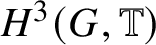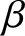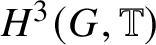1 Introduction
The notion of symmetry-protected topological phases was introduced by Gu and Wen [Reference Gu and WenGW]. It is defined as follows: We consider the set of all Hamiltonians with some symmetry which have a unique gapped ground state in the bulk and can be smoothly deformed into a common trivial gapped Hamiltonian without closing the gap. We say two such Hamiltonians are equivalent if they can be smoothly deformed into each other without breaking the symmetry. We call an equivalence class of this classification a symmetry-protected topological (SPT) phase. Based on tensor network or quantum field theory analysis [Reference Chen, Gu, Liu and WenCGLW, Reference Molnar, Ge, Schuch and CiracMGSC], it is conjectured that SPT phases with on-site finite group G symmetry for ![]() $\nu $-dimensional quantum spin systems have an
$\nu $-dimensional quantum spin systems have an ![]() $H^{\nu +1}(G,{\mathbb T})$-valued invariant. We proved that conjecture affirmatively in [Reference OgataO1] for
$H^{\nu +1}(G,{\mathbb T})$-valued invariant. We proved that conjecture affirmatively in [Reference OgataO1] for ![]() $\nu =1$. In this paper, we show that the conjecture is also true for
$\nu =1$. In this paper, we show that the conjecture is also true for ![]() $\nu =2$.
$\nu =2$.
We start by summarising the standard setup of ![]() $2$-dimensional quantum spin systems on the
$2$-dimensional quantum spin systems on the ![]() $2$-dimensional lattice
$2$-dimensional lattice ![]() ${\mathbb Z}^{2}$ [Reference Bratteli and RobinsonBR1, Reference Bratteli and RobinsonBR2]. We will freely use the basic notation in Section A. Throughout this paper, we fix some
${\mathbb Z}^{2}$ [Reference Bratteli and RobinsonBR1, Reference Bratteli and RobinsonBR2]. We will freely use the basic notation in Section A. Throughout this paper, we fix some ![]() $2\le d\in \mathbb {N}$. We denote the algebra of
$2\le d\in \mathbb {N}$. We denote the algebra of ![]() $d\times d$ matrices by
$d\times d$ matrices by ![]() $\mathop {\mathrm {M}}\nolimits _{d}$.
$\mathop {\mathrm {M}}\nolimits _{d}$.
For each subset ![]() $\Gamma $ of
$\Gamma $ of ![]() ${\mathbb Z}^2$, we denote the set of all finite subsets in
${\mathbb Z}^2$, we denote the set of all finite subsets in ![]() $\Gamma $ by
$\Gamma $ by ![]() ${\mathfrak S}_{\Gamma }$. We introduce the Euclidean metric on
${\mathfrak S}_{\Gamma }$. We introduce the Euclidean metric on ![]() ${\mathbb Z}^2$, inherited from
${\mathbb Z}^2$, inherited from ![]() ${\mathbb R}^2$. We denote by
${\mathbb R}^2$. We denote by ![]() $\mathrm {d}(S_1,S_2)$ the distance between
$\mathrm {d}(S_1,S_2)$ the distance between ![]() $S_1,S_2\subset {\mathbb Z}^2$. For a subset
$S_1,S_2\subset {\mathbb Z}^2$. For a subset ![]() $\Gamma $ of
$\Gamma $ of ![]() ${\mathbb Z}^2$ and
${\mathbb Z}^2$ and ![]() $r\in {\mathbb R}_{\ge 0}$,
$r\in {\mathbb R}_{\ge 0}$, ![]() $\hat \Gamma {(r)}$ denotes all the points in
$\hat \Gamma {(r)}$ denotes all the points in ![]() ${\mathbb R}^{2}$ whose distance from
${\mathbb R}^{2}$ whose distance from ![]() $\Gamma $ is less than or equal to r. We also set
$\Gamma $ is less than or equal to r. We also set ![]() $\Gamma (r):=\hat \Gamma {(r)}\cap {\mathbb Z}^{2}$. When we take a complement of
$\Gamma (r):=\hat \Gamma {(r)}\cap {\mathbb Z}^{2}$. When we take a complement of ![]() $\Gamma \subset {\mathbb Z}^{2}$, it means
$\Gamma \subset {\mathbb Z}^{2}$, it means ![]() $\Gamma ^{c}:={\mathbb Z}^{2}\setminus \Gamma $. For each
$\Gamma ^{c}:={\mathbb Z}^{2}\setminus \Gamma $. For each ![]() $n\in {\mathbb N}$, we denote
$n\in {\mathbb N}$, we denote ![]() $[-n,n]^2\cap {\mathbb Z}^2$ by
$[-n,n]^2\cap {\mathbb Z}^2$ by ![]() $\Lambda _n$.
$\Lambda _n$.
For each ![]() $z\in {\mathbb Z}^2$, let
$z\in {\mathbb Z}^2$, let ![]() ${\mathcal A}_{\{z\}}$ be an isomorphic copy of
${\mathcal A}_{\{z\}}$ be an isomorphic copy of ![]() $\mathop {\mathrm {M}}\nolimits _{d}$, and for any finite subset
$\mathop {\mathrm {M}}\nolimits _{d}$, and for any finite subset ![]() $\Lambda \subset {\mathbb Z}^2$, we set
$\Lambda \subset {\mathbb Z}^2$, we set ![]() ${\mathcal A}_{\Lambda } = \bigotimes _{z\in \Lambda }{\mathcal A}_{\{z\}}$. For finite
${\mathcal A}_{\Lambda } = \bigotimes _{z\in \Lambda }{\mathcal A}_{\{z\}}$. For finite ![]() $\Lambda $, the algebra
$\Lambda $, the algebra ![]() ${\mathcal A}_{\Lambda } $ can be regarded as the set of all bounded operators acting on the Hilbert space
${\mathcal A}_{\Lambda } $ can be regarded as the set of all bounded operators acting on the Hilbert space  $\bigotimes _{z\in \Lambda }{{\mathbb C}}^{d}$. We use this identification freely. If
$\bigotimes _{z\in \Lambda }{{\mathbb C}}^{d}$. We use this identification freely. If ![]() $\Lambda _1\subset \Lambda _2$, the algebra
$\Lambda _1\subset \Lambda _2$, the algebra ![]() ${\mathcal A}_{\Lambda _1}$ is naturally embedded in
${\mathcal A}_{\Lambda _1}$ is naturally embedded in ![]() ${\mathcal A}_{\Lambda _2}$ by tensoring its elements with the identity. For an infinite subset
${\mathcal A}_{\Lambda _2}$ by tensoring its elements with the identity. For an infinite subset ![]() $\Gamma \subset {\mathbb Z}^{2}$,
$\Gamma \subset {\mathbb Z}^{2}$, ![]() ${\mathcal A}_{\Gamma }$ is given as the inductive limit of the algebras
${\mathcal A}_{\Gamma }$ is given as the inductive limit of the algebras ![]() ${\mathcal A}_{\Lambda }$ with
${\mathcal A}_{\Lambda }$ with ![]() $\Lambda \in {\mathfrak S}_{\Gamma }$. We call
$\Lambda \in {\mathfrak S}_{\Gamma }$. We call ![]() ${\mathcal A}_{\Gamma }$ the quantum spin system on
${\mathcal A}_{\Gamma }$ the quantum spin system on ![]() $\Gamma $. For simplicity, we denote the
$\Gamma $. For simplicity, we denote the ![]() $2$-dimensional quantum spin system
$2$-dimensional quantum spin system ![]() ${\mathcal A}_{{\mathbb Z}^{2}}$ by
${\mathcal A}_{{\mathbb Z}^{2}}$ by ![]() ${\mathcal A}$. We also set
${\mathcal A}$. We also set  ${\mathcal A}_{\text {loc}}:=\bigcup _{\Lambda \in {\mathfrak S}_{{\mathbb Z}^{2}}}{\mathcal A}_{\Lambda } $. For a subset
${\mathcal A}_{\text {loc}}:=\bigcup _{\Lambda \in {\mathfrak S}_{{\mathbb Z}^{2}}}{\mathcal A}_{\Lambda } $. For a subset ![]() $\Gamma _1$ of
$\Gamma _1$ of ![]() $\Gamma \subset {\mathbb Z}^{2}$, the algebra
$\Gamma \subset {\mathbb Z}^{2}$, the algebra ![]() ${\mathcal A}_{\Gamma _1}$ can be regarded as a subalgebra of
${\mathcal A}_{\Gamma _1}$ can be regarded as a subalgebra of ![]() ${\mathcal A}_{\Gamma }$. With this identification, for
${\mathcal A}_{\Gamma }$. With this identification, for ![]() $A\in {\mathcal A}_{\Gamma _1}$ we occasionally use the same symbol A to denote
$A\in {\mathcal A}_{\Gamma _1}$ we occasionally use the same symbol A to denote ![]() $A\otimes \mathbb I_{{\mathcal A}_{\Gamma \setminus \Gamma _1}}\in {\mathcal A}_\Gamma $. Similarly, an automorphism
$A\otimes \mathbb I_{{\mathcal A}_{\Gamma \setminus \Gamma _1}}\in {\mathcal A}_\Gamma $. Similarly, an automorphism ![]() $\gamma $ on
$\gamma $ on ![]() ${\mathcal A}_{\Gamma _1}$ can be naturally regarded as an automorphism
${\mathcal A}_{\Gamma _1}$ can be naturally regarded as an automorphism ![]() $\gamma \otimes \mathop {\mathrm {id}}\nolimits _{{\mathcal A}_{\Gamma \setminus \Gamma _1}}$ on
$\gamma \otimes \mathop {\mathrm {id}}\nolimits _{{\mathcal A}_{\Gamma \setminus \Gamma _1}}$ on ![]() ${\mathcal A}_{\Gamma }$. We use this identification freely, and with a slight abuse of notation we occasionally denote
${\mathcal A}_{\Gamma }$. We use this identification freely, and with a slight abuse of notation we occasionally denote ![]() $\gamma \otimes \mathop {\mathrm {id}}\nolimits _{{\mathcal A}_{\Gamma \setminus \Gamma _1}}$ by
$\gamma \otimes \mathop {\mathrm {id}}\nolimits _{{\mathcal A}_{\Gamma \setminus \Gamma _1}}$ by ![]() $\gamma $. Similarly, for disjoint
$\gamma $. Similarly, for disjoint ![]() $\Gamma _-,\Gamma _+\subset {\mathbb Z}^{2}$ and
$\Gamma _-,\Gamma _+\subset {\mathbb Z}^{2}$ and ![]() $\alpha _\pm \in \mathop {\mathrm {Aut}}\nolimits {\mathcal A}_{\Gamma \pm }$, we occasionally write
$\alpha _\pm \in \mathop {\mathrm {Aut}}\nolimits {\mathcal A}_{\Gamma \pm }$, we occasionally write ![]() $\alpha _-\otimes \alpha _+$ to denote
$\alpha _-\otimes \alpha _+$ to denote ![]() $\left ( \alpha _-\otimes \mathop {\mathrm {id}}\nolimits _{\Gamma _-^c}\right ) \left ( \alpha _+\otimes \mathop {\mathrm {id}}\nolimits _{\Gamma _+^c}\right )$, under the given identification.
$\left ( \alpha _-\otimes \mathop {\mathrm {id}}\nolimits _{\Gamma _-^c}\right ) \left ( \alpha _+\otimes \mathop {\mathrm {id}}\nolimits _{\Gamma _+^c}\right )$, under the given identification.
Throughout this paper we fix a finite group G and a unitary representation U on ![]() ${\mathbb C}^{d}$. Let
${\mathbb C}^{d}$. Let ![]() $\Gamma \subset {\mathbb Z}^{2}$ be a nonempty subset. For each
$\Gamma \subset {\mathbb Z}^{2}$ be a nonempty subset. For each ![]() $g\in G$, there exists a unique automorphism
$g\in G$, there exists a unique automorphism ![]() $\beta ^{\Gamma }_g$ on
$\beta ^{\Gamma }_g$ on ![]() ${\mathcal A}_{\Gamma }$ such that
${\mathcal A}_{\Gamma }$ such that
 $$ \begin{align} \beta_{g}^{\Gamma}\left ( A\right )=\mathop{\mathrm{Ad}}\nolimits\left (\bigotimes_{I} U(g)\right )\left ( A\right ),\quad A\in{\mathcal A}_{I}, \ g\in G, \end{align} $$
$$ \begin{align} \beta_{g}^{\Gamma}\left ( A\right )=\mathop{\mathrm{Ad}}\nolimits\left (\bigotimes_{I} U(g)\right )\left ( A\right ),\quad A\in{\mathcal A}_{I}, \ g\in G, \end{align} $$for any finite subset I of ![]() $\Gamma $. We call the group homomorphism
$\Gamma $. We call the group homomorphism ![]() $\beta ^{\Gamma }: G\to \mathop {\mathrm {Aut}}\nolimits {\mathcal A}_{\Gamma }$ the on-site action of G on
$\beta ^{\Gamma }: G\to \mathop {\mathrm {Aut}}\nolimits {\mathcal A}_{\Gamma }$ the on-site action of G on ![]() ${\mathcal A}_{\Gamma }$ given by U. For simplicity, we denote
${\mathcal A}_{\Gamma }$ given by U. For simplicity, we denote  $\beta ^{{\mathbb Z}^{2}}_{g}$ by
$\beta ^{{\mathbb Z}^{2}}_{g}$ by ![]() $\beta _{g}$.
$\beta _{g}$.
A mathematical model of a quantum spin system is fully specified by its interaction ![]() $\Phi $. A uniformly bounded interaction on
$\Phi $. A uniformly bounded interaction on ![]() ${\mathcal A}$ is a map
${\mathcal A}$ is a map ![]() $\Phi : {\mathfrak S}_{{\mathbb Z}^{2}}\to {\mathcal A}_{\text {loc}}$ such that
$\Phi : {\mathfrak S}_{{\mathbb Z}^{2}}\to {\mathcal A}_{\text {loc}}$ such that
and
 $$ \begin{align} \sup_{X\in {\mathfrak S}_{{\mathbb Z}^{2}}}\left \lVert \Phi(X)\right \rVert<\infty. \end{align} $$
$$ \begin{align} \sup_{X\in {\mathfrak S}_{{\mathbb Z}^{2}}}\left \lVert \Phi(X)\right \rVert<\infty. \end{align} $$It is of finite range, with interaction length less than or equal to ![]() $R\in \mathbb {N}$ if
$R\in \mathbb {N}$ if ![]() $\Phi (X)=0$ for any
$\Phi (X)=0$ for any ![]() $X\in {\mathfrak S}_{{\mathbb Z}^{2}}$ whose diameter is larger than R. An on-site interaction – that is, an interaction with
$X\in {\mathfrak S}_{{\mathbb Z}^{2}}$ whose diameter is larger than R. An on-site interaction – that is, an interaction with ![]() $\Phi (X)=0$ unless X consists of a single point – is said to be trivial. An interaction
$\Phi (X)=0$ unless X consists of a single point – is said to be trivial. An interaction ![]() $\Phi $ is
$\Phi $ is ![]() $\beta $-invariant if
$\beta $-invariant if ![]() $\beta _g(\Phi (X))=\Phi (X)$ for any
$\beta _g(\Phi (X))=\Phi (X)$ for any ![]() $X\in {\mathfrak S}_{{\mathbb Z}^{2}}$. For a uniformly bounded and finite-range interaction
$X\in {\mathfrak S}_{{\mathbb Z}^{2}}$. For a uniformly bounded and finite-range interaction ![]() $\Phi $ and
$\Phi $ and ![]() $\Lambda \in {\mathfrak S}_{{\mathbb Z}^{2}}$, define the local Hamiltonian
$\Lambda \in {\mathfrak S}_{{\mathbb Z}^{2}}$, define the local Hamiltonian
 $$ \begin{align} \left ( H_\Phi\right )_\Lambda :=\sum_{X\subset\Lambda} \Phi(X) \end{align} $$
$$ \begin{align} \left ( H_\Phi\right )_\Lambda :=\sum_{X\subset\Lambda} \Phi(X) \end{align} $$and denote the dynamics
 $$ \begin{align} \tau^{(\Lambda)\Phi}_t (A):=e^{it\left ( H_\Phi\right )_\Lambda}Ae^{-it\left ( H_\Phi\right )_\Lambda}, \quad t\in {\mathbb R},\ A\in{\mathcal A}. \end{align} $$
$$ \begin{align} \tau^{(\Lambda)\Phi}_t (A):=e^{it\left ( H_\Phi\right )_\Lambda}Ae^{-it\left ( H_\Phi\right )_\Lambda}, \quad t\in {\mathbb R},\ A\in{\mathcal A}. \end{align} $$By the uniform boundedness and finite-rangeness of ![]() $\Phi $, for each
$\Phi $, for each ![]() $A\in {\mathcal A}$ the following limit exists
$A\in {\mathcal A}$ the following limit exists
 $$ \begin{align} \lim_{\Lambda\to{\mathbb Z}^{\nu}} \tau^{(\Lambda),\Phi}_t\left ( A\right )=: \tau^{\Phi}_t\left ( A\right ),\quad t\in{\mathbb R}, \end{align} $$
$$ \begin{align} \lim_{\Lambda\to{\mathbb Z}^{\nu}} \tau^{(\Lambda),\Phi}_t\left ( A\right )=: \tau^{\Phi}_t\left ( A\right ),\quad t\in{\mathbb R}, \end{align} $$which defines the dynamics ![]() $\tau ^{\Phi }$ on
$\tau ^{\Phi }$ on ![]() ${\mathcal A}$ [Reference Bratteli and RobinsonBR2]. For a uniformly bounded and finite-range interaction
${\mathcal A}$ [Reference Bratteli and RobinsonBR2]. For a uniformly bounded and finite-range interaction ![]() $\Phi $, a state
$\Phi $, a state ![]() $\varphi $ on
$\varphi $ on ![]() ${\mathcal A}$ is called a
${\mathcal A}$ is called a ![]() $\tau ^{\Phi }$-ground state if the inequality
$\tau ^{\Phi }$-ground state if the inequality ![]() $ -i\,\varphi (A^*{\delta _{\Phi }}(A))\ge 0 $ holds for any element A in the domain
$ -i\,\varphi (A^*{\delta _{\Phi }}(A))\ge 0 $ holds for any element A in the domain ![]() ${\mathcal D}({\delta _{\Phi }})$ of the generator
${\mathcal D}({\delta _{\Phi }})$ of the generator ![]() ${\delta _\Phi }$. Let
${\delta _\Phi }$. Let ![]() $\varphi $ be a
$\varphi $ be a ![]() $\tau ^\Phi $-ground state, with a Gelfand–Naimark–Segal (GNS) triple
$\tau ^\Phi $-ground state, with a Gelfand–Naimark–Segal (GNS) triple ![]() $\left ({\mathcal H}_\varphi ,\pi _\varphi ,\Omega _\varphi \right )$. Then there exists a unique positive operator
$\left ({\mathcal H}_\varphi ,\pi _\varphi ,\Omega _\varphi \right )$. Then there exists a unique positive operator ![]() $H_{\varphi ,\Phi }$ on
$H_{\varphi ,\Phi }$ on ![]() ${\mathcal H}_\varphi $ such that
${\mathcal H}_\varphi $ such that 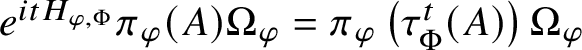 $e^{itH_{\varphi ,\Phi }}\pi _\varphi (A)\Omega _\varphi =\pi _\varphi \left (\tau ^t_\Phi (A)\right )\Omega _\varphi $, for all
$e^{itH_{\varphi ,\Phi }}\pi _\varphi (A)\Omega _\varphi =\pi _\varphi \left (\tau ^t_\Phi (A)\right )\Omega _\varphi $, for all ![]() $A\in {\mathcal A}$ and
$A\in {\mathcal A}$ and ![]() $t\in \mathbb R$. We call this
$t\in \mathbb R$. We call this ![]() $H_{\varphi ,\Phi }$ the bulk Hamiltonian associated with
$H_{\varphi ,\Phi }$ the bulk Hamiltonian associated with ![]() $\varphi $.
$\varphi $.
Definition 1.1. We say that an interaction ![]() $\Phi $ has a unique gapped ground state if (i) the
$\Phi $ has a unique gapped ground state if (i) the ![]() $\tau ^\Phi $-ground state, which we denote as
$\tau ^\Phi $-ground state, which we denote as ![]() $\omega _{\Phi }$, is unique and (ii) there exists a
$\omega _{\Phi }$, is unique and (ii) there exists a ![]() $\gamma>0$ such that
$\gamma>0$ such that ![]() $\sigma \left (H_{\omega _{\Phi },\Phi }\right )\setminus \{0\}\subset [\gamma ,\infty )$, where
$\sigma \left (H_{\omega _{\Phi },\Phi }\right )\setminus \{0\}\subset [\gamma ,\infty )$, where ![]() $\sigma \left (H_{\omega _{\Phi },\Phi }\right )$ is the spectrum of
$\sigma \left (H_{\omega _{\Phi },\Phi }\right )$ is the spectrum of ![]() $H_{\omega _{\Phi },\Phi }$. We denote by
$H_{\omega _{\Phi },\Phi }$. We denote by ![]() ${\mathcal P}_{UG} $ the set of all uniformly bounded finite-range interactions with unique gapped ground state. We denote by
${\mathcal P}_{UG} $ the set of all uniformly bounded finite-range interactions with unique gapped ground state. We denote by ![]() ${\mathcal P}_{UG\beta }$ the set of all uniformly bounded finite-range
${\mathcal P}_{UG\beta }$ the set of all uniformly bounded finite-range ![]() $\beta $-invariant interactions with unique gapped ground state.
$\beta $-invariant interactions with unique gapped ground state.
In this paper we consider a classification problem of a subset of ![]() ${\mathcal P}_{UG\beta }$, models with short-range entanglement. To describe the models with short-range entanglement, we need to explain the classification problem of unique gapped ground-state phases without symmetry. For
${\mathcal P}_{UG\beta }$, models with short-range entanglement. To describe the models with short-range entanglement, we need to explain the classification problem of unique gapped ground-state phases without symmetry. For ![]() $\Gamma \subset {\mathbb Z}^{2}$, we denote by
$\Gamma \subset {\mathbb Z}^{2}$, we denote by ![]() $\Pi _{\Gamma }:{\mathcal A}\to {\mathcal A}_{\Gamma }$ the conditional expectation with respect to the trace state. Let
$\Pi _{\Gamma }:{\mathcal A}\to {\mathcal A}_{\Gamma }$ the conditional expectation with respect to the trace state. Let ![]() $f:(0,\infty )\to (0,\infty )$ be a continuous decreasing function with
$f:(0,\infty )\to (0,\infty )$ be a continuous decreasing function with ![]() $\lim _{t\to \infty }f(t)=0$. For each
$\lim _{t\to \infty }f(t)=0$. For each ![]() $A\in {\mathcal A}$, define
$A\in {\mathcal A}$, define
 $$ \begin{align} \left \lVert A\right \rVert_f:=\left \lVert A\right \rVert + \sup_{N\in \mathbb{N}}\left (\frac{\left \lVert A-\Pi_{\Lambda_N} (A) \right \rVert} {f(N)} \right ). \end{align} $$
$$ \begin{align} \left \lVert A\right \rVert_f:=\left \lVert A\right \rVert + \sup_{N\in \mathbb{N}}\left (\frac{\left \lVert A-\Pi_{\Lambda_N} (A) \right \rVert} {f(N)} \right ). \end{align} $$We denote by ![]() ${\mathcal D}_f$ the set of all
${\mathcal D}_f$ the set of all ![]() $A\in {\mathcal A}$ such that
$A\in {\mathcal A}$ such that ![]() $\left \lVert A\right \rVert _f<\infty $.
$\left \lVert A\right \rVert _f<\infty $.
The classification of unique gapped ground-state phases ![]() ${\mathcal P}_{UG} $ without symmetry is the following:
${\mathcal P}_{UG} $ without symmetry is the following:
Definition 1.2. Two interactions ![]() $\Phi _0,\Phi _1\in {\mathcal P}_{UG} $ are equivalent if there is a path of interactions
$\Phi _0,\Phi _1\in {\mathcal P}_{UG} $ are equivalent if there is a path of interactions ![]() $\Phi : [0,1]\to {\mathcal P}_{UG} $ satisfying the following:
$\Phi : [0,1]\to {\mathcal P}_{UG} $ satisfying the following:
1.
 $\Phi (0)=\Phi _0$ and
$\Phi (0)=\Phi _0$ and  $\Phi (1)=\Phi _1$.
$\Phi (1)=\Phi _1$.2. For each
 $X\in {\mathfrak S}_{{\mathbb Z}^2}$, the map
$X\in {\mathfrak S}_{{\mathbb Z}^2}$, the map  $[0,1]\ni s\to \Phi (X;s)\in {\mathcal A}_{X}$ is
$[0,1]\ni s\to \Phi (X;s)\in {\mathcal A}_{X}$ is  $C^1$. We denote by
$C^1$. We denote by  $\dot {\Phi }(X;s)$ the corresponding derivatives. The interaction obtained by differentiation is denoted by
$\dot {\Phi }(X;s)$ the corresponding derivatives. The interaction obtained by differentiation is denoted by  $\dot \Phi (s)$, for each
$\dot \Phi (s)$, for each  $s\in [0,1]$.
$s\in [0,1]$.3. There is a number
 $R\in \mathbb {N}$ such that
$R\in \mathbb {N}$ such that  $X \in {\mathfrak S}_{{\mathbb Z}^2}$ and
$X \in {\mathfrak S}_{{\mathbb Z}^2}$ and  $\mathop {\mathrm {diam}}\nolimits {X}\ge R$ imply
$\mathop {\mathrm {diam}}\nolimits {X}\ge R$ imply  $\Phi (X;s)=0$, for all
$\Phi (X;s)=0$, for all  $s\in [0,1]$.
$s\in [0,1]$.4. Interactions are bounded as follows:
(1.8) $$ \begin{align} C_b^{\Phi}:=\sup_{s\in\left[0,1\right]}\sup_{X\in {\mathfrak S}_{{\mathbb Z}^2}} \left ( \left \lVert \Phi\left ( X;s\right ) \right \rVert+\left \lVert \dot{\Phi} \left ( X;s\right ) \right \rVert \right )<\infty. \end{align} $$
$$ \begin{align} C_b^{\Phi}:=\sup_{s\in\left[0,1\right]}\sup_{X\in {\mathfrak S}_{{\mathbb Z}^2}} \left ( \left \lVert \Phi\left ( X;s\right ) \right \rVert+\left \lVert \dot{\Phi} \left ( X;s\right ) \right \rVert \right )<\infty. \end{align} $$5. Setting
(1.9)for each $$ \begin{align} b(\varepsilon):=\sup_{Z\in{\mathfrak S}_{{\mathbb Z}^2}} \sup_{s,s_0 \in\left[0,1\right],0<\left \lvert s-s_0\right \rvert<\varepsilon} \left \lVert \frac{\Phi(Z;s)-\Phi(Z;s_0)}{s-s_0}-\dot{\Phi}(Z;s_0) \right \rVert \end{align} $$
$$ \begin{align} b(\varepsilon):=\sup_{Z\in{\mathfrak S}_{{\mathbb Z}^2}} \sup_{s,s_0 \in\left[0,1\right],0<\left \lvert s-s_0\right \rvert<\varepsilon} \left \lVert \frac{\Phi(Z;s)-\Phi(Z;s_0)}{s-s_0}-\dot{\Phi}(Z;s_0) \right \rVert \end{align} $$ $\varepsilon>0$, we have
$\varepsilon>0$, we have  $\lim _{\varepsilon \to 0} b(\varepsilon )=0$.
$\lim _{\varepsilon \to 0} b(\varepsilon )=0$.6. There exists a
 $\gamma>0$ such that
$\gamma>0$ such that  $\sigma \left (H_{\omega _{\Phi (s)},\Phi (s)}\right )\setminus \{0\}\subset [\gamma ,\infty )$ for all
$\sigma \left (H_{\omega _{\Phi (s)},\Phi (s)}\right )\setminus \{0\}\subset [\gamma ,\infty )$ for all  $s\in [0,1]$, where
$s\in [0,1]$, where  $\sigma \left (H_{\omega _{\Phi (s)},\Phi (s)}\right )$ is the spectrum of
$\sigma \left (H_{\omega _{\Phi (s)},\Phi (s)}\right )$ is the spectrum of  $H_{\omega _{\Phi (s)},\Phi (s)}$.
$H_{\omega _{\Phi (s)},\Phi (s)}$.7. There exists
 $0<\eta <1$ satisfying the following: Set
$0<\eta <1$ satisfying the following: Set  $\zeta (t):=e^{-t^{ \eta }}$. Then for each
$\zeta (t):=e^{-t^{ \eta }}$. Then for each  $A\in {\mathcal D}_\zeta $,
$A\in {\mathcal D}_\zeta $,  $\omega _{\Phi (s)}(A)$ is differentiable with respect to s, and there is a constant
$\omega _{\Phi (s)}(A)$ is differentiable with respect to s, and there is a constant  $C_\zeta $ such that (1.10)for any
$C_\zeta $ such that (1.10)for any $$ \begin{align} \left \lvert \frac{d}{ds}\omega_{\Phi(s)}(A) \right \rvert \le C_\zeta\left \lVert A\right \rVert_\zeta, \end{align} $$
$$ \begin{align} \left \lvert \frac{d}{ds}\omega_{\Phi(s)}(A) \right \rvert \le C_\zeta\left \lVert A\right \rVert_\zeta, \end{align} $$ $A\in {\mathcal D}_\zeta $. (Recall definition (1.7)).
$A\in {\mathcal D}_\zeta $. (Recall definition (1.7)).
We write ![]() $\Phi _0\sim \Phi _1$ if
$\Phi _0\sim \Phi _1$ if ![]() $\Phi _0$ and
$\Phi _0$ and ![]() $\Phi _1$ are equivalent. If
$\Phi _1$ are equivalent. If ![]() $\Phi _0,\Phi _1\in {\mathcal P}_{UG\beta }$ and we can take the path in
$\Phi _0,\Phi _1\in {\mathcal P}_{UG\beta }$ and we can take the path in ![]() ${\mathcal P}_{UG\beta }$ – that is, so that
${\mathcal P}_{UG\beta }$ – that is, so that ![]() $\beta _g\left ( \Phi (X;s)\right )=\Phi (X;s)$,
$\beta _g\left ( \Phi (X;s)\right )=\Phi (X;s)$, ![]() $g\in G$, for all
$g\in G$, for all ![]() $s\in [0,1]$ – then we say
$s\in [0,1]$ – then we say ![]() $\Phi _0$ and
$\Phi _0$ and ![]() $\Phi _1$ are
$\Phi _1$ are ![]() $\beta $-equivalent and write
$\beta $-equivalent and write ![]() $\Phi _0\sim _\beta \Phi _1$.
$\Phi _0\sim _\beta \Phi _1$.
The reason we require these conditions is that we rely on the result in [Reference Moon and OgataMO]. The object we classify in this paper is the following:
Definition 1.3. Fix a trivial interaction ![]() $\Phi _0\in {\mathcal P}_{UG} $. We denote by
$\Phi _0\in {\mathcal P}_{UG} $. We denote by ![]() ${\mathcal P}_{SL\beta }$ the set of all
${\mathcal P}_{SL\beta }$ the set of all ![]() $\Phi \in {\mathcal P}_{UG\beta }$ such that
$\Phi \in {\mathcal P}_{UG\beta }$ such that ![]() $\Phi \sim \Phi _0$. Connected components of
$\Phi \sim \Phi _0$. Connected components of ![]() ${\mathcal P}_{SL\beta }$ with respect to
${\mathcal P}_{SL\beta }$ with respect to ![]() $\sim _\beta $ are the SPT phases.
$\sim _\beta $ are the SPT phases.
Because we have ![]() $\Phi _0\sim \tilde \Phi _0$ for any trivial
$\Phi _0\sim \tilde \Phi _0$ for any trivial ![]() $\Phi _0,\tilde \Phi _{0}\in {\mathcal P}_{UG} $, the set
$\Phi _0,\tilde \Phi _{0}\in {\mathcal P}_{UG} $, the set ![]() ${\mathcal P}_{SL\beta }$ does not depend on the choice of
${\mathcal P}_{SL\beta }$ does not depend on the choice of ![]() $\Phi _0$.
$\Phi _0$.
Remark 1.4. From the automorphic equivalence (Theorem 5.1), ![]() $\Phi \sim \Phi _0$ means that the ground state of
$\Phi \sim \Phi _0$ means that the ground state of ![]() $\Phi $ has a short-range entanglement. This is because the automorphisms in Theorem 5.1 can be regarded as a version of a quantum circuit with finite depth, which is regarded as a quantum circuit that does not create long-range entanglement [Reference Bachmann and LangeBL].
$\Phi $ has a short-range entanglement. This is because the automorphisms in Theorem 5.1 can be regarded as a version of a quantum circuit with finite depth, which is regarded as a quantum circuit that does not create long-range entanglement [Reference Bachmann and LangeBL].
The main result of this paper is as follows:
Theorem 1.5. There is an ![]() $H^3(G,{\mathbb T})$-valued index on
$H^3(G,{\mathbb T})$-valued index on ![]() ${\mathcal P}_{SL\beta }$, which is an invariant of the classification
${\mathcal P}_{SL\beta }$, which is an invariant of the classification ![]() $\sim _\beta $ of
$\sim _\beta $ of ![]() ${\mathcal P}_{SL\beta }$.
${\mathcal P}_{SL\beta }$.
The paper is organised as follows. In Section 2, we define the ![]() $H^{3}(G,{\mathbb T})$-valued index for a class of states which are created from a fixed product state via ‘factorisable’ automorphisms, satisfying some additional condition. This additional condition is the existence of the set of automorphisms which (i) do not move the state and (ii) are almost like
$H^{3}(G,{\mathbb T})$-valued index for a class of states which are created from a fixed product state via ‘factorisable’ automorphisms, satisfying some additional condition. This additional condition is the existence of the set of automorphisms which (i) do not move the state and (ii) are almost like ![]() $\beta $-action restricted to the upper half-plane, except for some
$\beta $-action restricted to the upper half-plane, except for some ![]() $1$-dimensional perturbation. In Section 3, we show that the existence of such set of automorphisms is guaranteed in a suitable situation. Furthermore, in Section 4 we show the stability of the index – that is, a suitably
$1$-dimensional perturbation. In Section 3, we show that the existence of such set of automorphisms is guaranteed in a suitable situation. Furthermore, in Section 4 we show the stability of the index – that is, a suitably ![]() $\beta $-invariant automorphism does not change this index. Finally, in Section 5 we show our main theorem, Theorem 1.5, and that in our setting of Theorem 1.5, all the conditions required in Sections 2, 3 and 4 are satisfied. Although the index is defined in terms of GNS representations, in some good situation, we can calculate it without going through GNS representation; this is shown in Section 6. Reviews of this article can be found in [Reference OgataO3, Reference OgataO4].
$\beta $-invariant automorphism does not change this index. Finally, in Section 5 we show our main theorem, Theorem 1.5, and that in our setting of Theorem 1.5, all the conditions required in Sections 2, 3 and 4 are satisfied. Although the index is defined in terms of GNS representations, in some good situation, we can calculate it without going through GNS representation; this is shown in Section 6. Reviews of this article can be found in [Reference OgataO3, Reference OgataO4].
2 The  $H^{3}(G,{\mathbb T})$-valued index in
$H^{3}(G,{\mathbb T})$-valued index in  $2$-dimensional systems
$2$-dimensional systems
In this section, we associate an ![]() $H^{3}(G,{\mathbb T})$-index for some class of states. It will turn out later that this class includes SPT phases. For a nontrivial example of this index, see [Reference OgataO3]. It is also shown there that if a state is of product form of two states on half-planes, then our index is trivial. From the construction to follow, one can easily see that the group structure of
$H^{3}(G,{\mathbb T})$-index for some class of states. It will turn out later that this class includes SPT phases. For a nontrivial example of this index, see [Reference OgataO3]. It is also shown there that if a state is of product form of two states on half-planes, then our index is trivial. From the construction to follow, one can easily see that the group structure of ![]() $H^{3}(G,{\mathbb T})$, which is a simple pointwise multiplication, shows up when we tensor two systems.
$H^{3}(G,{\mathbb T})$, which is a simple pointwise multiplication, shows up when we tensor two systems.
2.1 An overview
We consider states of the form ![]() $\omega =\omega _{0}\circ \alpha $, where
$\omega =\omega _{0}\circ \alpha $, where ![]() $\omega _{0}$ is a pure infinite tensor product state (see definition (2.18)) and
$\omega _{0}$ is a pure infinite tensor product state (see definition (2.18)) and ![]() $\alpha $ an automorphism satisfying some factorisation property (2.8). In equation (2.8),
$\alpha $ an automorphism satisfying some factorisation property (2.8). In equation (2.8), ![]() $\alpha _{L}, \alpha _{R}$ are automorphisms localised to the left and right infinite planes
$\alpha _{L}, \alpha _{R}$ are automorphisms localised to the left and right infinite planes ![]() $H_{L}, H_{R}$, and
$H_{L}, H_{R}$, and ![]() $\Theta $ is localised in
$\Theta $ is localised in ![]() $\left ( C_{\theta }\right )^{c}$, where
$\left ( C_{\theta }\right )^{c}$, where ![]() $C_{\theta }$ is defined by definition (2.2). We then have
$C_{\theta }$ is defined by definition (2.2). We then have ![]() $\omega \simeq \left ( \omega _{L}\alpha _{L}\otimes \omega _{R}\alpha _{R}\right )\circ \Theta $ with pure states
$\omega \simeq \left ( \omega _{L}\alpha _{L}\otimes \omega _{R}\alpha _{R}\right )\circ \Theta $ with pure states ![]() $\omega _{L}, \omega _{R}$ on the left and right infinite planes. We further assume that the effective excitation caused by
$\omega _{L}, \omega _{R}$ on the left and right infinite planes. We further assume that the effective excitation caused by  $( \beta _{g}^{U})^{-1}$ (see formula (2.5)) on
$( \beta _{g}^{U})^{-1}$ (see formula (2.5)) on ![]() $\omega $ is localised around the x-axis, in the sense that for any
$\omega $ is localised around the x-axis, in the sense that for any ![]() $0<\theta <\frac \pi 2$, there are automorphisms
$0<\theta <\frac \pi 2$, there are automorphisms  $\eta _{g}^{L}, \eta _{g}^{R}$ localised in
$\eta _{g}^{L}, \eta _{g}^{R}$ localised in ![]() $C_{\theta }\cap H_{L}, C_{\theta }\cap H_{R}$ such that
$C_{\theta }\cap H_{L}, C_{\theta }\cap H_{R}$ such that  $\omega \circ ( \beta _{g}^{U})^{-1}$ is equivalent to
$\omega \circ ( \beta _{g}^{U})^{-1}$ is equivalent to  $\omega \circ (\eta _{g}^{L}\otimes \eta _{g}^{R} )$. This corresponds to thinking of
$\omega \circ (\eta _{g}^{L}\otimes \eta _{g}^{R} )$. This corresponds to thinking of ![]() ${\mathcal T}(\theta , (\tilde \beta _g) )$ (definition (2.22)) and
${\mathcal T}(\theta , (\tilde \beta _g) )$ (definition (2.22)) and ![]() $\mathop {\mathrm {IG}}\nolimits (\omega ,\theta )$ (definition (2.24)). Setting
$\mathop {\mathrm {IG}}\nolimits (\omega ,\theta )$ (definition (2.24)). Setting 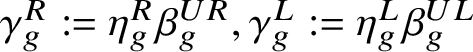 $\gamma _{g}^{R}:=\eta _{g}^{R}\beta _{g}^{UR}, \gamma _{g}^{L}:=\eta _{g}^{L}\beta _{g}^{UL}$, with
$\gamma _{g}^{R}:=\eta _{g}^{R}\beta _{g}^{UR}, \gamma _{g}^{L}:=\eta _{g}^{L}\beta _{g}^{UL}$, with  $\beta _{g}^{UR}, \beta _{g}^{UL}$ in formula (2.5), the condition given is
$\beta _{g}^{UR}, \beta _{g}^{UL}$ in formula (2.5), the condition given is  $\omega \simeq \omega \circ ( \gamma _{g}^{L}\otimes \gamma _{g}^{R} )$. Repeated use of this formula gives us
$\omega \simeq \omega \circ ( \gamma _{g}^{L}\otimes \gamma _{g}^{R} )$. Repeated use of this formula gives us  $\omega \simeq \omega \circ ( \gamma _{g}^{L}\gamma _{h}^{L}(\gamma _{gh}^{L} )^{-1} \otimes \gamma _{g}^{R}\gamma _{h}^{R} (\gamma _{gh}^{R} )^{-1} )$. Substituting the factorisation of
$\omega \simeq \omega \circ ( \gamma _{g}^{L}\gamma _{h}^{L}(\gamma _{gh}^{L} )^{-1} \otimes \gamma _{g}^{R}\gamma _{h}^{R} (\gamma _{gh}^{R} )^{-1} )$. Substituting the factorisation of ![]() $\omega $, we then have
$\omega $, we then have
 $$ \begin{align*} \left ( \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\right )\circ\Theta \simeq \left ( \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\right )\circ\Theta \left ( \gamma_{g}^{L}\gamma_{h}^{L}\left (\gamma_{gh}^{L}\right )^{-1} \otimes \gamma_{g}^{R}\gamma_{h}^{R}\left (\gamma_{gh}^{R}\right )^{-1}\right ). \end{align*} $$
$$ \begin{align*} \left ( \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\right )\circ\Theta \simeq \left ( \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\right )\circ\Theta \left ( \gamma_{g}^{L}\gamma_{h}^{L}\left (\gamma_{gh}^{L}\right )^{-1} \otimes \gamma_{g}^{R}\gamma_{h}^{R}\left (\gamma_{gh}^{R}\right )^{-1}\right ). \end{align*} $$However, because conjugation by  $\beta _g^U$ does not change the support of automorphisms, we see that this combination
$\beta _g^U$ does not change the support of automorphisms, we see that this combination  $\gamma _{g}^{R}\gamma _{h}^{R}(\gamma _{gh}^{R} )^{-1}$ is localised in
$\gamma _{g}^{R}\gamma _{h}^{R}(\gamma _{gh}^{R} )^{-1}$ is localised in ![]() $C_{\theta }\cap H_{R}$. As a result,
$C_{\theta }\cap H_{R}$. As a result,  $\gamma _{g}^{R}\gamma _{h}^{R}(\gamma _{gh}^{R})^{-1}$ – and also
$\gamma _{g}^{R}\gamma _{h}^{R}(\gamma _{gh}^{R})^{-1}$ – and also  $\gamma _{g}^{L}\gamma _{h}^{L}(\gamma _{gh}^{L} )^{-1}$ – commutes with
$\gamma _{g}^{L}\gamma _{h}^{L}(\gamma _{gh}^{L} )^{-1}$ – commutes with ![]() $\Theta $. Letting them commute, we obtain
$\Theta $. Letting them commute, we obtain
 $$ \begin{align*} \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\simeq \left ( \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\right )\circ \left ( \gamma_{g}^{L}\gamma_{h}^{L}\left (\gamma_{gh}^{L}\right )^{-1} \otimes \gamma_{g}^{R}\gamma_{h}^{R}\left (\gamma_{gh}^{R}\right )^{-1}\right ), \end{align*} $$
$$ \begin{align*} \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\simeq \left ( \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\right )\circ \left ( \gamma_{g}^{L}\gamma_{h}^{L}\left (\gamma_{gh}^{L}\right )^{-1} \otimes \gamma_{g}^{R}\gamma_{h}^{R}\left (\gamma_{gh}^{R}\right )^{-1}\right ), \end{align*} $$from which we can conclude  $ \omega _{R}\alpha _{R}\simeq \omega _{R}\alpha _{R} \gamma _{g}^{R}\gamma _{h}^{R}(\gamma _{gh}^{R})^{-1}$. This means that
$ \omega _{R}\alpha _{R}\simeq \omega _{R}\alpha _{R} \gamma _{g}^{R}\gamma _{h}^{R}(\gamma _{gh}^{R})^{-1}$. This means that 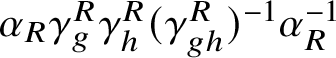 $\alpha _{R} \gamma _{g}^{R}\gamma _{h}^{R}(\gamma _{gh}^{R})^{-1}\alpha _{R}^{-1}$ is implementable by some unitary
$\alpha _{R} \gamma _{g}^{R}\gamma _{h}^{R}(\gamma _{gh}^{R})^{-1}\alpha _{R}^{-1}$ is implementable by some unitary ![]() $u(g,h)$ unitary in the GNS representation
$u(g,h)$ unitary in the GNS representation ![]() $\pi _{R}$ of
$\pi _{R}$ of ![]() $\omega _{R}$ (equation (2.19); see equation (2.27)). On the other hand, substituting the factorisation of
$\omega _{R}$ (equation (2.19); see equation (2.27)). On the other hand, substituting the factorisation of ![]() $\omega $ to
$\omega $ to  $\omega \simeq \omega \circ ( \gamma _{g}^{L}\otimes \gamma _{g}^{R} )$ implies
$\omega \simeq \omega \circ ( \gamma _{g}^{L}\otimes \gamma _{g}^{R} )$ implies
 $$ \begin{align} \left ( \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\right ) \simeq \left ( \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\right )\circ \Theta \circ\left ( \gamma_{g}^{L}\otimes \gamma_{g}^{R}\right )\circ \Theta^{-1}, \end{align} $$
$$ \begin{align} \left ( \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\right ) \simeq \left ( \omega_{L}\alpha_{L}\otimes \omega_{R}\alpha_{R}\right )\circ \Theta \circ\left ( \gamma_{g}^{L}\otimes \gamma_{g}^{R}\right )\circ \Theta^{-1}, \end{align} $$from which we can derive the implementability of  $\Theta \circ ( \gamma _{g}^{L}\otimes \gamma _{g}^{R} )\circ \Theta ^{-1}$ in the representation
$\Theta \circ ( \gamma _{g}^{L}\otimes \gamma _{g}^{R} )\circ \Theta ^{-1}$ in the representation ![]() $\pi _{L}\alpha _{L}\otimes \pi _{R}\alpha _{R}$ by some unitary
$\pi _{L}\alpha _{L}\otimes \pi _{R}\alpha _{R}$ by some unitary ![]() $W_{g}$ (see equation (2.26)). Using the definitions of
$W_{g}$ (see equation (2.26)). Using the definitions of ![]() $W_{g}$ and
$W_{g}$ and ![]() $u(g,h)$, we can see that they satisfy some nontrivial relation (2.52), with some
$u(g,h)$, we can see that they satisfy some nontrivial relation (2.52), with some ![]() $U(1)$-phase
$U(1)$-phase ![]() $c_{R}(g,h.k)$. In fact, this is quite a similar situation to that of cocycle actions [Reference JonesJ]. As in [Reference JonesJ], we can show that this
$c_{R}(g,h.k)$. In fact, this is quite a similar situation to that of cocycle actions [Reference JonesJ]. As in [Reference JonesJ], we can show that this ![]() $U(1)$-phase
$U(1)$-phase ![]() $c_{R}(g,h.k)$ is a
$c_{R}(g,h.k)$ is a ![]() $3$-cocycle and obtain an
$3$-cocycle and obtain an ![]() $H^{3}(G, {\mathbb T})$-index. The rest of this section is devoted to the proof that our index is independent of the choice of objects we introduced to define it. All of them follow from the fact that the difference of
$H^{3}(G, {\mathbb T})$-index. The rest of this section is devoted to the proof that our index is independent of the choice of objects we introduced to define it. All of them follow from the fact that the difference of ![]() $W_{g}$ and
$W_{g}$ and ![]() $u(g,h)$ caused by the different choice of objects can be implemented by some unitary, and the proof is rather straightforward.
$u(g,h)$ caused by the different choice of objects can be implemented by some unitary, and the proof is rather straightforward.
2.2 Definitions and the setting
For ![]() $0<\theta <\frac \pi 2$, a (double) cone
$0<\theta <\frac \pi 2$, a (double) cone ![]() $C_\theta $ is defined by
$C_\theta $ is defined by
 $$ \begin{align} C_\theta:= \left\{ (x,y)\in{\mathbb Z}^2\mid \lvert y\rvert\le \tan \theta\cdot \lvert x\rvert \right\}. \end{align} $$
$$ \begin{align} C_\theta:= \left\{ (x,y)\in{\mathbb Z}^2\mid \lvert y\rvert\le \tan \theta\cdot \lvert x\rvert \right\}. \end{align} $$Note that it consists of the left part ![]() $x\le -1$ and the right part
$x\le -1$ and the right part ![]() $0\le x$. For
$0\le x$. For ![]() $0<\theta _1<\theta _2\le \frac \pi 2$, we use the notation
$0<\theta _1<\theta _2\le \frac \pi 2$, we use the notation ![]() ${\mathcal C}_{\left (\theta _1,\theta _2\right ]}:=C_{\theta _2}\setminus C_{\theta _1}$ and
${\mathcal C}_{\left (\theta _1,\theta _2\right ]}:=C_{\theta _2}\setminus C_{\theta _1}$ and ![]() ${\mathcal C}_{\left [0,\theta _1\right ]}:=C_{\theta _1}$. Left, right, upper and lower half-planes are denoted by
${\mathcal C}_{\left [0,\theta _1\right ]}:=C_{\theta _1}$. Left, right, upper and lower half-planes are denoted by ![]() $H_L$,
$H_L$, ![]() $H_R$,
$H_R$, ![]() $H_U$ and
$H_U$ and ![]() $H_D$:
$H_D$:
 $$ \begin{align} H_L & :=\left\{ (x,y)\in{\mathbb Z}^2\mid x\le -1\right\}, & H_R & :=\left\{ (x,y)\in{\mathbb Z}^2\mid 0\le x\right\}, \end{align} $$
$$ \begin{align} H_L & :=\left\{ (x,y)\in{\mathbb Z}^2\mid x\le -1\right\}, & H_R & :=\left\{ (x,y)\in{\mathbb Z}^2\mid 0\le x\right\}, \end{align} $$ $$ \begin{align} H_U & :=\left\{ (x,y)\in{\mathbb Z}^2\mid 0\le y\right\}, & H_D & :=\left\{ (x,y)\in{\mathbb Z}^2\mid y\le -1\right\}. \end{align} $$
$$ \begin{align} H_U & :=\left\{ (x,y)\in{\mathbb Z}^2\mid 0\le y\right\}, & H_D & :=\left\{ (x,y)\in{\mathbb Z}^2\mid y\le -1\right\}. \end{align} $$We use the notation
 $$ \begin{align} \beta_g:=\beta_g^{{\mathbb Z}^2}, \quad \beta_g^U:=\beta_g^{H_U},\quad \beta_g^{RU}:=\beta_g^{H_R\cap H_U},\quad \beta_g^{LU}:=\beta_g^{H_L\cap H_U}. \end{align} $$
$$ \begin{align} \beta_g:=\beta_g^{{\mathbb Z}^2}, \quad \beta_g^U:=\beta_g^{H_U},\quad \beta_g^{RU}:=\beta_g^{H_R\cap H_U},\quad \beta_g^{LU}:=\beta_g^{H_L\cap H_U}. \end{align} $$ For each subset S of ![]() ${\mathbb Z}^2$, we set
${\mathbb Z}^2$, we set
We occasionally write ![]() ${\mathcal A}_{S,\sigma }, {\mathcal A}_{S,\zeta }, {\mathcal A}_{S,\sigma ,\zeta }$ to denote
${\mathcal A}_{S,\sigma }, {\mathcal A}_{S,\zeta }, {\mathcal A}_{S,\sigma ,\zeta }$ to denote ![]() ${\mathcal A}_{S_{\sigma }}, {\mathcal A}_{S_{\zeta }}, {\mathcal A}_{S_{\sigma \zeta }}$. For an automorphism
${\mathcal A}_{S_{\sigma }}, {\mathcal A}_{S_{\zeta }}, {\mathcal A}_{S_{\sigma \zeta }}$. For an automorphism ![]() $\alpha $ on
$\alpha $ on ![]() ${\mathcal A}$ and
${\mathcal A}$ and ![]() $0<\theta <\frac {\pi }2$, we denote by
$0<\theta <\frac {\pi }2$, we denote by ![]() ${\mathfrak D}^{\theta }_\alpha $ a set of all triples
${\mathfrak D}^{\theta }_\alpha $ a set of all triples ![]() $(\alpha _L,\alpha _R,\Theta )$ with
$(\alpha _L,\alpha _R,\Theta )$ with
decomposing ![]() $\alpha $ as
$\alpha $ as
For  $(\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{(\theta )}_\alpha $, we set
$(\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{(\theta )}_\alpha $, we set
The class of automorphisms which allow such decompositions for any directions is denoted by
 $$ \begin{align} \mathop{\mathrm{QAut}}\nolimits\left ( {\mathcal A}\right ) :=\left\{ \alpha\in \mathop{\mathrm{Aut}}\nolimits({\mathcal A})\mid {\mathfrak D}^{\theta}_\alpha\neq\emptyset \text{ for all } 0<\theta<\frac\pi 2 \right\}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{QAut}}\nolimits\left ( {\mathcal A}\right ) :=\left\{ \alpha\in \mathop{\mathrm{Aut}}\nolimits({\mathcal A})\mid {\mathfrak D}^{\theta}_\alpha\neq\emptyset \text{ for all } 0<\theta<\frac\pi 2 \right\}. \end{align} $$
Furthermore, for each
 $$ \begin{align} 0<\theta_{0.8}<\theta_1<\theta_{1.2}<\theta_{1.8}<\theta_2<\theta_{2.2}< \theta_{2.8}<\theta_3<\theta_{3.2}<\frac\pi 2, \end{align} $$
$$ \begin{align} 0<\theta_{0.8}<\theta_1<\theta_{1.2}<\theta_{1.8}<\theta_2<\theta_{2.2}< \theta_{2.8}<\theta_3<\theta_{3.2}<\frac\pi 2, \end{align} $$we consider decompositions of ![]() $\alpha \in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A})$ such that
$\alpha \in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A})$ such that
 $$ \begin{align} &\alpha=({\textrm{{inner}}})\circ\left ( \alpha_{\left[0,\theta_1\right]}\otimes\alpha_{\left(\theta_1,\theta_2\right]} \otimes \alpha_{\left(\theta_2,\theta_3\right]}\otimes \alpha_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \alpha_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ), \end{align} $$
$$ \begin{align} &\alpha=({\textrm{{inner}}})\circ\left ( \alpha_{\left[0,\theta_1\right]}\otimes\alpha_{\left(\theta_1,\theta_2\right]} \otimes \alpha_{\left(\theta_2,\theta_3\right]}\otimes \alpha_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \alpha_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ), \end{align} $$with
 $$ \begin{align} \begin{aligned} \alpha_X & :=\bigotimes_{\sigma=L,R, \: \zeta=D,U} \alpha_{X,\sigma,\zeta}, & \alpha_{\left[0,\theta_1\right]} & :=\bigotimes_{\sigma=L,R}\alpha_{\left[0,\theta_{1}\right],\sigma}, & \alpha_{\left(\theta_3,\frac\pi 2\right]} & :=\bigotimes_{\zeta=D,U} \alpha_{\left(\theta_3,\frac\pi 2\right],\zeta}, \\ \alpha_{X,\sigma,\zeta} & \in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{X,\sigma,\zeta}}\right ), & \alpha_{X,\sigma} & :=\bigotimes_{\zeta=U,D}\alpha_{X,\sigma,\zeta}, & \alpha_{X,\zeta} & :=\bigotimes_{\sigma=L,R}\alpha_{X,\sigma,\zeta}, \\ \alpha_{\left[0,\theta_{1}\right],\sigma} & \in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\left[0,\theta_{0}\right],\sigma}}\right ), & \alpha_{\left(\theta_3,\frac\pi 2\right],\zeta} &\in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\left(\theta_3,\frac\pi 2\right],\zeta}}\right ), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \alpha_X & :=\bigotimes_{\sigma=L,R, \: \zeta=D,U} \alpha_{X,\sigma,\zeta}, & \alpha_{\left[0,\theta_1\right]} & :=\bigotimes_{\sigma=L,R}\alpha_{\left[0,\theta_{1}\right],\sigma}, & \alpha_{\left(\theta_3,\frac\pi 2\right]} & :=\bigotimes_{\zeta=D,U} \alpha_{\left(\theta_3,\frac\pi 2\right],\zeta}, \\ \alpha_{X,\sigma,\zeta} & \in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{X,\sigma,\zeta}}\right ), & \alpha_{X,\sigma} & :=\bigotimes_{\zeta=U,D}\alpha_{X,\sigma,\zeta}, & \alpha_{X,\zeta} & :=\bigotimes_{\sigma=L,R}\alpha_{X,\sigma,\zeta}, \\ \alpha_{\left[0,\theta_{1}\right],\sigma} & \in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\left[0,\theta_{0}\right],\sigma}}\right ), & \alpha_{\left(\theta_3,\frac\pi 2\right],\zeta} &\in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\left(\theta_3,\frac\pi 2\right],\zeta}}\right ), \end{aligned} \end{align} $$for
The class of automorphisms on ![]() ${\mathcal A}$ which allow such decompositions for any directions
${\mathcal A}$ which allow such decompositions for any directions ![]() $\theta _{0.8}, \theta _1, \theta _{1.2}, \theta _{1.8},\theta _2,\theta _{2.2}, \theta _{2.8},\theta _3,\theta _{3.2}$ (satisfying formula (2.11)) is denoted by
$\theta _{0.8}, \theta _1, \theta _{1.2}, \theta _{1.8},\theta _2,\theta _{2.2}, \theta _{2.8},\theta _3,\theta _{3.2}$ (satisfying formula (2.11)) is denoted by ![]() $\mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$. Note that
$\mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$. Note that ![]() $\mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})\subset \mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$. The set of all
$\mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})\subset \mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$. The set of all ![]() $\alpha \in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$ with each of
$\alpha \in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$ with each of ![]() $\alpha _{I}$ in the decompositions required to commute with
$\alpha _{I}$ in the decompositions required to commute with  $\beta _g^{U}$,
$\beta _g^{U}$, ![]() $g\in G$, is denoted by
$g\in G$, is denoted by ![]() $\mathop {\mathrm {GSQAut}}\nolimits ({\mathcal A})$:
$\mathop {\mathrm {GSQAut}}\nolimits ({\mathcal A})$:
 $$ \begin{align} \begin{split} &\mathop{\mathrm{GSQAut}}\nolimits({\mathcal A})\\ &:=\left\{ \alpha\in \mathop{\mathrm{SQAut}}\nolimits({\mathcal A})\middle\vert \begin{gathered} \text{for any } \theta_{0.8}, \theta_1, \theta_{1.2},\theta_{1.8},\theta_2,\theta_{2.2}, \theta_{2.8},\theta_3,\theta_{3.2}\text{ satisfying formula (2.11),}\\\text{there is a decomposition }(2.12), (2.13), (2.14) \text{ satisfying}\\ \alpha_{I}\circ\beta_g^{U}=\beta_g^{U}\circ\alpha_{I},\ g\in G,\\ \text{for all }I=[0,\theta_1],(\theta_1,\theta_2], (\theta_2,\theta_3], \left(\theta_3,\frac\pi 2\right], (\theta_{0.8}, \theta_{1.2}], (\theta_{1.8},\theta_{2.2}], (\theta_{2.8},\theta_{3.2}] \end{gathered} \right\}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\mathop{\mathrm{GSQAut}}\nolimits({\mathcal A})\\ &:=\left\{ \alpha\in \mathop{\mathrm{SQAut}}\nolimits({\mathcal A})\middle\vert \begin{gathered} \text{for any } \theta_{0.8}, \theta_1, \theta_{1.2},\theta_{1.8},\theta_2,\theta_{2.2}, \theta_{2.8},\theta_3,\theta_{3.2}\text{ satisfying formula (2.11),}\\\text{there is a decomposition }(2.12), (2.13), (2.14) \text{ satisfying}\\ \alpha_{I}\circ\beta_g^{U}=\beta_g^{U}\circ\alpha_{I},\ g\in G,\\ \text{for all }I=[0,\theta_1],(\theta_1,\theta_2], (\theta_2,\theta_3], \left(\theta_3,\frac\pi 2\right], (\theta_{0.8}, \theta_{1.2}], (\theta_{1.8},\theta_{2.2}], (\theta_{2.8},\theta_{3.2}] \end{gathered} \right\}. \end{split} \end{align} $$We also define
 $$ \begin{align} \mathop{\mathrm{HAut}}\nolimits\left ( {\mathcal A}\right ):= \left\{\alpha\in\mathop{\mathrm{Aut}}\nolimits({\mathcal A})\middle\vert \begin{gathered} \text{for any } 0<\theta<\frac\pi 2, \text{ there exist }\alpha_{\sigma}\in \mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{{\left ( C_{\theta}\right )_\sigma}}\right ),\ \sigma=L,R,\\ \text{such that } \alpha=({\textrm{{inner}}})\circ\left ( \alpha_{L}\otimes \alpha_{R}\right ) \end{gathered} \right\}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{HAut}}\nolimits\left ( {\mathcal A}\right ):= \left\{\alpha\in\mathop{\mathrm{Aut}}\nolimits({\mathcal A})\middle\vert \begin{gathered} \text{for any } 0<\theta<\frac\pi 2, \text{ there exist }\alpha_{\sigma}\in \mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{{\left ( C_{\theta}\right )_\sigma}}\right ),\ \sigma=L,R,\\ \text{such that } \alpha=({\textrm{{inner}}})\circ\left ( \alpha_{L}\otimes \alpha_{R}\right ) \end{gathered} \right\}. \end{align} $$In Section 5, we will see that quasilocal automorphisms corresponding to paths in symmetric gapped phases belong to the following set:
 $$ \begin{align} \mathop{\mathrm{GUQAut}}\nolimits\left ({\mathcal A}\right ) :=\left\{ \gamma\in\mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}\right )\middle\vert \begin{gathered} \text{there are } \gamma_{H}\in \mathop{\mathrm{HAut}}\nolimits({\mathcal A}), \gamma_{C}\in \mathop{\mathrm{GSQAut}}\nolimits({\mathcal A}),\\ \text{such that } \gamma=\gamma_{C}\circ\gamma_{H} \end{gathered} \right\}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{GUQAut}}\nolimits\left ({\mathcal A}\right ) :=\left\{ \gamma\in\mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}\right )\middle\vert \begin{gathered} \text{there are } \gamma_{H}\in \mathop{\mathrm{HAut}}\nolimits({\mathcal A}), \gamma_{C}\in \mathop{\mathrm{GSQAut}}\nolimits({\mathcal A}),\\ \text{such that } \gamma=\gamma_{C}\circ\gamma_{H} \end{gathered} \right\}. \end{align} $$ We fix a reference state ![]() $\omega _0$ as follows: We fix a unit vector
$\omega _0$ as follows: We fix a unit vector ![]() ${\xi _x}\in {\mathbb C}^d$ and let
${\xi _x}\in {\mathbb C}^d$ and let ![]() $\rho _{\xi _x}$ be the vector state on
$\rho _{\xi _x}$ be the vector state on ![]() $\mathop {\mathrm {M}}\nolimits _d$ given by
$\mathop {\mathrm {M}}\nolimits _d$ given by ![]() ${\xi _x}$, for each
${\xi _x}$, for each ![]() $x\in {\mathbb Z}^2$. Then our reference state
$x\in {\mathbb Z}^2$. Then our reference state ![]() $\omega _0$ is given by
$\omega _0$ is given by
 $$ \begin{align} \omega_0:=\bigotimes_{x\in {\mathbb Z}^2} \rho_{\xi_x}. \end{align} $$
$$ \begin{align} \omega_0:=\bigotimes_{x\in {\mathbb Z}^2} \rho_{\xi_x}. \end{align} $$Throughout this section this ![]() $\omega _0$ is fixed. Let
$\omega _0$ is fixed. Let ![]() $({\mathcal H}_0,\pi _0,\Omega _0)$ be a GNS triple of
$({\mathcal H}_0,\pi _0,\Omega _0)$ be a GNS triple of ![]() $\omega _0$. Because of the product structure of
$\omega _0$. Because of the product structure of ![]() $\omega _0$, it is decomposed as
$\omega _0$, it is decomposed as
where ![]() $({\mathcal H}_\sigma ,\pi _\sigma ,\Omega _\sigma )$ is a GNS triple of
$({\mathcal H}_\sigma ,\pi _\sigma ,\Omega _\sigma )$ is a GNS triple of ![]() $\omega _\sigma :=\omega _0\rvert _{{\mathcal A}_{H_\sigma }}$ for
$\omega _\sigma :=\omega _0\rvert _{{\mathcal A}_{H_\sigma }}$ for ![]() $\sigma =L,R$. As
$\sigma =L,R$. As ![]() $\omega _0\rvert _{{\mathcal A}_{H_\sigma }}$ is pure,
$\omega _0\rvert _{{\mathcal A}_{H_\sigma }}$ is pure, ![]() $\pi _\sigma $ is irreducible. What we consider in this section is the set of states created via elements in
$\pi _\sigma $ is irreducible. What we consider in this section is the set of states created via elements in ![]() $\mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$ from our reference state
$\mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$ from our reference state ![]() $\omega _0$:
$\omega _0$:
Because any pure product states can be transformed to each other via an automorphism of product form ![]() $\tilde \alpha =\bigotimes _{x\in {\mathbb Z}^{2}}\tilde \alpha _{x}$, and
$\tilde \alpha =\bigotimes _{x\in {\mathbb Z}^{2}}\tilde \alpha _{x}$, and ![]() $\tilde \alpha \alpha $ belongs to
$\tilde \alpha \alpha $ belongs to ![]() $\mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$ for any
$\mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$ for any ![]() $\alpha \in \mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$,
$\alpha \in \mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$, ![]() $\mathop {\mathcal {SL}}\nolimits $ does not depend on the choice of
$\mathop {\mathcal {SL}}\nolimits $ does not depend on the choice of ![]() $\omega _0$. For each
$\omega _0$. For each ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $, we set
$\omega \in \mathop {\mathcal {SL}}\nolimits $, we set
By the definition of ![]() $\mathop {\mathcal {SL}}\nolimits $,
$\mathop {\mathcal {SL}}\nolimits $, ![]() $\mathop {\mathrm {EAut}}\nolimits (\omega )$ is not empty.
$\mathop {\mathrm {EAut}}\nolimits (\omega )$ is not empty.
For ![]() $0<\theta <\frac \pi 2$ and a set of automorphisms
$0<\theta <\frac \pi 2$ and a set of automorphisms  $\left (\tilde \beta _g\right )_{g\in G}\subset \mathop {\mathrm {Aut}}\nolimits ({{\mathcal A}})$, we introduce a set
$\left (\tilde \beta _g\right )_{g\in G}\subset \mathop {\mathrm {Aut}}\nolimits ({{\mathcal A}})$, we introduce a set
 $$ \begin{align} {\mathcal T}\left(\theta, (\tilde\beta_g )\right) :=\left\{ (\eta_{g}^\sigma )_{g\in G,\, \sigma=L,R } \middle\vert \begin{gathered} \eta_g^\sigma\in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{\left ( C_\theta\right )_\sigma}\right ), \\ \tilde\beta_g=({\textrm{{inner}}})\circ\left ( \eta_g^L\otimes\eta_g^R\right )\circ\beta_g^U,\\ \text{for all}\;g\in G,\ \sigma=L,R \end{gathered} \right\}. \end{align} $$
$$ \begin{align} {\mathcal T}\left(\theta, (\tilde\beta_g )\right) :=\left\{ (\eta_{g}^\sigma )_{g\in G,\, \sigma=L,R } \middle\vert \begin{gathered} \eta_g^\sigma\in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{\left ( C_\theta\right )_\sigma}\right ), \\ \tilde\beta_g=({\textrm{{inner}}})\circ\left ( \eta_g^L\otimes\eta_g^R\right )\circ\beta_g^U,\\ \text{for all}\;g\in G,\ \sigma=L,R \end{gathered} \right\}. \end{align} $$In a word, it is a set of decompositions of  $\tilde \beta _g\circ ( \beta _g^{U})^{-1}$ into tensors of
$\tilde \beta _g\circ ( \beta _g^{U})^{-1}$ into tensors of ![]() $\mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{( C_\theta )_L} ), \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{( C_\theta )_R} )$ modulo inner automorphisms. For
$\mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{( C_\theta )_L} ), \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{( C_\theta )_R} )$ modulo inner automorphisms. For  $(\eta _{g}^\sigma )_{g\in G,\, \sigma =L,R }\in {\mathcal T}(\theta , (\tilde \beta _g ))$, we set
$(\eta _{g}^\sigma )_{g\in G,\, \sigma =L,R }\in {\mathcal T}(\theta , (\tilde \beta _g ))$, we set
 $$ \begin{align} \eta_g:=\eta_g^L\otimes\eta_g^R,\quad g\in G. \end{align} $$
$$ \begin{align} \eta_g:=\eta_g^L\otimes\eta_g^R,\quad g\in G. \end{align} $$The following set of automorphisms is the key ingredient for the definition of our index: For ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ and
$\omega \in \mathop {\mathcal {SL}}\nolimits $ and ![]() $0<\theta <\frac \pi 2$, we set
$0<\theta <\frac \pi 2$, we set
 $$ \begin{align} \mathop{\mathrm{IG}}\nolimits\left (\omega,\theta\right ) :=\left\{ (\tilde\beta_g )_{g\in G}\in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}\right )^{\times G} \middle\vert \begin{gathered} \omega\circ\tilde\beta_g=\omega \text{ for all } g\in G\\ \text{and }{\mathcal T}\left(\theta, (\tilde\beta_g )\right)\neq\emptyset\end{gathered} \right\}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{IG}}\nolimits\left (\omega,\theta\right ) :=\left\{ (\tilde\beta_g )_{g\in G}\in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}\right )^{\times G} \middle\vert \begin{gathered} \omega\circ\tilde\beta_g=\omega \text{ for all } g\in G\\ \text{and }{\mathcal T}\left(\theta, (\tilde\beta_g )\right)\neq\emptyset\end{gathered} \right\}. \end{align} $$We also set
In this section we associate some third cohomology ![]() $h(\omega )$ for each
$h(\omega )$ for each ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ with
$\omega \in \mathop {\mathcal {SL}}\nolimits $ with ![]() $\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $.
$\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $.
2.3 Derivation of elements in  $Z^3(G,{\mathbb T})$
$Z^3(G,{\mathbb T})$
In this subsection, we derive ![]() $3$-cocycles out of
$3$-cocycles out of  $\omega , \alpha , \theta , (\tilde \beta _g ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta )$.
$\omega , \alpha , \theta , (\tilde \beta _g ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta )$.
Lemma 2.1. Set  $\omega \in \mathop {\mathcal {SL}}\nolimits , \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega ), 0<\theta <\frac \pi 2, (\tilde \beta _g)\in \mathop {\mathrm {IG}}\nolimits \left (\omega ,\theta \right ), (\eta _{g}^\sigma )\in {\mathcal T}(\theta , (\tilde \beta _g)), (\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $. Then the following hold:
$\omega \in \mathop {\mathcal {SL}}\nolimits , \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega ), 0<\theta <\frac \pi 2, (\tilde \beta _g)\in \mathop {\mathrm {IG}}\nolimits \left (\omega ,\theta \right ), (\eta _{g}^\sigma )\in {\mathcal T}(\theta , (\tilde \beta _g)), (\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $. Then the following hold:
(i) There are unitaries
 $W_g$,
$W_g$,  $g\in G$, on
$g\in G$, on  ${\mathcal H}_0$ such that (2.26)with the notation of definitions (2.9) and (2.23).
${\mathcal H}_0$ such that (2.26)with the notation of definitions (2.9) and (2.23). $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)\circ\pi_0 =\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1},\quad g\in G, \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)\circ\pi_0 =\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1},\quad g\in G, \end{align} $$(ii) There exists a unitary
 $u_\sigma (g,h)$ on
$u_\sigma (g,h)$ on  ${\mathcal H}_{\sigma }$, for each
${\mathcal H}_{\sigma }$, for each  $\sigma =L,R$ and for
$\sigma =L,R$ and for  $g,h\in G$, such that (2.27)and
$g,h\in G$, such that (2.27)and $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_\sigma(g,h)\right )\circ\pi_\sigma =\pi_\sigma\circ\alpha_\sigma\circ\eta_g^\sigma\beta_g^{\sigma U} \eta_h^\sigma\left (\beta_g^{\sigma U}\right )^{-1}\left ( \eta_{gh}^\sigma\right )^{-1} \circ\alpha_\sigma^{-1} \end{align} $$(2.28)Furthermore,
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_\sigma(g,h)\right )\circ\pi_\sigma =\pi_\sigma\circ\alpha_\sigma\circ\eta_g^\sigma\beta_g^{\sigma U} \eta_h^\sigma\left (\beta_g^{\sigma U}\right )^{-1}\left ( \eta_{gh}^\sigma\right )^{-1} \circ\alpha_\sigma^{-1} \end{align} $$(2.28)Furthermore, $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_L(g,h)\otimes u_R(g,h)\right )\pi_0 =\pi_0\circ\alpha_0\circ\eta_g\beta_g^U\eta_h\left ( \beta_g^U\right )^{-1}\left (\eta_{gh}\right )^{-1} \circ\alpha_0^{-1}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_L(g,h)\otimes u_R(g,h)\right )\pi_0 =\pi_0\circ\alpha_0\circ\eta_g\beta_g^U\eta_h\left ( \beta_g^U\right )^{-1}\left (\eta_{gh}\right )^{-1} \circ\alpha_0^{-1}. \end{align} $$ $u_{\sigma }(g,h)$ commutes with any element of
$u_{\sigma }(g,h)$ commutes with any element of  $ \pi _\sigma \circ \alpha _\sigma \left ( {\mathcal A}_{\left ( \left ( C_\theta \right )^c\right )_\sigma }\right )$.
$ \pi _\sigma \circ \alpha _\sigma \left ( {\mathcal A}_{\left ( \left ( C_\theta \right )^c\right )_\sigma }\right )$.
Definition 2.2. For  $\omega \in \mathop {\mathcal {SL}}\nolimits , \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega ), 0<\theta <\frac \pi 2, (\tilde \beta _g )\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta ), (\eta _{g}^\sigma)_{g\in G,\, \sigma =L,R }\in {\mathcal T}\left (\theta , \left (\tilde \beta _g\right )\right ), (\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $, we denote by
$\omega \in \mathop {\mathcal {SL}}\nolimits , \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega ), 0<\theta <\frac \pi 2, (\tilde \beta _g )\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta ), (\eta _{g}^\sigma)_{g\in G,\, \sigma =L,R }\in {\mathcal T}\left (\theta , \left (\tilde \beta _g\right )\right ), (\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $, we denote by
 $$ \begin{align} \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ) \end{align} $$
$$ \begin{align} \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ) \end{align} $$the set of ![]() $( (W_g)_{g\in G}, (u_\sigma (g,h))_{g,h\in G,\,\sigma =L,R} )$ with
$( (W_g)_{g\in G}, (u_\sigma (g,h))_{g,h\in G,\,\sigma =L,R} )$ with ![]() $W_{g}\in {\mathcal U}({\mathcal H}_{0} )$ and
$W_{g}\in {\mathcal U}({\mathcal H}_{0} )$ and ![]() $u_\sigma (g,h)\in {\mathcal U}\left ({\mathcal H}_{\sigma }\right )$ satisfying
$u_\sigma (g,h)\in {\mathcal U}\left ({\mathcal H}_{\sigma }\right )$ satisfying
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)\circ\pi_0 & =\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1},\quad g\in G, \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)\circ\pi_0 & =\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1},\quad g\in G, \end{align} $$and
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_{\sigma}(g,h)\right )\circ\pi_{\sigma} & =\pi_{\sigma}\circ\alpha_{\sigma}\circ\eta_g^{\sigma}\beta_g^{{\sigma} U} \eta_h^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}( \eta_{gh}^{\sigma})^{-1} \circ\alpha_{\sigma}^{-1},\quad g,h\in G, \ \sigma=L,R. \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_{\sigma}(g,h)\right )\circ\pi_{\sigma} & =\pi_{\sigma}\circ\alpha_{\sigma}\circ\eta_g^{\sigma}\beta_g^{{\sigma} U} \eta_h^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}( \eta_{gh}^{\sigma})^{-1} \circ\alpha_{\sigma}^{-1},\quad g,h\in G, \ \sigma=L,R. \end{align} $$(Here we used the notation of definition (2.9) and (2.23).) By Lemma 2.1, it is nonempty.
Proof. For a GNS triple ![]() $({\mathcal H}_0,\pi _0\circ \alpha ,\Omega _0)$ of
$({\mathcal H}_0,\pi _0\circ \alpha ,\Omega _0)$ of ![]() $\omega =\omega _0\circ \alpha $, there are unitaries
$\omega =\omega _0\circ \alpha $, there are unitaries ![]() $\tilde W_g$ on
$\tilde W_g$ on ![]() ${\mathcal H}_0$ such that
${\mathcal H}_0$ such that
because ![]() $\omega \circ \tilde \beta _g=\omega $.
$\omega \circ \tilde \beta _g=\omega $.
Because  $(\eta _{g}^\sigma )_{g\in G,\, \sigma =L,R }\in {\mathcal T}(\theta , (\tilde \beta _g ) )$ and
$(\eta _{g}^\sigma )_{g\in G,\, \sigma =L,R }\in {\mathcal T}(\theta , (\tilde \beta _g ) )$ and ![]() $(\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $, there are unitaries
$(\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $, there are unitaries ![]() $v_g, V\in {\mathcal U}\left ({\mathcal A}\right )$ such that
$v_g, V\in {\mathcal U}\left ({\mathcal A}\right )$ such that
 $$ \begin{align} \tilde\beta_g=\mathop{\mathrm{Ad}}\nolimits\left ( v_g\right )\circ\left ( \eta_g^L\otimes\eta_g^R\right )\circ\beta_g^U,\quad \alpha=\mathop{\mathrm{Ad}}\nolimits V\circ\alpha_0\circ\Theta. \end{align} $$
$$ \begin{align} \tilde\beta_g=\mathop{\mathrm{Ad}}\nolimits\left ( v_g\right )\circ\left ( \eta_g^L\otimes\eta_g^R\right )\circ\beta_g^U,\quad \alpha=\mathop{\mathrm{Ad}}\nolimits V\circ\alpha_0\circ\Theta. \end{align} $$Substituting these, we have
 $$ \begin{align} \begin{split} \mathop{\mathrm{Ad}}\nolimits \left ( \tilde W_g\pi_0(V)\right )\pi_0\circ\alpha_0\circ\Theta & =\pi_0\circ\alpha\tilde\beta_g =\pi_0\circ\alpha\circ\mathop{\mathrm{Ad}}\nolimits\left(v_g\right)\circ \eta_g\beta_g^U\\ &=\mathop{\mathrm{Ad}}\nolimits\left ( \left ( \pi_0\circ\alpha(v_g)\right )\pi_0(V) \right )\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathop{\mathrm{Ad}}\nolimits \left ( \tilde W_g\pi_0(V)\right )\pi_0\circ\alpha_0\circ\Theta & =\pi_0\circ\alpha\tilde\beta_g =\pi_0\circ\alpha\circ\mathop{\mathrm{Ad}}\nolimits\left(v_g\right)\circ \eta_g\beta_g^U\\ &=\mathop{\mathrm{Ad}}\nolimits\left ( \left ( \pi_0\circ\alpha(v_g)\right )\pi_0(V) \right )\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U. \end{split} \end{align} $$Therefore, setting  $W_g:=\pi _0(V)^*( \pi _0\circ \alpha (v_g^*))\tilde W_g\pi _0(V)\in {\mathcal U}({\mathcal H}_0)$, we obtain equation (2.26).
$W_g:=\pi _0(V)^*( \pi _0\circ \alpha (v_g^*))\tilde W_g\pi _0(V)\in {\mathcal U}({\mathcal H}_0)$, we obtain equation (2.26).
Using equation (2.26), we have
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( W_gW_h W_{gh}^*\right ) \pi_0 =\pi_0\circ\alpha_0\circ\Theta \circ\eta_g\beta_g^U\eta_h\left ( \beta_g^{U}\right )^{-1} \eta_{gh}^{-1}\Theta^{-1}\alpha_0^{-1}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( W_gW_h W_{gh}^*\right ) \pi_0 =\pi_0\circ\alpha_0\circ\Theta \circ\eta_g\beta_g^U\eta_h\left ( \beta_g^{U}\right )^{-1} \eta_{gh}^{-1}\Theta^{-1}\alpha_0^{-1}. \end{align} $$Note that because conjugation by  $\beta _g^U$ does not change the support of automorphisms,
$\beta _g^U$ does not change the support of automorphisms,  $\eta _g\beta _g^U\eta _h( \beta _g^{U} )^{-1} \eta _{gh}^{-1}$ belongs to
$\eta _g\beta _g^U\eta _h( \beta _g^{U} )^{-1} \eta _{gh}^{-1}$ belongs to ![]() $\mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_\theta } )$. On the other hand,
$\mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_\theta } )$. On the other hand, ![]() $\Theta $ belongs to
$\Theta $ belongs to ![]() $\mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{ ( C_\theta )^{c}} )$. Therefore, they commute and we obtain
$\mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{ ( C_\theta )^{c}} )$. Therefore, they commute and we obtain
 $$ \begin{align} \begin{split} \mathop{\mathrm{Ad}}\nolimits\left ( W_gW_h W_{gh}^*\right ) \pi_0 &= \text{equation }(2.35)=\pi_0\circ\alpha_0\circ\eta_g\beta_g^U\eta_h\left ( \beta_g^{U}\right )^{-1} \eta_{gh}^{-1}\alpha_0^{-1}\\ &=\bigotimes_{\sigma=L,R} \pi_\sigma\circ\alpha_\sigma\circ\eta_g^\sigma\beta_g^{\sigma U} \eta_h^\sigma\left (\beta_g^{\sigma U}\right )^{-1}\left ( \eta_{gh}^\sigma\right )^{-1} \circ\alpha_\sigma^{-1}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathop{\mathrm{Ad}}\nolimits\left ( W_gW_h W_{gh}^*\right ) \pi_0 &= \text{equation }(2.35)=\pi_0\circ\alpha_0\circ\eta_g\beta_g^U\eta_h\left ( \beta_g^{U}\right )^{-1} \eta_{gh}^{-1}\alpha_0^{-1}\\ &=\bigotimes_{\sigma=L,R} \pi_\sigma\circ\alpha_\sigma\circ\eta_g^\sigma\beta_g^{\sigma U} \eta_h^\sigma\left (\beta_g^{\sigma U}\right )^{-1}\left ( \eta_{gh}^\sigma\right )^{-1} \circ\alpha_\sigma^{-1}. \end{split} \end{align} $$From this and the irreducibility of ![]() $\pi _R$, we see that
$\pi _R$, we see that  $\mathop {\mathrm {Ad}}\nolimits ( W_gW_h W_{gh}^* )$ gives rise to a
$\mathop {\mathrm {Ad}}\nolimits ( W_gW_h W_{gh}^* )$ gives rise to a ![]() $*$-isomorphism
$*$-isomorphism ![]() $\tau $ on
$\tau $ on ![]() ${\mathcal B}({\mathcal H}_R)$. It is implemented by some unitary
${\mathcal B}({\mathcal H}_R)$. It is implemented by some unitary ![]() $u_R(g,h)$ on
$u_R(g,h)$ on ![]() ${\mathcal H}_R$ by the Wigner theorem, and we obtain
${\mathcal H}_R$ by the Wigner theorem, and we obtain
 $$ \begin{align} \begin{split} \mathbb I_{{\mathcal H}_L}\otimes \left ( \mathop{\mathrm{Ad}}\nolimits\left ( u_R(g,h) \right )\circ\pi_R(A)\right ) &=\mathbb I_{{\mathcal H}_L}\otimes \tau\left ( \pi_R(A)\right ) =\mathop{\mathrm{Ad}}\nolimits\left ( W_gW_h W_{gh}^*\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes \pi_R(A)\right )\\ &=\mathbb I_{{\mathcal H}_L}\otimes \pi_R\circ\alpha_R\circ\eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1} \circ\alpha_R^{-1}(A), \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathbb I_{{\mathcal H}_L}\otimes \left ( \mathop{\mathrm{Ad}}\nolimits\left ( u_R(g,h) \right )\circ\pi_R(A)\right ) &=\mathbb I_{{\mathcal H}_L}\otimes \tau\left ( \pi_R(A)\right ) =\mathop{\mathrm{Ad}}\nolimits\left ( W_gW_h W_{gh}^*\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes \pi_R(A)\right )\\ &=\mathbb I_{{\mathcal H}_L}\otimes \pi_R\circ\alpha_R\circ\eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1} \circ\alpha_R^{-1}(A), \end{split} \end{align} $$for any ![]() $A\in {\mathcal A}_{H_{R}}$. Hence we obtain equation (2.27) for
$A\in {\mathcal A}_{H_{R}}$. Hence we obtain equation (2.27) for ![]() $\sigma =R$.
$\sigma =R$.
To see that ![]() $u_R(g,h)$ belongs to
$u_R(g,h)$ belongs to  $\left ( \pi _R\circ \alpha _R\left ( {\mathcal A}_{\left ( \left ( C_\theta \right )^c\right )_R}\right )\right )'$, set
$\left ( \pi _R\circ \alpha _R\left ( {\mathcal A}_{\left ( \left ( C_\theta \right )^c\right )_R}\right )\right )'$, set ![]() $A\in {\mathcal A}_{\left ( \left ( C_\theta \right )^c\right )_R}$. Then because
$A\in {\mathcal A}_{\left ( \left ( C_\theta \right )^c\right )_R}$. Then because  $\eta _g^R\beta _g^{R U} \eta _h^R (\beta _g^{R U} )^{-1} ( \eta _{gh}^R )^{-1}$ belongs to
$\eta _g^R\beta _g^{R U} \eta _h^R (\beta _g^{R U} )^{-1} ( \eta _{gh}^R )^{-1}$ belongs to ![]() $\mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{\left ( C_\theta \right )_R}\right )$, we have
$\mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{\left ( C_\theta \right )_R}\right )$, we have
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_R(g,h)\right )\pi_R\left ( \alpha_R(A)\right ) =\pi_R\alpha_R \eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\alpha_R^{-1}\alpha_R(A) =\pi_R\alpha_R(A). \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_R(g,h)\right )\pi_R\left ( \alpha_R(A)\right ) =\pi_R\alpha_R \eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\alpha_R^{-1}\alpha_R(A) =\pi_R\alpha_R(A). \end{align} $$This proves that ![]() $u_R(g,h)$ belongs to
$u_R(g,h)$ belongs to 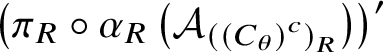 $\left ( \pi _R\circ \alpha _R\left ( {\mathcal A}_{\left ( \left ( C_\theta \right )^c\right )_R}\right )\right )'$. An analogous statement for
$\left ( \pi _R\circ \alpha _R\left ( {\mathcal A}_{\left ( \left ( C_\theta \right )^c\right )_R}\right )\right )'$. An analogous statement for ![]() $u_L(g,h)$ can be shown exactly the same way. The last statement of (ii), equation (2.28), is trivial from equation (2.27).
$u_L(g,h)$ can be shown exactly the same way. The last statement of (ii), equation (2.28), is trivial from equation (2.27).
Lemma 2.3. Set  $\omega \in \mathop {\mathcal {SL}}\nolimits , \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega ), 0<\theta <\frac \pi 2, \left (\tilde \beta _g\right )\in \mathop {\mathrm {IG}}\nolimits \left (\omega ,\theta \right ), (\eta _{g}^\sigma )\in {\mathcal T}(\theta , (\tilde \beta _g)), (\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $. Let
$\omega \in \mathop {\mathcal {SL}}\nolimits , \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega ), 0<\theta <\frac \pi 2, \left (\tilde \beta _g\right )\in \mathop {\mathrm {IG}}\nolimits \left (\omega ,\theta \right ), (\eta _{g}^\sigma )\in {\mathcal T}(\theta , (\tilde \beta _g)), (\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $. Let ![]() $( (W_g), (u_R(g,h))) $ be an element of
$( (W_g), (u_R(g,h))) $ be an element of  $\mathop {\mathrm {IP}}\nolimits ( \omega , \alpha , \theta , (\tilde \beta _g ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta ) )$.
$\mathop {\mathrm {IP}}\nolimits ( \omega , \alpha , \theta , (\tilde \beta _g ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta ) )$.
Then the following hold:
(i) For any
 $g,h,k\in G$, (2.39)
$g,h,k\in G$, (2.39) $$ \begin{align} &\mathop{\mathrm{Ad}}\nolimits\left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right )\circ\pi_0 \nonumber \\ &\quad =\pi_0\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_{L}}}\otimes \alpha_R\eta_g^R\beta_g^{RU} \left ( \eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1} \right ) \left ( \eta_g^R\beta_g^{RU}\right )^{-1} \alpha_R^{-1} \right ). \end{align} $$
$$ \begin{align} &\mathop{\mathrm{Ad}}\nolimits\left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right )\circ\pi_0 \nonumber \\ &\quad =\pi_0\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_{L}}}\otimes \alpha_R\eta_g^R\beta_g^{RU} \left ( \eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1} \right ) \left ( \eta_g^R\beta_g^{RU}\right )^{-1} \alpha_R^{-1} \right ). \end{align} $$(ii) For any
 $g,h\in G$, (2.40)on
$g,h\in G$, (2.40)on $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( \left ( u_L(g,h)\otimes u_R(g,h)\right ) W_{gh}\right ) =\mathop{\mathrm{Ad}}\nolimits \left ( W_gW_h\right ) \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( \left ( u_L(g,h)\otimes u_R(g,h)\right ) W_{gh}\right ) =\mathop{\mathrm{Ad}}\nolimits \left ( W_gW_h\right ) \end{align} $$ ${\mathcal B}({\mathcal H}_{0})$.
${\mathcal B}({\mathcal H}_{0})$.(iii) For any
 $g,h,k\in G$, (2.41)
$g,h,k\in G$, (2.41) $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) \in{\mathbb C}\mathbb I_{{\mathcal H}_L}\otimes{\mathcal B}({\mathcal H}_R). \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) \in{\mathbb C}\mathbb I_{{\mathcal H}_L}\otimes{\mathcal B}({\mathcal H}_R). \end{align} $$(iv) For any
 $g,h,k,f\in G$, (2.42)
$g,h,k,f\in G$, (2.42) $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( W_g W_h\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) =\left ( \mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h)\right ) W_{gh}\right ) \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ). \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( W_g W_h\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) =\left ( \mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h)\right ) W_{gh}\right ) \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ). \end{align} $$
Proof. We use the notation from definitions (2.9) and (2.23).
(i) Substituting equations (2.30) and (2.31), we have
 $$ \begin{align} \begin{split} \mathop{\mathrm{Ad}}\nolimits & \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right )\circ\pi_0 \\ &=\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1}\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_L}}\otimes \alpha_R\circ\eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1} \circ\alpha_R^{-1}\right )\\ &\quad \circ\alpha_0\circ\Theta\circ\left ( \eta_g\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1} \\ &=\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_L}}\otimes \eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1} \right ) \circ\Theta\circ\left ( \eta_g\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathop{\mathrm{Ad}}\nolimits & \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right )\circ\pi_0 \\ &=\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1}\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_L}}\otimes \alpha_R\circ\eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1} \circ\alpha_R^{-1}\right )\\ &\quad \circ\alpha_0\circ\Theta\circ\left ( \eta_g\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1} \\ &=\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_L}}\otimes \eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1} \right ) \circ\Theta\circ\left ( \eta_g\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}. \end{split} \end{align} $$Because  $\eta _h^R\beta _h^{R U} \eta _k^R(\beta _h^{R U} )^{-1}( \eta _{hk}^R)^{-1}$ belongs to
$\eta _h^R\beta _h^{R U} \eta _k^R(\beta _h^{R U} )^{-1}( \eta _{hk}^R)^{-1}$ belongs to ![]() $\mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{\left ( C_\theta \right )_R}\right )$, it commutes with
$\mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{\left ( C_\theta \right )_R}\right )$, it commutes with  $\Theta \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{\left ( C_\theta \right )^{c}}\right )$. Hence we obtain
$\Theta \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{\left ( C_\theta \right )^{c}}\right )$. Hence we obtain
 $$ \begin{align} & \text{equation }(2.43)\notag\\ & \quad = \pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ \left ( \mathbb I_{{\mathcal A}_{H_L}}\otimes \eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1} \right ) \circ\left ( \eta_g\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\notag\\ & \quad =\pi_0\circ\alpha_0\circ\Theta\circ \left ( \mathbb I_{{\mathcal A}_{H_L}}\otimes \eta_g^R\beta_g^{RU}\circ\eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1}\circ \left ( \eta_g^R\beta_g^{RU}\right )^{-1} \right ) \circ\Theta^{-1}\circ\alpha_0^{-1}. \end{align} $$
$$ \begin{align} & \text{equation }(2.43)\notag\\ & \quad = \pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ \left ( \mathbb I_{{\mathcal A}_{H_L}}\otimes \eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1} \right ) \circ\left ( \eta_g\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\notag\\ & \quad =\pi_0\circ\alpha_0\circ\Theta\circ \left ( \mathbb I_{{\mathcal A}_{H_L}}\otimes \eta_g^R\beta_g^{RU}\circ\eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1}\circ \left ( \eta_g^R\beta_g^{RU}\right )^{-1} \right ) \circ\Theta^{-1}\circ\alpha_0^{-1}. \end{align} $$Again, the term in parentheses in the last line is localised at ![]() $\left ( C_\theta \right )_R$, and it commutes with
$\left ( C_\theta \right )_R$, and it commutes with ![]() $\Theta $. Therefore, we have
$\Theta $. Therefore, we have
 $$ \begin{align} &\mathop{\mathrm{Ad}}\nolimits\left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right )\circ\pi_0\nonumber\\ &\qquad=\pi_0\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_L}}\otimes \alpha_R\circ\eta_g^R\beta_g^{RU}\circ\eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1}\circ \left ( \eta_g^R\beta_g^{RU}\right )^{-1} \circ\alpha_R^{-1}\right ). \end{align} $$
$$ \begin{align} &\mathop{\mathrm{Ad}}\nolimits\left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right )\circ\pi_0\nonumber\\ &\qquad=\pi_0\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_L}}\otimes \alpha_R\circ\eta_g^R\beta_g^{RU}\circ\eta_h^R\beta_h^{R U} \eta_k^R\left (\beta_h^{R U}\right )^{-1}\left ( \eta_{hk}^R\right )^{-1}\circ \left ( \eta_g^R\beta_g^{RU}\right )^{-1} \circ\alpha_R^{-1}\right ). \end{align} $$(ii) Again by equations (2.30) and (2.31), we have
 $$ \begin{align} \begin{split} \mathop{\mathrm{Ad}}\nolimits & \left ( \left ( u_L(g,h)\otimes u_R(g,h)\right ) W_{gh}\right )\circ\pi_0 =\pi_0\circ\alpha_0\circ\eta_g\beta_g^U\eta_h\left ( \beta_g^U\right )^{-1}\left (\eta_{gh}\right )^{-1} \circ\Theta\circ\eta_{gh}\beta_{gh}^U\circ\Theta^{-1}\circ\alpha_0^{-1} \\ &=\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\eta_h\left ( \beta_g^U\right )^{-1}\left (\eta_{gh}\right )^{-1} \circ\eta_{gh}\beta_{gh}^U\circ\Theta^{-1}\circ\alpha_0^{-1}\\ &=\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\eta_h\beta_{h}^U\circ\Theta^{-1}\circ\alpha_0^{-1}\\ &=\mathop{\mathrm{Ad}}\nolimits \left ( W_gW_h\right )\circ\pi_0. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathop{\mathrm{Ad}}\nolimits & \left ( \left ( u_L(g,h)\otimes u_R(g,h)\right ) W_{gh}\right )\circ\pi_0 =\pi_0\circ\alpha_0\circ\eta_g\beta_g^U\eta_h\left ( \beta_g^U\right )^{-1}\left (\eta_{gh}\right )^{-1} \circ\Theta\circ\eta_{gh}\beta_{gh}^U\circ\Theta^{-1}\circ\alpha_0^{-1} \\ &=\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\eta_h\left ( \beta_g^U\right )^{-1}\left (\eta_{gh}\right )^{-1} \circ\eta_{gh}\beta_{gh}^U\circ\Theta^{-1}\circ\alpha_0^{-1}\\ &=\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\eta_h\beta_{h}^U\circ\Theta^{-1}\circ\alpha_0^{-1}\\ &=\mathop{\mathrm{Ad}}\nolimits \left ( W_gW_h\right )\circ\pi_0. \end{split} \end{align} $$Here, for the second equality we again used the commutativity of ![]() $\eta $s and
$\eta $s and ![]() $\Theta $, due to their disjoint support. Because
$\Theta $, due to their disjoint support. Because ![]() $\pi _0$ is irreducible, we obtain equation (2.40).
$\pi _0$ is irreducible, we obtain equation (2.40).
(iii) For any ![]() $A\in {\mathcal A}_{H_L}$, we have
$A\in {\mathcal A}_{H_L}$, we have
 $$ \begin{align} \Theta^{-1}\circ\alpha_0^{-1}\left ( A\otimes \mathbb I_{{\mathcal A}_{H_R}}\right ) =\Theta^{-1}\circ\left ( \alpha_L^{-1}(A)\otimes \mathbb I_{{\mathcal A}_{H_R}}\right ) \in \Theta^{-1}\left ({\mathcal A}_{H_L}\otimes {\mathbb C}\mathbb I_{{\mathcal A}_{H_R}}\right ) \subset {\mathcal A}_{H_L\cup \left ( C_\theta^c\right )_R }, \end{align} $$
$$ \begin{align} \Theta^{-1}\circ\alpha_0^{-1}\left ( A\otimes \mathbb I_{{\mathcal A}_{H_R}}\right ) =\Theta^{-1}\circ\left ( \alpha_L^{-1}(A)\otimes \mathbb I_{{\mathcal A}_{H_R}}\right ) \in \Theta^{-1}\left ({\mathcal A}_{H_L}\otimes {\mathbb C}\mathbb I_{{\mathcal A}_{H_R}}\right ) \subset {\mathcal A}_{H_L\cup \left ( C_\theta^c\right )_R }, \end{align} $$because  $\Theta \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{\left ( C_\theta \right )^{c}}\right )$. Therefore,
$\Theta \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{\left ( C_\theta \right )^{c}}\right )$. Therefore,  $\eta _g^R\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{\left ( C_\theta \right )_R}\right )$ acts trivially on it and we have
$\eta _g^R\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{\left ( C_\theta \right )_R}\right )$ acts trivially on it and we have
 $$ \begin{align} \left ( \beta_g^U\right )^{-1}\left ( \eta_g\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\left ( A\otimes \mathbb I_{{\mathcal A}_{H_R}}\right ) \in {\mathcal A}_{H_L\cup \left ( C_\theta^c\right )_R }. \end{align} $$
$$ \begin{align} \left ( \beta_g^U\right )^{-1}\left ( \eta_g\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\left ( A\otimes \mathbb I_{{\mathcal A}_{H_R}}\right ) \in {\mathcal A}_{H_L\cup \left ( C_\theta^c\right )_R }. \end{align} $$As ![]() $\Theta $ preserves
$\Theta $ preserves  ${\mathcal A}_{H_L\cup \left ( C_\theta ^c\right )_R }$,
${\mathcal A}_{H_L\cup \left ( C_\theta ^c\right )_R }$,
 $$ \begin{align} \Theta\circ\left ( \beta_g^U\right )^{-1}\left ( \eta_g\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\left ( A\otimes \mathbb I_{{\mathcal A}_{H_R}}\right ) \end{align} $$
$$ \begin{align} \Theta\circ\left ( \beta_g^U\right )^{-1}\left ( \eta_g\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\left ( A\otimes \mathbb I_{{\mathcal A}_{H_R}}\right ) \end{align} $$also belongs to  ${\mathcal A}_{H_L\cup \left ( C_\theta ^c\right )_R }$. As a result,
${\mathcal A}_{H_L\cup \left ( C_\theta ^c\right )_R }$. As a result,
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( W_g^*\right )\left ( \pi_L(A)\otimes \mathbb I_{{\mathcal H}_R}\right ) =\pi_0\circ\alpha_0\circ\Theta\circ\left ( \beta_g^U\right )^{-1}\left ( \eta_g\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\left ( A\otimes \mathbb I_{{\mathcal A}_{H_R}}\right ) \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( W_g^*\right )\left ( \pi_L(A)\otimes \mathbb I_{{\mathcal H}_R}\right ) =\pi_0\circ\alpha_0\circ\Theta\circ\left ( \beta_g^U\right )^{-1}\left ( \eta_g\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\left ( A\otimes \mathbb I_{{\mathcal A}_{H_R}}\right ) \end{align} $$belongs to ![]() $\pi _L({\mathcal A}_{H_L})\otimes \pi _R\circ \alpha _R( {\mathcal A}_{( C_\theta ^c)_R } )$, and hence commutes with
$\pi _L({\mathcal A}_{H_L})\otimes \pi _R\circ \alpha _R( {\mathcal A}_{( C_\theta ^c)_R } )$, and hence commutes with ![]() $\mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)$. Hence
$\mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)$. Hence ![]() $\mathop {\mathrm {Ad}}\nolimits (W_g)\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k) \right )$ commutes with any elements in
$\mathop {\mathrm {Ad}}\nolimits (W_g)\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k) \right )$ commutes with any elements in ![]() $\pi _L({\mathcal A}_L)\otimes {\mathbb C}\mathbb I_{{\mathcal H}_R}$. Because
$\pi _L({\mathcal A}_L)\otimes {\mathbb C}\mathbb I_{{\mathcal H}_R}$. Because ![]() $\pi _L$ is irreducible,
$\pi _L$ is irreducible, ![]() $\mathop {\mathrm {Ad}}\nolimits (W_g)\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k) \right )$ belongs to
$\mathop {\mathrm {Ad}}\nolimits (W_g)\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k) \right )$ belongs to ![]() ${\mathbb C}\mathbb I_{{\mathcal H}_L}\otimes {\mathcal B}({\mathcal H}_R)$.
${\mathbb C}\mathbb I_{{\mathcal H}_L}\otimes {\mathcal B}({\mathcal H}_R)$.
(iv) By (iii), ![]() $\mathop {\mathrm {Ad}}\nolimits \left ( W_{gh}\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right )$ belongs to
$\mathop {\mathrm {Ad}}\nolimits \left ( W_{gh}\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right )$ belongs to ![]() ${\mathbb C}\mathbb I_{{\mathcal H}_L}\otimes {\mathcal B}({\mathcal H}_R)$. Therefore, from (ii), we have
${\mathbb C}\mathbb I_{{\mathcal H}_L}\otimes {\mathcal B}({\mathcal H}_R)$. Therefore, from (ii), we have
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( W_g W_h\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) & =\mathop{\mathrm{Ad}}\nolimits\left ( \left ( u_L(g,h)\otimes u_R(g,h)\right ) W_{gh}\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right )\notag\\ &=\mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h)\right ) W_{gh}\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ), \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( W_g W_h\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) & =\mathop{\mathrm{Ad}}\nolimits\left ( \left ( u_L(g,h)\otimes u_R(g,h)\right ) W_{gh}\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right )\notag\\ &=\mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h)\right ) W_{gh}\right )\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ), \end{align} $$obtaining (iv).
With this preparation, we may obtain some element of ![]() $Z^3(G,{\mathbb T})$ from
$Z^3(G,{\mathbb T})$ from ![]() $\left ((W_g), (u_\sigma (g,h))\right )$.
$\left ((W_g), (u_\sigma (g,h))\right )$.
Lemma 2.4. Set  $\omega \in \mathop {\mathcal {SL}}\nolimits , \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega ), 0<\theta <\frac \pi 2, (\tilde \beta _g)\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta ), (\eta _{g}^\sigma )\in {\mathcal T}(\theta , (\tilde \beta _g)), (\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $. Let
$\omega \in \mathop {\mathcal {SL}}\nolimits , \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega ), 0<\theta <\frac \pi 2, (\tilde \beta _g)\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta ), (\eta _{g}^\sigma )\in {\mathcal T}(\theta , (\tilde \beta _g)), (\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $. Let ![]() $( (W_g), (u_\sigma (g,h)))$ be an element of
$( (W_g), (u_\sigma (g,h)))$ be an element of  $ \mathop {\mathrm {IP}}\nolimits ( \omega , \alpha , \theta , (\tilde \beta _g ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta ) )$. Then there is a
$ \mathop {\mathrm {IP}}\nolimits ( \omega , \alpha , \theta , (\tilde \beta _g ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta ) )$. Then there is a ![]() $c_R\in Z^3(G,{\mathbb T})$ such that
$c_R\in Z^3(G,{\mathbb T})$ such that
 $$ \begin{align} \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h) u_R(gh,k) =c_R(g,h,k) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\right ), \end{align} $$
$$ \begin{align} \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h) u_R(gh,k) =c_R(g,h,k) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\right ), \end{align} $$for all ![]() $g,h,k\in G$.
$g,h,k\in G$.
Definition 2.5. We denote this ![]() $3$-cocycle
$3$-cocycle ![]() $c_R$ in Lemma 2.4 by
$c_R$ in Lemma 2.4 by
 $$ \begin{align} c_R\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ) \end{align} $$
$$ \begin{align} c_R\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ) \end{align} $$and its cohomology class by
 $$ \begin{align} &h^{(1)} \left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right )\nonumber\\ &\qquad\qquad\qquad:= \left [ c_R\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ) \right ]_{H^3\left(G,{\mathbb T}\right)}. \end{align} $$
$$ \begin{align} &h^{(1)} \left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right )\nonumber\\ &\qquad\qquad\qquad:= \left [ c_R\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ) \right ]_{H^3\left(G,{\mathbb T}\right)}. \end{align} $$Proof. First we prove that there is a number ![]() $c_R(g,h,k)\in {\mathbb T}$ satisfying equation (2.52). From equation (2.31), we have
$c_R(g,h,k)\in {\mathbb T}$ satisfying equation (2.52). From equation (2.31), we have
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h) u_R(gh,k) \right )\pi_0 =\pi_L\otimes \pi_R \circ \alpha_R\circ \left ( \eta_g^R\beta_g^{RU}\right ) \left ( \eta_h^R\beta_h^{RU}\right ) \left ( \eta_k^R\beta_k^{RU}\right ) \left ( \eta_{ghk}^R\beta_{ghk}^{RU}\right )^{-1} \alpha_R^{-1}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h) u_R(gh,k) \right )\pi_0 =\pi_L\otimes \pi_R \circ \alpha_R\circ \left ( \eta_g^R\beta_g^{RU}\right ) \left ( \eta_h^R\beta_h^{RU}\right ) \left ( \eta_k^R\beta_k^{RU}\right ) \left ( \eta_{ghk}^R\beta_{ghk}^{RU}\right )^{-1} \alpha_R^{-1}. \end{align} $$On the other hand, using Lemma 2.3(i), we have that
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\right )\right ) \pi_0 \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\right )\right ) \pi_0 \end{align} $$is also equal to the right-hand side of equation (2.55). Because ![]() $\pi _0$ is irreducible, this means that there is a number
$\pi _0$ is irreducible, this means that there is a number ![]() $c_R(g,h,k)\in {\mathbb T}$ satisfying equation (2.52).
$c_R(g,h,k)\in {\mathbb T}$ satisfying equation (2.52).
Now let us check that this ![]() $c_R$ is a
$c_R$ is a ![]() $3$-cocycle. For any
$3$-cocycle. For any ![]() $g,h,k,f\in G$, by repeated use of equation (2.52), we get
$g,h,k,f\in G$, by repeated use of equation (2.52), we get
 $$\begin{align*} \mathbb I_{{\mathcal H}_L} & \otimes u_R(g,h) u_R(gh,k)u_R(ghk,f) =\left [ \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h) u_R(gh,k)\right ]\cdot\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(ghk,f)\right ) \end{align*}$$
$$\begin{align*} \mathbb I_{{\mathcal H}_L} & \otimes u_R(g,h) u_R(gh,k)u_R(ghk,f) =\left [ \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h) u_R(gh,k)\right ]\cdot\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(ghk,f)\right ) \end{align*}$$ $$ \begin{align} \nonumber\\[-24pt] & =\left ( c_R(g,h,k) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\right )\right )\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(ghk,f)\right ) \nonumber \\ & =\left ( c_R(g,h,k) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k) \right ) W_g^*\right )\right )\cdot \left [ \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)u_R(ghk,f)\right ] \nonumber\\ & =\left ( c_R(g,h,k) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k) \right ) W_g^*\right )\right ) \nonumber\\ &\quad \cdot \left ( c_R(g,hk,f) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(hk,f)\right ) W_g^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hkf)\right ) \right )\nonumber\\ &= c_R(g,h,k) c_R(g,hk,f) \left ( W_g\left [ \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k) u_R(hk,f)\right ] W_g^*\right )\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hkf)\right ) \nonumber\\ &=c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f) \nonumber\\ &\quad W_g\left ( W_h \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) W_h^*\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,kf)\right )\right ) W_g^*\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hkf)\right )\nonumber\\ &=c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f)\nonumber\\ &\quad \cdot W_gW_h \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) W_h^*W_g^*\cdot \left [\left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,kf)\right ) W_g^*\right ) \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hkf)\right ] \nonumber\\ & =c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f) \overline{c(g,h,kf)} \cdot \left\{W_gW_h \left (\mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right) \left.W_h^*W_g^*\right)\right\} \nonumber\\ &\quad \cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}(g,h)u_{R}(gh,kf) \right ). \end{align} $$
$$ \begin{align} \nonumber\\[-24pt] & =\left ( c_R(g,h,k) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\right )\right )\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(ghk,f)\right ) \nonumber \\ & =\left ( c_R(g,h,k) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k) \right ) W_g^*\right )\right )\cdot \left [ \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)u_R(ghk,f)\right ] \nonumber\\ & =\left ( c_R(g,h,k) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k) \right ) W_g^*\right )\right ) \nonumber\\ &\quad \cdot \left ( c_R(g,hk,f) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(hk,f)\right ) W_g^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hkf)\right ) \right )\nonumber\\ &= c_R(g,h,k) c_R(g,hk,f) \left ( W_g\left [ \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k) u_R(hk,f)\right ] W_g^*\right )\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hkf)\right ) \nonumber\\ &=c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f) \nonumber\\ &\quad W_g\left ( W_h \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) W_h^*\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,kf)\right )\right ) W_g^*\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hkf)\right )\nonumber\\ &=c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f)\nonumber\\ &\quad \cdot W_gW_h \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) W_h^*W_g^*\cdot \left [\left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,kf)\right ) W_g^*\right ) \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hkf)\right ] \nonumber\\ & =c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f) \overline{c(g,h,kf)} \cdot \left\{W_gW_h \left (\mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right) \left.W_h^*W_g^*\right)\right\} \nonumber\\ &\quad \cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}(g,h)u_{R}(gh,kf) \right ). \end{align} $$Here and in the following, we apply equation (2.52) for terms in ![]() $\left [\cdot \right ]$ to get the succeeding equality. Applying Lemma 2.3(iv) to the
$\left [\cdot \right ]$ to get the succeeding equality. Applying Lemma 2.3(iv) to the ![]() $\{\cdot \}$ part of equation (2.57), we obtain
$\{\cdot \}$ part of equation (2.57), we obtain
 $$ \begin{align} \begin{split} \text{equation }(2.57) &=c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f)\overline{c(g,h,kf)}\\ &\quad \left ( \mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h)\right ) W_{gh}\right ) \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}(g,h)u_{R}(gh,kf) \right )\\ &=c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f)\overline{c(g,h,kf)}\\ &\quad \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h)\right ) \left [ W_{gh}\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) W_{gh}^{*} \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}(gh,kf) \right )\right ] \\ &=c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f)\overline{c(g,h,kf)}\overline{c_{R}(gh,k,f)}\\ &\quad \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h)u_R(gh, k)u_{R}(ghk,f)\right ). \end{split} \end{align} $$
$$ \begin{align} \begin{split} \text{equation }(2.57) &=c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f)\overline{c(g,h,kf)}\\ &\quad \left ( \mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h)\right ) W_{gh}\right ) \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}(g,h)u_{R}(gh,kf) \right )\\ &=c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f)\overline{c(g,h,kf)}\\ &\quad \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h)\right ) \left [ W_{gh}\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(k,f)\right ) W_{gh}^{*} \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}(gh,kf) \right )\right ] \\ &=c_R(g,h,k) c_R(g,hk,f) c_R(h,k,f)\overline{c(g,h,kf)}\overline{c_{R}(gh,k,f)}\\ &\quad \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h)u_R(gh, k)u_{R}(ghk,f)\right ). \end{split} \end{align} $$Hence, we obtain
This means ![]() $c_{R}\in Z^{3}(G,{\mathbb T})$.
$c_{R}\in Z^{3}(G,{\mathbb T})$.
2.4 The  $H^{3}(G,{\mathbb T})$-valued index
$H^{3}(G,{\mathbb T})$-valued index
From the previous subsection, we remark the following fact:
Lemma 2.6. For any ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ with
$\omega \in \mathop {\mathcal {SL}}\nolimits $ with ![]() $\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $, there are
$\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $, there are
 $$ \begin{align} \begin{split} \alpha\in \mathop{\mathrm{EAut}}\nolimits(\omega), \quad 0<\theta<\frac\pi 2,\quad (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits\left (\omega,\theta\right ),\quad (\eta_{g}^\sigma )\in {\mathcal T}\left(\theta, (\tilde\beta_g )\right),\quad (\alpha_L,\alpha_R,\Theta)\in{\mathfrak D}^{\theta}_\alpha,\\ ( (W_g), (u_R(g,h)))\in\mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ). \end{split} \end{align} $$
$$ \begin{align} \begin{split} \alpha\in \mathop{\mathrm{EAut}}\nolimits(\omega), \quad 0<\theta<\frac\pi 2,\quad (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits\left (\omega,\theta\right ),\quad (\eta_{g}^\sigma )\in {\mathcal T}\left(\theta, (\tilde\beta_g )\right),\quad (\alpha_L,\alpha_R,\Theta)\in{\mathfrak D}^{\theta}_\alpha,\\ ( (W_g), (u_R(g,h)))\in\mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ). \end{split} \end{align} $$Proof. Because ![]() $\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $, there is some
$\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $, there is some ![]() $0<\theta <\frac \pi 2$ such that
$0<\theta <\frac \pi 2$ such that ![]() $\mathop {\mathrm {IG}}\nolimits (\omega ,\theta )\neq \emptyset $, and hence
$\mathop {\mathrm {IG}}\nolimits (\omega ,\theta )\neq \emptyset $, and hence ![]() $\left (\tilde \beta _g\right )\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta )$ and
$\left (\tilde \beta _g\right )\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta )$ and  $(\eta _g^\sigma )\in {\mathcal T}\left (\theta , \left (\tilde \beta _g\right )\right )$ exist. Because
$(\eta _g^\sigma )\in {\mathcal T}\left (\theta , \left (\tilde \beta _g\right )\right )$ exist. Because ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $, by definition there exists some
$\omega \in \mathop {\mathcal {SL}}\nolimits $, by definition there exists some ![]() $\alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$, and by the definition of
$\alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$, and by the definition of ![]() $\mathop {\mathrm {EAut}}\nolimits (\omega )$, there is some
$\mathop {\mathrm {EAut}}\nolimits (\omega )$, there is some ![]() $(\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $. The existence of
$(\alpha _L,\alpha _R,\Theta )\in {\mathfrak D}^{\theta }_\alpha $. The existence of  $( (W_g), (u_R(g,h)))\in \mathop {\mathrm {IP}}\nolimits ( \omega , \alpha , \theta , (\tilde \beta _g ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta ) )$ is given by Lemma 2.1.
$( (W_g), (u_R(g,h)))\in \mathop {\mathrm {IP}}\nolimits ( \omega , \alpha , \theta , (\tilde \beta _g ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta ) )$ is given by Lemma 2.1.
By Lemma 2.4, for ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ with
$\omega \in \mathop {\mathcal {SL}}\nolimits $ with ![]() $\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $ and each choice of (2.60), we can associate some element of
$\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $ and each choice of (2.60), we can associate some element of ![]() $H^3(G,{\mathbb T})$:
$H^3(G,{\mathbb T})$:
 $$ \begin{align} h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ). \end{align} $$
$$ \begin{align} h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ). \end{align} $$In this subsection, we show that the third cohomology class does not depend on the choice of (2.60):
Theorem 2.7. For any ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ with
$\omega \in \mathop {\mathcal {SL}}\nolimits $ with ![]() $\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $,
$\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $,
 $$\begin{align*}h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ) \end{align*}$$
$$\begin{align*}h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ) \end{align*}$$is independent of the choice of
 $$\begin{align*}\alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta), ( (W_g), (u_\sigma(g,h))). \end{align*}$$
$$\begin{align*}\alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta), ( (W_g), (u_\sigma(g,h))). \end{align*}$$Definition 2.8. Let ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ with
$\omega \in \mathop {\mathcal {SL}}\nolimits $ with ![]() $\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $. We denote the third cohomology given in Theorem 2.7 by
$\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $. We denote the third cohomology given in Theorem 2.7 by
 $$\begin{align*}h(\omega):=h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ). \end{align*}$$
$$\begin{align*}h(\omega):=h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ). \end{align*}$$ First we show the independence from ![]() $( (W_g), (u_\sigma (g,h)))$.
$( (W_g), (u_\sigma (g,h)))$.
Lemma 2.9. Set
 $$ \begin{align} &\omega\in\mathop{\mathcal{SL}}\nolimits, \enspace \alpha\in \mathop{\mathrm{EAut}}\nolimits(\omega), \enspace 0<\theta<\frac\pi 2,\quad (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \quad (\eta_{g}^\sigma )\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ),\quad (\alpha_L,\alpha_R,\Theta)\in {\mathcal D}_{\alpha}^{\theta}, \end{align} $$
$$ \begin{align} &\omega\in\mathop{\mathcal{SL}}\nolimits, \enspace \alpha\in \mathop{\mathrm{EAut}}\nolimits(\omega), \enspace 0<\theta<\frac\pi 2,\quad (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \quad (\eta_{g}^\sigma )\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ),\quad (\alpha_L,\alpha_R,\Theta)\in {\mathcal D}_{\alpha}^{\theta}, \end{align} $$ $$ \begin{align} &( (W_g), (u_\sigma(g,h))), ( (\tilde W_g ), (\tilde u_\sigma(g,h)))\in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$
$$ \begin{align} &( (W_g), (u_\sigma(g,h))), ( (\tilde W_g ), (\tilde u_\sigma(g,h)))\in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$Then we have
 $$ \begin{align} &h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right )\nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad= h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (\tilde W_g ), (\tilde u_\sigma(g,h))) \right ). \end{align} $$
$$ \begin{align} &h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right )\nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad= h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (\tilde W_g ), (\tilde u_\sigma(g,h))) \right ). \end{align} $$Definition 2.10. From this lemma and because there is always ![]() $( (W_g), (u_R(g,h)))$ in
$( (W_g), (u_R(g,h)))$ in  $\mathop {\mathrm {IP}}\nolimits ( \omega , \alpha , \theta , (\tilde \beta _g ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta ) )$ by Lemma 2.1, we may define
$\mathop {\mathrm {IP}}\nolimits ( \omega , \alpha , \theta , (\tilde \beta _g ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta ) )$ by Lemma 2.1, we may define
 $$ \begin{align} h^{(2)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ) := h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ) \end{align} $$
$$ \begin{align} h^{(2)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ) := h^{(1)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ) \end{align} $$for any
 $$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \enspace \alpha\in \mathop{\mathrm{EAut}}\nolimits(\omega), \enspace 0<\theta<\frac\pi 2,\enspace (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \enspace (\eta_{g}^\sigma )\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ),\enspace (\alpha_L,\alpha_R,\Theta)\in {\mathcal D}_{\alpha}^{\theta}, \end{align} $$
$$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \enspace \alpha\in \mathop{\mathrm{EAut}}\nolimits(\omega), \enspace 0<\theta<\frac\pi 2,\enspace (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \enspace (\eta_{g}^\sigma )\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ),\enspace (\alpha_L,\alpha_R,\Theta)\in {\mathcal D}_{\alpha}^{\theta}, \end{align} $$independent of the choice of ![]() $( (W_g), (u_\sigma (g,h)))$.
$( (W_g), (u_\sigma (g,h)))$.
Proof. Because
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)\circ\pi_0 &=\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1} =\mathop{\mathrm{Ad}}\nolimits\left ( \tilde W_g\right )\circ\pi_0, \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)\circ\pi_0 &=\pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1} =\mathop{\mathrm{Ad}}\nolimits\left ( \tilde W_g\right )\circ\pi_0, \end{align} $$ $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_R(g,h)\right )\circ\pi_R &=\pi_R\circ\alpha_R\circ\eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1} \circ\alpha_R^{-1}=\mathop{\mathrm{Ad}}\nolimits\left ( \tilde u_R(g,h)\right )\circ\pi_R \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_R(g,h)\right )\circ\pi_R &=\pi_R\circ\alpha_R\circ\eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1} \circ\alpha_R^{-1}=\mathop{\mathrm{Ad}}\nolimits\left ( \tilde u_R(g,h)\right )\circ\pi_R \end{align} $$and ![]() $\pi _{0}, \pi _{R}$ are irreducible, there are
$\pi _{0}, \pi _{R}$ are irreducible, there are ![]() $b(g),a(g,h)\in {\mathbb T}$,
$b(g),a(g,h)\in {\mathbb T}$, ![]() $g,h\in G$, such that
$g,h\in G$, such that
Set
 $$ \begin{align} c_{R}&:=c_R\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ),\notag\\ \tilde c_R&:=c_{R}\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (\tilde W_g ), (\tilde u_\sigma(g,h))) \right ). \end{align} $$
$$ \begin{align} c_{R}&:=c_R\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ),\notag\\ \tilde c_R&:=c_{R}\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (\tilde W_g ), (\tilde u_\sigma(g,h))) \right ). \end{align} $$Then from the definition of these values and equation (2.69), we have
 $$ \begin{align} a(g,h)a(gh,k)&\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h) u_R(gh,k)\right ) = \mathbb I_{{\mathcal H}_L}\otimes \tilde u_R(g,h) \tilde u_R(gh,k)\notag\\ &=\tilde c_R(g,h,k) \left ( \tilde W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes \tilde u_R(h,k)\right ) \tilde W_g^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes \tilde u_R(g,hk)\right )\notag\\ &=\tilde c_R(g,h,k)a(h,k)a(g,hk) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_{g}^{*}\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\right )\notag\\ &=\tilde c_R(g,h,k)a(h,k)a(g,hk)\overline{c_{R}(g,h,k)} \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h) u_R(gh,k)\right ). \end{align} $$
$$ \begin{align} a(g,h)a(gh,k)&\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h) u_R(gh,k)\right ) = \mathbb I_{{\mathcal H}_L}\otimes \tilde u_R(g,h) \tilde u_R(gh,k)\notag\\ &=\tilde c_R(g,h,k) \left ( \tilde W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes \tilde u_R(h,k)\right ) \tilde W_g^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes \tilde u_R(g,hk)\right )\notag\\ &=\tilde c_R(g,h,k)a(h,k)a(g,hk) \left ( W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_{g}^{*}\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\right )\notag\\ &=\tilde c_R(g,h,k)a(h,k)a(g,hk)\overline{c_{R}(g,h,k)} \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,h) u_R(gh,k)\right ). \end{align} $$Hence we have ![]() $\tilde c_{R}(g,h,k)=c_R(g,h,k)\overline {a(h,k)a(g,hk)}a(g,h)a(gh,k)$, and we get
$\tilde c_{R}(g,h,k)=c_R(g,h,k)\overline {a(h,k)a(g,hk)}a(g,h)a(gh,k)$, and we get ![]() $[c_{R}]_{H^{3}\left (G,{\mathbb T}\right )}=\left [\tilde c_{R}\right ]_{H^{3}\left (G,{\mathbb T}\right )}$, proving the claim.
$[c_{R}]_{H^{3}\left (G,{\mathbb T}\right )}=\left [\tilde c_{R}\right ]_{H^{3}\left (G,{\mathbb T}\right )}$, proving the claim.
Next we show the independence from ![]() $\alpha , (\alpha _L,\alpha _R,\Theta )$:
$\alpha , (\alpha _L,\alpha _R,\Theta )$:
Lemma 2.11. Set
 $$ \begin{align} &\omega\in\mathop{\mathcal{SL}}\nolimits, \quad \alpha_{1},\alpha_{2}\in \mathop{\mathrm{EAut}}\nolimits(\omega), \quad 0<\theta<\frac\pi 2,\ (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \quad (\eta_{g}^\sigma )\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ), \end{align} $$
$$ \begin{align} &\omega\in\mathop{\mathcal{SL}}\nolimits, \quad \alpha_{1},\alpha_{2}\in \mathop{\mathrm{EAut}}\nolimits(\omega), \quad 0<\theta<\frac\pi 2,\ (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \quad (\eta_{g}^\sigma )\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ), \end{align} $$ $$ \begin{align} & \left(\alpha_{L,1},\alpha_{R,1},\Theta_{1}\right)\in {\mathcal D}_{\alpha_{1}}^{\theta},\quad \left(\alpha_{L,2},\alpha_{R,2},\Theta_{2}\right)\in {\mathcal D}_{\alpha_{2}}^{\theta}. \end{align} $$
$$ \begin{align} & \left(\alpha_{L,1},\alpha_{R,1},\Theta_{1}\right)\in {\mathcal D}_{\alpha_{1}}^{\theta},\quad \left(\alpha_{L,2},\alpha_{R,2},\Theta_{2}\right)\in {\mathcal D}_{\alpha_{2}}^{\theta}. \end{align} $$Then we have
 $$ \begin{align} h^{(2)} \left ( \omega, \alpha_{1} , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,1},\alpha_{R,1},\Theta_{1}\right) \right ) = h^{(2)} \left ( \omega, \alpha_{2} , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,2},\alpha_{R,2},\Theta_{2}\right) \right ). \end{align} $$
$$ \begin{align} h^{(2)} \left ( \omega, \alpha_{1} , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,1},\alpha_{R,1},\Theta_{1}\right) \right ) = h^{(2)} \left ( \omega, \alpha_{2} , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,2},\alpha_{R,2},\Theta_{2}\right) \right ). \end{align} $$Definition 2.12. From this lemma and because there are always ![]() $ \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ and
$ \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ and ![]() $(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta }$ for
$(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta }$ for ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ and
$\omega \in \mathop {\mathcal {SL}}\nolimits $ and ![]() $0<\theta <\frac \pi 2$ by the definition, we may define
$0<\theta <\frac \pi 2$ by the definition, we may define
 $$ \begin{align} h^{(3)} \left ( \omega, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ) \right ) := h^{(2)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_{L},\alpha_{R},\Theta) \right ) \end{align} $$
$$ \begin{align} h^{(3)} \left ( \omega, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ) \right ) := h^{(2)} \left ( \omega, \alpha , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_{L},\alpha_{R},\Theta) \right ) \end{align} $$for any
 $$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta<\frac\pi 2,\quad (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \quad (\eta_{g}^\sigma )\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ), \end{align} $$
$$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta<\frac\pi 2,\quad (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \quad (\eta_{g}^\sigma )\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ), \end{align} $$independent of the choice of ![]() $\alpha , (\alpha _L,\alpha _R,\Theta )$.
$\alpha , (\alpha _L,\alpha _R,\Theta )$.
Proof. By Lemma 2.1, there are
 $$ \begin{align} \left ( \left(W_{g,1}\right), \left(u_{\sigma,1}(g,h)\right)\right ) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha_{1}, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,1},\alpha_{R,1},\Theta_1\right) \right ). \end{align} $$
$$ \begin{align} \left ( \left(W_{g,1}\right), \left(u_{\sigma,1}(g,h)\right)\right ) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha_{1}, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,1},\alpha_{R,1},\Theta_1\right) \right ). \end{align} $$For each ![]() $i=1,2$, we have
$i=1,2$, we have ![]() $\Theta _{i}\in \mathop {\mathrm {Aut}}\nolimits {\mathcal A}_{C_{\theta }^{c}}$ and
$\Theta _{i}\in \mathop {\mathrm {Aut}}\nolimits {\mathcal A}_{C_{\theta }^{c}}$ and
setting
Because ![]() $\omega _{0}\circ \alpha _{1}=\omega =\omega _{0}\circ \alpha _{2}$, we have
$\omega _{0}\circ \alpha _{1}=\omega =\omega _{0}\circ \alpha _{2}$, we have  $\omega _{0}\circ \alpha _{2}\circ \alpha _{1}^{-1}=\omega _{0}$. Therefore, there is a unitary
$\omega _{0}\circ \alpha _{2}\circ \alpha _{1}^{-1}=\omega _{0}$. Therefore, there is a unitary ![]() $\tilde V$ on
$\tilde V$ on ![]() ${\mathcal H}_{0}$ such that
${\mathcal H}_{0}$ such that  $ \pi _{0}\circ \alpha _{2}\circ \alpha _{1}^{-1}=\mathop {\mathrm {Ad}}\nolimits \left ( \tilde V\right )\circ \pi _{0} $. Substituting equation (2.78) into this, we see that there is a unitary V on
$ \pi _{0}\circ \alpha _{2}\circ \alpha _{1}^{-1}=\mathop {\mathrm {Ad}}\nolimits \left ( \tilde V\right )\circ \pi _{0} $. Substituting equation (2.78) into this, we see that there is a unitary V on ![]() ${\mathcal H}_{0}$ satisfying
${\mathcal H}_{0}$ satisfying
From this, we obtain
 $$ \begin{align} \begin{split} &\mathop{\mathrm{Ad}}\nolimits\left ( V W_{g,1} V^{*}\right )\circ\pi_{0} \\ &\quad =\mathop{\mathrm{Ad}}\nolimits\left ( V W_{g,1}\right ) \pi_{0}\circ \alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}\\ &\quad =\mathop{\mathrm{Ad}}\nolimits\left ( V\right )\circ \pi_{0} \circ\alpha_{0,1}\circ\Theta_{1}\circ\eta_g\beta_g^U\circ\Theta_{1}^{-1}\circ\alpha_{0,1}^{-1} \circ \alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}\\ &\quad =\pi_{0}\circ\alpha_{0, 2}\circ\Theta_{2}\circ \Theta_{1}^{-1}\circ \alpha_{0, 1}^{-1} \circ\alpha_{0,1}\circ\Theta_{1}\circ\eta_g\beta_g^U\circ\Theta_{1}^{-1}\circ\alpha_{0,1}^{-1} \circ \alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}\\ &\quad =\pi_{0}\circ\alpha_{0, 2}\circ\Theta_{2} \circ\eta_g\beta_g^U \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\mathop{\mathrm{Ad}}\nolimits\left ( V W_{g,1} V^{*}\right )\circ\pi_{0} \\ &\quad =\mathop{\mathrm{Ad}}\nolimits\left ( V W_{g,1}\right ) \pi_{0}\circ \alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}\\ &\quad =\mathop{\mathrm{Ad}}\nolimits\left ( V\right )\circ \pi_{0} \circ\alpha_{0,1}\circ\Theta_{1}\circ\eta_g\beta_g^U\circ\Theta_{1}^{-1}\circ\alpha_{0,1}^{-1} \circ \alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}\\ &\quad =\pi_{0}\circ\alpha_{0, 2}\circ\Theta_{2}\circ \Theta_{1}^{-1}\circ \alpha_{0, 1}^{-1} \circ\alpha_{0,1}\circ\Theta_{1}\circ\eta_g\beta_g^U\circ\Theta_{1}^{-1}\circ\alpha_{0,1}^{-1} \circ \alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}\\ &\quad =\pi_{0}\circ\alpha_{0, 2}\circ\Theta_{2} \circ\eta_g\beta_g^U \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}, \end{split} \end{align} $$for all ![]() $g\in G$. Furthermore, we have
$g\in G$. Furthermore, we have
 $$ \begin{align} &\mathop{\mathrm{Ad}}\nolimits\left ( V\left (\mathbb I_{{\mathcal H}_{L}}\otimes u_{R,1}(g,h)\right ) V^{*} \right )\circ\pi_{0} = \mathop{\mathrm{Ad}}\nolimits\left ( V\left (\mathbb I_{{\mathcal H}_{L}}\otimes u_{R,1}(g,h)\right ) \right )\circ \pi_{0}\circ \alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}\notag\\ &=\mathop{\mathrm{Ad}}\nolimits\left ( V\right )\circ \pi_{0}\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_{L}}}\otimes \alpha_{R,1} \eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\alpha_{R,1}^{-1}\right ) \alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}\notag\\ &= \pi_{0}\circ \alpha_{0, 2}\circ\Theta_{2}\circ \Theta_{1}^{-1} \circ \alpha_{0, 1}^{-1}\left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_{L}}}\otimes \alpha_{R,1} \eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\alpha_{R,1}^{-1}\right ) \circ\alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1} \notag\\ &= \pi_{0}\circ \alpha_{0, 2}\circ\Theta_{2}\circ \Theta_{1}^{-1} \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_{L}}}\otimes \eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\right ) \circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}. \end{align} $$
$$ \begin{align} &\mathop{\mathrm{Ad}}\nolimits\left ( V\left (\mathbb I_{{\mathcal H}_{L}}\otimes u_{R,1}(g,h)\right ) V^{*} \right )\circ\pi_{0} = \mathop{\mathrm{Ad}}\nolimits\left ( V\left (\mathbb I_{{\mathcal H}_{L}}\otimes u_{R,1}(g,h)\right ) \right )\circ \pi_{0}\circ \alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}\notag\\ &=\mathop{\mathrm{Ad}}\nolimits\left ( V\right )\circ \pi_{0}\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_{L}}}\otimes \alpha_{R,1} \eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\alpha_{R,1}^{-1}\right ) \alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}\notag\\ &= \pi_{0}\circ \alpha_{0, 2}\circ\Theta_{2}\circ \Theta_{1}^{-1} \circ \alpha_{0, 1}^{-1}\left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_{L}}}\otimes \alpha_{R,1} \eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\alpha_{R,1}^{-1}\right ) \circ\alpha_{0, 1}\circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1} \notag\\ &= \pi_{0}\circ \alpha_{0, 2}\circ\Theta_{2}\circ \Theta_{1}^{-1} \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_{L}}}\otimes \eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\right ) \circ\Theta_{1} \circ \Theta_{2}^{-1}\circ \alpha_{0, 2}^{-1}. \end{align} $$Now, because  $\eta _g^R\beta _g^{R U} \eta _h^R\left (\beta _g^{R U}\right )^{-1}\left ( \eta _{gh}^R\right )^{-1}$ is an automorphism on
$\eta _g^R\beta _g^{R U} \eta _h^R\left (\beta _g^{R U}\right )^{-1}\left ( \eta _{gh}^R\right )^{-1}$ is an automorphism on ![]() ${\mathcal A}_{C_{\theta }}$ and
${\mathcal A}_{C_{\theta }}$ and  $\Theta _{2}\circ \Theta _{1}^{-1}$ is an automorphism on
$\Theta _{2}\circ \Theta _{1}^{-1}$ is an automorphism on ![]() ${\mathcal A}_{C_{\theta }^{c}}$, they commute. Therefore, we have
${\mathcal A}_{C_{\theta }^{c}}$, they commute. Therefore, we have
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits&\left ( V\left (\mathbb I_{{\mathcal H}_{L}}\otimes u_{R,1}(g,h)\right ) V^{*} \right )\circ\pi_{0}\notag\\ &= \text{equation }(2.83)= \pi_{0}\circ \alpha_{0, 2} \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_{L}}}\otimes \eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\right ) \circ \alpha_{0, 2}^{-1}\notag\\ &= \pi_{L}\otimes \left ( \pi_{R}\circ \alpha_{R,2}\eta_{g}^{R}\beta_{g}^{RU} \eta_{h}^{R}\left ( \beta_{g}^{RU}\right )^{-1} \left ( \eta_{gh}^{R}\right )^{-1}\left ( \alpha_{R,2}\right )^{-1}\right ). \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits&\left ( V\left (\mathbb I_{{\mathcal H}_{L}}\otimes u_{R,1}(g,h)\right ) V^{*} \right )\circ\pi_{0}\notag\\ &= \text{equation }(2.83)= \pi_{0}\circ \alpha_{0, 2} \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_{L}}}\otimes \eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\right ) \circ \alpha_{0, 2}^{-1}\notag\\ &= \pi_{L}\otimes \left ( \pi_{R}\circ \alpha_{R,2}\eta_{g}^{R}\beta_{g}^{RU} \eta_{h}^{R}\left ( \beta_{g}^{RU}\right )^{-1} \left ( \eta_{gh}^{R}\right )^{-1}\left ( \alpha_{R,2}\right )^{-1}\right ). \end{align} $$From this equality and the fact that ![]() $\pi _{L}$ is irreducible, we see that
$\pi _{L}$ is irreducible, we see that ![]() $V\left (\mathbb I_{{\mathcal H}_{L}}\otimes u_{R,1}(g,h)\right ) V^{*}$ is of the form
$V\left (\mathbb I_{{\mathcal H}_{L}}\otimes u_{R,1}(g,h)\right ) V^{*}$ is of the form ![]() $\mathbb I_{{\mathcal H}_{L}}\otimes u_{R,2}(g,h)$ with some unitary
$\mathbb I_{{\mathcal H}_{L}}\otimes u_{R,2}(g,h)$ with some unitary ![]() $u_{R,2}(g,h)$ on
$u_{R,2}(g,h)$ on ![]() ${\mathcal H}_{R}$. This
${\mathcal H}_{R}$. This ![]() $u_{R,2}(g,h)$ satisfies
$u_{R,2}(g,h)$ satisfies
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_{R,2}(g,h)\right )\circ\pi_{R} =\pi_{R}\circ \alpha_{R,2}\eta_{g}^{R}\beta_{g}^{RU} \eta_{h}^{R}\left ( \beta_{g}^{RU}\right )^{-1} \left ( \eta_{gh}^{R}\right )^{-1}\left ( \alpha_{R,2}\right )^{-1}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_{R,2}(g,h)\right )\circ\pi_{R} =\pi_{R}\circ \alpha_{R,2}\eta_{g}^{R}\beta_{g}^{RU} \eta_{h}^{R}\left ( \beta_{g}^{RU}\right )^{-1} \left ( \eta_{gh}^{R}\right )^{-1}\left ( \alpha_{R,2}\right )^{-1}. \end{align} $$Analogously, we obtain a unitary ![]() $u_{L,2}(g,h)$ on
$u_{L,2}(g,h)$ on ![]() ${\mathcal H}_{L}$ such that
${\mathcal H}_{L}$ such that
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_{L,2}(g,h)\right )\circ\pi_{L} &=\pi_{L}\circ \alpha_{L,2}\eta_{g}^{L}\beta_{g}^{LU} \eta_{h}^{L}\left ( \beta_{g}^{LU}\right )^{-1} \left ( \eta_{gh}^{L}\right )^{-1}\left ( \alpha_{L,2}\right )^{-1}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( u_{L,2}(g,h)\right )\circ\pi_{L} &=\pi_{L}\circ \alpha_{L,2}\eta_{g}^{L}\beta_{g}^{LU} \eta_{h}^{L}\left ( \beta_{g}^{LU}\right )^{-1} \left ( \eta_{gh}^{L}\right )^{-1}\left ( \alpha_{L,2}\right )^{-1}. \end{align} $$From equations (2.81), (2.84) and (2.85), we see that
 $$ \begin{align} \left ( \left ( V W_{g,1} V^{*}\right ) , \left ( u_{\sigma,2}(g,h)\right )\right )\in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha_{2}, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,2},\alpha_{R,2},\Theta\right) \right ). \end{align} $$
$$ \begin{align} \left ( \left ( V W_{g,1} V^{*}\right ) , \left ( u_{\sigma,2}(g,h)\right )\right )\in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha_{2}, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,2},\alpha_{R,2},\Theta\right) \right ). \end{align} $$Set
 $$ \begin{align} c_{R,1}&:=c_R\left ( \omega, \alpha_{1}, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,1},\alpha_{R,1},\Theta_{1}\right),\left ( \left(W_{g,1}\right), \left(u_{\sigma,1}(g,h)\right)\right ) \right ),\notag\\ c_{R,2}&:=c_{R}\left ( \omega, \alpha_{2}, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,2},\alpha_{R,2},\Theta_{2}\right), \left ( V W_{g,1} V^{*}\right ) , \left ( u_{\sigma,2}(g,h)\right ) \right ). \end{align} $$
$$ \begin{align} c_{R,1}&:=c_R\left ( \omega, \alpha_{1}, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,1},\alpha_{R,1},\Theta_{1}\right),\left ( \left(W_{g,1}\right), \left(u_{\sigma,1}(g,h)\right)\right ) \right ),\notag\\ c_{R,2}&:=c_{R}\left ( \omega, \alpha_{2}, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), \left(\alpha_{L,2},\alpha_{R,2},\Theta_{2}\right), \left ( V W_{g,1} V^{*}\right ) , \left ( u_{\sigma,2}(g,h)\right ) \right ). \end{align} $$It suffices to show that ![]() $c_{R,1}=c_{R,2}$. This can be checked directly as follows:
$c_{R,1}=c_{R,2}$. This can be checked directly as follows:
 $$ \begin{align} V& \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,1}(g,h) u_{R,1}(gh,k) \right ) V^{*} = \mathbb I_{{\mathcal H}_L}\otimes u_{R,2}(g,h) u_{R,2}(gh,k)\notag\\ &=c_{R,2}(g,h,k) \left ( V W_{g,1}V^{*}\left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,2}(h,k)\right ) VW_{g,1}^*V^{*}\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,2}(g,hk)\right )\notag\\ &=c_{R,2}(g,h,k)V \left ( W_{g,1}\left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,1}(h,k)\right ) W_{g,1}^{*}\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,1}(g,hk)\right ) V^{*}\notag\\ &= c_{R,2}(g,h,k)\overline{c_{R,1}(g,h,k)}V \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,1}(g,h) u_{R,1}(gh,k) \right ) V^{*}. \end{align} $$
$$ \begin{align} V& \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,1}(g,h) u_{R,1}(gh,k) \right ) V^{*} = \mathbb I_{{\mathcal H}_L}\otimes u_{R,2}(g,h) u_{R,2}(gh,k)\notag\\ &=c_{R,2}(g,h,k) \left ( V W_{g,1}V^{*}\left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,2}(h,k)\right ) VW_{g,1}^*V^{*}\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,2}(g,hk)\right )\notag\\ &=c_{R,2}(g,h,k)V \left ( W_{g,1}\left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,1}(h,k)\right ) W_{g,1}^{*}\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,1}(g,hk)\right ) V^{*}\notag\\ &= c_{R,2}(g,h,k)\overline{c_{R,1}(g,h,k)}V \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R,1}(g,h) u_{R,1}(gh,k) \right ) V^{*}. \end{align} $$Lemma 2.13. Set
 $$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta<\frac\pi 2,\quad (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \quad (\eta_{g}^\sigma ), \left(\tilde \eta_{g}^\sigma\right)\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ). \end{align} $$
$$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta<\frac\pi 2,\quad (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \quad (\eta_{g}^\sigma ), \left(\tilde \eta_{g}^\sigma\right)\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ). \end{align} $$Then we have
 $$ \begin{align} h^{(3)} \left ( \omega , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ) \right ) = h^{(3)} \left ( \omega, \theta, (\tilde\beta_g ), \left(\tilde \eta_{g}^\sigma\right) \right ). \end{align} $$
$$ \begin{align} h^{(3)} \left ( \omega , \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ) \right ) = h^{(3)} \left ( \omega, \theta, (\tilde\beta_g ), \left(\tilde \eta_{g}^\sigma\right) \right ). \end{align} $$Definition 2.14. From this lemma and the definition of ![]() $ \mathop {\mathrm {IG}}\nolimits (\omega ,\theta )$, we may define
$ \mathop {\mathrm {IG}}\nolimits (\omega ,\theta )$, we may define
 $$ \begin{align} h^{(4)} \left ( \omega, \theta, (\tilde\beta_g ) \right ) := h^{(3)} \left ( \omega, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ) \right ) \end{align} $$
$$ \begin{align} h^{(4)} \left ( \omega, \theta, (\tilde\beta_g ) \right ) := h^{(3)} \left ( \omega, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ) \right ) \end{align} $$for any
 $$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta<\frac\pi 2,\quad (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \quad (\eta_{g}^\sigma )\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ), \end{align} $$
$$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta<\frac\pi 2,\quad (\tilde\beta_g )\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta), \quad (\eta_{g}^\sigma )\in {\mathcal T}\left (\theta, (\tilde\beta_g )\right ), \end{align} $$independent of the choice of ![]() $(\eta _{g}^\sigma )$.
$(\eta _{g}^\sigma )$.
Proof. There are ![]() $ \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ and
$ \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ and ![]() $(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta }$ for
$(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta }$ for ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ by the definition. We set
$\omega \in \mathop {\mathcal {SL}}\nolimits $ by the definition. We set ![]() $\alpha _0:=\alpha _L\otimes \alpha _R$ and
$\alpha _0:=\alpha _L\otimes \alpha _R$ and  $\eta _g:=\eta _g^L\otimes \eta _g^R$,
$\eta _g:=\eta _g^L\otimes \eta _g^R$,  $\tilde \eta _g:=\tilde \eta _g^L\otimes \tilde \eta _g^R$. By Lemma 2.1, there is some
$\tilde \eta _g:=\tilde \eta _g^L\otimes \tilde \eta _g^R$. By Lemma 2.1, there is some
 $$ \begin{align} \left ( \left(W_{g}\right), (u_{\sigma}(g,h))\right ) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_{L},\alpha_{R},\Theta) \right ). \end{align} $$
$$ \begin{align} \left ( \left(W_{g}\right), (u_{\sigma}(g,h))\right ) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_{L},\alpha_{R},\Theta) \right ). \end{align} $$ Because  $ (\eta _{g}^\sigma ), \left (\tilde \eta _{g}^\sigma \right )\in {\mathcal T}\left (\theta , \left (\tilde \beta _g\right )\right )$, we have
$ (\eta _{g}^\sigma ), \left (\tilde \eta _{g}^\sigma \right )\in {\mathcal T}\left (\theta , \left (\tilde \beta _g\right )\right )$, we have
 $$ \begin{align} \tilde\beta_g=({\textrm{{inner}}})\circ\left ( \eta_g^L\otimes\eta_g^R\right )\circ\beta_g^U =({\textrm{{inner}}}) \circ\left (\tilde \eta_g^L\otimes\tilde \eta_g^R\right )\circ\beta_g^U. \end{align} $$
$$ \begin{align} \tilde\beta_g=({\textrm{{inner}}})\circ\left ( \eta_g^L\otimes\eta_g^R\right )\circ\beta_g^U =({\textrm{{inner}}}) \circ\left (\tilde \eta_g^L\otimes\tilde \eta_g^R\right )\circ\beta_g^U. \end{align} $$From this, we obtain
 $$ \begin{align} \tilde \eta_g^L\circ\left (\eta_g^L\right )^{-1}\otimes\tilde \eta_g^R\circ\left (\eta_g^R\right )^{-1} =({\textrm{{inner}}}), \end{align} $$
$$ \begin{align} \tilde \eta_g^L\circ\left (\eta_g^L\right )^{-1}\otimes\tilde \eta_g^R\circ\left (\eta_g^R\right )^{-1} =({\textrm{{inner}}}), \end{align} $$hence there are unitaries ![]() $v_g^\sigma \in {\mathcal A}_{H_\sigma }$,
$v_g^\sigma \in {\mathcal A}_{H_\sigma }$, ![]() $\sigma =L,R$, such that
$\sigma =L,R$, such that
 $$ \begin{align} \tilde \eta_g^\sigma\circ\left (\eta_g^\sigma\right )^{-1} =\mathop{\mathrm{Ad}}\nolimits\left ( v_g^\sigma\right ). \end{align} $$
$$ \begin{align} \tilde \eta_g^\sigma\circ\left (\eta_g^\sigma\right )^{-1} =\mathop{\mathrm{Ad}}\nolimits\left ( v_g^\sigma\right ). \end{align} $$Because ![]() $\tilde \eta _g^\sigma , \eta _g^\sigma $ are automorphisms on
$\tilde \eta _g^\sigma , \eta _g^\sigma $ are automorphisms on ![]() ${\mathcal A}_{C_\theta ,\sigma }$,
${\mathcal A}_{C_\theta ,\sigma }$, ![]() $v_g^\sigma $ belongs to
$v_g^\sigma $ belongs to ![]() ${\mathcal A}_{C_\theta ,\sigma }$. (See Lemma B.1.) Setting
${\mathcal A}_{C_\theta ,\sigma }$. (See Lemma B.1.) Setting  $v_g:=v_g^L\otimes v_g^R$, we obtain
$v_g:=v_g^L\otimes v_g^R$, we obtain ![]() $\tilde \eta _g=\mathop {\mathrm {Ad}}\nolimits \left ( v_g\right )\circ \eta _g$.
$\tilde \eta _g=\mathop {\mathrm {Ad}}\nolimits \left ( v_g\right )\circ \eta _g$.
Set
 $$ \begin{align} \tilde W_g&:=\left ( \left ( \pi_L\alpha_L\left ( v_g^L\right )\right ) \otimes \left ( \pi_R\alpha_R\left ( v_g^R\right )\right )\right ) W_g, \end{align} $$
$$ \begin{align} \tilde W_g&:=\left ( \left ( \pi_L\alpha_L\left ( v_g^L\right )\right ) \otimes \left ( \pi_R\alpha_R\left ( v_g^R\right )\right )\right ) W_g, \end{align} $$ $$ \begin{align} \tilde u_\sigma(g,h) &:= \pi_\sigma\left ( \alpha_\sigma\left ( v_g^\sigma \cdot \left ( \eta_g^\sigma\beta_g^{\sigma U}\right )\left ( v_h^\sigma\right )\right ) \right )\cdot u_\sigma\left ( g,h\right )\cdot \pi_\sigma\left (\alpha_\sigma\left ( \left ( v_{gh}^{\sigma}\right )^*\right )\right ), \end{align} $$
$$ \begin{align} \tilde u_\sigma(g,h) &:= \pi_\sigma\left ( \alpha_\sigma\left ( v_g^\sigma \cdot \left ( \eta_g^\sigma\beta_g^{\sigma U}\right )\left ( v_h^\sigma\right )\right ) \right )\cdot u_\sigma\left ( g,h\right )\cdot \pi_\sigma\left (\alpha_\sigma\left ( \left ( v_{gh}^{\sigma}\right )^*\right )\right ), \end{align} $$for each ![]() $g,h\in G$ and
$g,h\in G$ and ![]() $\sigma =L,R$. We claim that
$\sigma =L,R$. We claim that
 $$ \begin{align} \left (\left ( \tilde W_g\right ), \left ( \tilde u_\sigma(g,h)\right ) \right ) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, (\tilde\beta_g ), \left(\tilde \eta_{g}^\sigma\right), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$
$$ \begin{align} \left (\left ( \tilde W_g\right ), \left ( \tilde u_\sigma(g,h)\right ) \right ) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, (\tilde\beta_g ), \left(\tilde \eta_{g}^\sigma\right), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$First, we have
 $$ \begin{align} \begin{split} \pi_0&\circ\alpha_0\circ\Theta\circ\tilde \eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1} =\pi_0\circ\alpha_0\circ\Theta\circ \mathop{\mathrm{Ad}}\nolimits\left ( v_g\right )\circ\eta_g \beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1}\\ &=\pi_0\circ\alpha_0\circ\mathop{\mathrm{Ad}}\nolimits\left ( v_g\right )\circ\Theta \circ\eta_g \beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1}\\ &= \mathop{\mathrm{Ad}}\nolimits\left ( \left ( \pi_L\alpha_L\left ( v_g^L\right )\right ) \otimes \left ( \pi_R\alpha_R\left ( v_g^R\right )\right ) \right ) \pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1} = \mathop{\mathrm{Ad}}\nolimits\left ( \tilde W_g\right )\circ\pi_0. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \pi_0&\circ\alpha_0\circ\Theta\circ\tilde \eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1} =\pi_0\circ\alpha_0\circ\Theta\circ \mathop{\mathrm{Ad}}\nolimits\left ( v_g\right )\circ\eta_g \beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1}\\ &=\pi_0\circ\alpha_0\circ\mathop{\mathrm{Ad}}\nolimits\left ( v_g\right )\circ\Theta \circ\eta_g \beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1}\\ &= \mathop{\mathrm{Ad}}\nolimits\left ( \left ( \pi_L\alpha_L\left ( v_g^L\right )\right ) \otimes \left ( \pi_R\alpha_R\left ( v_g^R\right )\right ) \right ) \pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1} = \mathop{\mathrm{Ad}}\nolimits\left ( \tilde W_g\right )\circ\pi_0. \end{split} \end{align} $$For the first equality, we substituted ![]() $\tilde \eta _g=\mathop {\mathrm {Ad}}\nolimits \left ( v_g\right )\circ \eta _g$, and for the second equality, we used the fact that
$\tilde \eta _g=\mathop {\mathrm {Ad}}\nolimits \left ( v_g\right )\circ \eta _g$, and for the second equality, we used the fact that ![]() $v_g^\sigma $ belongs to
$v_g^\sigma $ belongs to ![]() ${\mathcal A}_{C_\theta ,\sigma }$, while
${\mathcal A}_{C_\theta ,\sigma }$, while ![]() $\Theta $ is an automorphism on
$\Theta $ is an automorphism on ![]() ${\mathcal A}_{\left ( C_\theta \right )^c,\sigma }$. The last equality follows from the definition of
${\mathcal A}_{\left ( C_\theta \right )^c,\sigma }$. The last equality follows from the definition of ![]() $W_g$. On the other hand, we have
$W_g$. On the other hand, we have
 $$ \begin{align} &\pi_{\sigma}\circ\alpha_{\sigma}\circ{\tilde\eta}_g^{\sigma}\beta_g^{{\sigma} U} {\tilde\eta}_h^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}\left ( {\tilde\eta}_{gh}^{\sigma}\right )^{-1} \circ\alpha_{\sigma}^{-1}\notag\\ &= \pi_{\sigma}\circ\alpha_{\sigma}\circ\mathop{\mathrm{Ad}}\nolimits\left ( v_g^\sigma\right )\circ\eta_g^{\sigma}\beta_g^{{\sigma} U} \mathop{\mathrm{Ad}}\nolimits\left ( v_h^\sigma\right )\circ\eta_h^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}( \eta_{gh}^{\sigma})^{-1} \mathop{\mathrm{Ad}}\nolimits\left ( {v_{gh}^\sigma}^*\right ) \circ\alpha_{\sigma}^{-1}\notag\\ &= \mathop{\mathrm{Ad}}\nolimits\left ( \pi_{\sigma}\circ\alpha_{\sigma} \left ( \left ( v_g^\sigma\right ) \eta_g^{\sigma}\beta_g^{{\sigma} U}\left ( v_h^\sigma\right )\right ) \right ) \pi_{\sigma}\circ\alpha_{\sigma}\eta_g^{\sigma}\beta_g^{{\sigma} U} \eta_h^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}( \eta_{gh}^{\sigma})^{-1} \circ\alpha_{\sigma}^{-1}\circ \mathop{\mathrm{Ad}}\nolimits\left (\alpha_\sigma\left ( {v_{gh}^\sigma}^*\right )\right )\notag\\ &= \mathop{\mathrm{Ad}}\nolimits\left ( \pi_{\sigma}\circ\alpha_{\sigma} \left ( \left ( v_g^\sigma\right ) \eta_g^{\sigma}\beta_g^{{\sigma} U}\left ( v_h^\sigma\right )\right )\right ) \circ \mathop{\mathrm{Ad}}\nolimits\left ( u_\sigma(g,h)\right ) \pi_\sigma\circ \mathop{\mathrm{Ad}}\nolimits\left (\alpha_\sigma\left ( {v_{gh}^\sigma}^*\right )\right ) = \mathop{\mathrm{Ad}}\nolimits\left ( \tilde u_{\sigma}(g,h)\right )\circ\pi_{\sigma}, \end{align} $$
$$ \begin{align} &\pi_{\sigma}\circ\alpha_{\sigma}\circ{\tilde\eta}_g^{\sigma}\beta_g^{{\sigma} U} {\tilde\eta}_h^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}\left ( {\tilde\eta}_{gh}^{\sigma}\right )^{-1} \circ\alpha_{\sigma}^{-1}\notag\\ &= \pi_{\sigma}\circ\alpha_{\sigma}\circ\mathop{\mathrm{Ad}}\nolimits\left ( v_g^\sigma\right )\circ\eta_g^{\sigma}\beta_g^{{\sigma} U} \mathop{\mathrm{Ad}}\nolimits\left ( v_h^\sigma\right )\circ\eta_h^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}( \eta_{gh}^{\sigma})^{-1} \mathop{\mathrm{Ad}}\nolimits\left ( {v_{gh}^\sigma}^*\right ) \circ\alpha_{\sigma}^{-1}\notag\\ &= \mathop{\mathrm{Ad}}\nolimits\left ( \pi_{\sigma}\circ\alpha_{\sigma} \left ( \left ( v_g^\sigma\right ) \eta_g^{\sigma}\beta_g^{{\sigma} U}\left ( v_h^\sigma\right )\right ) \right ) \pi_{\sigma}\circ\alpha_{\sigma}\eta_g^{\sigma}\beta_g^{{\sigma} U} \eta_h^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}( \eta_{gh}^{\sigma})^{-1} \circ\alpha_{\sigma}^{-1}\circ \mathop{\mathrm{Ad}}\nolimits\left (\alpha_\sigma\left ( {v_{gh}^\sigma}^*\right )\right )\notag\\ &= \mathop{\mathrm{Ad}}\nolimits\left ( \pi_{\sigma}\circ\alpha_{\sigma} \left ( \left ( v_g^\sigma\right ) \eta_g^{\sigma}\beta_g^{{\sigma} U}\left ( v_h^\sigma\right )\right )\right ) \circ \mathop{\mathrm{Ad}}\nolimits\left ( u_\sigma(g,h)\right ) \pi_\sigma\circ \mathop{\mathrm{Ad}}\nolimits\left (\alpha_\sigma\left ( {v_{gh}^\sigma}^*\right )\right ) = \mathop{\mathrm{Ad}}\nolimits\left ( \tilde u_{\sigma}(g,h)\right )\circ\pi_{\sigma}, \end{align} $$for all ![]() $g,h\in G$. For the first equality, we substituted
$g,h\in G$. For the first equality, we substituted ![]() $\tilde \eta _g=\mathop {\mathrm {Ad}}\nolimits \left ( v_g\right )\circ \eta _g$. The third equality is the definition of
$\tilde \eta _g=\mathop {\mathrm {Ad}}\nolimits \left ( v_g\right )\circ \eta _g$. The third equality is the definition of ![]() $u(g,h)$. Hence we have proven formula (2.100).
$u(g,h)$. Hence we have proven formula (2.100).
Set
 $$ \begin{align} c_{R}&:=c_R\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ),\notag\\ \tilde c_R&:=c_{R}\left ( \omega, \alpha, \theta, (\tilde\beta_g ), \left(\tilde \eta_{g}^\sigma\right), (\alpha_L,\alpha_R,\Theta),( (\tilde W_g ), (\tilde u_\sigma(g,h))) \right ). \end{align} $$
$$ \begin{align} c_{R}&:=c_R\left ( \omega, \alpha, \theta, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta),( (W_g), (u_\sigma(g,h))) \right ),\notag\\ \tilde c_R&:=c_{R}\left ( \omega, \alpha, \theta, (\tilde\beta_g ), \left(\tilde \eta_{g}^\sigma\right), (\alpha_L,\alpha_R,\Theta),( (\tilde W_g ), (\tilde u_\sigma(g,h))) \right ). \end{align} $$In order to show the statement of the lemma, it suffices to show that ![]() $c_R=\tilde c_R$. Substituting the definition of
$c_R=\tilde c_R$. Substituting the definition of ![]() $\tilde u_R$, we obtain
$\tilde u_R$, we obtain
 $$ \begin{align} \begin{split} &\tilde u_R(g,h) \tilde u_R(gh,k)\\ &\quad = \pi_R\left ( \alpha_R\left ( v_g^R \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\right ) \right )\cdot u_R\left ( g,h\right )\cdot \pi_R\left (\alpha_R\left ( \left ( v_{gh}^{R}\right )^*\right )\right )\\ &\pi_R\left ( \alpha_R\left ( v_{gh}^R \left ( \eta_{gh}^R\beta_{gh}^{R U}\right )( v_k^R)\right ) \right )\cdot u_R\left ( gh,k\right )\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right ) \\ &\quad = \pi_R\left ( \alpha_R\left ( v_g^R \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\right ) \right ) \\ &\qquad \cdot \left [ u_R\left ( g,h\right )\cdot \pi_R\left ( \alpha_R\left ( \left ( \eta_{gh}^R\beta_{gh}^{R U}\right )( v_k^R)\right ) \right ) \right ] u_R\left ( gh,k\right ) \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right ) \\ &\quad = \pi_R\left ( \alpha_R\left ( v_g^R \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\right ) \right )\\ &\quad \cdot \left [ \mathop{\mathrm{Ad}}\nolimits\left ( u_R\left ( g,h\right )\right )\left ( \pi_R\left ( \alpha_R\left ( \left ( \eta_{gh}^R\beta_{gh}^{R U}\right )( v_k^R)\right ) \right )\right ) \cdot u_R\left ( g,h\right ) \right ] u_R\left ( gh,k\right )\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right ) \\ &\quad = \pi_R\left ( \alpha_R\left ( v_g^R \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\right ) \right ) \\ &\qquad \cdot \left ( \pi_R\left (\alpha_R\circ\eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1} \circ\alpha_R^{-1} \alpha_R\left ( \left ( \eta_{gh}^R\beta_{gh}^{R U}\right )( v_k^R)\right ) \right )\right )\\ &\qquad \cdot u_R\left ( g,h\right ) u_R\left ( gh,k\right )\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right )\\ &\quad =\pi_R\left ( \alpha_R\left ( v_g^R \cdot \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\cdot \eta_g^R\beta_g^{R U} \eta_h^R\beta_{h}^{R U}( v_k^R)\right ) \right )\cdot u_R\left ( g,h\right ) u_R\left ( gh,k\right )\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right ). \end{split}\end{align} $$
$$ \begin{align} \begin{split} &\tilde u_R(g,h) \tilde u_R(gh,k)\\ &\quad = \pi_R\left ( \alpha_R\left ( v_g^R \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\right ) \right )\cdot u_R\left ( g,h\right )\cdot \pi_R\left (\alpha_R\left ( \left ( v_{gh}^{R}\right )^*\right )\right )\\ &\pi_R\left ( \alpha_R\left ( v_{gh}^R \left ( \eta_{gh}^R\beta_{gh}^{R U}\right )( v_k^R)\right ) \right )\cdot u_R\left ( gh,k\right )\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right ) \\ &\quad = \pi_R\left ( \alpha_R\left ( v_g^R \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\right ) \right ) \\ &\qquad \cdot \left [ u_R\left ( g,h\right )\cdot \pi_R\left ( \alpha_R\left ( \left ( \eta_{gh}^R\beta_{gh}^{R U}\right )( v_k^R)\right ) \right ) \right ] u_R\left ( gh,k\right ) \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right ) \\ &\quad = \pi_R\left ( \alpha_R\left ( v_g^R \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\right ) \right )\\ &\quad \cdot \left [ \mathop{\mathrm{Ad}}\nolimits\left ( u_R\left ( g,h\right )\right )\left ( \pi_R\left ( \alpha_R\left ( \left ( \eta_{gh}^R\beta_{gh}^{R U}\right )( v_k^R)\right ) \right )\right ) \cdot u_R\left ( g,h\right ) \right ] u_R\left ( gh,k\right )\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right ) \\ &\quad = \pi_R\left ( \alpha_R\left ( v_g^R \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\right ) \right ) \\ &\qquad \cdot \left ( \pi_R\left (\alpha_R\circ\eta_g^R\beta_g^{R U} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1} \circ\alpha_R^{-1} \alpha_R\left ( \left ( \eta_{gh}^R\beta_{gh}^{R U}\right )( v_k^R)\right ) \right )\right )\\ &\qquad \cdot u_R\left ( g,h\right ) u_R\left ( gh,k\right )\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right )\\ &\quad =\pi_R\left ( \alpha_R\left ( v_g^R \cdot \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\cdot \eta_g^R\beta_g^{R U} \eta_h^R\beta_{h}^{R U}( v_k^R)\right ) \right )\cdot u_R\left ( g,h\right ) u_R\left ( gh,k\right )\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right ). \end{split}\end{align} $$For the fourth equality, we used the definition of ![]() $u_R$. From this equation, applying equation (2.52) to the
$u_R$. From this equation, applying equation (2.52) to the ![]() $[\cdot ]$ part, we have
$[\cdot ]$ part, we have
 $$ \begin{align} &\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R(g,h) \tilde u_R(gh,k)\notag\\ &\quad = \mathbb I_{{\mathcal H}_L}\otimes \pi_R\left ( \alpha_R\left ( v_g^R \cdot \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\cdot \eta_g^R\beta_g^{R U} \eta_h^R\beta_{h}^{R U}( v_k^R)\right ) \right ) \notag\\ &\qquad \cdot \left [ u_R\left ( g,h\right ) u_R\left ( gh,k\right )\right ]\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right )\notag\\ &\quad =c_R(g,h,k)\left ( \mathbb I_{{\mathcal H}_L}\otimes \pi_R\left ( \alpha_R\left ( v_g^R \cdot \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\cdot \eta_g^R\beta_g^{R U} \eta_h^R\beta_{h}^{R U}( v_k^R)\right ) \right )\right )\notag\\ &\qquad \left\{ W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right\} \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\right ) \cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right ). \end{align} $$
$$ \begin{align} &\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R(g,h) \tilde u_R(gh,k)\notag\\ &\quad = \mathbb I_{{\mathcal H}_L}\otimes \pi_R\left ( \alpha_R\left ( v_g^R \cdot \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\cdot \eta_g^R\beta_g^{R U} \eta_h^R\beta_{h}^{R U}( v_k^R)\right ) \right ) \notag\\ &\qquad \cdot \left [ u_R\left ( g,h\right ) u_R\left ( gh,k\right )\right ]\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right )\notag\\ &\quad =c_R(g,h,k)\left ( \mathbb I_{{\mathcal H}_L}\otimes \pi_R\left ( \alpha_R\left ( v_g^R \cdot \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\cdot \eta_g^R\beta_g^{R U} \eta_h^R\beta_{h}^{R U}( v_k^R)\right ) \right )\right )\notag\\ &\qquad \left\{ W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\right\} \left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\right ) \cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right ). \end{align} $$Now from the definition of ![]() $\tilde u_R$, the
$\tilde u_R$, the ![]() $\{\cdot \}$ part becomes
$\{\cdot \}$ part becomes
 $$ \begin{align} W_g&\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^* \nonumber\\ &= \mathop{\mathrm{Ad}}\nolimits( W_g)\circ\pi_0\circ\left ( \mathop{\mathrm{id}}\nolimits_L\otimes \alpha_R\left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right ) \nonumber \\& \quad \cdot \mathop{\mathrm{Ad}}\nolimits( W_g)\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\cdot\left ( \mathop{\mathrm{Ad}}\nolimits( W_g)\pi_0\left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\left ( v_{hk}^{R}\right )\right ) \right ). \end{align} $$
$$ \begin{align} W_g&\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^* \nonumber\\ &= \mathop{\mathrm{Ad}}\nolimits( W_g)\circ\pi_0\circ\left ( \mathop{\mathrm{id}}\nolimits_L\otimes \alpha_R\left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right ) \nonumber \\& \quad \cdot \mathop{\mathrm{Ad}}\nolimits( W_g)\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\cdot\left ( \mathop{\mathrm{Ad}}\nolimits( W_g)\pi_0\left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\left ( v_{hk}^{R}\right )\right ) \right ). \end{align} $$Because ![]() $v_g^R$ belongs to
$v_g^R$ belongs to ![]() ${\mathcal A}_{C_\theta ,R}$ and
${\mathcal A}_{C_\theta ,R}$ and ![]() $\eta _g^R$ is an automorphism on
$\eta _g^R$ is an automorphism on ![]() ${\mathcal A}_{C_\theta ,R}$ while
${\mathcal A}_{C_\theta ,R}$ while ![]() $\Theta $ is an automorphism on
$\Theta $ is an automorphism on ![]() ${\mathcal A}_{\left ( C_\theta \right )^c}$ and
${\mathcal A}_{\left ( C_\theta \right )^c}$ and  $\beta _g^U\left ( {\mathcal A}_{C_\theta ,R}\right )={\mathcal A}_{C_\theta ,R}$, we have
$\beta _g^U\left ( {\mathcal A}_{C_\theta ,R}\right )={\mathcal A}_{C_\theta ,R}$, we have
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)&\circ\pi_0\circ\left ( \mathop{\mathrm{id}}\nolimits_L\otimes \alpha_R\left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right )\notag\\ &= \pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1} \circ \left ( \mathop{\mathrm{id}}\nolimits_L\otimes \alpha_R\left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right )\notag\\ &= \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right ),\quad \text{and}\notag\\ \mathop{\mathrm{Ad}}\nolimits( W_g)&\circ\pi_0\left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\left ( v_{hk}^{R}\right )\right ) =\pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( v_{hk}^{R} \right ) \right ). \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)&\circ\pi_0\circ\left ( \mathop{\mathrm{id}}\nolimits_L\otimes \alpha_R\left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right )\notag\\ &= \pi_0\circ\alpha_0\circ\Theta\circ\eta_g\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1} \circ \left ( \mathop{\mathrm{id}}\nolimits_L\otimes \alpha_R\left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right )\notag\\ &= \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right ),\quad \text{and}\notag\\ \mathop{\mathrm{Ad}}\nolimits( W_g)&\circ\pi_0\left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\left ( v_{hk}^{R}\right )\right ) =\pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( v_{hk}^{R} \right ) \right ). \end{align} $$Substituting this into equation (2.106), we obtain
 $$ \begin{align} &W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\nonumber\\ &\quad = \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right ) \notag\\ &\qquad\cdot \mathop{\mathrm{Ad}}\nolimits( W_g)\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\cdot \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( v_{hk}^{R} \right ) \right ). \end{align} $$
$$ \begin{align} &W_g\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(h,k)\right ) W_g^*\nonumber\\ &\quad = \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right ) \notag\\ &\qquad\cdot \mathop{\mathrm{Ad}}\nolimits( W_g)\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\cdot \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( v_{hk}^{R} \right ) \right ). \end{align} $$Substituting this to the ![]() $\{ \}$ part and the
$\{ \}$ part and the ![]() $\{\cdot \}$ part of equation (2.105), we obtain
$\{\cdot \}$ part of equation (2.105), we obtain
 $$ \begin{align} \mathbb I_{{\mathcal H}_L}&\otimes \tilde u_R(g,h) \tilde u_R(gh,k)\notag\\ &=c_R(g,h,k)\left ( \mathbb I_{{\mathcal H}_L}\otimes \pi_R\left ( \alpha_R\left ( v_g^R \cdot \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\cdot \eta_g^R\beta_g^{R U} \eta_h^R\beta_{h}^{R U}( v_k^R)\right ) \right )\right )\notag\\ & \quad \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right ) \nonumber \\ &\quad \cdot \mathop{\mathrm{Ad}}\nolimits( W_g)\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\cdot \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( v_{hk}^{R} \right ) \right )\notag\\ & \quad\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right )\right ) \notag\\ & =c_R(g,h,k)\left ( \mathbb I_{{\mathcal H}_L}\otimes \pi_R\left ( \alpha_R\left ( v_g^R \right ) \right )\right ) \mathop{\mathrm{Ad}}\nolimits( W_g)\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\cdot \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( v_{hk}^{R} \right ) \right )\notag\\ & \quad \pi_0\circ\left ( \mathop{\mathrm{id}}\nolimits_L\otimes \alpha_R\left ( \left ( v_g^R \cdot \eta_g^R\beta_g^{R U}\left ( v_{hk}^R\right )\right )^*\right ) \right ) \nonumber \\ &\qquad \cdot \left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R\left ( g,hk\right )\cdot\right ) \pi_0\left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\left ( v_{ghk}^{R}\right ) \alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right ) \right ) \notag\\ &= c_R(g,h,k) \mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes \pi_R\left ( \alpha_R\left ( v_g^R \right ) \right )\right ) W_g\right )\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\cdot \left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R\left ( g,hk\right )\right ) \notag\\ &=c_R(g,h,k) \left\{\mathop{\mathrm{Ad}}\nolimits\left ( \pi_L\left ( \alpha_L\left ({ v_g^L}^* \right )\otimes\mathbb I_{{\mathcal H}_R} \right )\right ) \mathop{\mathrm{Ad}}\nolimits \tilde W_g\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\right\}\cdot \left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R\left ( g,hk\right )\right ). \notag\\ \end{align} $$
$$ \begin{align} \mathbb I_{{\mathcal H}_L}&\otimes \tilde u_R(g,h) \tilde u_R(gh,k)\notag\\ &=c_R(g,h,k)\left ( \mathbb I_{{\mathcal H}_L}\otimes \pi_R\left ( \alpha_R\left ( v_g^R \cdot \left ( \eta_g^R\beta_g^{R U}\right )( v_h^R)\cdot \eta_g^R\beta_g^{R U} \eta_h^R\beta_{h}^{R U}( v_k^R)\right ) \right )\right )\notag\\ & \quad \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( \left ( v_h^R \cdot \eta_h^R\beta_h^{R U}( v_k^R)\right )^*\right ) \right ) \nonumber \\ &\quad \cdot \mathop{\mathrm{Ad}}\nolimits( W_g)\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\cdot \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( v_{hk}^{R} \right ) \right )\notag\\ & \quad\left ( \mathbb I_{{\mathcal H}_L}\otimes u_R(g,hk)\cdot \pi_R\left (\alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right )\right )\right ) \notag\\ & =c_R(g,h,k)\left ( \mathbb I_{{\mathcal H}_L}\otimes \pi_R\left ( \alpha_R\left ( v_g^R \right ) \right )\right ) \mathop{\mathrm{Ad}}\nolimits( W_g)\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\cdot \pi_0 \left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\circ \eta_g^R\beta_g^{R U} \left ( v_{hk}^{R} \right ) \right )\notag\\ & \quad \pi_0\circ\left ( \mathop{\mathrm{id}}\nolimits_L\otimes \alpha_R\left ( \left ( v_g^R \cdot \eta_g^R\beta_g^{R U}\left ( v_{hk}^R\right )\right )^*\right ) \right ) \nonumber \\ &\qquad \cdot \left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R\left ( g,hk\right )\cdot\right ) \pi_0\left ( \mathop{\mathrm{id}}\nolimits_L\otimes\alpha_R\left ( v_{ghk}^{R}\right ) \alpha_R\left ( \left ( v_{ghk}^{R}\right )^*\right ) \right ) \notag\\ &= c_R(g,h,k) \mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes \pi_R\left ( \alpha_R\left ( v_g^R \right ) \right )\right ) W_g\right )\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\cdot \left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R\left ( g,hk\right )\right ) \notag\\ &=c_R(g,h,k) \left\{\mathop{\mathrm{Ad}}\nolimits\left ( \pi_L\left ( \alpha_L\left ({ v_g^L}^* \right )\otimes\mathbb I_{{\mathcal H}_R} \right )\right ) \mathop{\mathrm{Ad}}\nolimits \tilde W_g\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )\right\}\cdot \left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R\left ( g,hk\right )\right ). \notag\\ \end{align} $$Because of Lemma 2.3(iii), the ![]() $\{\cdot \}$ part of the last equation is equal to
$\{\cdot \}$ part of the last equation is equal to ![]() $\mathop {\mathrm {Ad}}\nolimits \tilde W_g\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )$. Hence we obtain
$\mathop {\mathrm {Ad}}\nolimits \tilde W_g\left (\mathbb I_{{\mathcal H}_L}\otimes \tilde u_R( h,k)\right )$. Hence we obtain
This proves ![]() $c_R=\tilde c_R$, completing the proof.
$c_R=\tilde c_R$, completing the proof.
Lemma 2.15. Set
 $$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta<\frac\pi 2,\quad \left(\tilde\beta_{g}^{(1)}\right), \left(\tilde\beta_g^{(2)}\right)\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta). \end{align} $$
$$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta<\frac\pi 2,\quad \left(\tilde\beta_{g}^{(1)}\right), \left(\tilde\beta_g^{(2)}\right)\in \mathop{\mathrm{IG}}\nolimits(\omega,\theta). \end{align} $$Then we have
 $$ \begin{align} h^{(4)} \left ( \omega , \theta, \left(\tilde\beta_g^{(1)}\right) \right ) = h^{(4)} \left ( \omega, \theta, \left(\tilde\beta_g^{(2)}\right) \right ). \end{align} $$
$$ \begin{align} h^{(4)} \left ( \omega , \theta, \left(\tilde\beta_g^{(1)}\right) \right ) = h^{(4)} \left ( \omega, \theta, \left(\tilde\beta_g^{(2)}\right) \right ). \end{align} $$Definition 2.16. From this lemma we may define
 $$ \begin{align} h^{(5)} \left ( \omega, \theta \right ) := h^{(4)} \left ( \omega, \theta, (\tilde\beta_g ) \right ) \end{align} $$
$$ \begin{align} h^{(5)} \left ( \omega, \theta \right ) := h^{(4)} \left ( \omega, \theta, (\tilde\beta_g ) \right ) \end{align} $$for any
 $$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta<\frac\pi 2,\quad \text{with } \mathop{\mathrm{IG}}\nolimits(\omega,\theta)\neq \emptyset, \end{align} $$
$$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta<\frac\pi 2,\quad \text{with } \mathop{\mathrm{IG}}\nolimits(\omega,\theta)\neq \emptyset, \end{align} $$independent of the choice of ![]() $\left (\tilde \beta _g\right )$.
$\left (\tilde \beta _g\right )$.
Proof. By the definition of ![]() $\mathop {\mathrm {IG}}\nolimits (\omega ,\theta )$, there are
$\mathop {\mathrm {IG}}\nolimits (\omega ,\theta )$, there are
 $$ \begin{align} \left(\eta_{g,i}^{\sigma}\right)_{g\in G, \, \sigma=L,R} \in {\mathcal T}\left(\theta, \left(\tilde\beta_g^{(i)}\right)\right),\quad \text{for } i=1,2. \end{align} $$
$$ \begin{align} \left(\eta_{g,i}^{\sigma}\right)_{g\in G, \, \sigma=L,R} \in {\mathcal T}\left(\theta, \left(\tilde\beta_g^{(i)}\right)\right),\quad \text{for } i=1,2. \end{align} $$We set  $\eta _{g,i}:=\eta _{g,i}^L\otimes \eta _{g,i}^R$, for
$\eta _{g,i}:=\eta _{g,i}^L\otimes \eta _{g,i}^R$, for ![]() $i=1,2$. There are
$i=1,2$. There are ![]() $ \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ and
$ \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ and ![]() $(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta }$ for
$(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta }$ for ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ by the definition. Setting
$\omega \in \mathop {\mathcal {SL}}\nolimits $ by the definition. Setting ![]() $\alpha _0:=\alpha _L\otimes \alpha _R$, we have
$\alpha _0:=\alpha _L\otimes \alpha _R$, we have ![]() $\alpha =({\textrm {{inner}}})\circ \alpha _0\circ \Theta $. By Lemma 2.1, there is some
$\alpha =({\textrm {{inner}}})\circ \alpha _0\circ \Theta $. By Lemma 2.1, there is some
 $$ \begin{align} \left ( \left(W_{g,1}\right), \left(u_{\sigma}^{(1)}(g,h)\right)\right ) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, \left(\tilde\beta_g^{(1)}\right), \left(\eta_{g,1}^\sigma\right), (\alpha_{L},\alpha_{R},\Theta) \right ). \end{align} $$
$$ \begin{align} \left ( \left(W_{g,1}\right), \left(u_{\sigma}^{(1)}(g,h)\right)\right ) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, \left(\tilde\beta_g^{(1)}\right), \left(\eta_{g,1}^\sigma\right), (\alpha_{L},\alpha_{R},\Theta) \right ). \end{align} $$Set
 $$ \begin{align} K^\sigma_g:=\eta_{g,2}^\sigma\circ \left ( \eta_{g,1}^\sigma\right )^{-1}\in \mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{C_\theta,\sigma}\right ),\quad\text{for } \sigma=L,R,\ g\in G,\qquad K_g:=K_{g}^L\otimes K_g^R\in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{C_\theta}\right ). \end{align} $$
$$ \begin{align} K^\sigma_g:=\eta_{g,2}^\sigma\circ \left ( \eta_{g,1}^\sigma\right )^{-1}\in \mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{C_\theta,\sigma}\right ),\quad\text{for } \sigma=L,R,\ g\in G,\qquad K_g:=K_{g}^L\otimes K_g^R\in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{C_\theta}\right ). \end{align} $$ We claim that there are unitaries ![]() $V_g^\sigma $,
$V_g^\sigma $, ![]() $g\in G, \ \sigma =L,R$, on
$g\in G, \ \sigma =L,R$, on ![]() ${\mathcal H}_\sigma $ such that
${\mathcal H}_\sigma $ such that
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits \left ( V_g^\sigma\right )\circ\pi_\sigma =\pi_\sigma\circ\alpha_\sigma\circ K_g^\sigma\circ \left (\alpha_\sigma\right )^{-1}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits \left ( V_g^\sigma\right )\circ\pi_\sigma =\pi_\sigma\circ\alpha_\sigma\circ K_g^\sigma\circ \left (\alpha_\sigma\right )^{-1}. \end{align} $$To see this, note that
 $$ \begin{align} \omega=\omega\circ\tilde \beta_g^{(i)} =\omega_0\circ\alpha\circ\tilde \beta_g^{(i)} \sim_{\text{q.e.}} \omega_0\circ\alpha_0\circ\Theta\circ \left ( \eta_{g,i}^{L}\otimes \eta_{g,i}^{R} \right )\circ\beta_g^U,\quad i=1,2. \end{align} $$
$$ \begin{align} \omega=\omega\circ\tilde \beta_g^{(i)} =\omega_0\circ\alpha\circ\tilde \beta_g^{(i)} \sim_{\text{q.e.}} \omega_0\circ\alpha_0\circ\Theta\circ \left ( \eta_{g,i}^{L}\otimes \eta_{g,i}^{R} \right )\circ\beta_g^U,\quad i=1,2. \end{align} $$Therefore, we have
 $$ \begin{align} \omega_0\circ\alpha_0\circ\Theta\circ \left ( \eta_{g,1}^{L}\otimes \eta_{g,1}^{R} \right ) \sim_{\text{q.e.}} \omega\circ\left ( \beta_g^U\right )^{-1} \sim_{\text{q.e.}} \omega_0\circ\alpha_0\circ\Theta\circ \left ( \eta_{g,2}^{L}\otimes \eta_{g,2}^{R} \right ), \end{align} $$
$$ \begin{align} \omega_0\circ\alpha_0\circ\Theta\circ \left ( \eta_{g,1}^{L}\otimes \eta_{g,1}^{R} \right ) \sim_{\text{q.e.}} \omega\circ\left ( \beta_g^U\right )^{-1} \sim_{\text{q.e.}} \omega_0\circ\alpha_0\circ\Theta\circ \left ( \eta_{g,2}^{L}\otimes \eta_{g,2}^{R} \right ), \end{align} $$and then using the facts that  $\Theta \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{C_\theta ^c}\right )$ and
$\Theta \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{C_\theta ^c}\right )$ and ![]() $K_g\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{C_\theta }\right )$,
$K_g\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{C_\theta }\right )$,
 $$ \begin{align} \omega_0\sim_{\text{q.e.}} \omega_0\circ\alpha_0\circ\Theta\circ K_g\circ\Theta^{-1}\circ \alpha_0^{-1} =\omega_0\circ \alpha_0\circ K_g\circ \left ( \alpha_0\right )^{-1} =\bigotimes_{\sigma=L,R} \omega_\sigma \circ\alpha_\sigma K_g^\sigma \left ( \alpha_\sigma\right )^{-1}. \end{align} $$
$$ \begin{align} \omega_0\sim_{\text{q.e.}} \omega_0\circ\alpha_0\circ\Theta\circ K_g\circ\Theta^{-1}\circ \alpha_0^{-1} =\omega_0\circ \alpha_0\circ K_g\circ \left ( \alpha_0\right )^{-1} =\bigotimes_{\sigma=L,R} \omega_\sigma \circ\alpha_\sigma K_g^\sigma \left ( \alpha_\sigma\right )^{-1}. \end{align} $$This implies that ![]() $\omega _\sigma $ and
$\omega _\sigma $ and  $ \omega _\sigma \circ \alpha _\sigma K_g^\sigma \left ( \alpha _\sigma \right )^{-1}$ are quasiequivalent. Because
$ \omega _\sigma \circ \alpha _\sigma K_g^\sigma \left ( \alpha _\sigma \right )^{-1}$ are quasiequivalent. Because ![]() $\pi _\sigma $ is irreducible, this implies the existence of a unitary
$\pi _\sigma $ is irreducible, this implies the existence of a unitary ![]() $V_g^\sigma $ on
$V_g^\sigma $ on ![]() ${\mathcal H}_\sigma $ satisfying equation (2.118), proving the claim.
${\mathcal H}_\sigma $ satisfying equation (2.118), proving the claim.
Next we claim that there are unitaries  $v^\sigma _{g,h}$ on
$v^\sigma _{g,h}$ on ![]() ${\mathcal H}_\sigma $, for
${\mathcal H}_\sigma $, for ![]() $g,h\in G$ and
$g,h\in G$ and ![]() $\sigma =L,R$, such that
$\sigma =L,R$, such that
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits_{W_{g,1}}\left (\mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) =\mathbb I_{{\mathcal H}_L}\otimes v^{R}_{g,h},\qquad \mathop{\mathrm{Ad}}\nolimits_{W_{g,1}}\left ( V_h^L\otimes \mathbb I_{{\mathcal H}_R}\right ) =v^{L}_{g,h}\otimes\mathbb I_{{\mathcal H}_R} \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits_{W_{g,1}}\left (\mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) =\mathbb I_{{\mathcal H}_L}\otimes v^{R}_{g,h},\qquad \mathop{\mathrm{Ad}}\nolimits_{W_{g,1}}\left ( V_h^L\otimes \mathbb I_{{\mathcal H}_R}\right ) =v^{L}_{g,h}\otimes\mathbb I_{{\mathcal H}_R} \end{align} $$and
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( V_g^\sigma v^\sigma_{g,h} u_\sigma^{(1)}(g,h) \left ( V_{gh}^\sigma \right )^* \right )\pi_\sigma =\pi_\sigma\circ \alpha_\sigma \circ \eta_{g,2}^{\sigma}\beta_g^{{\sigma} U} \eta_{h,2}^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}\left ( \eta_{gh,2}^{\sigma}\right )^{-1}\circ \alpha_\sigma ^{-1}, \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( V_g^\sigma v^\sigma_{g,h} u_\sigma^{(1)}(g,h) \left ( V_{gh}^\sigma \right )^* \right )\pi_\sigma =\pi_\sigma\circ \alpha_\sigma \circ \eta_{g,2}^{\sigma}\beta_g^{{\sigma} U} \eta_{h,2}^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}\left ( \eta_{gh,2}^{\sigma}\right )^{-1}\circ \alpha_\sigma ^{-1}, \end{align} $$for any ![]() $g,h\in G$ and
$g,h\in G$ and ![]() $\sigma =L,R$. To see this, first we calculate
$\sigma =L,R$. To see this, first we calculate
 $$ \begin{align}& \mathop{\mathrm{Ad}}\nolimits\left ( W_{g,1}\left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \right ) \circ\pi_0 =\mathop{\mathrm{Ad}}\nolimits\left ( W_{g,1}\left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \right )\pi_0\circ \alpha_0\circ\Theta\circ\left ( {\eta_{g,1}}\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\notag\\ &\quad =\pi_0\circ \alpha_0\circ\Theta\circ {\eta_{g,1}}\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1} \circ \left ( \mathop{\mathrm{id}}\nolimits_{L}\otimes \alpha_R\circ K_h^R\circ \left (\alpha_R\right )^{-1} \right ) \circ \alpha_0\circ\Theta\circ\left ( {\eta_{g,1}}\beta_g^U\right )^{-1}\!\circ\Theta^{-1}\circ\alpha_0^{-1}\notag\\ &\quad = \pi_0\circ \alpha_0\circ\Theta\circ {\eta_{g,1}}\beta_g^U\circ\Theta^{-1} \circ \left ( \mathop{\mathrm{id}}\nolimits_{L}\otimes K_h^R \right ) \circ\Theta\circ\left ( {\eta_{g,1}}\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1} \notag\\ &\quad = \pi_0\circ \alpha_0\circ\Theta\circ {\eta_{g,1}}\beta_g^U \circ \left ( \mathop{\mathrm{id}}\nolimits_{L}\otimes K_h^R \right ) \circ\left ( {\eta_{g,1}}\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\notag\\ &\quad =\pi_0\circ\alpha_0\circ\Theta \circ \left ( \mathop{\mathrm{id}}\nolimits_{L}\otimes {\eta_{g,1}^R}\beta_g^{RU} K_h^R \left ( {\eta_{g,1}^R}\beta_g^{RU}\right )^{-1} \right ) \circ\Theta^{-1}\circ\alpha_0^{-1}\notag\\ &\quad = \pi_0\circ \left ( \mathop{\mathrm{id}}\nolimits_{L}\otimes \alpha_R\circ {\eta_{g,1}^R}\beta_g^{RU} K_h^R \left ( {\eta_{g,1}^R}\beta_g^{RU}\right )^{-1}\alpha_R^{-1} \right ). \end{align} $$
$$ \begin{align}& \mathop{\mathrm{Ad}}\nolimits\left ( W_{g,1}\left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \right ) \circ\pi_0 =\mathop{\mathrm{Ad}}\nolimits\left ( W_{g,1}\left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \right )\pi_0\circ \alpha_0\circ\Theta\circ\left ( {\eta_{g,1}}\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\notag\\ &\quad =\pi_0\circ \alpha_0\circ\Theta\circ {\eta_{g,1}}\beta_g^U\circ\Theta^{-1}\circ\alpha_0^{-1} \circ \left ( \mathop{\mathrm{id}}\nolimits_{L}\otimes \alpha_R\circ K_h^R\circ \left (\alpha_R\right )^{-1} \right ) \circ \alpha_0\circ\Theta\circ\left ( {\eta_{g,1}}\beta_g^U\right )^{-1}\!\circ\Theta^{-1}\circ\alpha_0^{-1}\notag\\ &\quad = \pi_0\circ \alpha_0\circ\Theta\circ {\eta_{g,1}}\beta_g^U\circ\Theta^{-1} \circ \left ( \mathop{\mathrm{id}}\nolimits_{L}\otimes K_h^R \right ) \circ\Theta\circ\left ( {\eta_{g,1}}\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1} \notag\\ &\quad = \pi_0\circ \alpha_0\circ\Theta\circ {\eta_{g,1}}\beta_g^U \circ \left ( \mathop{\mathrm{id}}\nolimits_{L}\otimes K_h^R \right ) \circ\left ( {\eta_{g,1}}\beta_g^U\right )^{-1}\circ\Theta^{-1}\circ\alpha_0^{-1}\notag\\ &\quad =\pi_0\circ\alpha_0\circ\Theta \circ \left ( \mathop{\mathrm{id}}\nolimits_{L}\otimes {\eta_{g,1}^R}\beta_g^{RU} K_h^R \left ( {\eta_{g,1}^R}\beta_g^{RU}\right )^{-1} \right ) \circ\Theta^{-1}\circ\alpha_0^{-1}\notag\\ &\quad = \pi_0\circ \left ( \mathop{\mathrm{id}}\nolimits_{L}\otimes \alpha_R\circ {\eta_{g,1}^R}\beta_g^{RU} K_h^R \left ( {\eta_{g,1}^R}\beta_g^{RU}\right )^{-1}\alpha_R^{-1} \right ). \end{align} $$In the fourth and sixth equalities, we used the fact that  $K_h^R, \eta _{g,1}^R\beta _g^{RU} K_h^R \left ( \eta _{g,1}^R\beta _g^{RU}\right )^{-1}\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{C_\theta }\right )$ and
$K_h^R, \eta _{g,1}^R\beta _g^{RU} K_h^R \left ( \eta _{g,1}^R\beta _g^{RU}\right )^{-1}\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{C_\theta }\right )$ and  $\Theta \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{C_\theta ^c}\right )$ commute, in order to remove
$\Theta \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{C_\theta ^c}\right )$ commute, in order to remove ![]() $\Theta $. Equation (2.124) and the fact that
$\Theta $. Equation (2.124) and the fact that ![]() $\pi _L$ is irreducible imply that there is a unitary
$\pi _L$ is irreducible imply that there is a unitary  $v^R_{g,h}$ satisfying equation (2.122). The same argument implies the existence of
$v^R_{g,h}$ satisfying equation (2.122). The same argument implies the existence of  $v^L_{g,h}$ satisfying equation (2.122).
$v^L_{g,h}$ satisfying equation (2.122).
For this  $v^R_{g,h}$, we would like to show equation (2.123). Rewriting
$v^R_{g,h}$, we would like to show equation (2.123). Rewriting
 $$ \begin{align} \begin{split} &\eta_{g,2}^{\sigma}\beta_g^{{\sigma} U} \eta_{h,2}^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}\left ( \eta_{gh,2}^{\sigma}\right )^{-1} \\ &\qquad\qquad\qquad=K_g^\sigma\circ\left ( \eta_{g,1}^{\sigma}\beta_g^{{\sigma} U} K_h^\sigma \left ( \eta_{g,1}^{\sigma}\beta_g^{{\sigma} U}\right )^{-1} \right )\circ \eta_{g,1}^{\sigma}\beta_g^{{\sigma} U} \eta_{h,1}^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}\left ( \eta_{gh,1}^{\sigma}\right )^{-1} \circ \left ( K_{gh}^{\sigma} \right )^{-1}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\eta_{g,2}^{\sigma}\beta_g^{{\sigma} U} \eta_{h,2}^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}\left ( \eta_{gh,2}^{\sigma}\right )^{-1} \\ &\qquad\qquad\qquad=K_g^\sigma\circ\left ( \eta_{g,1}^{\sigma}\beta_g^{{\sigma} U} K_h^\sigma \left ( \eta_{g,1}^{\sigma}\beta_g^{{\sigma} U}\right )^{-1} \right )\circ \eta_{g,1}^{\sigma}\beta_g^{{\sigma} U} \eta_{h,1}^{\sigma}\left (\beta_g^{{\sigma} U}\right )^{-1}\left ( \eta_{gh,1}^{\sigma}\right )^{-1} \circ \left ( K_{gh}^{\sigma} \right )^{-1}, \end{split} \end{align} $$we obtain
 $$ \begin{align} &\pi_L\otimes \pi_R\circ \alpha_R \eta_{g,2}^{R}\beta_g^{{R} U} \eta_{h,2}^{R}\left (\beta_g^{{R} U}\right )^{-1}\left ( \eta_{gh,2}^{R}\right )^{-1} \alpha_R ^{-1}\notag\\ &\quad =\pi_0\circ\left ( \mathop{\mathrm{id}}\nolimits_L\otimes \alpha_R\circ K_g^R\circ \left ( \eta_{g,1}^{R}\beta_g^{{R} U} K_h^R \left ( \eta_{g,1}^{R}\beta_g^{{R} U}\right )^{-1} \right ) \right.\nonumber \\ &\qquad\left.\, \circ\ \eta_{g,1}^{R}\beta_g^{{R} U} \eta_{h,1}^{R}\left (\beta_g^{{R} U}\right )^{-1}\left ( \eta_{gh,1}^{R}\right )^{-1} \circ \left ( K_{gh}^{R} \right )^{-1} \alpha_R^{-1} \right )\notag\\ &\quad = \pi_L\otimes \mathop{\mathrm{Ad}}\nolimits\left ( {V_g^R v_{g,h}^R u_R^{(1)}(g,h) \left ( V_{gh}^R\right )^*}\right ) \pi_R, \end{align} $$
$$ \begin{align} &\pi_L\otimes \pi_R\circ \alpha_R \eta_{g,2}^{R}\beta_g^{{R} U} \eta_{h,2}^{R}\left (\beta_g^{{R} U}\right )^{-1}\left ( \eta_{gh,2}^{R}\right )^{-1} \alpha_R ^{-1}\notag\\ &\quad =\pi_0\circ\left ( \mathop{\mathrm{id}}\nolimits_L\otimes \alpha_R\circ K_g^R\circ \left ( \eta_{g,1}^{R}\beta_g^{{R} U} K_h^R \left ( \eta_{g,1}^{R}\beta_g^{{R} U}\right )^{-1} \right ) \right.\nonumber \\ &\qquad\left.\, \circ\ \eta_{g,1}^{R}\beta_g^{{R} U} \eta_{h,1}^{R}\left (\beta_g^{{R} U}\right )^{-1}\left ( \eta_{gh,1}^{R}\right )^{-1} \circ \left ( K_{gh}^{R} \right )^{-1} \alpha_R^{-1} \right )\notag\\ &\quad = \pi_L\otimes \mathop{\mathrm{Ad}}\nolimits\left ( {V_g^R v_{g,h}^R u_R^{(1)}(g,h) \left ( V_{gh}^R\right )^*}\right ) \pi_R, \end{align} $$substituting equations (2.118), (2.124) and (2.122). This proves equation (2.123) for ![]() $\sigma =R$. An analogous result for
$\sigma =R$. An analogous result for ![]() $\sigma =L$ can be proven by the same argument. Hence we have proven the claim (2.124) and (2.123).
$\sigma =L$ can be proven by the same argument. Hence we have proven the claim (2.124) and (2.123).
Setting
 $$ \begin{align} V_g:=V_g^L\otimes V_g^R\in{\mathcal U}({\mathcal H}_0), \end{align} $$
$$ \begin{align} V_g:=V_g^L\otimes V_g^R\in{\mathcal U}({\mathcal H}_0), \end{align} $$we have
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( V_gW_{g,1}\right )\circ\pi_0 &=\pi_0\circ \alpha_0\circ K_g\circ \alpha_0^{-1}\circ \alpha_0\circ\Theta\circ \eta_{g,1} \circ\beta_g^U\circ \Theta^{-1}\circ \alpha_0^{-1}\notag\\ &=\pi_0\circ \alpha_0\circ\Theta\circ \eta_{g,2}\circ\beta_g^U\circ\Theta^{-1}\circ \alpha_0^{-1}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( V_gW_{g,1}\right )\circ\pi_0 &=\pi_0\circ \alpha_0\circ K_g\circ \alpha_0^{-1}\circ \alpha_0\circ\Theta\circ \eta_{g,1} \circ\beta_g^U\circ \Theta^{-1}\circ \alpha_0^{-1}\notag\\ &=\pi_0\circ \alpha_0\circ\Theta\circ \eta_{g,2}\circ\beta_g^U\circ\Theta^{-1}\circ \alpha_0^{-1}. \end{align} $$In the last equality, we used the definition of ![]() $K_g$ and the commutativity of
$K_g$ and the commutativity of ![]() $\Theta $ and
$\Theta $ and ![]() $K_g$ again. From equations (2.128) and (2.123), setting
$K_g$ again. From equations (2.128) and (2.123), setting
 $$ \begin{align} u_\sigma^{(2)}(g,h):= V_g^\sigma v^\sigma_{g,h} u_\sigma^{(1)}(g,h) \left ( V_{gh}^\sigma \right )^*, \end{align} $$
$$ \begin{align} u_\sigma^{(2)}(g,h):= V_g^\sigma v^\sigma_{g,h} u_\sigma^{(1)}(g,h) \left ( V_{gh}^\sigma \right )^*, \end{align} $$we see that
 $$ \begin{align} \left ( \left ( V_gW_{g,1}\right ), \left ( {u_{R}^{(2)}}(g,h )\right )\right ) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, \left(\tilde\beta_g^{(2)}\right), \left(\eta_{g,2}^\sigma\right), (\alpha_{L},\alpha_{R},\Theta) \right ) \end{align} $$
$$ \begin{align} \left ( \left ( V_gW_{g,1}\right ), \left ( {u_{R}^{(2)}}(g,h )\right )\right ) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta, \left(\tilde\beta_g^{(2)}\right), \left(\eta_{g,2}^\sigma\right), (\alpha_{L},\alpha_{R},\Theta) \right ) \end{align} $$and
 $$ \begin{align} \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(2)}}(g,h ) =\left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(g,h )\left ( V_{gh}^R\right )^* \right ). \end{align} $$
$$ \begin{align} \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(2)}}(g,h ) =\left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(g,h )\left ( V_{gh}^R\right )^* \right ). \end{align} $$Now we set
 $$ \begin{align} c_{R,1}&:=c_R\left ( \omega, \alpha, \theta, \left(\tilde\beta_g^{(1)}\right), \left(\eta_{g,1}^\sigma\right), (\alpha_{L},\alpha_{R},\Theta),\left ( (W_{g,1}), \left(u_{\sigma}^{(1)}(g,h)\right)\right ) \right ),\notag\\ c_{R,2}&:=c_{R}\left ( \omega, \alpha, \theta, \left(\tilde\beta_g^{(2)}\right), \left(\eta_{g,2}^\sigma\right), (\alpha_{L},\alpha_{R},\Theta), \left ( \left ( V_gW_{g,1}\right ), \left ( {u_{R}^{(2)}}(g,h )\right )\right ) \right ). \end{align} $$
$$ \begin{align} c_{R,1}&:=c_R\left ( \omega, \alpha, \theta, \left(\tilde\beta_g^{(1)}\right), \left(\eta_{g,1}^\sigma\right), (\alpha_{L},\alpha_{R},\Theta),\left ( (W_{g,1}), \left(u_{\sigma}^{(1)}(g,h)\right)\right ) \right ),\notag\\ c_{R,2}&:=c_{R}\left ( \omega, \alpha, \theta, \left(\tilde\beta_g^{(2)}\right), \left(\eta_{g,2}^\sigma\right), (\alpha_{L},\alpha_{R},\Theta), \left ( \left ( V_gW_{g,1}\right ), \left ( {u_{R}^{(2)}}(g,h )\right )\right ) \right ). \end{align} $$To prove the Lemma, it suffices to show ![]() $c_{R,1}=c_{R,2}$. By equation (2.131), we have
$c_{R,1}=c_{R,2}$. By equation (2.131), we have
 $$ \begin{align} \mathbb I_{{\mathcal H}_L}&\otimes u_R^{(2)}(g,h) u_R^{(2)}(gh,k) \nonumber\\ &=\left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(g,h )\left ( V_{gh}^R\right )^* \right )\nonumber\\& \quad \cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes V_{gh}^R\right ) W_{gh,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_k^R\right ) \left ( W_{gh,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(gh,k )\left ( V_{ghk}^R\right )^* \right )\nonumber\\ &= \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(g,h ) \right )\nonumber\\& \quad \cdot W_{gh,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_k^R\right ) \left ( W_{gh,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(gh,k )\left ( V_{ghk}^R\right )^* \right )\nonumber\\ &= \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \left\{\mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(g,h ) \right )\cdot W_{gh,1} \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_k^R\right ) \right\}\nonumber\\ & \quad \cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes \left [ {u_{R}^{(1)}}(g,h ){u_{R}^{(1)}}(gh,k )\right ]\left ( V_{ghk}^R\right )^* \right )\nonumber\\ & =c_{R,1}(g,h,k) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \left\{\mathop{\mathrm{Ad}}\nolimits\left ( W_{g,1}W_{h,1} \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_k^R\right ) \right\}\nonumber\\ & \quad \cdot \left ( W_{g,1}\left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(1)}(h,k)\right ) W_{g,1}^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(1)}(g,hk)\left ( V_{ghk}^R\right )^*\right ). \end{align} $$
$$ \begin{align} \mathbb I_{{\mathcal H}_L}&\otimes u_R^{(2)}(g,h) u_R^{(2)}(gh,k) \nonumber\\ &=\left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(g,h )\left ( V_{gh}^R\right )^* \right )\nonumber\\& \quad \cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes V_{gh}^R\right ) W_{gh,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_k^R\right ) \left ( W_{gh,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(gh,k )\left ( V_{ghk}^R\right )^* \right )\nonumber\\ &= \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(g,h ) \right )\nonumber\\& \quad \cdot W_{gh,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_k^R\right ) \left ( W_{gh,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(gh,k )\left ( V_{ghk}^R\right )^* \right )\nonumber\\ &= \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \left\{\mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes {u_{R}^{(1)}}(g,h ) \right )\cdot W_{gh,1} \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_k^R\right ) \right\}\nonumber\\ & \quad \cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes \left [ {u_{R}^{(1)}}(g,h ){u_{R}^{(1)}}(gh,k )\right ]\left ( V_{ghk}^R\right )^* \right )\nonumber\\ & =c_{R,1}(g,h,k) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left ( W_{g,1}\right )^* \left\{\mathop{\mathrm{Ad}}\nolimits\left ( W_{g,1}W_{h,1} \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_k^R\right ) \right\}\nonumber\\ & \quad \cdot \left ( W_{g,1}\left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(1)}(h,k)\right ) W_{g,1}^*\right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(1)}(g,hk)\left ( V_{ghk}^R\right )^*\right ). \end{align} $$ We used equation (2.52) for the ![]() $[\cdot ]$ part and Lemma 2.3(ii) and equation (2.122) for the
$[\cdot ]$ part and Lemma 2.3(ii) and equation (2.122) for the ![]() $\{\cdot \}$ part in the fourth equality. Again using equation (2.131), we have
$\{\cdot \}$ part in the fourth equality. Again using equation (2.131), we have
 $$ \begin{align} & \mathbb I_{{\mathcal H}_L} \otimes u_R^{(2)}(g,h) u_R^{(2)}(gh,k)= \text{equation }(2.134)\hspace{220pt} \nonumber \\ & =c_{R,1}(g,h,k) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left\{\mathop{\mathrm{Ad}}\nolimits\left ( W_{h,1} \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_k^R\right ) \right\}\notag\\ & \quad \cdot\left ( W_{h,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes \left ( V_k^R\right )^*\right ) \left ( W_{h,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(h,k) \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes \left ( V_{hk}^R\right ) \right ) \left ( W_{g,1}\right )^*\right )\notag\\ & \quad W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes \left ( V_{hk}^R\right )^*\right ) \left ( W_{g,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(g,hk) \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes \left ( V_{ghk}^R\right ) \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes \left ( V_{ghk}^R\right )^*\right )\notag\\ &= c_{R,1}(g,h,k) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \cdot\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(h,k) \right ) \right )\cdot \left ( W_{g,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(g,hk) \right )\notag\\ &= c_{R,1}(g,h,k)\cdot \mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \right ) \left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(h,k) \right ) \right )\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(g,hk) \right )\notag\\ &= c_{R,1}(g,h,k)\cdot \mathop{\mathrm{Ad}}\nolimits\left ( \left ( {V_g^L}^*\otimes \mathbb I_{{\mathcal H}_R}\right ) V_g W_{g,1} \right ) \left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(h,k) \right ) \right )\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(g,hk) \right )\notag\\ &= c_{R,1}(g,h,k)\cdot \mathop{\mathrm{Ad}}\nolimits\left ( V_g W_{g,1} \right ) \left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(h,k) \right ) \right )\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(g,hk) \right ) \end{align} $$
$$ \begin{align} & \mathbb I_{{\mathcal H}_L} \otimes u_R^{(2)}(g,h) u_R^{(2)}(gh,k)= \text{equation }(2.134)\hspace{220pt} \nonumber \\ & =c_{R,1}(g,h,k) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right ) \left\{\mathop{\mathrm{Ad}}\nolimits\left ( W_{h,1} \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_k^R\right ) \right\}\notag\\ & \quad \cdot\left ( W_{h,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes \left ( V_k^R\right )^*\right ) \left ( W_{h,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes V_h^R\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(h,k) \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes \left ( V_{hk}^R\right ) \right ) \left ( W_{g,1}\right )^*\right )\notag\\ & \quad W_{g,1} \left ( \mathbb I_{{\mathcal H}_L}\otimes \left ( V_{hk}^R\right )^*\right ) \left ( W_{g,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(g,hk) \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes \left ( V_{ghk}^R\right ) \right ) \left ( \mathbb I_{{\mathcal H}_L}\otimes \left ( V_{ghk}^R\right )^*\right )\notag\\ &= c_{R,1}(g,h,k) \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \cdot\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(h,k) \right ) \right )\cdot \left ( W_{g,1}\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right )^* \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(g,hk) \right )\notag\\ &= c_{R,1}(g,h,k)\cdot \mathop{\mathrm{Ad}}\nolimits\left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes V_g^R\right ) W_{g,1} \right ) \left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(h,k) \right ) \right )\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(g,hk) \right )\notag\\ &= c_{R,1}(g,h,k)\cdot \mathop{\mathrm{Ad}}\nolimits\left ( \left ( {V_g^L}^*\otimes \mathbb I_{{\mathcal H}_R}\right ) V_g W_{g,1} \right ) \left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(h,k) \right ) \right )\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(g,hk) \right )\notag\\ &= c_{R,1}(g,h,k)\cdot \mathop{\mathrm{Ad}}\nolimits\left ( V_g W_{g,1} \right ) \left ( \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(h,k) \right ) \right )\cdot \left ( \mathbb I_{{\mathcal H}_L}\otimes u_{R}^{(2)}(g,hk) \right ) \end{align} $$In the last line we used formula (2.130) and Lemma 2.3(iii) to remove  ${V_g^L}^*$. From this, we see that
${V_g^L}^*$. From this, we see that ![]() $c_{R,1}=c_{R,2}$, completing the proof.
$c_{R,1}=c_{R,2}$, completing the proof.
Lemma 2.17. Set
 $$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta_1<\theta_2<\frac\pi 2,\quad \text{with } \mathop{\mathrm{IG}}\nolimits(\omega,\theta_1),\ \mathop{\mathrm{IG}}\nolimits(\omega,\theta_2)\neq\emptyset. \end{align} $$
$$ \begin{align} \omega\in\mathop{\mathcal{SL}}\nolimits, \quad 0<\theta_1<\theta_2<\frac\pi 2,\quad \text{with } \mathop{\mathrm{IG}}\nolimits(\omega,\theta_1),\ \mathop{\mathrm{IG}}\nolimits(\omega,\theta_2)\neq\emptyset. \end{align} $$Then we have
Definition 2.18. From this lemma, for any ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ with
$\omega \in \mathop {\mathcal {SL}}\nolimits $ with ![]() $\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $, we may define
$\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $, we may define
independent of the choice of ![]() $\theta $. This is the index we associate to
$\theta $. This is the index we associate to ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ with
$\omega \in \mathop {\mathcal {SL}}\nolimits $ with ![]() $\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $.
$\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $.
Proof. By the assumption, there are some ![]() $\left (\tilde \beta _g\right )\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta _1)$ and
$\left (\tilde \beta _g\right )\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta _1)$ and  $(\eta _g^\sigma )\in {\mathcal T}\left ( \left (\theta _1, \tilde \beta _g\right )\right )$. Because
$(\eta _g^\sigma )\in {\mathcal T}\left ( \left (\theta _1, \tilde \beta _g\right )\right )$. Because ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $, there are
$\omega \in \mathop {\mathcal {SL}}\nolimits $, there are ![]() $ \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ and
$ \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ and ![]() $(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta _2}$ by the definition. Setting
$(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta _2}$ by the definition. Setting ![]() $\alpha _0:=\alpha _L\otimes \alpha _R$, we have
$\alpha _0:=\alpha _L\otimes \alpha _R$, we have ![]() $\alpha =({\textrm {{inner}}})\circ \alpha _0\circ \Theta $. Because
$\alpha =({\textrm {{inner}}})\circ \alpha _0\circ \Theta $. Because ![]() $0<\theta _1<\theta _2<\frac \pi 2$, we also have
$0<\theta _1<\theta _2<\frac \pi 2$, we also have  $(\eta _g^\sigma )\in {\mathcal T}( (\theta _2, \tilde \beta _g ))$, and
$(\eta _g^\sigma )\in {\mathcal T}( (\theta _2, \tilde \beta _g ))$, and ![]() $\left (\tilde \beta _g\right )\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta _2)$. For the same reason, we also have
$\left (\tilde \beta _g\right )\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta _2)$. For the same reason, we also have ![]() $(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta _1}$.
$(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta _1}$.
By Lemma 2.1, there is some
 $$ \begin{align} ( (W_g), (u_\sigma(g,h))) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta_1, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$
$$ \begin{align} ( (W_g), (u_\sigma(g,h))) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta_1, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$However, we also have
 $$ \begin{align} ( (W_g), (u_\sigma(g,h))) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta_2, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$
$$ \begin{align} ( (W_g), (u_\sigma(g,h))) \in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta_2, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$Therefore, we obtain ![]() $h^{(5)} \left ( \omega , \theta _1 \right ) = h^{(5)} \left ( \omega , \theta _2 \right ) $.
$h^{(5)} \left ( \omega , \theta _1 \right ) = h^{(5)} \left ( \omega , \theta _2 \right ) $.
This completes the proof of Theorem 2.7.
3 The existence of  $\tilde \beta $ for SPT phases
$\tilde \beta $ for SPT phases
In this section, we give a sufficient condition for ![]() $\mathop {\mathrm {IG}}\nolimits (\omega )$ to be nonempty. We consider the same setting as in Section 2.2.
$\mathop {\mathrm {IG}}\nolimits (\omega )$ to be nonempty. We consider the same setting as in Section 2.2.
Theorem 3.1. For any ![]() $0<\theta <\frac \pi 2$ and
$0<\theta <\frac \pi 2$ and ![]() $\alpha \in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$ satisfying
$\alpha \in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$ satisfying ![]() $ \omega _0\circ \alpha \circ \beta _g=\omega _0\circ \alpha $ for all
$ \omega _0\circ \alpha \circ \beta _g=\omega _0\circ \alpha $ for all ![]() $g\in G$,
$g\in G$, ![]() $\mathop {\mathrm {IG}}\nolimits (\omega _0\circ \alpha ,\theta )$ is not empty.
$\mathop {\mathrm {IG}}\nolimits (\omega _0\circ \alpha ,\theta )$ is not empty.
The strategy is as follows. Our infinite tensor product state ![]() $\omega _{0}$ can be written as
$\omega _{0}$ can be written as ![]() $\omega _{0}=\omega _{U}\otimes \omega _{D}$, with pure states
$\omega _{0}=\omega _{U}\otimes \omega _{D}$, with pure states ![]() $\omega _{U}, \omega _{D}$ on
$\omega _{U}, \omega _{D}$ on ![]() ${\mathcal A}_{H_{U}}, {\mathcal A}_{H_{D}}$. Using the factorisation property of
${\mathcal A}_{H_{U}}, {\mathcal A}_{H_{D}}$. Using the factorisation property of ![]() $\alpha \in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$, we can show that
$\alpha \in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$, we can show that
 $$ \begin{align} \alpha\circ\beta_{g}^{U}\circ\alpha^{-1} &=\left ( id_{{\mathcal A}_{H_{D}}}\otimes \tilde Y_{g,U}\right )\circ\left ( {\text{an automorphism localised at } C_{\theta_2}} \right )\circ({\textrm{{inner}}}), \end{align} $$
$$ \begin{align} \alpha\circ\beta_{g}^{U}\circ\alpha^{-1} &=\left ( id_{{\mathcal A}_{H_{D}}}\otimes \tilde Y_{g,U}\right )\circ\left ( {\text{an automorphism localised at } C_{\theta_2}} \right )\circ({\textrm{{inner}}}), \end{align} $$ $$ \begin{align} \alpha\circ\beta_{g}\circ\alpha^{-1} &=\left ( \tilde Y_{g,D}\otimes \tilde Y_{g,U}\right )\circ\left ( {\text{an automorphism localised at } C_{\theta_2}} \right )\circ({\textrm{{inner}}}), \end{align} $$
$$ \begin{align} \alpha\circ\beta_{g}\circ\alpha^{-1} &=\left ( \tilde Y_{g,D}\otimes \tilde Y_{g,U}\right )\circ\left ( {\text{an automorphism localised at } C_{\theta_2}} \right )\circ({\textrm{{inner}}}), \end{align} $$with  $\tilde Y_{g,U}:=\beta _{g}^{C_{\left (\theta _{0.8},\frac \pi 2\right ],U}}\xi _U, \tilde Y_{g,D}:=\beta _{g}^{C_{\left (\theta _{0.8},\frac \pi 2\right ],U}}\xi _D$ automorphisms on
$\tilde Y_{g,U}:=\beta _{g}^{C_{\left (\theta _{0.8},\frac \pi 2\right ],U}}\xi _U, \tilde Y_{g,D}:=\beta _{g}^{C_{\left (\theta _{0.8},\frac \pi 2\right ],U}}\xi _D$ automorphisms on ![]() $\left ( C_{\theta _{0.8}}\right )^c\cap H_{U}, \left ( C_{\theta _{0.8}}\right )^c\cap H_{D}$, respectively. The ‘automorphism localised at
$\left ( C_{\theta _{0.8}}\right )^c\cap H_{U}, \left ( C_{\theta _{0.8}}\right )^c\cap H_{D}$, respectively. The ‘automorphism localised at ![]() $C_{\theta _2}$’ can be split into left and right parts. (See equation (3.28).) From the latter equation and
$C_{\theta _2}$’ can be split into left and right parts. (See equation (3.28).) From the latter equation and ![]() $\omega _0\circ \alpha \circ \beta _g=\omega _0\circ \alpha $, one can show that
$\omega _0\circ \alpha \circ \beta _g=\omega _0\circ \alpha $, one can show that ![]() $\omega _{U} \tilde Y_{g,U}$ is quasiequivalent to a state of the form
$\omega _{U} \tilde Y_{g,U}$ is quasiequivalent to a state of the form ![]() $\varphi _{L}\otimes \varphi _{R}\otimes \omega _{C_{\theta _{2}}^{c}}$, where
$\varphi _{L}\otimes \varphi _{R}\otimes \omega _{C_{\theta _{2}}^{c}}$, where ![]() $\varphi _{L}, \varphi _{R}$ are states on
$\varphi _{L}, \varphi _{R}$ are states on ![]() ${\mathcal A}_{C_{\theta _{2}\cap H_{L}}}, {\mathcal A}_{C_{\theta _{2}\cap H_{R}}}$ and
${\mathcal A}_{C_{\theta _{2}\cap H_{L}}}, {\mathcal A}_{C_{\theta _{2}\cap H_{R}}}$ and ![]() $\omega _{C_{\theta _{2}}^{c}}$ is the pure state given as the restriction of
$\omega _{C_{\theta _{2}}^{c}}$ is the pure state given as the restriction of ![]() $\omega _{0}$ to
$\omega _{0}$ to  ${\mathcal A}_{{C_{\theta _{2}}^{c}}}$ (with
${\mathcal A}_{{C_{\theta _{2}}^{c}}}$ (with ![]() $\theta _{0.8}<\theta _{2}$). A general lemma proven in the following (Lemma 3.2), derived from the homogeneity of pure state spaces on UHF-algebras, then allows us to show the existence of automorphisms
$\theta _{0.8}<\theta _{2}$). A general lemma proven in the following (Lemma 3.2), derived from the homogeneity of pure state spaces on UHF-algebras, then allows us to show the existence of automorphisms ![]() $Z_{g,L}, Z_{g,R}$ on
$Z_{g,L}, Z_{g,R}$ on ![]() ${\mathcal A}_{C_{\theta _{2}\cap H_{L}}}, {\mathcal A}_{C_{\theta _{2}\cap H_{R}}}$ satisfying
${\mathcal A}_{C_{\theta _{2}\cap H_{L}}}, {\mathcal A}_{C_{\theta _{2}\cap H_{R}}}$ satisfying  $\omega _{U} \tilde Y_{g,U}\simeq \omega _{U}\circ \left ( Z_{g,L}\otimes Z_{g,R}\otimes \mathop {\mathrm {id}}\nolimits _{C_{\theta _{2}}^{c}}\right )$. Combining this with equation (3.1) basically gives the Theorem.
$\omega _{U} \tilde Y_{g,U}\simeq \omega _{U}\circ \left ( Z_{g,L}\otimes Z_{g,R}\otimes \mathop {\mathrm {id}}\nolimits _{C_{\theta _{2}}^{c}}\right )$. Combining this with equation (3.1) basically gives the Theorem.
Now let us start with a precise mathematical proof. We first prepare the general lemma just mentioned.
Lemma 3.2. Let ![]() ${\mathfrak A},{\mathfrak B}$ be UHF-algebras. Let
${\mathfrak A},{\mathfrak B}$ be UHF-algebras. Let ![]() $\omega $ be a pure state on
$\omega $ be a pure state on ![]() ${\mathfrak A}\otimes {\mathfrak B}$ and
${\mathfrak A}\otimes {\mathfrak B}$ and ![]() $\varphi _{{\mathfrak A}}, \varphi _{{\mathfrak B}}$ states on
$\varphi _{{\mathfrak A}}, \varphi _{{\mathfrak B}}$ states on ![]() ${\mathfrak A}, {\mathfrak B}$, respectively. Assume that
${\mathfrak A}, {\mathfrak B}$, respectively. Assume that ![]() $\omega $ is quasiequivalent to
$\omega $ is quasiequivalent to ![]() $\varphi _{{\mathfrak A}}\otimes \varphi _{{\mathfrak B}}$. Then for any pure states
$\varphi _{{\mathfrak A}}\otimes \varphi _{{\mathfrak B}}$. Then for any pure states ![]() $\psi _{{\mathfrak A}}, \psi _{{\mathfrak B}}$ on
$\psi _{{\mathfrak A}}, \psi _{{\mathfrak B}}$ on ![]() ${\mathfrak A}, {\mathfrak B}$, there are automorphisms
${\mathfrak A}, {\mathfrak B}$, there are automorphisms ![]() $\gamma _{{\mathfrak A}}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak A}\right ), \gamma _{{\mathfrak B}}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak B}\right )$ and a unitary
$\gamma _{{\mathfrak A}}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak A}\right ), \gamma _{{\mathfrak B}}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak B}\right )$ and a unitary ![]() $u\in {\mathcal U}\left ({\mathfrak A}\otimes {\mathfrak B}\right )$ such that
$u\in {\mathcal U}\left ({\mathfrak A}\otimes {\mathfrak B}\right )$ such that
If ![]() $\psi _{{\mathfrak A}}$ and
$\psi _{{\mathfrak A}}$ and ![]() $\varphi _{{\mathfrak A}}$ are quasiequivalent, then we may set
$\varphi _{{\mathfrak A}}$ are quasiequivalent, then we may set ![]() $\gamma _{{\mathfrak A}}=\mathop {\mathrm {id}}\nolimits _{{\mathfrak A}}$.
$\gamma _{{\mathfrak A}}=\mathop {\mathrm {id}}\nolimits _{{\mathfrak A}}$.
Proof. Let ![]() $({\mathcal H}_{\omega },\pi _{\omega },\Omega _{\omega }), \left ({\mathcal H}_{\varphi _{{\mathfrak A}}},\pi _{\varphi _{{\mathfrak A}}},\Omega _{\varphi _{{\mathfrak A}}}\right ), \left ({\mathcal H}_{\varphi _{{\mathfrak B}}},\pi _{\varphi _{{\mathfrak B}}},\Omega _{\varphi _{{\mathfrak B}}}\right )$ be GNS triples of
$({\mathcal H}_{\omega },\pi _{\omega },\Omega _{\omega }), \left ({\mathcal H}_{\varphi _{{\mathfrak A}}},\pi _{\varphi _{{\mathfrak A}}},\Omega _{\varphi _{{\mathfrak A}}}\right ), \left ({\mathcal H}_{\varphi _{{\mathfrak B}}},\pi _{\varphi _{{\mathfrak B}}},\Omega _{\varphi _{{\mathfrak B}}}\right )$ be GNS triples of ![]() $\omega , \varphi _{{\mathfrak A}}, \varphi _{{\mathfrak B}}$, respectively. Then
$\omega , \varphi _{{\mathfrak A}}, \varphi _{{\mathfrak B}}$, respectively. Then ![]() $\left ({\mathcal H}_{\varphi _{{\mathfrak A}}}\otimes {\mathcal H}_{\varphi _{{\mathfrak B}}},\pi _{\varphi _{{\mathfrak A}}}\otimes \pi _{\varphi _{{\mathfrak B}}},\Omega _{\varphi _{{\mathfrak A}}}\otimes \Omega _{\varphi _{{\mathfrak B}}}\right )$ is a GNS triple of
$\left ({\mathcal H}_{\varphi _{{\mathfrak A}}}\otimes {\mathcal H}_{\varphi _{{\mathfrak B}}},\pi _{\varphi _{{\mathfrak A}}}\otimes \pi _{\varphi _{{\mathfrak B}}},\Omega _{\varphi _{{\mathfrak A}}}\otimes \Omega _{\varphi _{{\mathfrak B}}}\right )$ is a GNS triple of ![]() $\varphi _{{\mathfrak A}}\otimes \varphi _{{\mathfrak B}}$. As
$\varphi _{{\mathfrak A}}\otimes \varphi _{{\mathfrak B}}$. As ![]() $\omega $ is quasiequivalent to
$\omega $ is quasiequivalent to ![]() $\varphi _{{\mathfrak A}}\otimes \varphi _{{\mathfrak B}}$, there is a
$\varphi _{{\mathfrak A}}\otimes \varphi _{{\mathfrak B}}$, there is a ![]() $*$-isomorphism
$*$-isomorphism ![]() $\tau :\pi _{\omega }\left ({\mathfrak A}\otimes {\mathfrak B}\right )''\to \pi _{\varphi _{{\mathfrak A}}}({\mathfrak A})''\otimes \pi _{\varphi _{{\mathfrak B}}}({\mathfrak B})''$ such that
$\tau :\pi _{\omega }\left ({\mathfrak A}\otimes {\mathfrak B}\right )''\to \pi _{\varphi _{{\mathfrak A}}}({\mathfrak A})''\otimes \pi _{\varphi _{{\mathfrak B}}}({\mathfrak B})''$ such that ![]() $\tau \circ \pi _{\omega }=\pi _{\varphi _{{\mathfrak A}}}\otimes \pi _{\varphi _{{\mathfrak B}}}$. Because
$\tau \circ \pi _{\omega }=\pi _{\varphi _{{\mathfrak A}}}\otimes \pi _{\varphi _{{\mathfrak B}}}$. Because ![]() $\omega $ is pure, we have
$\omega $ is pure, we have ![]() $\pi _{\omega }\left ({\mathfrak A}\otimes {\mathfrak B}\right )''={\mathcal B}({\mathcal H}_{\omega })$, and from the isomorphism
$\pi _{\omega }\left ({\mathfrak A}\otimes {\mathfrak B}\right )''={\mathcal B}({\mathcal H}_{\omega })$, and from the isomorphism ![]() $\tau $, we have that
$\tau $, we have that ![]() $\pi _{\varphi _{{\mathfrak A}}}({\mathfrak A})''\otimes \pi _{\varphi _{{\mathfrak B}}}({\mathfrak B})''$ is also a type I factor. Then from [Reference TakesakiT, Theorem 2.30V], both
$\pi _{\varphi _{{\mathfrak A}}}({\mathfrak A})''\otimes \pi _{\varphi _{{\mathfrak B}}}({\mathfrak B})''$ is also a type I factor. Then from [Reference TakesakiT, Theorem 2.30V], both ![]() $\pi _{\varphi _{{\mathfrak A}}}({\mathfrak A})''$ and
$\pi _{\varphi _{{\mathfrak A}}}({\mathfrak A})''$ and ![]() $\pi _{\varphi _{{\mathfrak B}}}({\mathfrak B})''$ are type I factors. The restriction of
$\pi _{\varphi _{{\mathfrak B}}}({\mathfrak B})''$ are type I factors. The restriction of ![]() $\tau $ to
$\tau $ to ![]() $\pi _{\omega }\left ({\mathfrak A}\otimes {\mathbb C}\mathbb I_{{\mathfrak B}}\right )''$ implies a
$\pi _{\omega }\left ({\mathfrak A}\otimes {\mathbb C}\mathbb I_{{\mathfrak B}}\right )''$ implies a ![]() $*$-isomorphism from
$*$-isomorphism from ![]() $\pi _{\omega }\left ({\mathfrak A}\otimes {\mathbb C}\mathbb I_{{\mathfrak B}}\right )''$ onto the type I factor
$\pi _{\omega }\left ({\mathfrak A}\otimes {\mathbb C}\mathbb I_{{\mathfrak B}}\right )''$ onto the type I factor ![]() $\pi _{\varphi _{{\mathfrak A}}}({\mathfrak A})''$. Hence we see that
$\pi _{\varphi _{{\mathfrak A}}}({\mathfrak A})''$. Hence we see that ![]() $\pi _{\omega }\left ({\mathfrak A}\otimes {\mathbb C}\mathbb I_{{\mathfrak B}}\right )''$ is a type I factor. Therefore, from [Reference TakesakiT, Theorem 1.31V], there are Hilbert spaces
$\pi _{\omega }\left ({\mathfrak A}\otimes {\mathbb C}\mathbb I_{{\mathfrak B}}\right )''$ is a type I factor. Therefore, from [Reference TakesakiT, Theorem 1.31V], there are Hilbert spaces ![]() ${\mathcal K}_{{\mathfrak A}},{\mathcal K}_{{\mathfrak B}}$ and a unitary
${\mathcal K}_{{\mathfrak A}},{\mathcal K}_{{\mathfrak B}}$ and a unitary ![]() $W: {\mathcal H}_\omega \to {\mathcal K}_{{\mathfrak A}}\otimes {\mathcal K}_{{\mathfrak B}}$ such that
$W: {\mathcal H}_\omega \to {\mathcal K}_{{\mathfrak A}}\otimes {\mathcal K}_{{\mathfrak B}}$ such that ![]() $\mathop {\mathrm {Ad}}\nolimits \left ( W\right )\left ( \pi _{\omega }\left ({\mathfrak A}\otimes {\mathbb C}\mathbb I_{{\mathfrak B}}\right )''\right )= {\mathcal B}\left ( {\mathcal K}_{{\mathfrak A}}\right )\otimes {\mathbb C}\mathbb I_{{\mathcal K}_{{\mathfrak B}}} $. Because
$\mathop {\mathrm {Ad}}\nolimits \left ( W\right )\left ( \pi _{\omega }\left ({\mathfrak A}\otimes {\mathbb C}\mathbb I_{{\mathfrak B}}\right )''\right )= {\mathcal B}\left ( {\mathcal K}_{{\mathfrak A}}\right )\otimes {\mathbb C}\mathbb I_{{\mathcal K}_{{\mathfrak B}}} $. Because ![]() $\omega $ is pure, we also have
$\omega $ is pure, we also have ![]() $\mathop {\mathrm {Ad}}\nolimits \left ( W\right )\left ( \pi _{\omega }\left ({\mathbb C}\mathbb I_{{\mathfrak A}} \otimes {\mathfrak B}\right )''\right )={\mathbb C}\mathbb I_{{\mathcal K}_{{\mathfrak A}}}\otimes {\mathcal B}({\mathcal K}_{{\mathfrak B}})$. From this, we see that there are irreducible representations
$\mathop {\mathrm {Ad}}\nolimits \left ( W\right )\left ( \pi _{\omega }\left ({\mathbb C}\mathbb I_{{\mathfrak A}} \otimes {\mathfrak B}\right )''\right )={\mathbb C}\mathbb I_{{\mathcal K}_{{\mathfrak A}}}\otimes {\mathcal B}({\mathcal K}_{{\mathfrak B}})$. From this, we see that there are irreducible representations ![]() $\rho _{{\mathfrak A}}, \rho _{{\mathfrak B}}$ of
$\rho _{{\mathfrak A}}, \rho _{{\mathfrak B}}$ of ![]() ${\mathfrak A}$ and
${\mathfrak A}$ and ![]() ${\mathfrak B}$ on
${\mathfrak B}$ on ![]() ${\mathcal K}_{{\mathfrak A}}, {\mathcal K}_{{\mathfrak B}}$ such that
${\mathcal K}_{{\mathfrak A}}, {\mathcal K}_{{\mathfrak B}}$ such that ![]() $\mathop {\mathrm {Ad}}\nolimits (W)\circ \pi _{\omega }=\rho _{{\mathfrak A}}\otimes \rho _{{\mathfrak B}}$. Fix some unit vectors
$\mathop {\mathrm {Ad}}\nolimits (W)\circ \pi _{\omega }=\rho _{{\mathfrak A}}\otimes \rho _{{\mathfrak B}}$. Fix some unit vectors ![]() $\xi _{{\mathfrak A}}\in {\mathcal K}_{{\mathfrak A}}, \xi _{{\mathfrak B}}\in {\mathcal K}_{{\mathfrak B}}$. Then because of the irreducibility of
$\xi _{{\mathfrak A}}\in {\mathcal K}_{{\mathfrak A}}, \xi _{{\mathfrak B}}\in {\mathcal K}_{{\mathfrak B}}$. Then because of the irreducibility of ![]() $\rho _{{\mathfrak B}}$ and
$\rho _{{\mathfrak B}}$ and ![]() $\rho _{{\mathfrak B}}$, we have that
$\rho _{{\mathfrak B}}$, we have that ![]() $\omega _{{\mathfrak A}}:=\left \langle \xi _{{\mathfrak A}},\rho _{{\mathfrak A}}\left (\cdot \right )\xi _{{\mathfrak A}}\right \rangle $ and
$\omega _{{\mathfrak A}}:=\left \langle \xi _{{\mathfrak A}},\rho _{{\mathfrak A}}\left (\cdot \right )\xi _{{\mathfrak A}}\right \rangle $ and ![]() $\omega _{{\mathfrak B}}:=\left \langle \xi _{{\mathfrak B}},\rho _{{\mathfrak B}}\left (\cdot \right )\xi _{{\mathfrak B}}\right \rangle $ are pure states on
$\omega _{{\mathfrak B}}:=\left \langle \xi _{{\mathfrak B}},\rho _{{\mathfrak B}}\left (\cdot \right )\xi _{{\mathfrak B}}\right \rangle $ are pure states on ![]() ${\mathfrak A}, {\mathfrak B}$. By [Reference Kishimoto, Ozawa and SakaiKOS, Theorem 1.1] (originally proved by Powers [Reference PowersP] for UHF-algebras), for any pure states
${\mathfrak A}, {\mathfrak B}$. By [Reference Kishimoto, Ozawa and SakaiKOS, Theorem 1.1] (originally proved by Powers [Reference PowersP] for UHF-algebras), for any pure states ![]() $\psi _{{\mathfrak A}}, \psi _{{\mathfrak B}}$ on
$\psi _{{\mathfrak A}}, \psi _{{\mathfrak B}}$ on ![]() ${\mathfrak A}, {\mathfrak B}$, there exist automorphisms
${\mathfrak A}, {\mathfrak B}$, there exist automorphisms ![]() $\gamma _{{\mathfrak A}}\in \mathop {\mathrm {Aut}}\nolimits ({\mathfrak A}), \gamma _{{\mathfrak B}}\in \mathop {\mathrm {Aut}}\nolimits ({\mathfrak B})$ such that
$\gamma _{{\mathfrak A}}\in \mathop {\mathrm {Aut}}\nolimits ({\mathfrak A}), \gamma _{{\mathfrak B}}\in \mathop {\mathrm {Aut}}\nolimits ({\mathfrak B})$ such that ![]() $\omega _{{\mathfrak A}}=\psi _{{\mathfrak A}}\circ \gamma _{{\mathfrak A}}$
$\omega _{{\mathfrak A}}=\psi _{{\mathfrak A}}\circ \gamma _{{\mathfrak A}}$ ![]() $\omega _{{\mathfrak B}}=\psi _{{\mathfrak B}}\circ \gamma _{{\mathfrak B}}$. Now for unit vectors
$\omega _{{\mathfrak B}}=\psi _{{\mathfrak B}}\circ \gamma _{{\mathfrak B}}$. Now for unit vectors ![]() $W^{*}\left (\xi _{{\mathfrak A}}\otimes \xi _{{\mathfrak B}}\right ),\Omega _{\omega }\in {\mathcal H}_{\omega }$, by Kadison’s transitivity theorem and the irreducibility of
$W^{*}\left (\xi _{{\mathfrak A}}\otimes \xi _{{\mathfrak B}}\right ),\Omega _{\omega }\in {\mathcal H}_{\omega }$, by Kadison’s transitivity theorem and the irreducibility of ![]() $\pi _\omega $ there exists a unitary
$\pi _\omega $ there exists a unitary ![]() $u\in {\mathcal U}\left ( {\mathfrak A}\otimes {\mathfrak B}\right )$ such that
$u\in {\mathcal U}\left ( {\mathfrak A}\otimes {\mathfrak B}\right )$ such that ![]() $\pi _{\omega }(u)\Omega _{\omega }=W^{*}\left (\xi _{{\mathfrak A}}\otimes \xi _{{\mathfrak B}}\right )$. Substituting this, we obtain
$\pi _{\omega }(u)\Omega _{\omega }=W^{*}\left (\xi _{{\mathfrak A}}\otimes \xi _{{\mathfrak B}}\right )$. Substituting this, we obtain
 $$ \begin{align} \omega&=\left\langle\Omega_{\omega},\pi_{\omega}\left (\cdot\right ) \Omega_{\omega}\right\rangle =\left\langle\pi_{\omega}(u^{*})W^{*}\left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right ),\pi_{\omega}\left (\cdot\right )\pi_{\omega}(u^{*})W^{*}\left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right )\right\rangle\notag\\ &=\left\langle W^{*}\left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right ),\pi_{\omega}\circ\mathop{\mathrm{Ad}}\nolimits(u)\left (\cdot\right ) W^{*}\left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right )\right\rangle\notag\\ &=\left\langle\left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right ),\left (\rho_{{\mathfrak A}}\otimes \rho_{{\mathfrak B}}\right )\circ\mathop{\mathrm{Ad}}\nolimits(u)\left (\cdot\right ) \left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right )\right\rangle \notag \\ &=\left ( \omega_{{\mathfrak A}}\otimes\omega_{{\mathfrak B}}\right )\circ \mathop{\mathrm{Ad}}\nolimits(u) =\left ( \psi_{{\mathfrak A}}\circ \gamma_{{\mathfrak A}}\otimes \psi_{{\mathfrak B}}\circ \gamma_{{\mathfrak B}}\right ) \circ \mathop{\mathrm{Ad}}\nolimits(u). \end{align} $$
$$ \begin{align} \omega&=\left\langle\Omega_{\omega},\pi_{\omega}\left (\cdot\right ) \Omega_{\omega}\right\rangle =\left\langle\pi_{\omega}(u^{*})W^{*}\left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right ),\pi_{\omega}\left (\cdot\right )\pi_{\omega}(u^{*})W^{*}\left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right )\right\rangle\notag\\ &=\left\langle W^{*}\left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right ),\pi_{\omega}\circ\mathop{\mathrm{Ad}}\nolimits(u)\left (\cdot\right ) W^{*}\left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right )\right\rangle\notag\\ &=\left\langle\left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right ),\left (\rho_{{\mathfrak A}}\otimes \rho_{{\mathfrak B}}\right )\circ\mathop{\mathrm{Ad}}\nolimits(u)\left (\cdot\right ) \left (\xi_{{\mathfrak A}}\otimes \xi_{{\mathfrak B}}\right )\right\rangle \notag \\ &=\left ( \omega_{{\mathfrak A}}\otimes\omega_{{\mathfrak B}}\right )\circ \mathop{\mathrm{Ad}}\nolimits(u) =\left ( \psi_{{\mathfrak A}}\circ \gamma_{{\mathfrak A}}\otimes \psi_{{\mathfrak B}}\circ \gamma_{{\mathfrak B}}\right ) \circ \mathop{\mathrm{Ad}}\nolimits(u). \end{align} $$Now assume that ![]() $\psi _{{\mathfrak A}}$ and
$\psi _{{\mathfrak A}}$ and ![]() $\varphi _{{\mathfrak A}}$ are quasiequivalent – that is, the GNS representations of
$\varphi _{{\mathfrak A}}$ are quasiequivalent – that is, the GNS representations of ![]() $\psi _{{\mathfrak A}}, \varphi _{{\mathfrak A}}$, denoted by
$\psi _{{\mathfrak A}}, \varphi _{{\mathfrak A}}$, denoted by ![]() $\pi _{\psi _{{\mathfrak A}}}$ and
$\pi _{\psi _{{\mathfrak A}}}$ and ![]() $\pi _{\varphi _{{\mathfrak A}}}$ are quasiequivalent. From the foregoing argument,
$\pi _{\varphi _{{\mathfrak A}}}$ are quasiequivalent. From the foregoing argument, ![]() $\pi _{\omega }\rvert _{{\mathfrak A}}$ and
$\pi _{\omega }\rvert _{{\mathfrak A}}$ and ![]() $\pi _{\varphi _{{\mathfrak A}}}$ are quasiequivalent. At the same time,
$\pi _{\varphi _{{\mathfrak A}}}$ are quasiequivalent. At the same time, ![]() $\pi _{\omega }\rvert _{{\mathfrak A}}$ and
$\pi _{\omega }\rvert _{{\mathfrak A}}$ and ![]() $\rho _{{\mathfrak A}}$ are quasiequivalent. Therefore,
$\rho _{{\mathfrak A}}$ are quasiequivalent. Therefore, ![]() $\pi _{\psi _{{\mathfrak A}}}$ and
$\pi _{\psi _{{\mathfrak A}}}$ and ![]() $\rho _{{\mathfrak A}}$ are quasiequivalent. Because both of them are irreducible, we see that a pure state
$\rho _{{\mathfrak A}}$ are quasiequivalent. Because both of them are irreducible, we see that a pure state ![]() ${\psi _{{\mathfrak A}}}$ can be represented by a unit vector
${\psi _{{\mathfrak A}}}$ can be represented by a unit vector ![]() $\zeta \in {\mathcal K}_{{\mathfrak A}}$, as
$\zeta \in {\mathcal K}_{{\mathfrak A}}$, as ![]() ${\psi _{{\mathfrak A}}}=\left \langle \zeta ,\rho _{{\mathfrak A}}\left (\cdot \right ) \zeta \right \rangle $. Because
${\psi _{{\mathfrak A}}}=\left \langle \zeta ,\rho _{{\mathfrak A}}\left (\cdot \right ) \zeta \right \rangle $. Because ![]() $\rho _{{\mathfrak A}}$ is irreducible, by Kadison’s transitivity theorem there exists a unitary
$\rho _{{\mathfrak A}}$ is irreducible, by Kadison’s transitivity theorem there exists a unitary ![]() $w\in {\mathcal U}\left ( {\mathfrak A}\right )$ such that
$w\in {\mathcal U}\left ( {\mathfrak A}\right )$ such that ![]() $\rho _{{\mathfrak A}}(w^{*})\zeta =\xi _{{\mathfrak A}}$. Hence we obtain
$\rho _{{\mathfrak A}}(w^{*})\zeta =\xi _{{\mathfrak A}}$. Hence we obtain ![]() ${\psi _{{\mathfrak A}}}\circ \mathop {\mathrm {Ad}}\nolimits (w)=\omega _{{\mathfrak A}}$. Substituting this instead of
${\psi _{{\mathfrak A}}}\circ \mathop {\mathrm {Ad}}\nolimits (w)=\omega _{{\mathfrak A}}$. Substituting this instead of ![]() $\omega _{{\mathfrak A}}=\psi _{{\mathfrak A}}\circ \gamma _{{\mathfrak A}}$ in equation (3.4), we obtain
$\omega _{{\mathfrak A}}=\psi _{{\mathfrak A}}\circ \gamma _{{\mathfrak A}}$ in equation (3.4), we obtain
proving the last claim.
Lemma 3.3. Let ![]() ${\mathfrak B},{\mathfrak A}_{1,L},{\mathfrak A}_{2,L},{\mathfrak A}_{1,R},{\mathfrak A}_{2,R}$ be UHF-algebras. Set
${\mathfrak B},{\mathfrak A}_{1,L},{\mathfrak A}_{2,L},{\mathfrak A}_{1,R},{\mathfrak A}_{2,R}$ be UHF-algebras. Set ![]() ${\mathfrak A}_{1}:={\mathfrak A}_{1,L}\otimes {\mathfrak A}_{1,R}$,
${\mathfrak A}_{1}:={\mathfrak A}_{1,L}\otimes {\mathfrak A}_{1,R}$, ![]() ${\mathfrak A}_{2}:={\mathfrak A}_{2,L}\otimes {\mathfrak A}_{2,R}$,
${\mathfrak A}_{2}:={\mathfrak A}_{2,L}\otimes {\mathfrak A}_{2,R}$, ![]() ${\mathfrak A}_{L}:={\mathfrak A}_{1,L}\otimes {\mathfrak A}_{2,L}$ and
${\mathfrak A}_{L}:={\mathfrak A}_{1,L}\otimes {\mathfrak A}_{2,L}$ and ![]() ${\mathfrak A}_{R}:={\mathfrak A}_{1,R}\otimes {\mathfrak A}_{2,R}$. Let
${\mathfrak A}_{R}:={\mathfrak A}_{1,R}\otimes {\mathfrak A}_{2,R}$. Let  $\omega , \varphi _{L}^{\left (1,2\right )}, \varphi _{R}^{\left (1,2\right )}, \psi $ be pure states on
$\omega , \varphi _{L}^{\left (1,2\right )}, \varphi _{R}^{\left (1,2\right )}, \psi $ be pure states on ![]() ${\mathfrak B}\otimes {\mathfrak A}_{1}, {\mathfrak A}_{L}, {\mathfrak A}_{R}, {\mathfrak B}$, respectively. Suppose that
${\mathfrak B}\otimes {\mathfrak A}_{1}, {\mathfrak A}_{L}, {\mathfrak A}_{R}, {\mathfrak B}$, respectively. Suppose that ![]() $\omega $ is quasiequivalent to
$\omega $ is quasiequivalent to  $\left .\left ( \psi \otimes \varphi _{L}^{\left (1,2\right )}\otimes \varphi _{R}^{\left (1,2\right )} \right )\right \rvert _{{\mathfrak B}\otimes {\mathfrak A}_{1}}$. Then for any pure states
$\left .\left ( \psi \otimes \varphi _{L}^{\left (1,2\right )}\otimes \varphi _{R}^{\left (1,2\right )} \right )\right \rvert _{{\mathfrak B}\otimes {\mathfrak A}_{1}}$. Then for any pure states  $\varphi _{L}^{(1)}, \varphi _{R}^{(1)}$ on
$\varphi _{L}^{(1)}, \varphi _{R}^{(1)}$ on ![]() ${\mathfrak A}_{1,L}, {\mathfrak A}_{1,R}$, respectively, there are automorphisms
${\mathfrak A}_{1,L}, {\mathfrak A}_{1,R}$, respectively, there are automorphisms  $\gamma _{L}^{(1)}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak A}_{1,L}\right ), \gamma _{R}^{(1)}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak A}_{1,R}\right )$ and a unitary
$\gamma _{L}^{(1)}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak A}_{1,L}\right ), \gamma _{R}^{(1)}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak A}_{1,R}\right )$ and a unitary ![]() $u\in {\mathcal U}\left ({\mathfrak B}\otimes {\mathfrak A}_{1}\right )$ such that
$u\in {\mathcal U}\left ({\mathfrak B}\otimes {\mathfrak A}_{1}\right )$ such that
 $$ \begin{align} \omega=\left ( \psi\otimes \left ( \varphi_{L}^{(1)}\circ\gamma_{L}^{(1)}\right ) \otimes \left ( \varphi_{R}^{(1)}\circ\gamma_{R}^{(1)}\right ) \right )\circ\mathop{\mathrm{Ad}}\nolimits u. \end{align} $$
$$ \begin{align} \omega=\left ( \psi\otimes \left ( \varphi_{L}^{(1)}\circ\gamma_{L}^{(1)}\right ) \otimes \left ( \varphi_{R}^{(1)}\circ\gamma_{R}^{(1)}\right ) \right )\circ\mathop{\mathrm{Ad}}\nolimits u. \end{align} $$Proof. Because the pure state ![]() $\omega $ is quasiequivalent to
$\omega $ is quasiequivalent to  $\left .\left ( \psi \otimes \varphi _{L}^{\left (1,2\right )}\otimes \varphi _{R}^{\left (1,2\right )} \right )\right \rvert _{{\mathfrak B}\otimes {\mathfrak A}_{1}} =\psi \otimes \left .\left ( \varphi _{L}^{\left (1,2\right )}\otimes \varphi _{R}^{\left (1,2\right )} \right )\right \rvert _{{\mathfrak A}_{1}}$, applying Lemma 3.2 means that for any pure states
$\left .\left ( \psi \otimes \varphi _{L}^{\left (1,2\right )}\otimes \varphi _{R}^{\left (1,2\right )} \right )\right \rvert _{{\mathfrak B}\otimes {\mathfrak A}_{1}} =\psi \otimes \left .\left ( \varphi _{L}^{\left (1,2\right )}\otimes \varphi _{R}^{\left (1,2\right )} \right )\right \rvert _{{\mathfrak A}_{1}}$, applying Lemma 3.2 means that for any pure states  $\varphi _{L}^{(1)}, \varphi _{R}^{(1)}$ on
$\varphi _{L}^{(1)}, \varphi _{R}^{(1)}$ on ![]() ${\mathfrak A}_{1,L}, {\mathfrak A}_{1,R}$, there exist an automorphism
${\mathfrak A}_{1,L}, {\mathfrak A}_{1,R}$, there exist an automorphism ![]() $S\in \mathop {\mathrm {Aut}}\nolimits {\mathfrak A}_1$ and a unitary
$S\in \mathop {\mathrm {Aut}}\nolimits {\mathfrak A}_1$ and a unitary ![]() $v\in {\mathcal U}\left ( {\mathfrak B}\otimes {\mathfrak A}_1\right )$ such that
$v\in {\mathcal U}\left ( {\mathfrak B}\otimes {\mathfrak A}_1\right )$ such that
 $$ \begin{align} \omega=\left ( \psi\otimes\left ( \left ( \varphi_{L}^{(1)} \otimes \varphi_{R}^{(1)}\right )\circ S\right ) \right )\circ \mathop{\mathrm{Ad}}\nolimits v. \end{align} $$
$$ \begin{align} \omega=\left ( \psi\otimes\left ( \left ( \varphi_{L}^{(1)} \otimes \varphi_{R}^{(1)}\right )\circ S\right ) \right )\circ \mathop{\mathrm{Ad}}\nolimits v. \end{align} $$From equation (3.7) and  $\omega \sim _{\text {q.e.}}\left .\left ( \psi \otimes \varphi _{L}^{\left (1,2\right )}\otimes \varphi _{R}^{\left (1,2\right )} \right )\right \rvert _{{\mathfrak B}\otimes {\mathfrak A}_{1}}$, we get
$\omega \sim _{\text {q.e.}}\left .\left ( \psi \otimes \varphi _{L}^{\left (1,2\right )}\otimes \varphi _{R}^{\left (1,2\right )} \right )\right \rvert _{{\mathfrak B}\otimes {\mathfrak A}_{1}}$, we get  $ \left ( \psi \otimes \left ( \left ( \varphi _{L}^{(1)} \otimes \varphi _{R}^{(1)}\right )\circ S\right ) \right )\sim _{\text {q.e.}} \left .\left ( \psi \otimes \varphi _{L}^{\left (1,2\right )}\otimes \varphi _{R}^{\left (1,2\right )} \right )\right \rvert _{{\mathfrak B}\otimes {\mathfrak A}_{1}}$, which implies
$ \left ( \psi \otimes \left ( \left ( \varphi _{L}^{(1)} \otimes \varphi _{R}^{(1)}\right )\circ S\right ) \right )\sim _{\text {q.e.}} \left .\left ( \psi \otimes \varphi _{L}^{\left (1,2\right )}\otimes \varphi _{R}^{\left (1,2\right )} \right )\right \rvert _{{\mathfrak B}\otimes {\mathfrak A}_{1}}$, which implies
 $$ \begin{align} \left ( \varphi_{L}^{(1)} \otimes \varphi_{R}^{(1)}\right )\circ S\sim_{\text{q.e.}} \left.\left ( \varphi_{L}^{\left(1,2\right)}\otimes \varphi_{R}^{\left(1,2\right)} \right )\right\rvert_{{\mathfrak A}_{1}}. \end{align} $$
$$ \begin{align} \left ( \varphi_{L}^{(1)} \otimes \varphi_{R}^{(1)}\right )\circ S\sim_{\text{q.e.}} \left.\left ( \varphi_{L}^{\left(1,2\right)}\otimes \varphi_{R}^{\left(1,2\right)} \right )\right\rvert_{{\mathfrak A}_{1}}. \end{align} $$Applying Lemma 3.2 to formula (3.8), there are automorphisms  $\gamma _{L}^{(1)}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak A}_{1,L}\right ), \gamma _{R}^{(1)}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak A}_{1,R}\right )$ and a unitary
$\gamma _{L}^{(1)}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak A}_{1,L}\right ), \gamma _{R}^{(1)}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathfrak A}_{1,R}\right )$ and a unitary ![]() $w\in {\mathcal U}\left ( {\mathfrak A}_{1}\right )$ such that
$w\in {\mathcal U}\left ( {\mathfrak A}_{1}\right )$ such that
 $$ \begin{align} \left ( \varphi_{L}^{(1)} \otimes \varphi_{R}^{(1)}\right )\circ S=\left (\left ( \varphi_{L}^{(1)}\circ\gamma_{L}^{(1)}\right ) \otimes \left ( \varphi_{R}^{(1)}\circ\gamma_{R}^{(1)}\right ) \right )\circ\mathop{\mathrm{Ad}}\nolimits w. \end{align} $$
$$ \begin{align} \left ( \varphi_{L}^{(1)} \otimes \varphi_{R}^{(1)}\right )\circ S=\left (\left ( \varphi_{L}^{(1)}\circ\gamma_{L}^{(1)}\right ) \otimes \left ( \varphi_{R}^{(1)}\circ\gamma_{R}^{(1)}\right ) \right )\circ\mathop{\mathrm{Ad}}\nolimits w. \end{align} $$Substituting this into equation (3.7), we obtain equation (3.6).
Lemma 3.4. Let ![]() ${\mathfrak A}_L, {\mathfrak A}_R, {\mathfrak B}_{LU}, {\mathfrak B}_{LD}, {\mathfrak B}_{RU}, {\mathfrak B}_{RD}, {\mathfrak C}_U, {\mathfrak C}_D$ be UHF-algebras, and set
${\mathfrak A}_L, {\mathfrak A}_R, {\mathfrak B}_{LU}, {\mathfrak B}_{LD}, {\mathfrak B}_{RU}, {\mathfrak B}_{RD}, {\mathfrak C}_U, {\mathfrak C}_D$ be UHF-algebras, and set
 $$ \begin{align} {\mathfrak B}_U&:={\mathfrak B}_{LU}\otimes{\mathfrak B}_{RU},& {\mathfrak B}_D&:={\mathfrak B}_{LD}\otimes{\mathfrak B}_{RD},& {\mathfrak B}_L&:={\mathfrak B}_{LD}\otimes{\mathfrak B}_{LU},& {\mathfrak B}_R&:={\mathfrak B}_{RD}\otimes{\mathfrak B}_{RU}, \notag\\ {\mathfrak A}&:={\mathfrak A}_L\otimes{\mathfrak A}_R,&{\mathfrak B}&:={\mathfrak B}_D\otimes{\mathfrak B}_U={\mathfrak B}_L\otimes{\mathfrak B}_R,& {\mathfrak C}&:={\mathfrak C}_D\otimes{\mathfrak C}_U,& {\mathfrak D}&:={\mathfrak A}\otimes{\mathfrak B}\otimes{\mathfrak C}. \end{align} $$
$$ \begin{align} {\mathfrak B}_U&:={\mathfrak B}_{LU}\otimes{\mathfrak B}_{RU},& {\mathfrak B}_D&:={\mathfrak B}_{LD}\otimes{\mathfrak B}_{RD},& {\mathfrak B}_L&:={\mathfrak B}_{LD}\otimes{\mathfrak B}_{LU},& {\mathfrak B}_R&:={\mathfrak B}_{RD}\otimes{\mathfrak B}_{RU}, \notag\\ {\mathfrak A}&:={\mathfrak A}_L\otimes{\mathfrak A}_R,&{\mathfrak B}&:={\mathfrak B}_D\otimes{\mathfrak B}_U={\mathfrak B}_L\otimes{\mathfrak B}_R,& {\mathfrak C}&:={\mathfrak C}_D\otimes{\mathfrak C}_U,& {\mathfrak D}&:={\mathfrak A}\otimes{\mathfrak B}\otimes{\mathfrak C}. \end{align} $$Let ![]() $\omega _X$ be a pure state on each
$\omega _X$ be a pure state on each ![]() $X={\mathfrak A}_L, {\mathfrak A}_R, {\mathfrak B}_{LU}, {\mathfrak B}_{LD}, {\mathfrak B}_{RU}, {\mathfrak B}_{RD}, {\mathfrak C}_U, {\mathfrak C}_D$, and set
$X={\mathfrak A}_L, {\mathfrak A}_R, {\mathfrak B}_{LU}, {\mathfrak B}_{LD}, {\mathfrak B}_{RU}, {\mathfrak B}_{RD}, {\mathfrak C}_U, {\mathfrak C}_D$, and set
 $$ \begin{align} \omega_{{\mathfrak B}{\mathfrak C}}^U&:=\omega_{{\mathfrak B}_{LU}}\otimes\omega_{{\mathfrak B}_{RU}}\otimes\omega_{{\mathfrak C}_U}\quad \text{on } {\mathfrak B}_U\otimes{\mathfrak C}_U,\notag\\ \omega_{{\mathfrak B}{\mathfrak C}}^D&:=\omega_{{\mathfrak B}_{LD}}\otimes\omega_{{\mathfrak B}_{RD}}\otimes\omega_{{\mathfrak C}_D}\quad \text{on } {\mathfrak B}_D\otimes{\mathfrak C}_D,\notag\\ \omega_{{\mathfrak A}}&:=\omega_{{\mathfrak A}_L}\otimes\omega_{{\mathfrak A}_R} \quad \text{on }{\mathfrak A},\notag\\ \omega_{{\mathfrak A}{\mathfrak B}}^L &:=\omega_{{\mathfrak A}_L}\otimes\omega_{{\mathfrak B}_{LU}}\otimes\omega_{{\mathfrak B}_{LD}} \quad \text{on } {\mathfrak A}_L\otimes{\mathfrak B}_L, \notag\\ \omega_{{\mathfrak A}{\mathfrak B}}^R &:=\omega_{{\mathfrak A}_R}\otimes\omega_{{\mathfrak B}_{RU}}\otimes\omega_{{\mathfrak B}_{RD}} \quad \text{on } {\mathfrak A}_R\otimes{\mathfrak B}_R, \notag\\ \omega_0&:=\bigotimes_{\substack{X={\mathfrak A}_L, {\mathfrak A}_R, {\mathfrak B}_{LU}, {\mathfrak B}_{LD},\\ {\mathfrak B}_{RU}, {\mathfrak B}_{RD}, {\mathfrak C}_U, {\mathfrak C}_D}}\omega_X\quad \text{on } {\mathfrak D}. \end{align} $$
$$ \begin{align} \omega_{{\mathfrak B}{\mathfrak C}}^U&:=\omega_{{\mathfrak B}_{LU}}\otimes\omega_{{\mathfrak B}_{RU}}\otimes\omega_{{\mathfrak C}_U}\quad \text{on } {\mathfrak B}_U\otimes{\mathfrak C}_U,\notag\\ \omega_{{\mathfrak B}{\mathfrak C}}^D&:=\omega_{{\mathfrak B}_{LD}}\otimes\omega_{{\mathfrak B}_{RD}}\otimes\omega_{{\mathfrak C}_D}\quad \text{on } {\mathfrak B}_D\otimes{\mathfrak C}_D,\notag\\ \omega_{{\mathfrak A}}&:=\omega_{{\mathfrak A}_L}\otimes\omega_{{\mathfrak A}_R} \quad \text{on }{\mathfrak A},\notag\\ \omega_{{\mathfrak A}{\mathfrak B}}^L &:=\omega_{{\mathfrak A}_L}\otimes\omega_{{\mathfrak B}_{LU}}\otimes\omega_{{\mathfrak B}_{LD}} \quad \text{on } {\mathfrak A}_L\otimes{\mathfrak B}_L, \notag\\ \omega_{{\mathfrak A}{\mathfrak B}}^R &:=\omega_{{\mathfrak A}_R}\otimes\omega_{{\mathfrak B}_{RU}}\otimes\omega_{{\mathfrak B}_{RD}} \quad \text{on } {\mathfrak A}_R\otimes{\mathfrak B}_R, \notag\\ \omega_0&:=\bigotimes_{\substack{X={\mathfrak A}_L, {\mathfrak A}_R, {\mathfrak B}_{LU}, {\mathfrak B}_{LD},\\ {\mathfrak B}_{RU}, {\mathfrak B}_{RD}, {\mathfrak C}_U, {\mathfrak C}_D}}\omega_X\quad \text{on } {\mathfrak D}. \end{align} $$Let ![]() $\alpha ,\hat \alpha $ be automorphisms on
$\alpha ,\hat \alpha $ be automorphisms on ![]() ${\mathfrak D}$ which allow the following decompositions:
${\mathfrak D}$ which allow the following decompositions:
 $$ \begin{align} \hat\alpha&=\left (\rho_{{\mathfrak B}{\mathfrak C}}^U\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak A}}\otimes \rho_{{\mathfrak B}{\mathfrak C}}^D\right ) \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_U}\otimes\hat\gamma_{{\mathfrak A}{\mathfrak B}}^L\otimes \hat\gamma_{{\mathfrak A}{\mathfrak B}}^R \otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_D} \right )\circ({\textrm{{inner}}}), \end{align} $$
$$ \begin{align} \hat\alpha&=\left (\rho_{{\mathfrak B}{\mathfrak C}}^U\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak A}}\otimes \rho_{{\mathfrak B}{\mathfrak C}}^D\right ) \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_U}\otimes\hat\gamma_{{\mathfrak A}{\mathfrak B}}^L\otimes \hat\gamma_{{\mathfrak A}{\mathfrak B}}^R \otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_D} \right )\circ({\textrm{{inner}}}), \end{align} $$ $$ \begin{align} \alpha&=\left (\rho_{{\mathfrak B}{\mathfrak C}}^U\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak A}}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak B}_D\otimes{\mathfrak C}_D}\right ) \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_U}\otimes\gamma_{{\mathfrak A}{\mathfrak B}}^L\otimes \gamma_{{\mathfrak A}{\mathfrak B}}^R \otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_D} \right )\circ({\textrm{{inner}}}). \end{align} $$
$$ \begin{align} \alpha&=\left (\rho_{{\mathfrak B}{\mathfrak C}}^U\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak A}}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak B}_D\otimes{\mathfrak C}_D}\right ) \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_U}\otimes\gamma_{{\mathfrak A}{\mathfrak B}}^L\otimes \gamma_{{\mathfrak A}{\mathfrak B}}^R \otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_D} \right )\circ({\textrm{{inner}}}). \end{align} $$Here,  $\rho _{{\mathfrak B}{\mathfrak C}}^U, \rho _{{\mathfrak B}{\mathfrak C}}^D$ are automorphisms on
$\rho _{{\mathfrak B}{\mathfrak C}}^U, \rho _{{\mathfrak B}{\mathfrak C}}^D$ are automorphisms on ![]() ${\mathfrak B}_U\otimes {\mathfrak C}_U, {\mathfrak B}_D\otimes {\mathfrak C}_D$, respectively. For each
${\mathfrak B}_U\otimes {\mathfrak C}_U, {\mathfrak B}_D\otimes {\mathfrak C}_D$, respectively. For each ![]() $\sigma =L,R$,
$\sigma =L,R$, ![]() $\gamma _{{\mathfrak A}{\mathfrak B}}^{\sigma },\hat \gamma _{{\mathfrak A}{\mathfrak B}}^{\sigma }$ are automorphisms on
$\gamma _{{\mathfrak A}{\mathfrak B}}^{\sigma },\hat \gamma _{{\mathfrak A}{\mathfrak B}}^{\sigma }$ are automorphisms on ![]() ${\mathfrak A}_{\sigma }\otimes {\mathfrak B}_{{\sigma }D}\otimes {\mathfrak B}_{{\sigma }U}$. Suppose that
${\mathfrak A}_{\sigma }\otimes {\mathfrak B}_{{\sigma }D}\otimes {\mathfrak B}_{{\sigma }U}$. Suppose that ![]() $\omega _0\circ \hat \alpha =\omega _0$. Then there are automorphisms
$\omega _0\circ \hat \alpha =\omega _0$. Then there are automorphisms ![]() $\eta _L,\eta _R$ on
$\eta _L,\eta _R$ on ![]() ${\mathfrak A}_L\otimes {\mathfrak B}_{LD}\otimes {\mathfrak B}_{LU}, {\mathfrak A}_R\otimes {\mathfrak B}_{RD}\otimes {\mathfrak B}_{RU}$ such that
${\mathfrak A}_L\otimes {\mathfrak B}_{LD}\otimes {\mathfrak B}_{LU}, {\mathfrak A}_R\otimes {\mathfrak B}_{RD}\otimes {\mathfrak B}_{RU}$ such that ![]() $\omega _0\circ \alpha $ is quasiequivalent to
$\omega _0\circ \alpha $ is quasiequivalent to ![]() $\omega _0\circ \left (\mathop {\mathrm {id}}\nolimits _{{\mathfrak C}_U}\otimes \eta _L\otimes \eta _R\otimes \mathop {\mathrm {id}}\nolimits _{{\mathfrak C}_D}\right )$.
$\omega _0\circ \left (\mathop {\mathrm {id}}\nolimits _{{\mathfrak C}_U}\otimes \eta _L\otimes \eta _R\otimes \mathop {\mathrm {id}}\nolimits _{{\mathfrak C}_D}\right )$.
Proof. First we claim that there are automorphisms  $\theta _{\mathfrak B}^{LU}\in \mathop {\mathrm {Aut}}\nolimits {{\mathfrak B}_{LU}}, \theta _{\mathfrak B}^{RU}\in \mathop {\mathrm {Aut}}\nolimits {\mathfrak B}_{RU}$ and a unitary
$\theta _{\mathfrak B}^{LU}\in \mathop {\mathrm {Aut}}\nolimits {{\mathfrak B}_{LU}}, \theta _{\mathfrak B}^{RU}\in \mathop {\mathrm {Aut}}\nolimits {\mathfrak B}_{RU}$ and a unitary ![]() $u\in {\mathcal U}\left ( {\mathfrak B}^U\otimes {\mathfrak C}^U\right )$ such that
$u\in {\mathcal U}\left ( {\mathfrak B}^U\otimes {\mathfrak C}^U\right )$ such that
 $$ \begin{align} \omega_{{\mathfrak B}{\mathfrak C}}^U\circ\rho_{{\mathfrak B}{\mathfrak C}}^U =\omega_{{\mathfrak B}{\mathfrak C}}^U\circ \left ( \theta_{{\mathfrak B}}^{LU}\otimes \theta_{{\mathfrak B}}^{RU}\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak C}^U}\right ) \circ\mathop{\mathrm{Ad}}\nolimits\left ( u\right ). \end{align} $$
$$ \begin{align} \omega_{{\mathfrak B}{\mathfrak C}}^U\circ\rho_{{\mathfrak B}{\mathfrak C}}^U =\omega_{{\mathfrak B}{\mathfrak C}}^U\circ \left ( \theta_{{\mathfrak B}}^{LU}\otimes \theta_{{\mathfrak B}}^{RU}\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak C}^U}\right ) \circ\mathop{\mathrm{Ad}}\nolimits\left ( u\right ). \end{align} $$To prove this, we first note that from ![]() $\omega _0\circ \hat \alpha =\omega _0$ and the decomposition (3.12), we have
$\omega _0\circ \hat \alpha =\omega _0$ and the decomposition (3.12), we have
 $$ \begin{align} \omega_{{\mathfrak B}{\mathfrak C}}^U\circ\rho_{{\mathfrak B}{\mathfrak C}}^U\otimes \omega_{{\mathfrak A}} \otimes \omega_{{\mathfrak B}{\mathfrak C}}^D\circ\rho_{{\mathfrak B}{\mathfrak C}}^D \sim_{\text{q.e.}} \omega_{{\mathfrak C}_U} \otimes\omega_{{\mathfrak A}{\mathfrak B}}^L\circ\left (\widehat{ \gamma_{{\mathfrak A}{\mathfrak B}}^L}\right )^{-1} \otimes \omega_{{\mathfrak A}{\mathfrak B}}^R\circ\left ( \widehat{\gamma_{{\mathfrak A}{\mathfrak B}}^R}\right )^{-1} \otimes\omega_{{\mathfrak C}_D}. \end{align} $$
$$ \begin{align} \omega_{{\mathfrak B}{\mathfrak C}}^U\circ\rho_{{\mathfrak B}{\mathfrak C}}^U\otimes \omega_{{\mathfrak A}} \otimes \omega_{{\mathfrak B}{\mathfrak C}}^D\circ\rho_{{\mathfrak B}{\mathfrak C}}^D \sim_{\text{q.e.}} \omega_{{\mathfrak C}_U} \otimes\omega_{{\mathfrak A}{\mathfrak B}}^L\circ\left (\widehat{ \gamma_{{\mathfrak A}{\mathfrak B}}^L}\right )^{-1} \otimes \omega_{{\mathfrak A}{\mathfrak B}}^R\circ\left ( \widehat{\gamma_{{\mathfrak A}{\mathfrak B}}^R}\right )^{-1} \otimes\omega_{{\mathfrak C}_D}. \end{align} $$From this, because both states are pure (hence the restrictions of their GNS representations onto ![]() ${\mathfrak C}_U\otimes {\mathfrak B}_U$ are factors), we have
${\mathfrak C}_U\otimes {\mathfrak B}_U$ are factors), we have
 $$ \begin{align} \omega_{{\mathfrak B}{\mathfrak C}}^U\circ\rho_{{\mathfrak B}{\mathfrak C}}^U&= \left.\left ( \omega_{{\mathfrak B}{\mathfrak C}}^U\circ\rho_{{\mathfrak B}{\mathfrak C}}^U\otimes \omega_{{\mathfrak A}} \otimes \omega_{{\mathfrak B}{\mathfrak C}}^D\circ\rho_{{\mathfrak B}{\mathfrak C}}^D \right ) \right\rvert_{{\mathfrak C}_U\otimes {\mathfrak B}_U}\notag\\ &\sim_{\text{q.e.}} \omega_{{\mathfrak C}_U} \otimes\left.\left ( \omega_{{\mathfrak A}{\mathfrak B}}^L\circ\left ( \widehat{\gamma_{{\mathfrak A}{\mathfrak B}}^L}\right )^{-1} \otimes \omega_{{\mathfrak A}{\mathfrak B}}^R\circ\left ( \widehat{\gamma_{{\mathfrak A}{\mathfrak B}}^R}\right )^{-1}\right )\right\rvert_{{\mathfrak B}_U}. \end{align} $$
$$ \begin{align} \omega_{{\mathfrak B}{\mathfrak C}}^U\circ\rho_{{\mathfrak B}{\mathfrak C}}^U&= \left.\left ( \omega_{{\mathfrak B}{\mathfrak C}}^U\circ\rho_{{\mathfrak B}{\mathfrak C}}^U\otimes \omega_{{\mathfrak A}} \otimes \omega_{{\mathfrak B}{\mathfrak C}}^D\circ\rho_{{\mathfrak B}{\mathfrak C}}^D \right ) \right\rvert_{{\mathfrak C}_U\otimes {\mathfrak B}_U}\notag\\ &\sim_{\text{q.e.}} \omega_{{\mathfrak C}_U} \otimes\left.\left ( \omega_{{\mathfrak A}{\mathfrak B}}^L\circ\left ( \widehat{\gamma_{{\mathfrak A}{\mathfrak B}}^L}\right )^{-1} \otimes \omega_{{\mathfrak A}{\mathfrak B}}^R\circ\left ( \widehat{\gamma_{{\mathfrak A}{\mathfrak B}}^R}\right )^{-1}\right )\right\rvert_{{\mathfrak B}_U}. \end{align} $$We apply Lemma 3.3 for  ${\mathfrak B}, {\mathfrak A}_{1L}, {\mathfrak A}_{1R}, {\mathfrak A}_{2L}, {\mathfrak A}_{2R}, \omega , \varphi _L^{(1,2)}, \varphi _R^{(1,2)}, \psi $, replaced by
${\mathfrak B}, {\mathfrak A}_{1L}, {\mathfrak A}_{1R}, {\mathfrak A}_{2L}, {\mathfrak A}_{2R}, \omega , \varphi _L^{(1,2)}, \varphi _R^{(1,2)}, \psi $, replaced by  ${\mathfrak C}_U, {\mathfrak B}_{LU}, {\mathfrak B}_{RU}, {\mathfrak A}_{L}\otimes {\mathfrak B}_{LD}, {\mathfrak A}_R\otimes {\mathfrak B}_{RD}, \omega _{{\mathfrak B}{\mathfrak C}}^U\circ \rho _{{\mathfrak B}{\mathfrak C}}^U, \omega _{{\mathfrak A}{\mathfrak B}}^L\circ \left (\widehat {\gamma _{{\mathfrak A}{\mathfrak B}}^L}\right )^{-1}, \omega _{{\mathfrak A}{\mathfrak B}}^R\circ \left ( \widehat {\gamma _{{\mathfrak A}{\mathfrak B}}^R}\right )^{-1}, \omega _{{\mathfrak C}_U}$, respectively. From equation (3.16), they satisfy the conditions in Lemma 3.3. Applying Lemma 3.3 – for pure states
${\mathfrak C}_U, {\mathfrak B}_{LU}, {\mathfrak B}_{RU}, {\mathfrak A}_{L}\otimes {\mathfrak B}_{LD}, {\mathfrak A}_R\otimes {\mathfrak B}_{RD}, \omega _{{\mathfrak B}{\mathfrak C}}^U\circ \rho _{{\mathfrak B}{\mathfrak C}}^U, \omega _{{\mathfrak A}{\mathfrak B}}^L\circ \left (\widehat {\gamma _{{\mathfrak A}{\mathfrak B}}^L}\right )^{-1}, \omega _{{\mathfrak A}{\mathfrak B}}^R\circ \left ( \widehat {\gamma _{{\mathfrak A}{\mathfrak B}}^R}\right )^{-1}, \omega _{{\mathfrak C}_U}$, respectively. From equation (3.16), they satisfy the conditions in Lemma 3.3. Applying Lemma 3.3 – for pure states  $\varphi _L^{(1)}=\omega _{{\mathfrak B}_{LU}}$ and
$\varphi _L^{(1)}=\omega _{{\mathfrak B}_{LU}}$ and  $\varphi _R^{(1)}=\omega _{{\mathfrak B}_{RU}}$ – we obtain automorphisms
$\varphi _R^{(1)}=\omega _{{\mathfrak B}_{RU}}$ – we obtain automorphisms  $\theta _{{\mathfrak B}}^{LU}\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathfrak B}_{LU}\right ), \theta _{{\mathfrak B}}^{RU}\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathfrak B}_{RU}\right )$ and a unitary
$\theta _{{\mathfrak B}}^{LU}\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathfrak B}_{LU}\right ), \theta _{{\mathfrak B}}^{RU}\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathfrak B}_{RU}\right )$ and a unitary ![]() $u\in {\mathcal U}\left ({\mathfrak B}_U\otimes {\mathfrak C}_U\right )$ satisfying equation (3.14).
$u\in {\mathcal U}\left ({\mathfrak B}_U\otimes {\mathfrak C}_U\right )$ satisfying equation (3.14).
We set
 $$ \begin{align} \begin{split} \eta_L&:=\left ( \theta^{LU}_{{\mathfrak B}}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak A}_L}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak B}_{LD}}\right ) \circ\gamma_{{\mathfrak A}{\mathfrak B}}^L \in \mathop{\mathrm{Aut}}\nolimits\left ({\mathfrak B}_{LU}\otimes {\mathfrak A}_L\otimes{\mathfrak B}_{LD}\right )\\ \eta_R&:=\left ( \theta^{RU}_{{\mathfrak B}}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak A}_R}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak B}_{RD}}\right ) \circ\gamma_{{\mathfrak A}{\mathfrak B}}^R \in \mathop{\mathrm{Aut}}\nolimits\left ( {\mathfrak B}_{RU}\otimes {\mathfrak A}_R\otimes{\mathfrak B}_{RD}\right ). \end{split} \end{align} $$
$$ \begin{align} \begin{split} \eta_L&:=\left ( \theta^{LU}_{{\mathfrak B}}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak A}_L}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak B}_{LD}}\right ) \circ\gamma_{{\mathfrak A}{\mathfrak B}}^L \in \mathop{\mathrm{Aut}}\nolimits\left ({\mathfrak B}_{LU}\otimes {\mathfrak A}_L\otimes{\mathfrak B}_{LD}\right )\\ \eta_R&:=\left ( \theta^{RU}_{{\mathfrak B}}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak A}_R}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak B}_{RD}}\right ) \circ\gamma_{{\mathfrak A}{\mathfrak B}}^R \in \mathop{\mathrm{Aut}}\nolimits\left ( {\mathfrak B}_{RU}\otimes {\mathfrak A}_R\otimes{\mathfrak B}_{RD}\right ). \end{split} \end{align} $$Then we have
 $$ \begin{align} \begin{split} \omega_0\circ\alpha&= \left ( \omega_{{\mathfrak A}_L}\otimes\omega_{{\mathfrak A}_R} \otimes \omega_{{\mathfrak B}{\mathfrak C}}^U\otimes \omega_{{\mathfrak B}{\mathfrak C}}^D \right )\circ\alpha\\ &\sim_{\text{q.e.}} \left ( \omega_{{\mathfrak A}_L}\otimes\omega_{{\mathfrak A}_R} \otimes \omega_{{\mathfrak B}{\mathfrak C}}^U\circ\rho_{{\mathfrak B}{\mathfrak C}}^U \otimes \omega_{{\mathfrak B}{\mathfrak C}}^D \right ) \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_U}\otimes \gamma_{{\mathfrak A}{\mathfrak B}}^L\otimes \gamma_{{\mathfrak A}{\mathfrak B}}^R \otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_D} \right )\\ &\sim_{\text{q.e.}} \left ( \omega_{{\mathfrak A}_L}\otimes\omega_{{\mathfrak A}_R} \otimes \omega_{{\mathfrak B}{\mathfrak C}}^U \otimes \omega_{{\mathfrak B}{\mathfrak C}}^D \right )\\ &\quad \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_U}\otimes \left ( \left ( \theta_{{\mathfrak B}}^{LU}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak A}_L}\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak B}_{LD}} \right )\circ\gamma_{{\mathfrak A}{\mathfrak B}}^L\right ) \otimes \left ( \left ( \theta_{{\mathfrak B}}^{RU}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak A}_R}\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak B}_{RD}} \right )\circ\gamma_{{\mathfrak A}{\mathfrak B}}^R\right ) \otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_D} \right )\\ &=\omega_0\circ\left (\mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_U}\otimes\eta_L\otimes\eta_R\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_D}\right ). \end{split} \end{align} $$
$$ \begin{align} \begin{split} \omega_0\circ\alpha&= \left ( \omega_{{\mathfrak A}_L}\otimes\omega_{{\mathfrak A}_R} \otimes \omega_{{\mathfrak B}{\mathfrak C}}^U\otimes \omega_{{\mathfrak B}{\mathfrak C}}^D \right )\circ\alpha\\ &\sim_{\text{q.e.}} \left ( \omega_{{\mathfrak A}_L}\otimes\omega_{{\mathfrak A}_R} \otimes \omega_{{\mathfrak B}{\mathfrak C}}^U\circ\rho_{{\mathfrak B}{\mathfrak C}}^U \otimes \omega_{{\mathfrak B}{\mathfrak C}}^D \right ) \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_U}\otimes \gamma_{{\mathfrak A}{\mathfrak B}}^L\otimes \gamma_{{\mathfrak A}{\mathfrak B}}^R \otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_D} \right )\\ &\sim_{\text{q.e.}} \left ( \omega_{{\mathfrak A}_L}\otimes\omega_{{\mathfrak A}_R} \otimes \omega_{{\mathfrak B}{\mathfrak C}}^U \otimes \omega_{{\mathfrak B}{\mathfrak C}}^D \right )\\ &\quad \circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_U}\otimes \left ( \left ( \theta_{{\mathfrak B}}^{LU}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak A}_L}\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak B}_{LD}} \right )\circ\gamma_{{\mathfrak A}{\mathfrak B}}^L\right ) \otimes \left ( \left ( \theta_{{\mathfrak B}}^{RU}\otimes \mathop{\mathrm{id}}\nolimits_{{\mathfrak A}_R}\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak B}_{RD}} \right )\circ\gamma_{{\mathfrak A}{\mathfrak B}}^R\right ) \otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_D} \right )\\ &=\omega_0\circ\left (\mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_U}\otimes\eta_L\otimes\eta_R\otimes\mathop{\mathrm{id}}\nolimits_{{\mathfrak C}_D}\right ). \end{split} \end{align} $$This completes the proof.
Now we are ready to prove Theorem 3.1.
Proof of Theorem 3.1.
Set ![]() $0<\theta <\frac \pi 2$ and
$0<\theta <\frac \pi 2$ and ![]() $\alpha \in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$ satisfying
$\alpha \in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$ satisfying ![]() $ \omega _0\circ \alpha \circ \beta _g=\omega _0\circ \alpha $ for all
$ \omega _0\circ \alpha \circ \beta _g=\omega _0\circ \alpha $ for all ![]() $g\in G$. We would like to show that
$g\in G$. We would like to show that ![]() $\mathop {\mathrm {IG}}\nolimits (\omega _0\circ \alpha ,\theta )$ is not empty.
$\mathop {\mathrm {IG}}\nolimits (\omega _0\circ \alpha ,\theta )$ is not empty.
Let us set ![]() $\theta _{2.2}:=\theta $ and consider
$\theta _{2.2}:=\theta $ and consider ![]() $\theta _{0.8}, \theta _1, \theta _{1.2}, \theta _{1.8}, \theta _2, \theta _{2.8}, \theta _3, \theta _{3.2}$ satisfying formula (2.11) for this
$\theta _{0.8}, \theta _1, \theta _{1.2}, \theta _{1.8}, \theta _2, \theta _{2.8}, \theta _3, \theta _{3.2}$ satisfying formula (2.11) for this ![]() $\theta _{2.2}$. Because
$\theta _{2.2}$. Because ![]() $\alpha \in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$, there is a decomposition given by formulas (2.12), (2.13) and (2.14). Using this decomposition, set
$\alpha \in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$, there is a decomposition given by formulas (2.12), (2.13) and (2.14). Using this decomposition, set
 $$ \begin{align} \begin{split} \alpha_1&:=\alpha_{1D}\otimes\alpha_{1U},\quad \text{where}\\ \alpha_{1\zeta} &:= \left ( \alpha_{\left(\theta_1,\theta_2\right],\zeta} \otimes \alpha_{\left(\theta_2,\theta_3\right],\zeta}\otimes \alpha_{\left(\theta_3,\frac\pi 2\right],\zeta} \right ) \\ &\quad \circ \left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\zeta}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right],\zeta} \otimes \alpha_{\left(\theta_{2.8},\theta_{3.2}\right],\zeta} \right )\in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{\left ( \left ( C_{\theta_{0.8}}\right )^c\right )_\zeta} \right ) ,\quad\zeta=U,D,\\ \alpha_2&:=\alpha_{\left[0,\theta_1\right]} \in\mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\theta_1}}\right ). \end{split} \end{align} $$
$$ \begin{align} \begin{split} \alpha_1&:=\alpha_{1D}\otimes\alpha_{1U},\quad \text{where}\\ \alpha_{1\zeta} &:= \left ( \alpha_{\left(\theta_1,\theta_2\right],\zeta} \otimes \alpha_{\left(\theta_2,\theta_3\right],\zeta}\otimes \alpha_{\left(\theta_3,\frac\pi 2\right],\zeta} \right ) \\ &\quad \circ \left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\zeta}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right],\zeta} \otimes \alpha_{\left(\theta_{2.8},\theta_{3.2}\right],\zeta} \right )\in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{\left ( \left ( C_{\theta_{0.8}}\right )^c\right )_\zeta} \right ) ,\quad\zeta=U,D,\\ \alpha_2&:=\alpha_{\left[0,\theta_1\right]} \in\mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\theta_1}}\right ). \end{split} \end{align} $$We have ![]() $\alpha =({\textrm {{inner}}})\circ \alpha _2\circ \alpha _1$.
$\alpha =({\textrm {{inner}}})\circ \alpha _2\circ \alpha _1$.
We would like to show that  $\left (\alpha \circ \beta _g^U\circ \alpha ^{-1}, \alpha \circ \beta _g\circ \alpha ^{-1}\right )$ satisfy the conditions of
$\left (\alpha \circ \beta _g^U\circ \alpha ^{-1}, \alpha \circ \beta _g\circ \alpha ^{-1}\right )$ satisfy the conditions of ![]() $(\alpha ,\hat \alpha )$ in Lemma 3.4. We first show that they satisfy a decomposition corresponding to equations (3.12) and (3.13). For
$(\alpha ,\hat \alpha )$ in Lemma 3.4. We first show that they satisfy a decomposition corresponding to equations (3.12) and (3.13). For ![]() $\Gamma ={\mathbb Z}^2, H_U$, we have
$\Gamma ={\mathbb Z}^2, H_U$, we have
 $$ \begin{align} \left ( \beta_g^\Gamma\right )^{-1}\alpha\circ\beta_g^\Gamma\circ\alpha^{-1} =({\textrm{{inner}}})\circ\left ( \beta_g^\Gamma\right )^{-1}\circ\left ( \alpha_1\beta_g^\Gamma\alpha_1^{-1}\right ) \left ( \alpha_1\beta_g^\Gamma\alpha_1^{-1}\right )^{-1} \alpha_2\alpha_1\beta_g^{\Gamma}\alpha_1^{-1}\alpha_2^{-1}. \end{align} $$
$$ \begin{align} \left ( \beta_g^\Gamma\right )^{-1}\alpha\circ\beta_g^\Gamma\circ\alpha^{-1} =({\textrm{{inner}}})\circ\left ( \beta_g^\Gamma\right )^{-1}\circ\left ( \alpha_1\beta_g^\Gamma\alpha_1^{-1}\right ) \left ( \alpha_1\beta_g^\Gamma\alpha_1^{-1}\right )^{-1} \alpha_2\alpha_1\beta_g^{\Gamma}\alpha_1^{-1}\alpha_2^{-1}. \end{align} $$The latter part,  $\left ( \alpha _1\beta _g^\Gamma \alpha _1^{-1}\right )^{-1} \alpha _2\alpha _1\beta _g^{\Gamma }\alpha _1^{-1}\alpha _2^{-1}$, decomposes to left and right. To see this, first note that
$\left ( \alpha _1\beta _g^\Gamma \alpha _1^{-1}\right )^{-1} \alpha _2\alpha _1\beta _g^{\Gamma }\alpha _1^{-1}\alpha _2^{-1}$, decomposes to left and right. To see this, first note that
 $$ \begin{align} \alpha_1^{-1}\alpha_2\alpha_1 =\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}^{-1}\alpha_{\left[0,\theta_1\right]}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]} \in \mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{C_{\theta_{1.2}}} \right ). \end{align} $$
$$ \begin{align} \alpha_1^{-1}\alpha_2\alpha_1 =\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}^{-1}\alpha_{\left[0,\theta_1\right]}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]} \in \mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{C_{\theta_{1.2}}} \right ). \end{align} $$Because the conjugation  $\left ( \beta _g^\Gamma \right )^{-1}\cdot \beta _g^{\Gamma }$ does not change the support of an automorphism,
$\left ( \beta _g^\Gamma \right )^{-1}\cdot \beta _g^{\Gamma }$ does not change the support of an automorphism,  $\left ( \beta _g^\Gamma \right )^{-1}\left ( \alpha _1^{-1}\alpha _2\alpha _1\right ) \beta _g^{\Gamma }$ is also supported on
$\left ( \beta _g^\Gamma \right )^{-1}\left ( \alpha _1^{-1}\alpha _2\alpha _1\right ) \beta _g^{\Gamma }$ is also supported on ![]() ${C_{\theta _{1.2}}}$. Therefore, we have
${C_{\theta _{1.2}}}$. Therefore, we have
 $$ \begin{align} &\alpha_1\left ( \left ( \beta_g^\Gamma\right )^{-1}\left ( \alpha_1^{-1}\alpha_2\alpha_1\right ) \beta_g^{\Gamma}\right ) \alpha_1^{-1} \notag \\ &=\alpha_{\left(\theta_1,\theta_2\right]}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]} \left ( \beta_g^\Gamma\right )^{-1} \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}^{-1}\alpha_{\left[0,\theta_1\right]}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]} \beta_g^\Gamma\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}^{-1}\alpha_{\left(\theta_1,\theta_2\right]}^{-1}. \end{align} $$
$$ \begin{align} &\alpha_1\left ( \left ( \beta_g^\Gamma\right )^{-1}\left ( \alpha_1^{-1}\alpha_2\alpha_1\right ) \beta_g^{\Gamma}\right ) \alpha_1^{-1} \notag \\ &=\alpha_{\left(\theta_1,\theta_2\right]}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]} \left ( \beta_g^\Gamma\right )^{-1} \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}^{-1}\alpha_{\left[0,\theta_1\right]}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]} \beta_g^\Gamma\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}^{-1}\alpha_{\left(\theta_1,\theta_2\right]}^{-1}. \end{align} $$Hence we get the left-right decomposition
 $$ \begin{align} \begin{split} \left ( \alpha_1\beta_g^\Gamma\alpha_1^{-1}\right )^{-1} &\alpha_2\alpha_1\beta_g^{\Gamma}\alpha_1^{-1}\alpha_2^{-1} =\alpha_1\left ( \left ( \beta_g^\Gamma\right )^{-1}\left ( \alpha_1^{-1}\alpha_2\alpha_1\right ) \beta_g^{\Gamma}\right ) \alpha_1^{-1}\alpha_2^{-1}\\ &=\alpha_{\left(\theta_1,\theta_2\right]}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]} \left ( \beta_g^\Gamma\right )^{-1} \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}^{-1}\alpha_{\left[0,\theta_1\right]}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]} \beta_g^\Gamma\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}^{-1}\alpha_{\left(\theta_1,\theta_2\right]}^{-1}\circ\alpha_{\left[0,\theta_1\right]}^{-1}\\ &=:\bigotimes_{\sigma=L,R}\Xi_{\Gamma,g,\sigma}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \left ( \alpha_1\beta_g^\Gamma\alpha_1^{-1}\right )^{-1} &\alpha_2\alpha_1\beta_g^{\Gamma}\alpha_1^{-1}\alpha_2^{-1} =\alpha_1\left ( \left ( \beta_g^\Gamma\right )^{-1}\left ( \alpha_1^{-1}\alpha_2\alpha_1\right ) \beta_g^{\Gamma}\right ) \alpha_1^{-1}\alpha_2^{-1}\\ &=\alpha_{\left(\theta_1,\theta_2\right]}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]} \left ( \beta_g^\Gamma\right )^{-1} \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}^{-1}\alpha_{\left[0,\theta_1\right]}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]} \beta_g^\Gamma\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}^{-1}\alpha_{\left(\theta_1,\theta_2\right]}^{-1}\circ\alpha_{\left[0,\theta_1\right]}^{-1}\\ &=:\bigotimes_{\sigma=L,R}\Xi_{\Gamma,g,\sigma}. \end{split} \end{align} $$Here we set
 $$ \begin{align} &\Xi_{\Gamma,g,\sigma}:=\left ( \alpha_{\left(\theta_1,\theta_2\right],\sigma}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma} \left ( \beta_g^{\Gamma_\sigma}\right )^{-1} \right. \notag\\ &\quad \left.\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}^{-1}\alpha_{\left[0,\theta_1\right],\sigma }\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma} \beta_g^{\Gamma_\sigma}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}^{-1}\alpha_{\left(\theta_1,\theta_2\right],\sigma}^{-1}\circ\alpha_{\left[0,\theta_1\right],\sigma}^{-1} \right )\quad \in\mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{\left ( C_{\theta_2}\right )_\sigma}\right ). \end{align} $$
$$ \begin{align} &\Xi_{\Gamma,g,\sigma}:=\left ( \alpha_{\left(\theta_1,\theta_2\right],\sigma}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma} \left ( \beta_g^{\Gamma_\sigma}\right )^{-1} \right. \notag\\ &\quad \left.\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}^{-1}\alpha_{\left[0,\theta_1\right],\sigma }\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma} \beta_g^{\Gamma_\sigma}\alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}^{-1}\alpha_{\left(\theta_1,\theta_2\right],\sigma}^{-1}\circ\alpha_{\left[0,\theta_1\right],\sigma}^{-1} \right )\quad \in\mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{\left ( C_{\theta_2}\right )_\sigma}\right ). \end{align} $$On the other hand, the first part of equation (3.20) with ![]() $\Gamma ={\mathbb Z}^2,H_U$ satisfies
$\Gamma ={\mathbb Z}^2,H_U$ satisfies
 $$ \begin{align} \begin{split} \beta_g^{-1}\alpha_1\beta_g\alpha_1^{-1} = \xi_D\otimes\xi_U, \qquad \left ( \beta_g^{U}\right )^{-1}\alpha_1\beta_g^U\alpha_1^{-1} = \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_D}}\otimes \xi_U, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \beta_g^{-1}\alpha_1\beta_g\alpha_1^{-1} = \xi_D\otimes\xi_U, \qquad \left ( \beta_g^{U}\right )^{-1}\alpha_1\beta_g^U\alpha_1^{-1} = \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_D}}\otimes \xi_U, \end{split} \end{align} $$where
 $$ \begin{align} \xi_\zeta:=\left ( \beta_g^{\zeta}\right )^{-1}\alpha_{1,\zeta}\beta_g^{\zeta}\alpha_{1,\zeta}^{-1}\in \mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{\left ( \left ( C_{\theta_{0.8}}\right )^c\right )_\zeta} \right ),\quad \zeta=U,D. \end{align} $$
$$ \begin{align} \xi_\zeta:=\left ( \beta_g^{\zeta}\right )^{-1}\alpha_{1,\zeta}\beta_g^{\zeta}\alpha_{1,\zeta}^{-1}\in \mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{\left ( \left ( C_{\theta_{0.8}}\right )^c\right )_\zeta} \right ),\quad \zeta=U,D. \end{align} $$Hence we obtain decompositions
 $$ \begin{align} \begin{split} \left ( \beta_g^U\right )^{-1}\circ\alpha\circ \beta_g^U\circ \alpha^{-1} &=({\textrm{{inner}}})\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_D}}\otimes \xi_U \right )\circ \left ( \Xi_{H_U,g,L}\otimes \Xi_{H_U,g,R}\right ),\\ \left ( \beta_g\right )^{-1}\circ\alpha\circ \beta_g\circ \alpha^{-1} &=({\textrm{{inner}}})\circ \left ( \xi_D\otimes\xi_U\right ) \circ \left ( \Xi_{{\mathbb Z}^2,g,L}\otimes \Xi_{{\mathbb Z}^2,g,R}\right ). \end{split} \end{align} $$
$$ \begin{align} \begin{split} \left ( \beta_g^U\right )^{-1}\circ\alpha\circ \beta_g^U\circ \alpha^{-1} &=({\textrm{{inner}}})\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_D}}\otimes \xi_U \right )\circ \left ( \Xi_{H_U,g,L}\otimes \Xi_{H_U,g,R}\right ),\\ \left ( \beta_g\right )^{-1}\circ\alpha\circ \beta_g\circ \alpha^{-1} &=({\textrm{{inner}}})\circ \left ( \xi_D\otimes\xi_U\right ) \circ \left ( \Xi_{{\mathbb Z}^2,g,L}\otimes \Xi_{{\mathbb Z}^2,g,R}\right ). \end{split} \end{align} $$Because  $\xi _{\zeta }\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{\left ( \left ( C_{\theta _{0.8}}\right )^c\right )_\zeta } \right )$ commutes with
$\xi _{\zeta }\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{\left ( \left ( C_{\theta _{0.8}}\right )^c\right )_\zeta } \right )$ commutes with  $\beta _{g}^{C_{\left [0,\theta _{0.8}\right ]}}$ and
$\beta _{g}^{C_{\left [0,\theta _{0.8}\right ]}}$ and  $\beta _{g}^{C_{\left [0,\theta _{0.8}\right ],U}}$, we get
$\beta _{g}^{C_{\left [0,\theta _{0.8}\right ],U}}$, we get
 $$ \begin{align} \alpha\circ \beta_g^U\circ \alpha^{-1} &=({\textrm{{inner}}})\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_D}}\otimes \beta_{g}^{C_{\left(\theta_{0.8},\frac\pi 2\right],U}}\xi_U \right )\circ \left ( \beta_{g}^{C_{\left[0,\theta_{0.8}\right],L,U}}\Xi_{H_U,g,L}\otimes \beta_{g}^{C_{\left[0,\theta_{0.8}\right],R,U}} \Xi_{H_U,g,R}\right ), \notag\\ \alpha\circ \beta_g\circ \alpha^{-1} &=({\textrm{{inner}}})\circ \left ( \beta_{g}^{C_{(\theta_{0.8},\frac\pi 2],D}} \xi_D\otimes\beta_{g}^{C_{(\theta_{0.8},\frac\pi 2],U}}\xi_U \!\right ) \circ \left ( \beta_{g}^{C_{[0,\theta_{0.8}],L}}\Xi_{{\mathbb Z}^2,g,L}\otimes \beta_{g}^{C_{[0,\theta_{0.8}],R}}\Xi_{{\mathbb Z}^2,g,R} \!\right ). \end{align} $$
$$ \begin{align} \alpha\circ \beta_g^U\circ \alpha^{-1} &=({\textrm{{inner}}})\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{H_D}}\otimes \beta_{g}^{C_{\left(\theta_{0.8},\frac\pi 2\right],U}}\xi_U \right )\circ \left ( \beta_{g}^{C_{\left[0,\theta_{0.8}\right],L,U}}\Xi_{H_U,g,L}\otimes \beta_{g}^{C_{\left[0,\theta_{0.8}\right],R,U}} \Xi_{H_U,g,R}\right ), \notag\\ \alpha\circ \beta_g\circ \alpha^{-1} &=({\textrm{{inner}}})\circ \left ( \beta_{g}^{C_{(\theta_{0.8},\frac\pi 2],D}} \xi_D\otimes\beta_{g}^{C_{(\theta_{0.8},\frac\pi 2],U}}\xi_U \!\right ) \circ \left ( \beta_{g}^{C_{[0,\theta_{0.8}],L}}\Xi_{{\mathbb Z}^2,g,L}\otimes \beta_{g}^{C_{[0,\theta_{0.8}],R}}\Xi_{{\mathbb Z}^2,g,R} \!\right ). \end{align} $$ Furthermore, from the ![]() $\beta _g$-invariance of
$\beta _g$-invariance of ![]() $\omega _0\circ \alpha $, we have
$\omega _0\circ \alpha $, we have
 $$ \begin{align} \omega_0\circ \alpha\circ \beta_g\circ \alpha^{-1} =\omega_0. \end{align} $$
$$ \begin{align} \omega_0\circ \alpha\circ \beta_g\circ \alpha^{-1} =\omega_0. \end{align} $$ Now we apply Lemma 3.4 for ![]() ${\mathfrak A}_\sigma , {\mathfrak B}_{\sigma \zeta }, {\mathfrak C}_\zeta $ replaced by
${\mathfrak A}_\sigma , {\mathfrak B}_{\sigma \zeta }, {\mathfrak C}_\zeta $ replaced by  ${\mathcal A}_{\left ( C_{\left [0,\theta _{0.8}\right ]}\right )_\sigma }, {\mathcal A}_{\left ( C_{\left (\theta _{0.8},\theta _{2}\right ]}\right )_{\sigma ,\zeta }}, {\mathcal A}_{\left ( C_{\left (\theta _2,\frac \pi 2\right ]}\right )_\zeta }$, for
${\mathcal A}_{\left ( C_{\left [0,\theta _{0.8}\right ]}\right )_\sigma }, {\mathcal A}_{\left ( C_{\left (\theta _{0.8},\theta _{2}\right ]}\right )_{\sigma ,\zeta }}, {\mathcal A}_{\left ( C_{\left (\theta _2,\frac \pi 2\right ]}\right )_\zeta }$, for ![]() $\sigma =L,R$,
$\sigma =L,R$, ![]() $\zeta =D,U$. By equations (3.29) and (3.28),
$\zeta =D,U$. By equations (3.29) and (3.28),  $\left (\alpha \circ \beta _g^U\circ \alpha ^{-1}, \alpha \circ \beta _g\circ \alpha ^{-1}\right )$ satisfy the conditions of
$\left (\alpha \circ \beta _g^U\circ \alpha ^{-1}, \alpha \circ \beta _g\circ \alpha ^{-1}\right )$ satisfy the conditions of ![]() $(\alpha ,\hat \alpha )$ in Lemma 3.4, for
$(\alpha ,\hat \alpha )$ in Lemma 3.4, for ![]() $\omega _0$ and its restrictions. Applying Lemma 3.4, there are
$\omega _0$ and its restrictions. Applying Lemma 3.4, there are  $\tilde \eta _{\sigma ,g}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{\left ( C_{\theta _2}\right )_\sigma }\right )$,
$\tilde \eta _{\sigma ,g}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{\left ( C_{\theta _2}\right )_\sigma }\right )$, ![]() $g\in G$,
$g\in G$, ![]() $\sigma =L,R$, such that
$\sigma =L,R$, such that
 $$ \begin{align} \omega_0\circ\alpha\circ \beta_g^U\circ \alpha^{-1} \sim_{\text{q.e.}} \omega_0\circ \left ( \tilde\eta_{Lg}\otimes \tilde\eta_{Rg} \right ),\quad g\in G. \end{align} $$
$$ \begin{align} \omega_0\circ\alpha\circ \beta_g^U\circ \alpha^{-1} \sim_{\text{q.e.}} \omega_0\circ \left ( \tilde\eta_{Lg}\otimes \tilde\eta_{Rg} \right ),\quad g\in G. \end{align} $$Because both  $\omega _0\circ \alpha \circ \beta _g^U\circ \alpha ^{-1}$ and
$\omega _0\circ \alpha \circ \beta _g^U\circ \alpha ^{-1}$ and ![]() $\omega _0\circ \left ( \tilde \eta _{Lg}\otimes \tilde \eta _{Rg} \right )$ are pure, by Kadison’s transitivity theorem there exists a unitary
$\omega _0\circ \left ( \tilde \eta _{Lg}\otimes \tilde \eta _{Rg} \right )$ are pure, by Kadison’s transitivity theorem there exists a unitary ![]() $\tilde v_g\in {\mathcal U}({\mathcal A})$ such that
$\tilde v_g\in {\mathcal U}({\mathcal A})$ such that
 $$ \begin{align} \omega_0\circ\alpha\circ \beta_g^U\circ \alpha^{-1} = \omega_0\circ\mathop{\mathrm{Ad}}\nolimits_{\tilde v_g}\circ \left ( \tilde\eta_{Lg}\otimes \tilde\eta_{Rg} \right ),\quad g\in G. \end{align} $$
$$ \begin{align} \omega_0\circ\alpha\circ \beta_g^U\circ \alpha^{-1} = \omega_0\circ\mathop{\mathrm{Ad}}\nolimits_{\tilde v_g}\circ \left ( \tilde\eta_{Lg}\otimes \tilde\eta_{Rg} \right ),\quad g\in G. \end{align} $$We define
 $$ \begin{align} \tilde \beta_g:= \mathop{\mathrm{Ad}}\nolimits\left ( \alpha^{-1}\left (\tilde v_{g^{-1}}\right )\right ) \circ\alpha^{-1} \circ\left ( \tilde\eta_{Lg^{-1}}\otimes \tilde\eta_{Rg^{-1}} \right )\circ\alpha\circ\beta_g^U,\quad g\in G. \end{align} $$
$$ \begin{align} \tilde \beta_g:= \mathop{\mathrm{Ad}}\nolimits\left ( \alpha^{-1}\left (\tilde v_{g^{-1}}\right )\right ) \circ\alpha^{-1} \circ\left ( \tilde\eta_{Lg^{-1}}\otimes \tilde\eta_{Rg^{-1}} \right )\circ\alpha\circ\beta_g^U,\quad g\in G. \end{align} $$It suffices to show that ![]() $\left (\tilde \beta _g\right )\in \mathop {\mathrm {IG}}\nolimits (\omega _0\circ \alpha ,\theta )=\mathop {\mathrm {IG}}\nolimits \left (\omega _0\circ \alpha ,\theta _{2.2}\right )$. By equation (3.31), we have
$\left (\tilde \beta _g\right )\in \mathop {\mathrm {IG}}\nolimits (\omega _0\circ \alpha ,\theta )=\mathop {\mathrm {IG}}\nolimits \left (\omega _0\circ \alpha ,\theta _{2.2}\right )$. By equation (3.31), we have ![]() $\omega _0\circ \alpha \circ \tilde \beta _g=\omega _0\circ \alpha $. Therefore, what is left to be proven is that there are
$\omega _0\circ \alpha \circ \tilde \beta _g=\omega _0\circ \alpha $. Therefore, what is left to be proven is that there are ![]() $\eta _{g}^\sigma \in \mathop {\mathrm {Aut}}\nolimits \left ( \left ( C_\theta \right )_\sigma \right )$,
$\eta _{g}^\sigma \in \mathop {\mathrm {Aut}}\nolimits \left ( \left ( C_\theta \right )_\sigma \right )$, ![]() $g\in G$,
$g\in G$, ![]() $\sigma =L,R$, such that
$\sigma =L,R$, such that
 $$ \begin{align} \tilde\beta_g=({\textrm{{inner}}})\circ\left ( \eta_g^L\otimes\eta_g^R\right )\circ\beta_g^U,\quad \text{for all } g\in G. \end{align} $$
$$ \begin{align} \tilde\beta_g=({\textrm{{inner}}})\circ\left ( \eta_g^L\otimes\eta_g^R\right )\circ\beta_g^U,\quad \text{for all } g\in G. \end{align} $$By the decomposition (2.12) and the fact that ![]() $\tilde \eta _{Lg^{-1}}\otimes \tilde \eta _{Rg^{-1}}$ has support in
$\tilde \eta _{Lg^{-1}}\otimes \tilde \eta _{Rg^{-1}}$ has support in ![]() $C_{\theta _2}$, we have
$C_{\theta _2}$, we have
 $$ \begin{align} \begin{split} \alpha^{-1} &\circ\left ( \tilde\eta_{Lg^{-1}}\otimes \tilde\eta_{Rg^{-1}} \right )\circ\alpha\\ &=({\textrm{{inner}}})\circ \left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right]} \right )^{-1} \left ( \alpha_{\left[0,\theta_1\right]}\otimes\alpha_{\left(\theta_1,\theta_2\right]} \right )^{-1} \left ( \tilde\eta_{Lg^{-1}}\otimes \tilde\eta_{Rg^{-1}} \right ) \left ( \alpha_{\left[0,\theta_1\right]}\otimes\alpha_{\left(\theta_1,\theta_2\right]} \right )\\ & \quad \circ \left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right]} \right )\\ &=({\textrm{{inner}}})\circ\left ( \eta_g^L\otimes\eta_g^R\right ), \end{split} \end{align} $$
$$ \begin{align} \begin{split} \alpha^{-1} &\circ\left ( \tilde\eta_{Lg^{-1}}\otimes \tilde\eta_{Rg^{-1}} \right )\circ\alpha\\ &=({\textrm{{inner}}})\circ \left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right]} \right )^{-1} \left ( \alpha_{\left[0,\theta_1\right]}\otimes\alpha_{\left(\theta_1,\theta_2\right]} \right )^{-1} \left ( \tilde\eta_{Lg^{-1}}\otimes \tilde\eta_{Rg^{-1}} \right ) \left ( \alpha_{\left[0,\theta_1\right]}\otimes\alpha_{\left(\theta_1,\theta_2\right]} \right )\\ & \quad \circ \left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right]} \right )\\ &=({\textrm{{inner}}})\circ\left ( \eta_g^L\otimes\eta_g^R\right ), \end{split} \end{align} $$where
 $$ \begin{align} \begin{split} \eta_{g}^\sigma&=\left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right],\sigma} \right )^{-1} \left ( \alpha_{\left[0,\theta_1\right],\sigma}\otimes\alpha_{\left(\theta_1,\theta_2\right],\sigma} \right )^{-1} \left ( \tilde\eta_{\sigma g^{-1}} \right ) \left ( \alpha_{\left[0,\theta_1\right],\sigma}\otimes\alpha_{\left(\theta_1,\theta_2\right],\sigma} \right ) \\ & \quad \circ \left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right], \sigma} \right )\\ &\quad \in \mathop{\mathrm{Aut}}\nolimits\left ( \left ( C_{\theta_{2.2}}\right )_\sigma\right ),\quad \sigma=L,R. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \eta_{g}^\sigma&=\left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right],\sigma} \right )^{-1} \left ( \alpha_{\left[0,\theta_1\right],\sigma}\otimes\alpha_{\left(\theta_1,\theta_2\right],\sigma} \right )^{-1} \left ( \tilde\eta_{\sigma g^{-1}} \right ) \left ( \alpha_{\left[0,\theta_1\right],\sigma}\otimes\alpha_{\left(\theta_1,\theta_2\right],\sigma} \right ) \\ & \quad \circ \left ( \alpha_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right], \sigma} \right )\\ &\quad \in \mathop{\mathrm{Aut}}\nolimits\left ( \left ( C_{\theta_{2.2}}\right )_\sigma\right ),\quad \sigma=L,R. \end{split} \end{align} $$Substituting this into formula (3.32), we obtain equation (3.33). This completes the proof.
4 The stability of the index  $h(\omega )$
$h(\omega )$
In this section we prove the stability of the index ![]() $h(\omega )$ with respect to
$h(\omega )$ with respect to ![]() $\gamma \in \mathop {\mathrm {GUQAut}}\nolimits ({\mathcal A})$.
$\gamma \in \mathop {\mathrm {GUQAut}}\nolimits ({\mathcal A})$.
Theorem 4.1. Set ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ with
$\omega \in \mathop {\mathcal {SL}}\nolimits $ with ![]() $\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $. Set
$\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $. Set ![]() $\gamma \in \mathop {\mathrm {GUQAut}}\nolimits \left ({\mathcal A}\right )$. Then we have
$\gamma \in \mathop {\mathrm {GUQAut}}\nolimits \left ({\mathcal A}\right )$. Then we have ![]() $\omega \circ \gamma \in \mathop {\mathcal {SL}}\nolimits $ with
$\omega \circ \gamma \in \mathop {\mathcal {SL}}\nolimits $ with ![]() $\mathop {\mathrm {IG}}\nolimits (\omega \circ \gamma )\neq \emptyset $ and
$\mathop {\mathrm {IG}}\nolimits (\omega \circ \gamma )\neq \emptyset $ and
Proof. The point of the proof is that we can derive  $\left (\hat \alpha _{L},\hat \alpha _{R},\hat \Theta \right )\in {\mathcal D}_{\alpha \gamma }^{\theta _{1.2}}$ (formulas (4.10) and (4.11)) and
$\left (\hat \alpha _{L},\hat \alpha _{R},\hat \Theta \right )\in {\mathcal D}_{\alpha \gamma }^{\theta _{1.2}}$ (formulas (4.10) and (4.11)) and  $\left ( \gamma ^{-1}\tilde \beta _{g}\gamma \right )\in \mathop {\mathrm {IG}}\nolimits (\omega \circ \gamma ,\theta _{1.2}), \left (\hat \eta _{g}^{\sigma }\right )\in {\mathcal T}\left (\theta _{1.2}, \left ( \gamma ^{-1}\tilde \beta _{g}\gamma \right )\right )$ (formula (4.16)) from the corresponding objects for
$\left ( \gamma ^{-1}\tilde \beta _{g}\gamma \right )\in \mathop {\mathrm {IG}}\nolimits (\omega \circ \gamma ,\theta _{1.2}), \left (\hat \eta _{g}^{\sigma }\right )\in {\mathcal T}\left (\theta _{1.2}, \left ( \gamma ^{-1}\tilde \beta _{g}\gamma \right )\right )$ (formula (4.16)) from the corresponding objects for ![]() $\alpha $, using the factorisation property of
$\alpha $, using the factorisation property of ![]() $\alpha ,\gamma $. And it is straightforward to see that the
$\alpha ,\gamma $. And it is straightforward to see that the  $\beta _{g}^{U}$-invariance of
$\beta _{g}^{U}$-invariance of ![]() $\gamma _{C}$ results in
$\gamma _{C}$ results in  $\mathop {\mathrm {IP}}\nolimits \left ( \omega , \alpha , \theta _{2}, \left (\tilde \beta _g\right ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta ) \right ) =\mathop {\mathrm {IP}}\nolimits \left ( \omega \circ \gamma , \alpha \circ \gamma , \theta _{1.2}, \left (\gamma ^{-1}\tilde \beta _g\gamma \right ), \left (\hat \eta _{g}^\sigma \right ), \left (\hat \alpha _L,\hat \alpha _R,\hat \Theta \right ) \right )$, which immediately implies the Theorem.
$\mathop {\mathrm {IP}}\nolimits \left ( \omega , \alpha , \theta _{2}, \left (\tilde \beta _g\right ), (\eta _{g}^\sigma ), (\alpha _L,\alpha _R,\Theta ) \right ) =\mathop {\mathrm {IP}}\nolimits \left ( \omega \circ \gamma , \alpha \circ \gamma , \theta _{1.2}, \left (\gamma ^{-1}\tilde \beta _g\gamma \right ), \left (\hat \eta _{g}^\sigma \right ), \left (\hat \alpha _L,\hat \alpha _R,\hat \Theta \right ) \right )$, which immediately implies the Theorem.
Step 1. From ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $, there is an
$\omega \in \mathop {\mathcal {SL}}\nolimits $, there is an ![]() $ \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$. For any
$ \alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$. For any ![]() $0<\theta <\frac \pi 2$ fixed, we show that
$0<\theta <\frac \pi 2$ fixed, we show that  ${\mathcal D}^{\theta }_{\alpha \circ \gamma }\neq \emptyset $, hence
${\mathcal D}^{\theta }_{\alpha \circ \gamma }\neq \emptyset $, hence ![]() $\alpha \circ \gamma \in \mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$ and
$\alpha \circ \gamma \in \mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$ and ![]() $\omega \circ \gamma =\omega _{0}\circ \alpha \gamma \in \mathop {\mathcal {SL}}\nolimits $. Set
$\omega \circ \gamma =\omega _{0}\circ \alpha \gamma \in \mathop {\mathcal {SL}}\nolimits $. Set ![]() $\theta _{1.2}:=\theta $ and choose
$\theta _{1.2}:=\theta $ and choose
 $$ \begin{align} 0<\theta_{0}<\theta_{0.8}<\theta_1<\theta_{1.2}:=\theta<\theta_{1.8}<\theta_2<\theta_{2.2}< \theta_{2.8}<\theta_3<\theta_{3.2}<\frac\pi 2. \end{align} $$
$$ \begin{align} 0<\theta_{0}<\theta_{0.8}<\theta_1<\theta_{1.2}:=\theta<\theta_{1.8}<\theta_2<\theta_{2.2}< \theta_{2.8}<\theta_3<\theta_{3.2}<\frac\pi 2. \end{align} $$Because ![]() $\alpha \in \mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$, there exists some
$\alpha \in \mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$, there exists some ![]() $(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta _{2}}$. Setting
$(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta _{2}}$. Setting ![]() $\alpha _0:=\alpha _L\otimes \alpha _R$, we have
$\alpha _0:=\alpha _L\otimes \alpha _R$, we have ![]() $\alpha =({\textrm {{inner}}})\circ \alpha _0\circ \Theta $. Because
$\alpha =({\textrm {{inner}}})\circ \alpha _0\circ \Theta $. Because ![]() $\gamma \in \mathop {\mathrm {GUQAut}}\nolimits \left ({\mathcal A}\right )$, there are
$\gamma \in \mathop {\mathrm {GUQAut}}\nolimits \left ({\mathcal A}\right )$, there are ![]() $\gamma _{H}\in \mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$ and
$\gamma _{H}\in \mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$ and ![]() $\gamma _{C}\in \mathop {\mathrm {GSQAut}}\nolimits ({\mathcal A})$ such that
$\gamma _{C}\in \mathop {\mathrm {GSQAut}}\nolimits ({\mathcal A})$ such that
Because ![]() $\gamma _{H}\in \mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$, we may decompose
$\gamma _{H}\in \mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$, we may decompose ![]() $\gamma _{H}$ as
$\gamma _{H}$ as
with some  $\gamma _{H, {\sigma }}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{{\left ( C_{\theta _{0}}\right )_\sigma }}\right )$,
$\gamma _{H, {\sigma }}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{{\left ( C_{\theta _{0}}\right )_\sigma }}\right )$, ![]() $\sigma =L,R$. We set
$\sigma =L,R$. We set  $\gamma _{0}:=\gamma _{H, {L}}\otimes \gamma _{H,R}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{{ C_{\theta _{0}}}}\right )$. By definition,
$\gamma _{0}:=\gamma _{H, {L}}\otimes \gamma _{H,R}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{{ C_{\theta _{0}}}}\right )$. By definition, ![]() $\gamma _{C}\in \mathop {\mathrm {GSQAut}}\nolimits ({\mathcal A})$ allows a decomposition
$\gamma _{C}\in \mathop {\mathrm {GSQAut}}\nolimits ({\mathcal A})$ allows a decomposition
 $$ \begin{align} \gamma_{C}&=({\textrm{{inner}}})\circ\gamma_{CS},\notag\\ \gamma_{CS}&=\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \otimes \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ), \end{align} $$
$$ \begin{align} \gamma_{C}&=({\textrm{{inner}}})\circ\gamma_{CS},\notag\\ \gamma_{CS}&=\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \otimes \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ), \end{align} $$with
 $$ \begin{align} \gamma_X&:=\bigotimes_{\sigma=L,R, \, \zeta=D,U} \gamma_{X,\sigma,\zeta},& \gamma_{\left[0,\theta_{1}\right]}&:=\bigotimes_{\sigma=L,R}\gamma_{\left[0,\theta_{1}\right],\sigma},& \gamma_{\left(\theta_3,\frac\pi 2\right]}&:=\bigotimes_{\zeta=D,U} \gamma_{\left(\theta_3,\frac\pi 2\right],\zeta}, \nonumber\\ \gamma_{X,\sigma,\zeta}&\in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{X,\sigma,\zeta}}\right ),& \gamma_{X,\sigma}&:=\bigotimes_{\zeta=U,D}\gamma_{X,\sigma,\zeta},& \gamma_{X,\zeta}&:=\bigotimes_{\sigma=L,R}\gamma_{X,\sigma,\zeta},\\ \gamma_{\left[0,\theta_{1}\right],\sigma}&\in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\left[0,\theta_{1}\right],\sigma}}\right ),& \gamma_{\left(\theta_3,\frac\pi 2\right],\zeta}&\in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\left(\theta_3,\frac\pi 2\right],\zeta}}\right ), \nonumber \end{align} $$
$$ \begin{align} \gamma_X&:=\bigotimes_{\sigma=L,R, \, \zeta=D,U} \gamma_{X,\sigma,\zeta},& \gamma_{\left[0,\theta_{1}\right]}&:=\bigotimes_{\sigma=L,R}\gamma_{\left[0,\theta_{1}\right],\sigma},& \gamma_{\left(\theta_3,\frac\pi 2\right]}&:=\bigotimes_{\zeta=D,U} \gamma_{\left(\theta_3,\frac\pi 2\right],\zeta}, \nonumber\\ \gamma_{X,\sigma,\zeta}&\in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{X,\sigma,\zeta}}\right ),& \gamma_{X,\sigma}&:=\bigotimes_{\zeta=U,D}\gamma_{X,\sigma,\zeta},& \gamma_{X,\zeta}&:=\bigotimes_{\sigma=L,R}\gamma_{X,\sigma,\zeta},\\ \gamma_{\left[0,\theta_{1}\right],\sigma}&\in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\left[0,\theta_{1}\right],\sigma}}\right ),& \gamma_{\left(\theta_3,\frac\pi 2\right],\zeta}&\in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\left(\theta_3,\frac\pi 2\right],\zeta}}\right ), \nonumber \end{align} $$for
Here we have
 $$ \begin{align} \gamma_{I}\circ\beta_g^{U}=\beta_g^{U}\circ\gamma_{I}\quad\text{for all } g\in G, \end{align} $$
$$ \begin{align} \gamma_{I}\circ\beta_g^{U}=\beta_g^{U}\circ\gamma_{I}\quad\text{for all } g\in G, \end{align} $$for any
 $$ \begin{align} I=[0,\theta_1],(\theta_1,\theta_2], (\theta_2,\theta_3], \left(\theta_3,\frac\pi 2\right], (\theta_{0.8}, \theta_{1.2}], (\theta_{1.8},\theta_{2.2}], (\theta_{2.8},\theta_{3.2}]. \end{align} $$
$$ \begin{align} I=[0,\theta_1],(\theta_1,\theta_2], (\theta_2,\theta_3], \left(\theta_3,\frac\pi 2\right], (\theta_{0.8}, \theta_{1.2}], (\theta_{1.8},\theta_{2.2}], (\theta_{2.8},\theta_{3.2}]. \end{align} $$Set
 $$ \begin{align} \hat\Theta:=\Theta\circ \left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ) \in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{C_{\theta_{1.8}}^{c}}\right ) \subset \mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{C_{\theta_{1.2}}^{c}}\right ) \end{align} $$
$$ \begin{align} \hat\Theta:=\Theta\circ \left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ) \in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{C_{\theta_{1.8}}^{c}}\right ) \subset \mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{C_{\theta_{1.2}}^{c}}\right ) \end{align} $$and
We claim
This means  $(\hat \alpha _{L},\hat \alpha _{R},\hat \Theta )\in {\mathcal D}_{\alpha \gamma }^{\theta _{1.2}}$, hence
$(\hat \alpha _{L},\hat \alpha _{R},\hat \Theta )\in {\mathcal D}_{\alpha \gamma }^{\theta _{1.2}}$, hence  ${\mathcal D}_{\alpha \gamma }^{\theta }={\mathcal D}_{\alpha \gamma }^{\theta _{1.2}}\neq \emptyset $. The claim (4.12) can be checked as follows. Note that
${\mathcal D}_{\alpha \gamma }^{\theta }={\mathcal D}_{\alpha \gamma }^{\theta _{1.2}}\neq \emptyset $. The claim (4.12) can be checked as follows. Note that ![]() $\gamma _{\left (\theta _2,\theta _3\right ]}\otimes \gamma _{\left (\theta _3,\frac \pi 2\right ]}$ and
$\gamma _{\left (\theta _2,\theta _3\right ]}\otimes \gamma _{\left (\theta _3,\frac \pi 2\right ]}$ and ![]() $\gamma _{\left (\theta _{0.8}, \theta _{1.2}\right ]}$ commute because of their disjoint supports. Because
$\gamma _{\left (\theta _{0.8}, \theta _{1.2}\right ]}$ commute because of their disjoint supports. Because  $\Theta \in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_{\theta _{2}}^{c}})$, it commutes with
$\Theta \in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_{\theta _{2}}^{c}})$, it commutes with ![]() $\gamma _{\left [0,\theta _1\right ]}\otimes \gamma _{\left (\theta _1,\theta _2\right ]}$ and
$\gamma _{\left [0,\theta _1\right ]}\otimes \gamma _{\left (\theta _1,\theta _2\right ]}$ and ![]() $\gamma _{\left (\theta _{0.8}, \theta _{1.2}\right ]}$. Therefore, we have
$\gamma _{\left (\theta _{0.8}, \theta _{1.2}\right ]}$. Therefore, we have
 $$ \begin{align} \alpha\circ\gamma&=({\textrm{{inner}}})\circ\alpha_{0}\circ \Theta\circ\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \otimes \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \notag\\ &\quad \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )\circ\gamma_{0}\notag\\ &=({\textrm{{inner}}})\circ\alpha_{0}\circ\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \right )\circ\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\circ \Theta\circ\left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]}\right ) \notag\\ &\quad \circ\left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )\circ\gamma_{0}\notag\\ &=({\textrm{{inner}}})\circ\alpha_{0}\circ\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \right )\circ\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\circ\hat\Theta\circ\gamma_{0}. \end{align} $$
$$ \begin{align} \alpha\circ\gamma&=({\textrm{{inner}}})\circ\alpha_{0}\circ \Theta\circ\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \otimes \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \notag\\ &\quad \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )\circ\gamma_{0}\notag\\ &=({\textrm{{inner}}})\circ\alpha_{0}\circ\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \right )\circ\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\circ \Theta\circ\left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]}\right ) \notag\\ &\quad \circ\left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )\circ\gamma_{0}\notag\\ &=({\textrm{{inner}}})\circ\alpha_{0}\circ\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \right )\circ\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\circ\hat\Theta\circ\gamma_{0}. \end{align} $$Because  $\gamma _{0}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{{ C_{\theta _{0}}}}\right )$ and
$\gamma _{0}\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{{ C_{\theta _{0}}}}\right )$ and  $\hat \Theta \in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{C_{\theta _{1.8}}^{c}}\right )$ commute, we have
$\hat \Theta \in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{C_{\theta _{1.8}}^{c}}\right )$ commute, we have
 $$ \begin{align} \alpha\circ\gamma&=\text{equation }(4.13)= ({\textrm{{inner}}})\circ\alpha_{0}\circ\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \right )\circ\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\circ\gamma_{0}\circ\hat\Theta \notag\\ &=({\textrm{{inner}}})\circ\left (\hat\alpha_{L}\otimes\hat \alpha_{R}\right )\circ\hat\Theta, \end{align} $$
$$ \begin{align} \alpha\circ\gamma&=\text{equation }(4.13)= ({\textrm{{inner}}})\circ\alpha_{0}\circ\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \right )\circ\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\circ\gamma_{0}\circ\hat\Theta \notag\\ &=({\textrm{{inner}}})\circ\left (\hat\alpha_{L}\otimes\hat \alpha_{R}\right )\circ\hat\Theta, \end{align} $$proving equation (4.12).
Step 2. From ![]() $\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $, we fix a
$\mathop {\mathrm {IG}}\nolimits (\omega )\neq \emptyset $, we fix a ![]() $0<\theta _{0}<\frac \pi 2$ such that
$0<\theta _{0}<\frac \pi 2$ such that ![]() $\mathop {\mathrm {IG}}\nolimits (\omega ,\theta _{0})\neq \emptyset $. We choose
$\mathop {\mathrm {IG}}\nolimits (\omega ,\theta _{0})\neq \emptyset $. We choose ![]() $\theta _{0.8},\theta _1,\theta _{1.2},\theta _{1.8},\theta _2,\theta _{2.2}, \theta _{2.8},\theta _3,\theta _{3.2}$ such that
$\theta _{0.8},\theta _1,\theta _{1.2},\theta _{1.8},\theta _2,\theta _{2.2}, \theta _{2.8},\theta _3,\theta _{3.2}$ such that
 $$ \begin{align} 0<\theta_{0}<\theta_{0.8}<\theta_1<\theta_{1.2}<\theta_{1.8}<\theta_2<\theta_{2.2}< \theta_{2.8}<\theta_3<\theta_{3.2}<\frac\pi 2. \end{align} $$
$$ \begin{align} 0<\theta_{0}<\theta_{0.8}<\theta_1<\theta_{1.2}<\theta_{1.8}<\theta_2<\theta_{2.2}< \theta_{2.8}<\theta_3<\theta_{3.2}<\frac\pi 2. \end{align} $$For these ![]() $\theta $s, we associate the decomposition of
$\theta $s, we associate the decomposition of ![]() $\gamma $ in step 1. Fix
$\gamma $ in step 1. Fix ![]() $\left ( \tilde \beta _{g}\right )\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta _{0})$ and
$\left ( \tilde \beta _{g}\right )\in \mathop {\mathrm {IG}}\nolimits (\omega ,\theta _{0})$ and  $ \left (\eta _{g}^{\sigma }\right )\in {\mathcal T}\left (\theta _{0}, \left (\tilde \beta _g\right )\right )$. Set
$ \left (\eta _{g}^{\sigma }\right )\in {\mathcal T}\left (\theta _{0}, \left (\tilde \beta _g\right )\right )$. Set  $\eta _{g}:=\eta _{g}^{L}\otimes \eta _{g}^{R}$. Note that
$\eta _{g}:=\eta _{g}^{L}\otimes \eta _{g}^{R}$. Note that  $\left (\eta _{g}^{\sigma }\right )$ also belongs to
$\left (\eta _{g}^{\sigma }\right )$ also belongs to ![]() ${\mathcal T}\left (\theta _{2}, \left (\tilde \beta _g\right )\right )$. Set
${\mathcal T}\left (\theta _{2}, \left (\tilde \beta _g\right )\right )$. Set
 $$ \begin{align} \hat\eta_{g}^{\sigma} &:= \left ( \gamma_{\left[0,\theta_1\right],\sigma}\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}\gamma_{H,\sigma}\right )^{-1} \eta_{g}^{\sigma}\left ( \beta_{g}^{\sigma U} \gamma_{\left[0,\theta_1\right],\sigma}\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}\gamma_{H,\sigma} \left ( \beta_{g}^{\sigma U} \right )^{-1}\right )\notag\\ &\quad \in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{\left ( C_{\theta_{1.2}}\right )_{\sigma}}\right ), \end{align} $$
$$ \begin{align} \hat\eta_{g}^{\sigma} &:= \left ( \gamma_{\left[0,\theta_1\right],\sigma}\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}\gamma_{H,\sigma}\right )^{-1} \eta_{g}^{\sigma}\left ( \beta_{g}^{\sigma U} \gamma_{\left[0,\theta_1\right],\sigma}\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],\sigma}\gamma_{H,\sigma} \left ( \beta_{g}^{\sigma U} \right )^{-1}\right )\notag\\ &\quad \in\mathop{\mathrm{Aut}}\nolimits\left ( {\mathcal A}_{\left ( C_{\theta_{1.2}}\right )_{\sigma}}\right ), \end{align} $$for ![]() $\sigma =L,R$. We also set
$\sigma =L,R$. We also set  $\hat \eta _{g}:=\hat \eta _{g}^{L}\otimes \hat \eta _{g}^{R}$. We claim that
$\hat \eta _{g}:=\hat \eta _{g}^{L}\otimes \hat \eta _{g}^{R}$. We claim that ![]() $\left ( \gamma ^{-1}\tilde \beta _{g}\gamma \right )\in \mathop {\mathrm {IG}}\nolimits (\omega \circ \gamma ,\theta _{1.2})$ with
$\left ( \gamma ^{-1}\tilde \beta _{g}\gamma \right )\in \mathop {\mathrm {IG}}\nolimits (\omega \circ \gamma ,\theta _{1.2})$ with  $\left (\hat \eta _{g}^{\sigma }\right )\in {\mathcal T}\left (\theta _{1.2}, \left ( \gamma ^{-1}\tilde \beta _{g}\gamma \right )\right )$. Clearly we have
$\left (\hat \eta _{g}^{\sigma }\right )\in {\mathcal T}\left (\theta _{1.2}, \left ( \gamma ^{-1}\tilde \beta _{g}\gamma \right )\right )$. Clearly we have
 $$ \begin{align} \omega\circ\gamma\circ\left ( \gamma^{-1}\tilde \beta_{g}\gamma\right ) =\omega\circ\tilde \beta_{g}\circ\gamma =\omega\circ\gamma. \end{align} $$
$$ \begin{align} \omega\circ\gamma\circ\left ( \gamma^{-1}\tilde \beta_{g}\gamma\right ) =\omega\circ\tilde \beta_{g}\circ\gamma =\omega\circ\gamma. \end{align} $$Therefore, what remains to be shown is
 $$ \begin{align} \gamma^{-1}\tilde \beta_{g}\gamma =({\textrm{{inner}}}) \circ\left (\hat\eta_{g}^L\otimes \hat\eta_{g}^R\right )\circ \beta_{g}^{U}. \end{align} $$
$$ \begin{align} \gamma^{-1}\tilde \beta_{g}\gamma =({\textrm{{inner}}}) \circ\left (\hat\eta_{g}^L\otimes \hat\eta_{g}^R\right )\circ \beta_{g}^{U}. \end{align} $$To see this, we first have
 $$ \begin{align} &\gamma^{-1}\circ\eta_{g}\circ\gamma=({\textrm{{inner}}})\circ\gamma_{0}^{-1}\circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )^{-1}\notag\\ &\quad \circ \left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \otimes \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right )^{-1}\notag\\ & \quad \circ\eta_{g}\circ\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \otimes \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ) \gamma_{0} \end{align} $$
$$ \begin{align} &\gamma^{-1}\circ\eta_{g}\circ\gamma=({\textrm{{inner}}})\circ\gamma_{0}^{-1}\circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )^{-1}\notag\\ &\quad \circ \left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \otimes \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right )^{-1}\notag\\ & \quad \circ\eta_{g}\circ\left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \otimes \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ) \gamma_{0} \end{align} $$from the decomposition of equations (4.3), (4.4) and (4.5). Because ![]() $\gamma _{\left (\theta _1,\theta _2\right ]} \otimes \gamma _{\left (\theta _2,\theta _3\right ]}\otimes \gamma _{\left (\theta _3,\frac \pi 2\right ]}$ commutes with
$\gamma _{\left (\theta _1,\theta _2\right ]} \otimes \gamma _{\left (\theta _2,\theta _3\right ]}\otimes \gamma _{\left (\theta _3,\frac \pi 2\right ]}$ commutes with ![]() $\eta _{g}\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{0}}}})$ and
$\eta _{g}\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{0}}}})$ and ![]() $\gamma _{\left (\theta _{1.8},\theta _{2.2}\right ]} \otimes \gamma _{\left (\theta _{2.8},\theta _{3.2}\right ]}$ commutes with
$\gamma _{\left (\theta _{1.8},\theta _{2.2}\right ]} \otimes \gamma _{\left (\theta _{2.8},\theta _{3.2}\right ]}$ commutes with  $\left ( \gamma _{\left [0,\theta _1\right ]}\right )^{-1}\eta _{g}\gamma _{[0,\theta _1]}\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1}}}})$, we have
$\left ( \gamma _{\left [0,\theta _1\right ]}\right )^{-1}\eta _{g}\gamma _{[0,\theta _1]}\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1}}}})$, we have
 $$ \begin{align} \gamma^{-1}&\circ\eta_{g}\circ\gamma\notag\\ &=\text{equation }(4.19) = ({\textrm{{inner}}})\circ\gamma_{0}^{-1}\circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )^{-1}\notag\\ &\quad\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\circ\eta_{g} \circ\left ( \gamma_{\left[0,\theta_1\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ) \gamma_{0}\notag\\ &=({\textrm{{inner}}})\circ\gamma_{0}^{-1}\circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\circ\eta_{g} \circ\left ( \gamma_{\left[0,\theta_1\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right ) \gamma_{0}. \end{align} $$
$$ \begin{align} \gamma^{-1}&\circ\eta_{g}\circ\gamma\notag\\ &=\text{equation }(4.19) = ({\textrm{{inner}}})\circ\gamma_{0}^{-1}\circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )^{-1}\notag\\ &\quad\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\circ\eta_{g} \circ\left ( \gamma_{\left[0,\theta_1\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\otimes \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ) \gamma_{0}\notag\\ &=({\textrm{{inner}}})\circ\gamma_{0}^{-1}\circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\circ\eta_{g} \circ\left ( \gamma_{\left[0,\theta_1\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right ) \gamma_{0}. \end{align} $$On the other hand, because ![]() $\gamma _{CS}$ and
$\gamma _{CS}$ and  $\beta _{g}^{U}$ commute, we have
$\beta _{g}^{U}$ commute, we have
 $$ \begin{align} \gamma^{-1}\circ\beta_{g}^{U}\circ\gamma=({\textrm{{inner}}})\gamma_{0}^{-1}\circ\gamma_{CS}^{-1}\beta_{g}^{U}\gamma_{CS}\gamma_{0} =({\textrm{{inner}}})\gamma_{0}^{-1}\circ\beta_{g}^{U}\gamma_{0}. \end{align} $$
$$ \begin{align} \gamma^{-1}\circ\beta_{g}^{U}\circ\gamma=({\textrm{{inner}}})\gamma_{0}^{-1}\circ\gamma_{CS}^{-1}\beta_{g}^{U}\gamma_{CS}\gamma_{0} =({\textrm{{inner}}})\gamma_{0}^{-1}\circ\beta_{g}^{U}\gamma_{0}. \end{align} $$Combining equations (4.20) and (4.21), we obtain
 $$ \begin{align} \gamma^{-1}\tilde \beta_{g}\gamma &=({\textrm{{inner}}})\circ \gamma_{0}^{-1} \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\circ\eta_{g} \circ\left ( \gamma_{\left[0,\theta_1\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right ) \gamma_{0} \circ \gamma_{0}^{-1}\circ\beta_{g}^{U}\gamma_{0}\notag\\ &=({\textrm{{inner}}})\circ \gamma_{0}^{-1} \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\circ\eta_{g}\beta_{g}^{U} \circ\left ( \gamma_{\left[0,\theta_1\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right ) \circ\gamma_{0}\notag\\ &=({\textrm{{inner}}}) \circ\left (\hat\eta_{g}^L\otimes \hat\eta_{g}^R\right )\circ \beta_{g}^{U}. \end{align} $$
$$ \begin{align} \gamma^{-1}\tilde \beta_{g}\gamma &=({\textrm{{inner}}})\circ \gamma_{0}^{-1} \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\circ\eta_{g} \circ\left ( \gamma_{\left[0,\theta_1\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right ) \gamma_{0} \circ \gamma_{0}^{-1}\circ\beta_{g}^{U}\gamma_{0}\notag\\ &=({\textrm{{inner}}})\circ \gamma_{0}^{-1} \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\circ\eta_{g}\beta_{g}^{U} \circ\left ( \gamma_{\left[0,\theta_1\right]} \right ) \circ \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right ) \circ\gamma_{0}\notag\\ &=({\textrm{{inner}}}) \circ\left (\hat\eta_{g}^L\otimes \hat\eta_{g}^R\right )\circ \beta_{g}^{U}. \end{align} $$In the second equality, we used the fact that ![]() $ \gamma _{[0,\theta _1]} \gamma _{(\theta _{0.8}, \theta _{1.2}]} $ and
$ \gamma _{[0,\theta _1]} \gamma _{(\theta _{0.8}, \theta _{1.2}]} $ and  $\beta _{g}^{U}$ commute. This completes the proof of the claim.
$\beta _{g}^{U}$ commute. This completes the proof of the claim.
Step 3. We use the setting and notation of steps 1 and 2 (with ![]() $\theta _{0}$ chosen in step 2). By Lemma 2.1, there exists
$\theta _{0}$ chosen in step 2). By Lemma 2.1, there exists
 $$ \begin{align} ( (W_g), (u_\sigma(g,h)))\in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta_{2}, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$
$$ \begin{align} ( (W_g), (u_\sigma(g,h)))\in \mathop{\mathrm{IP}}\nolimits\left ( \omega, \alpha, \theta_{2}, (\tilde\beta_g ), (\eta_{g}^\sigma ), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$Now we have
 $$ \begin{align} \begin{split} &\omega\circ\gamma\in \mathop{\mathcal{SL}}\nolimits,\qquad \alpha\circ\gamma\in \mathop{\mathrm{EAut}}\nolimits(\omega\circ\gamma),\qquad \left ( \gamma^{-1}\circ\tilde \beta_{g}\circ\gamma\right )\in \mathop{\mathrm{IG}}\nolimits(\omega\circ\gamma,\theta_{1.2}),\\ &\left(\hat\eta_{g}^{\sigma}\right)\in {\mathcal T}\left (\theta_{1.2}, \left ( \gamma^{-1}\tilde \beta_{g}\gamma\right )\right ),\qquad \left(\hat \alpha_L,\hat \alpha_R,\hat\Theta\right)\in{\mathcal D}_{\alpha\gamma}^{\theta_{1.2}}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\omega\circ\gamma\in \mathop{\mathcal{SL}}\nolimits,\qquad \alpha\circ\gamma\in \mathop{\mathrm{EAut}}\nolimits(\omega\circ\gamma),\qquad \left ( \gamma^{-1}\circ\tilde \beta_{g}\circ\gamma\right )\in \mathop{\mathrm{IG}}\nolimits(\omega\circ\gamma,\theta_{1.2}),\\ &\left(\hat\eta_{g}^{\sigma}\right)\in {\mathcal T}\left (\theta_{1.2}, \left ( \gamma^{-1}\tilde \beta_{g}\gamma\right )\right ),\qquad \left(\hat \alpha_L,\hat \alpha_R,\hat\Theta\right)\in{\mathcal D}_{\alpha\gamma}^{\theta_{1.2}}. \end{split} \end{align} $$We claim
 $$ \begin{align} ( (W_g), (u_\sigma(g,h)))\in \mathop{\mathrm{IP}}\nolimits\left ( \omega\circ\gamma, \alpha\circ\gamma, \theta_{1.2}, \left(\gamma^{-1}\tilde\beta_g\gamma\right), \left(\hat \eta_{g}^\sigma\right), \left(\hat \alpha_L,\hat \alpha_R,\hat \Theta\right) \right ). \end{align} $$
$$ \begin{align} ( (W_g), (u_\sigma(g,h)))\in \mathop{\mathrm{IP}}\nolimits\left ( \omega\circ\gamma, \alpha\circ\gamma, \theta_{1.2}, \left(\gamma^{-1}\tilde\beta_g\gamma\right), \left(\hat \eta_{g}^\sigma\right), \left(\hat \alpha_L,\hat \alpha_R,\hat \Theta\right) \right ). \end{align} $$This immediately implies ![]() $h(\omega )=h(\omega \circ \gamma )$. To prove the claim, we first see from formulas (4.10) and (4.11) that
$h(\omega )=h(\omega \circ \gamma )$. To prove the claim, we first see from formulas (4.10) and (4.11) that
 $$ \begin{align} &\left ( \hat \alpha_L\otimes\hat \alpha_R\right )\circ \hat\Theta\circ \gamma_{0}^{-1} \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\notag\\ &=\alpha_{0}\circ \left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \right ) \circ \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \circ\gamma_{0} \circ\Theta\circ \left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )\notag\\ &\quad \circ \gamma_{0}^{-1} \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\notag\\ &=\alpha_{0}\circ \left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \right ) \circ \Theta\circ \left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}, \end{align} $$
$$ \begin{align} &\left ( \hat \alpha_L\otimes\hat \alpha_R\right )\circ \hat\Theta\circ \gamma_{0}^{-1} \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\notag\\ &=\alpha_{0}\circ \left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \right ) \circ \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \circ\gamma_{0} \circ\Theta\circ \left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )\notag\\ &\quad \circ \gamma_{0}^{-1} \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}\notag\\ &=\alpha_{0}\circ \left ( \gamma_{\left[0,\theta_1\right]}\otimes\gamma_{\left(\theta_1,\theta_2\right]} \right ) \circ \Theta\circ \left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1}, \end{align} $$because ![]() $\gamma _{\left (\theta _{0.8}, \theta _{1.2}\right ]}\circ \gamma _{0}\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1.2}}}})$ and
$\gamma _{\left (\theta _{0.8}, \theta _{1.2}\right ]}\circ \gamma _{0}\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1.2}}}})$ and  $\Theta \circ ( \gamma _{(\theta _2,\theta _3 ]}\otimes \gamma _{\left (\theta _3,\frac \pi 2\right ]} ) \circ ( \gamma _{\left (\theta _{1.8},\theta _{2.2}\right ]} \otimes \gamma _{\left (\theta _{2.8},\theta _{3.2}\right ]} )\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1.8}}}^{c}})$ commute. Furthermore, because
$\Theta \circ ( \gamma _{(\theta _2,\theta _3 ]}\otimes \gamma _{\left (\theta _3,\frac \pi 2\right ]} ) \circ ( \gamma _{\left (\theta _{1.8},\theta _{2.2}\right ]} \otimes \gamma _{\left (\theta _{2.8},\theta _{3.2}\right ]} )\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1.8}}}^{c}})$ commute. Furthermore, because ![]() $\gamma _{\left [0,\theta _1\right ]}$ and
$\gamma _{\left [0,\theta _1\right ]}$ and  $\Theta \circ ( \gamma _{(\theta _2,\theta _3 ]}\otimes \gamma _{\left (\theta _3,\frac \pi 2\right ]} ) \circ \left ( \gamma _{\left (\theta _{1.8},\theta _{2.2}\right ]} \otimes \gamma _{\left (\theta _{2.8},\theta _{3.2}\right ]} \right ) \in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1.8}}}^{c}})$ commute and
$\Theta \circ ( \gamma _{(\theta _2,\theta _3 ]}\otimes \gamma _{\left (\theta _3,\frac \pi 2\right ]} ) \circ \left ( \gamma _{\left (\theta _{1.8},\theta _{2.2}\right ]} \otimes \gamma _{\left (\theta _{2.8},\theta _{3.2}\right ]} \right ) \in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1.8}}}^{c}})$ commute and ![]() $\gamma _{\left (\theta _1,\theta _2\right ]}$ and
$\gamma _{\left (\theta _1,\theta _2\right ]}$ and ![]() $\Theta \in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{2}}}^{c}} )$ commute, we have
$\Theta \in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{2}}}^{c}} )$ commute, we have
 $$ \begin{align} \left ( \hat \alpha_L\otimes\hat \alpha_R\right )&\circ \hat\Theta\circ \gamma_{0}^{-1} \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1} =\text{equation }(4.26) \notag\\ & =\alpha_{0}\circ \gamma_{\left(\theta_1,\theta_2\right]} \circ \Theta\circ \left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )\notag\\ &=\alpha_{0}\circ \Theta\circ\gamma_{\left(\theta_1,\theta_2\right]} \circ\left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ) =\alpha_{0}\circ \Theta \circ\hat\gamma. \end{align} $$
$$ \begin{align} \left ( \hat \alpha_L\otimes\hat \alpha_R\right )&\circ \hat\Theta\circ \gamma_{0}^{-1} \left ( \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]} \right )^{-1}\circ \left ( \gamma_{\left[0,\theta_1\right]} \right )^{-1} =\text{equation }(4.26) \notag\\ & =\alpha_{0}\circ \gamma_{\left(\theta_1,\theta_2\right]} \circ \Theta\circ \left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right )\notag\\ &=\alpha_{0}\circ \Theta\circ\gamma_{\left(\theta_1,\theta_2\right]} \circ\left ( \gamma_{\left(\theta_2,\theta_3\right]}\otimes \gamma_{\left(\theta_3,\frac\pi 2\right]} \right ) \circ \left ( \gamma_{\left(\theta_{1.8},\theta_{2.2}\right]} \otimes \gamma_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ) =\alpha_{0}\circ \Theta \circ\hat\gamma. \end{align} $$Here  $\hat \gamma :=\gamma _{(\theta _1,\theta _2 ]} \circ ( \gamma _{ (\theta _2,\theta _3 ]}\otimes \gamma _{\left (\theta _3,\frac \pi 2\right ]} ) \circ \left ( \gamma _{\left (\theta _{1.8},\theta _{2.2}\right ]} \otimes \gamma _{\left (\theta _{2.8},\theta _{3.2}\right ]} \right )\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1}}}^{c}} )$ commutes with
$\hat \gamma :=\gamma _{(\theta _1,\theta _2 ]} \circ ( \gamma _{ (\theta _2,\theta _3 ]}\otimes \gamma _{\left (\theta _3,\frac \pi 2\right ]} ) \circ \left ( \gamma _{\left (\theta _{1.8},\theta _{2.2}\right ]} \otimes \gamma _{\left (\theta _{2.8},\theta _{3.2}\right ]} \right )\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1}}}^{c}} )$ commutes with  $\beta _{g}^{U}$. Combining this and
$\beta _{g}^{U}$. Combining this and
 $$ \begin{align} \hat \eta_{g}\beta_{g}^{U}= \left ( \gamma_{\left[0,\theta_1\right]}\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\gamma_{0}\right )^{-1} \eta_{g} \beta_{g}^{ U} \gamma_{\left[0,\theta_1\right]}\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\gamma_{0}, \end{align} $$
$$ \begin{align} \hat \eta_{g}\beta_{g}^{U}= \left ( \gamma_{\left[0,\theta_1\right]}\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\gamma_{0}\right )^{-1} \eta_{g} \beta_{g}^{ U} \gamma_{\left[0,\theta_1\right]}\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right]}\gamma_{0}, \end{align} $$we obtain
 $$ \begin{align} \pi_{0}\circ \left ( \hat \alpha_L\otimes\hat \alpha_R\right )\circ \hat\Theta\circ\hat\eta_{g}\beta_{g}^{U} ( \hat\Theta )^{-1} \left ( \hat \alpha_L\otimes\hat \alpha_R\right )^{-1} =\pi_{0}\circ\alpha_{0}\circ \Theta \circ\hat\gamma\circ \eta_{g} \beta_{g}^{ U}\circ \hat\gamma^{-1}\circ\Theta^{-1}\circ \alpha_{0}^{-1}. \end{align} $$
$$ \begin{align} \pi_{0}\circ \left ( \hat \alpha_L\otimes\hat \alpha_R\right )\circ \hat\Theta\circ\hat\eta_{g}\beta_{g}^{U} ( \hat\Theta )^{-1} \left ( \hat \alpha_L\otimes\hat \alpha_R\right )^{-1} =\pi_{0}\circ\alpha_{0}\circ \Theta \circ\hat\gamma\circ \eta_{g} \beta_{g}^{ U}\circ \hat\gamma^{-1}\circ\Theta^{-1}\circ \alpha_{0}^{-1}. \end{align} $$Because ![]() $\hat \gamma $ commutes with
$\hat \gamma $ commutes with  $\beta _{g}^{U}$ and
$\beta _{g}^{U}$ and ![]() $ \eta _{g}\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{0}}}} )$ commutes with
$ \eta _{g}\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{0}}}} )$ commutes with ![]() $\hat \gamma \in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1}}}^{c}} )$, we have
$\hat \gamma \in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{1}}}^{c}} )$, we have
 $$ \begin{align} &\pi_{0}\circ \left ( \hat \alpha_L\otimes\hat \alpha_R\right )\circ \hat\Theta\circ\hat\eta_{g}\beta_{g}^{U} ( \hat\Theta )^{-1} \left ( \hat \alpha_L\otimes\hat \alpha_R\right )^{-1} \notag \\&\quad =\text{equation }(4.29) =\pi_{0}\circ\alpha_{0}\circ \Theta \circ \eta_{g} \beta_{g}^{ U} \circ\Theta^{-1}\circ \alpha_{0}^{-1} =\mathop{\mathrm{Ad}}\nolimits( W_{g} )\circ\pi_{0}. \end{align} $$
$$ \begin{align} &\pi_{0}\circ \left ( \hat \alpha_L\otimes\hat \alpha_R\right )\circ \hat\Theta\circ\hat\eta_{g}\beta_{g}^{U} ( \hat\Theta )^{-1} \left ( \hat \alpha_L\otimes\hat \alpha_R\right )^{-1} \notag \\&\quad =\text{equation }(4.29) =\pi_{0}\circ\alpha_{0}\circ \Theta \circ \eta_{g} \beta_{g}^{ U} \circ\Theta^{-1}\circ \alpha_{0}^{-1} =\mathop{\mathrm{Ad}}\nolimits( W_{g} )\circ\pi_{0}. \end{align} $$Hence the condition for ![]() $W_{g}$ in formula (4.25) is checked. On the other hand, substituting formulas (4.11) and (4.16), we get
$W_{g}$ in formula (4.25) is checked. On the other hand, substituting formulas (4.11) and (4.16), we get
 $$ \begin{align} \pi_R&\circ\hat \alpha_R\circ\hat \eta_g^R\beta_g^{R U} \hat \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \hat \eta_{gh}^R\right )^{-1}\hat\alpha_{R}^{-1}\notag\\ &= \pi_{R}\circ\alpha_R\circ \left ( \gamma_{\left[0,\theta_1\right],R}\otimes\gamma_{\left(\theta_1,\theta_2\right],R} \right ) \circ \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],R} \circ\gamma_{H,R} \circ \left ( \gamma_{\left[0,\theta_1\right],R}\circ\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],R}\circ\gamma_{H,R}\right )^{-1}\notag\\ & \quad \eta_g^R\beta_g^{RU} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\circ \gamma_{\left[0,\theta_1\right],R}\circ\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],R} \notag\\ &\quad\circ\gamma_{H,R} \circ \left ( \left ( \gamma_{\left[0,\theta_1\right],R}\otimes\gamma_{\left(\theta_1,\theta_2\right],R} \right ) \circ \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],R} \circ\gamma_{H,R} \right )^{-1}\alpha_R^{-1}\notag\\ &= \pi_{R}\circ\alpha_R\circ \gamma_{\left(\theta_1,\theta_2\right],R} \circ \eta_g^R\beta_g^{RU} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\circ \left ( \gamma_{\left(\theta_1,\theta_2\right],R} \right )^{-1}\circ\alpha_R^{-1}. \end{align} $$
$$ \begin{align} \pi_R&\circ\hat \alpha_R\circ\hat \eta_g^R\beta_g^{R U} \hat \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \hat \eta_{gh}^R\right )^{-1}\hat\alpha_{R}^{-1}\notag\\ &= \pi_{R}\circ\alpha_R\circ \left ( \gamma_{\left[0,\theta_1\right],R}\otimes\gamma_{\left(\theta_1,\theta_2\right],R} \right ) \circ \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],R} \circ\gamma_{H,R} \circ \left ( \gamma_{\left[0,\theta_1\right],R}\circ\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],R}\circ\gamma_{H,R}\right )^{-1}\notag\\ & \quad \eta_g^R\beta_g^{RU} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\circ \gamma_{\left[0,\theta_1\right],R}\circ\gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],R} \notag\\ &\quad\circ\gamma_{H,R} \circ \left ( \left ( \gamma_{\left[0,\theta_1\right],R}\otimes\gamma_{\left(\theta_1,\theta_2\right],R} \right ) \circ \gamma_{\left(\theta_{0.8}, \theta_{1.2}\right],R} \circ\gamma_{H,R} \right )^{-1}\alpha_R^{-1}\notag\\ &= \pi_{R}\circ\alpha_R\circ \gamma_{\left(\theta_1,\theta_2\right],R} \circ \eta_g^R\beta_g^{RU} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1}\circ \left ( \gamma_{\left(\theta_1,\theta_2\right],R} \right )^{-1}\circ\alpha_R^{-1}. \end{align} $$Because  $ \eta _g^R\beta _g^{RU} \eta _h^R(\beta _g^{R U})^{-1}( \eta _{gh}^R)^{-1}\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{0}}}})$ commutes with
$ \eta _g^R\beta _g^{RU} \eta _h^R(\beta _g^{R U})^{-1}( \eta _{gh}^R)^{-1}\in \mathop {\mathrm {Aut}}\nolimits ( {\mathcal A}_{{ C_{\theta _{0}}}})$ commutes with ![]() $\gamma _{\left (\theta _1,\theta _2\right ],R}$, we obtain
$\gamma _{\left (\theta _1,\theta _2\right ],R}$, we obtain
 $$ \begin{align} \pi_R&\circ\hat \alpha_R\circ\hat \eta_g^R\beta_g^{R U} \hat \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \hat \eta_{gh}^R\right )^{-1}\hat\alpha_{R}^{-1} =\text{equation }(4.31)\notag\\ &=\pi_{R}\circ\alpha_R\circ \eta_g^R\beta_g^{RU} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1} \alpha_R^{-1} =\mathop{\mathrm{Ad}}\nolimits\left ( u_{R}(g,h)\right )\circ\pi_{R}. \end{align} $$
$$ \begin{align} \pi_R&\circ\hat \alpha_R\circ\hat \eta_g^R\beta_g^{R U} \hat \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \hat \eta_{gh}^R\right )^{-1}\hat\alpha_{R}^{-1} =\text{equation }(4.31)\notag\\ &=\pi_{R}\circ\alpha_R\circ \eta_g^R\beta_g^{RU} \eta_h^R\left (\beta_g^{R U}\right )^{-1}\left ( \eta_{gh}^R\right )^{-1} \alpha_R^{-1} =\mathop{\mathrm{Ad}}\nolimits\left ( u_{R}(g,h)\right )\circ\pi_{R}. \end{align} $$An analogous statement for ![]() $\sigma =L$ also holds. This completes the proof of formula (4.25). Hence the statement of the theorem is proven.
$\sigma =L$ also holds. This completes the proof of formula (4.25). Hence the statement of the theorem is proven.
5 Proof of Theorem 1.5
In this section, we prove Theorem 1.5. The proof relies heavily on the machinery of quasilocal automorphisms developed in [Reference Bachmann, Michalakis, Nachtergaele and SimsBMNS, Reference Nachtergaele, Sims and YoungNSY, Reference Moon and OgataMO]. (A summary is given in Appendix D.) We use terminology and facts from Appendixes C and D freely. We introduce a set of F-functions with fast decay, ![]() ${\mathcal F}_a$, as Definition C.2. A crucial point for us is the following:
${\mathcal F}_a$, as Definition C.2. A crucial point for us is the following:
Theorem 5.1. Set ![]() $\Phi _0,\Phi _1\in {\mathcal P}_{UG}$ and let
$\Phi _0,\Phi _1\in {\mathcal P}_{UG}$ and let ![]() $\omega _{\Phi _0}, \omega _{\Phi _1}$ be their unique gapped ground states. Suppose that
$\omega _{\Phi _0}, \omega _{\Phi _1}$ be their unique gapped ground states. Suppose that ![]() $\Phi _0\sim \Phi _1$ holds, via a path
$\Phi _0\sim \Phi _1$ holds, via a path ![]() $\Phi : [0,1]\to {\mathcal P}_{UG}$. Then there exists some
$\Phi : [0,1]\to {\mathcal P}_{UG}$. Then there exists some ![]() $\Psi \in \hat {\mathcal B}_F([0,1])$ with
$\Psi \in \hat {\mathcal B}_F([0,1])$ with ![]() $\Psi _{1}\in \hat {\mathcal B}_{F}([0,1])$ for some
$\Psi _{1}\in \hat {\mathcal B}_{F}([0,1])$ for some ![]() $F\in {\mathcal F}_a$ of the form
$F\in {\mathcal F}_a$ of the form  $F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant
$F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant ![]() $0<\theta <1$, such that
$0<\theta <1$, such that  $\omega _{\Phi _{1}}=\omega _{\Phi _0}\circ \tau _{1,0}^{\Psi }$. If
$\omega _{\Phi _{1}}=\omega _{\Phi _0}\circ \tau _{1,0}^{\Psi }$. If ![]() $\Phi _0,\Phi _1\in {\mathcal P}_{UG\beta }$ and
$\Phi _0,\Phi _1\in {\mathcal P}_{UG\beta }$ and ![]() $\Phi \sim _\beta \Phi _0$, we may take
$\Phi \sim _\beta \Phi _0$, we may take ![]() $\Psi $ to be
$\Psi $ to be ![]() $\beta $-invariant.
$\beta $-invariant.
For the proof, see Appendix D.
From this and Theorems 3.1 and 4.1, in order to show Theorem 1.5 it suffices to show the following, which says that the automorphism  $\tau _{1,0}^{\Psi }$ in Theorem 5.1 satisfies all the good factorisation properties which we assumed in previous sections:
$\tau _{1,0}^{\Psi }$ in Theorem 5.1 satisfies all the good factorisation properties which we assumed in previous sections:
Theorem 5.2. Let ![]() $F\in {\mathcal F}_a$ be an F-function of the form
$F\in {\mathcal F}_a$ be an F-function of the form  $F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant
$F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant ![]() $0<\theta <1$. Let
$0<\theta <1$. Let ![]() $\Psi \in \hat {\mathcal B}_{F}([0,1])$ be a path of interactions satisfying
$\Psi \in \hat {\mathcal B}_{F}([0,1])$ be a path of interactions satisfying ![]() $\Psi _1\in \hat {\mathcal B}_F([0,1])$. Then we have
$\Psi _1\in \hat {\mathcal B}_F([0,1])$. Then we have  $\tau _{1,0}^{\Psi }\in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$. Furthermore, if
$\tau _{1,0}^{\Psi }\in \mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$. Furthermore, if ![]() $\Psi $ is
$\Psi $ is  $\beta _{g}^{U}$-invariant – that is,
$\beta _{g}^{U}$-invariant – that is,  $\beta _{g}^U\left ( \Psi (X;t)\right )=\Psi (X;t)$ for any
$\beta _{g}^U\left ( \Psi (X;t)\right )=\Psi (X;t)$ for any ![]() $X\in {\mathfrak S}_{{\mathbb Z}^2}$,
$X\in {\mathfrak S}_{{\mathbb Z}^2}$, ![]() $t\in [0,1]$ and
$t\in [0,1]$ and ![]() $g\in G$ – then we have
$g\in G$ – then we have  $\tau _{1,0}^{\Psi }\in \mathop {\mathrm {GSQAut}}\nolimits ({\mathcal A})$.
$\tau _{1,0}^{\Psi }\in \mathop {\mathrm {GSQAut}}\nolimits ({\mathcal A})$.
Proof. Fix arbitrary
 $$ \begin{align} 0<\theta_{0.8}<\theta_1<\theta_{1.2}<\theta_{1.8}<\theta_2<\theta_{2.2}< \theta_{2.8}<\theta_3<\theta_{3.2}<\frac\pi 2. \end{align} $$
$$ \begin{align} 0<\theta_{0.8}<\theta_1<\theta_{1.2}<\theta_{1.8}<\theta_2<\theta_{2.2}< \theta_{2.8}<\theta_3<\theta_{3.2}<\frac\pi 2. \end{align} $$We show the existence of the decomposition
 $$ \begin{align} \begin{split} \tau_{1,0}^\Psi=&\mathop{\mathrm{Ad}}\nolimits(u)\circ \left ( \alpha_{\left(0,\theta_1\right]}\otimes \alpha_{\left(\theta_1,\theta_2\right]}\otimes \alpha_{\left(\theta_2,\theta_3\right]} \otimes \alpha_{\left(\theta_3,\frac\pi 2\right]} \right )\\ &\circ \left ( \alpha_{\left(\theta_{0.8},\theta_{1.2}\right]} \alpha_{\left(\theta_{1.8},\theta_{2.2}\right]}\otimes \alpha_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ), \end{split} \end{align} $$
$$ \begin{align} \begin{split} \tau_{1,0}^\Psi=&\mathop{\mathrm{Ad}}\nolimits(u)\circ \left ( \alpha_{\left(0,\theta_1\right]}\otimes \alpha_{\left(\theta_1,\theta_2\right]}\otimes \alpha_{\left(\theta_2,\theta_3\right]} \otimes \alpha_{\left(\theta_3,\frac\pi 2\right]} \right )\\ &\circ \left ( \alpha_{\left(\theta_{0.8},\theta_{1.2}\right]} \alpha_{\left(\theta_{1.8},\theta_{2.2}\right]}\otimes \alpha_{\left(\theta_{2.8},\theta_{3.2}\right]} \right ), \end{split} \end{align} $$with ![]() $\alpha $s of the forms in formulas (2.13) and (2.14). We follow the strategy of [Reference Naaijkens and OgataNO].
$\alpha $s of the forms in formulas (2.13) and (2.14). We follow the strategy of [Reference Naaijkens and OgataNO].
Step 1. Fix some ![]() $0<\theta '<\theta $ and set
$0<\theta '<\theta $ and set
 $$ \begin{align} \tilde F(r):=\frac{\exp\left ( {-r^{\theta'}}\right )}{(1+r)^{4}}. \end{align} $$
$$ \begin{align} \tilde F(r):=\frac{\exp\left ( {-r^{\theta'}}\right )}{(1+r)^{4}}. \end{align} $$With a suitably chosen constant ![]() $c_{1}>0$, we have
$c_{1}>0$, we have
 $$ \begin{align} \max\left\{ F\left (\frac r 3\right ), \left ( F\left ( \left [ \frac r 3 \right ] \right )\right )^{\frac 12}\right\}\le c_{1}\tilde F(r),\quad r\ge 0. \end{align} $$
$$ \begin{align} \max\left\{ F\left (\frac r 3\right ), \left ( F\left ( \left [ \frac r 3 \right ] \right )\right )^{\frac 12}\right\}\le c_{1}\tilde F(r),\quad r\ge 0. \end{align} $$Namely, ![]() $c_{1}\tilde F(r)$ satisfy the condition on
$c_{1}\tilde F(r)$ satisfy the condition on ![]() $\tilde F_{\theta }$ in Definition C.2(ii) for our
$\tilde F_{\theta }$ in Definition C.2(ii) for our  $F=\frac {\exp \left ( {-cr^{\theta }}\right )}{(1+r)^{4}}$ and
$F=\frac {\exp \left ( {-cr^{\theta }}\right )}{(1+r)^{4}}$ and  $\theta =\frac 12$. Set
$\theta =\frac 12$. Set
 $$ \begin{align} {\mathcal C}_{0}&:=\left\{ \begin{gathered} C_{\left[0,\theta_1\right],\sigma}, \ C_{\left(\theta_1,\theta_2\right], \sigma,\zeta}, \ C_{\left(\theta_2,\theta_3\right], \sigma,\zeta}, \ C_{\left(\theta_3,\frac\pi 2\right], \zeta},\\ \sigma=L,R,\ \zeta=D,U \end{gathered} \right\}, \end{align} $$
$$ \begin{align} {\mathcal C}_{0}&:=\left\{ \begin{gathered} C_{\left[0,\theta_1\right],\sigma}, \ C_{\left(\theta_1,\theta_2\right], \sigma,\zeta}, \ C_{\left(\theta_2,\theta_3\right], \sigma,\zeta}, \ C_{\left(\theta_3,\frac\pi 2\right], \zeta},\\ \sigma=L,R,\ \zeta=D,U \end{gathered} \right\}, \end{align} $$ $$ \begin{align} {\mathcal C}_{1}&:=\left\{ \begin{gathered} C_{\left(\theta_{0.8},\theta_{1.2}\right),\sigma,\zeta}, \ C_{\left(\theta_{1.8},\theta_{2.2}\right), \sigma,\zeta}, \ C_{\left(\theta_{2.8},\theta_{3.2}\right), \sigma,\zeta},\\ \sigma=L,R,\ \zeta=D,U \end{gathered} \right\}. \end{align} $$
$$ \begin{align} {\mathcal C}_{1}&:=\left\{ \begin{gathered} C_{\left(\theta_{0.8},\theta_{1.2}\right),\sigma,\zeta}, \ C_{\left(\theta_{1.8},\theta_{2.2}\right), \sigma,\zeta}, \ C_{\left(\theta_{2.8},\theta_{3.2}\right), \sigma,\zeta},\\ \sigma=L,R,\ \zeta=D,U \end{gathered} \right\}. \end{align} $$Define ![]() $\Psi ^{(0)}, \Psi ^{(1)}\in \hat {\mathcal B}_{F}([0,1])$ by
$\Psi ^{(0)}, \Psi ^{(1)}\in \hat {\mathcal B}_{F}([0,1])$ by
 $$ \begin{align} \begin{split} \Psi^{(0)}\left ( X; t\right )&:= \begin{cases} \Psi\left ( X; t\right ) & \text{if there exists a } C\in{\mathcal C}_0 \text{ such that } X\subset C, \\ 0 & \text{otherwise}, \end{cases} \\ \Psi^{(1)}\left ( X; t\right )&:=\Psi^{(0)}\left ( X; t\right )-\Psi\left ( X; t\right ), \end{split} \end{align} $$
$$ \begin{align} \begin{split} \Psi^{(0)}\left ( X; t\right )&:= \begin{cases} \Psi\left ( X; t\right ) & \text{if there exists a } C\in{\mathcal C}_0 \text{ such that } X\subset C, \\ 0 & \text{otherwise}, \end{cases} \\ \Psi^{(1)}\left ( X; t\right )&:=\Psi^{(0)}\left ( X; t\right )-\Psi\left ( X; t\right ), \end{split} \end{align} $$for each ![]() $X\in {\mathfrak S}_{{\mathbb Z}^2}$,
$X\in {\mathfrak S}_{{\mathbb Z}^2}$, ![]() $t\in [0,1]$.
$t\in [0,1]$.
First we would like to represent  $ ( \tau _{1,0}^{\Psi ^{(0)}})^{-1}\circ \tau _{1,0}^{ \Psi }$ as some quasilocal automorphism. Set
$ ( \tau _{1,0}^{\Psi ^{(0)}})^{-1}\circ \tau _{1,0}^{ \Psi }$ as some quasilocal automorphism. Set ![]() $t,s\in [0,1]$. We apply Proposition D.6 for
$t,s\in [0,1]$. We apply Proposition D.6 for ![]() $\Psi $ replaced by
$\Psi $ replaced by ![]() $\Psi ^{(1)}$ and
$\Psi ^{(1)}$ and ![]() $\tilde \Psi $ by
$\tilde \Psi $ by ![]() $\Psi $. Hence we set
$\Psi $. Hence we set
 $$ \begin{align} \Xi^{(s)}\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)=Z} \Delta_{X(m)}\left ( \tau_{t,s}^{\Psi}\left ( \Psi^{(1)}\left ( X; t\right ) \right ) \right ) \end{align} $$
$$ \begin{align} \Xi^{(s)}\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)=Z} \Delta_{X(m)}\left ( \tau_{t,s}^{\Psi}\left ( \Psi^{(1)}\left ( X; t\right ) \right ) \right ) \end{align} $$and
 $$ \begin{align} \Xi^{(n)(s)}\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z, \, X(m)\cap\Lambda_{n}=Z} \Delta_{X(m)}\left ( \tau_{t,s}^{\left(\Lambda_n\right)\Psi}\left ( \Psi^{{(1)}}\left ( X; t\right ) \right ) \right ). \end{align} $$
$$ \begin{align} \Xi^{(n)(s)}\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z, \, X(m)\cap\Lambda_{n}=Z} \Delta_{X(m)}\left ( \tau_{t,s}^{\left(\Lambda_n\right)\Psi}\left ( \Psi^{{(1)}}\left ( X; t\right ) \right ) \right ). \end{align} $$Corresponding to equation (D.31), we obtain
 $$ \begin{align} \tau_{t,s}^{\left(\Lambda_n\right),\Psi} \left ( H_{\Lambda_n,\Psi^{(1)}}(t) \right ) = H_{\Lambda_n,\Xi^{(n)(s)}}(t). \end{align} $$
$$ \begin{align} \tau_{t,s}^{\left(\Lambda_n\right),\Psi} \left ( H_{\Lambda_n,\Psi^{(1)}}(t) \right ) = H_{\Lambda_n,\Xi^{(n)(s)}}(t). \end{align} $$Applying Proposition D.6. we have ![]() $\Xi ^{(n)(s)}, \Xi ^{(s)}\in \hat {\mathcal B}_{\tilde F}([0,1])$, and
$\Xi ^{(n)(s)}, \Xi ^{(s)}\in \hat {\mathcal B}_{\tilde F}([0,1])$, and
 $$ \begin{align} \lim_{n\to\infty}\left \lVert \tau_{t,u}^{\Xi^{(n)(s)}}\left ( A\right ) -\tau_{t,u}^{\Xi^{(s)}}\left ( A\right ) \right \rVert=0,\quad A\in{\mathcal A},\ t,u\in [0,1], \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\left \lVert \tau_{t,u}^{\Xi^{(n)(s)}}\left ( A\right ) -\tau_{t,u}^{\Xi^{(s)}}\left ( A\right ) \right \rVert=0,\quad A\in{\mathcal A},\ t,u\in [0,1], \end{align} $$holds. Two functions 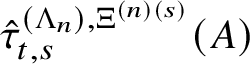 $\hat \tau _{t,s}^{(\Lambda _n), \Xi ^{(n)(s)}}(A)$ and
$\hat \tau _{t,s}^{(\Lambda _n), \Xi ^{(n)(s)}}(A)$ and  $ \tau _{t,s}^{(\Lambda _n ), \Psi }\circ ( \tau _{t,s}^{(\Lambda _n ),\Psi ^{(0)}} )^{-1}(A)$ satisfy the same differential equation and initial condition. Therefore we obtain
$ \tau _{t,s}^{(\Lambda _n ), \Psi }\circ ( \tau _{t,s}^{(\Lambda _n ),\Psi ^{(0)}} )^{-1}(A)$ satisfy the same differential equation and initial condition. Therefore we obtain
 $$ \begin{align} \hat\tau_{t,s}^{\left(\Lambda_n\right), \Xi^{(n)(s)}}(A)= \tau_{t,s}^{\left(\Lambda_n\right), \Psi}\circ \left ( \tau_{t,s}^{\left(\Lambda_n\right),\Psi^{(0)}}\right )^{-1}(A),\quad t\in [0,1],\ A\in{\mathcal A}. \end{align} $$
$$ \begin{align} \hat\tau_{t,s}^{\left(\Lambda_n\right), \Xi^{(n)(s)}}(A)= \tau_{t,s}^{\left(\Lambda_n\right), \Psi}\circ \left ( \tau_{t,s}^{\left(\Lambda_n\right),\Psi^{(0)}}\right )^{-1}(A),\quad t\in [0,1],\ A\in{\mathcal A}. \end{align} $$From the fact that  $ \hat \tau _{t,u}^{\left (\Lambda _n\right ), \Xi ^{(n)(s)}}=\tau _{u,t}^{\left (\Lambda _n\right ), \Xi ^{(n)(s)}}=\tau _{u,t}^{\Xi ^{(n)(s)}}$ converges strongly to an automorphism
$ \hat \tau _{t,u}^{\left (\Lambda _n\right ), \Xi ^{(n)(s)}}=\tau _{u,t}^{\left (\Lambda _n\right ), \Xi ^{(n)(s)}}=\tau _{u,t}^{\Xi ^{(n)(s)}}$ converges strongly to an automorphism  $\tau _{u,t}^{\Xi ^{(s)}}$ on
$\tau _{u,t}^{\Xi ^{(s)}}$ on ![]() ${\mathcal A}$ (equation (5.11)), we have
${\mathcal A}$ (equation (5.11)), we have
 $$ \begin{align} \lim_{n\to\infty}\left \lVert \hat\tau_{t,s}^{\left(\Lambda_{n}\right)\Xi^{(n)(s)}}\left ( A\right ) -\tau_{s,t}^{\Xi^{(s)}}\left ( A\right ) \right \rVert=0,\quad A\in{\mathcal A}. \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\left \lVert \hat\tau_{t,s}^{\left(\Lambda_{n}\right)\Xi^{(n)(s)}}\left ( A\right ) -\tau_{s,t}^{\Xi^{(s)}}\left ( A\right ) \right \rVert=0,\quad A\in{\mathcal A}. \end{align} $$On the other hand, by Theorem D.3 we have, for ![]() $t \in [0,1]$ and
$t \in [0,1]$ and ![]() $A \in {\mathcal A}$,
$A \in {\mathcal A}$,
 $$ \begin{align} \lim_{n\to\infty}\left \lVert \tau_{t,s}^{\left(\Lambda_n\right), \Psi}\circ \left ( \tau_{t,s}^{\left(\Lambda_n\right),\Psi^{(0)}}\right )^{-1}(A) -\tau_{t,s}^{ \Psi}\circ \left ( \tau_{t,s}^{\Psi^{(0)}}\right )^{-1}(A) \right \rVert=0. \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\left \lVert \tau_{t,s}^{\left(\Lambda_n\right), \Psi}\circ \left ( \tau_{t,s}^{\left(\Lambda_n\right),\Psi^{(0)}}\right )^{-1}(A) -\tau_{t,s}^{ \Psi}\circ \left ( \tau_{t,s}^{\Psi^{(0)}}\right )^{-1}(A) \right \rVert=0. \end{align} $$Therefore, taking the ![]() $n\to \infty $ limit in equation (5.12), we obtain
$n\to \infty $ limit in equation (5.12), we obtain
 $$ \begin{align} \tau_{s,t}^{ \Xi^{(s)}}(A)= \tau_{t,s}^{\Psi}\circ \left ( \tau_{t,s}^{\Psi^{(0)}}\right )^{-1}(A),\quad t,s\in [0,1],\ A\in{\mathcal A}. \end{align} $$
$$ \begin{align} \tau_{s,t}^{ \Xi^{(s)}}(A)= \tau_{t,s}^{\Psi}\circ \left ( \tau_{t,s}^{\Psi^{(0)}}\right )^{-1}(A),\quad t,s\in [0,1],\ A\in{\mathcal A}. \end{align} $$Hence we have
 $$ \begin{align} \tau_{s,t}^{\Psi}=\left ( \tau_{t,s}^{\Psi}\right )^{-1} =\left ( \tau_{t,s}^{\Psi^{(0)}}\right )^{-1}\left (\tau_{s,t}^{ \Xi^{(s)}}\right )^{-1}= \tau_{s,t}^{\Psi^{(0)}}\tau_{t,s}^{ \Xi^{(s)}}. \end{align} $$
$$ \begin{align} \tau_{s,t}^{\Psi}=\left ( \tau_{t,s}^{\Psi}\right )^{-1} =\left ( \tau_{t,s}^{\Psi^{(0)}}\right )^{-1}\left (\tau_{s,t}^{ \Xi^{(s)}}\right )^{-1}= \tau_{s,t}^{\Psi^{(0)}}\tau_{t,s}^{ \Xi^{(s)}}. \end{align} $$In particular, we get
 $$ \begin{align} \tau_{1,0}^{\Psi}= \tau_{1,0}^{\Psi^{(0)}}\tau_{0,1}^{ \Xi^{(1)}}. \end{align} $$
$$ \begin{align} \tau_{1,0}^{\Psi}= \tau_{1,0}^{\Psi^{(0)}}\tau_{0,1}^{ \Xi^{(1)}}. \end{align} $$Step 2. We show
 $$ \begin{align} \sum_{\substack{Z\in{\mathfrak S}\left({\mathbb Z}^2\right), \\\not\exists C\in{\mathcal C}_{1}\text{ s.t. }Z\subset C}} \sup_{t\in \left[0,1\right]}\left \lVert \Xi^{(1)}\left ( Z,t\right )\right \rVert<\infty. \end{align} $$
$$ \begin{align} \sum_{\substack{Z\in{\mathfrak S}\left({\mathbb Z}^2\right), \\\not\exists C\in{\mathcal C}_{1}\text{ s.t. }Z\subset C}} \sup_{t\in \left[0,1\right]}\left \lVert \Xi^{(1)}\left ( Z,t\right )\right \rVert<\infty. \end{align} $$From this,
 $$ \begin{align} V(t):=\sum_{\substack{Z\in{\mathfrak S}\left({\mathbb Z}^2\right), \\\not\exists C\in{\mathcal C}_{1}\text{ s.t. }Z\subset C}} \Xi^{(1)}\left ( Z,t\right ) \in{\mathcal A} \end{align} $$
$$ \begin{align} V(t):=\sum_{\substack{Z\in{\mathfrak S}\left({\mathbb Z}^2\right), \\\not\exists C\in{\mathcal C}_{1}\text{ s.t. }Z\subset C}} \Xi^{(1)}\left ( Z,t\right ) \in{\mathcal A} \end{align} $$converges absolutely in the norm topology and defines an element in ![]() ${\mathcal A}$. Furthermore, for
${\mathcal A}$. Furthermore, for
 $$ \begin{align} V_{n}(t):=\sum_{\substack{Z\in{\mathfrak S}\left({\mathbb Z}^2\right),\, Z\subset \Lambda_{n} \\\not\exists C\in{\mathcal C}_{1}\text{ s.t. }Z\subset C} } \Xi^{(1)}\left ( Z,t\right ) \in{\mathcal A}_{\Lambda_{n}},\quad n\in\mathbb{N}, \end{align} $$
$$ \begin{align} V_{n}(t):=\sum_{\substack{Z\in{\mathfrak S}\left({\mathbb Z}^2\right),\, Z\subset \Lambda_{n} \\\not\exists C\in{\mathcal C}_{1}\text{ s.t. }Z\subset C} } \Xi^{(1)}\left ( Z,t\right ) \in{\mathcal A}_{\Lambda_{n}},\quad n\in\mathbb{N}, \end{align} $$we get
 $$ \begin{align} \lim_{n\to\infty}\sup_{t\in\left[0,1\right]}\left \lVert V_{n}(t)-V(t)\right \rVert=0 \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\sup_{t\in\left[0,1\right]}\left \lVert V_{n}(t)-V(t)\right \rVert=0 \end{align} $$from formula (5.18).
To prove formula (5.18), we first bound
 $$ \begin{align} \begin{split} \sum_{\substack{Z\in{\mathfrak S}\left({\mathbb Z}^2\right) \\ \not\exists C\in{\mathcal C}_{1}\text{ s.t. }Z\subset C } } &\sup_{t\in\left[0,1\right]} \left \lVert \Xi^{(1)}\left ( Z,t\right ) \right \rVert \\ &\le \sum_{\substack{Z\in{\mathfrak S}\left({\mathbb Z}^2\right), \\ \not\exists C\in{\mathcal C}_{1}\text{ s.t. }Z\subset C } } \sum_{m\ge 0} \sum_{\substack{X: X\subset Z\\ X(m)=Z}} \left[ \sup_{t\in\left[0,1\right]}\left \lVert \Delta_{X(m)}\left ( \tau_{t,1}^{\Psi}\left ( \Psi^{(1)}\left ( X; t\right ) \right ) \right ) \right \rVert \right]\\ &\le \sum_{m\ge 0} \sum_{\substack{X: \\ \not\exists C\in{\mathcal C}_{1}\text{ s.t. }X(m)\subset C}} \sup_{t\in\left[0,1\right]}\left \lVert \Delta_{X(m)}\left ( \tau_{t,1}^{\Psi}\left ( \Psi^{(1)}\left ( X; t\right ) \right ) \right ) \right \rVert\\ & \le \sum_{m\ge 0} \sum_{\substack{X: \\ \not\exists C\in{\mathcal C}_{1}\text{ s.t. }X(m)\subset C}} \left[ \sup_{t\in\left[0,1\right]} \frac{8\left \lVert \Psi^{(1)}\left ( X; t\right ) \right \rVert}{C_{F}}\left ( e^{2I_{F}(\Psi)}-1\right )\left \lvert X\right \rvert G_{F}\left ( m\right ) \right] \\ &=\frac{8}{C_{F}}\left ( e^{2I_F(\Psi)}-1\right ) \sum_{m\ge 0} \sum_{\substack{X: \\ \not\exists C\in{\mathcal C}_{1}\text{ s.t. }X(m)\subset C}} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi^{(1)}\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right]. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \sum_{\substack{Z\in{\mathfrak S}\left({\mathbb Z}^2\right) \\ \not\exists C\in{\mathcal C}_{1}\text{ s.t. }Z\subset C } } &\sup_{t\in\left[0,1\right]} \left \lVert \Xi^{(1)}\left ( Z,t\right ) \right \rVert \\ &\le \sum_{\substack{Z\in{\mathfrak S}\left({\mathbb Z}^2\right), \\ \not\exists C\in{\mathcal C}_{1}\text{ s.t. }Z\subset C } } \sum_{m\ge 0} \sum_{\substack{X: X\subset Z\\ X(m)=Z}} \left[ \sup_{t\in\left[0,1\right]}\left \lVert \Delta_{X(m)}\left ( \tau_{t,1}^{\Psi}\left ( \Psi^{(1)}\left ( X; t\right ) \right ) \right ) \right \rVert \right]\\ &\le \sum_{m\ge 0} \sum_{\substack{X: \\ \not\exists C\in{\mathcal C}_{1}\text{ s.t. }X(m)\subset C}} \sup_{t\in\left[0,1\right]}\left \lVert \Delta_{X(m)}\left ( \tau_{t,1}^{\Psi}\left ( \Psi^{(1)}\left ( X; t\right ) \right ) \right ) \right \rVert\\ & \le \sum_{m\ge 0} \sum_{\substack{X: \\ \not\exists C\in{\mathcal C}_{1}\text{ s.t. }X(m)\subset C}} \left[ \sup_{t\in\left[0,1\right]} \frac{8\left \lVert \Psi^{(1)}\left ( X; t\right ) \right \rVert}{C_{F}}\left ( e^{2I_{F}(\Psi)}-1\right )\left \lvert X\right \rvert G_{F}\left ( m\right ) \right] \\ &=\frac{8}{C_{F}}\left ( e^{2I_F(\Psi)}-1\right ) \sum_{m\ge 0} \sum_{\substack{X: \\ \not\exists C\in{\mathcal C}_{1}\text{ s.t. }X(m)\subset C}} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi^{(1)}\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right]. \end{split} \end{align} $$For the third inequality, we used Theorem D.3 3. For any cone ![]() $C_1,C_2$ of
$C_1,C_2$ of ![]() ${\mathbb Z}^2$ with its apex at the origin, we set
${\mathbb Z}^2$ with its apex at the origin, we set
 $$ \begin{align} M(C_1,C_2):= \sum_{m\ge 0} \sum_{\substack{X: \\ \forall C\in{\mathcal C}_{1}, \, X\cap \left ( \left ( C^{c}\right )(m)\right )\neq\emptyset,\\ X\cap C_{1}\neq\emptyset,\, X\cap C_{2}\neq\emptyset }} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi^{(1)}\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right]. \end{align} $$
$$ \begin{align} M(C_1,C_2):= \sum_{m\ge 0} \sum_{\substack{X: \\ \forall C\in{\mathcal C}_{1}, \, X\cap \left ( \left ( C^{c}\right )(m)\right )\neq\emptyset,\\ X\cap C_{1}\neq\emptyset,\, X\cap C_{2}\neq\emptyset }} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi^{(1)}\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right]. \end{align} $$From the definition of ![]() $ \Psi ^{(1)}$, we have
$ \Psi ^{(1)}$, we have ![]() $ \Psi ^{(1)}\left ( X; t\right ) =0, $ unless X has a nonempty intersection with at least two elements in
$ \Psi ^{(1)}\left ( X; t\right ) =0, $ unless X has a nonempty intersection with at least two elements in ![]() ${\mathcal C}_{0}$. Therefore, if X gives a nonzero contribution in formula (5.22), then it has to satisfy
${\mathcal C}_{0}$. Therefore, if X gives a nonzero contribution in formula (5.22), then it has to satisfy
 $$ \begin{gather*} X\cap \left ( \left ( C^{c}\right )(m)\right )\neq\emptyset,\quad \text{for all } C\in{\mathcal C}_{1},\\ \exists C_{1},C_{2}\in{\mathcal C}_{0}\text{ such that } C_1\neq C_2, \ X\cap C_{1}\neq\emptyset,\ X\cap C_{2}\neq\emptyset. \end{gather*} $$
$$ \begin{gather*} X\cap \left ( \left ( C^{c}\right )(m)\right )\neq\emptyset,\quad \text{for all } C\in{\mathcal C}_{1},\\ \exists C_{1},C_{2}\in{\mathcal C}_{0}\text{ such that } C_1\neq C_2, \ X\cap C_{1}\neq\emptyset,\ X\cap C_{2}\neq\emptyset. \end{gather*} $$Hence we have
 $$ \begin{align} \begin{split} \text{formula }(5.22)\le \frac{8}{C_{F}}\left ( e^{2I_F(\Psi)}-1\right ) \sum_{\substack{C_{1},C_{2}\in{\mathcal C}_{0}\\C_1\neq C_2 } } M({C_1,C_2}). \end{split} \end{align} $$
$$ \begin{align} \begin{split} \text{formula }(5.22)\le \frac{8}{C_{F}}\left ( e^{2I_F(\Psi)}-1\right ) \sum_{\substack{C_{1},C_{2}\in{\mathcal C}_{0}\\C_1\neq C_2 } } M({C_1,C_2}). \end{split} \end{align} $$Hence it suffices to show that ![]() $M({C_1,C_2})<\infty $ for all
$M({C_1,C_2})<\infty $ for all ![]() $C_{1},C_{2}\in {\mathcal C}_{0}$ with
$C_{1},C_{2}\in {\mathcal C}_{0}$ with ![]() $C_1\neq C_2$.
$C_1\neq C_2$.
In order to proceed, we prepare two estimates. We will freely identify ![]() ${\mathbb C}$ and
${\mathbb C}$ and ![]() ${\mathbb R}^{2}$ in an obvious manner. In particular,
${\mathbb R}^{2}$ in an obvious manner. In particular, ![]() $\arg z$ of
$\arg z$ of ![]() $z\in {\mathbb Z}^{2}\subset {\mathbb R}^{2}$ in the following definition is considered with this identification: For
$z\in {\mathbb Z}^{2}\subset {\mathbb R}^{2}$ in the following definition is considered with this identification: For ![]() $\varphi _{1}<\varphi _{2}$, we set
$\varphi _{1}<\varphi _{2}$, we set
 $$ \begin{align} \check C_{\left[\varphi_{1},\varphi_{2}\right]}:= \left\{ z\in {\mathbb Z}^{2}\mid \arg z\in [\varphi_{1},\varphi_{2}] \right\}. \end{align} $$
$$ \begin{align} \check C_{\left[\varphi_{1},\varphi_{2}\right]}:= \left\{ z\in {\mathbb Z}^{2}\mid \arg z\in [\varphi_{1},\varphi_{2}] \right\}. \end{align} $$We define  $\check C_{\left (\varphi _{1},\varphi _{2}\right )}$ and so on analogously. Set
$\check C_{\left (\varphi _{1},\varphi _{2}\right )}$ and so on analogously. Set
 $$ \begin{align} {c^{(0)}}_{\zeta_1,\zeta_2,\zeta_3,\zeta_4} :=\sqrt{1-\max\left\{\cos (\zeta_3-\zeta_2),\cos (\zeta_4-\zeta_1),0\right\}},\quad \zeta_1,\zeta_2,\zeta_3,\zeta_4 \in {\mathbb R}. \end{align} $$
$$ \begin{align} {c^{(0)}}_{\zeta_1,\zeta_2,\zeta_3,\zeta_4} :=\sqrt{1-\max\left\{\cos (\zeta_3-\zeta_2),\cos (\zeta_4-\zeta_1),0\right\}},\quad \zeta_1,\zeta_2,\zeta_3,\zeta_4 \in {\mathbb R}. \end{align} $$Lemma 5.3. Set ![]() $\varphi _1<\varphi _2<\varphi _3<\varphi _4$ with
$\varphi _1<\varphi _2<\varphi _3<\varphi _4$ with ![]() $\varphi _4-\varphi _1<2\pi $. Then
$\varphi _4-\varphi _1<2\pi $. Then
 $$ \begin{align*} \begin{split} b_0(\varphi_1,\varphi_2,\varphi_3,\varphi_4) &:= \sum_{m\ge 0} \sum_{\substack{X: \\ X\cap \check C_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset\\ X\cap \check C_{\left[\varphi_3,\varphi_4\right]}\neq\emptyset }} \left[ \sup_{t\in\left[0,1\right]}\left (\left \lVert \Psi\left ( X; t\right )\right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right] \notag\\ &\le (64)^3 \frac {3^{4}\kappa_{1, 4, F}}{\left ( c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}\right ) ^{4}} \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_{F}\right ) \left ( \sum_{m\ge 0}G_{F}\left ( m\right )\right )<\infty. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} b_0(\varphi_1,\varphi_2,\varphi_3,\varphi_4) &:= \sum_{m\ge 0} \sum_{\substack{X: \\ X\cap \check C_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset\\ X\cap \check C_{\left[\varphi_3,\varphi_4\right]}\neq\emptyset }} \left[ \sup_{t\in\left[0,1\right]}\left (\left \lVert \Psi\left ( X; t\right )\right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right] \notag\\ &\le (64)^3 \frac {3^{4}\kappa_{1, 4, F}}{\left ( c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}\right ) ^{4}} \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_{F}\right ) \left ( \sum_{m\ge 0}G_{F}\left ( m\right )\right )<\infty. \end{split} \end{align*} $$Proof. Substituting Lemma C.4, we obtain
 $$ \begin{align} b_0(\varphi_1,\varphi_2,\varphi_3,\varphi_4) &:= \sum_{m\ge 0} \sum_{\substack{X: \\ X\cap \check {C}_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset\\ X\cap \check {C}_{\left[\varphi_3,\varphi_4\right]}\neq\emptyset }} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right] \notag\\ &\le \sum_{m\ge 0} \sum_{\substack{x\in \check {C}_{\left[\varphi_1,\varphi_2\right]} \\y\in \check {C}_{\left[\varphi_3,\varphi_4\right]}}} \sum_{X\ni x,y}\left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right]\notag\\ &\le \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_{F}\right ) \sum_{\substack{x\in \check {C}_{\left[\varphi_1,\varphi_2\right]}\\ y\in \check {C}_{\left[\varphi_3,\varphi_4\right]}}} F\left ( {\mathrm{d}}(x,y)\right ) \left ( \sum_{m\ge 0}G_{F}\left ( m\right )\right )\notag\\ &\le (64)^3 \frac {3^{4}\kappa_{1, 4, F}}{\left ( c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}\right ) ^{4}} \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_{F}\right ) \left ( \sum_{m\ge 0}G_{F}\left ( m\right )\right )<\infty. \end{align} $$
$$ \begin{align} b_0(\varphi_1,\varphi_2,\varphi_3,\varphi_4) &:= \sum_{m\ge 0} \sum_{\substack{X: \\ X\cap \check {C}_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset\\ X\cap \check {C}_{\left[\varphi_3,\varphi_4\right]}\neq\emptyset }} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right] \notag\\ &\le \sum_{m\ge 0} \sum_{\substack{x\in \check {C}_{\left[\varphi_1,\varphi_2\right]} \\y\in \check {C}_{\left[\varphi_3,\varphi_4\right]}}} \sum_{X\ni x,y}\left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right]\notag\\ &\le \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_{F}\right ) \sum_{\substack{x\in \check {C}_{\left[\varphi_1,\varphi_2\right]}\\ y\in \check {C}_{\left[\varphi_3,\varphi_4\right]}}} F\left ( {\mathrm{d}}(x,y)\right ) \left ( \sum_{m\ge 0}G_{F}\left ( m\right )\right )\notag\\ &\le (64)^3 \frac {3^{4}\kappa_{1, 4, F}}{\left ( c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}\right ) ^{4}} \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_{F}\right ) \left ( \sum_{m\ge 0}G_{F}\left ( m\right )\right )<\infty. \end{align} $$We used Lemma C.4 in the last inequality. The last value is finite by equation (C.14) for our ![]() $F\in {\mathcal F}_{a}$.
$F\in {\mathcal F}_{a}$.
Set
 $$ \begin{align} {c^{(1)}}_{\zeta_1,\zeta_2,\zeta_3} :=\sqrt{1-\max\left\{\cos (\zeta_1-\zeta_2),\cos (\zeta_1-\zeta_3)\right\}},\quad \zeta_1,\zeta_2,\zeta_3\in [0,2\pi). \end{align} $$
$$ \begin{align} {c^{(1)}}_{\zeta_1,\zeta_2,\zeta_3} :=\sqrt{1-\max\left\{\cos (\zeta_1-\zeta_2),\cos (\zeta_1-\zeta_3)\right\}},\quad \zeta_1,\zeta_2,\zeta_3\in [0,2\pi). \end{align} $$Lemma 5.4. For ![]() $\varphi _1<\varphi _2<\varphi _3$ with
$\varphi _1<\varphi _2<\varphi _3$ with ![]() $\varphi _3-\varphi _1<\frac \pi 2$, we have
$\varphi _3-\varphi _1<\frac \pi 2$, we have
 $$ \begin{align} \begin{split} b_1(\varphi_1,\varphi_2,\varphi_3) &:=\sum_{m\ge 0} \sum_{\substack{X: \\ X\subset \check {C}_{\left[\varphi_1,\varphi_3\right]}\\ X\cap \check {C}_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset\\ X\cap \check C_{\left[\varphi_2,\varphi_3\right]}\neq\emptyset\\ X\cap \left ( \left ( \left ( \check C_{\left(\varphi_1,\varphi_3\right)}\right )^c\right )(m)\right )\neq \emptyset }} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right]\\ &\le64\cdot 144\cdot 24\cdot \left ( \pi \kappa_{1,2,F}+F(0) \right ) \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_F\right ) \left ( \sum_{m\ge 0} (m+1)^{4}G_{F}\left ( m\right )\right ) \\ &\quad \left ( \left ( {c^{(1)}}_{\varphi_{1},\varphi_{2},\varphi_{3}}\right )^{-4} +\left ( {c^{(1)}}_{\varphi_{3},\varphi_{1},\varphi_2}\right )^{-4} \right ) <\infty. \end{split} \end{align} $$
$$ \begin{align} \begin{split} b_1(\varphi_1,\varphi_2,\varphi_3) &:=\sum_{m\ge 0} \sum_{\substack{X: \\ X\subset \check {C}_{\left[\varphi_1,\varphi_3\right]}\\ X\cap \check {C}_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset\\ X\cap \check C_{\left[\varphi_2,\varphi_3\right]}\neq\emptyset\\ X\cap \left ( \left ( \left ( \check C_{\left(\varphi_1,\varphi_3\right)}\right )^c\right )(m)\right )\neq \emptyset }} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right]\\ &\le64\cdot 144\cdot 24\cdot \left ( \pi \kappa_{1,2,F}+F(0) \right ) \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_F\right ) \left ( \sum_{m\ge 0} (m+1)^{4}G_{F}\left ( m\right )\right ) \\ &\quad \left ( \left ( {c^{(1)}}_{\varphi_{1},\varphi_{2},\varphi_{3}}\right )^{-4} +\left ( {c^{(1)}}_{\varphi_{3},\varphi_{1},\varphi_2}\right )^{-4} \right ) <\infty. \end{split} \end{align} $$Proof. Set
 $$ \begin{align} L_\varphi:= \left\{ z\in{\mathbb R}^2\mid \arg z=\varphi \right\},\quad \varphi\in [0,2\pi). \end{align} $$
$$ \begin{align} L_\varphi:= \left\{ z\in{\mathbb R}^2\mid \arg z=\varphi \right\},\quad \varphi\in [0,2\pi). \end{align} $$Note that if ![]() $X\in {\mathfrak S}_{{\mathbb Z}^2}$ satisfies
$X\in {\mathfrak S}_{{\mathbb Z}^2}$ satisfies  $X\subset \check {C}_{\left [\varphi _1,\varphi _3\right ]}$ and
$X\subset \check {C}_{\left [\varphi _1,\varphi _3\right ]}$ and  $X\cap ( ( ( \check C_{ (\varphi _1,\varphi _3 )} )^c )(m) )\neq \emptyset $, then we have
$X\cap ( ( ( \check C_{ (\varphi _1,\varphi _3 )} )^c )(m) )\neq \emptyset $, then we have
Therefore, we have
 $$ \begin{align}\sum_{m\ge 0}& \sum_{\substack{X: \\ X\subset \check {C}_{\left[\varphi_1,\varphi_3\right]}\\ X\cap \check {C}_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset\\ X\cap \check C_{\left[\varphi_2,\varphi_3\right]}\neq\emptyset\\ X\cap \left ( \left ( \left ( \check C_{\left(\varphi_1,\varphi_3\right)}\right )^c\right )(m)\right )\neq \emptyset }} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right] \nonumber \\ &\le\sum_{m\ge 0} G_{F}\left ( m\right ) \left ( \sum_{\substack{X: \\ X\cap \check C_{\left[\varphi_2,\varphi_3\right]}\neq\emptyset\\ d\left(X, L_{\varphi_1}\right)\le m }} +\sum_{\substack{X: \\ X\cap \check{C}_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset\\ d\left(X, L_{\varphi_3}\right)\le m }} \right ) \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert \right] \nonumber\\ &\le \sum_{m\ge 0} G_{F}\left ( m\right ) \left ( \sum_{\substack{x\in \check C_{\left[\varphi_2,\varphi_3\right]}\\ y\in L_{\varphi_1}(m) }} +\sum_{\substack{x\in \check {C}_{\left[\varphi_1,\varphi_2\right]}\\ y\in L_{\varphi_3}(m) }} \right ) \sum_{\substack{X: X\ni x,y }} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert \right] \nonumber\\ &\le \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_F\right ) \sum_{m\ge 0} G_{F}\left ( m\right ) \left ( \sum_{\substack{x\in \check C_{\left[\varphi_2,\varphi_3\right]}\\ y\in L_{\varphi_1}(m) }} +\sum_{\substack{x\in \check {C}_{\left[\varphi_1,\varphi_2\right]}\\ y\in L_{\varphi_3}(m) }} \right ) F\left ( {\mathrm{d}}(x,y)\right )\nonumber\\ &\le 64\cdot 144\cdot 24\cdot \left ( \pi \kappa_{1,2,F}+F(0) \right ) \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_F\right )\nonumber \\ &\quad \left ( \sum_{m\ge 0} (m+1)^{4}G_{F}\left ( m\right )\right ) \left ( \left ( {c^{(1)}}_{\varphi_{1},\varphi_{2},\varphi_{3}}\right )^{-4} +\left ( {c^{(1)}}_{\varphi_{3},\varphi_{1},\varphi_2}\right )^{-4} \right ). \end{align} $$
$$ \begin{align}\sum_{m\ge 0}& \sum_{\substack{X: \\ X\subset \check {C}_{\left[\varphi_1,\varphi_3\right]}\\ X\cap \check {C}_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset\\ X\cap \check C_{\left[\varphi_2,\varphi_3\right]}\neq\emptyset\\ X\cap \left ( \left ( \left ( \check C_{\left(\varphi_1,\varphi_3\right)}\right )^c\right )(m)\right )\neq \emptyset }} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right] \nonumber \\ &\le\sum_{m\ge 0} G_{F}\left ( m\right ) \left ( \sum_{\substack{X: \\ X\cap \check C_{\left[\varphi_2,\varphi_3\right]}\neq\emptyset\\ d\left(X, L_{\varphi_1}\right)\le m }} +\sum_{\substack{X: \\ X\cap \check{C}_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset\\ d\left(X, L_{\varphi_3}\right)\le m }} \right ) \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert \right] \nonumber\\ &\le \sum_{m\ge 0} G_{F}\left ( m\right ) \left ( \sum_{\substack{x\in \check C_{\left[\varphi_2,\varphi_3\right]}\\ y\in L_{\varphi_1}(m) }} +\sum_{\substack{x\in \check {C}_{\left[\varphi_1,\varphi_2\right]}\\ y\in L_{\varphi_3}(m) }} \right ) \sum_{\substack{X: X\ni x,y }} \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert \right] \nonumber\\ &\le \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_F\right ) \sum_{m\ge 0} G_{F}\left ( m\right ) \left ( \sum_{\substack{x\in \check C_{\left[\varphi_2,\varphi_3\right]}\\ y\in L_{\varphi_1}(m) }} +\sum_{\substack{x\in \check {C}_{\left[\varphi_1,\varphi_2\right]}\\ y\in L_{\varphi_3}(m) }} \right ) F\left ( {\mathrm{d}}(x,y)\right )\nonumber\\ &\le 64\cdot 144\cdot 24\cdot \left ( \pi \kappa_{1,2,F}+F(0) \right ) \left ( \left \lVert\left \lvert \Psi_1\right \rVert\right \rvert_F\right )\nonumber \\ &\quad \left ( \sum_{m\ge 0} (m+1)^{4}G_{F}\left ( m\right )\right ) \left ( \left ( {c^{(1)}}_{\varphi_{1},\varphi_{2},\varphi_{3}}\right )^{-4} +\left ( {c^{(1)}}_{\varphi_{3},\varphi_{1},\varphi_2}\right )^{-4} \right ). \end{align} $$In the last inequality, we used Lemma C.5 with ![]() $\varphi _3-\varphi _1<\frac \pi 2$. Because
$\varphi _3-\varphi _1<\frac \pi 2$. Because ![]() $\varphi _3-\varphi _1<\frac \pi 2$ and because of formula (C.14), the last value is finite.
$\varphi _3-\varphi _1<\frac \pi 2$ and because of formula (C.14), the last value is finite.
Now let us go back to the estimate of formula (5.23). If ![]() $C_1,C_2\in {\mathcal C}_0$ are
$C_1,C_2\in {\mathcal C}_0$ are  $C_1=\check {C}_{\left [\varphi _1,\varphi _2\right ]}, C_2=\check {C}_{\left [\varphi _3,\varphi _4\right ]}$ with
$C_1=\check {C}_{\left [\varphi _1,\varphi _2\right ]}, C_2=\check {C}_{\left [\varphi _3,\varphi _4\right ]}$ with ![]() $\varphi _1<\varphi _2<\varphi _3<\varphi _4, \varphi _4-\varphi _1<2\pi $, then from Lemma 5.3, we have
$\varphi _1<\varphi _2<\varphi _3<\varphi _4, \varphi _4-\varphi _1<2\pi $, then from Lemma 5.3, we have
Now suppose that ![]() $C_1,C_2\in {\mathcal C}_0$ are
$C_1,C_2\in {\mathcal C}_0$ are  $C_1=\check {C}_{\left [\varphi _1,\varphi _2\right ]}, C_2=\check C_{\left [\varphi _2,\varphi _3\right ]}$ with
$C_1=\check {C}_{\left [\varphi _1,\varphi _2\right ]}, C_2=\check C_{\left [\varphi _2,\varphi _3\right ]}$ with ![]() $\varphi _1<\varphi _2<\varphi _3, \varphi _3-\varphi _1<2\pi $. (Recall definition (5.5).) By the definition of
$\varphi _1<\varphi _2<\varphi _3, \varphi _3-\varphi _1<2\pi $. (Recall definition (5.5).) By the definition of ![]() ${\mathcal C}_0$ and
${\mathcal C}_0$ and ![]() ${\mathcal C}_1$, there is some
${\mathcal C}_1$, there is some ![]() $C=C_{\left (\zeta _1,\zeta _2\right )}\in {\mathcal C}_1$ such that
$C=C_{\left (\zeta _1,\zeta _2\right )}\in {\mathcal C}_1$ such that ![]() $\varphi _1<\zeta _1<\varphi _2<\zeta _2<\varphi _3$ and
$\varphi _1<\zeta _1<\varphi _2<\zeta _2<\varphi _3$ and ![]() $\zeta _2-\zeta _1<\frac \pi 2$. For
$\zeta _2-\zeta _1<\frac \pi 2$. For ![]() $X\in {\mathfrak S}_{{\mathbb Z}^2}$ to give a nonzero contribution in formula (5.23), it has to satisfy
$X\in {\mathfrak S}_{{\mathbb Z}^2}$ to give a nonzero contribution in formula (5.23), it has to satisfy
 $$ \begin{align} X(m)\cap ( \check C_{\left[\zeta_1,\zeta_2\right]})^c\neq\emptyset,\qquad X\cap \check {C}_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset,\qquad X\cap \check C_{\left[\varphi_2,\varphi_3\right]}\neq\emptyset. \end{align} $$
$$ \begin{align} X(m)\cap ( \check C_{\left[\zeta_1,\zeta_2\right]})^c\neq\emptyset,\qquad X\cap \check {C}_{\left[\varphi_1,\varphi_2\right]}\neq\emptyset,\qquad X\cap \check C_{\left[\varphi_2,\varphi_3\right]}\neq\emptyset. \end{align} $$For such an X, one of the following occurs:
(i)
 $X\cap \check C_{\left [\zeta _2,\varphi _3\right ]}\neq \emptyset $ and
$X\cap \check C_{\left [\zeta _2,\varphi _3\right ]}\neq \emptyset $ and  $X\cap \check {C}_{\left [\varphi _1,\varphi _2\right ]}\neq \emptyset $.
$X\cap \check {C}_{\left [\varphi _1,\varphi _2\right ]}\neq \emptyset $.(ii)
 $X\cap \check C_{\left [\varphi _1,\zeta _1\right ]}\neq \emptyset $ and
$X\cap \check C_{\left [\varphi _1,\zeta _1\right ]}\neq \emptyset $ and  $X\cap \check C_{\left [\varphi _2,\varphi _3\right ]}\neq \emptyset $.
$X\cap \check C_{\left [\varphi _2,\varphi _3\right ]}\neq \emptyset $.(iii)
 $X\cap \check C_{\left [\varphi _2, \zeta _2\right ]}\neq \emptyset (\text {and } X\cap \check C_{\left [\zeta _1,\varphi _2\right ]}\neq \emptyset )$ and
$X\cap \check C_{\left [\varphi _2, \zeta _2\right ]}\neq \emptyset (\text {and } X\cap \check C_{\left [\zeta _1,\varphi _2\right ]}\neq \emptyset )$ and  $X\cap \check C_{\left [\varphi _3,\varphi _1+2\pi \right ]}\neq \emptyset $.
$X\cap \check C_{\left [\varphi _3,\varphi _1+2\pi \right ]}\neq \emptyset $.(iv)
 $X\subset \check C_{\zeta _1,\zeta _2}$,
$X\subset \check C_{\zeta _1,\zeta _2}$,  $X\cap ( ( \check C_{\zeta _1,\zeta _2} )^c )(m)\neq \emptyset $,
$X\cap ( ( \check C_{\zeta _1,\zeta _2} )^c )(m)\neq \emptyset $,  $X\cap \check C_{\left [\varphi _2, \zeta _2\right ]}\neq \emptyset $ and
$X\cap \check C_{\left [\varphi _2, \zeta _2\right ]}\neq \emptyset $ and  $X\cap \check C_{\left [\zeta _1,\varphi _2\right ]}\neq \emptyset $.
$X\cap \check C_{\left [\zeta _1,\varphi _2\right ]}\neq \emptyset $.
Hence we get
 $$ \begin{align} \begin{split} M({C_1,C_2}) &\le b_0(\varphi_1,\varphi_2, \zeta_2,\varphi_3) +b_0(\varphi_1,\zeta_1, \varphi_2,\varphi_3) +b_0(\varphi_2, \zeta_2, \varphi_3,\varphi_1+2\pi) +b_1(\zeta_1,\varphi_2,\zeta_2)\\ &<\infty. \end{split} \end{align} $$
$$ \begin{align} \begin{split} M({C_1,C_2}) &\le b_0(\varphi_1,\varphi_2, \zeta_2,\varphi_3) +b_0(\varphi_1,\zeta_1, \varphi_2,\varphi_3) +b_0(\varphi_2, \zeta_2, \varphi_3,\varphi_1+2\pi) +b_1(\zeta_1,\varphi_2,\zeta_2)\\ &<\infty. \end{split} \end{align} $$Hence we have proven the claim of step 2.
Step 3. Next we set
 $$ \begin{align} \tilde\Xi(Z,t):= \begin{cases} \Xi^{(1)}(Z,t) & \text{if }\exists C\in{\mathcal C}_{1}\text{ s.t. } Z\subset C,\\ 0&\text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} \tilde\Xi(Z,t):= \begin{cases} \Xi^{(1)}(Z,t) & \text{if }\exists C\in{\mathcal C}_{1}\text{ s.t. } Z\subset C,\\ 0&\text{otherwise}. \end{cases} \end{align} $$ Clearly, we have ![]() $\tilde \Xi \in \hat {\mathcal B}_{\tilde F}([0,1])$. Note that
$\tilde \Xi \in \hat {\mathcal B}_{\tilde F}([0,1])$. Note that
As a uniform limit of ![]() $[0,1]\ni t\mapsto V_{n}(t)\in {\mathcal A}$ (equation (5.21)),
$[0,1]\ni t\mapsto V_{n}(t)\in {\mathcal A}$ (equation (5.21)), ![]() $[0,1]\ni t\mapsto V(t)\in {\mathcal A}$ is norm-continuous. Because
$[0,1]\ni t\mapsto V(t)\in {\mathcal A}$ is norm-continuous. Because ![]() $\tilde \Xi \in \hat {\mathcal B}_{\tilde F}([0,1])$,
$\tilde \Xi \in \hat {\mathcal B}_{\tilde F}([0,1])$,  $[0,1]\ni t\mapsto \tau _{t,s}^{\tilde \Xi }\left ( V(t)\right )\in {\mathcal A}$ is also norm-continuous, for each
$[0,1]\ni t\mapsto \tau _{t,s}^{\tilde \Xi }\left ( V(t)\right )\in {\mathcal A}$ is also norm-continuous, for each ![]() $s\in [0,1]$. Therefore, for each
$s\in [0,1]$. Therefore, for each ![]() $s\in [0,1]$, there is a unique norm-differentiable map
$s\in [0,1]$, there is a unique norm-differentiable map ![]() $[0,1]\ni t \mapsto W^{(s)}(t) \in {\mathcal U}\left ( {\mathcal A}\right )$ such that
$[0,1]\ni t \mapsto W^{(s)}(t) \in {\mathcal U}\left ( {\mathcal A}\right )$ such that
 $$ \begin{align} \frac{d}{dt} W^{(s)}(t)=-i \tau_{t,s}^{\tilde\Xi}\left ( V(t)\right ) W^{(s)}(t),\quad W^{(s)}(s)=\mathbb I. \end{align} $$
$$ \begin{align} \frac{d}{dt} W^{(s)}(t)=-i \tau_{t,s}^{\tilde\Xi}\left ( V(t)\right ) W^{(s)}(t),\quad W^{(s)}(s)=\mathbb I. \end{align} $$It is given by
 $$ \begin{align} W^{(s)}(t) :=\sum_{k=0}^{\infty }(-i)^{k} \int_{s}^{t}ds_{1}\int_{s}^{s_{1}}ds_{2}\dotsi \int_{s}^{s_{k-1}}ds_{k} \tau_{s_{1},s}^{\tilde\Xi}\left ( V(s_{1})\right ) \dotsm \tau_{s_{k},s}^{\tilde\Xi}\left ( V(s_{k})\right ). \end{align} $$
$$ \begin{align} W^{(s)}(t) :=\sum_{k=0}^{\infty }(-i)^{k} \int_{s}^{t}ds_{1}\int_{s}^{s_{1}}ds_{2}\dotsi \int_{s}^{s_{k-1}}ds_{k} \tau_{s_{1},s}^{\tilde\Xi}\left ( V(s_{1})\right ) \dotsm \tau_{s_{k},s}^{\tilde\Xi}\left ( V(s_{k})\right ). \end{align} $$Analogously, for each ![]() $s\in [0,1]$ and
$s\in [0,1]$ and ![]() $n\in \mathbb {N}$, we define a unique norm-differentiable map from
$n\in \mathbb {N}$, we define a unique norm-differentiable map from ![]() $[0,1]$ to
$[0,1]$ to ![]() $ {\mathcal U}\left ( {\mathcal A}\right )$ such that
$ {\mathcal U}\left ( {\mathcal A}\right )$ such that
 $$ \begin{align} \frac{d}{dt} W_{n}^{(s)}(t)=-i \tau_{t,s}^{(\Lambda_{n})\tilde\Xi}\left ( V_{n}(t)\right ) W_{n}^{(s)}(t),\quad W_{n}^{(s)}(s)=\mathbb I. \end{align} $$
$$ \begin{align} \frac{d}{dt} W_{n}^{(s)}(t)=-i \tau_{t,s}^{(\Lambda_{n})\tilde\Xi}\left ( V_{n}(t)\right ) W_{n}^{(s)}(t),\quad W_{n}^{(s)}(s)=\mathbb I. \end{align} $$It is given by
 $$ \begin{align} W_{n}^{(s)}(t) :=\sum_{k=0}^{\infty }(-i)^{k} \int_{s}^{t}ds_{1}\int_{s}^{s_{1}}ds_{2}\dotsi \int_{s}^{s_{k-1}}ds_{k} \tau_{s_{1},s}^{\left(\Lambda_{n}\right)\tilde\Xi}\left ( V_{n}(s_{1})\right ) \dotsm \tau_{s_{k},s}^{\left(\Lambda_{n}\right)\tilde\Xi}\left ( V_{n}(s_{k})\right ). \end{align} $$
$$ \begin{align} W_{n}^{(s)}(t) :=\sum_{k=0}^{\infty }(-i)^{k} \int_{s}^{t}ds_{1}\int_{s}^{s_{1}}ds_{2}\dotsi \int_{s}^{s_{k-1}}ds_{k} \tau_{s_{1},s}^{\left(\Lambda_{n}\right)\tilde\Xi}\left ( V_{n}(s_{1})\right ) \dotsm \tau_{s_{k},s}^{\left(\Lambda_{n}\right)\tilde\Xi}\left ( V_{n}(s_{k})\right ). \end{align} $$By the uniform convergence (5.21) and Lemma D.3, we have
 $$ \begin{align}\lim_{n\to\infty} \sup_{t\in\left[0,1\right]}\left \lVert \tau_{t,s}^{\left(\Lambda_{n}\right)\tilde\Xi}\left ( V_{n}(t)\right ) -\tau_{t,s}^{\tilde\Xi}\left ( V(t)\right )\right \rVert=0. \end{align} $$
$$ \begin{align}\lim_{n\to\infty} \sup_{t\in\left[0,1\right]}\left \lVert \tau_{t,s}^{\left(\Lambda_{n}\right)\tilde\Xi}\left ( V_{n}(t)\right ) -\tau_{t,s}^{\tilde\Xi}\left ( V(t)\right )\right \rVert=0. \end{align} $$From this and formulas (5.39) and (5.41), we obtain
 $$ \begin{align} \lim_{n\to\infty}\sup_{t\in\left[0,1\right]}\left \lVert W_{n}^{(s)}(t)- W^{(s)}(t) \right \rVert =0. \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\sup_{t\in\left[0,1\right]}\left \lVert W_{n}^{(s)}(t)- W^{(s)}(t) \right \rVert =0. \end{align} $$This and Theorem D.3 4 for ![]() $\Xi ^{(1)}, \tilde \Xi \in {\mathcal B}_{\tilde F}([0,1])$ imply
$\Xi ^{(1)}, \tilde \Xi \in {\mathcal B}_{\tilde F}([0,1])$ imply
 $$ \begin{align} \begin{split} \lim_{n\to\infty} \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A)&= \tau_{s,t}^{ \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W^{(s)}(t)\right ) (A),\\ \lim_{n\to\infty} \tau_{s,t}^{\left(\Lambda_{n}\right), \Xi^{(1)}}(A)&= \tau_{s,t}^{ \Xi^{(1)}}(A), \end{split} \end{align} $$
$$ \begin{align} \begin{split} \lim_{n\to\infty} \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A)&= \tau_{s,t}^{ \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W^{(s)}(t)\right ) (A),\\ \lim_{n\to\infty} \tau_{s,t}^{\left(\Lambda_{n}\right), \Xi^{(1)}}(A)&= \tau_{s,t}^{ \Xi^{(1)}}(A), \end{split} \end{align} $$for any ![]() $A\in {\mathcal A}$.
$A\in {\mathcal A}$.
Note that for any ![]() $A\in {\mathcal A}$,
$A\in {\mathcal A}$,
 $$ \begin{align*} \begin{split} \frac{d}{dt} \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) &=-i\left[ H_{\Lambda_{n}, \tilde\Xi}(t), \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) \right] \\ &\quad -i\tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\left ( \left[ \tau_{t,s}^{\left(\Lambda_{n}\right), \tilde\Xi}\left ( V_{n}(t)\right ), \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) \right] \right ) \\ &=-i\left[ H_{\Lambda_{n}, \tilde\Xi}(t)+V_{n}(t), \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) \right]\nonumber\\ &=-i\left[ H_{\Lambda_{n}, \Xi^{(1)}}(t), \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) \right]. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \frac{d}{dt} \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) &=-i\left[ H_{\Lambda_{n}, \tilde\Xi}(t), \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) \right] \\ &\quad -i\tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\left ( \left[ \tau_{t,s}^{\left(\Lambda_{n}\right), \tilde\Xi}\left ( V_{n}(t)\right ), \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) \right] \right ) \\ &=-i\left[ H_{\Lambda_{n}, \tilde\Xi}(t)+V_{n}(t), \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) \right]\nonumber\\ &=-i\left[ H_{\Lambda_{n}, \Xi^{(1)}}(t), \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) \right]. \end{split} \end{align*} $$We used equation (D.10) for the second equality and equation (5.37) for the third. On the other hand, for any ![]() $A\in {\mathcal A}$, we have
$A\in {\mathcal A}$, we have
 $$ \begin{align} \frac{d}{dt} \tau_{s,t}^{\left(\Lambda_{n}\right), \Xi^{(1)}} (A)=-i\left[ H_{\Lambda_{n}, \Xi^{(1)}}(t), \tau_{s,t}^{\left(\Lambda_{n}\right), \Xi^{(1)}} (A) \right]. \end{align} $$
$$ \begin{align} \frac{d}{dt} \tau_{s,t}^{\left(\Lambda_{n}\right), \Xi^{(1)}} (A)=-i\left[ H_{\Lambda_{n}, \Xi^{(1)}}(t), \tau_{s,t}^{\left(\Lambda_{n}\right), \Xi^{(1)}} (A) \right]. \end{align} $$Therefore,  $\tau _{s,t}^{\left (\Lambda _{n}\right ), \tilde \Xi }\circ \mathop {\mathrm {Ad}}\nolimits ( W_{n}^{(s)}(t) ) (A)$ and
$\tau _{s,t}^{\left (\Lambda _{n}\right ), \tilde \Xi }\circ \mathop {\mathrm {Ad}}\nolimits ( W_{n}^{(s)}(t) ) (A)$ and  $ \tau _{s,t}^{\left (\Lambda _{n}\right ), \Xi ^{(1)}} (A)$ satisfy the same differential equation. Also note that we have
$ \tau _{s,t}^{\left (\Lambda _{n}\right ), \Xi ^{(1)}} (A)$ satisfy the same differential equation. Also note that we have  $\tau _{s,s}^{\left (\Lambda _{n}\right ), \tilde \Xi }\circ \mathop {\mathrm {Ad}}\nolimits ( W_{n}^{(s)}(s) ) (A)= \tau _{s,s}^{\left (\Lambda _{n}\right ), \Xi ^{(1)}} (A)=A$. Therefore, we get
$\tau _{s,s}^{\left (\Lambda _{n}\right ), \tilde \Xi }\circ \mathop {\mathrm {Ad}}\nolimits ( W_{n}^{(s)}(s) ) (A)= \tau _{s,s}^{\left (\Lambda _{n}\right ), \Xi ^{(1)}} (A)=A$. Therefore, we get
 $$ \begin{align} \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) =\tau_{s,t}^{\left(\Lambda_{n}\right), \Xi^{(1)}} (A). \end{align} $$
$$ \begin{align} \tau_{s,t}^{\left(\Lambda_{n}\right), \tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W_{n}^{(s)}(t)\right ) (A) =\tau_{s,t}^{\left(\Lambda_{n}\right), \Xi^{(1)}} (A). \end{align} $$By equation (5.44), we obtain
 $$ \begin{align} \tau_{s,t}^{\tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W^{(s)}(t)\right ) (A) =\tau_{s,t}^{\Xi^{(1)}} (A),\quad A\in{\mathcal A}, \ t,s\in[0,1]. \end{align} $$
$$ \begin{align} \tau_{s,t}^{\tilde\Xi}\circ \mathop{\mathrm{Ad}}\nolimits \left ( W^{(s)}(t)\right ) (A) =\tau_{s,t}^{\Xi^{(1)}} (A),\quad A\in{\mathcal A}, \ t,s\in[0,1]. \end{align} $$Taking the inverse, we get
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits \left ( W^{(s)^{*}}(t)\right )\circ\tau_{t,s }^{\tilde\Xi} =\tau_{t,s}^{\Xi^{(1)}},\quad t,s\in[0,1]. \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits \left ( W^{(s)^{*}}(t)\right )\circ\tau_{t,s }^{\tilde\Xi} =\tau_{t,s}^{\Xi^{(1)}},\quad t,s\in[0,1]. \end{align} $$Step 4. Combining equations (5.17) and (5.48), we have
 $$ \begin{align} \tau_{1,0}^{\Psi}= \tau_{1,0}^{\Psi^{(0)}}\tau_{0,1}^{ \Xi^{(1)}} =\tau_{1,0}^{\Psi^{(0)}}\circ\mathop{\mathrm{Ad}}\nolimits \left ( \left ( W^{(1)}(0)\right )^{*}\right )\circ\tau_{0,1 }^{\tilde\Xi}. \end{align} $$
$$ \begin{align} \tau_{1,0}^{\Psi}= \tau_{1,0}^{\Psi^{(0)}}\tau_{0,1}^{ \Xi^{(1)}} =\tau_{1,0}^{\Psi^{(0)}}\circ\mathop{\mathrm{Ad}}\nolimits \left ( \left ( W^{(1)}(0)\right )^{*}\right )\circ\tau_{0,1 }^{\tilde\Xi}. \end{align} $$By the definitions of ![]() $\Psi ^{(0)}$ and
$\Psi ^{(0)}$ and ![]() $\tilde \Xi $, we obtain decompositions
$\tilde \Xi $, we obtain decompositions
 $$ \begin{align} \begin{split} \tau_{1,0}^{\Psi^{(0)}} &=\alpha_{\left[0,\theta_{1}\right]}\otimes \alpha_{\left(\theta_1,\theta_2\right]}\otimes \alpha_{\left(\theta_2,\theta_3\right]} \otimes \alpha_{\left(\theta_3,\frac\pi 2\right]},\\ \tau_{0,1}^{\tilde\Xi} &= \alpha_{\left(\theta_{0.8},\theta_{1.2}\right]}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right]}\otimes \alpha_{\left(\theta_{2.8},\theta_{3.2}\right]}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \tau_{1,0}^{\Psi^{(0)}} &=\alpha_{\left[0,\theta_{1}\right]}\otimes \alpha_{\left(\theta_1,\theta_2\right]}\otimes \alpha_{\left(\theta_2,\theta_3\right]} \otimes \alpha_{\left(\theta_3,\frac\pi 2\right]},\\ \tau_{0,1}^{\tilde\Xi} &= \alpha_{\left(\theta_{0.8},\theta_{1.2}\right]}\otimes \alpha_{\left(\theta_{1.8},\theta_{2.2}\right]}\otimes \alpha_{\left(\theta_{2.8},\theta_{3.2}\right]}, \end{split} \end{align} $$with ![]() $\alpha $s in the form of formulas (2.13) and (2.14). This completes the proof of the first part.
$\alpha $s in the form of formulas (2.13) and (2.14). This completes the proof of the first part.
Step 5. Suppose that  $\beta _{g}^{U}\left ( \Psi (X;t)\right )=\Psi (X;t)$ for any
$\beta _{g}^{U}\left ( \Psi (X;t)\right )=\Psi (X;t)$ for any ![]() $X\in {\mathfrak S}_{{\mathbb Z}^2}$,
$X\in {\mathfrak S}_{{\mathbb Z}^2}$, ![]() $t\in [0,1]$ and
$t\in [0,1]$ and ![]() $g\in G$. Then clearly we have
$g\in G$. Then clearly we have  $\beta _{g}^{U}\left ( \Psi ^{(0)}(X;t)\right )=\Psi ^{(0)}(X;t)$ for any
$\beta _{g}^{U}\left ( \Psi ^{(0)}(X;t)\right )=\Psi ^{(0)}(X;t)$ for any ![]() $X\in {\mathfrak S}_{{\mathbb Z}^2}$,
$X\in {\mathfrak S}_{{\mathbb Z}^2}$, ![]() $t\in [0,1]$ and
$t\in [0,1]$ and ![]() $g\in G$. By Theorem D.3 5, this implies
$g\in G$. By Theorem D.3 5, this implies  $\tau _{1,0}^{\Psi ^{(0)}}{\beta _g^U}={\beta _g^U}\tau _{1,0}^{\Psi ^{(0)}}$. From the decomposition (5.50), this means that all of
$\tau _{1,0}^{\Psi ^{(0)}}{\beta _g^U}={\beta _g^U}\tau _{1,0}^{\Psi ^{(0)}}$. From the decomposition (5.50), this means that all of ![]() $\alpha _{\left [0,\theta _{1}\right ],\sigma }, \alpha _{\left (\theta _1,\theta _2\right ],\sigma ,\zeta }, \alpha _{\left (\theta _2,\theta _3\right ],\sigma ,\zeta }, \alpha _{\left (\theta _3,\frac \pi 2\right ],\zeta }$,
$\alpha _{\left [0,\theta _{1}\right ],\sigma }, \alpha _{\left (\theta _1,\theta _2\right ],\sigma ,\zeta }, \alpha _{\left (\theta _2,\theta _3\right ],\sigma ,\zeta }, \alpha _{\left (\theta _3,\frac \pi 2\right ],\zeta }$, ![]() $\sigma =L,R, \zeta =U,D$, commute with
$\sigma =L,R, \zeta =U,D$, commute with  ${\beta _g^U}$. Because
${\beta _g^U}$. Because ![]() $\Pi _{X}$ commutes with
$\Pi _{X}$ commutes with  $\beta _{g}^{U}$,
$\beta _{g}^{U}$,  $\tau _{t,s}^{\Psi }$ commutes with
$\tau _{t,s}^{\Psi }$ commutes with  $\beta _{g}^{U}$ (Theorem D.3 5), and
$\beta _{g}^{U}$ (Theorem D.3 5), and ![]() $\Psi ^{(1)}$ and
$\Psi ^{(1)}$ and ![]() $\Xi ^{(s)}$ are
$\Xi ^{(s)}$ are  $\beta _{g}^{U}$-invariant from the definition (5.8). Therefore, from the definition (5.36),
$\beta _{g}^{U}$-invariant from the definition (5.8). Therefore, from the definition (5.36), ![]() $\tilde \Xi $ is also
$\tilde \Xi $ is also  $\beta _{g}^{U}$-invariant. Hence by Theorem D.3 5,
$\beta _{g}^{U}$-invariant. Hence by Theorem D.3 5,  $\tau _{0,1}^{ \tilde \Xi }$ commutes with
$\tau _{0,1}^{ \tilde \Xi }$ commutes with  ${\beta _g^U}$. The decomposition (5.50) then implies that
${\beta _g^U}$. The decomposition (5.50) then implies that ![]() $\alpha _{\left (\theta _{0.8},\theta _{1.2}\right ],\sigma ,\zeta }, \alpha _{\left (\theta _{1.8},\theta _{2.2}\right ],\sigma ,\zeta }, \alpha _{\left (\theta _{2.8},\theta _{3.2}\right ],\sigma ,\zeta }$,
$\alpha _{\left (\theta _{0.8},\theta _{1.2}\right ],\sigma ,\zeta }, \alpha _{\left (\theta _{1.8},\theta _{2.2}\right ],\sigma ,\zeta }, \alpha _{\left (\theta _{2.8},\theta _{3.2}\right ],\sigma ,\zeta }$, ![]() $\sigma =L,R, \ \zeta =U,D$, commute with
$\sigma =L,R, \ \zeta =U,D$, commute with  ${\beta _g^U}$.
${\beta _g^U}$.
An analogous proof shows the following:
Proposition 5.5. Let ![]() $F\in {\mathcal F}_a$ be an F-function of the form
$F\in {\mathcal F}_a$ be an F-function of the form  $F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant
$F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant ![]() $0<\theta <1$. Let
$0<\theta <1$. Let ![]() $\Psi \in \hat {\mathcal B}_{F}([0,1])$ be a path of interactions satisfying
$\Psi \in \hat {\mathcal B}_{F}([0,1])$ be a path of interactions satisfying ![]() $\Psi _1\in \hat {\mathcal B}_F([0,1])$. Define
$\Psi _1\in \hat {\mathcal B}_F([0,1])$. Define ![]() $\Psi ^{(0)}\in \hat {\mathcal B}_{F}([0,1])$ by
$\Psi ^{(0)}\in \hat {\mathcal B}_{F}([0,1])$ by
 $$ \begin{align} \begin{split} & \Psi^{(0)}\left ( X; t\right ):= \begin{cases} \Psi\left ( X; t\right ) & \text{if } X\subset H_U\text{ or } X\subset H_D, \\ 0& \text{otherwise}, \end{cases} \end{split} \end{align} $$
$$ \begin{align} \begin{split} & \Psi^{(0)}\left ( X; t\right ):= \begin{cases} \Psi\left ( X; t\right ) & \text{if } X\subset H_U\text{ or } X\subset H_D, \\ 0& \text{otherwise}, \end{cases} \end{split} \end{align} $$for each ![]() $X\in {\mathfrak S}_{{\mathbb Z}^2}, t\in [0,1]$. Then
$X\in {\mathfrak S}_{{\mathbb Z}^2}, t\in [0,1]$. Then  $ \left (\tau _{1,0}^{\Psi ^{(0)}}\right )^{-1}\tau _{1,0}^{\Psi }$ belongs to
$ \left (\tau _{1,0}^{\Psi ^{(0)}}\right )^{-1}\tau _{1,0}^{\Psi }$ belongs to ![]() $\mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$.
$\mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$.
Proof. Define ![]() $\tilde F$ as in formula (5.3) with some
$\tilde F$ as in formula (5.3) with some ![]() $0<\theta '<\theta $. The same argument as in Theorem 5.2, step 2, implies that there exists
$0<\theta '<\theta $. The same argument as in Theorem 5.2, step 2, implies that there exists ![]() $\Xi ^{(1)}\in \hat {\mathcal B}_{\tilde F}[0,1]$ with
$\Xi ^{(1)}\in \hat {\mathcal B}_{\tilde F}[0,1]$ with ![]() $\tilde F\in {\mathcal F}_a$, such that
$\tilde F\in {\mathcal F}_a$, such that
 $$ \begin{align} \tau_{1,0}^{\Psi}= \tau_{1,0}^{\Psi^{(0)}}\tau_{0,1}^{ \Xi^{(1)}}. \end{align} $$
$$ \begin{align} \tau_{1,0}^{\Psi}= \tau_{1,0}^{\Psi^{(0)}}\tau_{0,1}^{ \Xi^{(1)}}. \end{align} $$This ![]() $\Xi ^{(1)}$ is given by formula (5.8) for current
$\Xi ^{(1)}$ is given by formula (5.8) for current ![]() $\Psi $ and
$\Psi $ and ![]() $\Psi ^{(1)}\left ( X; t\right ):=\Psi ^{(0)}\left ( X; t\right )-\Psi \left ( X; t\right )$. To prove the theorem, it suffices to show that
$\Psi ^{(1)}\left ( X; t\right ):=\Psi ^{(0)}\left ( X; t\right )-\Psi \left ( X; t\right )$. To prove the theorem, it suffices to show that  $\tau _{0,1}^{ \Xi ^{(1)}}$ belongs to
$\tau _{0,1}^{ \Xi ^{(1)}}$ belongs to ![]() $\mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$. Indeed, for any
$\mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$. Indeed, for any ![]() $0<\theta _0<\frac \pi 4$, as in Theorem 5.2, step 2, we have
$0<\theta _0<\frac \pi 4$, as in Theorem 5.2, step 2, we have
 $$ \begin{align} &\sum_{\substack{Z: Z\nsubseteq C_{\left[0,\theta_0\right],L} \\Z\nsubseteq C_{\left[0,\theta_0\right],R} }} \sup_{t\in \left[0,1\right]}\left \lVert \Xi^{(1)}\left ( Z,t\right )\right \rVert\nonumber\\ &\qquad\qquad\le \frac{8}{C_{F}}\left ( e^{2I_F(\Psi)}-1\right ) \sum_{m\ge 0} \sum_{\substack{X: X(m)\nsubseteq C_{\left[0,\theta_0\right],L} \\X(m)\nsubseteq C_{\left[0,\theta_0\right],R} } } \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi^{(1)}\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right] <\infty. \end{align} $$
$$ \begin{align} &\sum_{\substack{Z: Z\nsubseteq C_{\left[0,\theta_0\right],L} \\Z\nsubseteq C_{\left[0,\theta_0\right],R} }} \sup_{t\in \left[0,1\right]}\left \lVert \Xi^{(1)}\left ( Z,t\right )\right \rVert\nonumber\\ &\qquad\qquad\le \frac{8}{C_{F}}\left ( e^{2I_F(\Psi)}-1\right ) \sum_{m\ge 0} \sum_{\substack{X: X(m)\nsubseteq C_{\left[0,\theta_0\right],L} \\X(m)\nsubseteq C_{\left[0,\theta_0\right],R} } } \left[ \sup_{t\in\left[0,1\right]}\left ( \left \lVert \Psi^{(1)}\left ( X; t\right ) \right \rVert\right ) \left \lvert X\right \rvert G_{F}\left ( m\right ) \right] <\infty. \end{align} $$To see this, note that if X in the last line has a nonzero contribution to the sum, then at least one of the following occurs:
(i)
 $X\cap C_{\left [\theta _{0}, \frac \pi 2\right ],U}\neq \emptyset $ and
$X\cap C_{\left [\theta _{0}, \frac \pi 2\right ],U}\neq \emptyset $ and  $X\cap H_{D}\neq \emptyset $.
$X\cap H_{D}\neq \emptyset $.(ii)
 $X\cap C_{\left [\theta _{0}, \frac \pi 2\right ],D}\neq \emptyset $ and
$X\cap C_{\left [\theta _{0}, \frac \pi 2\right ],D}\neq \emptyset $ and  $X\cap H_{U}\neq \emptyset $.
$X\cap H_{U}\neq \emptyset $.(iii)
 $X\subset C_{\left [0,\theta _{0}\right ]}$ and
$X\subset C_{\left [0,\theta _{0}\right ]}$ and(1)
 $X\cap C_{\left [0,\theta _{0}\right ],L}\neq \emptyset $ and
$X\cap C_{\left [0,\theta _{0}\right ],L}\neq \emptyset $ and  $X\cap C_{\left [0,\theta _{0}\right ],R}\neq \emptyset $, or
$X\cap C_{\left [0,\theta _{0}\right ],R}\neq \emptyset $, or(2)
 $X\subset C_{\left [0,\theta _{0}\right ], R}$,
$X\subset C_{\left [0,\theta _{0}\right ], R}$,  $X\cap \check C_{\left [0,\theta _{0}\right ]}\neq \emptyset $,
$X\cap \check C_{\left [0,\theta _{0}\right ]}\neq \emptyset $,  $X\cap \check C_{\left [-\theta _{0},0\right ]}\neq \emptyset $ and
$X\cap \check C_{\left [-\theta _{0},0\right ]}\neq \emptyset $ and  $X{(m)}\cap \left ( C_{\left [0,\theta _{0}\right ], R}\right )^{c}\neq \emptyset $, or
$X{(m)}\cap \left ( C_{\left [0,\theta _{0}\right ], R}\right )^{c}\neq \emptyset $, or(3)
 $X\subset C_{\left [0,\theta _{0}\right ], L}$,
$X\subset C_{\left [0,\theta _{0}\right ], L}$,  $X\cap \check C_{\left [\pi -\theta _{0},\pi \right ]}\neq \emptyset $,
$X\cap \check C_{\left [\pi -\theta _{0},\pi \right ]}\neq \emptyset $,  $X\cap \check C_{\left [\pi , \pi +\theta _{0}\right ]}\neq \emptyset $ and
$X\cap \check C_{\left [\pi , \pi +\theta _{0}\right ]}\neq \emptyset $ and  $X{(m)}\cap \left ( C_{\left [0,\theta _{0}\right ], L}\right )^{c}\neq \emptyset $.
$X{(m)}\cap \left ( C_{\left [0,\theta _{0}\right ], L}\right )^{c}\neq \emptyset $.
Therefore, the summation in the second line of formula (5.53) is bounded by
 $$ \begin{align*} \frac{8}{C_{F}}\left ( e^{2I_F(\Psi)}-1\right ) \left ( \begin{gathered} b_{0}(\theta_{0}, \pi-\theta_{0}, \pi, 2\pi) +b_{0}(0,\pi, \pi+\theta_{0}, 2\pi-\theta_{0}) +b_{0}(-\theta_{0}, \theta_{0}, \pi-\theta_{0}, \pi+\theta_{0})\\ +b_{1}(-\theta_{0}, 0,\theta_{0}) +b_{1}(\pi-\theta_{0}, \pi, \pi+\theta_{0}) \end{gathered} \right )<\infty, \end{align*} $$
$$ \begin{align*} \frac{8}{C_{F}}\left ( e^{2I_F(\Psi)}-1\right ) \left ( \begin{gathered} b_{0}(\theta_{0}, \pi-\theta_{0}, \pi, 2\pi) +b_{0}(0,\pi, \pi+\theta_{0}, 2\pi-\theta_{0}) +b_{0}(-\theta_{0}, \theta_{0}, \pi-\theta_{0}, \pi+\theta_{0})\\ +b_{1}(-\theta_{0}, 0,\theta_{0}) +b_{1}(\pi-\theta_{0}, \pi, \pi+\theta_{0}) \end{gathered} \right )<\infty, \end{align*} $$from Lemmas 5.3 and 5.4, proving formula (5.53).
Therefore, as in step 3 of Theorem 5.2, setting
 $$ \begin{align} \tilde\Xi(Z,t):= \begin{cases} \Xi^{(1)}(Z,t)&\text{if } Z\subseteq C_{\left[0,\theta_0\right],L} \text{ or }Z\subseteq C_{\left[0,\theta_0\right],R}, \\ 0&\text{otherwise}, \end{cases} \end{align} $$
$$ \begin{align} \tilde\Xi(Z,t):= \begin{cases} \Xi^{(1)}(Z,t)&\text{if } Z\subseteq C_{\left[0,\theta_0\right],L} \text{ or }Z\subseteq C_{\left[0,\theta_0\right],R}, \\ 0&\text{otherwise}, \end{cases} \end{align} $$we obtain  $\tau _{0,1}^{ \Xi ^{(1)}}=({\textrm {{inner}}})\circ \tau _{0,1}^{ \tilde \Xi }$. By the definition,
$\tau _{0,1}^{ \Xi ^{(1)}}=({\textrm {{inner}}})\circ \tau _{0,1}^{ \tilde \Xi }$. By the definition,  $\tau _{0,1}^{ \tilde \Xi }$ decomposes as
$\tau _{0,1}^{ \tilde \Xi }$ decomposes as  $\tau _{0,1}^{ \tilde \Xi }= \zeta _L\otimes \zeta _R$, with some
$\tau _{0,1}^{ \tilde \Xi }= \zeta _L\otimes \zeta _R$, with some  $\zeta _\sigma \in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_{\left [0,\theta _0\right ],\sigma }} )$,
$\zeta _\sigma \in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_{\left [0,\theta _0\right ],\sigma }} )$, ![]() $\sigma =L,R$. As this holds for any
$\sigma =L,R$. As this holds for any ![]() $0<\theta _0<\frac \pi 4$, we conclude
$0<\theta _0<\frac \pi 4$, we conclude  $\tau _{0,1}^{ \Xi ^{(1)}}\in \mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$.
$\tau _{0,1}^{ \Xi ^{(1)}}\in \mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$.
Theorem 5.6. Let ![]() $F\in {\mathcal F}_a$ be an F-function of the form
$F\in {\mathcal F}_a$ be an F-function of the form  $F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant
$F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant ![]() $0<\theta <1$. Let
$0<\theta <1$. Let ![]() $\Psi \in \hat {\mathcal B}_{F}([0,1])$ be a path of interactions satisfying
$\Psi \in \hat {\mathcal B}_{F}([0,1])$ be a path of interactions satisfying ![]() $\Psi _1\in \hat {\mathcal B}_F([0,1])$. If
$\Psi _1\in \hat {\mathcal B}_F([0,1])$. If ![]() $\Psi $ is
$\Psi $ is ![]() $\beta $-invariant, then
$\beta $-invariant, then  $\tau _{1,0}^{\Psi }$ belongs to
$\tau _{1,0}^{\Psi }$ belongs to ![]() $\mathop {\mathrm {GUQAut}}\nolimits ({\mathcal A})$.
$\mathop {\mathrm {GUQAut}}\nolimits ({\mathcal A})$.
Proof. Define ![]() $\Psi ^{(0)}$ as in formula (5.51) for our
$\Psi ^{(0)}$ as in formula (5.51) for our ![]() $\Psi $. By Proposition 5.5, we have
$\Psi $. By Proposition 5.5, we have  $ (\tau _{1,0}^{\Psi ^{(0)}} )^{-1}\tau _{1,0}^{\Psi }\in \mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$. On the other hand, applying Theorem 5.2 to
$ (\tau _{1,0}^{\Psi ^{(0)}} )^{-1}\tau _{1,0}^{\Psi }\in \mathop {\mathrm {HAut}}\nolimits ({\mathcal A})$. On the other hand, applying Theorem 5.2 to ![]() $\Psi ^{(0)}\in \hat {\mathcal B}_F([0,1])$, we see that
$\Psi ^{(0)}\in \hat {\mathcal B}_F([0,1])$, we see that  $\tau _{1,0}^{\Psi ^{(0)}}$ belongs to
$\tau _{1,0}^{\Psi ^{(0)}}$ belongs to ![]() $\mathop {\mathrm {SQAut}}\nolimits ({\mathcal A}).$ Note that
$\mathop {\mathrm {SQAut}}\nolimits ({\mathcal A}).$ Note that ![]() $\Psi ^{(0)}(X;t)$ is nonzero only if
$\Psi ^{(0)}(X;t)$ is nonzero only if ![]() $X\subset H_U$ or
$X\subset H_U$ or ![]() $X\subset H_D$, and it coincides with
$X\subset H_D$, and it coincides with ![]() $\Psi (X;t)$ when it is nonzero. Therefore, if
$\Psi (X;t)$ when it is nonzero. Therefore, if ![]() $\Psi $ is
$\Psi $ is ![]() $\beta $-invariant,
$\beta $-invariant, ![]() $\Psi ^{(0)}$ is
$\Psi ^{(0)}$ is  $\beta _g^U$-invariant. Therefore, by Theorem 5.2, we have
$\beta _g^U$-invariant. Therefore, by Theorem 5.2, we have  $\tau _{1,0}^{\Psi ^{(0)}}\in \mathop {\mathrm {GSQAut}}\nolimits ({\mathcal A})$. Hence we have
$\tau _{1,0}^{\Psi ^{(0)}}\in \mathop {\mathrm {GSQAut}}\nolimits ({\mathcal A})$. Hence we have  $\tau _{1,0}^{\Psi }\in \mathop {\mathrm {GUQAut}}\nolimits ({\mathcal A})$.
$\tau _{1,0}^{\Psi }\in \mathop {\mathrm {GUQAut}}\nolimits ({\mathcal A})$.
Proof of Theorem 1.5.
Let ![]() $\Phi _0\in {\mathcal P}_{UG}$ be the fixed trivial interaction with a unique gapped ground state. Its ground state
$\Phi _0\in {\mathcal P}_{UG}$ be the fixed trivial interaction with a unique gapped ground state. Its ground state ![]() $\omega _0:=\omega _{\Phi _0}$ is of a product form (formula (2.18)). For any
$\omega _0:=\omega _{\Phi _0}$ is of a product form (formula (2.18)). For any ![]() $\Phi \in {\mathcal P}_{SL\beta }$, we have
$\Phi \in {\mathcal P}_{SL\beta }$, we have ![]() $\Phi _0\sim \Phi $. Then by Theorem 5.1, there exists some
$\Phi _0\sim \Phi $. Then by Theorem 5.1, there exists some ![]() $\Psi \in \hat {\mathcal B}_F([0,1])$ with
$\Psi \in \hat {\mathcal B}_F([0,1])$ with ![]() $\Psi _{1}\in \hat {\mathcal B}_{F}([0,1])$ for some
$\Psi _{1}\in \hat {\mathcal B}_{F}([0,1])$ for some ![]() $F\in {\mathcal F}_a$ of the form
$F\in {\mathcal F}_a$ of the form  $F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with
$F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with ![]() $0<\theta <1$, such that
$0<\theta <1$, such that  $\omega _{\Phi }=\omega _{\Phi _0}\circ \tau _{1,0}^{\Psi }$. From Theorem 5.2,
$\omega _{\Phi }=\omega _{\Phi _0}\circ \tau _{1,0}^{\Psi }$. From Theorem 5.2,  $\tau _{1,0}^\Psi $ belongs to
$\tau _{1,0}^\Psi $ belongs to ![]() $\mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$. Because
$\mathop {\mathrm {SQAut}}\nolimits ({\mathcal A})$. Because ![]() $\Phi \in {\mathcal P}_{SL\beta }$,
$\Phi \in {\mathcal P}_{SL\beta }$,  $\omega _{\Phi }=\omega _{\Phi _0}\circ \tau _{1,0}^{\Psi }$ is
$\omega _{\Phi }=\omega _{\Phi _0}\circ \tau _{1,0}^{\Psi }$ is ![]() $\beta $-invariant. Then, by Theorem 3.1,
$\beta $-invariant. Then, by Theorem 3.1, ![]() $\mathop {\mathrm {IG}}\nolimits (\omega _{\Phi })$ is not empty. Therefore, we may define
$\mathop {\mathrm {IG}}\nolimits (\omega _{\Phi })$ is not empty. Therefore, we may define ![]() $h_\Phi :=h(\omega _{\Phi })$ by Definition 2.18.
$h_\Phi :=h(\omega _{\Phi })$ by Definition 2.18.
To see that ![]() $h_\Phi $ is an invariant of
$h_\Phi $ is an invariant of ![]() $\sim _\beta $, set
$\sim _\beta $, set ![]() $\Phi _1,\Phi _2\in {\mathcal P}_{SL\beta }$ with
$\Phi _1,\Phi _2\in {\mathcal P}_{SL\beta }$ with ![]() $\Phi _1\sim _\beta \Phi _2$. Then by Theorem 5.1, there exists some
$\Phi _1\sim _\beta \Phi _2$. Then by Theorem 5.1, there exists some ![]() $\beta $-invariant
$\beta $-invariant ![]() $\Psi \in \hat {\mathcal B}_F([0,1])$ with
$\Psi \in \hat {\mathcal B}_F([0,1])$ with ![]() $\Psi _{1}\in \hat {\mathcal B}_F([0,1])$ for some
$\Psi _{1}\in \hat {\mathcal B}_F([0,1])$ for some ![]() $F\in {\mathcal F}_a$ of the form
$F\in {\mathcal F}_a$ of the form  $F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant
$F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant ![]() $0<\theta <1$ such that
$0<\theta <1$ such that  $\omega _{\Phi _2}=\omega _{\Phi _1}\circ \tau _{1,0}^{\Psi }$. Applying Theorem 5.6 to this
$\omega _{\Phi _2}=\omega _{\Phi _1}\circ \tau _{1,0}^{\Psi }$. Applying Theorem 5.6 to this ![]() $\Psi $, we see that
$\Psi $, we see that  $\tau _{1,0}^{\Psi }$ belongs to
$\tau _{1,0}^{\Psi }$ belongs to ![]() $\mathop {\mathrm {GUQAut}}\nolimits ({\mathcal A})$. Then Theorem 4.1 implies
$\mathop {\mathrm {GUQAut}}\nolimits ({\mathcal A})$. Then Theorem 4.1 implies
 $$ \begin{align} h_{\Phi_2}=h(\omega_{\Phi_2}) =h\left(\omega_{\Phi_1}\circ\tau_{1,0}^{\Psi}\right)=h(\omega_{\Phi_1}) =h_{\Phi_1}, \end{align} $$
$$ \begin{align} h_{\Phi_2}=h(\omega_{\Phi_2}) =h\left(\omega_{\Phi_1}\circ\tau_{1,0}^{\Psi}\right)=h(\omega_{\Phi_1}) =h_{\Phi_1}, \end{align} $$proving the stability.
6 Automorphisms with factorised  $d^{0}_{H_{U}}\alpha $
$d^{0}_{H_{U}}\alpha $
When ![]() $\alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ has some good factorisation property with respect to the action of
$\alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ has some good factorisation property with respect to the action of  $\beta _{g}^{U}$, the index
$\beta _{g}^{U}$, the index ![]() $h(\omega )$ can be calculated without going through GNS representations.
$h(\omega )$ can be calculated without going through GNS representations.
Definition 6.1. For ![]() $\alpha \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}\right )$, we set
$\alpha \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}\right )$, we set
 $$ \begin{align} \left ( d^{0}_{H_{U}}\alpha\right ) (g):=\alpha^{-1}\beta_{g}^{U}\circ \alpha\circ \left ( \beta_{g}^{U}\right )^{-1},\quad g\in G. \end{align} $$
$$ \begin{align} \left ( d^{0}_{H_{U}}\alpha\right ) (g):=\alpha^{-1}\beta_{g}^{U}\circ \alpha\circ \left ( \beta_{g}^{U}\right )^{-1},\quad g\in G. \end{align} $$We say that  $d^{0}_{H_{U}}\alpha $ is factorised into left and right if there are automorphisms
$d^{0}_{H_{U}}\alpha $ is factorised into left and right if there are automorphisms ![]() $\gamma _{g,\sigma }\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{H_{\sigma }}\right )$,
$\gamma _{g,\sigma }\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{H_{\sigma }}\right )$, ![]() $g\in G, \sigma =L,R$, such that
$g\in G, \sigma =L,R$, such that
 $$ \begin{align} \left ( d^{0}_{H_{U}}\alpha\right ) (g)=({\textrm{{inner}}})\circ \left ( \gamma_{g,L}\otimes\gamma_{g,R}\right ),\quad g\in G. \end{align} $$
$$ \begin{align} \left ( d^{0}_{H_{U}}\alpha\right ) (g)=({\textrm{{inner}}})\circ \left ( \gamma_{g,L}\otimes\gamma_{g,R}\right ),\quad g\in G. \end{align} $$ For known examples of ![]() $2$-dimensional SPT phases like [Reference Chen, Gu, Liu and WenCGLW, Reference Miller and MiyakeMM, Reference YoshidaY, Reference Dijkgraaf and WittenDW] or injective projected entangled-pair states [Reference Molnar, Ge, Schuch and CiracMGSC], this property holds. Namely, with a bit of effort, states in these models can be written in the form
$2$-dimensional SPT phases like [Reference Chen, Gu, Liu and WenCGLW, Reference Miller and MiyakeMM, Reference YoshidaY, Reference Dijkgraaf and WittenDW] or injective projected entangled-pair states [Reference Molnar, Ge, Schuch and CiracMGSC], this property holds. Namely, with a bit of effort, states in these models can be written in the form ![]() $\omega _0\alpha $, where
$\omega _0\alpha $, where ![]() $\omega _0$ is a pure infinite tensor product state and
$\omega _0$ is a pure infinite tensor product state and ![]() $\alpha $ is an automorphism satisfying the property in Definition 6.1. From such an automorphism, we can derive an outer action of G.
$\alpha $ is an automorphism satisfying the property in Definition 6.1. From such an automorphism, we can derive an outer action of G.
Lemma 6.2. Let ![]() $\alpha \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}\right )$ be an automorphism. Suppose that
$\alpha \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}\right )$ be an automorphism. Suppose that  $d^{0}_{H_{U}}\alpha $ is factorised into left and right – that is, there are automorphisms
$d^{0}_{H_{U}}\alpha $ is factorised into left and right – that is, there are automorphisms ![]() $\gamma _{g,\sigma }\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{H_{\sigma }}\right )$,
$\gamma _{g,\sigma }\in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}_{H_{\sigma }}\right )$, ![]() $g\in G, \sigma =L,R$, such that
$g\in G, \sigma =L,R$, such that
 $$ \begin{align} \left ( d^{0}_{H_{U}}\alpha\right ) (g)=({\textrm{{inner}}})\circ \left ( \gamma_{g,L}\otimes\gamma_{g,R}\right ),\quad g\in G. \end{align} $$
$$ \begin{align} \left ( d^{0}_{H_{U}}\alpha\right ) (g)=({\textrm{{inner}}})\circ \left ( \gamma_{g,L}\otimes\gamma_{g,R}\right ),\quad g\in G. \end{align} $$Then there are unitaries ![]() $v_{\sigma }(g,h)\in {\mathcal U}\left ( {\mathcal A}_{H_{\sigma }}\right )$,
$v_{\sigma }(g,h)\in {\mathcal U}\left ( {\mathcal A}_{H_{\sigma }}\right )$, ![]() $g,h\in G, \sigma =L,R$, such that
$g,h\in G, \sigma =L,R$, such that
 $$ \begin{align} \gamma_{g,{\sigma}}\beta_{g}^{{\sigma}U}\gamma_{h,{\sigma}}\beta_{h}^{{\sigma}U} \left ( \gamma_{gh,{\sigma}}\beta_{gh}^{{\sigma}U}\right )^{-1} =\mathop{\mathrm{Ad}}\nolimits( v_{\sigma}(g,h)). \end{align} $$
$$ \begin{align} \gamma_{g,{\sigma}}\beta_{g}^{{\sigma}U}\gamma_{h,{\sigma}}\beta_{h}^{{\sigma}U} \left ( \gamma_{gh,{\sigma}}\beta_{gh}^{{\sigma}U}\right )^{-1} =\mathop{\mathrm{Ad}}\nolimits( v_{\sigma}(g,h)). \end{align} $$Proof. Because  $\beta _{g}^{U}$ is a group action, substituting equation (6.3) we get
$\beta _{g}^{U}$ is a group action, substituting equation (6.3) we get
 $$ \begin{align} \mathop{\mathrm{id}}\nolimits_{{\mathcal A}} &=\alpha^{-1}\beta_{g}^{U}\alpha\circ\alpha^{-1}\beta_{h}^{U}\alpha\circ \left ( \alpha^{-1}\beta_{gh}^{U}\alpha\right )^{-1}\notag\\ &=({\textrm{{inner}}})\circ \left ( \gamma_{g,L}\beta_{g}^{LU}\otimes\gamma_{g,R}\beta_{g}^{RU}\right ) \circ \left ( \gamma_{h,L}\beta_{h}^{LU}\otimes\gamma_{h,R}\beta_{h}^{RU}\right ) \circ \left ( \gamma_{gh,L}\beta_{gh}^{LU}\otimes\gamma_{gh,R}\beta_{gh}^{RU}\right )^{-1}\notag\\ &=({\textrm{{inner}}})\circ \left ( \gamma_{g,L}\beta_{g}^{LU}\gamma_{h,L}\beta_{h}^{LU} \left ( \gamma_{gh,L}\beta_{gh}^{LU}\right )^{-1} \otimes\gamma_{g,R}\beta_{g}^{RU} \gamma_{h,R}\beta_{h}^{RU}\left ( \gamma_{gh,R}\beta_{gh}^{RU}\right )^{-1}\right ). \end{align} $$
$$ \begin{align} \mathop{\mathrm{id}}\nolimits_{{\mathcal A}} &=\alpha^{-1}\beta_{g}^{U}\alpha\circ\alpha^{-1}\beta_{h}^{U}\alpha\circ \left ( \alpha^{-1}\beta_{gh}^{U}\alpha\right )^{-1}\notag\\ &=({\textrm{{inner}}})\circ \left ( \gamma_{g,L}\beta_{g}^{LU}\otimes\gamma_{g,R}\beta_{g}^{RU}\right ) \circ \left ( \gamma_{h,L}\beta_{h}^{LU}\otimes\gamma_{h,R}\beta_{h}^{RU}\right ) \circ \left ( \gamma_{gh,L}\beta_{gh}^{LU}\otimes\gamma_{gh,R}\beta_{gh}^{RU}\right )^{-1}\notag\\ &=({\textrm{{inner}}})\circ \left ( \gamma_{g,L}\beta_{g}^{LU}\gamma_{h,L}\beta_{h}^{LU} \left ( \gamma_{gh,L}\beta_{gh}^{LU}\right )^{-1} \otimes\gamma_{g,R}\beta_{g}^{RU} \gamma_{h,R}\beta_{h}^{RU}\left ( \gamma_{gh,R}\beta_{gh}^{RU}\right )^{-1}\right ). \end{align} $$By Lemma B.1, we then see that there are unitaries ![]() $v_{\sigma }(g,h)\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{H_{\sigma }}\right )$,
$v_{\sigma }(g,h)\in \mathop {\mathrm {Aut}}\nolimits \left ( {\mathcal A}_{H_{\sigma }}\right )$, ![]() $g\in G, \sigma =L,R$, satisfying equation (6.4).
$g\in G, \sigma =L,R$, satisfying equation (6.4).
It is well known that a third cohomology class can be associated to cocycle actions [Reference ConnesC, Reference JonesJ].
Lemma 6.3. Let ![]() $\alpha \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}\right )$ be an automorphism such that
$\alpha \in \mathop {\mathrm {Aut}}\nolimits \left ({\mathcal A}\right )$ be an automorphism such that  $d^{0}_{H_{U}}\alpha $ is factorised into left and right as in equation (6.3). Let
$d^{0}_{H_{U}}\alpha $ is factorised into left and right as in equation (6.3). Let ![]() $v_{\sigma }(g,h)\in {\mathcal U}\left ( {\mathcal A}_{H_{\sigma }}\right )$,
$v_{\sigma }(g,h)\in {\mathcal U}\left ( {\mathcal A}_{H_{\sigma }}\right )$, ![]() $g,h\in G, \sigma =L,R$, be unitaries satisfying equation (6.4). Then there is some
$g,h\in G, \sigma =L,R$, be unitaries satisfying equation (6.4). Then there is some ![]() $c_{{\sigma }}\in C^{3}(G,{\mathbb T})$,
$c_{{\sigma }}\in C^{3}(G,{\mathbb T})$, ![]() $\sigma =L,R$, such that
$\sigma =L,R$, such that
 $$ \begin{align} v_{{\sigma}}(g,h) v_{{\sigma}}(gh,k) =c_{{\sigma}}(g,h,k) \left ( \gamma_{g,{\sigma}}\circ\beta_{g}^{{\sigma}U}\left ( v_{{\sigma}}(h,k)\right )\right ) v_{{\sigma}}\left ( g, hk\right ),\quad g,h,k\in G. \end{align} $$
$$ \begin{align} v_{{\sigma}}(g,h) v_{{\sigma}}(gh,k) =c_{{\sigma}}(g,h,k) \left ( \gamma_{g,{\sigma}}\circ\beta_{g}^{{\sigma}U}\left ( v_{{\sigma}}(h,k)\right )\right ) v_{{\sigma}}\left ( g, hk\right ),\quad g,h,k\in G. \end{align} $$Proof. By equation (6.4), we have
for  $ \hat \gamma _{g,\sigma }:=\gamma _{g,{\sigma }}\beta _{g}^{{\sigma }U} $. Using this, we have
$ \hat \gamma _{g,\sigma }:=\gamma _{g,{\sigma }}\beta _{g}^{{\sigma }U} $. Using this, we have
 $$ \begin{align} &\mathop{\mathrm{Ad}}\nolimits( v_{\sigma}(g,h))\circ\mathop{\mathrm{Ad}}\nolimits\left ( v_{\sigma}(gh,k)\right )\circ\hat\gamma_{ghk,\sigma} \notag \\ &\quad =\mathop{\mathrm{Ad}}\nolimits( v_{\sigma}(g,h))\circ \hat\gamma_{gh,\sigma}\circ\hat\gamma_{k,\sigma} =\hat\gamma_{g,\sigma}\hat\gamma_{h,\sigma}\hat\gamma_{k,\sigma} =\hat\gamma_{g,\sigma}\circ \mathop{\mathrm{Ad}}\nolimits\left ( v_{\sigma}(h,k)\right )\circ\hat\gamma_{hk,\sigma}\notag\\ &\quad =\mathop{\mathrm{Ad}}\nolimits\left ( \hat\gamma_{g,\sigma}\left ( v_{\sigma}(h,k)\right )\right ) \hat\gamma_{g,\sigma}\circ \hat\gamma_{hk,\sigma} =\mathop{\mathrm{Ad}}\nolimits\left ( \hat\gamma_{g,\sigma}\left ( v_{\sigma}(h,k)\right ) v_{\sigma}(g,hk) \right )\circ\hat\gamma_{ghk,\sigma}. \end{align} $$
$$ \begin{align} &\mathop{\mathrm{Ad}}\nolimits( v_{\sigma}(g,h))\circ\mathop{\mathrm{Ad}}\nolimits\left ( v_{\sigma}(gh,k)\right )\circ\hat\gamma_{ghk,\sigma} \notag \\ &\quad =\mathop{\mathrm{Ad}}\nolimits( v_{\sigma}(g,h))\circ \hat\gamma_{gh,\sigma}\circ\hat\gamma_{k,\sigma} =\hat\gamma_{g,\sigma}\hat\gamma_{h,\sigma}\hat\gamma_{k,\sigma} =\hat\gamma_{g,\sigma}\circ \mathop{\mathrm{Ad}}\nolimits\left ( v_{\sigma}(h,k)\right )\circ\hat\gamma_{hk,\sigma}\notag\\ &\quad =\mathop{\mathrm{Ad}}\nolimits\left ( \hat\gamma_{g,\sigma}\left ( v_{\sigma}(h,k)\right )\right ) \hat\gamma_{g,\sigma}\circ \hat\gamma_{hk,\sigma} =\mathop{\mathrm{Ad}}\nolimits\left ( \hat\gamma_{g,\sigma}\left ( v_{\sigma}(h,k)\right ) v_{\sigma}(g,hk) \right )\circ\hat\gamma_{ghk,\sigma}. \end{align} $$Because ![]() ${\mathcal A}'\cap {\mathcal A}=\mathbb I_{{\mathcal A}}$, it must be the case that
${\mathcal A}'\cap {\mathcal A}=\mathbb I_{{\mathcal A}}$, it must be the case that ![]() $\hat \gamma _{g,\sigma }\left ( v_{\sigma }(h,k)\right ) v_{\sigma }(g,hk)$ and
$\hat \gamma _{g,\sigma }\left ( v_{\sigma }(h,k)\right ) v_{\sigma }(g,hk)$ and ![]() $v_{\sigma }(g,h)v_{\sigma }(gh,k)$ are proportional to each other, proving the lemma.
$v_{\sigma }(g,h)v_{\sigma }(gh,k)$ are proportional to each other, proving the lemma.
By the same argument as in Lemma 2.4, we can show that this ![]() $c_{R}$ is actually a
$c_{R}$ is actually a ![]() $3$-cocycle. If
$3$-cocycle. If ![]() $\omega \in \mathop {\mathcal {SL}}\nolimits $ is given by an automorphism
$\omega \in \mathop {\mathcal {SL}}\nolimits $ is given by an automorphism ![]() $\alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ with factorised
$\alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega )$ with factorised  $d^{0}_{H_{U}}\alpha $, and if
$d^{0}_{H_{U}}\alpha $, and if ![]() $\omega _{0}$ is invariant under
$\omega _{0}$ is invariant under  $\beta _{g}^{U}$, then we have
$\beta _{g}^{U}$, then we have ![]() $h(\omega )=[c_{R}]_{H^{3}\left (G,{\mathbb T}\right )}$, for
$h(\omega )=[c_{R}]_{H^{3}\left (G,{\mathbb T}\right )}$, for ![]() $c_R$ given in Lemma 6.3.
$c_R$ given in Lemma 6.3.
Theorem 6.4. Let ![]() $\omega _{0}$ be a reference state of the form in formula (2.18), and assume that
$\omega _{0}$ be a reference state of the form in formula (2.18), and assume that  $\omega _{0}\circ \beta _{g}^{U}=\omega _{0}$ for any
$\omega _{0}\circ \beta _{g}^{U}=\omega _{0}$ for any ![]() $g\in G$. Let
$g\in G$. Let ![]() $\alpha \in \mathop {\mathrm {QAut}}\nolimits \left ( {\mathcal A}\right )$ be an automorphism. Suppose that
$\alpha \in \mathop {\mathrm {QAut}}\nolimits \left ( {\mathcal A}\right )$ be an automorphism. Suppose that  $d^{0}_{H_{U}}\alpha $ is factorised into left and right as in equation (6.3) with some
$d^{0}_{H_{U}}\alpha $ is factorised into left and right as in equation (6.3) with some ![]() $\gamma _{g,\sigma }\in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_{\theta _{0}},\sigma } )$ and
$\gamma _{g,\sigma }\in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_{\theta _{0}},\sigma } )$ and ![]() $0<\theta _{0}<\frac \pi 2$, for
$0<\theta _{0}<\frac \pi 2$, for ![]() $\sigma =L,R$. Let
$\sigma =L,R$. Let ![]() $v_{\sigma }(g,h)\in {\mathcal U}\left ( {\mathcal A}_{H_{\sigma }}\right )$,
$v_{\sigma }(g,h)\in {\mathcal U}\left ( {\mathcal A}_{H_{\sigma }}\right )$, ![]() $g,h\in G, \sigma =L,R$, be unitaries satisfying equation (6.4) and
$g,h\in G, \sigma =L,R$, be unitaries satisfying equation (6.4) and ![]() $c_{R}\in C^{3}(G,{\mathbb T})$ satisfying equation (6.6) for these
$c_{R}\in C^{3}(G,{\mathbb T})$ satisfying equation (6.6) for these ![]() $v_{R}(g,h)$ which are given in Lemma 6.2 and Lemma 6.3. Then we have
$v_{R}(g,h)$ which are given in Lemma 6.2 and Lemma 6.3. Then we have ![]() $\omega _{0}\circ \alpha \in \mathop {\mathcal {SL}}\nolimits $ with
$\omega _{0}\circ \alpha \in \mathop {\mathcal {SL}}\nolimits $ with ![]() $\mathop {\mathrm {IG}}\nolimits (\omega _{0}\circ \alpha )\neq \emptyset $,
$\mathop {\mathrm {IG}}\nolimits (\omega _{0}\circ \alpha )\neq \emptyset $, ![]() $c_{R}\in Z^{3}(G,{\mathbb T})$, and
$c_{R}\in Z^{3}(G,{\mathbb T})$, and ![]() $h(\omega _{0}\circ \alpha )=[c_{R}]_{H^{3}\left (G,{\mathbb T}\right )}$.
$h(\omega _{0}\circ \alpha )=[c_{R}]_{H^{3}\left (G,{\mathbb T}\right )}$.
Remark 6.5. The situation of this theorem is special. We do not expect that it always occurs.
Proof. That ![]() $\omega _{0}\circ \alpha \in \mathop {\mathcal {SL}}\nolimits $ is by definition. Because
$\omega _{0}\circ \alpha \in \mathop {\mathcal {SL}}\nolimits $ is by definition. Because
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( v_{\sigma}(g,h)) = \gamma_{g,{\sigma}}\beta_{g}^{{\sigma}U}\gamma_{h,{\sigma}}\beta_{h}^{{\sigma}U} \left ( \gamma_{gh,{\sigma}}\beta_{gh}^{{\sigma}U}\right )^{-1} \in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\theta_{0}},\sigma}\right ), \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( v_{\sigma}(g,h)) = \gamma_{g,{\sigma}}\beta_{g}^{{\sigma}U}\gamma_{h,{\sigma}}\beta_{h}^{{\sigma}U} \left ( \gamma_{gh,{\sigma}}\beta_{gh}^{{\sigma}U}\right )^{-1} \in \mathop{\mathrm{Aut}}\nolimits\left ({\mathcal A}_{C_{\theta_{0}},\sigma}\right ), \end{align} $$our ![]() $ v_{\sigma }(g,h)$ belongs to
$ v_{\sigma }(g,h)$ belongs to ![]() ${\mathcal U}({\mathcal A}_{C_{\theta _{0}},\sigma } )$. Because
${\mathcal U}({\mathcal A}_{C_{\theta _{0}},\sigma } )$. Because
 $$ \begin{align} \omega_{0}\alpha\circ\alpha^{-1}\beta_{g}^{U}\alpha =\omega_{0}\beta_{g}^{U}\alpha =\omega_{0}\alpha \end{align} $$
$$ \begin{align} \omega_{0}\alpha\circ\alpha^{-1}\beta_{g}^{U}\alpha =\omega_{0}\beta_{g}^{U}\alpha =\omega_{0}\alpha \end{align} $$and
 $$ \begin{align} \alpha^{-1}\beta_{g}^{U}\alpha =({\textrm{{inner}}})\circ \left ( \gamma_{g,L}\otimes\gamma_{g,R}\right )\circ\beta_{g}^{U}, \end{align} $$
$$ \begin{align} \alpha^{-1}\beta_{g}^{U}\alpha =({\textrm{{inner}}})\circ \left ( \gamma_{g,L}\otimes\gamma_{g,R}\right )\circ\beta_{g}^{U}, \end{align} $$with ![]() $\gamma _{g,\sigma }\in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_{\theta _{0},\sigma }} )$, we have
$\gamma _{g,\sigma }\in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_{\theta _{0},\sigma }} )$, we have  $(\alpha ^{-1}\beta _{g}^{U}\alpha )\in \mathop {\mathrm {IG}}\nolimits (\omega _{0}\alpha , \theta _{0})$, and
$(\alpha ^{-1}\beta _{g}^{U}\alpha )\in \mathop {\mathrm {IG}}\nolimits (\omega _{0}\alpha , \theta _{0})$, and  $ (\gamma _{g,\sigma } )\in {\mathcal T}(\theta _{0}, \alpha ^{-1}\beta _{g}^{U}\alpha )$. Clearly
$ (\gamma _{g,\sigma } )\in {\mathcal T}(\theta _{0}, \alpha ^{-1}\beta _{g}^{U}\alpha )$. Clearly ![]() $\alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega _{0}\circ \alpha )$, and there is
$\alpha \in \mathop {\mathrm {EAut}}\nolimits (\omega _{0}\circ \alpha )$, and there is ![]() $(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta _{0}}$ because
$(\alpha _L,\alpha _R,\Theta )\in {\mathcal D}_{\alpha }^{\theta _{0}}$ because ![]() $\alpha \in \mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$. Set
$\alpha \in \mathop {\mathrm {QAut}}\nolimits ({\mathcal A})$. Set ![]() $\gamma _{g}:=\gamma _{g,L}\otimes \gamma _{g,R}$. From Lemma 2.1, there is some
$\gamma _{g}:=\gamma _{g,L}\otimes \gamma _{g,R}$. From Lemma 2.1, there is some ![]() $W_{g}\in {\mathcal U}({\mathcal H}_{0}) g\in G$ satisfying
$W_{g}\in {\mathcal U}({\mathcal H}_{0}) g\in G$ satisfying
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)\circ\pi_0 =\pi_0\circ\left ( \alpha_L\otimes\alpha_{R}\right ) \circ\Theta\circ\gamma_g\beta_g^U\circ\Theta^{-1}\circ \left ( \alpha_L\otimes\alpha_{R}\right )^{-1},\quad g\in G. \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)\circ\pi_0 =\pi_0\circ\left ( \alpha_L\otimes\alpha_{R}\right ) \circ\Theta\circ\gamma_g\beta_g^U\circ\Theta^{-1}\circ \left ( \alpha_L\otimes\alpha_{R}\right )^{-1},\quad g\in G. \end{align} $$In particular, because ![]() $ v_{R}(h,k)$ belongs to
$ v_{R}(h,k)$ belongs to  ${\mathcal U}({\mathcal A}_{( C_{\theta _{0}})_{R}} )$,
${\mathcal U}({\mathcal A}_{( C_{\theta _{0}})_{R}} )$,  $\Theta \in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_{\theta _{0}}^{c}})$, and
$\Theta \in \mathop {\mathrm {Aut}}\nolimits ({\mathcal A}_{C_{\theta _{0}}^{c}})$, and  $\gamma _g\beta _g^U$ preserves
$\gamma _g\beta _g^U$ preserves  ${\mathcal A}_{\left ( C_{\theta _{0}}\right )_{R}}$, we have
${\mathcal A}_{\left ( C_{\theta _{0}}\right )_{R}}$, we have
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)&\circ \pi_0\circ\left ( \alpha_L\otimes\alpha_{R}\right ) \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{{L}}}\otimes \left ( v_{R}(h,k)\right )\right ) \notag \\ &=\pi_0\circ\left ( \alpha_L\otimes\alpha_{R}\right ) \circ\Theta\circ\gamma_g\beta_g^U\circ\Theta^{-1}\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{{L}}}\otimes \left ( v_{R}(h,k)\right )\right )\notag\\ &=\pi_0\circ\left ( \alpha_L\otimes\alpha_{R}\right ) \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{{L}}}\otimes \gamma_{g,R}\beta_g^{RU}\left ( v_{R}(h,k)\right )\right ) =\mathbb I_{{\mathcal H}_{L}}\otimes \pi_R\circ \alpha_{R}\circ \gamma_{g,R}\beta_g^{RU}( v_{R}(h,k) ). \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits( W_g)&\circ \pi_0\circ\left ( \alpha_L\otimes\alpha_{R}\right ) \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{{L}}}\otimes \left ( v_{R}(h,k)\right )\right ) \notag \\ &=\pi_0\circ\left ( \alpha_L\otimes\alpha_{R}\right ) \circ\Theta\circ\gamma_g\beta_g^U\circ\Theta^{-1}\circ \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{{L}}}\otimes \left ( v_{R}(h,k)\right )\right )\notag\\ &=\pi_0\circ\left ( \alpha_L\otimes\alpha_{R}\right ) \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal A}_{{L}}}\otimes \gamma_{g,R}\beta_g^{RU}\left ( v_{R}(h,k)\right )\right ) =\mathbb I_{{\mathcal H}_{L}}\otimes \pi_R\circ \alpha_{R}\circ \gamma_{g,R}\beta_g^{RU}( v_{R}(h,k) ). \end{align} $$On the other hand, equation (6.4) means
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( \pi_{\sigma}\circ\alpha_{\sigma}( v_{\sigma}(g,h)) \right )\pi_{\sigma} =\pi_{\sigma}\circ\alpha_{\sigma}\circ \gamma_{g,{\sigma}}\beta_{g}^{{\sigma}U}\gamma_{h,{\sigma}}\left ( \beta_{g}^{{\sigma}U}\right )^{-1} ( \gamma_{gh,{\sigma}})^{-1}\circ\alpha_{\sigma}^{-1}. \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits\left ( \pi_{\sigma}\circ\alpha_{\sigma}( v_{\sigma}(g,h)) \right )\pi_{\sigma} =\pi_{\sigma}\circ\alpha_{\sigma}\circ \gamma_{g,{\sigma}}\beta_{g}^{{\sigma}U}\gamma_{h,{\sigma}}\left ( \beta_{g}^{{\sigma}U}\right )^{-1} ( \gamma_{gh,{\sigma}})^{-1}\circ\alpha_{\sigma}^{-1}. \end{align} $$From equations (6.12) and (6.14), we have
 $$ \begin{align} \left ( (W_g), (\pi_{\sigma}\circ\alpha_{\sigma}( v_{\sigma}(g,h)))\right )\in \mathop{\mathrm{IP}}\nolimits\left ( \omega_{0}\circ\alpha, \alpha, \theta_{0}, \left(\alpha^{-1}\beta_{g}^{U}\alpha\right), \left(\gamma_{g,\sigma}\right), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$
$$ \begin{align} \left ( (W_g), (\pi_{\sigma}\circ\alpha_{\sigma}( v_{\sigma}(g,h)))\right )\in \mathop{\mathrm{IP}}\nolimits\left ( \omega_{0}\circ\alpha, \alpha, \theta_{0}, \left(\alpha^{-1}\beta_{g}^{U}\alpha\right), \left(\gamma_{g,\sigma}\right), (\alpha_L,\alpha_R,\Theta) \right ). \end{align} $$Now from equations (6.6) and then (6.13), we obtain
 $$ \begin{align} &\mathbb{I}_{{\mathcal H}_{L}}\otimes\pi_{R}\circ\alpha_{R}\left ( v_{R}(g,h)v_{R}(gh,k)\right ) \notag \\ &\quad =c_{{R}}(g,h,k) \mathbb I_{{\mathcal H}_{L}}\otimes\pi_{R}\circ\alpha_{R}\left ( \left ( \gamma_{g,{R}}\circ\beta_{g}^{{R}U}\left ( v_{{R}}(h,k)\right )\right ) v_{{R}}( g, hk ) \right)\notag\\ &\quad =c_{{R}}(g,h,k) \left ( \mathop{\mathrm{Ad}}\nolimits( W_g) \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal H}_{{L}}}\otimes \pi_{R}\alpha_{R}\left ( v_{R}(h,k)\right )\right )\right ) \cdot \left ( \mathbb I_{{\mathcal H}_{L}}\otimes\pi_{R}\circ\alpha_{R}\left ( v_{{R}}\left ( g, hk\right )\right )\right ). \end{align} $$
$$ \begin{align} &\mathbb{I}_{{\mathcal H}_{L}}\otimes\pi_{R}\circ\alpha_{R}\left ( v_{R}(g,h)v_{R}(gh,k)\right ) \notag \\ &\quad =c_{{R}}(g,h,k) \mathbb I_{{\mathcal H}_{L}}\otimes\pi_{R}\circ\alpha_{R}\left ( \left ( \gamma_{g,{R}}\circ\beta_{g}^{{R}U}\left ( v_{{R}}(h,k)\right )\right ) v_{{R}}( g, hk ) \right)\notag\\ &\quad =c_{{R}}(g,h,k) \left ( \mathop{\mathrm{Ad}}\nolimits( W_g) \left ( \mathop{\mathrm{id}}\nolimits_{{\mathcal H}_{{L}}}\otimes \pi_{R}\alpha_{R}\left ( v_{R}(h,k)\right )\right )\right ) \cdot \left ( \mathbb I_{{\mathcal H}_{L}}\otimes\pi_{R}\circ\alpha_{R}\left ( v_{{R}}\left ( g, hk\right )\right )\right ). \end{align} $$This means
 $$ \begin{align} c_{R}=c_R\left ( \omega_{0}\circ\alpha, \alpha, \theta_{0}, \left(\alpha^{-1}\beta_g^{U}\alpha\right), \left(\gamma_{g,\sigma}\right), (\alpha_L,\alpha_R,\Theta),\left ( (W_g), ((\pi_{\sigma}\circ\alpha_{\sigma}( v_{\sigma}(g,h))))\right ) \right ) \end{align} $$
$$ \begin{align} c_{R}=c_R\left ( \omega_{0}\circ\alpha, \alpha, \theta_{0}, \left(\alpha^{-1}\beta_g^{U}\alpha\right), \left(\gamma_{g,\sigma}\right), (\alpha_L,\alpha_R,\Theta),\left ( (W_g), ((\pi_{\sigma}\circ\alpha_{\sigma}( v_{\sigma}(g,h))))\right ) \right ) \end{align} $$in Definition 2.5. Hence we get ![]() $c_{R}\in Z^{3}(G,{\mathbb T})$, and
$c_{R}\in Z^{3}(G,{\mathbb T})$, and ![]() $h(\omega _{0}\circ \alpha )=[c_{R}]_{H^{3}\left (G,{\mathbb T}\right )}$.
$h(\omega _{0}\circ \alpha )=[c_{R}]_{H^{3}\left (G,{\mathbb T}\right )}$.
A Basic notation
For a finite set S, ![]() $\#S$ indicates the number of elements in S. For
$\#S$ indicates the number of elements in S. For ![]() $t\in {\mathbb R}$,
$t\in {\mathbb R}$, ![]() $[t]$ denotes the smallest integer less than or equal to t.
$[t]$ denotes the smallest integer less than or equal to t.
For a Hilbert space ![]() ${\mathcal H}$,
${\mathcal H}$, ![]() $B({\mathcal H})$ denotes the set of all bounded operators on
$B({\mathcal H})$ denotes the set of all bounded operators on ![]() ${\mathcal H}$. If
${\mathcal H}$. If ![]() $V:{\mathcal H}_1\to {\mathcal H}_2$ is a linear map from a Hilbert space
$V:{\mathcal H}_1\to {\mathcal H}_2$ is a linear map from a Hilbert space ![]() ${\mathcal H}_1$ to another Hilbert space
${\mathcal H}_1$ to another Hilbert space ![]() ${\mathcal H}_2$, then
${\mathcal H}_2$, then ![]() $\mathop {\mathrm {Ad}}\nolimits (V):B({\mathcal H}_1)\to B({\mathcal H}_2)$ denotes the map
$\mathop {\mathrm {Ad}}\nolimits (V):B({\mathcal H}_1)\to B({\mathcal H}_2)$ denotes the map ![]() $\mathop {\mathrm {Ad}}\nolimits (V)(x):=V x V^*$,
$\mathop {\mathrm {Ad}}\nolimits (V)(x):=V x V^*$, ![]() $x\in B({\mathcal H}_1)$. Occasionally we write
$x\in B({\mathcal H}_1)$. Occasionally we write ![]() $\mathop {\mathrm {Ad}}\nolimits _V$ instead of
$\mathop {\mathrm {Ad}}\nolimits _V$ instead of ![]() $\mathop {\mathrm {Ad}}\nolimits (V)$. For a
$\mathop {\mathrm {Ad}}\nolimits (V)$. For a ![]() $C^{*}$-algebra
$C^{*}$-algebra ![]() ${\mathcal B}$ and
${\mathcal B}$ and ![]() $v\in {\mathcal B}$, we set
$v\in {\mathcal B}$, we set ![]() $\mathop {\mathrm {Ad}}\nolimits (v)(x):=\mathop {\mathrm {Ad}}\nolimits _{v}(x):=vxv^{*}$,
$\mathop {\mathrm {Ad}}\nolimits (v)(x):=\mathop {\mathrm {Ad}}\nolimits _{v}(x):=vxv^{*}$, ![]() $x\in {\mathcal B}$.
$x\in {\mathcal B}$.
For a state ![]() $\omega , \varphi $ on a
$\omega , \varphi $ on a ![]() $C^{*}$-algebra
$C^{*}$-algebra ![]() ${\mathcal B}$, we write
${\mathcal B}$, we write ![]() $\omega \sim _{\text {q.e.}}\varphi $ when they are quasiequivalent (see [Reference Bratteli and RobinsonBR1]). We also write
$\omega \sim _{\text {q.e.}}\varphi $ when they are quasiequivalent (see [Reference Bratteli and RobinsonBR1]). We also write ![]() $\omega \simeq \varphi $ when they are equivalent. We denote by
$\omega \simeq \varphi $ when they are equivalent. We denote by ![]() $\mathop {\mathrm {Aut}}\nolimits {\mathcal B}$ the group of automorphisms on a
$\mathop {\mathrm {Aut}}\nolimits {\mathcal B}$ the group of automorphisms on a ![]() $C^{*}$-algebra
$C^{*}$-algebra ![]() ${\mathcal B}$. The group of inner automorphisms on a unital
${\mathcal B}$. The group of inner automorphisms on a unital ![]() $C^{*}$-algebra
$C^{*}$-algebra ![]() ${\mathcal B}$ is denoted by
${\mathcal B}$ is denoted by ![]() $\mathop {\mathrm {Inn}}\nolimits {\mathcal B}$. For
$\mathop {\mathrm {Inn}}\nolimits {\mathcal B}$. For ![]() $\gamma _1,\gamma _2\in \mathop {\mathrm {Aut}}\nolimits ({\mathcal B})$,
$\gamma _1,\gamma _2\in \mathop {\mathrm {Aut}}\nolimits ({\mathcal B})$, ![]() $\gamma _1=({\textrm {{inner}}})\circ \gamma _2$ means there is some unitary u in
$\gamma _1=({\textrm {{inner}}})\circ \gamma _2$ means there is some unitary u in ![]() ${\mathcal B}$ such that
${\mathcal B}$ such that ![]() $\gamma _1=\mathop {\mathrm {Ad}}\nolimits (u)\circ \gamma _2$. For a unital
$\gamma _1=\mathop {\mathrm {Ad}}\nolimits (u)\circ \gamma _2$. For a unital ![]() $C^{*}$-algebra
$C^{*}$-algebra ![]() ${\mathcal B}$, the unit of
${\mathcal B}$, the unit of ![]() ${\mathcal B}$ is denoted by
${\mathcal B}$ is denoted by ![]() $\mathbb I_{{\mathcal B}}$. For a Hilbert space we write
$\mathbb I_{{\mathcal B}}$. For a Hilbert space we write ![]() $\mathbb I_{{\mathcal H}}:=\mathbb I_{{\mathcal B}({\mathcal H})}$. For a unital
$\mathbb I_{{\mathcal H}}:=\mathbb I_{{\mathcal B}({\mathcal H})}$. For a unital ![]() $C^{*}$-algebra
$C^{*}$-algebra ![]() ${\mathcal B}$, by
${\mathcal B}$, by ![]() ${\mathcal U}({\mathcal B})$ we mean the set of all unitary elements in
${\mathcal U}({\mathcal B})$ we mean the set of all unitary elements in ![]() ${\mathcal B}$. For a Hilbert space we write
${\mathcal B}$. For a Hilbert space we write ![]() ${\mathcal U}({\mathcal H})$ for
${\mathcal U}({\mathcal H})$ for ![]() ${\mathcal U}({\mathcal B}({\mathcal H}))$.
${\mathcal U}({\mathcal B}({\mathcal H}))$.
For a state ![]() $\varphi $ on
$\varphi $ on ![]() ${\mathcal B}$ and a
${\mathcal B}$ and a ![]() $C^{*}$-subalgebra
$C^{*}$-subalgebra ![]() ${\mathcal C}$ of
${\mathcal C}$ of ![]() ${\mathcal B}$,
${\mathcal B}$, ![]() $\varphi \rvert _{{\mathcal C}}$ indicates the restriction of
$\varphi \rvert _{{\mathcal C}}$ indicates the restriction of ![]() $\varphi $ to
$\varphi $ to ![]() ${\mathcal C}$.
${\mathcal C}$.
To denote the composition of automorphisms ![]() $\alpha _1, \alpha _2$, all of
$\alpha _1, \alpha _2$, all of ![]() $\alpha _1\circ \alpha _2, \alpha _1\alpha _2, \alpha _1\cdot \alpha _2$ are used. Frequently, the first one serves as a bracket to visually separate a group of operators.
$\alpha _1\circ \alpha _2, \alpha _1\alpha _2, \alpha _1\cdot \alpha _2$ are used. Frequently, the first one serves as a bracket to visually separate a group of operators.
B Automorphisms on UHF-algebras
Lemma B.1. Let ![]() $\mathfrak A, \mathfrak B$ be UHF-algebras. If automorphisms
$\mathfrak A, \mathfrak B$ be UHF-algebras. If automorphisms ![]() $\gamma _{\mathfrak A}\in \mathop {\mathrm {Aut}}\nolimits (\mathfrak A), \gamma _{\mathfrak B}\in \mathop {\mathrm {Aut}}\nolimits (\mathfrak B)$ and a unitary
$\gamma _{\mathfrak A}\in \mathop {\mathrm {Aut}}\nolimits (\mathfrak A), \gamma _{\mathfrak B}\in \mathop {\mathrm {Aut}}\nolimits (\mathfrak B)$ and a unitary ![]() $W\in {\mathcal U}\left ({\mathfrak A}\otimes \mathfrak B\right )$ satisfy
$W\in {\mathcal U}\left ({\mathfrak A}\otimes \mathfrak B\right )$ satisfy
then there are unitaries ![]() $u_{\mathfrak A}\in {\mathcal U}(\mathfrak A)$ and
$u_{\mathfrak A}\in {\mathcal U}(\mathfrak A)$ and ![]() $u_{\mathfrak B}\in {\mathcal U}(\mathfrak B)$ such that
$u_{\mathfrak B}\in {\mathcal U}(\mathfrak B)$ such that
 $$ \begin{align} \begin{split} \gamma_{\mathfrak A}\left ( X_{\mathfrak A}\right ) &=\mathop{\mathrm{Ad}}\nolimits_{u_{\mathfrak A}}(X_{\mathfrak A}) ,\quad X_{\mathfrak A}\in{\mathfrak A},\\ \gamma_{\mathfrak B}\left ( X_{\mathfrak B}\right )&=\mathop{\mathrm{Ad}}\nolimits_{u_{\mathfrak B}}(X_{\mathfrak B}) ,\quad X_{\mathfrak B}\in{\mathfrak B}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \gamma_{\mathfrak A}\left ( X_{\mathfrak A}\right ) &=\mathop{\mathrm{Ad}}\nolimits_{u_{\mathfrak A}}(X_{\mathfrak A}) ,\quad X_{\mathfrak A}\in{\mathfrak A},\\ \gamma_{\mathfrak B}\left ( X_{\mathfrak B}\right )&=\mathop{\mathrm{Ad}}\nolimits_{u_{\mathfrak B}}(X_{\mathfrak B}) ,\quad X_{\mathfrak B}\in{\mathfrak B}. \end{split} \end{align} $$Proof. Fix some irreducible representations ![]() $({\mathcal H}_{\mathfrak A},\pi _{\mathfrak A}), ({\mathcal H}_{\mathfrak B},\pi _{\mathfrak B})$, of
$({\mathcal H}_{\mathfrak A},\pi _{\mathfrak A}), ({\mathcal H}_{\mathfrak B},\pi _{\mathfrak B})$, of ![]() $\mathfrak A, \mathfrak B$. We claim that there are unitaries
$\mathfrak A, \mathfrak B$. We claim that there are unitaries ![]() $v_{\mathfrak A}\in {\mathcal U}({\mathcal H}_{\mathfrak A})$ and
$v_{\mathfrak A}\in {\mathcal U}({\mathcal H}_{\mathfrak A})$ and ![]() $v_{{\mathfrak B}}\in {\mathcal U}({\mathcal H}_{{\mathfrak B}})$ such that
$v_{{\mathfrak B}}\in {\mathcal U}({\mathcal H}_{{\mathfrak B}})$ such that
 $$ \begin{align} \begin{split} \mathop{\mathrm{Ad}}\nolimits_{v_{{\mathfrak A}}}\left ( \pi_{{\mathfrak A}}(X_{{\mathfrak A}})\right )&=\pi_{{\mathfrak A}}\circ\gamma_{{\mathfrak A}} (X_{{\mathfrak A}}),\quad X_{{\mathfrak A}}\in{\mathfrak A},\\ \mathop{\mathrm{Ad}}\nolimits_{v_{{\mathfrak B}}}\left ( \pi_{{\mathfrak B}}(X_{{\mathfrak B}})\right )&=\pi_{{\mathfrak B}}\circ\gamma_{{\mathfrak B}} (X_{{\mathfrak B}}),\quad X_{{\mathfrak B}}\in{\mathfrak B}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathop{\mathrm{Ad}}\nolimits_{v_{{\mathfrak A}}}\left ( \pi_{{\mathfrak A}}(X_{{\mathfrak A}})\right )&=\pi_{{\mathfrak A}}\circ\gamma_{{\mathfrak A}} (X_{{\mathfrak A}}),\quad X_{{\mathfrak A}}\in{\mathfrak A},\\ \mathop{\mathrm{Ad}}\nolimits_{v_{{\mathfrak B}}}\left ( \pi_{{\mathfrak B}}(X_{{\mathfrak B}})\right )&=\pi_{{\mathfrak B}}\circ\gamma_{{\mathfrak B}} (X_{{\mathfrak B}}),\quad X_{{\mathfrak B}}\in{\mathfrak B}. \end{split} \end{align} $$To see this, note that
From this, ![]() $\pi _{{\mathfrak A}}\circ \gamma _{{\mathfrak A}}$ (resp.,
$\pi _{{\mathfrak A}}\circ \gamma _{{\mathfrak A}}$ (resp., ![]() $\pi _{{\mathfrak B}}\circ \gamma _{{\mathfrak B}}$) is quasiequivalent to
$\pi _{{\mathfrak B}}\circ \gamma _{{\mathfrak B}}$) is quasiequivalent to ![]() $\pi _{{\mathfrak A}}$ (resp.,
$\pi _{{\mathfrak A}}$ (resp., ![]() $\pi _{{\mathfrak B}}$). Because
$\pi _{{\mathfrak B}}$). Because ![]() $\pi _{{\mathfrak A}}$ and
$\pi _{{\mathfrak A}}$ and ![]() $\pi _{{\mathfrak B}}$ are irreducible, by the Wigner theorem there are unitaries
$\pi _{{\mathfrak B}}$ are irreducible, by the Wigner theorem there are unitaries ![]() $v_{\mathfrak A}\in {\mathcal U}({\mathcal H}_{\mathfrak A})$ and
$v_{\mathfrak A}\in {\mathcal U}({\mathcal H}_{\mathfrak A})$ and ![]() $v_{{\mathfrak B}}\in {\mathcal U}({\mathcal H}_{{\mathfrak B}})$ satisfying equation (B.3).
$v_{{\mathfrak B}}\in {\mathcal U}({\mathcal H}_{{\mathfrak B}})$ satisfying equation (B.3).
We then have
 $$ \begin{align} \mathop{\mathrm{Ad}}\nolimits_{\left ( \pi_{{\mathfrak A}}\otimes \pi_{{\mathfrak B}}\right )(W)}\circ\left ( \pi_{{\mathfrak A}}\otimes\pi_{{\mathfrak B}}\right ) &=\left ( \pi_{{\mathfrak A}}\circ\gamma_{{\mathfrak A}}\right )\otimes \left ( \pi_{{\mathfrak B}}\circ\gamma_{{\mathfrak B}}\right ) \notag \\ &=\left ( \mathop{\mathrm{Ad}}\nolimits_{v_{{\mathfrak A}}}\circ\pi_{{\mathfrak A}}\right )\otimes \left ( \mathop{\mathrm{Ad}}\nolimits_{v_{{\mathfrak B}}}\circ\pi_{{\mathfrak B}}\right ) =\mathop{\mathrm{Ad}}\nolimits_{v_{{\mathfrak A}}\otimes v_{{\mathfrak B}}}\circ \left (\pi_{{\mathfrak A}}\otimes\pi_{{\mathfrak B}}\right ). \end{align} $$
$$ \begin{align} \mathop{\mathrm{Ad}}\nolimits_{\left ( \pi_{{\mathfrak A}}\otimes \pi_{{\mathfrak B}}\right )(W)}\circ\left ( \pi_{{\mathfrak A}}\otimes\pi_{{\mathfrak B}}\right ) &=\left ( \pi_{{\mathfrak A}}\circ\gamma_{{\mathfrak A}}\right )\otimes \left ( \pi_{{\mathfrak B}}\circ\gamma_{{\mathfrak B}}\right ) \notag \\ &=\left ( \mathop{\mathrm{Ad}}\nolimits_{v_{{\mathfrak A}}}\circ\pi_{{\mathfrak A}}\right )\otimes \left ( \mathop{\mathrm{Ad}}\nolimits_{v_{{\mathfrak B}}}\circ\pi_{{\mathfrak B}}\right ) =\mathop{\mathrm{Ad}}\nolimits_{v_{{\mathfrak A}}\otimes v_{{\mathfrak B}}}\circ \left (\pi_{{\mathfrak A}}\otimes\pi_{{\mathfrak B}}\right ). \end{align} $$Because ![]() $\pi _{{\mathfrak A}}\otimes \pi _{{\mathfrak B}}$ is irreducible, there is a
$\pi _{{\mathfrak A}}\otimes \pi _{{\mathfrak B}}$ is irreducible, there is a ![]() $c\in {\mathbb T}$ such that
$c\in {\mathbb T}$ such that
We claim there is a unitary ![]() $u_{\mathfrak B}\in {\mathcal U}(\mathfrak B)$ such that
$u_{\mathfrak B}\in {\mathcal U}(\mathfrak B)$ such that
Choose a unit vector ![]() $\xi \in {\mathcal H}_{\mathfrak A}$ with
$\xi \in {\mathcal H}_{\mathfrak A}$ with ![]() $\left \langle \xi , v_{{\mathfrak A}}\xi \right \rangle \neq 0$. For each
$\left \langle \xi , v_{{\mathfrak A}}\xi \right \rangle \neq 0$. For each ![]() $x\in {\mathcal B}({\mathcal H}_{\mathfrak A}\otimes {\mathcal H}_{{\mathfrak B}})$, the map
$x\in {\mathcal B}({\mathcal H}_{\mathfrak A}\otimes {\mathcal H}_{{\mathfrak B}})$, the map
is a bounded sesquilinear form. Therefore, there is a unique ![]() $\Phi _\xi (x)\in {\mathcal B}({\mathcal H}_{\mathfrak B})$ such that
$\Phi _\xi (x)\in {\mathcal B}({\mathcal H}_{\mathfrak B})$ such that
 $$ \begin{align} \left\langle\eta_1,\Phi_\xi(x)\eta_2\right\rangle =\left\langle\left ( \xi\otimes \eta_1\right ),x \left ( \xi\otimes \eta_2\right )\right\rangle,\quad (\eta_1,\eta_2)\in {\mathcal H}_{\mathfrak B}\times {\mathcal H}_{\mathfrak B}. \end{align} $$
$$ \begin{align} \left\langle\eta_1,\Phi_\xi(x)\eta_2\right\rangle =\left\langle\left ( \xi\otimes \eta_1\right ),x \left ( \xi\otimes \eta_2\right )\right\rangle,\quad (\eta_1,\eta_2)\in {\mathcal H}_{\mathfrak B}\times {\mathcal H}_{\mathfrak B}. \end{align} $$The map ![]() $\Phi _\xi :{\mathcal B}\left ({\mathcal H}_{\mathfrak A}\otimes {\mathcal H}_{{\mathfrak B}}\right )\to {\mathcal B}({\mathcal H}_{\mathfrak B})$ is linear and
$\Phi _\xi :{\mathcal B}\left ({\mathcal H}_{\mathfrak A}\otimes {\mathcal H}_{{\mathfrak B}}\right )\to {\mathcal B}({\mathcal H}_{\mathfrak B})$ is linear and
 $$ \begin{align} \left \lVert\Phi_\xi(x)\right \rVert\le \left \lVert x\right \rVert,\quad x\in{\mathcal B}({\mathcal H}). \end{align} $$
$$ \begin{align} \left \lVert\Phi_\xi(x)\right \rVert\le \left \lVert x\right \rVert,\quad x\in{\mathcal B}({\mathcal H}). \end{align} $$Because W belongs to ![]() $\mathfrak A\otimes \mathfrak B$, there are sequences
$\mathfrak A\otimes \mathfrak B$, there are sequences
 $$ \begin{align} z_N=\sum_{i=1}^{n_N} a_i^{(N)}\otimes b_i^{(N)},\quad \text{with } a_i^{(N)}\in{\mathfrak A},\ b_i^{(N)}\in{\mathfrak B}, \end{align} $$
$$ \begin{align} z_N=\sum_{i=1}^{n_N} a_i^{(N)}\otimes b_i^{(N)},\quad \text{with } a_i^{(N)}\in{\mathfrak A},\ b_i^{(N)}\in{\mathfrak B}, \end{align} $$such that
 $$ \begin{align} \left \lVert W-z_N \right \rVert<\frac 1N. \end{align} $$
$$ \begin{align} \left \lVert W-z_N \right \rVert<\frac 1N. \end{align} $$Because of formula (B.10), we have
 $$ \begin{align} \left \lVert \Phi_{\xi}\left ( \left ( \pi_{\mathfrak A}\otimes\pi_{\mathfrak B}\right )\left ( W-z_N\right )\right ) \right \rVert<\frac 1N. \end{align} $$
$$ \begin{align} \left \lVert \Phi_{\xi}\left ( \left ( \pi_{\mathfrak A}\otimes\pi_{\mathfrak B}\right )\left ( W-z_N\right )\right ) \right \rVert<\frac 1N. \end{align} $$Note that
 $$ \begin{align} \Phi_{\xi}\left ( \left ( \pi_{\mathfrak A}\otimes\pi_{\mathfrak B}\right )\left ( z_N\right )\right ) =\sum_{i=1}^{n_N} \left\langle\xi, \pi_{\mathfrak A}\left ( a_i^{(N)}\right )\xi\right\rangle\pi_{\mathfrak B}\left ( b_i^{(N)}\right ) \in\pi_{\mathfrak B}(\mathfrak B). \end{align} $$
$$ \begin{align} \Phi_{\xi}\left ( \left ( \pi_{\mathfrak A}\otimes\pi_{\mathfrak B}\right )\left ( z_N\right )\right ) =\sum_{i=1}^{n_N} \left\langle\xi, \pi_{\mathfrak A}\left ( a_i^{(N)}\right )\xi\right\rangle\pi_{\mathfrak B}\left ( b_i^{(N)}\right ) \in\pi_{\mathfrak B}(\mathfrak B). \end{align} $$Therefore, we have
 $$ \begin{align} c\left\langle\xi,v_{{\mathfrak A}}\xi\right\rangle v_{{\mathfrak B}} =\Phi_{\xi}\left ( c\left ( v_{{\mathfrak A}}\otimes v_{{\mathfrak B}}\right ) \right ) =\Phi_{\xi}\left ( \left ( \pi_{{\mathfrak A}}\otimes\pi_{{\mathfrak B}}\right )(W)\right ) \in\overline{\pi_{\mathfrak B}(\mathfrak B)}^n, \end{align} $$
$$ \begin{align} c\left\langle\xi,v_{{\mathfrak A}}\xi\right\rangle v_{{\mathfrak B}} =\Phi_{\xi}\left ( c\left ( v_{{\mathfrak A}}\otimes v_{{\mathfrak B}}\right ) \right ) =\Phi_{\xi}\left ( \left ( \pi_{{\mathfrak A}}\otimes\pi_{{\mathfrak B}}\right )(W)\right ) \in\overline{\pi_{\mathfrak B}(\mathfrak B)}^n, \end{align} $$where ![]() $\overline {\cdot }^{n}$ denotes the norm closure. Because
$\overline {\cdot }^{n}$ denotes the norm closure. Because ![]() $\pi _{{\mathfrak B}}\left (\mathfrak B\right )$ is norm-closed, we have
$\pi _{{\mathfrak B}}\left (\mathfrak B\right )$ is norm-closed, we have  $\overline {\pi _{\mathfrak B}\left (\mathfrak B\right )}^n =\pi _{\mathfrak B}\left (\mathfrak B\right )$. Hence we have
$\overline {\pi _{\mathfrak B}\left (\mathfrak B\right )}^n =\pi _{\mathfrak B}\left (\mathfrak B\right )$. Hence we have ![]() $v_{{\mathfrak B}}\in \pi _{\mathfrak B}\left (\mathfrak B\right )$ – that is, there is a unitary
$v_{{\mathfrak B}}\in \pi _{\mathfrak B}\left (\mathfrak B\right )$ – that is, there is a unitary ![]() $u_{\mathfrak B}\in \mathfrak B$ such that
$u_{\mathfrak B}\in \mathfrak B$ such that ![]() $v_{{\mathfrak B}}=\pi _{\mathfrak B}\left ( u_{{\mathfrak B}}\right )$.
$v_{{\mathfrak B}}=\pi _{\mathfrak B}\left ( u_{{\mathfrak B}}\right )$.
We then have
As ![]() ${\mathfrak B}$ is simple,
${\mathfrak B}$ is simple, ![]() $\mathop {\mathrm {Ad}}\nolimits _{u_{{\mathfrak B}}}(X)=\gamma _{\mathfrak B}(X)$ for all
$\mathop {\mathrm {Ad}}\nolimits _{u_{{\mathfrak B}}}(X)=\gamma _{\mathfrak B}(X)$ for all ![]() $ X\in {\mathfrak B}$.
$ X\in {\mathfrak B}$.
The proof for ![]() ${\mathfrak A}$ is the same.
${\mathfrak A}$ is the same.
C F-functions
In this section, we collect various estimates about F-functions. These estimates are useful for the proof of the factorisation property. Let us first start from the definition:
Definition C.1. An F-function F on ![]() $\left ({{\mathbb Z}^2}, \mathrm {d}\right )$ is a nonincreasing function
$\left ({{\mathbb Z}^2}, \mathrm {d}\right )$ is a nonincreasing function ![]() $F:[0,\infty )\to (0,\infty )$ such that
$F:[0,\infty )\to (0,\infty )$ such that
(i)
 $\left \lVert F\right \rVert :=\sup _{x\in {{\mathbb Z}^2}}\left ( \sum _{y\in {{\mathbb Z}^2}}F\left ( {\mathrm {d}}(x,y)\right )\right )<\infty $ and
$\left \lVert F\right \rVert :=\sup _{x\in {{\mathbb Z}^2}}\left ( \sum _{y\in {{\mathbb Z}^2}}F\left ( {\mathrm {d}}(x,y)\right )\right )<\infty $ and(ii)
 $C_{F}:=\sup _{x,y\in {{\mathbb Z}^2}}\left ( \sum _{z\in {{\mathbb Z}^2}} \frac {F\left ( {\mathrm {d}}\left (x,z\right )\right ) F\left ( {\mathrm {d}}\left (z,y\right )\right )}{F\left ( {\mathrm {d}}\left (x,y\right )\right )}\right )<\infty $.
$C_{F}:=\sup _{x,y\in {{\mathbb Z}^2}}\left ( \sum _{z\in {{\mathbb Z}^2}} \frac {F\left ( {\mathrm {d}}\left (x,z\right )\right ) F\left ( {\mathrm {d}}\left (z,y\right )\right )}{F\left ( {\mathrm {d}}\left (x,y\right )\right )}\right )<\infty $.
These properties are called uniform integrability and the convolution identity, respectively.
We denote by ![]() ${\mathcal F}_{a}$ a class of F-functions which decay quickly.
${\mathcal F}_{a}$ a class of F-functions which decay quickly.
Definition C.2. We say an F-function F belongs to ![]() ${\mathcal F}_{a}$ if
${\mathcal F}_{a}$ if
(i) for any
 $k\in {\mathbb N}\cup \{0\}$ and
$k\in {\mathbb N}\cup \{0\}$ and  $0<\vartheta \le 1$, we have (C.1)and
$0<\vartheta \le 1$, we have (C.1)and $$ \begin{align} \kappa_{\vartheta,k, F}:=\sum_{n=0}^{\infty} (n+1)^{k}\left ( F(n)\right )^{\vartheta}<\infty \end{align} $$
$$ \begin{align} \kappa_{\vartheta,k, F}:=\sum_{n=0}^{\infty} (n+1)^{k}\left ( F(n)\right )^{\vartheta}<\infty \end{align} $$(ii) for any
 $0<\vartheta <1$, there is an F-function
$0<\vartheta <1$, there is an F-function  $\tilde F_{\vartheta }$ such that (C.2)
$\tilde F_{\vartheta }$ such that (C.2) $$ \begin{align} \max\left\{ F\left (\frac r 3\right ), \left ( F\left ( \left [ \frac r 3 \right ] \right )\right )^{\vartheta}\right\}\le \tilde F_{\vartheta}(r),\quad r\ge 0. \end{align} $$
$$ \begin{align} \max\left\{ F\left (\frac r 3\right ), \left ( F\left ( \left [ \frac r 3 \right ] \right )\right )^{\vartheta}\right\}\le \tilde F_{\vartheta}(r),\quad r\ge 0. \end{align} $$
For example, a function  $F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant
$F(r)=\frac {\exp \left ( {-r^{\theta }}\right )}{(1+r)^{4}}$ with a constant ![]() $0<\theta <1$ belongs to
$0<\theta <1$ belongs to ![]() ${\mathcal F}_a$. (See [Reference Nachtergaele, Sims and YoungNSY, Appendix] for (i). The proof of (ii) is rather standard.)
${\mathcal F}_a$. (See [Reference Nachtergaele, Sims and YoungNSY, Appendix] for (i). The proof of (ii) is rather standard.)
In this appendix, we derive inequalities about ![]() $F\in {\mathcal F}_{a}$. In order for that, the following lemma is useful. We will freely identify
$F\in {\mathcal F}_{a}$. In order for that, the following lemma is useful. We will freely identify ![]() ${\mathbb C}$ and
${\mathbb C}$ and ![]() ${\mathbb R}^{2}$ in an obvious manner.
${\mathbb R}^{2}$ in an obvious manner.
Lemma C.3. For ![]() $0\le \theta _1<\theta _2\le 2\pi $,
$0\le \theta _1<\theta _2\le 2\pi $, ![]() $c>0$, and
$c>0$, and ![]() $r\ge 0$, set
$r\ge 0$, set
 $$ \begin{align} S_{r,c}^{\left[\theta_1,\theta_2\right]} := \left\{ s e^{i\theta}\in{\mathbb R}^2\mid r\le s< r+c,\quad \theta\in [\theta_1,\theta_2] \right\}. \end{align} $$
$$ \begin{align} S_{r,c}^{\left[\theta_1,\theta_2\right]} := \left\{ s e^{i\theta}\in{\mathbb R}^2\mid r\le s< r+c,\quad \theta\in [\theta_1,\theta_2] \right\}. \end{align} $$Then we have
 $$ \begin{align} \#\left ( S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2 \right ) \le \pi \left ( 2\sqrt 2+c\right )^{2}(r+1). \end{align} $$
$$ \begin{align} \#\left ( S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2 \right ) \le \pi \left ( 2\sqrt 2+c\right )^{2}(r+1). \end{align} $$In particular, we have
 $$ \begin{align} \#\left ( S_{r,1}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2 \right ) \le 64 (r+1). \end{align} $$
$$ \begin{align} \#\left ( S_{r,1}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2 \right ) \le 64 (r+1). \end{align} $$Proof. Because the diameter of a ![]() $2$-dimensional unit square is
$2$-dimensional unit square is ![]() $\sqrt 2$, any unit square B of
$\sqrt 2$, any unit square B of ![]() ${\mathbb Z}^2$ with
${\mathbb Z}^2$ with  $B\cap S_{r,c}^{\left [\theta _1,\theta _2\right ]}\cap {\mathbb Z}^2\neq \emptyset $ satisfies
$B\cap S_{r,c}^{\left [\theta _1,\theta _2\right ]}\cap {\mathbb Z}^2\neq \emptyset $ satisfies  $B\subset \hat S_{r,c}^{[\theta _1,\theta _2 ]}(\sqrt 2 )$. Therefore, we have
$B\subset \hat S_{r,c}^{[\theta _1,\theta _2 ]}(\sqrt 2 )$. Therefore, we have
 $$ \begin{align} \#\left\{B\mid \text{unit square of } {\mathbb Z}^2 \text{ with } B\cap S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\neq \emptyset\right\} =\sum_{B: B\cap S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\neq \emptyset} 1 \le \left \lvert \hat S_{r,c}^{\left[\theta_1,\theta_2\right]}(\sqrt{2})\right \rvert. \end{align} $$
$$ \begin{align} \#\left\{B\mid \text{unit square of } {\mathbb Z}^2 \text{ with } B\cap S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\neq \emptyset\right\} =\sum_{B: B\cap S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\neq \emptyset} 1 \le \left \lvert \hat S_{r,c}^{\left[\theta_1,\theta_2\right]}(\sqrt{2})\right \rvert. \end{align} $$Note that the area of  $ \hat S_{r,c}^{\left [\theta _1,\theta _2\right ]}\left (\sqrt 2\right )$, denoted by
$ \hat S_{r,c}^{\left [\theta _1,\theta _2\right ]}\left (\sqrt 2\right )$, denoted by  $\left \lvert \hat S_{r,c}^{\left [\theta _1,\theta _2\right ]}\left (\sqrt 2\right )\right \rvert $, is less than
$\left \lvert \hat S_{r,c}^{\left [\theta _1,\theta _2\right ]}\left (\sqrt 2\right )\right \rvert $, is less than
 $$ \begin{align} \left \lvert \hat S_{r,c}^{\left[\theta_1,\theta_2\right]}(\sqrt{2})\right \rvert\le \pi\left ( \left(r+c+\sqrt 2\right)^2-\left(r-\sqrt 2\right)^2)\right ) \le \pi (2r+c) \left(2\sqrt 2+c\right) \le \pi\left ( 2\sqrt 2+c\right )^{2}(r+1) \end{align} $$
$$ \begin{align} \left \lvert \hat S_{r,c}^{\left[\theta_1,\theta_2\right]}(\sqrt{2})\right \rvert\le \pi\left ( \left(r+c+\sqrt 2\right)^2-\left(r-\sqrt 2\right)^2)\right ) \le \pi (2r+c) \left(2\sqrt 2+c\right) \le \pi\left ( 2\sqrt 2+c\right )^{2}(r+1) \end{align} $$if ![]() $r>\sqrt 2$. For
$r>\sqrt 2$. For ![]() $r\le \sqrt 2$, we have
$r\le \sqrt 2$, we have
 $$ \begin{align} \left \lvert \hat S_{r,c}^{\left[\theta_1,\theta_2\right]}(\sqrt{2})\right \rvert \le \pi\left ( \left(r+c+\sqrt 2\right)^2\right ) \le \pi\cdot \left(2\sqrt 2+c\right)^2 \le \pi\left ( 2\sqrt 2+c\right )^{2}(r+1). \end{align} $$
$$ \begin{align} \left \lvert \hat S_{r,c}^{\left[\theta_1,\theta_2\right]}(\sqrt{2})\right \rvert \le \pi\left ( \left(r+c+\sqrt 2\right)^2\right ) \le \pi\cdot \left(2\sqrt 2+c\right)^2 \le \pi\left ( 2\sqrt 2+c\right )^{2}(r+1). \end{align} $$Hence, in any case we have
 $$ \begin{align} \left \lvert \hat S_{r,c}^{\left[\theta_1,\theta_2\right]}(\sqrt{2})\right \rvert \le \pi\left ( 2\sqrt 2+c\right )^{2}(r+1). \end{align} $$
$$ \begin{align} \left \lvert \hat S_{r,c}^{\left[\theta_1,\theta_2\right]}(\sqrt{2})\right \rvert \le \pi\left ( 2\sqrt 2+c\right )^{2}(r+1). \end{align} $$Substituting this into equation (C.6), we obtain
 $$ \begin{align} \#\left\{B\mid \text{unit square of } {\mathbb Z}^2 \text{ with } B\cap S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\neq \emptyset\right\} \le \pi\left ( 2\sqrt 2+c\right )^{2}(r+1). \end{align} $$
$$ \begin{align} \#\left\{B\mid \text{unit square of } {\mathbb Z}^2 \text{ with } B\cap S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\neq \emptyset\right\} \le \pi\left ( 2\sqrt 2+c\right )^{2}(r+1). \end{align} $$On the other hand, we have
 $$ \begin{align} \#\left\{S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\right\} &=\sum_{z\in S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2}1 = \sum_{z\in S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2} \sum_{B: \text{unit square of }{\mathbb Z}^2} \frac 14 \mathbb I_{z\in B}\notag\\ &=\sum_{B: \text{unit square of }{\mathbb Z}^2} \sum_{z\in S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2}\frac 14 \mathbb I_{z\in B} \le \sum_{\substack{B: \\ \text{unit square of }{\mathbb Z}^2\\ B\cap S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\neq \emptyset}} 1\notag\\ &=\#\left\{B\mid \text{unit square of } {\mathbb Z}^2 \text{ with } B\cap S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\neq \emptyset\right\} \le \pi\left ( 2\sqrt 2+c\right )^{2}(r+1). \end{align} $$
$$ \begin{align} \#\left\{S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\right\} &=\sum_{z\in S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2}1 = \sum_{z\in S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2} \sum_{B: \text{unit square of }{\mathbb Z}^2} \frac 14 \mathbb I_{z\in B}\notag\\ &=\sum_{B: \text{unit square of }{\mathbb Z}^2} \sum_{z\in S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2}\frac 14 \mathbb I_{z\in B} \le \sum_{\substack{B: \\ \text{unit square of }{\mathbb Z}^2\\ B\cap S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\neq \emptyset}} 1\notag\\ &=\#\left\{B\mid \text{unit square of } {\mathbb Z}^2 \text{ with } B\cap S_{r,c}^{\left[\theta_1,\theta_2\right]}\cap {\mathbb Z}^2\neq \emptyset\right\} \le \pi\left ( 2\sqrt 2+c\right )^{2}(r+1). \end{align} $$ For an F-function ![]() $F\in {\mathcal F}_{a}$, define a function
$F\in {\mathcal F}_{a}$, define a function ![]() $G_{F}$ on
$G_{F}$ on ![]() $t\ge 0$ by
$t\ge 0$ by
 $$ \begin{align} G_{F}(t):= \sup_{x\in{{\mathbb Z}^2}}\left ( \sum_{y\in{{\mathbb Z}^2}, {\mathrm{d}}\left(x,y\right)\ge t} F\left ( {\mathrm{d}}(x,y)\right ) \right ),\quad t\ge 0. \end{align} $$
$$ \begin{align} G_{F}(t):= \sup_{x\in{{\mathbb Z}^2}}\left ( \sum_{y\in{{\mathbb Z}^2}, {\mathrm{d}}\left(x,y\right)\ge t} F\left ( {\mathrm{d}}(x,y)\right ) \right ),\quad t\ge 0. \end{align} $$Note that by uniform integrability, the supremum is finite for all t. In particular, for any ![]() $0<\theta <1$ we have
$0<\theta <1$ we have
 $$ \begin{align} \begin{split} G_F(t) &\le \sum_{r=[t]}^\infty\sum_{\substack{y\in {\mathbb Z}^2 :\\ r\le \mathrm{d}\left(0,y\right)<r+1 }} F\left ( \mathrm{d}(0,y)\right ) \le \sum_{r=[t]}^\infty\sum_{y\in S_{r,1}^{\left[0,2\pi\right]}\cap{\mathbb Z}^2} F(r) \le \sum_{r=[t]}^\infty \# \left ( S_{r,1}^{\left[0,2\pi\right]}\cap{\mathbb Z}^2\right ) F(r)\\[4pt] &\le 64 \sum_{r=[t]}^\infty (r+1) F(r) = 64 \sum_{r=[t]}^\infty (r+1) F(r)^{\theta} F(r)^{1-\theta} \le 64 \left ( \sum_{r=0}^\infty (r+1) F(r)^{\theta}\right ) F([t])^{1-\theta}\\[4pt] &\le 64 \cdot \kappa_{\theta, 1, F}\cdot F([t])^{1-\theta} <\infty. \end{split} \end{align} $$
$$ \begin{align} \begin{split} G_F(t) &\le \sum_{r=[t]}^\infty\sum_{\substack{y\in {\mathbb Z}^2 :\\ r\le \mathrm{d}\left(0,y\right)<r+1 }} F\left ( \mathrm{d}(0,y)\right ) \le \sum_{r=[t]}^\infty\sum_{y\in S_{r,1}^{\left[0,2\pi\right]}\cap{\mathbb Z}^2} F(r) \le \sum_{r=[t]}^\infty \# \left ( S_{r,1}^{\left[0,2\pi\right]}\cap{\mathbb Z}^2\right ) F(r)\\[4pt] &\le 64 \sum_{r=[t]}^\infty (r+1) F(r) = 64 \sum_{r=[t]}^\infty (r+1) F(r)^{\theta} F(r)^{1-\theta} \le 64 \left ( \sum_{r=0}^\infty (r+1) F(r)^{\theta}\right ) F([t])^{1-\theta}\\[4pt] &\le 64 \cdot \kappa_{\theta, 1, F}\cdot F([t])^{1-\theta} <\infty. \end{split} \end{align} $$Substituting this, for any ![]() $0<\alpha \le 1$,
$0<\alpha \le 1$, ![]() $0<\theta ,\varphi <1$, and
$0<\theta ,\varphi <1$, and ![]() $k\in {\mathbb N}\cup \{0\}$, we have
$k\in {\mathbb N}\cup \{0\}$, we have
 $$ \begin{align} \begin{split} \sum_{n=0}^{\infty} (1+n)^{k} \left ( G_{F}(n)\right )^{\alpha} &\le\left ( 64 \cdot \kappa_{\theta, 1, F}\right )^{\alpha} \sum_{n=0}^{\infty}(1+n)^{k} \cdot F(n)^{\alpha\left ( 1-\theta\right )} =\left ( 64 \cdot \kappa_{\theta, 1, F}\right )^{\alpha} \kappa_{\alpha\left ( 1-\theta\right ), k, F}<\infty,\\[4pt] \sum_{n=\left[\frac r3\right]}^{\infty} (1+n)^{k} \left ( G_{F}(n)\right )^{\alpha} &\le\left ( 64 \cdot \kappa_{\theta, 1, F}\right )^{\alpha} \sum_{n=\left[\frac r 3\right]}^{\infty}(1+n)^{k} \cdot \left ( F(n)^{\alpha\left ( 1-\theta\right )}\right )^{\left(1-\varphi\right)} \left ( F(n)^{\alpha\left ( 1-\theta\right )}\right )^{\varphi}\\[4pt] & \le\left ( 64 \cdot \kappa_{\theta, 1, F}\right )^{\alpha} \kappa_{\alpha\left ( 1-\theta\right )\left (1-\varphi\right ), k, F} F\left ( \left [\frac r3\right ]\right )^{\alpha\left ( 1-\theta\right )\varphi}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \sum_{n=0}^{\infty} (1+n)^{k} \left ( G_{F}(n)\right )^{\alpha} &\le\left ( 64 \cdot \kappa_{\theta, 1, F}\right )^{\alpha} \sum_{n=0}^{\infty}(1+n)^{k} \cdot F(n)^{\alpha\left ( 1-\theta\right )} =\left ( 64 \cdot \kappa_{\theta, 1, F}\right )^{\alpha} \kappa_{\alpha\left ( 1-\theta\right ), k, F}<\infty,\\[4pt] \sum_{n=\left[\frac r3\right]}^{\infty} (1+n)^{k} \left ( G_{F}(n)\right )^{\alpha} &\le\left ( 64 \cdot \kappa_{\theta, 1, F}\right )^{\alpha} \sum_{n=\left[\frac r 3\right]}^{\infty}(1+n)^{k} \cdot \left ( F(n)^{\alpha\left ( 1-\theta\right )}\right )^{\left(1-\varphi\right)} \left ( F(n)^{\alpha\left ( 1-\theta\right )}\right )^{\varphi}\\[4pt] & \le\left ( 64 \cdot \kappa_{\theta, 1, F}\right )^{\alpha} \kappa_{\alpha\left ( 1-\theta\right )\left (1-\varphi\right ), k, F} F\left ( \left [\frac r3\right ]\right )^{\alpha\left ( 1-\theta\right )\varphi}. \end{split} \end{align} $$For any ![]() $0<c\le 1$, we have
$0<c\le 1$, we have
 $$ \begin{align} \begin{split} \sum_{r=0}^{\infty} F(cr) (r+2)^{3} &=\sum_{l=0}^{\infty} \sum_{\substack{r\in{\mathbb Z}_{\ge 0}\\[4pt] l\le cr< l+1}}F(cr) (r+2)^{3} \le \sum_{l=0}^{\infty} \sum_{\substack{r\in{\mathbb Z}_{\ge 0}\\\frac{l}c\le r<\frac{l+1}c}}F(l) \left ( \frac{l+1}c+2\right )^{3}\\ &\le \sum_{l=0}^{\infty} F(l) \left ( \frac{l+1}c+2\right )^{3}\left ( \frac{l+1}c-\left(\frac lc-1\right)+1\right ) \le \sum_{l=0}^{\infty} F(l) \left ( \frac{l+1}c+2\right )^{4}\\[4pt] &\le \frac 1{c^{4}}\sum_{l=0}^{\infty} F(l) \left ( l+3\right )^{4}\le \frac {3^{4}\kappa_{1, 4, F}}{c^{4}} <\infty. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \sum_{r=0}^{\infty} F(cr) (r+2)^{3} &=\sum_{l=0}^{\infty} \sum_{\substack{r\in{\mathbb Z}_{\ge 0}\\[4pt] l\le cr< l+1}}F(cr) (r+2)^{3} \le \sum_{l=0}^{\infty} \sum_{\substack{r\in{\mathbb Z}_{\ge 0}\\\frac{l}c\le r<\frac{l+1}c}}F(l) \left ( \frac{l+1}c+2\right )^{3}\\ &\le \sum_{l=0}^{\infty} F(l) \left ( \frac{l+1}c+2\right )^{3}\left ( \frac{l+1}c-\left(\frac lc-1\right)+1\right ) \le \sum_{l=0}^{\infty} F(l) \left ( \frac{l+1}c+2\right )^{4}\\[4pt] &\le \frac 1{c^{4}}\sum_{l=0}^{\infty} F(l) \left ( l+3\right )^{4}\le \frac {3^{4}\kappa_{1, 4, F}}{c^{4}} <\infty. \end{split} \end{align} $$We also have, for ![]() $m\in {\mathbb Z}_{\ge 0}$ and
$m\in {\mathbb Z}_{\ge 0}$ and ![]() $0<c\le 1$,
$0<c\le 1$,
 $$\begin{align*}\sum_{r_1=0}^\infty\sum_{\substack{r\in{{\mathbb Z}_{\ge 0}}: \\\sqrt{r^2+r_1^2}c\ge (m+1)} } &(r_1+1) F\left ( \sqrt{r^2+r_1^2}c-(m+1) \right )\\ & \le \sum_{l=0}^{\infty} \sum_{\substack{r_{1}, r\in{\mathbb Z}_{\ge 0}\\ l\le \sqrt{r^2+r_1^2}c- (m+1)< l+1 }} (r_1+1) F\left ( \sqrt{r^2+r_1^2}c-(m+1) \right )\end{align*}$$
$$\begin{align*}\sum_{r_1=0}^\infty\sum_{\substack{r\in{{\mathbb Z}_{\ge 0}}: \\\sqrt{r^2+r_1^2}c\ge (m+1)} } &(r_1+1) F\left ( \sqrt{r^2+r_1^2}c-(m+1) \right )\\ & \le \sum_{l=0}^{\infty} \sum_{\substack{r_{1}, r\in{\mathbb Z}_{\ge 0}\\ l\le \sqrt{r^2+r_1^2}c- (m+1)< l+1 }} (r_1+1) F\left ( \sqrt{r^2+r_1^2}c-(m+1) \right )\end{align*}$$ $$\begin{align} \begin{split} &\le\sum_{l=0}^{\infty} \sum_{\substack{r_{1}, r\in{\mathbb Z}_{\ge 0}\\ l\le \sqrt{r^2+r_1^2}c- (m+1)< l+1 }} \left ( \frac{l+m+2}{c}+1\right ) \cdot F(l)\\[9pt] &\le \sum_{l=0}^{\infty} \#\left\{ {\mathbb Z}^{2}\cap S_{\frac{l+m+1}{c}, \frac 1c}^{\left[0,2\pi\right]} \right\} \left ( \frac{l+m+2}{c}+1\right ) \cdot F(l)\\[9pt] &\le \sum_{l=0}^{\infty}\pi \left ( 2\sqrt 2+\frac 1c\right )^{2}\left ( \frac{l+m+1}{c}+1\right )\cdot \left ( \frac{l+m+2}{c}+1\right ) \cdot F(l)\\[9pt] &\le \sum_{l=0}^{\infty}\pi \left ( 2\sqrt 2+\frac 1c\right )^{2} \left ( \frac{l+m+3}{c}\right )^{2}\cdot F(l)\\[9pt] &\le \pi \left ( 2\sqrt 2+\frac 1c\right )^{2} \frac{(m+3)^{2}}{c^{2}} \sum_{l=0}^{\infty}\left ( l+1\right )^{2} F(l)\\[9pt] &\le\pi \left ( 2\sqrt 2+\frac 1c\right )^{2} \frac{(m+3)^{2}}{c^{2}} \kappa_{1,2,F} \le \left (\frac 3 c\right )^{2}\left ( 2\sqrt 2+\frac 1c\right )^{2}\pi {(m+1)^{2}} \kappa_{1,2,F}. \end{split} \end{align}$$
$$\begin{align} \begin{split} &\le\sum_{l=0}^{\infty} \sum_{\substack{r_{1}, r\in{\mathbb Z}_{\ge 0}\\ l\le \sqrt{r^2+r_1^2}c- (m+1)< l+1 }} \left ( \frac{l+m+2}{c}+1\right ) \cdot F(l)\\[9pt] &\le \sum_{l=0}^{\infty} \#\left\{ {\mathbb Z}^{2}\cap S_{\frac{l+m+1}{c}, \frac 1c}^{\left[0,2\pi\right]} \right\} \left ( \frac{l+m+2}{c}+1\right ) \cdot F(l)\\[9pt] &\le \sum_{l=0}^{\infty}\pi \left ( 2\sqrt 2+\frac 1c\right )^{2}\left ( \frac{l+m+1}{c}+1\right )\cdot \left ( \frac{l+m+2}{c}+1\right ) \cdot F(l)\\[9pt] &\le \sum_{l=0}^{\infty}\pi \left ( 2\sqrt 2+\frac 1c\right )^{2} \left ( \frac{l+m+3}{c}\right )^{2}\cdot F(l)\\[9pt] &\le \pi \left ( 2\sqrt 2+\frac 1c\right )^{2} \frac{(m+3)^{2}}{c^{2}} \sum_{l=0}^{\infty}\left ( l+1\right )^{2} F(l)\\[9pt] &\le\pi \left ( 2\sqrt 2+\frac 1c\right )^{2} \frac{(m+3)^{2}}{c^{2}} \kappa_{1,2,F} \le \left (\frac 3 c\right )^{2}\left ( 2\sqrt 2+\frac 1c\right )^{2}\pi {(m+1)^{2}} \kappa_{1,2,F}. \end{split} \end{align}$$Recall formulas (5.25) and (5.26).
Lemma C.4. Let ![]() $\varphi _1<\varphi _2<\varphi _3<\varphi _4$ with
$\varphi _1<\varphi _2<\varphi _3<\varphi _4$ with ![]() $\varphi _4-\varphi _1<2\pi $. Then we have
$\varphi _4-\varphi _1<2\pi $. Then we have
 $$ \begin{align} \sum_{\substack{x\in \check C_{\left[\varphi_1,\varphi_2\right]}\\y\in \check C_{\left[\varphi_3,\varphi_4\right]}}} F\left ( {\mathrm{d}}(x,y)\right )\le (64)^3 \frac {3^{4}\kappa_{1, 4, F}}{\left ( c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}\right ) ^{4}}. \end{align} $$
$$ \begin{align} \sum_{\substack{x\in \check C_{\left[\varphi_1,\varphi_2\right]}\\y\in \check C_{\left[\varphi_3,\varphi_4\right]}}} F\left ( {\mathrm{d}}(x,y)\right )\le (64)^3 \frac {3^{4}\kappa_{1, 4, F}}{\left ( c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}\right ) ^{4}}. \end{align} $$Proof. Let  $x=s_1e^{i\phi _1}\in \check C_{\left [\varphi _1,\varphi _2\right ]}$ and
$x=s_1e^{i\phi _1}\in \check C_{\left [\varphi _1,\varphi _2\right ]}$ and  $y=s_2e^{i\phi _2}\in \check C_{\left [\varphi _3,\varphi _4\right ]}$, with
$y=s_2e^{i\phi _2}\in \check C_{\left [\varphi _3,\varphi _4\right ]}$, with ![]() $s_1,s_2\ge 0$. If
$s_1,s_2\ge 0$. If ![]() $\cos \left ( \phi _2-\phi _1\right )\ge 0$, then we have
$\cos \left ( \phi _2-\phi _1\right )\ge 0$, then we have
 $$ \begin{align} \begin{split} {\mathrm{d}}(x,y)&=\sqrt{s_1^2+s_2^2-2s_1s_2\cos\left ( \phi_2-\phi_1\right )} \ge \sqrt{s_1^2+s_2^2} \sqrt{1-\cos\left ( \phi_2-\phi_1\right )} \\[5pt] &\ge \sqrt{1- \max\left\{ \cos\left ( \varphi_3-\varphi_2\right ), \cos\left ( \varphi_4-\varphi_1\right ),0 \right\}} \sqrt{s_1^2+s_2^2}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} {\mathrm{d}}(x,y)&=\sqrt{s_1^2+s_2^2-2s_1s_2\cos\left ( \phi_2-\phi_1\right )} \ge \sqrt{s_1^2+s_2^2} \sqrt{1-\cos\left ( \phi_2-\phi_1\right )} \\[5pt] &\ge \sqrt{1- \max\left\{ \cos\left ( \varphi_3-\varphi_2\right ), \cos\left ( \varphi_4-\varphi_1\right ),0 \right\}} \sqrt{s_1^2+s_2^2}. \end{split} \end{align} $$If ![]() $\cos \left ( \phi _2-\phi _1\right )<0$, then we have
$\cos \left ( \phi _2-\phi _1\right )<0$, then we have
 $$ \begin{align} \begin{split} &{\mathrm{d}}(x,y)=\sqrt{s_1^2+s_2^2-2s_1s_2\cos\left ( \phi_2-\phi_1\right )} \ge \sqrt{s_1^2+s_2^2}.\\ \end{split} \end{align} $$
$$ \begin{align} \begin{split} &{\mathrm{d}}(x,y)=\sqrt{s_1^2+s_2^2-2s_1s_2\cos\left ( \phi_2-\phi_1\right )} \ge \sqrt{s_1^2+s_2^2}.\\ \end{split} \end{align} $$Hence for any  $x=s_1e^{i\phi _1}\in \check C_{\left [\varphi _1,\varphi _2\right ]}$ and
$x=s_1e^{i\phi _1}\in \check C_{\left [\varphi _1,\varphi _2\right ]}$ and  $y=s_2e^{i\phi _2}\in \check C_{\left [\varphi _3,\varphi _4\right ]}$ with
$y=s_2e^{i\phi _2}\in \check C_{\left [\varphi _3,\varphi _4\right ]}$ with ![]() $s_1,s_2\ge 0$, we have
$s_1,s_2\ge 0$, we have
 $$ \begin{align} {\mathrm{d}}(x,y)\ge \sqrt{1- \max\left\{ \cos\left ( \varphi_3-\varphi_2\right ), \cos\left ( \varphi_4-\varphi_1\right ),0 \right\}} \sqrt{s_1^2+s_2^2} =c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}\sqrt{s_1^2+s_2^2}. \end{align} $$
$$ \begin{align} {\mathrm{d}}(x,y)\ge \sqrt{1- \max\left\{ \cos\left ( \varphi_3-\varphi_2\right ), \cos\left ( \varphi_4-\varphi_1\right ),0 \right\}} \sqrt{s_1^2+s_2^2} =c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}\sqrt{s_1^2+s_2^2}. \end{align} $$Substituting this estimate, we obtain
 $$ \begin{align} \begin{split} \sum_{\substack{x\in \check C_{\left[\varphi_1,\varphi_2\right]}\\y\in \check C_{\left[\varphi_3,\varphi_4\right]}}} F\left ( {\mathrm{d}}(x,y)\right ) &\le \sum_{r_1=0}^\infty\sum_{r_2=0}^\infty \sum_{\substack{x\in S_{r_1,1}^{\left[\varphi_1,\varphi_2\right]}\cap {\mathbb Z}^2\\ y\in S_{r_2,1}^{\left[\varphi_3,\varphi_4\right]}\cap {\mathbb Z}^2}} F\left ( {\mathrm{d}}(x,y)\right ) \\ &\le \sum_{r_1=0}^\infty\sum_{r_2=0}^\infty F\left ( {c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}} \sqrt{r_1^2+r_2^2} \right )\#\left ( S_{r_1,1}^{\left[\varphi_1,\varphi_2\right]}\cap {\mathbb Z}^2 \right ) \#\left ( S_{r_2,1}^{\left[\varphi_3,\varphi_4\right]}\cap {\mathbb Z}^2 \right ) \\ &\le (64)^2 \sum_{r_1=0}^\infty\sum_{r_2=0}^\infty F\left ( {c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}} \sqrt{r_1^2+r_2^2} \right )(r_1+1)(r_2+1)\\ &\le (64)^2 \sum_{r=0}^\infty \sum_{\substack{r_{1}, r_{2}\in{\mathbb Z}_{\ge 0}\\ \left(r_{1}, r_{2}\right)\in S_{r, 1}^{\left[0,\frac\pi 2\right]}\cap{\mathbb Z}^{2} } } F\left ( {c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}} \sqrt{r_1^2+r_2^2} \right )(r_1+1)(r_2+1)\\ & \le (64)^2 \sum_{r=0}^\infty F\left ( {c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}} r \right ) (r+2)^2\cdot \#\left ( S_{r}^{\left[0,\frac\pi 2\right]}\cap {\mathbb Z}^2 \right ) \\ &\le (64)^3 \sum_{r=0}^\infty F\left ( {c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}} r \right ) (r+2)^3 \\ &\le(64)^3 \frac {3^{4}\kappa_{1, 4, F}}{\left ( c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}\right ) ^{4}}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \sum_{\substack{x\in \check C_{\left[\varphi_1,\varphi_2\right]}\\y\in \check C_{\left[\varphi_3,\varphi_4\right]}}} F\left ( {\mathrm{d}}(x,y)\right ) &\le \sum_{r_1=0}^\infty\sum_{r_2=0}^\infty \sum_{\substack{x\in S_{r_1,1}^{\left[\varphi_1,\varphi_2\right]}\cap {\mathbb Z}^2\\ y\in S_{r_2,1}^{\left[\varphi_3,\varphi_4\right]}\cap {\mathbb Z}^2}} F\left ( {\mathrm{d}}(x,y)\right ) \\ &\le \sum_{r_1=0}^\infty\sum_{r_2=0}^\infty F\left ( {c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}} \sqrt{r_1^2+r_2^2} \right )\#\left ( S_{r_1,1}^{\left[\varphi_1,\varphi_2\right]}\cap {\mathbb Z}^2 \right ) \#\left ( S_{r_2,1}^{\left[\varphi_3,\varphi_4\right]}\cap {\mathbb Z}^2 \right ) \\ &\le (64)^2 \sum_{r_1=0}^\infty\sum_{r_2=0}^\infty F\left ( {c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}} \sqrt{r_1^2+r_2^2} \right )(r_1+1)(r_2+1)\\ &\le (64)^2 \sum_{r=0}^\infty \sum_{\substack{r_{1}, r_{2}\in{\mathbb Z}_{\ge 0}\\ \left(r_{1}, r_{2}\right)\in S_{r, 1}^{\left[0,\frac\pi 2\right]}\cap{\mathbb Z}^{2} } } F\left ( {c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}} \sqrt{r_1^2+r_2^2} \right )(r_1+1)(r_2+1)\\ & \le (64)^2 \sum_{r=0}^\infty F\left ( {c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}} r \right ) (r+2)^2\cdot \#\left ( S_{r}^{\left[0,\frac\pi 2\right]}\cap {\mathbb Z}^2 \right ) \\ &\le (64)^3 \sum_{r=0}^\infty F\left ( {c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}} r \right ) (r+2)^3 \\ &\le(64)^3 \frac {3^{4}\kappa_{1, 4, F}}{\left ( c^{(0)}_{\varphi_1,\varphi_2,\varphi_3,\varphi_4}\right ) ^{4}}. \end{split} \end{align} $$We used Lemma C.3 to bound  $\#\left ( S_{r,1}^{\left [0,\frac \pi 2\right ]}\cap {\mathbb Z}^2 \right )$ and so on, and in the last inequality we used equation (C.15).
$\#\left ( S_{r,1}^{\left [0,\frac \pi 2\right ]}\cap {\mathbb Z}^2 \right )$ and so on, and in the last inequality we used equation (C.15).
Set
 $$ \begin{align} L_\varphi:= \left\{ z\in{\mathbb R}^2\mid \arg z=\varphi \right\},\quad \varphi\in [0,2\pi), \end{align} $$
$$ \begin{align} L_\varphi:= \left\{ z\in{\mathbb R}^2\mid \arg z=\varphi \right\},\quad \varphi\in [0,2\pi), \end{align} $$and
 $$ \begin{align} c^{(1)}_{\zeta_1,\zeta_2,\zeta_3} :=\sqrt{1-\max\left\{\cos (\zeta_1-\zeta_2),\cos (\zeta_1-\zeta_3)\right\}},\quad \zeta_1,\zeta_2,\zeta_3\in [0,2\pi). \end{align} $$
$$ \begin{align} c^{(1)}_{\zeta_1,\zeta_2,\zeta_3} :=\sqrt{1-\max\left\{\cos (\zeta_1-\zeta_2),\cos (\zeta_1-\zeta_3)\right\}},\quad \zeta_1,\zeta_2,\zeta_3\in [0,2\pi). \end{align} $$Lemma C.5. Set ![]() $\varphi , \theta _1,\theta _2\in {\mathbb R}$ with
$\varphi , \theta _1,\theta _2\in {\mathbb R}$ with ![]() $\theta _1<\theta _2$ and
$\theta _1<\theta _2$ and ![]() $0<\left \lvert \varphi -\theta _0\right \rvert <\frac \pi 2$ for all
$0<\left \lvert \varphi -\theta _0\right \rvert <\frac \pi 2$ for all ![]() $\theta _0\in [\theta _1,\theta _2] $. Then we have
$\theta _0\in [\theta _1,\theta _2] $. Then we have
 $$ \begin{align} \sum_{x\in \check C_{\left[\theta_1,\theta_2\right]}}\sum_{y\in L_\varphi(m)} F\left ( {\mathrm{d}}(x,y)\right ) \le 64\cdot 144\cdot 24\cdot \left ( {c^{(1)}}_{\varphi,\theta_1,\theta_2}\right )^{-4} \left ( \pi \kappa_{1,2,F}+F(0) \right )(m+1)^{4}, \end{align} $$
$$ \begin{align} \sum_{x\in \check C_{\left[\theta_1,\theta_2\right]}}\sum_{y\in L_\varphi(m)} F\left ( {\mathrm{d}}(x,y)\right ) \le 64\cdot 144\cdot 24\cdot \left ( {c^{(1)}}_{\varphi,\theta_1,\theta_2}\right )^{-4} \left ( \pi \kappa_{1,2,F}+F(0) \right )(m+1)^{4}, \end{align} $$for any ![]() $m\in {\mathbb N}\cup \{0\}$.
$m\in {\mathbb N}\cup \{0\}$.
Proof. For each ![]() $r\in {\mathbb Z}$, set
$r\in {\mathbb Z}$, set
 $$ \begin{align} T_{\varphi, r,m}:= \left\{ se^{i\theta}\in {\mathbb R}^{2}\mid r\le s\cos(\theta-\varphi)\le r+1,\ -m\le s\sin(\theta-\varphi)\le m \right\}. \end{align} $$
$$ \begin{align} T_{\varphi, r,m}:= \left\{ se^{i\theta}\in {\mathbb R}^{2}\mid r\le s\cos(\theta-\varphi)\le r+1,\ -m\le s\sin(\theta-\varphi)\le m \right\}. \end{align} $$Note that ![]() $s\cos (\theta -\varphi )$ is a projection of
$s\cos (\theta -\varphi )$ is a projection of ![]() $se^{i\theta }$ onto
$se^{i\theta }$ onto ![]() $L_\varphi $ and
$L_\varphi $ and ![]() $\left \lvert s\sin (\theta -\varphi )\right \rvert $ is the distance of
$\left \lvert s\sin (\theta -\varphi )\right \rvert $ is the distance of ![]() $se^{i\theta }$ from the line including
$se^{i\theta }$ from the line including ![]() $L_\varphi $. Then we have
$L_\varphi $. Then we have
 $$ \begin{align} L_\varphi(m)\subset \cup_{r=-m}^\infty T_{\varphi, r,m}\cap{\mathbb Z}^2\quad\text{and}\quad \left \lvert \hat T_{\varphi, r,m}(\sqrt{2}) \right \rvert\le \left(2\sqrt 2+1\right)\left(2m+2\sqrt 2\right)\le 12(m+1). \end{align} $$
$$ \begin{align} L_\varphi(m)\subset \cup_{r=-m}^\infty T_{\varphi, r,m}\cap{\mathbb Z}^2\quad\text{and}\quad \left \lvert \hat T_{\varphi, r,m}(\sqrt{2}) \right \rvert\le \left(2\sqrt 2+1\right)\left(2m+2\sqrt 2\right)\le 12(m+1). \end{align} $$Because the diameter of a ![]() $2$-dimensional unit square is
$2$-dimensional unit square is ![]() $\sqrt 2$, any unit square B of
$\sqrt 2$, any unit square B of ![]() ${\mathbb Z}^2$ with
${\mathbb Z}^2$ with ![]() $B\cap T_{\varphi , r,m} \cap {\mathbb Z}^2\neq \emptyset $ satisfies
$B\cap T_{\varphi , r,m} \cap {\mathbb Z}^2\neq \emptyset $ satisfies  $B\subset \hat T_{\varphi , r,m}\left (\sqrt 2\right )$. Therefore, using formula (C.26) we have
$B\subset \hat T_{\varphi , r,m}\left (\sqrt 2\right )$. Therefore, using formula (C.26) we have
 $$ \begin{align} \begin{split} \#\left\{B\mid \text{unit square of } {\mathbb Z}^2 \text{ with } B\cap T_{\varphi, r,m} \cap {\mathbb Z}^2\neq \emptyset\right\} &=\sum_{B: B\cap T_{\varphi, r,m} \cap {\mathbb Z}^2\neq \emptyset} 1\\ &\le \left \lvert \hat T_{\varphi, r,m}(\sqrt{2}) \right \rvert\le 12(m+1). \end{split} \end{align} $$
$$ \begin{align} \begin{split} \#\left\{B\mid \text{unit square of } {\mathbb Z}^2 \text{ with } B\cap T_{\varphi, r,m} \cap {\mathbb Z}^2\neq \emptyset\right\} &=\sum_{B: B\cap T_{\varphi, r,m} \cap {\mathbb Z}^2\neq \emptyset} 1\\ &\le \left \lvert \hat T_{\varphi, r,m}(\sqrt{2}) \right \rvert\le 12(m+1). \end{split} \end{align} $$On the other hand, we have
 $$ \begin{align} \#\left\{T_{\varphi,r,m}\cap {\mathbb Z}^2\right\} &=\sum_{z\in T_{\varphi,r,m}\cap {\mathbb Z}^2}1 = \sum_{z\in T_{\varphi,r,m}\cap {\mathbb Z}^2} \sum_{B: \text{unit square of }{\mathbb Z}^2} \frac 14 \mathbb I_{z\in B}\notag\\ &=\sum_{B: \text{unit square of }{\mathbb Z}^2} \sum_{z\in T_{\varphi,r,m}\cap {\mathbb Z}^2}\frac 14 \mathbb I_{z\in B} \le \sum_{\substack{B: \\ \text{unit square of }{\mathbb Z}^2\\ B\cap T_{\varphi,r,m}\cap {\mathbb Z}^2\neq \emptyset}} 1\notag\\ &=\#\left\{B\mid \text{unit square of } {\mathbb Z}^2 \text{ with } B\cap T_{\varphi,r,m}\cap {\mathbb Z}^2\neq \emptyset\right\} \le 12(m+1). \end{align} $$
$$ \begin{align} \#\left\{T_{\varphi,r,m}\cap {\mathbb Z}^2\right\} &=\sum_{z\in T_{\varphi,r,m}\cap {\mathbb Z}^2}1 = \sum_{z\in T_{\varphi,r,m}\cap {\mathbb Z}^2} \sum_{B: \text{unit square of }{\mathbb Z}^2} \frac 14 \mathbb I_{z\in B}\notag\\ &=\sum_{B: \text{unit square of }{\mathbb Z}^2} \sum_{z\in T_{\varphi,r,m}\cap {\mathbb Z}^2}\frac 14 \mathbb I_{z\in B} \le \sum_{\substack{B: \\ \text{unit square of }{\mathbb Z}^2\\ B\cap T_{\varphi,r,m}\cap {\mathbb Z}^2\neq \emptyset}} 1\notag\\ &=\#\left\{B\mid \text{unit square of } {\mathbb Z}^2 \text{ with } B\cap T_{\varphi,r,m}\cap {\mathbb Z}^2\neq \emptyset\right\} \le 12(m+1). \end{align} $$If  $x\in \check C_{\left [\theta _1,\theta _2\right ]}$, we have
$x\in \check C_{\left [\theta _1,\theta _2\right ]}$, we have ![]() $x=r_0 e^{i\theta _0}$ for some
$x=r_0 e^{i\theta _0}$ for some ![]() $r_0\ge 0$ and
$r_0\ge 0$ and ![]() $\theta _0\in [\theta _1,\theta _2]$. By the assumption, we have
$\theta _0\in [\theta _1,\theta _2]$. By the assumption, we have ![]() $0<|\theta _0-\varphi |<\frac \pi 2$, hence
$0<|\theta _0-\varphi |<\frac \pi 2$, hence ![]() $0<\cos (\varphi -\theta _0)<1$. Therefore, for any
$0<\cos (\varphi -\theta _0)<1$. Therefore, for any ![]() $r\in {\mathbb R}$, we have
$r\in {\mathbb R}$, we have
 $$ \begin{align} \begin{split} \mathrm{d}\left(x, r e^{i\varphi}\right) &=\sqrt{r^2+r_0^2-2r_0r\cos (\theta_0-\varphi)} \ge \sqrt{r^2+r_0^2}\sqrt{1-\cos (\theta_0-\varphi)}\\ &\ge \sqrt{r^2+r_0^2}\sqrt{1-\max\left\{\cos (\theta_1-\varphi),\cos (\theta_2-\varphi)\right\}}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathrm{d}\left(x, r e^{i\varphi}\right) &=\sqrt{r^2+r_0^2-2r_0r\cos (\theta_0-\varphi)} \ge \sqrt{r^2+r_0^2}\sqrt{1-\cos (\theta_0-\varphi)}\\ &\ge \sqrt{r^2+r_0^2}\sqrt{1-\max\left\{\cos (\theta_1-\varphi),\cos (\theta_2-\varphi)\right\}}. \end{split} \end{align} $$Therefore, for any  $x\in \check C_{\left [\theta _1,\theta _2\right ]}$ and
$x\in \check C_{\left [\theta _1,\theta _2\right ]}$ and ![]() $y\in T_{\varphi , r,m}$, we have
$y\in T_{\varphi , r,m}$, we have
 $$ \begin{align} \begin{split} {\mathrm{d}}(x,y) \ge \mathrm{d} \left(x, r e^{i\varphi}\right)-(m+1) =\sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1). \end{split} \end{align} $$
$$ \begin{align} \begin{split} {\mathrm{d}}(x,y) \ge \mathrm{d} \left(x, r e^{i\varphi}\right)-(m+1) =\sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1). \end{split} \end{align} $$From this and formulas (C.26) and (C.28), for any ![]() $x=r_0 e^{i\theta _0}\in C_{\left [\theta _1,\theta _2\right ]}$,
$x=r_0 e^{i\theta _0}\in C_{\left [\theta _1,\theta _2\right ]}$, ![]() $r_0\ge 0$, we have
$r_0\ge 0$, we have
 $$ \begin{align} \sum_{y\in L_\varphi(m)} F\left ( {\mathrm{d}}(x,y)\right ) &\le \sum_{r=-m}^\infty \sum_{y\in\left ( T_{\varphi, r,m}\cap{\mathbb Z}^2\right )} F\left ( {\mathrm{d}}(x,y)\right ) \le \sum_{r=-\infty}^\infty \sum_{y\in\left ( T_{\varphi, r,m}\cap{\mathbb Z}^2\right )} F\left ( {\mathrm{d}}(x,y)\right ) \notag \\ & \le \sum_{\substack{r\in{\mathbb Z}: \\ \sqrt{r^2+r_0^2} {c^{(1)}}_{\varphi,\theta_1,\theta_2}\ge (m+1)}} \sum_{y\in\left ( T_{\varphi, r,m}\cap{\mathbb Z}^2\right )} F\left ( \sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1) \right ) \notag \\ & \quad +\sum_{\substack{ r\in{\mathbb Z}: \\ \sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}<(m+1)}} \sum_{y\in\left ( T_{\varphi, r,m}\cap{\mathbb Z}^2\right )} F\left ( 0\right ) \notag \\ &\le \sum_{\substack{r\in{\mathbb Z}: \\\sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}\ge (m+1)}} 12(m+1) F\left ( \sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1) \right )\\ & \quad +\sum_{\substack{r\in{\mathbb Z}:\\ \sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}<(m+1)}} 12(m+1) F\left ( 0\right )\notag\\ &\le \sum_{\substack{r\in{{\mathbb Z}_{\ge 0}}: \\\sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}\ge (m+1)} } 24(m+1) F\left ( \sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1) \right )\notag\\ & \quad +36\frac{(m+1)^2}{{c^{(1)}}_{\varphi,\theta_1,\theta_2}}F(0)\mathbb I_{r_0\le \frac{m+1}{ {c^{(1)}}_{\varphi,\theta_1,\theta_2}}}. \notag\end{align} $$
$$ \begin{align} \sum_{y\in L_\varphi(m)} F\left ( {\mathrm{d}}(x,y)\right ) &\le \sum_{r=-m}^\infty \sum_{y\in\left ( T_{\varphi, r,m}\cap{\mathbb Z}^2\right )} F\left ( {\mathrm{d}}(x,y)\right ) \le \sum_{r=-\infty}^\infty \sum_{y\in\left ( T_{\varphi, r,m}\cap{\mathbb Z}^2\right )} F\left ( {\mathrm{d}}(x,y)\right ) \notag \\ & \le \sum_{\substack{r\in{\mathbb Z}: \\ \sqrt{r^2+r_0^2} {c^{(1)}}_{\varphi,\theta_1,\theta_2}\ge (m+1)}} \sum_{y\in\left ( T_{\varphi, r,m}\cap{\mathbb Z}^2\right )} F\left ( \sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1) \right ) \notag \\ & \quad +\sum_{\substack{ r\in{\mathbb Z}: \\ \sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}<(m+1)}} \sum_{y\in\left ( T_{\varphi, r,m}\cap{\mathbb Z}^2\right )} F\left ( 0\right ) \notag \\ &\le \sum_{\substack{r\in{\mathbb Z}: \\\sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}\ge (m+1)}} 12(m+1) F\left ( \sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1) \right )\\ & \quad +\sum_{\substack{r\in{\mathbb Z}:\\ \sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}<(m+1)}} 12(m+1) F\left ( 0\right )\notag\\ &\le \sum_{\substack{r\in{{\mathbb Z}_{\ge 0}}: \\\sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}\ge (m+1)} } 24(m+1) F\left ( \sqrt{r^2+r_0^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1) \right )\notag\\ & \quad +36\frac{(m+1)^2}{{c^{(1)}}_{\varphi,\theta_1,\theta_2}}F(0)\mathbb I_{r_0\le \frac{m+1}{ {c^{(1)}}_{\varphi,\theta_1,\theta_2}}}. \notag\end{align} $$We then get
 $$ \begin{align} &\sum_{x\in \check C_{\left[\theta_1,\theta_2\right]}}\sum_{y\in L_\varphi(m)} F\left ( {\mathrm{d}}(x,y)\right ) \nonumber \\&\quad \le \sum_{r_1=0}^\infty \sum_{x\in S_{r_1,1}^{\left[\theta_1,\theta_2\right]}\cap{\mathbb Z}^2} \left (\begin{array}{c} \displaystyle\sum\limits_{\substack{r\in{{\mathbb Z}_{\ge 0}}: \\\sqrt{r^2+r_1^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}\ge (m+1)} } 24(m+1) F\left ( \sqrt{r^2+r_1^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1) \right )\\\\[-6pt]+ 36\frac{(m+1)^2}{{c^{(1)}}_{\varphi,\theta_1,\theta_2}}F(0)\mathbb I_{r_1\le \frac{m+1}{ {c^{(1)}}_{\varphi,\theta_1,\theta_2} }} \end{array}\right) \nonumber\\&\quad \le \sum_{r_1=0}^\infty 64(r_1+1) \left ( \begin{array}{c} \displaystyle\sum\limits_{\substack{r\in{{\mathbb Z}_{\ge 0}}: \\\sqrt{r^2+r_1^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}\ge (m+1)} } 24(m+1) F\left ( \sqrt{r^2+r_1^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1) \right )\\\\[-6pt]+36\frac{(m+1)^2}{{c^{(1)}}_{\varphi,\theta_1,\theta_2}}F(0)\mathbb I_{r_1\le \frac{m+1}{ {c^{(1)}}_{\varphi,\theta_1,\theta_2}}} \end{array}\right)\nonumber\\&\quad \le 64\cdot 24\cdot \left (\frac 3 {c^{(1)}}_{\varphi,\theta_1,\theta_2}\right )^{2}\left ( 2\sqrt 2+\frac 1{c^{(1)}}_{\varphi,\theta_1,\theta_2}\right )^{2}\pi {(m+1)^{3}} \kappa_{1,2,F} \nonumber\\&\qquad +64\cdot 36\cdot \frac{(m+1)^2}{{c^{(1)}}_{\varphi,\theta_1,\theta_2}}F(0) \left (\frac{m+1}{{c^{(1)}}_{\varphi,\theta_1,\theta_2}}+1\right )^{2}\nonumber\\&\quad \le 64\cdot 144\cdot 24\cdot \left ( {c^{(1)}}_{\varphi,\theta_1,\theta_2}\right )^{-4} \left ( \pi \kappa_{1,2,F}+F(0) \right )(m+1)^{4}. \end{align} $$
$$ \begin{align} &\sum_{x\in \check C_{\left[\theta_1,\theta_2\right]}}\sum_{y\in L_\varphi(m)} F\left ( {\mathrm{d}}(x,y)\right ) \nonumber \\&\quad \le \sum_{r_1=0}^\infty \sum_{x\in S_{r_1,1}^{\left[\theta_1,\theta_2\right]}\cap{\mathbb Z}^2} \left (\begin{array}{c} \displaystyle\sum\limits_{\substack{r\in{{\mathbb Z}_{\ge 0}}: \\\sqrt{r^2+r_1^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}\ge (m+1)} } 24(m+1) F\left ( \sqrt{r^2+r_1^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1) \right )\\\\[-6pt]+ 36\frac{(m+1)^2}{{c^{(1)}}_{\varphi,\theta_1,\theta_2}}F(0)\mathbb I_{r_1\le \frac{m+1}{ {c^{(1)}}_{\varphi,\theta_1,\theta_2} }} \end{array}\right) \nonumber\\&\quad \le \sum_{r_1=0}^\infty 64(r_1+1) \left ( \begin{array}{c} \displaystyle\sum\limits_{\substack{r\in{{\mathbb Z}_{\ge 0}}: \\\sqrt{r^2+r_1^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}\ge (m+1)} } 24(m+1) F\left ( \sqrt{r^2+r_1^2}{c^{(1)}}_{\varphi,\theta_1,\theta_2}-(m+1) \right )\\\\[-6pt]+36\frac{(m+1)^2}{{c^{(1)}}_{\varphi,\theta_1,\theta_2}}F(0)\mathbb I_{r_1\le \frac{m+1}{ {c^{(1)}}_{\varphi,\theta_1,\theta_2}}} \end{array}\right)\nonumber\\&\quad \le 64\cdot 24\cdot \left (\frac 3 {c^{(1)}}_{\varphi,\theta_1,\theta_2}\right )^{2}\left ( 2\sqrt 2+\frac 1{c^{(1)}}_{\varphi,\theta_1,\theta_2}\right )^{2}\pi {(m+1)^{3}} \kappa_{1,2,F} \nonumber\\&\qquad +64\cdot 36\cdot \frac{(m+1)^2}{{c^{(1)}}_{\varphi,\theta_1,\theta_2}}F(0) \left (\frac{m+1}{{c^{(1)}}_{\varphi,\theta_1,\theta_2}}+1\right )^{2}\nonumber\\&\quad \le 64\cdot 144\cdot 24\cdot \left ( {c^{(1)}}_{\varphi,\theta_1,\theta_2}\right )^{-4} \left ( \pi \kappa_{1,2,F}+F(0) \right )(m+1)^{4}. \end{align} $$We used formula (C.16).
D Quasilocal automorphisms
In this appendix we collect some results from [Reference Nachtergaele, Sims and YoungNSY] and prove Theorem 5.1.
Definition D.1. A norm-continuous interaction on ![]() ${\mathcal A}$ defined on an interval
${\mathcal A}$ defined on an interval ![]() $[0,1]$ is a map
$[0,1]$ is a map ![]() $\Phi :{\mathfrak S}_{{\mathbb Z}^2}\times [0,1]\to {\mathcal A}_{\textrm {loc}}$ such that
$\Phi :{\mathfrak S}_{{\mathbb Z}^2}\times [0,1]\to {\mathcal A}_{\textrm {loc}}$ such that
(i) for any
 $t\in [0,1]$,
$t\in [0,1]$,  $\Phi (\cdot , t):{\mathfrak S}_{{\mathbb Z}^2}\to {\mathcal A}_{\textrm {loc}}$ is an interaction and
$\Phi (\cdot , t):{\mathfrak S}_{{\mathbb Z}^2}\to {\mathcal A}_{\textrm {loc}}$ is an interaction and(ii) for any
 $Z\in {\mathfrak S}_{{\mathbb Z}^2}$, the map
$Z\in {\mathfrak S}_{{\mathbb Z}^2}$, the map  $\Phi (Z,\cdot ):[0,1]\to {\mathcal A}_{Z}$ is norm-continuous.
$\Phi (Z,\cdot ):[0,1]\to {\mathcal A}_{Z}$ is norm-continuous.
To ensure that the interactions induce quasilocal automorphisms we need to impose sufficient decay properties on the interaction strength.
Definition D.2. Let F be an F-function on ![]() $\left ({{\mathbb Z}^2},\mathrm {d}\right )$. We denote by
$\left ({{\mathbb Z}^2},\mathrm {d}\right )$. We denote by ![]() ${\mathcal B}_{F}([0,1])$ the set of all norm-continuous interactions
${\mathcal B}_{F}([0,1])$ the set of all norm-continuous interactions ![]() $\Phi $ on
$\Phi $ on ![]() ${\mathcal A}$ defined on an interval
${\mathcal A}$ defined on an interval ![]() $[0,1]$ such that the function
$[0,1]$ such that the function ![]() $\left \lVert \Phi \right \rVert _{F}: [0,1]\to {\mathbb R}$ defined by
$\left \lVert \Phi \right \rVert _{F}: [0,1]\to {\mathbb R}$ defined by
 $$ \begin{align} \left \lVert \Phi \right \rVert_F(t):= \sup_{x,y\in{{\mathbb Z}^2}}\frac{1}{F\left ( {\mathrm{d}}(x,y)\right )}\sum_{Z\in{\mathfrak S}_{{\mathbb Z}^2},\, Z\ni x,y} \left \lVert\Phi(Z;t)\right \rVert,\quad t\in[0,1], \end{align} $$
$$ \begin{align} \left \lVert \Phi \right \rVert_F(t):= \sup_{x,y\in{{\mathbb Z}^2}}\frac{1}{F\left ( {\mathrm{d}}(x,y)\right )}\sum_{Z\in{\mathfrak S}_{{\mathbb Z}^2},\, Z\ni x,y} \left \lVert\Phi(Z;t)\right \rVert,\quad t\in[0,1], \end{align} $$is uniformly bounded – that is, ![]() $\sup _{t\in \left [0,1\right ]}\left \lVert \Phi \right \rVert (t)<\infty $. It follows that
$\sup _{t\in \left [0,1\right ]}\left \lVert \Phi \right \rVert (t)<\infty $. It follows that ![]() $t \mapsto \left \lVert \Phi \right \rVert _F(t)$ is integrable, and we set
$t \mapsto \left \lVert \Phi \right \rVert _F(t)$ is integrable, and we set
 $$ \begin{align} I_F(\Phi):=I_{1,0}(\Phi):= C_{F} \int_{0}^{1} dt\left \lVert \Phi \right \rVert_F(t), \end{align} $$
$$ \begin{align} I_F(\Phi):=I_{1,0}(\Phi):= C_{F} \int_{0}^{1} dt\left \lVert \Phi \right \rVert_F(t), \end{align} $$with ![]() $C_F$ given in Definition C.1. We also set
$C_F$ given in Definition C.1. We also set
 $$ \begin{align} \left \lVert\left \lvert \Phi\right \rVert\right \rvert_F:= \sup_{x,y\in{{\mathbb Z}^2}}\frac{1}{F\left ( {\mathrm{d}}(x,y)\right )}\sum_{Z\in{\mathfrak S}_{{\mathbb Z}^2},\, Z\ni x,y} \sup_{t\in \left[0,1\right]}\left ( \left \lVert\Phi(Z;t)\right \rVert\right ) \end{align} $$
$$ \begin{align} \left \lVert\left \lvert \Phi\right \rVert\right \rvert_F:= \sup_{x,y\in{{\mathbb Z}^2}}\frac{1}{F\left ( {\mathrm{d}}(x,y)\right )}\sum_{Z\in{\mathfrak S}_{{\mathbb Z}^2},\, Z\ni x,y} \sup_{t\in \left[0,1\right]}\left ( \left \lVert\Phi(Z;t)\right \rVert\right ) \end{align} $$and denote by ![]() $\hat {\mathcal B}_{F}([0,1])$ the set of all
$\hat {\mathcal B}_{F}([0,1])$ the set of all ![]() $\Phi \in {\mathcal B}_{F}([0,1])$ with
$\Phi \in {\mathcal B}_{F}([0,1])$ with ![]() $\left \lVert \left \lvert \Phi \right \rVert \right \rvert _F<\infty $.
$\left \lVert \left \lvert \Phi \right \rVert \right \rvert _F<\infty $.
We will need some more notation. For ![]() $\Phi \in {\mathcal B}_{F}([0,1])$ and
$\Phi \in {\mathcal B}_{F}([0,1])$ and ![]() $0\le m\in {\mathbb R}$, we introduce a path of interactions
$0\le m\in {\mathbb R}$, we introduce a path of interactions ![]() $\Phi _{m}$ by
$\Phi _{m}$ by
 $$ \begin{align} \Phi_{m}\left ( X;t\right ):=\left \lvert X\right \rvert^{m}\Phi\left ( X;t\right ),\quad X\in{\mathfrak S}\left({\mathbb Z}^2\right),\ t\in[0,1]. \end{align} $$
$$ \begin{align} \Phi_{m}\left ( X;t\right ):=\left \lvert X\right \rvert^{m}\Phi\left ( X;t\right ),\quad X\in{\mathfrak S}\left({\mathbb Z}^2\right),\ t\in[0,1]. \end{align} $$An interaction gives rise to local (and here, time-dependent) Hamiltonians via
 $$ \begin{align} H_{\Lambda,\Phi}(t):=\sum_{Z\in\Lambda}\Phi(Z,t),\quad t\in[0,1],\ \Lambda\in{\mathfrak S}_{{\mathbb Z}^2}. \end{align} $$
$$ \begin{align} H_{\Lambda,\Phi}(t):=\sum_{Z\in\Lambda}\Phi(Z,t),\quad t\in[0,1],\ \Lambda\in{\mathfrak S}_{{\mathbb Z}^2}. \end{align} $$We denote by ![]() $U_{\Lambda ,\Phi }(t;s)$, the solution of
$U_{\Lambda ,\Phi }(t;s)$, the solution of
 $$ \begin{align} \frac{d}{dt} U_{\Lambda,\Phi}(t;s)&=-iH_{\Lambda,\Phi}(t) U_{\Lambda,\Phi}(t;s),\quad s, t\in[0,1], \end{align} $$
$$ \begin{align} \frac{d}{dt} U_{\Lambda,\Phi}(t;s)&=-iH_{\Lambda,\Phi}(t) U_{\Lambda,\Phi}(t;s),\quad s, t\in[0,1], \end{align} $$We define corresponding automorphisms  $\tau _{t,s}^{(\Lambda ),\Phi }, \hat {\tau }_{t,s}^{(\Lambda ), \Phi }$ on
$\tau _{t,s}^{(\Lambda ),\Phi }, \hat {\tau }_{t,s}^{(\Lambda ), \Phi }$ on ![]() ${\mathcal A}$ by
${\mathcal A}$ by
 $$ \begin{align} \tau_{t,s}^{(\Lambda), \Phi}(A)&:=U_{\Lambda,\Phi}(t;s)^{*}AU_{\Lambda,\Phi}(t;s), \end{align} $$
$$ \begin{align} \tau_{t,s}^{(\Lambda), \Phi}(A)&:=U_{\Lambda,\Phi}(t;s)^{*}AU_{\Lambda,\Phi}(t;s), \end{align} $$ $$ \begin{align} \hat{\tau}_{t,s}^{(\Lambda), \Phi}(A)&:=U_{\Lambda,\Phi}(t;s)AU_{\Lambda,\Phi}(t;s)^{*}, \end{align} $$
$$ \begin{align} \hat{\tau}_{t,s}^{(\Lambda), \Phi}(A)&:=U_{\Lambda,\Phi}(t;s)AU_{\Lambda,\Phi}(t;s)^{*}, \end{align} $$with ![]() $A \in {\mathcal A}$. Note that
$A \in {\mathcal A}$. Note that
 $$ \begin{align} \hat{\tau}_{t,s}^{(\Lambda), \Phi}={\tau}_{s,t}^{(\Lambda), \Phi}, \end{align} $$
$$ \begin{align} \hat{\tau}_{t,s}^{(\Lambda), \Phi}={\tau}_{s,t}^{(\Lambda), \Phi}, \end{align} $$by the uniqueness of the solution of the differential equation.
Theorem D.3 [Reference Nachtergaele, Sims and YoungNSY]
Let F be an F-function on ![]() $\left ({{\mathbb Z}^2}, \mathrm {d}\right )$. Suppose that
$\left ({{\mathbb Z}^2}, \mathrm {d}\right )$. Suppose that ![]() $\Phi \in {\mathcal B}_F([0,1])$. Then the following hold:
$\Phi \in {\mathcal B}_F([0,1])$. Then the following hold:
1. The limits
(D.11)exist and define strongly continuous families of automorphisms on $$ \begin{align} \tau_{t,s}^{\Phi}(A):=\lim_{\Lambda \nearrow{{\mathbb Z}^2}}\tau_{t,s}^{(\Lambda), \Phi}(A),\qquad \hat \tau_{t,s}^{\Phi}(A):=\lim_{\Lambda \nearrow{{\mathbb Z}^2}}\hat \tau_{t,s}^{(\Lambda), \Phi}(A),\quad A\in{\mathcal A}, \ t,s\in[0,1], \end{align} $$
$$ \begin{align} \tau_{t,s}^{\Phi}(A):=\lim_{\Lambda \nearrow{{\mathbb Z}^2}}\tau_{t,s}^{(\Lambda), \Phi}(A),\qquad \hat \tau_{t,s}^{\Phi}(A):=\lim_{\Lambda \nearrow{{\mathbb Z}^2}}\hat \tau_{t,s}^{(\Lambda), \Phi}(A),\quad A\in{\mathcal A}, \ t,s\in[0,1], \end{align} $$ ${\mathcal A}$ such that
${\mathcal A}$ such that  $\hat \tau _{t,s}^{\Phi }=\tau _{s,t}^{\Phi }={\tau _{t,s}^{\Phi }}^{-1}$ and (D.12)
$\hat \tau _{t,s}^{\Phi }=\tau _{s,t}^{\Phi }={\tau _{t,s}^{\Phi }}^{-1}$ and (D.12) $$ \begin{align} \hat \tau_{t,s}^{\Phi}\circ\hat \tau_{s,u}^{\Phi}=\hat \tau_{t,u}^{\Phi},\qquad \tau_{t,t}^{\Phi}=\mathop{\mathrm{id}}\nolimits_{{\mathcal A}}, \quad t,s,u\in[0,1]. \end{align} $$
$$ \begin{align} \hat \tau_{t,s}^{\Phi}\circ\hat \tau_{s,u}^{\Phi}=\hat \tau_{t,u}^{\Phi},\qquad \tau_{t,t}^{\Phi}=\mathop{\mathrm{id}}\nolimits_{{\mathcal A}}, \quad t,s,u\in[0,1]. \end{align} $$2. For any
 $X,Y\in {\mathfrak S}_{{\mathbb Z}^2}$ with
$X,Y\in {\mathfrak S}_{{\mathbb Z}^2}$ with  $X\cap Y=\emptyset $, the bound (D.13)holds for all
$X\cap Y=\emptyset $, the bound (D.13)holds for all $$ \begin{align} \left \lVert \left[ \tau_{t,s}^{\Phi}(A), B \right] \right \rVert \le \frac{2\left \lVert A\right \rVert\left \lVert B\right \rVert}{C_{F}}\left ( e^{2I_F(\Phi)}-1\right )\left \lvert X\right \rvert G_{F}\left ( d(X,Y)\right ) \end{align} $$
$$ \begin{align} \left \lVert \left[ \tau_{t,s}^{\Phi}(A), B \right] \right \rVert \le \frac{2\left \lVert A\right \rVert\left \lVert B\right \rVert}{C_{F}}\left ( e^{2I_F(\Phi)}-1\right )\left \lvert X\right \rvert G_{F}\left ( d(X,Y)\right ) \end{align} $$ $A\in {\mathcal A}_{X}$,
$A\in {\mathcal A}_{X}$,  $B\in {\mathcal A}_{Y}$, and
$B\in {\mathcal A}_{Y}$, and  $t,s\in [0,1]$.
$t,s\in [0,1]$.If
 $\Lambda \in {\mathfrak S}_{{\mathbb Z}^2}$ and
$\Lambda \in {\mathfrak S}_{{\mathbb Z}^2}$ and  $X \cup Y \subset \Lambda $, a similar bound holds for
$X \cup Y \subset \Lambda $, a similar bound holds for  $\tau _{t,s}^{(\Lambda ),\Phi }$.
$\tau _{t,s}^{(\Lambda ),\Phi }$.3. For any
 $X\in {\mathfrak S}_{{\mathbb Z}^2}$, we have (D.14)for
$X\in {\mathfrak S}_{{\mathbb Z}^2}$, we have (D.14)for $$ \begin{align} &\left \lVert \Delta_{X(m)}\left ( \tau_{t,s}^{\Phi}(A)\right ) \right \rVert \le \frac{8\left \lVert A\right \rVert}{C_{F}}\left ( e^{2I_F(\Phi)}-1\right )\left \lvert X\right \rvert G_{F}\left ( m\right ), \end{align} $$
$$ \begin{align} &\left \lVert \Delta_{X(m)}\left ( \tau_{t,s}^{\Phi}(A)\right ) \right \rVert \le \frac{8\left \lVert A\right \rVert}{C_{F}}\left ( e^{2I_F(\Phi)}-1\right )\left \lvert X\right \rvert G_{F}\left ( m\right ), \end{align} $$ $A\in {\mathcal A}_{X}$. Here we set
$A\in {\mathcal A}_{X}$. Here we set  $\Delta _{X(0)}:=\Pi _{X}$ and
$\Delta _{X(0)}:=\Pi _{X}$ and  $\Delta _{X(m)}:=\Pi _{X(m)}-\Pi _{X(m-1)}$ for
$\Delta _{X(m)}:=\Pi _{X(m)}-\Pi _{X(m-1)}$ for  $m\in {\mathbb N}$. A similar bound holds for
$m\in {\mathbb N}$. A similar bound holds for  $\tau _{t,s}^{(\Lambda ),\Phi }$. (See formula (C.12) for the definition of
$\tau _{t,s}^{(\Lambda ),\Phi }$. (See formula (C.12) for the definition of  $G_F$.)
$G_F$.)4. For any
 $X,\Lambda \in {\mathfrak S}\left ({\mathbb Z}^2\right )$, with
$X,\Lambda \in {\mathfrak S}\left ({\mathbb Z}^2\right )$, with  $X\subset \Lambda $, and
$X\subset \Lambda $, and  $A \in {\mathcal A}_X$, we have (D.15)
$A \in {\mathcal A}_X$, we have (D.15) $$ \begin{align} \left \lVert \tau_{t,s}^{(\Lambda), \Phi}(A)-\tau_{t,s}^{\Phi}(A) \right \rVert \le\frac{2}{C_{F}} \left \lVert A\right \rVert e^{2I_F(\Phi)}I_F(\Phi) \left \lvert X\right \rvert G_{F}\left ( d\left ( X,{{\mathbb Z}^2}\setminus\Lambda\right ) \right ). \end{align} $$
$$ \begin{align} \left \lVert \tau_{t,s}^{(\Lambda), \Phi}(A)-\tau_{t,s}^{\Phi}(A) \right \rVert \le\frac{2}{C_{F}} \left \lVert A\right \rVert e^{2I_F(\Phi)}I_F(\Phi) \left \lvert X\right \rvert G_{F}\left ( d\left ( X,{{\mathbb Z}^2}\setminus\Lambda\right ) \right ). \end{align} $$5. If
 $\beta _{g}^U\left ( \Phi (X;t)\right )=\Phi (X;t)$ for any
$\beta _{g}^U\left ( \Phi (X;t)\right )=\Phi (X;t)$ for any  $X\in {\mathfrak S}_{{\mathbb Z}^2}$,
$X\in {\mathfrak S}_{{\mathbb Z}^2}$,  $t\in [0,1]$, and
$t\in [0,1]$, and  $g\in G$, then we have
$g\in G$, then we have  $\beta _g^U\circ \tau _{t,s}^{ \Phi }=\tau _{t,s}^{\Phi }\circ \beta _g^U$ for any
$\beta _g^U\circ \tau _{t,s}^{ \Phi }=\tau _{t,s}^{\Phi }\circ \beta _g^U$ for any  $t,s\in [0,1]$ and
$t,s\in [0,1]$ and  $g\in G$,
$g\in G$,
Proof. Item 1 is [Reference Nachtergaele, Sims and YoungNSY, Theorem 3.5], and 2 and 4 follow from Corollary 3.6 of the same paper by, respectively, a straightforward bounding of ![]() $D(X,Y)$ and the summation in [Reference Nachtergaele, Sims and YoungNSY, equation (3.80)]. Item 3 can be obtained using 2 and [Reference Nachtergaele, Sims and YoungNSY, Corollary 4.4].
$D(X,Y)$ and the summation in [Reference Nachtergaele, Sims and YoungNSY, equation (3.80)]. Item 3 can be obtained using 2 and [Reference Nachtergaele, Sims and YoungNSY, Corollary 4.4].
Suppose that  ${\beta _g^U}\left ( \Phi (X;t)\right )=\Phi (X;t)$ for any
${\beta _g^U}\left ( \Phi (X;t)\right )=\Phi (X;t)$ for any ![]() $X\in {\mathfrak S}_{{\mathbb Z}^2}$,
$X\in {\mathfrak S}_{{\mathbb Z}^2}$, ![]() $t\in [0,1]$, and
$t\in [0,1]$, and ![]() $g\in G$. Then we have
$g\in G$. Then we have
 $$ \begin{align} \frac{d}{dt} {\beta_g^U}\left ( U_{\Lambda,\Phi}(t;s)\right ) =-{\beta_g^U}\left ( iH_{\Lambda,\Phi}(t)\right ) {\beta_g^U}\left ( U_{\Lambda,\Phi}(t;s)\right ) =- iH_{\Lambda,\Phi}(t){\beta_g^U}\left ( U_{\Lambda,\Phi}(t;s)\right ),\quad t\in[0,1], \end{align} $$
$$ \begin{align} \frac{d}{dt} {\beta_g^U}\left ( U_{\Lambda,\Phi}(t;s)\right ) =-{\beta_g^U}\left ( iH_{\Lambda,\Phi}(t)\right ) {\beta_g^U}\left ( U_{\Lambda,\Phi}(t;s)\right ) =- iH_{\Lambda,\Phi}(t){\beta_g^U}\left ( U_{\Lambda,\Phi}(t;s)\right ),\quad t\in[0,1], \end{align} $$and  ${\beta _g^U}\left ( U_{\Lambda ,\Phi }(s;s)\right )=\mathbb I$. Hence
${\beta _g^U}\left ( U_{\Lambda ,\Phi }(s;s)\right )=\mathbb I$. Hence  ${\beta _g^U}\left ( U_{\Lambda ,\Phi }(t;s)\right )$ and
${\beta _g^U}\left ( U_{\Lambda ,\Phi }(t;s)\right )$ and ![]() $U_{\Lambda ,\Phi }(t;s)$ satisfy the same differential equation and initial condition. Therefore we get
$U_{\Lambda ,\Phi }(t;s)$ satisfy the same differential equation and initial condition. Therefore we get  ${\beta _g^U}\left ( U_{\Lambda ,\Phi }(t;s)\right )=U_{\Lambda ,\Phi }(t;s)$. From this, we obtain
${\beta _g^U}\left ( U_{\Lambda ,\Phi }(t;s)\right )=U_{\Lambda ,\Phi }(t;s)$. From this, we obtain  ${\beta _g^U}\tau _{t,s}^{(\Lambda ), \Phi }=\tau _{t,s}^{(\Lambda ), \Phi }{\beta _g^U}$, and taking
${\beta _g^U}\tau _{t,s}^{(\Lambda ), \Phi }=\tau _{t,s}^{(\Lambda ), \Phi }{\beta _g^U}$, and taking ![]() $\Lambda \uparrow {\mathbb Z}^2$, we obtain
$\Lambda \uparrow {\mathbb Z}^2$, we obtain  ${\beta _g^U}\circ \tau _{t,s}^{ \Phi }=\tau _{t,s}^{\Phi }\circ {\beta _g^U}$.
${\beta _g^U}\circ \tau _{t,s}^{ \Phi }=\tau _{t,s}^{\Phi }\circ {\beta _g^U}$.
The following is slightly strengthened version of [Reference Nachtergaele, Sims and YoungNSY, Assumption 5.15]:
Assumption D.4 [Reference Nachtergaele, Sims and YoungNSY]
We assume that the family of linear maps ![]() $\{{\mathcal K}_t:{\mathcal A}_{\textrm {loc}}\to {\mathcal A}\}_{t\in \left [0,1\right ]}$ is norm-continuous and satisfies the following: There is a family of linear maps
$\{{\mathcal K}_t:{\mathcal A}_{\textrm {loc}}\to {\mathcal A}\}_{t\in \left [0,1\right ]}$ is norm-continuous and satisfies the following: There is a family of linear maps  $\left \{ {\mathcal K}_t^{(n)} : {\mathcal A}_{\Lambda _n} \to {\mathcal A}_{\Lambda _n} \right \}_{t\in \left [0,1\right ]} $ for each
$\left \{ {\mathcal K}_t^{(n)} : {\mathcal A}_{\Lambda _n} \to {\mathcal A}_{\Lambda _n} \right \}_{t\in \left [0,1\right ]} $ for each ![]() $n\ge 1$ such that the following are true:
$n\ge 1$ such that the following are true:
(i) For each
 $n\ge 1$, the family
$n\ge 1$, the family  $\left \{{\mathcal K}_t^{(n)} : {\mathcal A}_{\Lambda _n}\to {\mathcal A}_{\Lambda _n}\right \}_{t\in \left [0,1\right ]}$ satisfies the following conditions:
$\left \{{\mathcal K}_t^{(n)} : {\mathcal A}_{\Lambda _n}\to {\mathcal A}_{\Lambda _n}\right \}_{t\in \left [0,1\right ]}$ satisfies the following conditions:(a) For each
 $t\in [0,1]$,
$t\in [0,1]$,  $\left ( {\mathcal K}_t^{(n)}(A)\right )^*= {\mathcal K}_t^{(n)}(A^*)$ for all
$\left ( {\mathcal K}_t^{(n)}(A)\right )^*= {\mathcal K}_t^{(n)}(A^*)$ for all  ${\mathcal A}_{\Lambda _n}$.
${\mathcal A}_{\Lambda _n}$.(b) For each
 $A\in {\mathcal A}_{\Lambda _n}$, the function
$A\in {\mathcal A}_{\Lambda _n}$, the function  $[0,1]\ni t\to {\mathcal K}_t^{(n)}(A)$ is norm-continuous.
$[0,1]\ni t\to {\mathcal K}_t^{(n)}(A)$ is norm-continuous.(c) For each
 $t\in [0,1]$, the map
$t\in [0,1]$, the map  ${\mathcal K}_t^{(n)}: {\mathcal A}_{\Lambda _n}\to {\mathcal A}_{\Lambda _n}$ is norm-continuous, and moreover, this continuity is uniform on
${\mathcal K}_t^{(n)}: {\mathcal A}_{\Lambda _n}\to {\mathcal A}_{\Lambda _n}$ is norm-continuous, and moreover, this continuity is uniform on  $[0,1]$.
$[0,1]$.
(ii) There is some
 $p\ge 0$ and a constant
$p\ge 0$ and a constant  $B_1>0$ for which, given any
$B_1>0$ for which, given any  $X\in {\mathfrak S}_{{\mathbb Z}^2}$ and
$X\in {\mathfrak S}_{{\mathbb Z}^2}$ and  $n\ge 1$ large enough so that
$n\ge 1$ large enough so that  $X\subset \Lambda _n$,
$X\subset \Lambda _n$,  $$\begin{align*}\left \lVert {\mathcal K}^{(n)}_t(A)\right \rVert\le B_1 \left \lvert X\right \rvert^p\left \lVert A \right \rVert,\quad \text{ for all } A\in{\mathcal A}_{X} \quad\text{and}\quad t\in [0,1]. \end{align*}$$
$$\begin{align*}\left \lVert {\mathcal K}^{(n)}_t(A)\right \rVert\le B_1 \left \lvert X\right \rvert^p\left \lVert A \right \rVert,\quad \text{ for all } A\in{\mathcal A}_{X} \quad\text{and}\quad t\in [0,1]. \end{align*}$$(iii) There is some
 $q\ge 0$, a nonnegative, nonincreasing function G with
$q\ge 0$, a nonnegative, nonincreasing function G with  $G(x)\to 0$ as
$G(x)\to 0$ as  $x\to \infty $, and a constant
$x\to \infty $, and a constant  $C_1>0$ for which, given any sets
$C_1>0$ for which, given any sets  $X,Y\in {\mathfrak S}_{{\mathbb Z}^2}$ and
$X,Y\in {\mathfrak S}_{{\mathbb Z}^2}$ and  $n\ge 1$ large enough so that
$n\ge 1$ large enough so that  $X\cup Y\subset \Lambda _n$,
$X\cup Y\subset \Lambda _n$,  $$\begin{align*}\left \lVert\left [ {\mathcal K}^{(n)}_t(A), B\right ] \right \rVert\le C_1\left \lvert X\right \rvert^q\left \lVert A \right \rVert\left \lVert B\right \rVert G\left (\mathrm{d}(X,Y)\right ),\quad \text{ for all } A\in{\mathcal A}_{X},\ B\in{\mathcal A}_{Y}, \ t\in [0,1]. \end{align*}$$
$$\begin{align*}\left \lVert\left [ {\mathcal K}^{(n)}_t(A), B\right ] \right \rVert\le C_1\left \lvert X\right \rvert^q\left \lVert A \right \rVert\left \lVert B\right \rVert G\left (\mathrm{d}(X,Y)\right ),\quad \text{ for all } A\in{\mathcal A}_{X},\ B\in{\mathcal A}_{Y}, \ t\in [0,1]. \end{align*}$$(iv) There is some
 $r\ge 0$, a nonnegative, nonincreasing function H with
$r\ge 0$, a nonnegative, nonincreasing function H with  $H(x)\to 0$ as
$H(x)\to 0$ as  $x\to \infty $, and a constant
$x\to \infty $, and a constant  $D_1>0$ for which, given any
$D_1>0$ for which, given any  $X\in {\mathfrak S}_{{\mathbb Z}^2}$, there exists
$X\in {\mathfrak S}_{{\mathbb Z}^2}$, there exists  $N\ge 1$ such that for
$N\ge 1$ such that for  $n\ge N$, for all
$n\ge N$, for all $$\begin{align*}\left \lVert {\mathcal K}_t^{(n)} (A)-{\mathcal K}_t(A)\right \rVert \le D_{1} \left \lvert X\right \rvert^r \left \lVert A\right \rVert H\left ( \mathrm{d} \left(X,{\mathbb Z}^2\setminus \Lambda_n\right)\right ) \end{align*}$$
$$\begin{align*}\left \lVert {\mathcal K}_t^{(n)} (A)-{\mathcal K}_t(A)\right \rVert \le D_{1} \left \lvert X\right \rvert^r \left \lVert A\right \rVert H\left ( \mathrm{d} \left(X,{\mathbb Z}^2\setminus \Lambda_n\right)\right ) \end{align*}$$ $A\in {\mathcal A}_X$ and
$A\in {\mathcal A}_X$ and  $t\in [0,1]$.
$t\in [0,1]$.
The following theorem is a slight modification of [Reference Nachtergaele, Sims and YoungNSY, Theorem 5.17]:
Theorem D.5. Set ![]() $F\in {\mathcal F}_a$, with
$F\in {\mathcal F}_a$, with ![]() $\tilde F_\theta $ in formula (C.2) for each
$\tilde F_\theta $ in formula (C.2) for each ![]() $0<\theta <1$. Assume that
$0<\theta <1$. Assume that ![]() $\{{\mathcal K}_t\}_{t\in \left [0,1\right ]}$ is a family of linear maps satisfying Assumption D.4, with
$\{{\mathcal K}_t\}_{t\in \left [0,1\right ]}$ is a family of linear maps satisfying Assumption D.4, with ![]() $G=G_{F}$ in part (iii). (Recall Definition C.2 and formula (C.12)). Let
$G=G_{F}$ in part (iii). (Recall Definition C.2 and formula (C.12)). Let ![]() $\Phi \in {\mathcal B}_F([0,1])$ be an interaction satisfying
$\Phi \in {\mathcal B}_F([0,1])$ be an interaction satisfying ![]() $\Phi _m\in {\mathcal B}_F([0,1])$ for
$\Phi _m\in {\mathcal B}_F([0,1])$ for ![]() $m=\max \{p,q,r\}$, where
$m=\max \{p,q,r\}$, where ![]() $p,q,r$ are numbers in Assumption D.4. Then the right-hand side of the sum
$p,q,r$ are numbers in Assumption D.4. Then the right-hand side of the sum
 $$ \begin{align} \Psi\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)=Z} \Delta_{X(m)}\left ( {\mathcal K}_t\left ( \Phi\left ( X; t\right ) \right ) \right ),\quad Z\in {\mathfrak S}_{{\mathbb Z}^2},\ t\in [0,1] \end{align} $$
$$ \begin{align} \Psi\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)=Z} \Delta_{X(m)}\left ( {\mathcal K}_t\left ( \Phi\left ( X; t\right ) \right ) \right ),\quad Z\in {\mathfrak S}_{{\mathbb Z}^2},\ t\in [0,1] \end{align} $$defines a path of interaction such that ![]() $\Psi \in {\mathcal B}_{\tilde F_{\theta }}([0,1])$, for any
$\Psi \in {\mathcal B}_{\tilde F_{\theta }}([0,1])$, for any ![]() $0<\theta <1$. Furthermore, the formula
$0<\theta <1$. Furthermore, the formula
 $$ \begin{align} \Psi^{(n)}\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)\cap\Lambda_{n}=Z} \Delta_{X(m)}\left ( {\mathcal K}_t^{(n)}\left ( \Phi\left ( X; t\right ) \right ) \right ) \end{align} $$
$$ \begin{align} \Psi^{(n)}\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)\cap\Lambda_{n}=Z} \Delta_{X(m)}\left ( {\mathcal K}_t^{(n)}\left ( \Phi\left ( X; t\right ) \right ) \right ) \end{align} $$defines  $\Psi ^{{(n)}}\in {\mathcal B}_{\tilde F_{\theta }}([0,1])$, for any
$\Psi ^{{(n)}}\in {\mathcal B}_{\tilde F_{\theta }}([0,1])$, for any ![]() $0<\theta <1$, such that
$0<\theta <1$, such that ![]() $\Psi ^{(n)}\left ( Z, t \right )=0$ unless
$\Psi ^{(n)}\left ( Z, t \right )=0$ unless ![]() $Z\subset \Lambda _{n}$, and satisfies
$Z\subset \Lambda _{n}$, and satisfies
 $$ \begin{align} {\mathcal K}_t^{(n)} \left ( H_{\Lambda_n, \Phi}(t)\right ) =H_{\Lambda_n, \Psi^{(n)}}(t). \end{align} $$
$$ \begin{align} {\mathcal K}_t^{(n)} \left ( H_{\Lambda_n, \Phi}(t)\right ) =H_{\Lambda_n, \Psi^{(n)}}(t). \end{align} $$For any ![]() $t,u\in [0,1]$, we have
$t,u\in [0,1]$, we have
 $$ \begin{align} \lim_{n\to\infty}\left \lVert \tau_{t,u}^{\Psi^{(n)}}\left ( A\right ) -\tau_{t,u}^{\Psi}\left ( A\right ) \right \rVert=0,\quad A\in{\mathcal A}. \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\left \lVert \tau_{t,u}^{\Psi^{(n)}}\left ( A\right ) -\tau_{t,u}^{\Psi}\left ( A\right ) \right \rVert=0,\quad A\in{\mathcal A}. \end{align} $$Furthermore, if ![]() $\Phi _{m+k}\in \hat {\mathcal B}_{F}([0,1])$ for
$\Phi _{m+k}\in \hat {\mathcal B}_{F}([0,1])$ for ![]() $k\in {\mathbb N}\cup \{0\}$, then we have
$k\in {\mathbb N}\cup \{0\}$, then we have  $\Psi _k^{{(n)}}, \Psi _k\in \hat {\mathcal B}_{\tilde F_{\theta }}([0,1])$ for any
$\Psi _k^{{(n)}}, \Psi _k\in \hat {\mathcal B}_{\tilde F_{\theta }}([0,1])$ for any ![]() $0<\theta <1$.
$0<\theta <1$.
Proof. Because of ![]() $F\in {\mathcal F}_{a}$, we see from formula (C.14) that for any
$F\in {\mathcal F}_{a}$, we see from formula (C.14) that for any ![]() $0<\alpha <1$ and
$0<\alpha <1$ and ![]() $k\in {\mathbb N}$,
$k\in {\mathbb N}$, ![]() $G_{F}^{\alpha }$ has a finite k-moment. We also recall formulas (C.2) and (C.14) to see that
$G_{F}^{\alpha }$ has a finite k-moment. We also recall formulas (C.2) and (C.14) to see that
 $$ \begin{align} \max\left\{ F\left (\frac r 3\right ), \sum_{n=\left[\frac r3\right]}^{\infty }(1+n)^{5}G_{F}(n)^{\alpha} \right\}\le \tilde C \tilde F_{\alpha(1-\theta')\varphi}(r),\quad r\ge 0, \end{align} $$
$$ \begin{align} \max\left\{ F\left (\frac r 3\right ), \sum_{n=\left[\frac r3\right]}^{\infty }(1+n)^{5}G_{F}(n)^{\alpha} \right\}\le \tilde C \tilde F_{\alpha(1-\theta')\varphi}(r),\quad r\ge 0, \end{align} $$for any ![]() $0<\alpha ,\theta ',\varphi <1$. As this holds for any
$0<\alpha ,\theta ',\varphi <1$. As this holds for any ![]() $0<\alpha ,\theta ',\varphi <1$, the condition in [Reference Nachtergaele, Sims and YoungNSY, Theorem 5.17(ii)] holds for any
$0<\alpha ,\theta ',\varphi <1$, the condition in [Reference Nachtergaele, Sims and YoungNSY, Theorem 5.17(ii)] holds for any ![]() $\tilde F_{\theta }$. Therefore, from [Reference Nachtergaele, Sims and YoungNSY, Theorem 5.17(ii)], we get
$\tilde F_{\theta }$. Therefore, from [Reference Nachtergaele, Sims and YoungNSY, Theorem 5.17(ii)], we get  $\Psi ,\Psi ^{(n)}\in {\mathcal B}_{\tilde F_{\theta }}\left ([0,1]\right )$ and
$\Psi ,\Psi ^{(n)}\in {\mathcal B}_{\tilde F_{\theta }}\left ([0,1]\right )$ and ![]() $\Psi ^{(n)}$ converges locally in F-norm to
$\Psi ^{(n)}$ converges locally in F-norm to ![]() $\Psi $ with respect to
$\Psi $ with respect to ![]() $\tilde F_{\theta }$, for any
$\tilde F_{\theta }$, for any ![]() $0<\theta <1$.
$0<\theta <1$.
From [Reference Nachtergaele, Sims and YoungNSY, Theorem 5.13] we have the implication
 $$ \begin{align} \sup_{n}\int_{0}^{1}\left \lVert \Psi^{(n)}\right \rVert_{\tilde F_{\theta}}(t) dt<\infty \end{align} $$
$$ \begin{align} \sup_{n}\int_{0}^{1}\left \lVert \Psi^{(n)}\right \rVert_{\tilde F_{\theta}}(t) dt<\infty \end{align} $$(see also [Reference Nachtergaele, Sims and YoungNSY, equation (5.101)]. Therefore, from [Reference Nachtergaele, Sims and YoungNSY, Theorem 3.8], we obtain equation (D.20).
By the proofs of [Reference Nachtergaele, Sims and YoungNSY, Theorems 5.17 and 5.13, equation (5.87)], if ![]() $\Phi _{k+m}\in \hat {\mathcal B}_{F}([0,1])$ for some
$\Phi _{k+m}\in \hat {\mathcal B}_{F}([0,1])$ for some ![]() $k\in {\mathbb N}$, then we have
$k\in {\mathbb N}$, then we have  $\Psi _k^{{(n)(s)}}, \Psi _k^{{(s)}}\in \hat {\mathcal B}_{\tilde F}([0,1])$. More precisely, instead of [Reference Nachtergaele, Sims and YoungNSY, equation (5.88)], we obtain
$\Psi _k^{{(n)(s)}}, \Psi _k^{{(s)}}\in \hat {\mathcal B}_{\tilde F}([0,1])$. More precisely, instead of [Reference Nachtergaele, Sims and YoungNSY, equation (5.88)], we obtain
 $$ \begin{align} \begin{split} &\sum_{\substack{Z\in{\mathfrak S}_{{\mathbb Z}^2}\\Z\ni x,y }} \left \lvert Z\right \rvert^{k}\sup_{t\in\left[0,1\right]}\left \lVert\Psi(Z;t) \right \rVert\\ &\quad \le B_1 \sum_{\substack{Z\in{\mathfrak S}_{{\mathbb Z}^2}\\Z\ni x,y }} \left \lvert Z\right \rvert^{k+p}\sup_{t\in\left[0,1\right]}\left \lVert\Phi(Z;t) \right \rVert +4C_1 \sum_{n=0}^\infty G_F(n) \sum_{X: X(n+1)\ni x,y} \left \lvert X\right \rvert^q\left \lvert X(n+1)\right \rvert^k \sup_{t\in\left[0,1\right]} \left \lVert\Phi(X;t)\right \rVert\\ &\quad \le B_1 \left \lVert\left \lvert \Phi_{k+p}\right \rvert\right \rVert_F F( \mathrm{d}(x,y)) +4C_1 \sum_{n=0}^\infty G_F(n)(2n+3)^{2k} \sum_{X:X(n+1)\ni x,y} \left \lvert X\right \rvert^{q+k} \sup_{t\in\left[0,1\right]} \left \lVert\Phi(X;t)\right \rVert\\ &\quad \le B_1 \left \lVert\left \lvert \Phi_{k+p}\right \rvert\right \rVert_F F( \mathrm{d}(x,y)) +\tilde C_{\theta}\tilde F_{\theta}( \mathrm{d}(x,y)) \left \lVert\left \lvert \Phi_{q+k}\right \rvert\right \rVert_F<\infty, \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\sum_{\substack{Z\in{\mathfrak S}_{{\mathbb Z}^2}\\Z\ni x,y }} \left \lvert Z\right \rvert^{k}\sup_{t\in\left[0,1\right]}\left \lVert\Psi(Z;t) \right \rVert\\ &\quad \le B_1 \sum_{\substack{Z\in{\mathfrak S}_{{\mathbb Z}^2}\\Z\ni x,y }} \left \lvert Z\right \rvert^{k+p}\sup_{t\in\left[0,1\right]}\left \lVert\Phi(Z;t) \right \rVert +4C_1 \sum_{n=0}^\infty G_F(n) \sum_{X: X(n+1)\ni x,y} \left \lvert X\right \rvert^q\left \lvert X(n+1)\right \rvert^k \sup_{t\in\left[0,1\right]} \left \lVert\Phi(X;t)\right \rVert\\ &\quad \le B_1 \left \lVert\left \lvert \Phi_{k+p}\right \rvert\right \rVert_F F( \mathrm{d}(x,y)) +4C_1 \sum_{n=0}^\infty G_F(n)(2n+3)^{2k} \sum_{X:X(n+1)\ni x,y} \left \lvert X\right \rvert^{q+k} \sup_{t\in\left[0,1\right]} \left \lVert\Phi(X;t)\right \rVert\\ &\quad \le B_1 \left \lVert\left \lvert \Phi_{k+p}\right \rvert\right \rVert_F F( \mathrm{d}(x,y)) +\tilde C_{\theta}\tilde F_{\theta}( \mathrm{d}(x,y)) \left \lVert\left \lvert \Phi_{q+k}\right \rvert\right \rVert_F<\infty, \end{split} \end{align} $$with some constant ![]() $\tilde C_{\theta }$, for each
$\tilde C_{\theta }$, for each ![]() $0<\theta <1$. In the last line we used formula (C.14) and [Reference Nachtergaele, Sims and YoungNSY, Lemma 8.9]. Hence we get
$0<\theta <1$. In the last line we used formula (C.14) and [Reference Nachtergaele, Sims and YoungNSY, Lemma 8.9]. Hence we get  $\Psi _k^{{(n)}}, \Psi _k\in \hat {\mathcal B}_{\tilde F_{\theta }}([0,1])$.
$\Psi _k^{{(n)}}, \Psi _k\in \hat {\mathcal B}_{\tilde F_{\theta }}([0,1])$.
Proof of Theorem 5.1.
Suppose ![]() $\Phi _{0}\sim \Phi _{1}$ via a path
$\Phi _{0}\sim \Phi _{1}$ via a path ![]() $\Phi $. Our definition of
$\Phi $. Our definition of ![]() $\Phi _0\sim \Phi _1$ means the existence of a path of interactions satisfying [Reference Moon and OgataMO, Assumption 1.2]. Therefore, [Reference Moon and OgataMO, Theorem 1.3] guarantees the existence of a path of quasilocal automorphisms
$\Phi _0\sim \Phi _1$ means the existence of a path of interactions satisfying [Reference Moon and OgataMO, Assumption 1.2]. Therefore, [Reference Moon and OgataMO, Theorem 1.3] guarantees the existence of a path of quasilocal automorphisms ![]() $\alpha _t$ satisfying
$\alpha _t$ satisfying ![]() $\omega _{\Phi _1}=\omega _{\Phi _0}\circ \alpha _1$. From the proof in [Reference Moon and OgataMO], the automorphism
$\omega _{\Phi _1}=\omega _{\Phi _0}\circ \alpha _1$. From the proof in [Reference Moon and OgataMO], the automorphism ![]() $\alpha _t$ is given by a family of interactions
$\alpha _t$ is given by a family of interactions
 $$ \begin{align} \Psi\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)=Z} \Delta_{X(m)}\left ( {\mathcal K}_t\left ( \dot \Phi\left ( X; t\right ) \right ) \right ),\quad Z\in {\mathfrak S}_{{\mathbb Z}^2},\ t\in [0,1], \end{align} $$
$$ \begin{align} \Psi\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)=Z} \Delta_{X(m)}\left ( {\mathcal K}_t\left ( \dot \Phi\left ( X; t\right ) \right ) \right ),\quad Z\in {\mathfrak S}_{{\mathbb Z}^2},\ t\in [0,1], \end{align} $$with
 $$ \begin{align} {\mathcal K}_t(A):=-\int du W_\gamma(u)\tau_{u}^{\Phi(t)}(A), \end{align} $$
$$ \begin{align} {\mathcal K}_t(A):=-\int du W_\gamma(u)\tau_{u}^{\Phi(t)}(A), \end{align} $$as  $\alpha _{t}=\tau _{t,0}^{\Psi }$. (Note that by the partial integral of [Reference Moon and OgataMO, equation (1.19)], we obtain [Reference Nachtergaele, Sims and YoungNSY, equation (6.103)] with function
$\alpha _{t}=\tau _{t,0}^{\Psi }$. (Note that by the partial integral of [Reference Moon and OgataMO, equation (1.19)], we obtain [Reference Nachtergaele, Sims and YoungNSY, equation (6.103)] with function ![]() $W_\gamma $ in [Reference Nachtergaele, Sims and YoungNSY, equation (6.35)]).) The interaction
$W_\gamma $ in [Reference Nachtergaele, Sims and YoungNSY, equation (6.35)]).) The interaction ![]() $\Psi $ actually belongs to
$\Psi $ actually belongs to  $\hat {\mathcal B}_{F_3}([0,1])$ for some
$\hat {\mathcal B}_{F_3}([0,1])$ for some ![]() $F_3\in {\mathcal F}_a$. To see this, note that the path
$F_3\in {\mathcal F}_a$. To see this, note that the path ![]() $\Phi $ in Definition 1.2 satisfies [Reference Nachtergaele, Sims and YoungNSY, Assumption 6.12] for any F-function, because
$\Phi $ in Definition 1.2 satisfies [Reference Nachtergaele, Sims and YoungNSY, Assumption 6.12] for any F-function, because
 $$ \begin{align} \sum_{\substack{X\in{\mathfrak S}_{{\mathbb Z}^2}\\ X\ni x,y }}\left ( \left \lVert \Phi\left ( X;s\right ) \right \rVert+\left \lvert X\right \rvert\left \lVert \dot{\Phi} \left ( X;s\right ) \right \rVert \right ) \le \frac{ 2^{(2R+1)^2}C_b^\Phi}{F(R)} F(\mathrm{d}(x,y)), \end{align} $$
$$ \begin{align} \sum_{\substack{X\in{\mathfrak S}_{{\mathbb Z}^2}\\ X\ni x,y }}\left ( \left \lVert \Phi\left ( X;s\right ) \right \rVert+\left \lvert X\right \rvert\left \lVert \dot{\Phi} \left ( X;s\right ) \right \rVert \right ) \le \frac{ 2^{(2R+1)^2}C_b^\Phi}{F(R)} F(\mathrm{d}(x,y)), \end{align} $$with  $C_b^\Phi $ and R given in Definition 1.2 3 and 4. In particular, it satisfies [Reference Nachtergaele, Sims and YoungNSY, Assumption 6.12] with respect to the F-function (see [Reference Nachtergaele, Sims and YoungNSY, Section 8])
$C_b^\Phi $ and R given in Definition 1.2 3 and 4. In particular, it satisfies [Reference Nachtergaele, Sims and YoungNSY, Assumption 6.12] with respect to the F-function (see [Reference Nachtergaele, Sims and YoungNSY, Section 8])  $ F_1(r):=\frac {e^{-r}}{(1+r)^{4}} $. By [Reference Nachtergaele, Sims and YoungNSY, Section 8],
$ F_1(r):=\frac {e^{-r}}{(1+r)^{4}} $. By [Reference Nachtergaele, Sims and YoungNSY, Section 8], ![]() $F_1$ belongs to
$F_1$ belongs to ![]() ${\mathcal F}_a$. Fix any
${\mathcal F}_a$. Fix any ![]() $0<\alpha <1$. Then by [Reference Nachtergaele, Sims and YoungNSY, Proposition 6.13] and its proof, the family of maps given by formula (D.25) [Reference Nachtergaele, Sims and YoungNSY, equation (6.102)] satisfies Assumption D.4, with
$0<\alpha <1$. Then by [Reference Nachtergaele, Sims and YoungNSY, Proposition 6.13] and its proof, the family of maps given by formula (D.25) [Reference Nachtergaele, Sims and YoungNSY, equation (6.102)] satisfies Assumption D.4, with ![]() $p=0$,
$p=0$, ![]() $q=1$,
$q=1$, ![]() $r=1$ and
$r=1$ and ![]() $G=G_{F_{2}}$, where
$G=G_{F_{2}}$, where ![]() $F_{2}(r)=(1+r)^{-4} \exp \left ( - r^{\alpha }\right )$. Furthermore, we have
$F_{2}(r)=(1+r)^{-4} \exp \left ( - r^{\alpha }\right )$. Furthermore, we have ![]() $\dot {\Phi }_m\in \hat {\mathcal B}_{F_2}([0,1])$ for any
$\dot {\Phi }_m\in \hat {\mathcal B}_{F_2}([0,1])$ for any ![]() $m\in {\mathbb N}$, because
$m\in {\mathbb N}$, because
 $$ \begin{align} \left \lVert\left \lvert \dot \Phi_m\right \rVert\right \rvert_{F_2}:= \sup_{x,y\in{{\mathbb Z}^2}}\frac{1}{F_2\left ( {\mathrm{d}}(x,y)\right )}\sum_{Z\in{\mathfrak S}_{{\mathbb Z}^2},\, Z\ni x,y} \sup_{t\in \left[0,1\right]}\left \lvert Z\right \rvert^m \left ( \left \lVert\dot\Phi(Z;t)\right \rVert\right ) \le \frac{2^{(2R+1)^2} (2R+1)^{2m}C_b^\Phi}{F_2(R)}<\infty. \end{align} $$
$$ \begin{align} \left \lVert\left \lvert \dot \Phi_m\right \rVert\right \rvert_{F_2}:= \sup_{x,y\in{{\mathbb Z}^2}}\frac{1}{F_2\left ( {\mathrm{d}}(x,y)\right )}\sum_{Z\in{\mathfrak S}_{{\mathbb Z}^2},\, Z\ni x,y} \sup_{t\in \left[0,1\right]}\left \lvert Z\right \rvert^m \left ( \left \lVert\dot\Phi(Z;t)\right \rVert\right ) \le \frac{2^{(2R+1)^2} (2R+1)^{2m}C_b^\Phi}{F_2(R)}<\infty. \end{align} $$We have ![]() $F_{2}\in {\mathcal F}_{a}$, and fixing any
$F_{2}\in {\mathcal F}_{a}$, and fixing any ![]() $0<\alpha '<\alpha $,
$0<\alpha '<\alpha $,  $\tilde F_{2}(r):= (1+r)^{-4} \exp \left ( - r^{\alpha '}\right )$ satisfies
$\tilde F_{2}(r):= (1+r)^{-4} \exp \left ( - r^{\alpha '}\right )$ satisfies
 $$ \begin{align} \max\left\{ F_{2}\left (\frac r 3\right ), \left ( F_{2}\left ( \left [ \frac r 3 \right ] \right )\right )^{\theta}\right\}\le C_{2,\theta,\alpha'}\tilde F_{2}(r),\quad r\ge 0, \end{align} $$
$$ \begin{align} \max\left\{ F_{2}\left (\frac r 3\right ), \left ( F_{2}\left ( \left [ \frac r 3 \right ] \right )\right )^{\theta}\right\}\le C_{2,\theta,\alpha'}\tilde F_{2}(r),\quad r\ge 0, \end{align} $$for a suitable constant ![]() $C_{2,\theta ,\alpha '}$.
$C_{2,\theta ,\alpha '}$.
Therefore, by Theorem D.5, ![]() $\Psi $ given by formula (D.24) for this
$\Psi $ given by formula (D.24) for this ![]() ${\mathcal K}_t$ and
${\mathcal K}_t$ and ![]() $\dot \Phi $ satisfy
$\dot \Phi $ satisfy  $\Psi _1,\Psi \in \hat {\mathcal B}_{\tilde F_2}([0,1])$ for
$\Psi _1,\Psi \in \hat {\mathcal B}_{\tilde F_2}([0,1])$ for ![]() $\tilde F_2\in {\mathcal F}_a$.
$\tilde F_2\in {\mathcal F}_a$.
If ![]() $\Phi $ is
$\Phi $ is ![]() $\beta _{g}$-invariant, then
$\beta _{g}$-invariant, then ![]() $\tau ^{\Phi (t)}$ commutes with
$\tau ^{\Phi (t)}$ commutes with ![]() $\beta _{g}$, hence
$\beta _{g}$, hence ![]() ${\mathcal K}_{t}$ commutes with
${\mathcal K}_{t}$ commutes with ![]() $\beta _{g}$. As
$\beta _{g}$. As ![]() $\Pi _{X}$ commutes with
$\Pi _{X}$ commutes with ![]() $\beta _{g}$ and
$\beta _{g}$ and ![]() $\dot \Phi $ is
$\dot \Phi $ is ![]() $\beta _{g}$-invariant, we see that
$\beta _{g}$-invariant, we see that ![]() $\Psi $ is
$\Psi $ is ![]() $\beta _{g}$-invariant.
$\beta _{g}$-invariant.
Proposition D.6. Let ![]() $F,\tilde F\in {\mathcal F}_a$ be F-functions of the form
$F,\tilde F\in {\mathcal F}_a$ be F-functions of the form  $F(r)=(1+r)^{-4} \exp \left ( - r^{\theta }\right ), \tilde F(r):=(1+r)^{-4} \exp \left ( - r^{\theta '}\right )$ with some constants
$F(r)=(1+r)^{-4} \exp \left ( - r^{\theta }\right ), \tilde F(r):=(1+r)^{-4} \exp \left ( - r^{\theta '}\right )$ with some constants ![]() $0<\theta '<\theta <1$. Let
$0<\theta '<\theta <1$. Let ![]() $\Psi ,\tilde \Psi \in {\mathcal B}_{F}([0,1])$ be a path of interactions such that
$\Psi ,\tilde \Psi \in {\mathcal B}_{F}([0,1])$ be a path of interactions such that ![]() $\Psi _{1}\in {\mathcal B}_{F}([0,1])$. Finally, let
$\Psi _{1}\in {\mathcal B}_{F}([0,1])$. Finally, let  $\tau _{t,s}^{\tilde \Psi }$ and
$\tau _{t,s}^{\tilde \Psi }$ and  $\tau _{t,s}^{\left (\Lambda _n\right ),{\tilde \Psi }}$ be automorphisms given by
$\tau _{t,s}^{\left (\Lambda _n\right ),{\tilde \Psi }}$ be automorphisms given by ![]() $\Psi ,\tilde \Psi $ from Theorem D.3.
$\Psi ,\tilde \Psi $ from Theorem D.3.
Then, with ![]() $s \in [0,1]$, the right-hand side of the sum
$s \in [0,1]$, the right-hand side of the sum
 $$ \begin{align} \Xi^{(s)}\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)=Z} \Delta_{X(m)}\left ( \tau_{t,s}^{\tilde \Psi}\left ( \Psi\left ( X; t\right ) \right ) \right ),\quad Z\in{\mathfrak S}_{{\mathbb Z}^2},\ t\in [0,1], \end{align} $$
$$ \begin{align} \Xi^{(s)}\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)=Z} \Delta_{X(m)}\left ( \tau_{t,s}^{\tilde \Psi}\left ( \Psi\left ( X; t\right ) \right ) \right ),\quad Z\in{\mathfrak S}_{{\mathbb Z}^2},\ t\in [0,1], \end{align} $$defines a path of interaction such that ![]() $\Xi ^{(s)}\in {\mathcal B}_{\tilde F}([0,1])$. Furthermore, the formula
$\Xi ^{(s)}\in {\mathcal B}_{\tilde F}([0,1])$. Furthermore, the formula
 $$ \begin{align} \Xi^{(n)(s)}\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)\cap\Lambda_{n}=Z} \Delta_{X(m)}\left ( \tau_{t,s}^{\left(\Lambda_n\right), \tilde \Psi}\left ( \Psi\left ( X; t\right ) \right ) \right ) \end{align} $$
$$ \begin{align} \Xi^{(n)(s)}\left ( Z, t \right ):= \sum_{m\ge 0} \sum_{X\subset Z,\, X(m)\cap\Lambda_{n}=Z} \Delta_{X(m)}\left ( \tau_{t,s}^{\left(\Lambda_n\right), \tilde \Psi}\left ( \Psi\left ( X; t\right ) \right ) \right ) \end{align} $$defines ![]() $\Xi ^{{(n)(s)}}\in {\mathcal B}_{\tilde F}([0,1])$ such that
$\Xi ^{{(n)(s)}}\in {\mathcal B}_{\tilde F}([0,1])$ such that ![]() $\Xi ^{(n)}\left ( Z, t \right )=0$ unless
$\Xi ^{(n)}\left ( Z, t \right )=0$ unless ![]() $Z\subset \Lambda _{n}$, and satisfies
$Z\subset \Lambda _{n}$, and satisfies
 $$ \begin{align} \tau_{t,s}^{\left(\Lambda_n\right), \tilde \Psi} \left ( H_{\Lambda_n, \Psi}(t)\right ) =H_{\Lambda_n, \Xi^{(n)(s)}}(t). \end{align} $$
$$ \begin{align} \tau_{t,s}^{\left(\Lambda_n\right), \tilde \Psi} \left ( H_{\Lambda_n, \Psi}(t)\right ) =H_{\Lambda_n, \Xi^{(n)(s)}}(t). \end{align} $$For any ![]() $t,u\in [0,1]$, we have
$t,u\in [0,1]$, we have
 $$ \begin{align} \lim_{n\to\infty}\left \lVert \tau_{t,u}^{\Xi^{(n)(s)}}\left ( A\right ) -\tau_{t,u}^{\Xi^{(s)}}\left ( A\right ) \right \rVert=0,\quad A\in{\mathcal A}. \end{align} $$
$$ \begin{align} \lim_{n\to\infty}\left \lVert \tau_{t,u}^{\Xi^{(n)(s)}}\left ( A\right ) -\tau_{t,u}^{\Xi^{(s)}}\left ( A\right ) \right \rVert=0,\quad A\in{\mathcal A}. \end{align} $$Furthermore, if ![]() $\Psi _1\in \hat {\mathcal B}_{F}([0,1])$, then we have
$\Psi _1\in \hat {\mathcal B}_{F}([0,1])$, then we have ![]() $\Xi ^{{(n)(s)}}, \Xi ^{{(s)}}\in \hat {\mathcal B}_{\tilde F}([0,1])$.
$\Xi ^{{(n)(s)}}, \Xi ^{{(s)}}\in \hat {\mathcal B}_{\tilde F}([0,1])$.
Acknowledgments
The author is grateful to Hal Tasaki for a stimulating discussion of the ![]() $2$-dimensional Dijkgraaf–Witten model, and to Yasuyuki Kawahigashi for introducing the author to various papers from operator algebra.
$2$-dimensional Dijkgraaf–Witten model, and to Yasuyuki Kawahigashi for introducing the author to various papers from operator algebra.
Conflict of Interest
None.
Financial support
This work was supported by JSPS KAKENHI grants 16K05171 and 19K03534. It was also supported by JST CREST grant JPMJCR19T2.Footnote 1