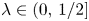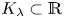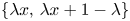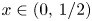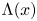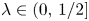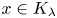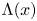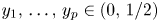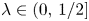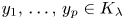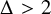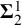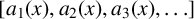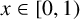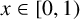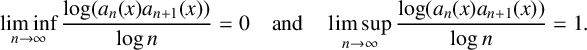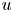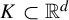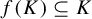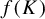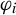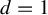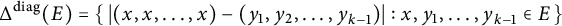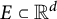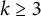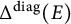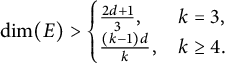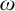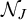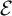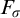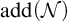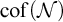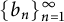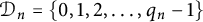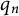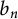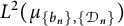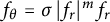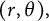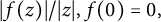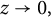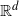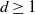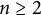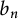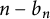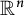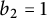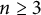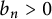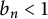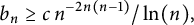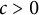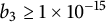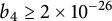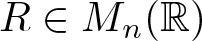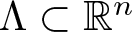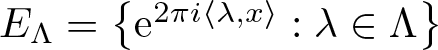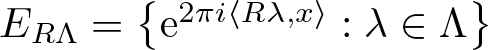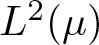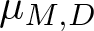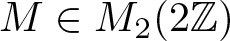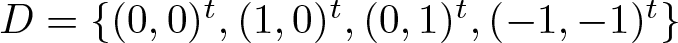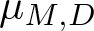317 results in 28Axx
On a class of self-similar sets which contain finitely many common points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-22
-
- Article
- Export citation
A reproducing kernel approach to Lebesgue decomposition
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON HOMOMORPHISM GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 May 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-invertible planar self-affine sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-17
-
- Article
- Export citation
Weighted topological pressure revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-37
-
- Article
- Export citation
ASYMPTOTIC BEHAVIOUR FOR PRODUCTS OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1-12
-
- Article
- Export citation
Sharp conditions for the validity of the Bourgain–Brezis–Mironescu formula
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-24
-
- Article
- Export citation
On a self-embedding problem for self-similar sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 14 February 2024, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On restricted Falconer distance sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 05 February 2024, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joint partial equidistribution of Farey rays in negatively curved manifolds and trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 January 2024, pp. 1-37
-
- Article
- Export citation
LEBESGUE MEASURE ZERO MODULO IDEALS ON THE NATURAL NUMBERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 December 2023, pp. 1-31
-
- Article
- Export citation
Tree structure of spectra of spectral Moran measures with consecutive digits
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1-18
-
- Article
- Export citation
Slices of the Takagi function
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 20 December 2023, pp. 1-38
-
- Article
- Export citation
Nonlinear Beltrami equation: lower estimates of Schwarz lemma’s type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 29 November 2023, pp. 1-11
-
- Article
- Export citation
Almost sure convergence and second moments of geometric functionals of fractal percolation
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-33
-
- Article
- Export citation
Lower bounds on Bourgain’s constant for harmonic measure
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-20
-
- Article
- Export citation
An elementary proof that the Rauzy gasket is fractal
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 1913-1922
- Print publication:
- July 2024
-
- Article
- Export citation
On the dimension of planar self-affine sets with non-invertible maps
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-16
-
- Article
- Export citation
Coupling capacity in C*-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The spectral eigenmatrix problems of planar self-affine measures with four digits
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 897-918
-
- Article
- Export citation