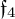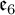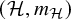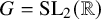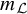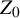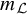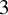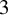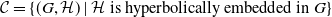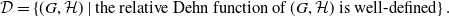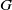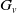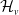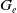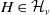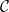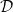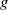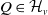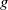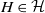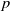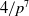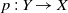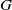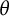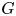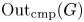225 results in 57Mxx
EXCEPTIONAL SIMPLE REAL LIE ALGEBRAS
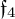 $\mathfrak {f}_4$ AND
$\mathfrak {f}_4$ AND 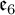 $\mathfrak {e}_6$ VIA CONTACTIFICATIONS
$\mathfrak {e}_6$ VIA CONTACTIFICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 03 July 2024, pp. 1-45
-
- Article
-
- You have access
- HTML
- Export citation
Adjoint Reidemeister torsions of some 3-manifolds obtained by Dehn surgeries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Singer conjecture for varieties with semismall Albanese map and residually finite fundamental group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-7
-
- Article
-
- You have access
- HTML
- Export citation
On the ergodic theory of the real Rel foliation
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Canonical decompositions and algorithmic recognition of spatial graphs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 14 March 2024, pp. 388-430
-
- Article
-
- You have access
- HTML
- Export citation
RADU GROUPS ACTING ON TREES ARE CCR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-38
-
- Article
-
- You have access
- HTML
- Export citation
LIMIT SETS OF UNFOLDING PATHS IN OUTER SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 15 February 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Length functions in Teichmüller and anti-de Sitter geometry
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 November 2023, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR GROWTH OF TRANSLATION LENGTHS OF RANDOM ISOMETRIES ON GROMOV HYPERBOLIC SPACES AND TEICHMÜLLER SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1751-1795
- Print publication:
- July 2024
-
- Article
-
- You have access
- HTML
- Export citation
Relative Dehn functions, hyperbolically embedded subgroups and combination theorems
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 25 August 2023, pp. 1-23
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Jones polynomial modulo primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 August 2023, pp. 730-734
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation
Subrepresentations in the homology of finite covers of graphs
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 06 July 2023, pp. 582-594
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Foliated affine and projective structures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1153-1187
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper extensions of the 2-sphere’s conformal group present entropy and are 4-transitive
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 03 May 2023, pp. 1102-1122
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Concordance of spatial graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 March 2023, pp. 1091-1108
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Braiding groups of automorphisms and almost-automorphisms of trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 March 2023, pp. 555-593
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant Heegaard genus of reducible 3-manifolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 13 February 2023, pp. 51-87
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On automorphisms and splittings of special groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 10 February 2023, pp. 232-305
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Residual torsion-free nilpotence, bi-orderability, and two-bridge links
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 25 January 2023, pp. 394-457
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Equivariant Brill–Noether theory for elliptic operators and superrigidity of J-holomorphic maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 January 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation