Hostname: page-component-84b7d79bbc-g78kv Total loading time: 0 Render date: 2024-07-27T17:25:56.423Z Has data issue: false hasContentIssue false
  • English
  • Français

EXCEPTIONAL SIMPLE REAL LIE ALGEBRAS 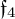$\mathfrak {f}_4$ AND 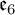$\mathfrak {e}_6$ VIA CONTACTIFICATIONS

Part of: Classical differential geometry Low-dimensional topology Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  03 July 2024

Paweł Nurowski Open the ORCID record for Paweł Nurowski [Opens in a new window]
Paweł Nurowski*
Affiliation:
Center for Theoretical Physics, Polish Academy of Sciences, Al. Lotników 32/46, 02-668 Warszawa, Poland
*
nurowski@fuw.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

In Cartan’s PhD thesis, there is a formula defining a certain rank 8 vector distribution in dimension 15, whose algebra of authomorphism is the split real form of the simple exceptional complex Lie algebra 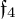$\mathfrak {f}_4$. Cartan’s formula is written in the standard Cartesian coordinates in 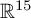$\mathbb {R}^{15}$. In the present paper, we explain how to find analogous formulae for the flat models of any bracket generating distribution 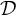$\mathcal D$ whose symbol algebra 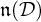$\mathfrak {n}({\mathcal D})$ is constant and 2-step graded, 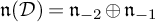$\mathfrak {n}({\mathcal D})=\mathfrak {n}_{-2}\oplus \mathfrak {n}_{-1}$.

The formula is given in terms of a solution to a certain system of linear algebraic equations determined by two representations 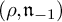$(\rho ,\mathfrak {n}_{-1})$ and 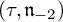$(\tau ,\mathfrak {n}_{-2})$ of a Lie algebra 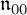$\mathfrak {n}_{00}$ contained in the 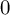$0$th order Tanaka prolongation 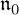$\mathfrak {n}_0$ of 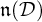$\mathfrak {n}({\mathcal D})$.

Numerous examples are provided, with particular emphasis put on the distributions with symmetries being real forms of simple exceptional Lie algebras 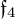$\mathfrak {f}_4$ and 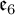$\mathfrak {e}_6$.

Keywords

contactificationsexceptional simple Lie algebrasreal forms

MSC classification

Primary: 17B05: Structure theory
Secondary: 17B10: Representations, algebraic theory (weights) 17B60: Lie (super)algebras associated with other structures (associative, Jordan, etc.) 17B70: Graded Lie (super)algebras 53A35: Non-Euclidean differential geometry 53A55: Differential invariants (local theory), geometric objects 57M50: Geometric structures on low-dimensional manifolds
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , First View , pp. 1 - 45
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research was funded from the Norwegian Financial Mechanism 2014-2021 with project registration number 2019/34/H/ST1/00636

References

Anderson, I., Nie, Z. and Nurowski, P. (2015) Non-rigid parabolic geometries of Monge type. Adv. Math. 277, 24–55. DOI: https://doi.org/10.1016/j.aim.2015.01.021.CrossRefGoogle Scholar
Michael, A. and Berndt, J. (2003) Projective planes, Severi varieties and spheres. In Surveys in Differential Geometry. Vol. VIII. 1–27.Google Scholar
Alekseevsky, DV. and Cortes, V. (1997) Classification of N-(super)-extended Poincaré algebras and bilinear invariants of the spinor representation of Spin(p, q). Comm. Math. Phys. 183(3), 477–510.CrossRefGoogle Scholar
Altomani, A. and Santi, A. (2014) Tanaka structures modeled on extended Poincaré algebras. Indiana Univ. Math. J. 63(1), 91–117.CrossRefGoogle Scholar
Biquard, O., Quaternionic contact structures. In Quaternionic Structures in Mathematics and Physics. 23–30. DOI: 10.1142/9789812810038_0003, available at https://www.worldscientific.com/doi/pdf/10.1142/9789812810038_0003.Google Scholar
Biquard, O. (2015) From G2 geometry to quaternionic Kahler metrics. J. Geom. Phys. 91, 101–107.CrossRefGoogle Scholar
Brown, RB. and Gray, A. (1972) Riemannian manifolds with holonomy group Spin(9). In Differential Geometry; in Honor of Kentaro Yano. 41–59.Google Scholar
Cartan, E. (1893) Über die einfachen Transformationsgruppen. Ber. Verh. k. Sachs. Ges. d. Wiss. Leipzig, 395–420.Google Scholar
Cartan, E. (1894) Sur la structure des grupes de transformations finis et continus. Oeuvres 1, 137–287.Google Scholar
Cartan, E. (1910) Les systèmes de Pfaff à cinq variables et les équations aux dérivées partielles du second ordre. Ann. Sci. Éc. Norm. Supér. 27, 109–192.CrossRefGoogle Scholar
Čap, A. and Slovák, J. (2009) Parabolic Geometries. I. Mathematical Surveys and Monographs. Vol. 154. Providence, RI: American Mathematical Society. MR2532439Google Scholar
Duchemin, D. (2006) Quaternionic contact structures in dimension 7. Ann. Inst. Fourier 56(4), 851–885 (eng).CrossRefGoogle Scholar
Helgason, S. (1977) Invariant differential equations on homogeneous manifolds. BAMS 83, 751–756.CrossRefGoogle Scholar
Hill, CD., Merker, J., Nie, Z. and Nurowski, P. (2023) Accidental CR structures. arXiv preprint 2302.03119. Available at https://arxiv.org/abs/2302.03119.Google Scholar
Kraśkiewicz, W. and Weyman, J. (2012) Geometry of orbit closures for the representations associated to gradings of Lie algebras of types E6, F4 and G2. arXiv preprint 1201.1102. Available at https://arxiv.org/abs/1201.1102.Google Scholar
Molina, MG., Kruglikov, B., Markina, I. and Vasil’ev, A. (2018) Rigidity of 2-step Carnot groups. J. Geom. Anal. 28, 1477–1501.CrossRefGoogle Scholar
Nurowski, P. (2005) Differential equations and conformal structures. J. Geom. Phys. 55, 19–49. DOI: https://doi.org/10.1016/j.geomphys.2004.11.006.CrossRefGoogle Scholar
Tanaka, N. (1970) On differential systems, graded Lie algebras and pseudogroups. Kyoto J. Math. 10, 1–82.CrossRefGoogle Scholar
Trautman, A. (2006) Clifford algebras and their representations. In Naber, GL., Tsou, ST. and Françoise, JP. (eds), Encyclopedia of Mathematical Physics. Vol. 1. Oxford: Elsevier. http://trautman.fuw.edu.pl.Google Scholar