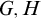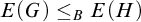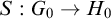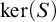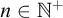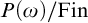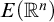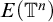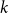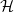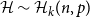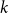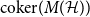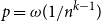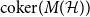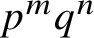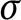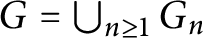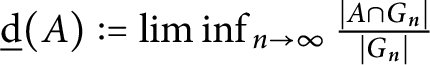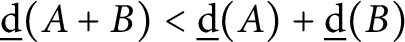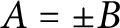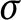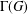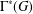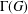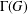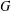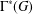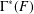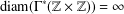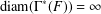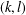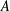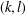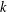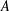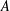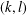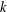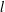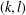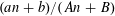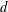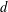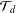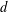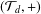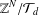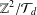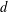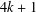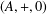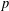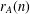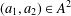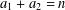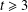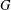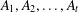41 results in 20Kxx
The Reidemeister spectrum of finite abelian groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 06 September 2023, pp. 940-959
-
- Article
- Export citation
ON EQUIVALENCE RELATIONS INDUCED BY LOCALLY COMPACT ABELIAN POLISH GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1-16
-
- Article
- Export citation
Abelian groups from random hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 654-664
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the dynamics of extensions of free-abelian times free groups endomorphisms to the completion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 12 August 2022, pp. 705-735
-
- Article
- Export citation
On the structure of spectral and tiling subsets of cyclic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kneser’s theorem in
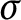 $\sigma $
-finite abelian groups
$\sigma $
-finite abelian groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 936-942
- Print publication:
- December 2022
-
- Article
- Export citation
Proof of the Brown–Erdős–Sós conjecture in groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 04 July 2019, pp. 323-333
- Print publication:
- September 2020
-
- Article
- Export citation
THE NUMBER OF CYCLIC SUBGROUPS OF FINITE ABELIAN GROUPS AND MENON’S IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 201-206
- Print publication:
- April 2020
-
- Article
- Export citation
THE GENERATING GRAPH OF INFINITE ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 68-75
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Approximations, ghosts and derived equivalences
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 813-840
- Print publication:
- April 2020
-
- Article
- Export citation
THE MAXIMUM SIZE OF
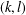 $(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
$(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 184-194
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
A STRUCTURED DESCRIPTION OF THE GENUS SPECTRUM OF ABELIAN p-GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 10 July 2018, pp. 381-423
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
On the Square Subgroup of a Mixed SI-Group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 295-304
-
- Article
- Export citation
HARMONIC ANALYSIS ON THE POSITIVE RATIONALS. DETERMINATION OF THE GROUP GENERATED BY THE RATIOS
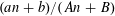 $(an+b)/(An+B)$
$(an+b)/(An+B)$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 919-943
- Print publication:
- 2017
-
- Article
- Export citation
ALGEBRAIC AND GEOMETRIC PROPERTIES OF LATTICE WALKS WITH STEPS OF EQUAL LENGTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 338-346
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
ON VARIETIES OF ABELIAN TOPOLOGICAL GROUPS WITH COPRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 54-65
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
A TORSION-FREE ABELIAN GROUP EXISTS WHOSE QUOTIENT GROUP MODULO THE SQUARE SUBGROUP IS NOT A NIL-GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 30 August 2016, pp. 449-456
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
On n-Sums in an Abelian Group
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 419-435
-
- Article
- Export citation
ON A PARTITION PROBLEM OF FINITE ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 29 April 2015, pp. 24-31
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
STRONGLY INVARIANT SUBGROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 431-443
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation