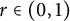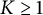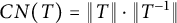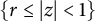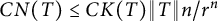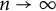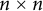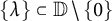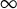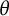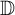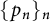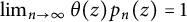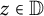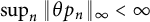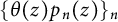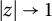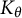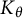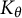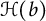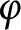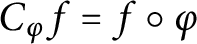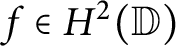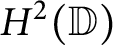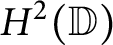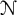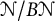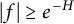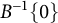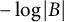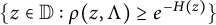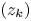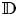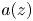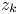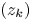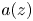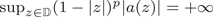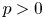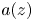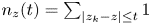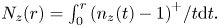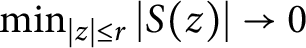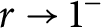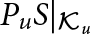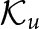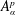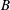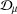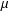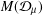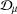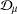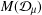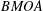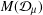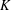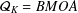14 results in 30Jxx
On the condition number of a Kreiss matrix
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1376-1390
- Print publication:
- December 2023
-
- Article
- Export citation
Constructions of some families of smooth Cauchy transforms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 26 January 2023, pp. 319-344
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cyclic inner functions in growth classes and applications to approximation problems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 749-760
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Model spaces invariant under composition operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 25 March 2022, pp. 204-217
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weakly separated Bessel systems of model spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 04 October 2021, pp. 723-742
- Print publication:
- September 2022
-
- Article
- Export citation
Invertibility Threshold for Nevanlinna Quotient Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 September 2021, pp. 225-244
- Print publication:
- February 2023
-
- Article
- Export citation
On non-separated zero sequences of solutions of a linear differential equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 247-261
-
- Article
- Export citation
Characterizations of Hankel operators in the essential commutant of quasicontinuous Toeplitz operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 44-51
- Print publication:
- March 2022
-
- Article
- Export citation
On the decay of singular inner functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 902-905
- Print publication:
- December 2021
-
- Article
- Export citation
The Dual of the Compressed Shift
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 April 2020, pp. 98-111
- Print publication:
- March 2021
-
- Article
- Export citation
Derivatives of Blaschke Products and Model Space Functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 12 November 2019, pp. 716-725
- Print publication:
- December 2020
-
- Article
- Export citation
Range Spaces of Co-Analytic Toeplitz Operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 6 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1261-1283
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
MÖBIUS INVARIANT FUNCTION SPACES AND DIRICHLET SPACES WITH SUPERHARMONIC WEIGHTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 12 July 2018, pp. 1-18
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
ON THE COMPLEXITY OF FINDING A NECESSARY AND SUFFICIENT CONDITION FOR BLASCHKE-OSCILLATORY EQUATIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 543-554
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation