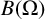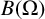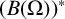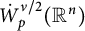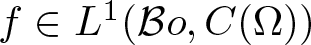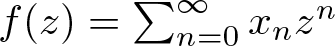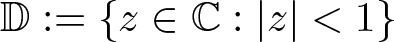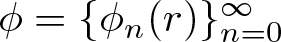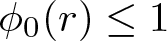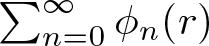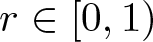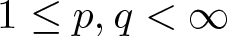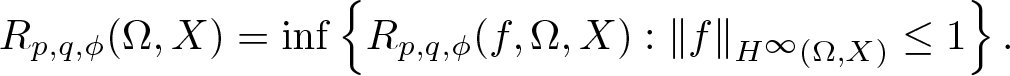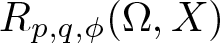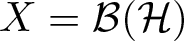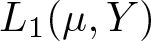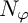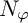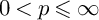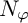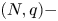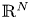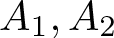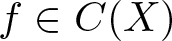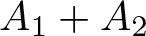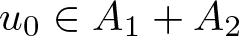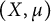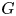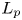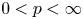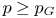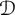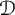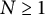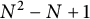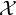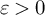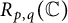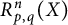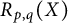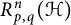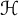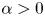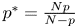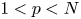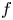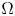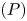195 results in 46Exx
EVALUATION FUNCTIONS AND REFLEXIVITY OF BANACH SPACES OF HOLOMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1-14
-
- Article
- Export citation
Dirichlet-type spaces of the unit bidisc and toral 2-isometries
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sobolev trace-type inequalities via time-space fractional heat equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The degree one Laguerre–Pólya class and the shuffle-word-embedding conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 28 February 2024, pp. 1-8
-
- Article
- Export citation
Multidimensional Frank–Laptev–Weidl improvement of the hardy inequality
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 151-167
-
- Article
- Export citation
On traces of Bochner representable operators on the space of bounded measurable functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 224-235
-
- Article
- Export citation
Linear homeomorphisms of function spaces and the position of a space in its compactification
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-22
-
- Article
- Export citation
Bohr radius for Banach spaces on simply connected domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 113-141
-
- Article
- Export citation
On weakly almost square Banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 05 October 2023, pp. 979-997
-
- Article
- Export citation
MULTIPLIERS AND CHARACTERIZATION OF THE DUAL OF NEVANLINNA-TYPE SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 216-240
- Print publication:
- March 2024
-
- Article
- Export citation
A weighted Trudinger–Moser inequalities and applications to some weighted $(N,q)-$
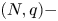 Laplacian equation in $\mathbb {R}^N$
Laplacian equation in $\mathbb {R}^N$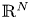 with new exponential growth conditions
with new exponential growth conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-52
-
- Article
- Export citation
A Chebyshev-type alternation theorem for best approximation by a sum of two algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 01 September 2023, pp. 971-978
-
- Article
- Export citation
Uncertainty principles in holomorphic function spaces on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 122-136
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Families of Young functions and limits of Orlicz norms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 26-39
- Print publication:
- March 2024
-
- Article
- Export citation
Isometric actions on Lp-spaces: dependence on the value of p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1300-1313
- Print publication:
- June 2023
-
- Article
- Export citation
REFLEXIVITY INDEX OF THE PRODUCT OF SOME TOPOLOGICAL SPACES AND LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 376-387
- Print publication:
- April 2024
-
- Article
- Export citation
Determining sets for holomorphic functions on the symmetrized bidisk
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 984-996
- Print publication:
- September 2023
-
- Article
- Export citation
BANACH SPACES IN WHICH LARGE SUBSETS OF SPHERES CONCENTRATE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 737-752
- Print publication:
- March 2024
-
- Article
- Export citation
Estimates for generalized Bohr radii in one and higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 682-699
- Print publication:
- June 2023
-
- Article
- Export citation
Multiple solutions for a class of quasilinear problems with double criticality
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 21 October 2022, pp. 1011-1047
-
- Article
- Export citation