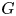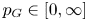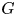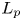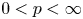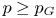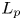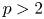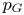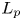1. Introduction
The study of affine isometric actions of groups on Banach spaces is an important theme in mathematics that is related to many other topics such as group cohomology, fixed point properties and geometric group theory. The case of actions on Hilbert spaces is very well-studied. For example, it is known that a second countable locally compact group ![]() $G$ has an affine isometric action on Hilbert spaces without fixed points (respectively, proper) if and only if
$G$ has an affine isometric action on Hilbert spaces without fixed points (respectively, proper) if and only if ![]() $G$ does not have Kazhdan's property (T) (respectively, has the Haagerup property). The question of the behaviour of actions on other
$G$ does not have Kazhdan's property (T) (respectively, has the Haagerup property). The question of the behaviour of actions on other ![]() $L^p$ spaces (raised by Gromov in [Reference GromovGro93, §
$L^p$ spaces (raised by Gromov in [Reference GromovGro93, § ![]() $6.D_3$]) is less well-understood. There are interesting phenomena that can occur: while the groups
$6.D_3$]) is less well-understood. There are interesting phenomena that can occur: while the groups ![]() $G=\mathrm {Sp}(n,1)$ have property (T), Pansu showed in [Reference PansuPan89] that they admit affine isometric actions without fixed points on
$G=\mathrm {Sp}(n,1)$ have property (T), Pansu showed in [Reference PansuPan89] that they admit affine isometric actions without fixed points on ![]() $L_p(G)$ for all
$L_p(G)$ for all ![]() $p > 4n+2$ (and actually proper actions by [Reference De Cornulier, Tessera and ValetteDCTV08]). This was generalized by Bourdon and Pajot in [Reference Bourdon and PajotBP03]. In [Reference YuYu05], Yu proved that any hyperbolic group
$p > 4n+2$ (and actually proper actions by [Reference De Cornulier, Tessera and ValetteDCTV08]). This was generalized by Bourdon and Pajot in [Reference Bourdon and PajotBP03]. In [Reference YuYu05], Yu proved that any hyperbolic group ![]() $\Gamma$ admits a proper affine isometric action on
$\Gamma$ admits a proper affine isometric action on ![]() $\ell ^p(\Gamma \times \Gamma )$ for all
$\ell ^p(\Gamma \times \Gamma )$ for all ![]() $p$ large enough, see also [Reference NicaNic13]. For more results and references, we refer to [Reference Bader, Furman, Gelander and MonodBFGM07] where a systematic study of affine isometric actions of groups on
$p$ large enough, see also [Reference NicaNic13]. For more results and references, we refer to [Reference Bader, Furman, Gelander and MonodBFGM07] where a systematic study of affine isometric actions of groups on ![]() $L_p$-spaces was undertaken. As suggested by the previous results, it is natural to expect that for a given group
$L_p$-spaces was undertaken. As suggested by the previous results, it is natural to expect that for a given group ![]() $G$, it should be ‘easier’ to act isometrically on an
$G$, it should be ‘easier’ to act isometrically on an ![]() $L_p$-space when the value of
$L_p$-space when the value of ![]() $p$ gets larger. The following questions by Chatterji, Druţu and Haglund makes this expectation precise.
$p$ gets larger. The following questions by Chatterji, Druţu and Haglund makes this expectation precise.
Question 1.1 [Reference Chatterji, Druţu and HaglundCDH10, Question 1.8]
Let ![]() $G$ be a group and
$G$ be a group and ![]() $p>q \geq 2$. If every isometric action of
$p>q \geq 2$. If every isometric action of ![]() $G$ on an
$G$ on an ![]() $L^p$ space has a fixed point, is the same true for
$L^p$ space has a fixed point, is the same true for ![]() $L^q$ spaces? If
$L^q$ spaces? If ![]() $G$ admits a proper isometric action on an
$G$ admits a proper isometric action on an ![]() $L^q$ space, does it also admit a proper isometric action on an
$L^q$ space, does it also admit a proper isometric action on an ![]() $L^p$ space?
$L^p$ space?
The fact that these questions have a positive answer is sometimes referred to as Druţu's conjecture [Reference NowakNow15, Reference Lavy and OlivierLO21].
The main result of this paper confirms this intuition and, in particular, answers these questions. In this statement as in the whole paper, ![]() $L_p$ space means
$L_p$ space means ![]() $L_p(X,\mu )$ for a standard measure space
$L_p(X,\mu )$ for a standard measure space ![]() $(X,\mu )$.
$(X,\mu )$.
Theorem 1 Let ![]() $G$ be a topological group. Take
$G$ be a topological group. Take ![]() $0 < p \leq q < \infty$. Then for every continuous affine isometric action
$0 < p \leq q < \infty$. Then for every continuous affine isometric action ![]() $\alpha : G \curvearrowright L_p$, there exists a continuous affine isometric action
$\alpha : G \curvearrowright L_p$, there exists a continuous affine isometric action ![]() $\beta : G \curvearrowright L_q$ such that
$\beta : G \curvearrowright L_q$ such that ![]() $\| \alpha _g(0) \|^p_{L_p}=\| \beta _g(0) \|^q_{L_q}$ for all
$\| \alpha _g(0) \|^p_{L_p}=\| \beta _g(0) \|^q_{L_q}$ for all ![]() $g \in G$.
$g \in G$.
Theorem 1 implies, in particular, that if a group ![]() $G$ has a continuous action by isometries on an
$G$ has a continuous action by isometries on an ![]() $L_p$ space with unbounded (respectively, metrically proper) orbits, then it has such an action on an
$L_p$ space with unbounded (respectively, metrically proper) orbits, then it has such an action on an ![]() $L_q$ space.
$L_q$ space.
Corollary 2 For every topological group ![]() $G$:
$G$:
(i) the set of values of
 $p \in (0,\infty )$ such that
$p \in (0,\infty )$ such that  $G$ admits a continuous action by isometries on an
$G$ admits a continuous action by isometries on an  $L_p$ space with unbounded orbits is an interval of the form
$L_p$ space with unbounded orbits is an interval of the form  $(p_G,\infty )$ or
$(p_G,\infty )$ or  $[p_G,\infty )$ for some
$[p_G,\infty )$ for some  $p_G \in \{0\} \cup [2,\infty ]$;
$p_G \in \{0\} \cup [2,\infty ]$;(ii) the set of values of
 $p \in (0,\infty )$ such that
$p \in (0,\infty )$ such that  $G$ admits a proper continuous action by isometries on an
$G$ admits a proper continuous action by isometries on an  $L_p$ space is an interval of the form
$L_p$ space is an interval of the form  $(p'_G,\infty )$ or
$(p'_G,\infty )$ or  $[p'_G,\infty )$ for some
$[p'_G,\infty )$ for some  $p'_G \in \{0\} \cup [2,\infty ]$.
$p'_G \in \{0\} \cup [2,\infty ]$.
Recall that for ![]() $1 \leq p<\infty$, an action by isometries on an
$1 \leq p<\infty$, an action by isometries on an ![]() $L_p$ space has a fixed point if and only if it has bounded orbits ([Reference Bader, Furman, Gelander and MonodBFGM07, Lemma 2.14] for
$L_p$ space has a fixed point if and only if it has bounded orbits ([Reference Bader, Furman, Gelander and MonodBFGM07, Lemma 2.14] for ![]() $p \neq 1$, [Reference Bader, Gelander and MonodBGM12] for
$p \neq 1$, [Reference Bader, Gelander and MonodBGM12] for ![]() $p=1$). Thus, Corollary 2 answers positively Question 1.1. A partial answer for
$p=1$). Thus, Corollary 2 answers positively Question 1.1. A partial answer for ![]() $\ell _p$ spaces had already been obtained independently by Czuroń [Reference CzurońCzu17] and Lavy and Olivier [Reference Lavy and OlivierLO21]. In [Reference Lavy and OlivierLO21] actions coming from ergodic probability measure-preserving actions were also covered. Unlike these previous results, it is worth mentioning that in Theorem 1, the linear part of the action
$\ell _p$ spaces had already been obtained independently by Czuroń [Reference CzurońCzu17] and Lavy and Olivier [Reference Lavy and OlivierLO21]. In [Reference Lavy and OlivierLO21] actions coming from ergodic probability measure-preserving actions were also covered. Unlike these previous results, it is worth mentioning that in Theorem 1, the linear part of the action ![]() $\beta$ that we construct is very different from the linear part of the original action
$\beta$ that we construct is very different from the linear part of the original action ![]() $\alpha$. We refer to Theorem 4.3 for a more precise statement.
$\alpha$. We refer to Theorem 4.3 for a more precise statement.
When ![]() $G$ is a second countable locally compact group, it is known that
$G$ is a second countable locally compact group, it is known that ![]() $p_G > 0$ if and only if
$p_G > 0$ if and only if ![]() $G$ has property (T) [Reference Bader, Furman, Gelander and MonodBFGM07], in which case we must have
$G$ has property (T) [Reference Bader, Furman, Gelander and MonodBFGM07], in which case we must have ![]() $p_G \geq 2$ (in fact, by an argument of Fisher and Margulis from [Reference Fisher and MargulisFM05] that appears in [Reference Bader, Furman, Gelander and MonodBFGM07], one can even show that
$p_G \geq 2$ (in fact, by an argument of Fisher and Margulis from [Reference Fisher and MargulisFM05] that appears in [Reference Bader, Furman, Gelander and MonodBFGM07], one can even show that ![]() $p_G > 2$ and that
$p_G > 2$ and that ![]() $G$ admits a continuous action by isometries on an
$G$ admits a continuous action by isometries on an ![]() $L_p$ space without fixed points for
$L_p$ space without fixed points for ![]() $p=p_G$, see also [Reference Lavy and OlivierLO21, Reference Druţu and KapovichDK18, Reference de la SalleSal19]). Similarly, it is known that
$p=p_G$, see also [Reference Lavy and OlivierLO21, Reference Druţu and KapovichDK18, Reference de la SalleSal19]). Similarly, it is known that ![]() $p'_G > 0$ if and only if
$p'_G > 0$ if and only if ![]() $G$ does not have the Haagerup property, in which case
$G$ does not have the Haagerup property, in which case ![]() $p'_G \geq 2$ (see [Reference NowakNow06]). This last fact, as well as the fact that
$p'_G \geq 2$ (see [Reference NowakNow06]). This last fact, as well as the fact that ![]() $p_G \notin (0,2)$, if often stated for second countable locally compact groups, but they are true for arbitrary topological groups, see Proposition 3.1 (but the fact that
$p_G \notin (0,2)$, if often stated for second countable locally compact groups, but they are true for arbitrary topological groups, see Proposition 3.1 (but the fact that ![]() $p'_G \notin (0,2)$ is meaningful only for locally compact groups, as
$p'_G \notin (0,2)$ is meaningful only for locally compact groups, as ![]() $p'_G=\infty$ trivially for nonlocally compact groups). The critical constant
$p'_G=\infty$ trivially for nonlocally compact groups). The critical constant ![]() $p_G$ and
$p_G$ and ![]() $p'_G$ are different in general. For example, if
$p'_G$ are different in general. For example, if ![]() $G$ is a locally compact group that has neither Kazhdan's property (T) nor Haagerup property, then
$G$ is a locally compact group that has neither Kazhdan's property (T) nor Haagerup property, then ![]() $p_G=0$ and
$p_G=0$ and ![]() $p'_G \geq 2$. It is also known that, among Gromov-hyperbolic groups, the value of
$p'_G \geq 2$. It is also known that, among Gromov-hyperbolic groups, the value of ![]() $p_G$ is unbounded, and explicit lower bounds have been obtained for random groups [Reference Druţu and MackayDM19] (see also [Reference de Laat and de la SalleLS21, Reference OppenheinOpp20]).
$p_G$ is unbounded, and explicit lower bounds have been obtained for random groups [Reference Druţu and MackayDM19] (see also [Reference de Laat and de la SalleLS21, Reference OppenheinOpp20]).
The linear part of the action ![]() $\beta$ constructed in Theorem 1 comes from an action on
$\beta$ constructed in Theorem 1 comes from an action on ![]() $(X,\mu )$ preserving an infinite measure. It is not possible to achieve the same with a finite measure. Indeed, when
$(X,\mu )$ preserving an infinite measure. It is not possible to achieve the same with a finite measure. Indeed, when ![]() $G$ has property (T), any affine action on
$G$ has property (T), any affine action on ![]() $L_p$ (
$L_p$ (![]() $1\leq p<\infty$) whose linear part comes from a probability measure-preserving action has a fixed point. This is known when
$1\leq p<\infty$) whose linear part comes from a probability measure-preserving action has a fixed point. This is known when ![]() $G$ is discrete [Reference Lavy and OlivierLO21] or when
$G$ is discrete [Reference Lavy and OlivierLO21] or when ![]() $G$ admits a finite Kazhdan set [Reference Czuroń and KalantarCK20]. In general, this is a particular case of the following result dealing with noncommutative
$G$ admits a finite Kazhdan set [Reference Czuroń and KalantarCK20]. In general, this is a particular case of the following result dealing with noncommutative ![]() $L_p$ spaces. Its proof relies on a general observation of independent interest: under a spectral gap and uniform convexity assumption, any cohomology class with values in an isometric representation has a unique harmonic representant (Lemma 5.1).
$L_p$ spaces. Its proof relies on a general observation of independent interest: under a spectral gap and uniform convexity assumption, any cohomology class with values in an isometric representation has a unique harmonic representant (Lemma 5.1).
Theorem 3 Let ![]() $G$ be a locally compact property (T) group. An action
$G$ be a locally compact property (T) group. An action ![]() $\alpha : G \curvearrowright L_p(M)$ by affine isometries on the noncommutative
$\alpha : G \curvearrowright L_p(M)$ by affine isometries on the noncommutative ![]() $L_p$ space of a von Neumann algebra
$L_p$ space of a von Neumann algebra ![]() $M$ has a fixed point in the following two cases:
$M$ has a fixed point in the following two cases:
•
 $1< p\leq 2$ and
$1< p\leq 2$ and  $M=B(H)$ for a Hilbert space
$M=B(H)$ for a Hilbert space  $H$;
$H$;•
 $2 \leq p <\infty$ and the linear part of
$2 \leq p <\infty$ and the linear part of  $\alpha$ comes from an action by automorphisms of
$\alpha$ comes from an action by automorphisms of  $M$ preserving a faithful normal state.
$M$ preserving a faithful normal state.
We insist that the first conclusion of the theorem is not trivial. It is indeed an open question by Masato Mimura whether a locally compact property (T) group can have an unbounded action by isometries on a noncommutative ![]() $L_p$ space for
$L_p$ space for ![]() $p<2$ (as explained previously this is not possible for usual
$p<2$ (as explained previously this is not possible for usual ![]() $L_p$ spaces), and the previous result provides a negative answer for Schatten classes.
$L_p$ spaces), and the previous result provides a negative answer for Schatten classes.
It is known that the metric space ![]() $(L_p,\|\cdot \|_p^{ {p}/{q}})$ isometrically embeds into
$(L_p,\|\cdot \|_p^{ {p}/{q}})$ isometrically embeds into ![]() $(L_q,\|\cdot \|_q)$ when
$(L_q,\|\cdot \|_q)$ when ![]() $p \leq q$ (see [Reference Mendel and NaorMN04, Remark 5.10]). This implies the following inequalities for the compression exponents [Reference Naor and PeresNP11] of a compactly generated group
$p \leq q$ (see [Reference Mendel and NaorMN04, Remark 5.10]). This implies the following inequalities for the compression exponents [Reference Naor and PeresNP11] of a compactly generated group ![]() $G$
$G$
As a consequence of Theorem 1, we obtain the same inequalities for the equivariant compression exponents:
This inequality is often strict, see [Reference Naor and PeresNP11].
We also note that Theorem 1 can be applied to the whole isometry group of ![]() $L_p$ and this yields the following corollary.
$L_p$ and this yields the following corollary.
Corollary 4 Take ![]() $0 < p \leq q < \infty$. Then
$0 < p \leq q < \infty$. Then ![]() $\mathord {\text { Isom}}(L_p)$ is isomorphic as a topological group to a closed subgroup of
$\mathord {\text { Isom}}(L_p)$ is isomorphic as a topological group to a closed subgroup of ![]() $\mathord {\text { Isom}}(L_q)$.
$\mathord {\text { Isom}}(L_q)$.
Note that if ![]() $p > 2$, the subgroup of translations
$p > 2$, the subgroup of translations ![]() $L_p \subset \mathord {\text { Isom}}(L_p)$ is not unitarily representable [Reference MegrelishviliMeg08, Theorem 3.1]. In particular, it cannot be embedded as a closed subgroup of
$L_p \subset \mathord {\text { Isom}}(L_p)$ is not unitarily representable [Reference MegrelishviliMeg08, Theorem 3.1]. In particular, it cannot be embedded as a closed subgroup of ![]() $\mathord {\text { Isom}}(L_2)$, which is unitarily representable (by using the affine Gaussian functor [Reference Arano, Isono and MarrakchiAIM21, Proposition 4.8] for example).
$\mathord {\text { Isom}}(L_2)$, which is unitarily representable (by using the affine Gaussian functor [Reference Arano, Isono and MarrakchiAIM21, Proposition 4.8] for example).
In view of Corollary 2, it is interesting to determine the parameters ![]() $p_G$ and
$p_G$ and ![]() $p'_G$, at least for some classes of groups. This motivates the study of their permanence properties, that we initiate in the last section of his paper. In particular, we prove the following result, which shows that they behave nicely with respect to
$p'_G$, at least for some classes of groups. This motivates the study of their permanence properties, that we initiate in the last section of his paper. In particular, we prove the following result, which shows that they behave nicely with respect to ![]() $L_p$-measure equivalence (see Theorem 5 and the definitions preceding it). This answers a question by David Fisher (private communication).
$L_p$-measure equivalence (see Theorem 5 and the definitions preceding it). This answers a question by David Fisher (private communication).
Theorem 5 If two compactly generated locally compact groups ![]() $G_1$ and
$G_1$ and ![]() $G_2$ are
$G_2$ are ![]() $L_p$ measure equivalent, then the critical constants defined in Corollary 2 satisfy
$L_p$ measure equivalent, then the critical constants defined in Corollary 2 satisfy
This paper is organized as follows. After some preliminaries in § 2, Theorem 1 and its Corollary 4 are proved in § 3 for ![]() $p=2$ and § 4 in the general case. Section 5 deals with harmonic cocycles and the proof of Theorem 3. In § 6, stability properties of the constants
$p=2$ and § 4 in the general case. Section 5 deals with harmonic cocycles and the proof of Theorem 3. In § 6, stability properties of the constants ![]() $p_G$ and
$p_G$ and ![]() $p'_G$ are investigated and in particular, Theorem 5 is proved.
$p'_G$ are investigated and in particular, Theorem 5 is proved.
2. Preliminaries
2.1 Nonsingular actions
Let ![]() $(X,\mu )$ be a
$(X,\mu )$ be a ![]() $\sigma$-finite standard measure space (we always assume that our measure spaces are standard and we omit the
$\sigma$-finite standard measure space (we always assume that our measure spaces are standard and we omit the ![]() $\sigma$-algebra). We denote by
$\sigma$-algebra). We denote by ![]() $[\mu ]$ the measure class of
$[\mu ]$ the measure class of ![]() $\mu$. We denote by
$\mu$. We denote by ![]() $\mathord {\text { Aut}}(X,[\mu ])$ the group of all nonsingular (preserving the measure class
$\mathord {\text { Aut}}(X,[\mu ])$ the group of all nonsingular (preserving the measure class ![]() $[\mu ]$) automorphisms of
$[\mu ]$) automorphisms of ![]() $(X,\mu )$ up to equality almost everywhere. It is known that
$(X,\mu )$ up to equality almost everywhere. It is known that ![]() $\mathord {\text { Aut}}(X,[\mu ])$ is a Polish group for the topology of pointwise convergence on probability measures: a sequence
$\mathord {\text { Aut}}(X,[\mu ])$ is a Polish group for the topology of pointwise convergence on probability measures: a sequence ![]() $\theta _n \in \mathord {\text { Aut}}(X,[\mu ])$ converges to the identity if and only if
$\theta _n \in \mathord {\text { Aut}}(X,[\mu ])$ converges to the identity if and only if ![]() $\lim _n \| (\theta _n)_* \nu - \nu \|_1=0$ for every probability measure
$\lim _n \| (\theta _n)_* \nu - \nu \|_1=0$ for every probability measure ![]() $\nu \in [\mu ]$. We denote by
$\nu \in [\mu ]$. We denote by ![]() $\mathord {\text { Aut}}(X,\mu )$ the group of all measure-preserving automorphisms of
$\mathord {\text { Aut}}(X,\mu )$ the group of all measure-preserving automorphisms of ![]() $(X,\mu )$ up to equality almost everywhere. It is a closed subgroup of
$(X,\mu )$ up to equality almost everywhere. It is a closed subgroup of ![]() $\mathord {\text { Aut}}(X,[\mu ])$. A continuous nonsingular action
$\mathord {\text { Aut}}(X,[\mu ])$. A continuous nonsingular action ![]() $\sigma : G \curvearrowright (X,\mu )$ of a topological group
$\sigma : G \curvearrowright (X,\mu )$ of a topological group ![]() $G$ is a continuous homomorphism
$G$ is a continuous homomorphism ![]() $\sigma : G \ni g \mapsto \sigma _g \in \mathord {\text { Aut}}(X,[\mu ])$.
$\sigma : G \ni g \mapsto \sigma _g \in \mathord {\text { Aut}}(X,[\mu ])$.
2.2 Cohomology
Let ![]() $\pi : G \curvearrowright V$ be a continuous linear representation of a topological group
$\pi : G \curvearrowright V$ be a continuous linear representation of a topological group ![]() $G$ on a topological vector space
$G$ on a topological vector space ![]() $V$. We denote by
$V$. We denote by ![]() $Z^1(G,\pi,V)$ the set of all continuous
$Z^1(G,\pi,V)$ the set of all continuous ![]() $1$-cocycles, i.e. all continuous maps
$1$-cocycles, i.e. all continuous maps ![]() $c : G \rightarrow V$ such that
$c : G \rightarrow V$ such that ![]() $c(gh)=c(g)+g \cdot c(h)$ for all
$c(gh)=c(g)+g \cdot c(h)$ for all ![]() $g,h \in G$. We denote by
$g,h \in G$. We denote by ![]() $B^1(G,\pi,V) \subset Z^1(G,\pi,V)$ the set of all coboundaries, i.e. cocycles
$B^1(G,\pi,V) \subset Z^1(G,\pi,V)$ the set of all coboundaries, i.e. cocycles ![]() $c$ of the form
$c$ of the form ![]() $c(g)=g \cdot v -v$ for some
$c(g)=g \cdot v -v$ for some ![]() $v \in V$.
$v \in V$.
Let ![]() $\sigma : G \curvearrowright (X,\mu )$ be a continuous nonsingular action of a topological group
$\sigma : G \curvearrowright (X,\mu )$ be a continuous nonsingular action of a topological group ![]() $G$. Let
$G$. Let ![]() $A$ be an abelian topological group (here we use the additive notation for
$A$ be an abelian topological group (here we use the additive notation for ![]() $A$ but this might change sometimes when
$A$ but this might change sometimes when ![]() $A=\mathbf {T}$). We denote by
$A=\mathbf {T}$). We denote by ![]() $Z^1_\sigma (G,A)$ the set of all
$Z^1_\sigma (G,A)$ the set of all ![]() $A$-valued
$A$-valued ![]() $1$-cocycles of
$1$-cocycles of ![]() $\sigma$, i.e. all continuous functions
$\sigma$, i.e. all continuous functions ![]() $c : G \mapsto L_0(X,\mu,A)$ such that
$c : G \mapsto L_0(X,\mu,A)$ such that ![]() $c(gh)=c(g)+\sigma _g(c(h))$. Here for every
$c(gh)=c(g)+\sigma _g(c(h))$. Here for every ![]() $f \in L_0(X,\mu,A)$, we use the notation
$f \in L_0(X,\mu,A)$, we use the notation ![]() $\sigma _g(f)=f \circ \sigma _g^{-1}$. We denote by
$\sigma _g(f)=f \circ \sigma _g^{-1}$. We denote by ![]() $B^1_\sigma (G,A)$ the set of all
$B^1_\sigma (G,A)$ the set of all ![]() $1$-coboundaries, i.e. cocycles of the form
$1$-coboundaries, i.e. cocycles of the form ![]() $g \mapsto \sigma _g(f)-f$ for some
$g \mapsto \sigma _g(f)-f$ for some ![]() $f \in L_0(X,\mu,A)$. Finally, we denote by
$f \in L_0(X,\mu,A)$. Finally, we denote by ![]() $H^1_\sigma (G,A)=Z^1_\sigma (G,A)/B^1_\sigma (G,A)$ the cohomology group of
$H^1_\sigma (G,A)=Z^1_\sigma (G,A)/B^1_\sigma (G,A)$ the cohomology group of ![]() $\sigma$.
$\sigma$.
2.3 Skew-product actions
Let ![]() $\sigma : G \curvearrowright (X,\mu )$ be a continuous nonsingular action of a topological group
$\sigma : G \curvearrowright (X,\mu )$ be a continuous nonsingular action of a topological group ![]() $G$. Suppose that
$G$. Suppose that ![]() $A$ is a locally compact abelian group and let
$A$ is a locally compact abelian group and let ![]() $m$ be the Haar measure of
$m$ be the Haar measure of ![]() $A$. Then for every
$A$. Then for every ![]() $c \in Z^1_\sigma (G,A)$, we can define a new continuous nonsingular action
$c \in Z^1_\sigma (G,A)$, we can define a new continuous nonsingular action ![]() $\sigma \rtimes c$ of
$\sigma \rtimes c$ of ![]() $G$ on
$G$ on ![]() $(X \times A, \mu \otimes m)$ by the formula
$(X \times A, \mu \otimes m)$ by the formula
The action ![]() $\sigma \rtimes c$ is called the skew-product action of
$\sigma \rtimes c$ is called the skew-product action of ![]() $\sigma$ by
$\sigma$ by ![]() $c$. Define a function
$c$. Define a function ![]() $h : X \times A \rightarrow A$ by
$h : X \times A \rightarrow A$ by ![]() $h(x,a)=a$ for all
$h(x,a)=a$ for all ![]() $(x,a) \in X \times A$. Then, by construction, we have
$(x,a) \in X \times A$. Then, by construction, we have ![]() $c(g) \otimes 1=(\sigma \rtimes c)_g(h)-h$. Thus, the skew-product action
$c(g) \otimes 1=(\sigma \rtimes c)_g(h)-h$. Thus, the skew-product action ![]() $\sigma \rtimes c$ turns the cocycle
$\sigma \rtimes c$ turns the cocycle ![]() $c$ into a coboundary.
$c$ into a coboundary.
2.4 The Maharam extension
Let ![]() $\sigma : G \curvearrowright (X,\mu )$ be a continuous nonsingular action of a topological group
$\sigma : G \curvearrowright (X,\mu )$ be a continuous nonsingular action of a topological group ![]() $G$. Then we can define the Radon–Nikodym cocycle
$G$. Then we can define the Radon–Nikodym cocycle ![]() $D \in Z^1_\sigma (G,\mathbf {R}^*_+)$ by the formula
$D \in Z^1_\sigma (G,\mathbf {R}^*_+)$ by the formula ![]() $D(g)= {{d} (\sigma _g)_* \mu }/{{d}\mu }$ for all
$D(g)= {{d} (\sigma _g)_* \mu }/{{d}\mu }$ for all ![]() $g \in G$. The skew-product action
$g \in G$. The skew-product action ![]() $\widetilde {\sigma }=\sigma \rtimes D^{-1} : G \curvearrowright X \times \mathbf {R}^*_+$ is called the Maharam extension of
$\widetilde {\sigma }=\sigma \rtimes D^{-1} : G \curvearrowright X \times \mathbf {R}^*_+$ is called the Maharam extension of ![]() $\sigma$. Note that
$\sigma$. Note that ![]() $\widetilde {\sigma }$ preserves the measure
$\widetilde {\sigma }$ preserves the measure ![]() $\mu \otimes {d} \lambda$ where
$\mu \otimes {d} \lambda$ where ![]() $d \lambda$ is the restriction to
$d \lambda$ is the restriction to ![]() $\mathbf {R}^*_+$ of the Lebesgue measure of
$\mathbf {R}^*_+$ of the Lebesgue measure of ![]() $\mathbf {R}$.
$\mathbf {R}$.
2.5 Isometric actions on  $L_p$-spaces
$L_p$-spaces
Take ![]() $p > 0$ and let
$p > 0$ and let ![]() $(X,\mu )$ be a
$(X,\mu )$ be a ![]() $\sigma$-finite measure space. For every
$\sigma$-finite measure space. For every ![]() $\theta : \mathord {\text { Aut}}(X,[\mu ])$, we define a linear isometry of
$\theta : \mathord {\text { Aut}}(X,[\mu ])$, we define a linear isometry of ![]() $L_p(X,\mu )$ given by
$L_p(X,\mu )$ given by
 \[ f \mapsto \bigg( \frac{\theta_* \mu}{\mu} \bigg)^{1/p} \theta(f). \]
\[ f \mapsto \bigg( \frac{\theta_* \mu}{\mu} \bigg)^{1/p} \theta(f). \]
The group ![]() $L_0(X,[\mu ],\mathbf {T})$ also acts by multiplication on
$L_0(X,[\mu ],\mathbf {T})$ also acts by multiplication on ![]() $L_p(X,\mu )$. We thus obtain a continuous linear isometric representation
$L_p(X,\mu )$. We thus obtain a continuous linear isometric representation
It follows from the Banach–Lamperti theorem that this map is surjective when ![]() $p \neq 2$. Note that if
$p \neq 2$. Note that if ![]() $\nu \in [\mu ]$, the canonical isometry
$\nu \in [\mu ]$, the canonical isometry ![]() $L_p(X,\mu ) \rightarrow L_p(X,\nu )$ given by
$L_p(X,\mu ) \rightarrow L_p(X,\nu )$ given by ![]() $f \mapsto ( {\mu }/{\nu } )^{1/p}f$ is equivariant with respect to the natural actions
$f \mapsto ( {\mu }/{\nu } )^{1/p}f$ is equivariant with respect to the natural actions ![]() $\pi ^{p,\mu }$ and
$\pi ^{p,\mu }$ and ![]() $\pi ^{p,\nu }$ of
$\pi ^{p,\nu }$ of ![]() $\mathord {\text { Aut}}(X,[\mu ]) \ltimes L_0(X,[\mu ],\mathbf {T})$.
$\mathord {\text { Aut}}(X,[\mu ]) \ltimes L_0(X,[\mu ],\mathbf {T})$.
Let ![]() $\sigma : G \rightarrow \mathord {\text { Aut}}(X,[\mu ])$ be a continuous nonsingular action of a topological group
$\sigma : G \rightarrow \mathord {\text { Aut}}(X,[\mu ])$ be a continuous nonsingular action of a topological group ![]() $G$. Then
$G$. Then ![]() $\sigma ^{p,\mu } =\pi ^{p,\mu } \circ \sigma$ is a continuous linear isometric representation of
$\sigma ^{p,\mu } =\pi ^{p,\mu } \circ \sigma$ is a continuous linear isometric representation of ![]() $G$ on
$G$ on ![]() $L_p(X,\mu )$. Let
$L_p(X,\mu )$. Let ![]() $D \in Z^1_\sigma (G,R^*_+)$ be the Radon–Nikodym cocycle. Then for every
$D \in Z^1_\sigma (G,R^*_+)$ be the Radon–Nikodym cocycle. Then for every ![]() $p > 0$ and every
$p > 0$ and every ![]() $g \in G$, the isometry
$g \in G$, the isometry ![]() $\sigma ^{p,\mu }(g)$ is given by the formula
$\sigma ^{p,\mu }(g)$ is given by the formula
Now take some cocycle ![]() $\omega \in Z^1_\sigma (G,\mathbf {T})$. Then the map
$\omega \in Z^1_\sigma (G,\mathbf {T})$. Then the map ![]() $g \mapsto \omega (g) \sigma ^p_g$ is again a continuous linear isometric representation of
$g \mapsto \omega (g) \sigma ^p_g$ is again a continuous linear isometric representation of ![]() $G$ on
$G$ on ![]() $L_p(X,\mu )$. Conversely, if
$L_p(X,\mu )$. Conversely, if ![]() $p \neq 2$, it follows from the Banach–Lamperti theorem that every continuous linear isometric representation of
$p \neq 2$, it follows from the Banach–Lamperti theorem that every continuous linear isometric representation of ![]() $G$ on
$G$ on ![]() $L_p(X,\mu )$ is of the form
$L_p(X,\mu )$ is of the form ![]() $\pi : g \mapsto \omega (g) \sigma ^{p,\mu }_g$ for some continuous nonsingular action
$\pi : g \mapsto \omega (g) \sigma ^{p,\mu }_g$ for some continuous nonsingular action ![]() $\sigma$ of
$\sigma$ of ![]() $G$ and some cocycle
$G$ and some cocycle ![]() $\omega \in Z^1_\sigma (G,\mathbf {T})$.
$\omega \in Z^1_\sigma (G,\mathbf {T})$.
Let ![]() $\alpha$ be an affine isometric action of
$\alpha$ be an affine isometric action of ![]() $G$ on some
$G$ on some ![]() $L_p$-space. As the affine isometry group
$L_p$-space. As the affine isometry group ![]() $\mathord {\text { Isom}}(L_p(X,\mu ))$ decomposes as a semi-direct product
$\mathord {\text { Isom}}(L_p(X,\mu ))$ decomposes as a semi-direct product
where ![]() $L_p(X,\mu )$ acts by translations, we see that
$L_p(X,\mu )$ acts by translations, we see that ![]() $\alpha$ is of the form
$\alpha$ is of the form ![]() $\alpha _g(f)=\pi (g)f+c(g)$ where
$\alpha _g(f)=\pi (g)f+c(g)$ where ![]() $\pi$ is an isometric linear representation of
$\pi$ is an isometric linear representation of ![]() $G$ on
$G$ on ![]() $L_p(X,\mu )$ and
$L_p(X,\mu )$ and ![]() $c \in Z^1(G,\pi,L_p(X,\mu ))$ is a cocycle. Observe that even when
$c \in Z^1(G,\pi,L_p(X,\mu ))$ is a cocycle. Observe that even when ![]() $\pi =\sigma ^{p,\mu }$ for some nonsingular action
$\pi =\sigma ^{p,\mu }$ for some nonsingular action ![]() $\sigma : G \curvearrowright (X,\mu )$, we do not have
$\sigma : G \curvearrowright (X,\mu )$, we do not have ![]() $Z^1(G,\sigma ^{p,\mu },L_p(X,\mu )) \subset Z^1_\sigma (G,\mathbf {C})$ unless
$Z^1(G,\sigma ^{p,\mu },L_p(X,\mu )) \subset Z^1_\sigma (G,\mathbf {C})$ unless ![]() $\sigma$ preserves the measure
$\sigma$ preserves the measure ![]() $\mu$.
$\mu$.
3. The case  $p=2$
$p=2$
Let ![]() $G$ be a topological group and let
$G$ be a topological group and let ![]() $p > 0$. We denote by
$p > 0$. We denote by ![]() $K^p(G)$ the set of all continuous functions
$K^p(G)$ the set of all continuous functions ![]() $\psi : G \rightarrow \mathbf {R}_+$ of the form
$\psi : G \rightarrow \mathbf {R}_+$ of the form ![]() $\psi (g)=\| \alpha _g(0)\|_{L_p}^p$ for some continuous affine isometric action
$\psi (g)=\| \alpha _g(0)\|_{L_p}^p$ for some continuous affine isometric action ![]() $\alpha$ of
$\alpha$ of ![]() $G$ on some
$G$ on some ![]() $L_p$-space. Note that
$L_p$-space. Note that ![]() $K^2(G)$ is the set of all continuous functions on
$K^2(G)$ is the set of all continuous functions on ![]() $G$ that are conditionally of negative type.
$G$ that are conditionally of negative type.
By using the Gaussian functor, one has the following (classical) result.
Proposition 3.1 Let ![]() $G$ be a topological group. Take
$G$ be a topological group. Take ![]() $\psi \in K^2(G)$ and
$\psi \in K^2(G)$ and ![]() $p > 0$. Then there exists a continuous probability measure-preserving action
$p > 0$. Then there exists a continuous probability measure-preserving action ![]() $\sigma : G \curvearrowright (X,\mu )$ and a cocycle
$\sigma : G \curvearrowright (X,\mu )$ and a cocycle ![]() $c \in Z^1_\sigma (G,\mathbf {R})$ such that
$c \in Z^1_\sigma (G,\mathbf {R})$ such that ![]() $\psi (g)^{ {p}/{2}}=\| c(g) \|_{L_p}^p$ for all
$\psi (g)^{ {p}/{2}}=\| c(g) \|_{L_p}^p$ for all ![]() $g \in G$. In particular,
$g \in G$. In particular, ![]() $\psi ^{ {p}/{2}} \in K^p(G)$ for all
$\psi ^{ {p}/{2}} \in K^p(G)$ for all ![]() $p > 0$.
$p > 0$.
Proof. By definition, there exists an orthogonal representation ![]() $\pi : G \rightarrow \mathcal {O}(H)$ on some Hilbert space
$\pi : G \rightarrow \mathcal {O}(H)$ on some Hilbert space ![]() $H$ and a cocycle
$H$ and a cocycle ![]() $c \in Z^1(G,\pi, H)$ such that
$c \in Z^1(G,\pi, H)$ such that ![]() $\psi (g)=\|c(g)\|^2$ for all
$\psi (g)=\|c(g)\|^2$ for all ![]() $g \in G$. Let
$g \in G$. Let ![]() $\sigma _\pi : G \curvearrowright (X,\mu )$ be the Gaussian action associated to
$\sigma _\pi : G \curvearrowright (X,\mu )$ be the Gaussian action associated to ![]() $\sigma$; see, for example, the construction in [Reference Cherix, Cowling, Jolissaint, Julg and ValetteCCJ+01, Proof of Theorem 2.2.2]. This means that there exists a linear map
$\sigma$; see, for example, the construction in [Reference Cherix, Cowling, Jolissaint, Julg and ValetteCCJ+01, Proof of Theorem 2.2.2]. This means that there exists a linear map ![]() $\xi \mapsto \widehat {\xi } \in L_0(X,\mu,\mathbf {R})$ such that
$\xi \mapsto \widehat {\xi } \in L_0(X,\mu,\mathbf {R})$ such that ![]() $\widehat {\xi }$ is a centered Gaussian random variable of variance
$\widehat {\xi }$ is a centered Gaussian random variable of variance ![]() $\| \xi \|^2$ for all
$\| \xi \|^2$ for all ![]() $\xi \in H$, and that
$\xi \in H$, and that ![]() $\sigma _{\pi }(\widehat {\xi })=\widehat {\pi (g) \xi }$ for all
$\sigma _{\pi }(\widehat {\xi })=\widehat {\pi (g) \xi }$ for all ![]() $\xi \in H$. Let
$\xi \in H$. Let ![]() $\widehat {c}(g)=\widehat {c(g)} \in L_p(X,\mu )$ for all
$\widehat {c}(g)=\widehat {c(g)} \in L_p(X,\mu )$ for all ![]() $g \in G$. Then
$g \in G$. Then ![]() $\widehat {c}$ is a cocycle for
$\widehat {c}$ is a cocycle for ![]() $\sigma _{\pi }$ and a computation shows that
$\sigma _{\pi }$ and a computation shows that ![]() $\| \widehat {c}(g) \|^p_{L_p}=C_p \| c(g)\|^p$ for all
$\| \widehat {c}(g) \|^p_{L_p}=C_p \| c(g)\|^p$ for all ![]() $g \in G$ and some constant
$g \in G$ and some constant ![]() $C_p > 0$.
$C_p > 0$.
Corollary 3.2 For every topological group ![]() $G$, we have
$G$, we have ![]() $K^2(G) \subset K^p(G)$ for all
$K^2(G) \subset K^p(G)$ for all ![]() $p \geq 2$.
$p \geq 2$.
Proof. The function ![]() $x \mapsto x^\alpha$ is a Bernstein function for all
$x \mapsto x^\alpha$ is a Bernstein function for all ![]() $0 < \alpha \leq 1$. It follows that for every
$0 < \alpha \leq 1$. It follows that for every ![]() $\psi \in K^2(G)$, we have
$\psi \in K^2(G)$, we have ![]() $\psi ^{\alpha } \in K^2(G)$, hence
$\psi ^{\alpha } \in K^2(G)$, hence ![]() $\psi ^{\alpha ({p}/{2})} \in K^p(G)$. The conclusion follows by taking
$\psi ^{\alpha ({p}/{2})} \in K^p(G)$. The conclusion follows by taking ![]() $\alpha = {2}/{p}$.
$\alpha = {2}/{p}$.
4. Proof of the main theorem
Proposition 4.1 Let ![]() $G$ be a topological group. For every
$G$ be a topological group. For every ![]() $p > 0$ and every
$p > 0$ and every ![]() $\psi \in K^p(G)$, there exists a continuous nonsingular action
$\psi \in K^p(G)$, there exists a continuous nonsingular action ![]() $\sigma : G \curvearrowright (X,\mu )$ and a cocycle
$\sigma : G \curvearrowright (X,\mu )$ and a cocycle ![]() $c \in Z^1(G, \sigma ^{p,\mu },L_p(X,\mu ))$ such that
$c \in Z^1(G, \sigma ^{p,\mu },L_p(X,\mu ))$ such that ![]() $\psi (g)=\| c(g)\|_{L_p}^p$ for all
$\psi (g)=\| c(g)\|_{L_p}^p$ for all ![]() $g \in G$.
$g \in G$.
Proof. We may assume that ![]() $p \neq 2$ thanks to Proposition 3.1. By definition, there exists an affine isometric action
$p \neq 2$ thanks to Proposition 3.1. By definition, there exists an affine isometric action ![]() $\alpha : G \curvearrowright L_p(X,\mu )$ for some probability space
$\alpha : G \curvearrowright L_p(X,\mu )$ for some probability space ![]() $(X,\mu )$ such that
$(X,\mu )$ such that ![]() $\psi (g)=\| \alpha _g(0)\|_{L_p}^p$ for all
$\psi (g)=\| \alpha _g(0)\|_{L_p}^p$ for all ![]() $g \in G$. Write
$g \in G$. Write ![]() $\alpha _g(f)=\pi _g(f)+c(g)$ where
$\alpha _g(f)=\pi _g(f)+c(g)$ where ![]() $\pi$ is an isometric linear representation of
$\pi$ is an isometric linear representation of ![]() $G$ on
$G$ on ![]() $L_p(X,\mu )$ and
$L_p(X,\mu )$ and ![]() $c \in Z^1(G,\pi,L_p(X,\mu ))$. As
$c \in Z^1(G,\pi,L_p(X,\mu ))$. As ![]() $p \neq 2$, we can write
$p \neq 2$, we can write ![]() $\pi (g)=\omega (g) \sigma ^{p,\mu }_g$ where
$\pi (g)=\omega (g) \sigma ^{p,\mu }_g$ where ![]() $\sigma : G \curvearrowright (X,\mu )$ is some nonsingular action and
$\sigma : G \curvearrowright (X,\mu )$ is some nonsingular action and ![]() $\omega \in Z^1_\sigma (G,\mathbf {T})$. Consider the skew-product nonsingular action
$\omega \in Z^1_\sigma (G,\mathbf {T})$. Consider the skew-product nonsingular action ![]() $\tilde {\sigma }=\sigma \rtimes \omega : G \curvearrowright (X \times \mathbf {T}, \mu \otimes m)$ where
$\tilde {\sigma }=\sigma \rtimes \omega : G \curvearrowright (X \times \mathbf {T}, \mu \otimes m)$ where ![]() $m$ is the Haar measure of
$m$ is the Haar measure of ![]() $\mathbf {T}$. Observe that
$\mathbf {T}$. Observe that ![]() $\tilde {\sigma }_g(u)u^*=\omega (g) \otimes 1$ where
$\tilde {\sigma }_g(u)u^*=\omega (g) \otimes 1$ where ![]() $u$ is the function on
$u$ is the function on ![]() $X \times \mathbf {T}$ given by
$X \times \mathbf {T}$ given by ![]() $u(x,z)=z$ for all
$u(x,z)=z$ for all ![]() $(x,z) \in X \times \mathbf {T}$. It follows that
$(x,z) \in X \times \mathbf {T}$. It follows that ![]() $\tilde {c}: g \mapsto u c(g)$ defines an element
$\tilde {c}: g \mapsto u c(g)$ defines an element ![]() $\tilde {c} \in Z^1(G,\tilde {\sigma }^p, L_p(X \times \mathbf {T},\mu \otimes m))$ such that
$\tilde {c} \in Z^1(G,\tilde {\sigma }^p, L_p(X \times \mathbf {T},\mu \otimes m))$ such that ![]() $\| \tilde {c}(g)\|_p=\| c(g)\|_p$ for all
$\| \tilde {c}(g)\|_p=\| c(g)\|_p$ for all ![]() $g \in G$, where
$g \in G$, where ![]() $m$ is the Haar measure of
$m$ is the Haar measure of ![]() $\mathbf {T}$.
$\mathbf {T}$.
Lemma 4.2 Take ![]() $0 < p < q < \infty$. Let
$0 < p < q < \infty$. Let ![]() $\varphi : \mathbf {C} \rightarrow \mathbf {R}$ be a nonzero, radial, compactly supported, Lipschitz function. Then there exists a constant
$\varphi : \mathbf {C} \rightarrow \mathbf {R}$ be a nonzero, radial, compactly supported, Lipschitz function. Then there exists a constant ![]() $C(q) > 0$ such that for all
$C(q) > 0$ such that for all ![]() $w \in \mathbf {C}$, we have
$w \in \mathbf {C}$, we have
Proof. Let ![]() $S$ be the Lebesgue measure of the support of
$S$ be the Lebesgue measure of the support of ![]() $\varphi$,
$\varphi$, ![]() $M=\| \varphi \|_\infty$ and let
$M=\| \varphi \|_\infty$ and let ![]() $K$ be the Lipschitz constant of
$K$ be the Lipschitz constant of ![]() $\varphi$. Then we have
$\varphi$. Then we have ![]() $|\varphi (z+\lambda ^{-1/p}) - \varphi (z)| \leq \min ( 2M,K \lambda ^{-1/p})$ for all
$|\varphi (z+\lambda ^{-1/p}) - \varphi (z)| \leq \min ( 2M,K \lambda ^{-1/p})$ for all ![]() $z \in \mathbf {C}$ and all
$z \in \mathbf {C}$ and all ![]() $\lambda \in \mathbf {R}^*_+$. Therefore, we have
$\lambda \in \mathbf {R}^*_+$. Therefore, we have
As ![]() $q > p$, the function
$q > p$, the function ![]() $\lambda \mapsto \min ( (2M)^q, K^q \lambda ^{-q/p})$ is integrable on
$\lambda \mapsto \min ( (2M)^q, K^q \lambda ^{-q/p})$ is integrable on ![]() $\mathbf {R}^*_+$. Therefore, we can define
$\mathbf {R}^*_+$. Therefore, we can define
As ![]() $\varphi$ is not constant, we have
$\varphi$ is not constant, we have ![]() $C(q) > 0$. Finally, the statement for all
$C(q) > 0$. Finally, the statement for all ![]() $w \in \mathbf {C}$ follows from the change of variable
$w \in \mathbf {C}$ follows from the change of variable ![]() $\lambda \mapsto |w|^p\lambda$ and the fact that
$\lambda \mapsto |w|^p\lambda$ and the fact that ![]() $\varphi$ is radial.
$\varphi$ is radial.
Theorem 4.3 Let ![]() $G$ be a topological group. Take
$G$ be a topological group. Take ![]() $0 < p < q < \infty$. Then for every
$0 < p < q < \infty$. Then for every ![]() $\psi \in K^p(G)$, there exists a continuous measure-preserving action
$\psi \in K^p(G)$, there exists a continuous measure-preserving action ![]() $\sigma : G \curvearrowright (Y,\nu )$ and a function
$\sigma : G \curvearrowright (Y,\nu )$ and a function ![]() $h \in L_\infty (Y,\nu )$ such that
$h \in L_\infty (Y,\nu )$ such that ![]() $b(g)=\sigma _g(h)-h \in L_q(Y,\nu )$ with
$b(g)=\sigma _g(h)-h \in L_q(Y,\nu )$ with ![]() $\psi (g)=\| b(g)\|_{L_q}^q$ for all
$\psi (g)=\| b(g)\|_{L_q}^q$ for all ![]() $g \in G$. In particular,
$g \in G$. In particular, ![]() $\psi \in K^q(G)$.
$\psi \in K^q(G)$.
Proof. By Proposition 4.1, there exists a nonsingular action ![]() $\sigma : G \curvearrowright (X,\mu )$ and a cocycle
$\sigma : G \curvearrowright (X,\mu )$ and a cocycle ![]() $c \in Z^1(G, \sigma ^{p,\mu },L_p(X,\mu ))$ such that
$c \in Z^1(G, \sigma ^{p,\mu },L_p(X,\mu ))$ such that ![]() $\psi (g)=\| c(g)\|_{L_p}^p$ for all
$\psi (g)=\| c(g)\|_{L_p}^p$ for all ![]() $g \in G$. Let
$g \in G$. Let ![]() $\widetilde {\sigma } : G {\curvearrowright } (\widetilde {X},\widetilde {\mu })$ be the Maharam extension of
$\widetilde {\sigma } : G {\curvearrowright } (\widetilde {X},\widetilde {\mu })$ be the Maharam extension of ![]() $\sigma$. This means that
$\sigma$. This means that ![]() $(\widetilde {X},\widetilde {\mu }) = (X \times \mathbf {R}^*_+,\mu \otimes d \lambda )$ where
$(\widetilde {X},\widetilde {\mu }) = (X \times \mathbf {R}^*_+,\mu \otimes d \lambda )$ where ![]() $d \lambda$ is the restriction to
$d \lambda$ is the restriction to ![]() $\mathbf {R}^*_+$ of the Lebesgue measure of
$\mathbf {R}^*_+$ of the Lebesgue measure of ![]() $\mathbf {R}$ and
$\mathbf {R}$ and ![]() $\widetilde {\sigma } : G {\curvearrowright } (\widetilde {X},\widetilde {\mu })$ is the measure-preserving action given by
$\widetilde {\sigma } : G {\curvearrowright } (\widetilde {X},\widetilde {\mu })$ is the measure-preserving action given by ![]() $g(x,\lambda ) = (gx,( ({d g^{-1} \mu }/{d\mu })(x))^{-1} \lambda )$. Define
$g(x,\lambda ) = (gx,( ({d g^{-1} \mu }/{d\mu })(x))^{-1} \lambda )$. Define ![]() $\widetilde c \in Z^1_{\widetilde {\sigma }}(G,\mathbf {C})$ by the formula
$\widetilde c \in Z^1_{\widetilde {\sigma }}(G,\mathbf {C})$ by the formula ![]() $\widetilde {c}(g,x,\lambda ) = \lambda ^{- {1}/{p}} c(g,x)$ (observe that
$\widetilde {c}(g,x,\lambda ) = \lambda ^{- {1}/{p}} c(g,x)$ (observe that ![]() $\widetilde {c}$ indeed satisfies the cocycle relation thanks to the term
$\widetilde {c}$ indeed satisfies the cocycle relation thanks to the term ![]() $\lambda ^{-1/p}$). Let
$\lambda ^{-1/p}$). Let ![]() $\rho : G {\curvearrowright } (Y,\nu )$ be the skew-product action of
$\rho : G {\curvearrowright } (Y,\nu )$ be the skew-product action of ![]() $\widetilde {\sigma }$ by
$\widetilde {\sigma }$ by ![]() $\widetilde c$. This is the measure space
$\widetilde c$. This is the measure space ![]() $(Y,\nu )=(\widetilde X \times \mathbf {C}, \widetilde {\mu } \otimes {d}z )$ and
$(Y,\nu )=(\widetilde X \times \mathbf {C}, \widetilde {\mu } \otimes {d}z )$ and ![]() $\rho$ is the measure-preserving action given by
$\rho$ is the measure-preserving action given by ![]() $g(\widetilde x,z) = (g \widetilde x,z+\widetilde c(g^{-1},\widetilde x))$. Let
$g(\widetilde x,z) = (g \widetilde x,z+\widetilde c(g^{-1},\widetilde x))$. Let ![]() $\varphi \colon \mathbf {C} \to \mathbf {R}$ be a nonzero, radial, compactly supported, Lipschitz function. Define a function
$\varphi \colon \mathbf {C} \to \mathbf {R}$ be a nonzero, radial, compactly supported, Lipschitz function. Define a function ![]() $h \in L_\infty (Y,\nu )$ by
$h \in L_\infty (Y,\nu )$ by ![]() $h(\widetilde x,z)=\varphi (z)$, and let
$h(\widetilde x,z)=\varphi (z)$, and let ![]() $b(g) = \rho _g(h) - h$ for all
$b(g) = \rho _g(h) - h$ for all ![]() $g \in G$. Then Lemma 4.2 shows that
$g \in G$. Then Lemma 4.2 shows that ![]() $b$ is a cocycle with values in
$b$ is a cocycle with values in ![]() $L_q(Y,\nu )$ that satisfies the conclusion of the theorem up to a constant
$L_q(Y,\nu )$ that satisfies the conclusion of the theorem up to a constant ![]() $C(q) > 0$.
$C(q) > 0$.
Remark 4.4 The idea of the proof of Theorem 4.3 and of the cocycle ![]() $\widetilde {c}$ becomes very natural if one uses the notion of modular bundle and Haagerup's canonical
$\widetilde {c}$ becomes very natural if one uses the notion of modular bundle and Haagerup's canonical ![]() $L_p$-spaces as explained in [Reference Arano, Isono and MarrakchiAIM21, §§ A.2 and A.3]. Indeed, by viewing the canonical
$L_p$-spaces as explained in [Reference Arano, Isono and MarrakchiAIM21, §§ A.2 and A.3]. Indeed, by viewing the canonical ![]() $L_p$-space
$L_p$-space ![]() $L_p(X)$ as a subspace of
$L_p(X)$ as a subspace of ![]() $L_0(\mathrm {Mod}(X))$, the isometric linear representation
$L_0(\mathrm {Mod}(X))$, the isometric linear representation ![]() $\sigma ^p : G \curvearrowright L_p(X)$ associated to some nonsingular action
$\sigma ^p : G \curvearrowright L_p(X)$ associated to some nonsingular action ![]() $\sigma : G \curvearrowright X$ is identified with the restriction to
$\sigma : G \curvearrowright X$ is identified with the restriction to ![]() $L_p(X)$ of the Maharam extension
$L_p(X)$ of the Maharam extension ![]() $\mathrm {Mod}(\sigma ) : G \curvearrowright \mathrm {Mod}(X)$. We can therefore identify every cocycle
$\mathrm {Mod}(\sigma ) : G \curvearrowright \mathrm {Mod}(X)$. We can therefore identify every cocycle ![]() $c \in Z^1(G,\sigma ^p,L_p(X))$ with a cocycle
$c \in Z^1(G,\sigma ^p,L_p(X))$ with a cocycle ![]() $\widetilde {c} \in Z^1_{\mathrm {Mod}(\sigma )}(G,\mathbf {C})$. This is crucial in order to be able to use the skew-product construction.
$\widetilde {c} \in Z^1_{\mathrm {Mod}(\sigma )}(G,\mathbf {C})$. This is crucial in order to be able to use the skew-product construction.
Proof of Corollary 4 Let ![]() $G=\mathord {\text { Isom}}(L_p)$ with its canonical affine isometric action on
$G=\mathord {\text { Isom}}(L_p)$ with its canonical affine isometric action on ![]() $L_p$. By applying Theorem 1, we obtain a continuous homomorphism
$L_p$. By applying Theorem 1, we obtain a continuous homomorphism ![]() $\Psi : \mathord {\text { Isom}}(L_p) \rightarrow \mathord {\text { Isom}}(L_q)$ such that
$\Psi : \mathord {\text { Isom}}(L_p) \rightarrow \mathord {\text { Isom}}(L_q)$ such that
We have to show that ![]() $\Psi$ is a homeomorphism on its range. Take
$\Psi$ is a homeomorphism on its range. Take ![]() $(g_n)_{n \in \mathbf {N}}$ a sequence in
$(g_n)_{n \in \mathbf {N}}$ a sequence in ![]() $\mathord {\text { Isom}}(L_p)$ and suppose that
$\mathord {\text { Isom}}(L_p)$ and suppose that ![]() $\Psi (g_n) \to \text {id}$. We have to show that
$\Psi (g_n) \to \text {id}$. We have to show that ![]() $g_n \to \text {id}$. Take
$g_n \to \text {id}$. Take ![]() $f \in L_p$ and let
$f \in L_p$ and let ![]() $\tau _f \in \mathord {\text { Isom}}(L_p)$ be the translation by
$\tau _f \in \mathord {\text { Isom}}(L_p)$ be the translation by ![]() $f$. Then
$f$. Then
As ![]() $\Psi (g_n) \to \text {id}$, we also have
$\Psi (g_n) \to \text {id}$, we also have ![]() $\Psi (\tau _f^{-1} \circ g_n \circ \tau _f)= \Psi (\tau _f)^{-1} \circ \Psi (g_n) \circ \Psi (\tau _f) \to \text {id}$. This yields
$\Psi (\tau _f^{-1} \circ g_n \circ \tau _f)= \Psi (\tau _f)^{-1} \circ \Psi (g_n) \circ \Psi (\tau _f) \to \text {id}$. This yields
As this holds for all ![]() $f \in L_p$, we conclude that
$f \in L_p$, we conclude that ![]() $g_n \to \text {id}$ as we wanted.
$g_n \to \text {id}$ as we wanted.
Question 4.5 Is Theorem 4.3 still true when ![]() $q=p$? Can we at least realize
$q=p$? Can we at least realize ![]() $\psi$ with an affine isometric action whose linear part comes from a measure-preserving action of
$\psi$ with an affine isometric action whose linear part comes from a measure-preserving action of ![]() $G$? One can show that if a measurable function
$G$? One can show that if a measurable function ![]() $\varphi : \mathbf {R} \rightarrow \mathbf {R}$ satisfies
$\varphi : \mathbf {R} \rightarrow \mathbf {R}$ satisfies
for some ![]() $p \geq 1$, then
$p \geq 1$, then ![]() $\varphi$ is almost surely constant. Therefore, our method for the proof of Theorem 4.3 cannot work when
$\varphi$ is almost surely constant. Therefore, our method for the proof of Theorem 4.3 cannot work when ![]() $q=p$.
$q=p$.
Question 4.6 Take ![]() $0 < p,q < \infty$. Is it true that
$0 < p,q < \infty$. Is it true that ![]() $\mathord {\text { Isom}}(L_p)$ embeds as a closed subgroup of
$\mathord {\text { Isom}}(L_p)$ embeds as a closed subgroup of ![]() $\mathord {\text { Isom}}(L_q)$ if and only if
$\mathord {\text { Isom}}(L_q)$ if and only if ![]() $p \leq \max (2,q)$?
$p \leq \max (2,q)$?
5. Harmonic cocycles and state-preserving actions
Let ![]() $E$ be a uniformly convex Banach space and let
$E$ be a uniformly convex Banach space and let ![]() $\pi$ be a continuous representation of a locally compact group
$\pi$ be a continuous representation of a locally compact group ![]() $G$ on
$G$ on ![]() $E$. Then we can decompose
$E$. Then we can decompose ![]() $E$ as a
$E$ as a ![]() $\pi$-invariant direct sum
$\pi$-invariant direct sum ![]() $E=E_\pi \oplus E^\pi$ where
$E=E_\pi \oplus E^\pi$ where ![]() $E^\pi$ is the subspace of
$E^\pi$ is the subspace of ![]() $\pi$-invariant vectors and
$\pi$-invariant vectors and ![]() $E_\pi$ is its natural complement (defined as the orthogonal of
$E_\pi$ is its natural complement (defined as the orthogonal of ![]() $(E^*)^{\pi ^*}$ where
$(E^*)^{\pi ^*}$ where ![]() $\pi ^*$ is the dual representation of
$\pi ^*$ is the dual representation of ![]() $\pi$ on
$\pi$ on ![]() $E^*$), see [Reference Bader, Furman, Gelander and MonodBFGM07]. We say that
$E^*$), see [Reference Bader, Furman, Gelander and MonodBFGM07]. We say that ![]() $\pi$ has spectral gap if
$\pi$ has spectral gap if ![]() $\pi |_{E_\pi }$ has no almost invariant vectors. By [Reference Druţu and NowakDN19, Theorem 1.1], this is equivalent to the existence of a symmetric compactly supported probability measure
$\pi |_{E_\pi }$ has no almost invariant vectors. By [Reference Druţu and NowakDN19, Theorem 1.1], this is equivalent to the existence of a symmetric compactly supported probability measure ![]() $\mu$ on
$\mu$ on ![]() $G$ such that
$G$ such that ![]() $\|\pi (\mu )|_{E_\pi }\| < 1$.
$\|\pi (\mu )|_{E_\pi }\| < 1$.
Lemma 5.1 Let ![]() $G$ be a locally compact group and let
$G$ be a locally compact group and let ![]() $\pi$ be a representation of
$\pi$ be a representation of ![]() $G$ on a uniformly convex Banach space
$G$ on a uniformly convex Banach space ![]() $E$ that has spectral gap. Let
$E$ that has spectral gap. Let ![]() $\mu$ be a symmetric compactly supported probability measure
$\mu$ be a symmetric compactly supported probability measure ![]() $\mu$ on
$\mu$ on ![]() $G$ such that
$G$ such that ![]() $\| \pi (\mu )|_{E_\pi } \| < 1$. Then every cohomology class in
$\| \pi (\mu )|_{E_\pi } \| < 1$. Then every cohomology class in ![]() $H^1(G,\pi,E)$ admits a unique
$H^1(G,\pi,E)$ admits a unique ![]() $\mu$-harmonic representant.
$\mu$-harmonic representant.
Proof. By decomposing ![]() $E=E_\pi \oplus E^\pi$, we can reduce the problem to the case where
$E=E_\pi \oplus E^\pi$, we can reduce the problem to the case where ![]() $\pi$ is either trivial or has no invariant vectors.
$\pi$ is either trivial or has no invariant vectors.
Assume first that ![]() $\pi$ is trivial. Then
$\pi$ is trivial. Then ![]() $B^1(G,\pi,E)=0$ and an element of
$B^1(G,\pi,E)=0$ and an element of ![]() $Z^1(G,\pi,E)$ is just a group homomorphism from
$Z^1(G,\pi,E)$ is just a group homomorphism from ![]() $G$ to
$G$ to ![]() $E$. Thus, because
$E$. Thus, because ![]() $\mu$ is symmetric, every element of
$\mu$ is symmetric, every element of ![]() $Z^1(G,\pi,E)$ is
$Z^1(G,\pi,E)$ is ![]() $\mu$-harmonic.
$\mu$-harmonic.
Now, assume that ![]() $\pi$ has no invariant vectors, i.e.
$\pi$ has no invariant vectors, i.e. ![]() $E=E_\pi$. Take
$E=E_\pi$. Take ![]() $c \in Z^1(G,\pi,E)$. Let
$c \in Z^1(G,\pi,E)$. Let ![]() $\alpha$ be the affine isometric action of
$\alpha$ be the affine isometric action of ![]() $G$ on
$G$ on ![]() $E$ associated to
$E$ associated to ![]() $c$. Then the affine map
$c$. Then the affine map ![]() $\alpha (\mu )=\int _{g \in G} \alpha _g \,{d} \mu (g)$ is
$\alpha (\mu )=\int _{g \in G} \alpha _g \,{d} \mu (g)$ is ![]() $k$-Lipschitz with
$k$-Lipschitz with ![]() $k=\|\pi (\mu )\| <1$. Therefore,
$k=\|\pi (\mu )\| <1$. Therefore, ![]() $\alpha (\mu )$ has a fixed point
$\alpha (\mu )$ has a fixed point ![]() $\xi \in E$ for some
$\xi \in E$ for some ![]() $\xi \in E$. Let
$\xi \in E$. Let ![]() $c'(g)=c(g)+\pi (g)\xi -\xi$. Then we get
$c'(g)=c(g)+\pi (g)\xi -\xi$. Then we get ![]() $\int _G c'(g) \,{d} \mu (g) =\alpha (\mu ) \xi -\xi =0$. We conclude that
$\int _G c'(g) \,{d} \mu (g) =\alpha (\mu ) \xi -\xi =0$. We conclude that ![]() $c'$ is a
$c'$ is a ![]() $\mu$-harmonic representant of the cohomology class of
$\mu$-harmonic representant of the cohomology class of ![]() $c$. For the uniqueness part, observe that if we have a coboundary
$c$. For the uniqueness part, observe that if we have a coboundary ![]() $b(g)=\pi (g)\xi -\xi$ that is
$b(g)=\pi (g)\xi -\xi$ that is ![]() $\mu$-harmonic, then
$\mu$-harmonic, then ![]() $\pi (\mu )\xi =\xi$, hence
$\pi (\mu )\xi =\xi$, hence ![]() $\xi =0$ because
$\xi =0$ because ![]() $\| \pi (\mu ) \| < 1$.
$\| \pi (\mu ) \| < 1$.
Lemma 5.2 Let ![]() $G$ be a compactly generated locally compact group and let
$G$ be a compactly generated locally compact group and let ![]() $\pi _1,\pi _2$ be two representations of
$\pi _1,\pi _2$ be two representations of ![]() $G$ on two strictly convex Banach spaces
$G$ on two strictly convex Banach spaces ![]() $E_1$ and
$E_1$ and ![]() $E_2$. Suppose moreover that
$E_2$. Suppose moreover that ![]() $E_1$ is uniformly convex and that
$E_1$ is uniformly convex and that ![]() $\pi _1$ has spectral gap. Then every injective continuous
$\pi _1$ has spectral gap. Then every injective continuous ![]() $G$-equivariant linear map
$G$-equivariant linear map ![]() $\psi : E_1 \rightarrow E_2$ induces an injective map
$\psi : E_1 \rightarrow E_2$ induces an injective map ![]() $\psi _* : H^1(G,\pi _1,E_1) \rightarrow H^1(G,\pi _2,E_2)$.
$\psi _* : H^1(G,\pi _1,E_1) \rightarrow H^1(G,\pi _2,E_2)$.
Proof. As ![]() $\pi _1$ has spectral gap and
$\pi _1$ has spectral gap and ![]() $E_1$ is uniformly convex, we can find a symmetric compactly supported probability measure
$E_1$ is uniformly convex, we can find a symmetric compactly supported probability measure ![]() $\mu$ on
$\mu$ on ![]() $G$ such that
$G$ such that ![]() $\| \pi _1(\mu )_{E_{\pi _1}} \| < 1$. As
$\| \pi _1(\mu )_{E_{\pi _1}} \| < 1$. As ![]() $G$ is compactly generated, we can assume that the support of
$G$ is compactly generated, we can assume that the support of ![]() $\mu$ generates
$\mu$ generates ![]() $G$.
$G$.
Take ![]() $\omega \in H^1(G,\pi _1,E_1)$. By Lemma 5.1
$\omega \in H^1(G,\pi _1,E_1)$. By Lemma 5.1 ![]() $\omega$ admits a
$\omega$ admits a ![]() $\mu$-harmonic representant
$\mu$-harmonic representant ![]() $c \in Z^1(G,\pi _1,E_1)$. Then
$c \in Z^1(G,\pi _1,E_1)$. Then ![]() $\psi _*\omega \in H^1(G,\pi _1,E_1)$ is represented by the cocycle
$\psi _*\omega \in H^1(G,\pi _1,E_1)$ is represented by the cocycle ![]() $c' : g \mapsto \psi (c(g))$. Note that
$c' : g \mapsto \psi (c(g))$. Note that ![]() $c'$ is still
$c'$ is still ![]() $\mu$-harmonic. Suppose that
$\mu$-harmonic. Suppose that ![]() $\psi _*\omega =0$. This means that
$\psi _*\omega =0$. This means that ![]() $c'$ is a coboundary, i.e.
$c'$ is a coboundary, i.e. ![]() $c'(g)=\pi _2(g) \xi -\xi$ for some
$c'(g)=\pi _2(g) \xi -\xi$ for some ![]() $\xi \in E_2$ and all
$\xi \in E_2$ and all ![]() $g \in G$. As
$g \in G$. As ![]() $c'$ is
$c'$ is ![]() $\mu$-harmonic, we have
$\mu$-harmonic, we have ![]() $\int _G \pi _2(g)\xi \,{d} \mu (g) = \xi$. As
$\int _G \pi _2(g)\xi \,{d} \mu (g) = \xi$. As ![]() $E_2$ is strictly convex, this implies that
$E_2$ is strictly convex, this implies that ![]() $\pi _2(g)\xi =\xi$ for all
$\pi _2(g)\xi =\xi$ for all ![]() $g$ in the support of
$g$ in the support of ![]() $\mu$, hence for all
$\mu$, hence for all ![]() $g \in G$. We conclude that
$g \in G$. We conclude that ![]() $c'=0$, hence
$c'=0$, hence ![]() $c=0$ because
$c=0$ because ![]() $\psi$ is injective.
$\psi$ is injective.
Remark 5.3 The previous lemma applies, for example, when ![]() $\sigma : G \curvearrowright (X,\mu )$ is a continuous probability measure-preserving action of a compactly generated locally compact group,
$\sigma : G \curvearrowright (X,\mu )$ is a continuous probability measure-preserving action of a compactly generated locally compact group, ![]() $(\pi _i,E_i) =(\sigma ^{p_i,\mu }, L^{p_i}(X,\mu ))$ for
$(\pi _i,E_i) =(\sigma ^{p_i,\mu }, L^{p_i}(X,\mu ))$ for ![]() $\infty >p_1 \geq p_2>1$ and
$\infty >p_1 \geq p_2>1$ and ![]() $\psi$ is the inclusion map
$\psi$ is the inclusion map ![]() $L^{p_1} \to L^{p_2}$. The lemma shows that
$L^{p_1} \to L^{p_2}$. The lemma shows that
Indeed, the assumption that ![]() $H^1(G,\sigma ^{p_2,\mu }) =0$ implies that
$H^1(G,\sigma ^{p_2,\mu }) =0$ implies that ![]() $\sigma ^{p_2,\mu }$ has spectral gap, which implies that
$\sigma ^{p_2,\mu }$ has spectral gap, which implies that ![]() $\sigma ^{p_1,\mu }$ has spectral gap, see [Reference Bader, Furman, Gelander and MonodBFGM07]. In particular, if
$\sigma ^{p_1,\mu }$ has spectral gap, see [Reference Bader, Furman, Gelander and MonodBFGM07]. In particular, if ![]() $G$ is a locally compact property (T) group,
$G$ is a locally compact property (T) group, ![]() $H^1(G,\sigma ^{p,\mu })=0$ for every
$H^1(G,\sigma ^{p,\mu })=0$ for every ![]() $p\in [1,\infty )$. This was already known when
$p\in [1,\infty )$. This was already known when ![]() $G$ is discrete [Reference Lavy and OlivierLO21], or
$G$ is discrete [Reference Lavy and OlivierLO21], or ![]() $G$ admits a finite Kazhdan set [Reference Czuroń and KalantarCK20].
$G$ admits a finite Kazhdan set [Reference Czuroń and KalantarCK20].
More generally, the lemma applies to the actions on noncommutative ![]() $L_p$ spaces associated to state-preserving actions on von Neumann algebras, and also for actions on Schatten
$L_p$ spaces associated to state-preserving actions on von Neumann algebras, and also for actions on Schatten ![]() $p$-classes. We start with the latter as it is more elementary.
$p$-classes. We start with the latter as it is more elementary.
For a Hilbert space ![]() $H$, we denote by
$H$, we denote by ![]() $S_p(H)$ the Schatten
$S_p(H)$ the Schatten ![]() $p$-class, that is, the space of operators on
$p$-class, that is, the space of operators on ![]() $H$ such that
$H$ such that ![]() $\|T\|_p:= (\mathrm {Tr}(|T|^p))^{ {1}/{p}}<\infty$. We say that a group has
$\|T\|_p:= (\mathrm {Tr}(|T|^p))^{ {1}/{p}}<\infty$. We say that a group has ![]() $FS_p$ if for every
$FS_p$ if for every ![]() $H$ and every continuous isometric representation
$H$ and every continuous isometric representation ![]() $\pi : G \curvearrowright S_p(H))$,
$\pi : G \curvearrowright S_p(H))$, ![]() $H^1(G,\pi,S_p(H))=0$.
$H^1(G,\pi,S_p(H))=0$.
Theorem 5.4 If ![]() $G$ is a
$G$ is a ![]() $\sigma$-compact locally compact group, then the set of
$\sigma$-compact locally compact group, then the set of ![]() $1< p<\infty$ such that
$1< p<\infty$ such that ![]() $G$ has
$G$ has ![]() $FS_p$ is empty if
$FS_p$ is empty if ![]() $G$ does not have property (T), and is an interval containing
$G$ does not have property (T), and is an interval containing ![]() $(1,2]$ otherwise.
$(1,2]$ otherwise.
Proof. Assume that ![]() $G$ does not have property (T). By Guichardet's theorem, there is a unitary representation
$G$ does not have property (T). By Guichardet's theorem, there is a unitary representation ![]() $\pi$ on a Hilbert space
$\pi$ on a Hilbert space ![]() $H$ and an unbounded cocycle
$H$ and an unbounded cocycle ![]() $b \in Z^1(G,\pi )$. If
$b \in Z^1(G,\pi )$. If ![]() $\xi \in H^*$ is a unit vector, then the formula
$\xi \in H^*$ is a unit vector, then the formula ![]() $g \cdot T = \pi (g) T + b(g) \otimes \xi$ defines an unbounded action by isometries on
$g \cdot T = \pi (g) T + b(g) \otimes \xi$ defines an unbounded action by isometries on ![]() $S_p(H)$ for every
$S_p(H)$ for every ![]() $1 \leq p \leq \infty$. Thus,
$1 \leq p \leq \infty$. Thus, ![]() $G$ does not have
$G$ does not have ![]() $FS_p$.
$FS_p$.
If ![]() $G$ has property (T), then
$G$ has property (T), then ![]() $G$ is compactly generated, and has
$G$ is compactly generated, and has ![]() $FS_2$ by Delorme's theorem (
$FS_2$ by Delorme's theorem (![]() $S_2(H)$ is a Hilbert space). We have to prove that, if
$S_2(H)$ is a Hilbert space). We have to prove that, if ![]() $1< p< q<\infty$ are such that
$1< p< q<\infty$ are such that ![]() $G$ has
$G$ has ![]() $FS_q$, then
$FS_q$, then ![]() $G$ has
$G$ has ![]() $FS_p$. We can assume that
$FS_p$. We can assume that ![]() $p \neq 2$. Let
$p \neq 2$. Let ![]() $\pi \colon G \to O(S_p(H))$ be an orthogonal representation. By [Reference YeadonYea81],
$\pi \colon G \to O(S_p(H))$ be an orthogonal representation. By [Reference YeadonYea81], ![]() $\pi _g$ is of the form
$\pi _g$ is of the form ![]() $\pi _g(T) = W_g J_g(T)$ for a unitary
$\pi _g(T) = W_g J_g(T)$ for a unitary ![]() $W_g$ and a Jordan automorphism
$W_g$ and a Jordan automorphism ![]() $J_g$ of
$J_g$ of ![]() $B(H)$. In particular, the same formula gives rise to an isometric representation on
$B(H)$. In particular, the same formula gives rise to an isometric representation on ![]() $S_q(H)$ and the inclusion
$S_q(H)$ and the inclusion ![]() $S_p(H) \subset S_q(G)$ is equivariant. Moreover, both representations have spectral gap [Reference YeadonYea81], and the Schatten spaces are uniformly convex when
$S_p(H) \subset S_q(G)$ is equivariant. Moreover, both representations have spectral gap [Reference YeadonYea81], and the Schatten spaces are uniformly convex when ![]() $1< p<\infty$. We conclude by Lemma 5.2 that
$1< p<\infty$. We conclude by Lemma 5.2 that ![]() $H^1(G,S_p(H)) \to H^1(G,S_q(H))=0$ is injective and
$H^1(G,S_p(H)) \to H^1(G,S_q(H))=0$ is injective and ![]() $H^1(G,S_p(H))=0$.
$H^1(G,S_p(H))=0$.
To state our result about state-preserving actions, we need to recall Haagerup's general definition of noncommutative ![]() $L_p$ spaces [Reference HaagerupHaa79]. We follow the approach in [Reference MarrakchiMar19, § 2.1]. If
$L_p$ spaces [Reference HaagerupHaa79]. We follow the approach in [Reference MarrakchiMar19, § 2.1]. If ![]() $M$ is a von Neumann algebra, the core of
$M$ is a von Neumann algebra, the core of ![]() $M$ is the unique (up to unique isomorphism) tuple
$M$ is the unique (up to unique isomorphism) tuple ![]() $(c(M),\tau,\theta,\iota )$ of a von Neumann algebra
$(c(M),\tau,\theta,\iota )$ of a von Neumann algebra ![]() $c(M)$, a normal faithful semifinite trace
$c(M)$, a normal faithful semifinite trace ![]() $\tau$ on
$\tau$ on ![]() $c(M)$, a continuous homomorphism
$c(M)$, a continuous homomorphism ![]() $\theta :\mathbf {R} \to \mathrm {Aut}(M)$, and a normal injective
$\theta :\mathbf {R} \to \mathrm {Aut}(M)$, and a normal injective ![]() $*$-homomorphism
$*$-homomorphism ![]() $\iota : M \to c(M)$ satisfying
$\iota : M \to c(M)$ satisfying ![]() $\tau \circ \theta _s = e^{-s}\tau$ and
$\tau \circ \theta _s = e^{-s}\tau$ and ![]() $\{x \in c(M) \mid \forall s \in \mathbf {R}, \theta _s (x)=x\} = \iota (M)$. In the following, we identify
$\{x \in c(M) \mid \forall s \in \mathbf {R}, \theta _s (x)=x\} = \iota (M)$. In the following, we identify ![]() $M$ with its image in
$M$ with its image in ![]() $c(M)$ and write
$c(M)$ and write ![]() $x$ instead of
$x$ instead of ![]() $\iota (x)$. For example, if
$\iota (x)$. For example, if ![]() $\phi$ is a normal faithful weight on
$\phi$ is a normal faithful weight on ![]() $M$, the core can be realized as
$M$, the core can be realized as ![]() $c(M) = M \rtimes _{\sigma ^\phi } \mathbf {R}$, the crossed product by the modular automorphism group of
$c(M) = M \rtimes _{\sigma ^\phi } \mathbf {R}$, the crossed product by the modular automorphism group of ![]() $\phi$. In that case,
$\phi$. In that case, ![]() $\theta$ is given by the dual action and
$\theta$ is given by the dual action and ![]() $\iota$ the natural inclusion. For details on the construction and the existence of a trace
$\iota$ the natural inclusion. For details on the construction and the existence of a trace ![]() $\tau$ as required, see [Reference TakesakiTak03]. Then
$\tau$ as required, see [Reference TakesakiTak03]. Then ![]() $L_p(M)$ is defined as the space of
$L_p(M)$ is defined as the space of ![]() $\tau$-measurable operators affiliated to
$\tau$-measurable operators affiliated to ![]() $c(M)$ such that
$c(M)$ such that ![]() $\theta _s(h)= e^{-s/p} h$ for all
$\theta _s(h)= e^{-s/p} h$ for all ![]() $s \in \mathbf {R}$. By [Reference HaagerupHaa79, Theorems 1.2 and 1.3], for every normal state
$s \in \mathbf {R}$. By [Reference HaagerupHaa79, Theorems 1.2 and 1.3], for every normal state ![]() $\varphi$ on
$\varphi$ on ![]() $M$, there is a unique element of
$M$, there is a unique element of ![]() $L_1(M)$, that we also denote
$L_1(M)$, that we also denote ![]() $\varphi$, satisfying
$\varphi$, satisfying
for every nonnegative ![]() $x \in c(M)$. Moreover, this map extends by linearity to an isomorphism
$x \in c(M)$. Moreover, this map extends by linearity to an isomorphism ![]() $M_* \to L_1(M)$. This allows us to define, for
$M_* \to L_1(M)$. This allows us to define, for ![]() $1\leq p<\infty$ and
$1\leq p<\infty$ and ![]() $h \in L_p(M)$,
$h \in L_p(M)$, ![]() $\|h\|_p := \| |h|^p \|_{M_*}^{ {1}/{p}}$. This turns
$\|h\|_p := \| |h|^p \|_{M_*}^{ {1}/{p}}$. This turns ![]() $L_p(M)$ into a Banach space that is uniformly convex if
$L_p(M)$ into a Banach space that is uniformly convex if ![]() $1< p<\infty$, and the
$1< p<\infty$, and the ![]() $\|\cdot \|_p$ norms satisfy Hölder's inequality.
$\|\cdot \|_p$ norms satisfy Hölder's inequality.
By the uniqueness of the core, any continuous action by automorphisms of ![]() $G$ on
$G$ on ![]() $M$ gives rise to a continuous action by isometries on
$M$ gives rise to a continuous action by isometries on ![]() $L_p(M)$, that we call the
$L_p(M)$, that we call the ![]() $p$-Koopman representation.
$p$-Koopman representation.
Theorem 5.5 Let ![]() $G$ be a locally compact group with property (T). Let
$G$ be a locally compact group with property (T). Let ![]() $\sigma : G \rightarrow \mathord {\text { Aut}}(M)$ be an action on a von Neumann algebra
$\sigma : G \rightarrow \mathord {\text { Aut}}(M)$ be an action on a von Neumann algebra ![]() $M$ that preserves some faithful normal state
$M$ that preserves some faithful normal state ![]() $\varphi$ on
$\varphi$ on ![]() $M$. Take
$M$. Take ![]() $p \geq 2$ and let
$p \geq 2$ and let ![]() $\pi ^p : G \rightarrow O(L_p(M))$ be the
$\pi ^p : G \rightarrow O(L_p(M))$ be the ![]() $p$-Koopman representation associated to
$p$-Koopman representation associated to ![]() $\sigma$. Then
$\sigma$. Then ![]() $H^1(G,\pi ^p,L_p(M))=0$.
$H^1(G,\pi ^p,L_p(M))=0$.
Proof. First, ![]() $\pi _p$ has spectral gap by [Reference OlivierOli12].
$\pi _p$ has spectral gap by [Reference OlivierOli12].
Define a continuous linear map ![]() $\psi : L_p(M) \rightarrow L_2(M)$ by the formula
$\psi : L_p(M) \rightarrow L_2(M)$ by the formula
for all ![]() $x \in M$. This map is well-defined because
$x \in M$. This map is well-defined because ![]() $M\varphi ^{1/p}$ is dense in
$M\varphi ^{1/p}$ is dense in ![]() $L_p(M)$ and for all
$L_p(M)$ and for all ![]() $x \in M$, we have
$x \in M$, we have
where ![]() $ {1}/{p}+ {1}/{q}=\frac {1}{2}$. Observe that
$ {1}/{p}+ {1}/{q}=\frac {1}{2}$. Observe that ![]() $\pi ^p(g)(x\varphi ^{1/p})=\sigma (g)(x)\varphi ^{1/p}$ for all
$\pi ^p(g)(x\varphi ^{1/p})=\sigma (g)(x)\varphi ^{1/p}$ for all ![]() $x \in M$, because
$x \in M$, because ![]() $\sigma$ preserves
$\sigma$ preserves ![]() $\varphi$, and we have the same formula for
$\varphi$, and we have the same formula for ![]() $p=2$. This implies that
$p=2$. This implies that ![]() $\psi$ is
$\psi$ is ![]() $G$-equivariant with respect to the Koopman representations of
$G$-equivariant with respect to the Koopman representations of ![]() $\sigma$. Thus, it induces an injective map from
$\sigma$. Thus, it induces an injective map from ![]() $H^1(G,\pi ^p,L_p(M))$ into
$H^1(G,\pi ^p,L_p(M))$ into ![]() $H^1(G,\pi ^2,L_2(M))$ by Lemma 5.2. As
$H^1(G,\pi ^2,L_2(M))$ by Lemma 5.2. As ![]() $G$ has property (T), we know that
$G$ has property (T), we know that ![]() $H^1(G,\pi ^2,L_2(M))=0$. We conclude that
$H^1(G,\pi ^2,L_2(M))=0$. We conclude that ![]() $H^1(G,\pi ^p,L_p(M))=0$.
$H^1(G,\pi ^p,L_p(M))=0$.
6. Stability properties of the constants  $p_G$ and
$p_G$ and  $p'_G$
$p'_G$
We start with some elementary stability properties.
Proposition 6.1 Let ![]() $G$ be a locally compact group and let
$G$ be a locally compact group and let ![]() $H< G$ be a closed subgroup. Then
$H< G$ be a closed subgroup. Then ![]() $p'_H \leq p'_G$. If
$p'_H \leq p'_G$. If ![]() $H \triangleleft G$ is a closed normal subgroup, then
$H \triangleleft G$ is a closed normal subgroup, then ![]() $p_{G/H} \geq p_G$.
$p_{G/H} \geq p_G$.
Proof. Any proper action of ![]() $G$ on an
$G$ on an ![]() $L_p$ space restricts to a proper action of
$L_p$ space restricts to a proper action of ![]() $H$, so
$H$, so ![]() $p'_H \leq p'_G$. If
$p'_H \leq p'_G$. If ![]() $H$ is normal, any action of
$H$ is normal, any action of ![]() $G/H$ with unbounded orbits on an
$G/H$ with unbounded orbits on an ![]() $L_p$ space can be seen as an action of
$L_p$ space can be seen as an action of ![]() $G$, so
$G$, so ![]() $p_{G/H} \geq p_G$.
$p_{G/H} \geq p_G$.
Proposition 6.2 Let ![]() $G_1,G_2$ be two locally compact groups. Then
$G_1,G_2$ be two locally compact groups. Then
Proof. The inequalities ![]() $p_{G_1 \times G_2} \leq \min (p_{G_1},p_{G_2})$ and
$p_{G_1 \times G_2} \leq \min (p_{G_1},p_{G_2})$ and ![]() $p'_{G_1 \times G_2} \geq \max (p'_{G_1},p'_{G_2})$ follow from Proposition 6.1.
$p'_{G_1 \times G_2} \geq \max (p'_{G_1},p'_{G_2})$ follow from Proposition 6.1.
For the inequality ![]() $p_{G_1 \times G_2} \geq \min (p_{G_1},p_{G_2})$, observe that if
$p_{G_1 \times G_2} \geq \min (p_{G_1},p_{G_2})$, observe that if ![]() $G_1 \times G_2 \curvearrowright L_p$ has unbounded orbits, then its restriction to either
$G_1 \times G_2 \curvearrowright L_p$ has unbounded orbits, then its restriction to either ![]() $G_1$ or
$G_1$ or ![]() $G_2$ also has unbounded orbits.
$G_2$ also has unbounded orbits.
For the inequality ![]() $p'_{G_1 \times G_2} \leq \max (p'_{G_1},p'_{G_2})$, observe that given two isometric actions
$p'_{G_1 \times G_2} \leq \max (p'_{G_1},p'_{G_2})$, observe that given two isometric actions ![]() $G_1 \curvearrowright L_p(\Omega _1)$ and
$G_1 \curvearrowright L_p(\Omega _1)$ and ![]() $G_1 \curvearrowright L_p(\Omega _2)$, one can construct the action of
$G_1 \curvearrowright L_p(\Omega _2)$, one can construct the action of ![]() $G_1 \times G_2$ on
$G_1 \times G_2$ on ![]() $L_p(\Omega _1 \cup \Omega _2)$, which is proper whenever both actions were proper.
$L_p(\Omega _1 \cup \Omega _2)$, which is proper whenever both actions were proper.
Proposition 6.3 Let ![]() $G$ be a locally compact group and let
$G$ be a locally compact group and let ![]() $K \triangleleft G$ be a normal compact subgroup. Then
$K \triangleleft G$ be a normal compact subgroup. Then
Proof. The only thing to note is that the space of ![]() $K$-invariant vectors for an isometric representation of
$K$-invariant vectors for an isometric representation of ![]() $G$ on an
$G$ on an ![]() $L_p$-space is isometric to an
$L_p$-space is isometric to an ![]() $L_p$-space. This either follows from the general form of isometries of
$L_p$-space. This either follows from the general form of isometries of ![]() $L_p$-space, or from the classical result [Reference TzafririTza69] that the range of a norm
$L_p$-space, or from the classical result [Reference TzafririTza69] that the range of a norm ![]() $1$ projection in
$1$ projection in ![]() $B(L_p)$ is isometric to an
$B(L_p)$ is isometric to an ![]() $L_p$-space.
$L_p$-space.
We now investigate the stability of the constants ![]() $p_G$ and
$p_G$ and ![]() $p'_G$ under measure equivalence. For this we need to recall some definitions.
$p'_G$ under measure equivalence. For this we need to recall some definitions.
Let ![]() $G$ be a locally compact group
$G$ be a locally compact group ![]() $G$ with left Haar measure
$G$ with left Haar measure ![]() $m_G$. A measure-preserving action of
$m_G$. A measure-preserving action of ![]() $G$ on
$G$ on ![]() $(X,\mu )$ is called principal if there is a measure-preserving conjugacy between
$(X,\mu )$ is called principal if there is a measure-preserving conjugacy between ![]() $G \curvearrowright (X,\mu )$ and an action of the form
$G \curvearrowright (X,\mu )$ and an action of the form ![]() $G \curvearrowright (G \times \Omega, m_G \otimes \nu )$ where
$G \curvearrowright (G \times \Omega, m_G \otimes \nu )$ where ![]() $G$ acts by translation of the left coordinate and
$G$ acts by translation of the left coordinate and ![]() $(\Omega, \nu )$ is a measure space with finite measure. In that case, we can identify
$(\Omega, \nu )$ is a measure space with finite measure. In that case, we can identify ![]() $\Omega$ with
$\Omega$ with ![]() $X/G$ and, thus, equip
$X/G$ and, thus, equip ![]() $X/G$ with the finite measure space structure coming from this identification. The finite measure on
$X/G$ with the finite measure space structure coming from this identification. The finite measure on ![]() $X/G$ coming from this identification is denoted
$X/G$ coming from this identification is denoted ![]() $\mu /G$.
$\mu /G$.
Let ![]() $G_1$ and
$G_1$ and ![]() $G_2$ be two locally compact groups. The groups
$G_2$ be two locally compact groups. The groups ![]() $G_1,G_2$ are said to be measure equivalent if there is a measure equivalence coupling, that is a measure space
$G_1,G_2$ are said to be measure equivalent if there is a measure equivalence coupling, that is a measure space ![]() $(X,\mu )$ equipped with two commuting measure-preserving principal actions of
$(X,\mu )$ equipped with two commuting measure-preserving principal actions of ![]() $G_1$ and
$G_1$ and ![]() $G_2$. Observe that we then obtain a measure-preserving action of
$G_2$. Observe that we then obtain a measure-preserving action of ![]() $G_2$ on
$G_2$ on ![]() $(X/G_1,\mu /{G_1})$ and of
$(X/G_1,\mu /{G_1})$ and of ![]() $G_1$ on
$G_1$ on ![]() $(X/G_2,\mu /{G_2})$. We use the notation
$(X/G_2,\mu /{G_2})$. We use the notation ![]() $\mu _1=\mu /G_1$ and
$\mu _1=\mu /G_1$ and ![]() $\mu _2=\mu /G_2$.
$\mu _2=\mu /G_2$.
Let ![]() $p_1 : X \rightarrow G_1$ be a
$p_1 : X \rightarrow G_1$ be a ![]() $G_1$-equivariant map (it always exists because the action of
$G_1$-equivariant map (it always exists because the action of ![]() $G_1$ is principal). Then for every
$G_1$ is principal). Then for every ![]() $g_2 \in G$, the map
$g_2 \in G$, the map
is ![]() $G_1$-invariant. Thus, one can define a cocycle
$G_1$-invariant. Thus, one can define a cocycle ![]() $c_1 : G_2 \times X/G_1 \rightarrow G_1$ by the formula
$c_1 : G_2 \times X/G_1 \rightarrow G_1$ by the formula
where ![]() $\omega \in X$ is any representant of
$\omega \in X$ is any representant of ![]() $\omega _1 \in X/G_1$. Observe that the cocycle
$\omega _1 \in X/G_1$. Observe that the cocycle ![]() $c_1$ depends on the section
$c_1$ depends on the section ![]() $p_1$.
$p_1$.
Now, suppose that ![]() $G_1$ is compactly generated. Take
$G_1$ is compactly generated. Take ![]() $p > 0$. We say that the measure equivalence coupling
$p > 0$. We say that the measure equivalence coupling ![]() $(X,\mu )$ is
$(X,\mu )$ is ![]() $L_p$-integrable over
$L_p$-integrable over ![]() $G_1$ if there exists a
$G_1$ if there exists a ![]() $G_1$-equivariant map
$G_1$-equivariant map ![]() $p_1 : X \rightarrow G_1$ such that the associated cocycle
$p_1 : X \rightarrow G_1$ such that the associated cocycle ![]() $c_1$ defined previously satisfies the following
$c_1$ defined previously satisfies the following ![]() $L_p$-integrability condition:
$L_p$-integrability condition:
where ![]() $| \cdot |_{G_1}$ is the word length with respect to any compact generating set of
$| \cdot |_{G_1}$ is the word length with respect to any compact generating set of ![]() $G_1$ (the integrability condition does not depend on the choice).
$G_1$ (the integrability condition does not depend on the choice).
We say that two compactly generated groups ![]() $G_1$ and
$G_1$ and ![]() $G_2$ are
$G_2$ are ![]() $L_p$-measure equivalent if there exists a measure equivalence coupling that is
$L_p$-measure equivalent if there exists a measure equivalence coupling that is ![]() $L_p$-integrable over both
$L_p$-integrable over both ![]() $G_1$ and
$G_1$ and ![]() $G_2$. Thanks to the construction in [Reference FurmanFur99, Theorem 3.3], we know that
$G_2$. Thanks to the construction in [Reference FurmanFur99, Theorem 3.3], we know that ![]() $L_p$-measure equivalence is more general than
$L_p$-measure equivalence is more general than ![]() $L_p$-orbit equivalence.
$L_p$-orbit equivalence.
More details on measure equivalence of locally compact groups and ![]() $L_p$-measure equivalence can be found in [Reference Bader, Furman and SauerBFS13, § 1.2] and the references therein.
$L_p$-measure equivalence can be found in [Reference Bader, Furman and SauerBFS13, § 1.2] and the references therein.
Theorem 6.4 Let ![]() $G_1$ and
$G_1$ and ![]() $G_2$ be two locally compact groups. Let
$G_2$ be two locally compact groups. Let ![]() $1 \leq p < \infty$. Suppose that
$1 \leq p < \infty$. Suppose that ![]() $G_1$ is compactly generated and that there exists a measure equivalence coupling between
$G_1$ is compactly generated and that there exists a measure equivalence coupling between ![]() $G_1$ and
$G_1$ and ![]() $G_2$ that is
$G_2$ that is ![]() $L_p$-integrable over
$L_p$-integrable over ![]() $G_1$.
$G_1$.
(i) If
 $G_1$ admits an affine isometric action without fixed points on some
$G_1$ admits an affine isometric action without fixed points on some  $L_p$-space, then so does
$L_p$-space, then so does  $G_2$.
$G_2$.(ii) If
 $G_1$ admits a proper affine isometric action on some
$G_1$ admits a proper affine isometric action on some  $L_p$-space, then so does
$L_p$-space, then so does  $G_2$.
$G_2$.
Proof. We use the standard tool of induction of Banach-space actions as in [Reference Bader, Furman, Gelander and MonodBFGM07, § 8.b]. Let ![]() $(X,\mu )$ be measure equivalence coupling that is
$(X,\mu )$ be measure equivalence coupling that is ![]() $L_p$-integrable over
$L_p$-integrable over ![]() $G_1$. Let
$G_1$. Let ![]() $p_1$ and
$p_1$ and ![]() $c_1$ be as in the definition.
$c_1$ be as in the definition.
Let ![]() $\alpha \colon G_1 \curvearrowright E$ be an action by affine isometries of
$\alpha \colon G_1 \curvearrowright E$ be an action by affine isometries of ![]() $G_1$ on a Banach space
$G_1$ on a Banach space ![]() $E$. Let
$E$. Let ![]() $L_0(X,\mu,E)^{G_1}$ be the set of all
$L_0(X,\mu,E)^{G_1}$ be the set of all ![]() $G_1$-equivariant Bochner-measurable maps from
$G_1$-equivariant Bochner-measurable maps from ![]() $X$ to
$X$ to ![]() $E$. Note that
$E$. Note that ![]() $L_0(X,\mu,E)^{G_1}$ is only an affine subspace of
$L_0(X,\mu,E)^{G_1}$ is only an affine subspace of ![]() $L_0(X,\mu,E)$ (it does not contain
$L_0(X,\mu,E)$ (it does not contain ![]() $0$). Observe that we have a natural affine action
$0$). Observe that we have a natural affine action ![]() $\beta : G_2 \curvearrowright L_0(X,\mu, E)^{G_1}$ given by
$\beta : G_2 \curvearrowright L_0(X,\mu, E)^{G_1}$ given by ![]() $\beta _{g_2}(f)(x)=f(g_2^{-1}x)$ for all
$\beta _{g_2}(f)(x)=f(g_2^{-1}x)$ for all ![]() $x \in X$. If
$x \in X$. If ![]() $f,h \in L_0(X,\mu,E)^{G_1}$, then the map
$f,h \in L_0(X,\mu,E)^{G_1}$, then the map ![]() $\| f-h\|_E : X \rightarrow \mathbf {R}_+$ is
$\| f-h\|_E : X \rightarrow \mathbf {R}_+$ is ![]() $G_1$-invariant and, thus, we can define
$G_1$-invariant and, thus, we can define
 \[ \| f-h\|_{p,G_1} = \bigg( \int_{X/G_1} \|f-h\|_E^p \,{d}\mu_1 \bigg)^{1/p}. \]
\[ \| f-h\|_{p,G_1} = \bigg( \int_{X/G_1} \|f-h\|_E^p \,{d}\mu_1 \bigg)^{1/p}. \]
We clearly have ![]() $\| \beta _{g_2}(f)-\beta _{g_2}(h) \| = \| f-h\|$ for all
$\| \beta _{g_2}(f)-\beta _{g_2}(h) \| = \| f-h\|$ for all ![]() $g_2 \in G_2$ (because the action of
$g_2 \in G_2$ (because the action of ![]() $G_2$ on
$G_2$ on ![]() $X/G_1$ preserves the measure).
$X/G_1$ preserves the measure).
Take ![]() $x \in E$ and define
$x \in E$ and define ![]() $f_0 \in L_0(X,\mu,E)^{G_1}$ by the formula
$f_0 \in L_0(X,\mu,E)^{G_1}$ by the formula ![]() $f_0(\omega )=p_1(\omega ) \cdot x$. Now, define an affine subspace
$f_0(\omega )=p_1(\omega ) \cdot x$. Now, define an affine subspace
Note that the space ![]() $F$ is isometric to
$F$ is isometric to ![]() $L_p( X/G_1,\mu _1, E)$. In particular, if
$L_p( X/G_1,\mu _1, E)$. In particular, if ![]() $E$ is an
$E$ is an ![]() $L_p$-space, then
$L_p$-space, then ![]() $F$ is also an
$F$ is also an ![]() $L_p$-space.
$L_p$-space.
Now, a key observation is that ![]() $\beta _{g_2}(f_0) \in F$ for all
$\beta _{g_2}(f_0) \in F$ for all ![]() $g_2 \in G_2$. Indeed, we have
$g_2 \in G_2$. Indeed, we have
 \[ \| \beta_{g_2}(f_0) - f_0 \|_{p,G_1}=\bigg( \int_{X/G_1} \| c_1(g_2,\omega_1) \cdot x -x\|_E^p \,{d} \mu_1(\omega_1) \bigg)^{1/p} \]
\[ \| \beta_{g_2}(f_0) - f_0 \|_{p,G_1}=\bigg( \int_{X/G_1} \| c_1(g_2,\omega_1) \cdot x -x\|_E^p \,{d} \mu_1(\omega_1) \bigg)^{1/p} \]
and this integral is finite because of the ![]() $L_p$-integrability of
$L_p$-integrability of ![]() $c_1$ and the fact that the function
$c_1$ and the fact that the function ![]() $g_1 \mapsto \| g_1 \cdot x-x\|_E$ grows sublinearly: there exists a constant
$g_1 \mapsto \| g_1 \cdot x-x\|_E$ grows sublinearly: there exists a constant ![]() $C > 0$ such that
$C > 0$ such that ![]() $\| g_1 \cdot x- x\|_E \leq C|g_1|_{G_1}$ for all
$\| g_1 \cdot x- x\|_E \leq C|g_1|_{G_1}$ for all ![]() $g_1 \in G_1$.
$g_1 \in G_1$.
As ![]() $\beta _{g_2}(f_0) \in F$ for all
$\beta _{g_2}(f_0) \in F$ for all ![]() $g_2 \in G_2$, it follows that
$g_2 \in G_2$, it follows that ![]() $F$ is globally invariant under the action
$F$ is globally invariant under the action ![]() $\beta$. We conclude that the action
$\beta$. We conclude that the action ![]() $\beta : G_2 \curvearrowright L_0(X,\mu,E)^{G_1}$ restricts to an affine isometric action, still denoted
$\beta : G_2 \curvearrowright L_0(X,\mu,E)^{G_1}$ restricts to an affine isometric action, still denoted ![]() $\beta$, of
$\beta$, of ![]() $G_2$ on
$G_2$ on ![]() $F$. We call the affine isometric action
$F$. We call the affine isometric action ![]() $\beta : G_2 \curvearrowright F$ the induced action of
$\beta : G_2 \curvearrowright F$ the induced action of ![]() $\alpha$ (note that it depends on the choice of
$\alpha$ (note that it depends on the choice of ![]() $p_1$).
$p_1$).
To prove item (i), it is enough to check that if ![]() $\beta$ has a fixed point then
$\beta$ has a fixed point then ![]() $\alpha$ also has a fixed point. Let
$\alpha$ also has a fixed point. Let ![]() $f \in F$ be a fixed point for
$f \in F$ be a fixed point for ![]() $\beta$. This means that
$\beta$. This means that ![]() $f : X \rightarrow E$ is a
$f : X \rightarrow E$ is a ![]() $G_1$-equivariant measurable map that is also
$G_1$-equivariant measurable map that is also ![]() $G_2$-invariant. Thus, we can view
$G_2$-invariant. Thus, we can view ![]() $f$ as a
$f$ as a ![]() $G_1$-equivariant map from
$G_1$-equivariant map from ![]() $X/G_2$ to
$X/G_2$ to ![]() $E$. As
$E$. As ![]() $X/G_2$ admits a
$X/G_2$ admits a ![]() $G_1$-invariant probability measure
$G_1$-invariant probability measure ![]() $\mu _2$, we can push it forward by
$\mu _2$, we can push it forward by ![]() $f$ to obtain a
$f$ to obtain a ![]() $G_1$-invariant probability measure on
$G_1$-invariant probability measure on ![]() $E$. We conclude by [Reference Bader, Furman, Gelander and MonodBFGM07, Lemma 2.14] that
$E$. We conclude by [Reference Bader, Furman, Gelander and MonodBFGM07, Lemma 2.14] that ![]() $\alpha$ has a fixed point.
$\alpha$ has a fixed point.
To prove item (ii), it is enough to check that if ![]() $\alpha$ is proper, then
$\alpha$ is proper, then ![]() $\beta$ is also proper. We have
$\beta$ is also proper. We have
 \[ \| \beta_{g_2}(f_0) - f_0 \|_{p,G_1} = \bigg(\int_{X/G_1} \| c_1(g_2,\omega_1) \cdot x-x \|_E^p \,{d}\mu_1(\omega_1)\bigg)^{{1}/{p}}. \]
\[ \| \beta_{g_2}(f_0) - f_0 \|_{p,G_1} = \bigg(\int_{X/G_1} \| c_1(g_2,\omega_1) \cdot x-x \|_E^p \,{d}\mu_1(\omega_1)\bigg)^{{1}/{p}}. \]
Take ![]() $R > 0$. As
$R > 0$. As ![]() $\alpha$ is proper, we can choose a compact subset
$\alpha$ is proper, we can choose a compact subset ![]() $K_1 \subset G_1$ such that
$K_1 \subset G_1$ such that ![]() $\| g_1 x-x\| \geq R$ for all
$\| g_1 x-x\| \geq R$ for all ![]() $g_1 \in G_1 \setminus K_1$. Observe that
$g_1 \in G_1 \setminus K_1$. Observe that
 \begin{align*} & \mu_1 \{ \omega_1 \in X/G_1 \mid c(g_2, \omega_1) \in K_1 \} \\ &\quad =\frac{1}{m_{G_1}(K_1)} \mu \{ \omega \in X \mid p_1(\omega) \in K_1 \text{ and } p_1(g_2 \omega)^{-1}p_1(\omega) \in K_1 \} \\ &\quad \leq \frac{1}{m_{G_1}(K_1)} \mu \{ \omega \in X \mid p_1(\omega) \in K_1 \text{ and } p_1(g_2 \omega) \in K_1^{-1} K_1 \}. \end{align*}
\begin{align*} & \mu_1 \{ \omega_1 \in X/G_1 \mid c(g_2, \omega_1) \in K_1 \} \\ &\quad =\frac{1}{m_{G_1}(K_1)} \mu \{ \omega \in X \mid p_1(\omega) \in K_1 \text{ and } p_1(g_2 \omega)^{-1}p_1(\omega) \in K_1 \} \\ &\quad \leq \frac{1}{m_{G_1}(K_1)} \mu \{ \omega \in X \mid p_1(\omega) \in K_1 \text{ and } p_1(g_2 \omega) \in K_1^{-1} K_1 \}. \end{align*}
As ![]() $\mu (p_1^{-1}(K_1 \cup K_1^{-1} K_1))<+\infty$, there exists a compact subset
$\mu (p_1^{-1}(K_1 \cup K_1^{-1} K_1))<+\infty$, there exists a compact subset ![]() $K_2 \subset G_2$ such that
$K_2 \subset G_2$ such that ![]() $\mu (p_1^{-1}(K_1 \cup K_1^{-1}K_1) \setminus p_2^{-1}(K_2) ) \leq \frac {1}{4} m_{G_1}(K_1)$. Take
$\mu (p_1^{-1}(K_1 \cup K_1^{-1}K_1) \setminus p_2^{-1}(K_2) ) \leq \frac {1}{4} m_{G_1}(K_1)$. Take ![]() $g_2 \in G_2 \setminus K_2 K_2^{-1}$. Then, we cannot have
$g_2 \in G_2 \setminus K_2 K_2^{-1}$. Then, we cannot have ![]() $p_2(\omega ) \in K_2$
$p_2(\omega ) \in K_2$ ![]() $p_2(g_2 \omega ) \in K_2$ at the same time. Therefore, we obtain
$p_2(g_2 \omega ) \in K_2$ at the same time. Therefore, we obtain
which yields
By the choice of ![]() $K_1$, this means that
$K_1$, this means that
hence
This holds for all ![]() $g_2 \in G_2$ outside of the compact subset
$g_2 \in G_2$ outside of the compact subset ![]() $K_2 K_2^{-1}$. We conclude that
$K_2 K_2^{-1}$. We conclude that ![]() $\beta$ is proper.
$\beta$ is proper.
When ![]() $G$ is a locally compact group and
$G$ is a locally compact group and ![]() $\Gamma < G$ is a lattice, then
$\Gamma < G$ is a lattice, then ![]() $(G,m_G)$ is measure equivalence coupling between
$(G,m_G)$ is measure equivalence coupling between ![]() $G$ and
$G$ and ![]() $\Gamma$. Therefore, Theorem 6.4 covers, in particular, the following corollary which is already implicit in [Reference Bader, Furman, Gelander and MonodBFGM07].
$\Gamma$. Therefore, Theorem 6.4 covers, in particular, the following corollary which is already implicit in [Reference Bader, Furman, Gelander and MonodBFGM07].
Corollary 6.5 [Reference Bader, Furman, Gelander and MonodBFGM07]
Let ![]() $G$ be a locally compact compactly generated group and let
$G$ be a locally compact compactly generated group and let ![]() $\Gamma < G$ be a lattice. Then
$\Gamma < G$ be a lattice. Then ![]() $p_{\Gamma } \leq p_G$ and
$p_{\Gamma } \leq p_G$ and ![]() $p'_{\Gamma } \leq p'_G$. If
$p'_{\Gamma } \leq p'_G$. If ![]() $\Gamma$ is
$\Gamma$ is ![]() $L_p$-integrable for some
$L_p$-integrable for some ![]() $p \geq p_\Gamma$ (respectively,
$p \geq p_\Gamma$ (respectively, ![]() $p \geq p'_\Gamma$), then
$p \geq p'_\Gamma$), then ![]() $p_G=p_{\Gamma }$ (respectively,
$p_G=p_{\Gamma }$ (respectively, ![]() $p'_G=p'_{\Gamma }$).
$p'_G=p'_{\Gamma }$).
Acknowledgements
We are grateful to David Fisher for his question on ![]() $L_p$-measure equivalence which led us to Theorem 5. We also thank Piotr Nowak for his comments which helped us to improve the presentation of this paper. We thank Romain Tessera for providing us with useful references.
$L_p$-measure equivalence which led us to Theorem 5. We also thank Piotr Nowak for his comments which helped us to improve the presentation of this paper. We thank Romain Tessera for providing us with useful references.