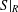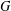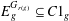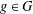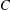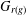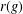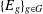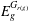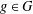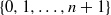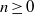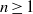32 results in 18Bxx
Functorial Fast-Growing Hierarchies
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 January 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper Ehresmann semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 758-788
-
- Article
-
- You have access
- HTML
- Export citation
Correspondence theorems for Hopf algebroids with applications to affine groupoids
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 830-880
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
COHOMOLOGICAL MACKEY 2-FUNCTORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 August 2022, pp. 279-309
- Print publication:
- January 2024
-
- Article
- Export citation
A GENERALISATION OF HIGHER-RANK GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 26 July 2021, pp. 257-266
- Print publication:
- April 2022
-
- Article
- Export citation
INFINITARY GENERALIZATIONS OF DELIGNE’S COMPLETENESS THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 1147-1162
- Print publication:
- September 2020
-
- Article
- Export citation
CATEGORICAL SEMANTICS OF METRIC SPACES AND CONTINUOUS LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1044-1078
- Print publication:
- September 2020
-
- Article
- Export citation
DERIVED NON-ARCHIMEDEAN ANALYTIC HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 26 August 2020, pp. 335-366
- Print publication:
- January 2022
-
- Article
- Export citation
Étale groupoid algebras with coefficients in a sheaf and skew inverse semigroup rings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 07 August 2020, pp. 1592-1626
- Print publication:
- December 2021
-
- Article
- Export citation
A BRIDGE BETWEEN Q-WORLDS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 02 July 2020, pp. 447-486
- Print publication:
- June 2021
-
- Article
- Export citation
EXACT COMPLETION AND CONSTRUCTIVE THEORIES OF SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 563-584
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- Export citation
GCR and CCR Steinberg Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 1581-1606
- Print publication:
- December 2020
-
- Article
- Export citation
Topos points of quasi-coherent sheaves over monoid schemes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 31-74
- Print publication:
- July 2020
-
- Article
- Export citation
CHARACTERIZING n-ISOCLINIC CLASSES OF CROSSED MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 08 October 2018, pp. 637-656
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Perforation conditions and almost algebraic order in Cuntz semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 18 April 2018, pp. 669-702
- Print publication:
- August 2018
-
- Article
- Export citation
A CHARACTERISATION FOR A GROUPOID GALOIS EXTENSION USING PARTIAL ISOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 59-68
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
SYNTHETIC LIE THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 10 February 2016, pp. 516-517
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ASPECTS OF GLOBULAR HIGHER CATEGORY THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 19 May 2014, pp. 172-173
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
A DUALIZING OBJECT APPROACH TO NONCOMMUTATIVE STONE DUALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 19 August 2013, pp. 383-403
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
THE ÉTALE GROUPOID OF AN INVERSE SEMIGROUP AS A GROUPOID OF FILTERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 15 May 2013, pp. 234-256
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation

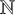
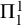

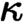
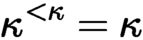
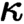
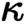
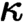
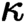
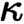
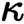
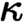
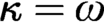
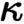
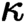
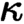
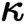
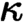
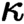
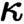
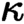
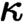
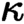
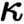
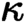
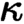
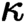
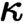
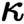
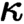
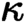
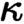
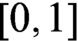
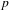
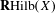
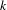
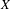
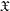
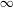
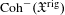
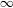
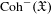
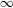
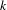
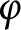
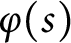
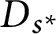
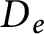
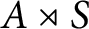
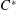
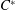
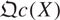 of quasi-coherent sheaves over
of quasi-coherent sheaves over 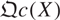 is of this form if
is of this form if 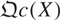 and
and 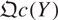 are equivalent.
are equivalent.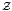 ) in terms of Cu(
) in terms of Cu(