The optimal expansion of a power system with reduced carbon footprint entails dealing with uncertainty about the distribution of the random variables involved in the decision process. Optimisation under ambiguity sets provides a mechanism to suitably deal with such a setting. For two-stage stochastic linear programs, we propose a new model that is between the optimistic and pessimistic paradigms in distributionally robust stochastic optimisation. When using Wasserstein balls as ambiguity sets, the resulting optimisation problem has nonsmooth convex constraints depending on the number of scenarios and a bilinear objective function. We propose a decomposition method along scenarios that converges to a solution, provided a global optimisation solver for bilinear programs with polyhedral feasible sets is available. The solution procedure is applied to a case study on expansion of energy generation that takes into account sustainability goals for 2050 in Europe, under uncertain future market conditions.

Some optimal choices for a parameter of the Dai–Liao conjugate gradient method are proposed by conducting matrix analyses of the method. More precisely, first the $\ell _{1}$ and $\ell _{\infty }$ norm condition numbers of the search direction matrix are minimized, yielding two adaptive choices for the Dai–Liao parameter. Then we show that a recent formula for computing this parameter which guarantees the descent property can be considered as a minimizer of the spectral condition number as well as the well-known measure function for a symmetrized version of the search direction matrix. Brief convergence analyses are also carried out. Finally, some numerical experiments on a set of test problems related to constrained and unconstrained testing environment, are conducted using a well-known performance profile.

A direct search quasi-Newton algorithm is presented for local minimization of Lipschitz continuous black-box functions. The method estimates the gradient via central differences using a maximal frame around each iterate. When nonsmoothness prevents progress, a global direction search is used to locate a descent direction. Almost sure convergence to Clarke stationary point(s) is shown, where convergence is independent of the accuracy of the gradient estimates. Numerical results show that the method is effective in practice.

In this paper, we generalize monotone operators, their resolvents and the proximal point algorithm to complete CAT(0) spaces. We study some properties of monotone operators and their resolvents. We show that the sequence generated by the inexact proximal point algorithm $\unicode[STIX]{x1D6E5}$-converges to a zero of the monotone operator in complete CAT(0) spaces. A strong convergence (convergence in metric) result is also presented. Finally, we consider two important special cases of monotone operators and we prove that they satisfy the range condition (see Section 4 for the definition), which guarantees the existence of the sequence generated by the proximal point algorithm.

This article addresses the resolution of the inverse problem for the parameter identification in orthotropic materials with a number of measurements merely on the boundaries. The inverse problem is formulated as an optimization problem of a residual functional which evaluates the differences between the experimental and predicted displacements. The singular boundary method, an integration-free, mathematically simple and boundary-only meshless method, is employed to numerically determine the predicted displacements. The residual functional is minimized by the Levenberg-Marquardt method. Three numerical examples are carried out to illustrate the robustness, efficiency, and accuracy of the proposed scheme. In addition, different levels of noise are added into the boundary conditions to verify the stability of the present methodology.

In this paper, a primal-dual interior point method is proposed for general constrained optimization, which incorporated a penalty function and a kind of new identification technique of the active set. At each iteration, the proposed algorithm only needs to solve two or three reduced systems of linear equations with the same coefficient matrix. The size of systems of linear equations can be decreased due to the introduction of the working set, which is an estimate of the active set. The penalty parameter is automatically updated and the uniformly positive definiteness condition on the Hessian approximation of the Lagrangian is relaxed. The proposed algorithm possesses global and superlinear convergence under some mild conditions. Finally, some preliminary numerical results are reported.

In this paper, we study to use nonlocal bounded variation (NLBV) techniques to decompose an image intensity into the illumination and reflectance components. By considering spatial smoothness of the illumination component and nonlocal total variation (NLTV) of the reflectance component in the decomposition framework, an energy functional is constructed. We establish the theoretical results of the space of NLBV functions such as lower semicontinuity, approximation and compactness. These essential properties of NLBV functions are important tools to show the existence of solution of the proposed energy functional. Experimental results on both grey-level and color images are shown to illustrate the usefulness of the nonlocal total variation image decomposition model, and demonstrate the performance of the proposed method is better than the other testing methods.

A new hybrid variational model for recovering blurred images in the presence of multiplicative noise is proposed. Inspired by previous work on multiplicative noise removal, an I-divergence technique is used to build a strictly convex model under a condition that ensures the uniqueness of the solution and the stability of the algorithm. A split-Bregman algorithm is adopted to solve the constrained minimisation problem in the new hybrid model efficiently. Numerical tests for simultaneous deblurring and denoising of the images subject to multiplicative noise are then reported. Comparison with other methods clearly demonstrates the good performance of our new approach.

Robust optimization is an approach for the design of a mechanical structure which takes into account the uncertainties of the design variables. It requires at each iteration the evaluation of some robust measures of the objective function and the constraints. In a previous work, the authors have proposed a method which efficiently generates a design of experiments with respect to the design variable uncertainties to compute the robust measures using the polynomial chaos expansion. This paper extends the proposed method to the case of the robust optimization. The generated design of experiments is used to build a surrogate model for the robust measures over a certain trust region. This leads to a trust region optimization method which only requires one evaluation of the design of experiments per iteration (single loop method). Unlike other single loop methods which are only based on a first order approximation of robust measure of the constraints and which does not handle a robust measure for the objective function, the proposed method can handle any approximation order and any choice for the robust measures. Some numerical experiments based on finite element functions are performed to show the efficiency of the method.

Image deconvolution problems with a symmetric point-spread function arise in many areas of science and engineering. These problems often are solved by the Richardson-Lucy method, a nonlinear iterative method. We first show a convergence result for the Richardson-Lucy method. The proof sheds light on why the method may converge slowly. Subsequently, we describe an iterative active set method that imposes the same constraints on the computed solution as the Richardson-Lucy method. Computed examples show the latter method to yield better restorations than the Richardson-Lucy method and typically require less computational effort.

Numerical methods of a 3D multiphysics, two-phase transport model of proton exchange membrane fuel cell (PEMFC) is studied in this paper. Due to the coexistence of multiphase regions, the standard finite element/finite volume method may fail to obtain a convergent nonlinear iteration for a two-phase transport model of PEMFC [49,50]. By introducing Kirchhoff transformation technique and a combined finite element-upwind finite volume approach, we efficiently achieve a fast convergence and reasonable solutions for this multiphase, multiphysics PEMFC model. Numerical implementation is done by using a novel automated finite element/finite volume program generator (FEPG). By virtue of a high-level algorithm description language (script), component programming and human intelligence technologies, FEPG can quickly generate finite element/finite volume source code for PEMFC simulation. Thus, one can focus on the efficient algorithm research without being distracted by the tedious computer programming on finite element/finite volume methods. Numerical success confirms that FEPG is an efficient tool for both algorithm research and software development of a 3D, multiphysics PEMFC model with multicomponent and multiphase mechanism.

The classical discrete element approach (DEM) based on Newtonian dynamics can be divided into two major groups, event-driven methods (EDM) and time-driven methods (TDM). Generally speaking, TDM simulations are suited for cases with high volume fractions where there are collisions between multiple objects. EDM simulations are suited for cases with low volume fractions from the viewpoint of CPU time. A method combining EDM and TDM called Hybrid Algorithm of event-driven and time-driven methods (HAET) is presented in this paper. The HAET method employs TDM for the areas with high volume fractions and EDM for the remaining areas with low volume fractions. It can decrease the CPU time for simulating granular flows with strongly non-uniform volume fractions. In addition, a modified EDM algorithm using a constant time as the lower time step limit is presented. Finally, an example is presented to demonstrate the hybrid algorithm.

In this paper we use two numerical methods to solve constrained optimal control problems governed by elliptic equations with rapidly oscillating coefficients: one is finite element method and the other is multiscale finite element method. We derive the convergence analysis for those two methods. Analytical results show that finite element method can not work when the parameter ε is small enough, while multiscale finite element method is useful for any parameter ε.

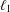
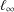
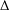
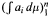An important question in the study of moment problems is to determine when a fixed point in ℝn lies in the moment cone of vectors , with μ a nonnegative measure. In associated optimization problems it is also important to be able to distinguish between the interior and boundary of the moment cone. Recent work of Dachuna-Castelle, Gamboa and Gassiat derived elegant computational characterizations for these problems, and for related questions with an upper bound on μ. Their technique involves a probabilistic interpretation and large deviations theory. In this paper a purely convex analytic approach is used, giving a more direct understanding of the underlying duality, and allowing the relaxation of their assumptions.