Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-26T12:58:10.153Z Has data issue: false hasContentIssue false
  • English
  • Français

MONOTONE OPERATORS AND THE PROXIMAL POINT ALGORITHM IN COMPLETE CAT(0) METRIC SPACES

Part of: Nonlinear operators and their properties Equations and inequalities involving nonlinear operators

Published online by Cambridge University Press:  23 September 2016

HADI KHATIBZADEH  and
SAJAD RANJBAR
HADI KHATIBZADEH*
Affiliation:
Department of Mathematics, University of Zanjan, Zanjan, PO Box 45195-313, Iran email hkhatibzadeh@znu.ac.ir
SAJAD RANJBAR
Affiliation:
Department of Mathematics, University of Zanjan, Zanjan, PO Box 45195-313, Iran email sranjbar74@yahoo.com Department of Mathematics, College of Sciences, Higher Education Center of Eghlid, Eghlid, Iran email sranjbar@eghlid.ac.ir
*
✉hkhatibzadeh@znu.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

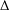In this paper, we generalize monotone operators, their resolvents and the proximal point algorithm to complete CAT(0) spaces. We study some properties of monotone operators and their resolvents. We show that the sequence generated by the inexact proximal point algorithm $\unicode[STIX]{x1D6E5}$-converges to a zero of the monotone operator in complete CAT(0) spaces. A strong convergence (convergence in metric) result is also presented. Finally, we consider two important special cases of monotone operators and we prove that they satisfy the range condition (see Section 4 for the definition), which guarantees the existence of the sequence generated by the proximal point algorithm.

Keywords

Hadamard spacemonotone operatorproximal point algorithm𝛥-convergencesubdifferentialnonexpansive mapping

MSC classification

Primary: 47H05: Monotone operators and generalizations
Secondary: 47J05: Equations involving nonlinear operators (general) 47J20: Variational and other types of inequalities involving nonlinear operators (general) 65K05: Mathematical programming methods
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 1 , August 2017 , pp. 70 - 90
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

The authors are grateful to the referees for valuable comments and suggestions. The second author was supported by Higher Education Center of Eghlid in Iran.

References

Ahmadi, P. and Khatibzadeh, H., ‘On the convergence of inexact proximal point algorithm on Hadamard manifolds’, Taiwanese J. Math. 18 (2014), 419–433.CrossRefGoogle Scholar
Ahmadi Kakavandi, B., ‘Weak topologies in complete CAT(0) metric spaces’, Proc. Amer. Math. Soc. 141 (2013), 1029–1039.CrossRefGoogle Scholar
Ahmadi Kakavandi, B. and Amini, M., ‘Duality and subdifferential for convex functions on complete CAT(0) metric spaces’, Nonlinear Anal. 73 (2010), 3450–3455.Google Scholar
Bačák, M., ‘The proximal point algorithm in metric spaces’, Israel J. Math. 194 (2013), 689–701.CrossRefGoogle Scholar
Bačák, M., ‘Convergence of nonlinear semigroups under nonpositive curvature’, Trans. Amer. Math. Soc. 367 (2015), 3929–3953.Google Scholar
Berg, I. D. and Nikolaev, I. G., ‘Quasilinearization and curvature of Alexandrov spaces’, Geom. Dedicata 133 (2008), 195–218.CrossRefGoogle Scholar
Brézis, H. and Lions, P. L., ‘Produits infinis derésolvantes’, Israel J. Math. 29 (1978), 329–345.CrossRefGoogle Scholar
Bridson, M. and Haefliger, A., Metric Spaces of Non-Positive Curvature, Vol. 319 (Springer, Berlin, 1999).Google Scholar
Burago, D., Burago, Y. and Ivanov, S., A Course in Metric Geometry, Graduate Studies in Mathematics, 33 (American Mathematical Society, Providence, RI, 2001).CrossRefGoogle Scholar
Dehghan, H. and Rooin, J., ‘Metric projection and convergence theorems for nonexpansive mappings in Hadamard spaces’, J. Nonlinear Convex Anal., to appear.Google Scholar
Dhompongsa, S. and Panyanak, B., ‘On 𝛥-convergence theorems in CAT(0) spaces’, Comput. Math. Appl. 56 (2008), 2572–2579.Google Scholar
Djafari Rouhani, B. and Khatibzadeh, H., ‘On the proximal point algorithm’, J. Optim. Theory Appl. 137 (2008), 411–417.CrossRefGoogle Scholar
Espínola, R. and Fernández-León, A., ‘CAT(𝜅)-spaces, weak convergence and fixed points’, J. Math. Anal. Appl. 353 (2009), 410–427.Google Scholar
Gromov, M. and Bates, S.M., Metric Structures for Riemannian and Non-Riemannian Spaces, Progress in Mathematics, 152 (eds. Lafontaine, J. and Pansu, P.) (Birkhäuser, Boston, 1999), with appendices by M. Katz, P. Pansu and S. Semmes.Google Scholar
Güler, O., ‘On the convergence of the proximal point algorithm for convex minimization’, SIAM J. Control Optim. 29 (1991), 403–419.CrossRefGoogle Scholar
Jöst, J., Nonpositive Curvature: Geometric and Analytic Aspects, Lectures in Mathematics (Birkhäuser, Basel, 1997).CrossRefGoogle Scholar
Kirk, W. A. and Panyanak, B., ‘A concept of convergence in geodesic spaces’, Nonlinear Anal. 68 (2008), 3689–3696.Google Scholar
Li, C., López, G. and Martín-Márquez, V., ‘Monotone vector fields and the proximal point algorithm’, J. London Math. Soc. 679 (2009), 663–683.CrossRefGoogle Scholar
Lim, T. C., ‘Remarks on some fixed point theorems’, Proc. Amer. Math. Soc. 60 (1976), 179–182.Google Scholar
Martinet, B., ‘Régularisation d’Inéquations Variationnelles par Approximations Successives’, Rev. Franćaise d’Inform. et de Rech. Opérationnelle 3 (1970), 154–158.Google Scholar
Morosanu, G., Nonlinear Evolution Equations and Applications (Editura Academiei Romane and D. Reidel publishing Company, Bucharest, 1988).Google Scholar
Ranjbar, S. and Khatibzadeh, H., ‘𝛥-convergence and w-convergence of the modified Mann iteration for a family of asymptotically nonexpansive type mappings in complete CAT(0) spaces’, Fixed Point Theory 17 (2016), 151–158.Google Scholar
Rockafellar, R. T., ‘Monotone operators and the proximal point algorithm’, SIAM J. Control Optim. 14 (1976), 877–898.Google Scholar