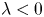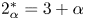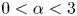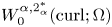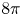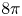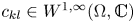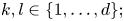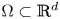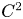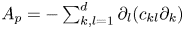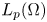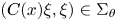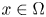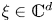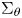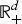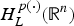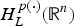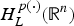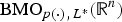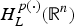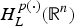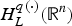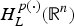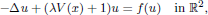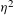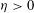26 results
On a critical time-harmonic Maxwell equation in nonlocal media
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-45
-
- Article
- Export citation
Groundstates of the planar Schrödinger–Poisson system with potential well and lack of symmetry
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radial solvability for Pucci-Lane-Emden systems in annuli
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 March 2023, pp. 494-507
- Print publication:
- April 2024
-
- Article
- Export citation
Stationary solutions to the Keller–Segel equation on curved planes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 327-343
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On sectoriality of degenerate elliptic operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 18 August 2021, pp. 689-710
-
- Article
- Export citation
A continuum limit for the PageRank algorithm
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 27 April 2021, pp. 472-504
-
- Article
-
- You have access
- Open access
- Export citation
Comparing the best-reply strategy and mean-field games: The stationary case
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 20 November 2020, pp. 79-110
-
- Article
- Export citation
Bloch wave homogenisation of quasiperiodic media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 58-78
-
- Article
- Export citation
ESTIMATES AND RIGIDITY FOR STABLE SOLUTIONS TO SOME NONLINEAR ELLIPTIC PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 10 September 2020, pp. 335-337
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
Decay rates at infinity for solutions to periodic Schrödinger equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1113-1126
- Print publication:
- June 2020
-
- Article
- Export citation
On the boundary regularity of phase-fields for Willmore's energy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1017-1035
- Print publication:
- August 2019
-
- Article
- Export citation
A quantitative Carleman estimate for second-order elliptic operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 915-938
- Print publication:
- August 2019
-
- Article
- Export citation
RECOVERY OF NON-COMPACTLY SUPPORTED COEFFICIENTS OF ELLIPTIC EQUATIONS ON AN INFINITE WAVEGUIDE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 05 November 2018, pp. 1573-1600
- Print publication:
- September 2020
-
- Article
- Export citation
On a Class of Fully Nonlinear Elliptic Equations Containing Gradient Terms on Compact Hermitian Manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 4 / 01 August 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 943-960
- Print publication:
- 01 August 2018
-
- Article
-
- You have access
- Export citation
Variable Hardy Spaces Associated with Operators Satisfying Davies–Gaffney Estimates
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 759-810
-
- Article
- Export citation
Multiplicity of Multi-Bump Type Nodal Solutions for A Class of Elliptic Problems with Exponential Critical Growth in ℝ2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 273-297
-
- Article
- Export citation
HOMOGENIZATION OF THE SYSTEM OF HIGH-CONTRAST MAXWELL EQUATIONS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 27 February 2015, pp. 475-500
- Print publication:
- May 2015
-
- Article
-
- You have access
- Open access
- Export citation
The Weyl Problem With Nonnegative Gauss Curvature In Hyperbolic Space
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 1 / 01 February 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 107-131
- Print publication:
- 01 February 2015
-
- Article
-
- You have access
- Export citation
Immersed Finite Element Method for Interface Problems with Algebraic Multigrid Solver
-
- Journal:
- Communications in Computational Physics / Volume 15 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1045-1067
- Print publication:
- April 2014
-
- Article
- Export citation
New global stability estimates for the Calderón problem in two dimensions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 07 June 2012, pp. 553-569
- Print publication:
- July 2013
-
- Article
- Export citation