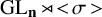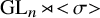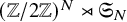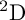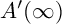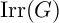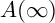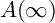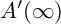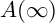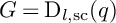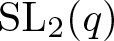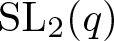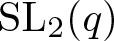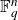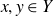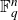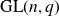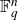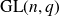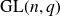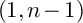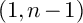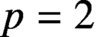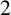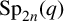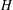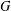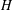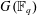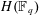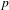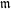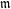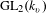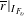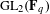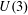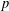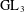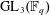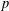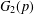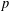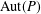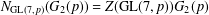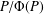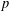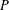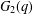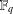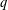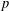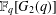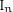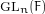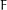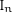34 results
E-Polynomials of Generic
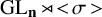 $\mathbf {\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!}~$-Character Varieties: Branched Case
$\mathbf {\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!}~$-Character Varieties: Branched Case
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSIONS OF CHARACTERS IN TYPE D AND THE INDUCTIVE MCKAY CONDITION, I
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 08 September 2023, pp. 906-958
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weights in a Benson-Solomon block
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trivial source character tables of
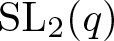 $\operatorname{SL}_2(q)$, part II
$\operatorname{SL}_2(q)$, part II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 30 June 2023, pp. 689-709
-
- Article
- Export citation
Intersection theorems for finite general linear groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 16 February 2023, pp. 129-160
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COHOMOLOGY OF THE BRUHAT–TITS STRATA IN THE UNRAMIFIED UNITARY RAPOPORT–ZINK SPACE OF SIGNATURE
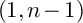 $(1,n-1)$
$(1,n-1)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 470-497
- Print publication:
- June 2023
-
- Article
- Export citation
Products of derangements in simple permutation groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 September 2022, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-isolated blocks and the Alperin–McKay conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 June 2022, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum to ‘Endoscopy for Hecke categories, character sheaves and representations’
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 30 November 2021, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The fields of values of characters of degree not divisible by p
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 15 February 2021, e2
-
- Article
-
- You have access
- Open access
- Export citation
Low-dimensional representations of finite orthogonal groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 26 January 2021, pp. 585-606
- Print publication:
- November 2021
-
- Article
- Export citation
THE INDUCTIVE BLOCKWISE ALPERIN WEIGHT CONDITION FOR TYPE
 ${\boldsymbol{\mathsf{C}}}$
AND THE PRIME
${\boldsymbol{\mathsf{C}}}$
AND THE PRIME
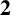 $\textbf{2}$
$\textbf{2}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 06 November 2020, pp. 1-20
- Print publication:
- August 2022
-
- Article
- Export citation
ENDOSCOPY FOR HECKE CATEGORIES, CHARACTER SHEAVES AND REPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 May 2020, e12
-
- Article
-
- You have access
- Open access
- Export citation
MULTIPLICITY ONE AT FULL CONGRUENCE LEVEL
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 15 May 2020, pp. 637-658
- Print publication:
- March 2022
-
- Article
- Export citation
SERRE WEIGHTS AND BREUIL’S LATTICE CONJECTURE IN DIMENSION THREE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 25 March 2020, e5
-
- Article
-
- You have access
- Open access
- Export citation
CHARACTER LEVELS AND CHARACTER BOUNDS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 24 January 2020, e2
-
- Article
-
- You have access
- Open access
- Export citation
ON
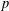 $p$-GROUPS WITH AUTOMORPHISM GROUPS RELATED TO THE CHEVALLEY GROUP
$p$-GROUPS WITH AUTOMORPHISM GROUPS RELATED TO THE CHEVALLEY GROUP 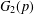 $G_{2}(p)$
$G_{2}(p)$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 321-331
- Print publication:
- June 2020
-
- Article
- Export citation
TAME BLOCK ALGEBRAS OF HECKE ALGEBRAS OF CLASSICAL TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 20 September 2019, pp. 179-201
- Print publication:
- October 2021
-
- Article
- Export citation
The Structure of Root Data and Smooth Regular Embeddings of Reductive Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 523-552
-
- Article
- Export citation
A VARIANT OF HARISH-CHANDRA FUNCTORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 14 August 2017, pp. 993-1049
- Print publication:
- September 2019
-
- Article
- Export citation