Hostname: page-component-7479d7b7d-k7p5g Total loading time: 0 Render date: 2024-07-13T07:23:40.288Z Has data issue: false hasContentIssue false
  • English
  • Français

THE INDUCTIVE BLOCKWISE ALPERIN WEIGHT CONDITION FOR TYPE ${\boldsymbol{\mathsf{C}}}$ AND THE PRIME 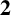$\textbf{2}$

Part of: Representation theory of groups

Published online by Cambridge University Press:  06 November 2020

ZHICHENG FENG  and
GUNTER MALLE
ZHICHENG FENG
Affiliation:
School of Mathematics and Physics, University of Science and Technology Beijing, Beijing100083, China e-mail: zfeng@pku.edu.cn
GUNTER MALLE*
Affiliation:
FB Mathematik, TU Kaiserslautern, Postfach 3049, 67653Kaiserslautern, Germany
*
e-mail: malle@mathematik.uni-kl.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish the inductive blockwise Alperin weight condition for simple groups of Lie type $\mathsf C$ and the bad prime 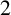$2$ . As a main step, we derive a labelling set for the irreducible 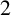$2$ -Brauer characters of the finite symplectic groups 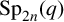$\operatorname {Sp}_{2n}(q)$ (with odd q), together with the action of automorphisms. As a further important ingredient, we prove a Jordan decomposition for weights.

Keywords

action of automorphisms on Brauer charactersAlperin weight conjecturesymplectic groupsunipotent classes

MSC classification

Primary: 20C20: Modular representations and characters
Secondary: 20C33: Representations of finite groups of Lie type
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 113 , Issue 1 , August 2022 , pp. 1 - 20
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Anthony Henderson

The first author gratefully acknowledges financial support by NSFC (11631001 and 11901028) and Fundamental Research Funds for the Central Universities (No. FRF-TP-19-036A1). The second author gratefully acknowledges financial support by SFB TRR 195.

References

Alperin, J. L., ‘Weights for finite groups’, in: The Arcata Conference on Representations of Finite Groups, Arcata, CA (1986), Part I, Proceedings of Symposia in Pure Mathematics, 47 (American Mathematical Society, Providence, RI, 1987), 369–379.CrossRefGoogle Scholar
Alperin, J. L. and Fong, P., ‘Weights for symmetric and general linear groups’, J. Algebra 131 (1990), 2–22.10.1016/0021-8693(90)90163-ICrossRefGoogle Scholar
An, J., ‘2-weights for general linear groups’, J. Algebra 149 (1992), 500–527.10.1016/0021-8693(92)90030-PCrossRefGoogle Scholar
An, J., ‘ $2$ -weights for classical groups’, J. reine angew. Math. 439 (1993), 159–204.Google Scholar
An, J., ‘2-weights for unitary groups’, Trans. Amer. Math. Soc. 339 (1993), 251–278.CrossRefGoogle Scholar
An, J., ‘Weights for classical groups’, Trans. Amer. Math. Soc. 342 (1994), 1–42.10.1090/S0002-9947-1994-1136543-7CrossRefGoogle Scholar
Bonnafé, C. and Rouquier, R., ‘Catégories dérivées et variétés de Deligne–Lusztig’, Publ. Math. Inst. Hautes Études Sci. 97 (2003), 1–59.CrossRefGoogle Scholar
Broué, M., ‘Les $l$ -bslocs des groupes $GL(n,q)$ et U $(n,{q}^2)$ et leurs structures locales’, Astérisque 133–134 (1986), 159–188.Google Scholar
Brough, J. and Späth, B., ‘A criterion for the inductive Alperin weight condition’, arXiv:2009.02074.Google Scholar
Cabanes, M. and Enguehard, M., ‘On unipotent blocks and their ordinary characters’, Invent. Math. 117 (1994), 149–164.10.1007/BF01232237CrossRefGoogle Scholar
Cabanes, M. and Enguehard, M., Representation Theory of Finite Reductive Groups, New Mathematical Monographs, 1 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Cabanes, M. and Späth, B., ‘Inductive McKay condition for finite simple groups of type C’, Represent. Theory 21 (2017), 61–81.10.1090/ert/497CrossRefGoogle Scholar
Carter, R., Finite Groups of Lie Type: Conjugacy Classes and Complex Characters (Wiley, Chichester, 1985).Google Scholar
Chaneb, R., ‘Basic sets for unipotent blocks of finite reductive groups in bad characteristic’, Int. Math. Res. Not. IMRN (2020), https://doi.org/10.1093/imrn/rnaa019.CrossRefGoogle Scholar
Feng, Z., ‘The blocks and weights of finite special linear and unitary groups’, J. Algebra 523 (2019), 53–92.10.1016/j.jalgebra.2019.01.004CrossRefGoogle Scholar
Feng, Z., Li, Z. and Zhang, J., ‘On the inductive blockwise Alperin weight condition for classical groups’, J. Algebra 537 (2019), 381–434.10.1016/j.jalgebra.2019.07.022CrossRefGoogle Scholar
Fong, P. and Srinivasan, B., ‘The blocks of finite general linear and unitary groups’, Invent. Math. 69 (1982), 109–153.10.1007/BF01389188CrossRefGoogle Scholar
Fong, P. and Srinivasan, B., ‘The blocks of finite classical groups’, J. reine angew. Math. 396 (1989), 122–191.Google Scholar
Geck, M., ‘On the decomposition numbers of the finite unitary groups in non-defining characteristic’, Math. Z. 207 (1991), 83–89.CrossRefGoogle Scholar
Geck, M. and Hézard, D., ‘On the unipotent support of character sheaves’, Osaka J. Math. 45 (2008), 819–831.Google Scholar
Geck, M. and Malle, G., The Character Theory of Finite Groups of Lie Type: A Guided Tour (Cambridge University Press, Cambridge, 2020).10.1017/9781108779081CrossRefGoogle Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The Classification of the Finite Simple Groups, Number 3, Mathematical Surveys and Monographs, 40 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 6th edn (Oxford University Press, Oxford, 2008).Google Scholar
Hézard, D., ‘Sur le support unipotent des faisceaux-caractères’, Thèse, Université Claude Bernard – Lyon I, 2004, https://tel.archives-ouvertes.fr/tel-00012071.Google Scholar
Li, C., ‘An equivariant bijection between irreducible Brauer characters and weights for $Sp\left(2n,q\right)$ ’, J. Algebra 539 (2019), 84–117.10.1016/j.jalgebra.2019.07.031CrossRefGoogle Scholar
Li, C. and Li, Z., ‘The inductive blockwise Alperin weight condition for ${PSp}_4(q)$ ’, Algebra Colloq . 26 (2019), 361–386.10.1142/S1005386719000270CrossRefGoogle Scholar
Li, C. and Zhang, J., ‘The inductive blockwise Alperin weight condition for ${\mathsf{PSL}}_n(q)$ and ${\mathrm{PSU}}_n(q)$ with cyclic outer automorphism groups’, J. Algebra 495 (2018), 130–149.CrossRefGoogle Scholar
Malle, G., ‘On the inductive Alperin–McKay and Alperin weight conjecture for groups with abelian Sylow subgroups’, J. Algebra 397 (2014), 190–208.10.1016/j.jalgebra.2013.09.013CrossRefGoogle Scholar
Malle, G., ‘Local–global conjectures in the representation theory of finite groups’, in: Representation Theory – Current Trends and Perspectives, EMS Series of Congress Reports, 11 (European Mathematical Society, Zürich, 2017), 519–539.10.4171/171-1/17CrossRefGoogle Scholar
Navarro, G., Characters and Blocks of Finite Groups, London Mathematical Society Lecture Note Series, 250 (Cambridge University Press, Cambridge, 1998).CrossRefGoogle Scholar
Navarro, G. and Tiep, P. H., ‘A reduction theorem for the Alperin weight conjecture’, Invent. Math. 184 (2011), 529–565.10.1007/s00222-010-0295-2CrossRefGoogle Scholar
Olsson, J. B., Combinatorics and Representations of Finite Groups, Vorlesungen aus dem Fachbereich Mathematik der Universität Essen, 20 (Universität Essen, Essen, 1993).Google Scholar
Schulte, E., ‘The inductive blockwise Alperin weight condition for ${G}_2(q)$ and ${}^3{D}_4(q)$ ’, J. Algebra 466 (2016), 314–369.CrossRefGoogle Scholar
Spaltenstein, N., Classes Unipotentes et Sous-Groupes de Borel, Lecture Notes in Mathematics, 946 (Springer, Berlin–New York, 1982).CrossRefGoogle Scholar
Späth, B., ‘A reduction theorem for the blockwise Alperin weight conjecture’, J. Group Theory 16 (2013), 159–220.10.1515/jgt-2012-0032CrossRefGoogle Scholar
Taylor, J., ‘On unipotent supports of reductive groups with a disconnected centre’, PhD thesis, University of Aberdeen, 2012, https://tel.archives-ouvertes.fr/tel-00709051.Google Scholar
Taylor, J., ‘On unipotent supports of reductive groups with a disconnected centre’, J. Algebra 391 (2013), 41–61.CrossRefGoogle Scholar
Taylor, J., ‘Action of automorphisms on irreducible characters of symplectic groups’, J. Algebra 505 (2018), 211–246.CrossRefGoogle Scholar
Wall, G. E., ‘On the conjugacy classes in the unitary, symplectic and orthogonal groups’, J. Aust. Math. Soc. 3 (1963), 1–62. 10.1017/S1446788700027622CrossRefGoogle Scholar