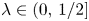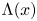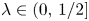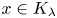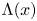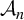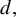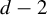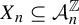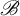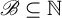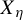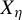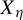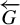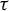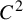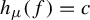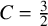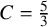115 results
Indistinguishable asymptotic pairs and multidimensional Sturmian configurations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1-59
-
- Article
-
- You have access
- HTML
- Export citation
On a class of self-similar sets which contain finitely many common points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-22
-
- Article
- Export citation
Minimal subdynamics and minimal flows without characteristic measures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Similarities and differences between specification and non-uniform specification
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-29
-
- Article
- Export citation
THERMODYNAMIC FORMALISM FOR AMENABLE GROUPS AND COUNTABLE STATE SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measure transfer and S-adic developments for subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-35
-
- Article
- Export citation
Invariant measures for
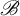 $\mathscr {B}$-free systems revisited
$\mathscr {B}$-free systems revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-32
-
- Article
- Export citation
On the Ziv–Merhav theorem beyond Markovianity I
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An embedding theorem for subshifts over amenable groups with the comparison property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant measures of Toeplitz subshifts on non-amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shifts of finite type on locally finite groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measures of maximal entropy of bounded density shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 20 February 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant sets and nilpotency of endomorphisms of algebraic sofic shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 15 February 2024, pp. 1-42
-
- Article
- Export citation
BRATTELI–VERSHIKISABILITY OF POLYGONAL BILLIARDS ON THE HYPERBOLIC PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 15 December 2023, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant measures for substitutions on countable alphabets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 11 December 2023, pp. 1-32
-
- Article
- Export citation
Conditional intermediate entropy and Birkhoff average properties of hyperbolic flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 14 November 2023, pp. 1-32
-
- Article
- Export citation
Stabilized automorphism group of odometers and of Toeplitz subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 November 2023, pp. 1-19
-
- Article
- Export citation
Markov capacity for factor codes with an unambiguous symbol
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 07 November 2023, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometrical representation of subshifts for primitive substitutions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 1885-1912
- Print publication:
- July 2024
-
- Article
- Export citation
Low complexity subshifts have discrete spectrum
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 October 2023, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation