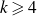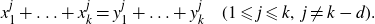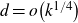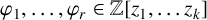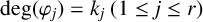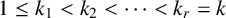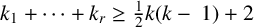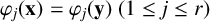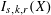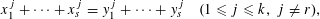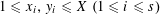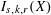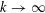30 results
Paucity problems and some relatives of Vinogradov’s mean value theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 05 April 2023, pp. 327-343
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PAUCITY PROBLEM FOR CERTAIN SYMMETRIC DIOPHANTINE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 29-39
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
VINOGRADOV SYSTEMS WITH A SLICE OFF
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 797-817
- Print publication:
- 2017
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APPROXIMATING THE MAIN CONJECTURE IN VINOGRADOV’S MEAN VALUE THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 21 December 2016, pp. 292-350
- Print publication:
- 2017
-
- Article
- Export citation
ON WARING’S PROBLEM: TWO SQUARES AND THREE BIQUADRATES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 28 June 2013, pp. 153-165
- Print publication:
- January 2014
-
- Article
- Export citation
Asymptotic Formulae for Pairs of Diagonal Cubic Equations
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 1 / 01 February 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 38-54
- Print publication:
- 01 February 2011
-
- Article
-
- You have access
- Export citation
On Waring’s problem: Three cubes and a minicube
-
- Journal:
- Nagoya Mathematical Journal / Volume 200 / December 2010
- Published online by Cambridge University Press:
- 11 January 2016, pp. 59-91
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
DAVENPORT’S METHOD AND SLIM EXCEPTIONAL SETS: THE ASYMPTOTIC FORMULAE IN WARING’S PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 13 July 2010, pp. 305-321
- Print publication:
- July 2010
-
- Article
- Export citation
A NOTE ON SIMULTANEOUS CONGRUENCES, II: MORDELL REVISED
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 25 March 2010, pp. 261-275
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Asymptotic formulae for pairs of diagonal equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 137 / Issue 1 / July 2004
- Published online by Cambridge University Press:
- 07 July 2004, pp. 227-235
- Print publication:
- July 2004
-
- Article
- Export citation
A light-weight version of Waring's problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-316
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
Slim exceptional sets and the asymptotic formula in Waring’s problem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 134 / Issue 2 / March 2003
- Published online by Cambridge University Press:
- 01 May 2003, pp. 193-206
- Print publication:
- March 2003
-
- Article
- Export citation
HUA'S LEMMA AND SIMULTANEOUS DIAGONAL EQUATIONS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 34 / Issue 3 / May 2002
- Published online by Cambridge University Press:
- 22 May 2002, pp. 279-283
- Print publication:
- May 2002
-
- Article
- Export citation
Slim Exceptional Sets for Sums of Cubes
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 2 / 01 April 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-448
- Print publication:
- 01 April 2002
-
- Article
-
- You have access
- Export citation
On Pairs of Diagonal Quintic Forms
-
- Journal:
- Compositio Mathematica / Volume 131 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 04 December 2007, pp. 61-96
- Print publication:
- March 2002
-
- Article
-
- You have access
- Export citation
SLIM EXCEPTIONAL SETS FOR SUMS OF FOUR SQUARES
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 85 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 09 July 2002, pp. 1-21
- Print publication:
- March 2002
-
- Article
- Export citation
On Waring’s problem: Three cubes and a sixth power
-
- Journal:
- Nagoya Mathematical Journal / Volume 163 / September 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 13-53
- Print publication:
- September 2001
-
- Article
-
- You have access
- Export citation
ON THE WARING–GOLDBACH PROBLEM FOR FOURTH AND FIFTH POWERS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 83 / Issue 1 / July 2001
- Published online by Cambridge University Press:
- 20 August 2001, pp. 1-50
- Print publication:
- July 2001
-
- Article
- Export citation
ON WARING'S PROBLEM FOR CUBES AND SMOOTH WEYL SUMS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 82 / Issue 1 / January 2001
- Published online by Cambridge University Press:
- 12 January 2001, pp. 89-109
- Print publication:
- January 2001
-
- Article
- Export citation
Sums of three cubes
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 53-61
- Print publication:
- December 2000
-
- Article
- Export citation