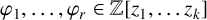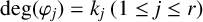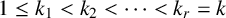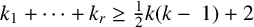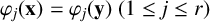1 Introduction
Our focus in this paper is on systems of simultaneous Diophantine equations defined by symmetric polynomials. Let
![]() $\varphi _1,\ldots ,\varphi _r\in {\mathbb Z}[z_1,\ldots ,z_k]$
be symmetric polynomials with
$\varphi _1,\ldots ,\varphi _r\in {\mathbb Z}[z_1,\ldots ,z_k]$
be symmetric polynomials with
![]() $\text {deg}(\varphi _j)=k_j\ (1\le j\le r)$
, so that, for any permutation
$\text {deg}(\varphi _j)=k_j\ (1\le j\le r)$
, so that, for any permutation
![]() $\pi $
of
$\pi $
of
![]() $\{1,2,\ldots ,k\}$
, one has
$\{1,2,\ldots ,k\}$
, one has
Given any such permutation
![]() $\pi $
, the system of Diophantine equations
$\pi $
, the system of Diophantine equations
plainly has the trivial solutions obtained by putting
![]() $y_i=x_{\pi i}\ (1\le i\le k)$
. Denoting by
$y_i=x_{\pi i}\ (1\le i\le k)$
. Denoting by
![]() $T_k(X)$
the number of these trivial solutions with
$T_k(X)$
the number of these trivial solutions with
![]() $1\le x_i,y_i\le X\ (1\le i\le k)$
, one is led to the question of whether there is a paucity of nondiagonal solutions. Thus, fixing k and
$1\le x_i,y_i\le X\ (1\le i\le k)$
, one is led to the question of whether there is a paucity of nondiagonal solutions. Thus, fixing k and
![]() ${\boldsymbol \varphi }$
and writing
${\boldsymbol \varphi }$
and writing
![]() $N_k(X;{\boldsymbol \varphi })$
for the number of solutions of the system (1.1) in this range, one may ask whether as
$N_k(X;{\boldsymbol \varphi })$
for the number of solutions of the system (1.1) in this range, one may ask whether as
![]() $X\rightarrow \infty $
, one has
$X\rightarrow \infty $
, one has
or equivalently, whether
![]() $N_k(X;{\boldsymbol \varphi })=k!X^k+o(X^k)$
. This question has been examined extensively in the diagonal case where the polynomials under consideration take the shape
$N_k(X;{\boldsymbol \varphi })=k!X^k+o(X^k)$
. This question has been examined extensively in the diagonal case where the polynomials under consideration take the shape
![]() $\varphi _j({\mathbf x})=x_1^{k_j}+\cdots +x_k^{k_j}$
, as can be surmised from the references cited in this paper. Relatively little consideration has been afforded to more general symmetric polynomials. It transpires that by adapting a strategy applied previously in a special case of Vinogradov’s mean value theorem (see [Reference Vaughan and Wooley17]), we are able to settle this paucity problem for numerous systems of the type (1.1) in a particularly strong form.
$\varphi _j({\mathbf x})=x_1^{k_j}+\cdots +x_k^{k_j}$
, as can be surmised from the references cited in this paper. Relatively little consideration has been afforded to more general symmetric polynomials. It transpires that by adapting a strategy applied previously in a special case of Vinogradov’s mean value theorem (see [Reference Vaughan and Wooley17]), we are able to settle this paucity problem for numerous systems of the type (1.1) in a particularly strong form.
Further notation is required to describe our conclusions. Define the elementary symmetric polynomials
![]() ${\sigma }_j({\mathbf z})\in {\mathbb Z}[z_1,\ldots ,z_k]$
for
${\sigma }_j({\mathbf z})\in {\mathbb Z}[z_1,\ldots ,z_k]$
for
![]() $j\ge 0$
by means of the generating function identity
$j\ge 0$
by means of the generating function identity
 $$ \begin{align} \sum_{j=0}^k{\sigma}_j({\mathbf z})t^{k-j}=\prod_{i=1}^k(t+z_i). \end{align} $$
$$ \begin{align} \sum_{j=0}^k{\sigma}_j({\mathbf z})t^{k-j}=\prod_{i=1}^k(t+z_i). \end{align} $$
We restrict attention primarily to symmetric polynomials of the shape
 $$ \begin{align} \varphi_j({\mathbf z})=\sum_{l=1}^ka_{jl}\sigma_l({\mathbf z})\quad (1\le j\le r), \end{align} $$
$$ \begin{align} \varphi_j({\mathbf z})=\sum_{l=1}^ka_{jl}\sigma_l({\mathbf z})\quad (1\le j\le r), \end{align} $$
with fixed coefficients
![]() $a_{jl}\in {\mathbb Z}$
for
$a_{jl}\in {\mathbb Z}$
for
![]() $1\le j\le r$
and
$1\le j\le r$
and
![]() $1\le l\le k$
. By taking appropriate integral linear combinations of the polynomials
$1\le l\le k$
. By taking appropriate integral linear combinations of the polynomials
![]() $\varphi _1,\ldots ,\varphi _r$
, it is evident that in our investigations concerning
$\varphi _1,\ldots ,\varphi _r$
, it is evident that in our investigations concerning
![]() $N_k(X;{\boldsymbol \varphi })$
, we may suppose that
$N_k(X;{\boldsymbol \varphi })$
, we may suppose that
![]() $\text {deg}(\varphi _j)=k_j\ (1\le j\le r)$
, where the exponents
$\text {deg}(\varphi _j)=k_j\ (1\le j\le r)$
, where the exponents
![]() $k_j$
satisfy the condition
$k_j$
satisfy the condition
This can be seen by applying elementary row operations on the reversed
![]() $r\times k$
matrix of coefficients
$r\times k$
matrix of coefficients
![]() $A=(a_{j,k-l+1})$
, reducing to an equivalent system having the same number of solutions, in which the new coefficient matrix
$A=(a_{j,k-l+1})$
, reducing to an equivalent system having the same number of solutions, in which the new coefficient matrix
![]() $A'$
has upper triangular form and
$A'$
has upper triangular form and
![]() $r'\le r$
nonvanishing rows.
$r'\le r$
nonvanishing rows.
A simple paucity result is provided by our first theorem. It is useful here and elsewhere to introduce the auxiliary quantity
Here and throughout this paper, implicit constants in the notations of Landau and Vinogradov may depend on
![]() $\varepsilon $
, k and the coefficients of
$\varepsilon $
, k and the coefficients of
![]() ${\boldsymbol \varphi }$
.
${\boldsymbol \varphi }$
.
Theorem 1.1. Let
![]() $\varphi _1,\ldots ,\varphi _r$
be symmetric polynomials of the shape (1.3), having respective degrees
$\varphi _1,\ldots ,\varphi _r$
be symmetric polynomials of the shape (1.3), having respective degrees
![]() $k_1,\ldots ,k_r$
satisfying (1.4). Then, for each
$k_1,\ldots ,k_r$
satisfying (1.4). Then, for each
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
In particular, when
![]() $k_1+\cdots +k_r\ge \tfrac {1}{2}k(k-1)+2$
, one has
$k_1+\cdots +k_r\ge \tfrac {1}{2}k(k-1)+2$
, one has
A specialisation of the system (1.1) illustrates the kind of results made available by Theorem 1.1. Fix a choice of coefficients
![]() $a_{jl}\in {\mathbb Z}$
for
$a_{jl}\in {\mathbb Z}$
for
![]() $1\le l\le k-r$
and
$1\le l\le k-r$
and
![]() $k-r+1\le j\le k$
, and denote by
$k-r+1\le j\le k$
, and denote by
![]() $M_{k,r}(X;{\mathbf a})$
the number of integral solutions of the simultaneous equations
$M_{k,r}(X;{\mathbf a})$
the number of integral solutions of the simultaneous equations
 $$ \begin{align} {\sigma}_j({\mathbf x})+\sum_{l=1}^{k-r}a_{jl}{\sigma}_l({\mathbf x}) ={\sigma}_j({\mathbf y})+\sum_{l=1}^{k-r}a_{jl}{\sigma}_l({\mathbf y})\quad (k-r+1\le j\le k), \end{align} $$
$$ \begin{align} {\sigma}_j({\mathbf x})+\sum_{l=1}^{k-r}a_{jl}{\sigma}_l({\mathbf x}) ={\sigma}_j({\mathbf y})+\sum_{l=1}^{k-r}a_{jl}{\sigma}_l({\mathbf y})\quad (k-r+1\le j\le k), \end{align} $$
in variables
![]() ${\mathbf x}=(x_1,\ldots ,x_k)$
and
${\mathbf x}=(x_1,\ldots ,x_k)$
and
![]() ${\mathbf y}=(y_1,\ldots ,y_k)$
with
${\mathbf y}=(y_1,\ldots ,y_k)$
with
![]() $1\le x_i,y_i\le X$
.
$1\le x_i,y_i\le X$
.
Corollary 1.2. Suppose that
![]() $k,r\in {\mathbb N}$
and
$k,r\in {\mathbb N}$
and
![]() $(k-r)(k-r+1)<2k-2$
. Then there is a paucity of nondiagonal solutions in the system of equations (1.6). In particular, for each
$(k-r)(k-r+1)<2k-2$
. Then there is a paucity of nondiagonal solutions in the system of equations (1.6). In particular, for each
![]() $\varepsilon>0$
, one has
$\varepsilon>0$
, one has
Results analogous to those of Theorem 1.1 and Corollary 1.2 for diagonal Diophantine systems involving r equations are almost always limited to systems possessing only
![]() $r+1$
pairs of variables, and these we now describe. In the case
$r+1$
pairs of variables, and these we now describe. In the case
![]() $r=1$
, Hooley applied sieve methods to investigate the equation
$r=1$
, Hooley applied sieve methods to investigate the equation
with
![]() $k\ge 3$
, and ultimately established the paucity of nondiagonal solutions with a power saving (see [Reference Hooley9, Reference Hooley10]). Strong conclusions have been derived when
$k\ge 3$
, and ultimately established the paucity of nondiagonal solutions with a power saving (see [Reference Hooley9, Reference Hooley10]). Strong conclusions have been derived when
![]() $k=3$
by Heath-Brown [Reference Heath-Brown8] using ideas based on quadratic forms, enhancing earlier work of the author that extends from cubes to general cubic polynomials [Reference Wooley20]. When
$k=3$
by Heath-Brown [Reference Heath-Brown8] using ideas based on quadratic forms, enhancing earlier work of the author that extends from cubes to general cubic polynomials [Reference Wooley20]. When
![]() $r=2$
,
$r=2$
,
![]() $k_1<k_2$
and
$k_1<k_2$
and
![]() $k_2\ge 3$
, the paucity of nondiagonal solutions has been established for the pair of simultaneous equations
$k_2\ge 3$
, the paucity of nondiagonal solutions has been established for the pair of simultaneous equations
 $$ \begin{align*} \left. \begin{aligned} x_1^{k_1}+x_2^{k_1}+x_3^{k_1}&=y_1^{k_1}+y_2^{k_1}+y_3^{k_1}\\ x_1^{k_2}+x_2^{k_2}+x_3^{k_2}&=y_1^{k_2}+y_2^{k_2}+y_3^{k_2} \end{aligned}\right\}. \end{align*} $$
$$ \begin{align*} \left. \begin{aligned} x_1^{k_1}+x_2^{k_1}+x_3^{k_1}&=y_1^{k_1}+y_2^{k_1}+y_3^{k_1}\\ x_1^{k_2}+x_2^{k_2}+x_3^{k_2}&=y_1^{k_2}+y_2^{k_2}+y_3^{k_2} \end{aligned}\right\}. \end{align*} $$
Sharp results are available in the case
![]() $(k_1,k_2)=(1,3)$
(see [Reference Vaughan and Wooley16]), with nontrivial conclusions available for the exponent pair
$(k_1,k_2)=(1,3)$
(see [Reference Vaughan and Wooley16]), with nontrivial conclusions available for the exponent pair
![]() $(1,k)$
when
$(1,k)$
when
![]() $k\ge 3$
(see [Reference Greaves5, Reference Skinner and Wooley14]). The cases
$k\ge 3$
(see [Reference Greaves5, Reference Skinner and Wooley14]). The cases
![]() $(2,3)$
and
$(2,3)$
and
![]() $(2,4)$
were tackled successfully via affine slicing methods (see [Reference Tsui and Wooley15, Reference Wooley, Berndt, Diamond and Hildebrand19]), with the remaining cases of this type covered by Salberger [Reference Salberger, Duke and Tschinkel12] using variants of the determinant method. Most other examples in which it is known that there is a paucity of nondiagonal solutions are closely related to the Vinogradov system of equations
$(2,4)$
were tackled successfully via affine slicing methods (see [Reference Tsui and Wooley15, Reference Wooley, Berndt, Diamond and Hildebrand19]), with the remaining cases of this type covered by Salberger [Reference Salberger, Duke and Tschinkel12] using variants of the determinant method. Most other examples in which it is known that there is a paucity of nondiagonal solutions are closely related to the Vinogradov system of equations
The paucity problem has been solved here by Vaughan and the author [Reference Vaughan and Wooley17], with similar conclusions when the equation of degree r is replaced by one of degree
![]() $r+1$
. Recent work [Reference Wooley21] shows that the missing equation of degree r in this last result can be replaced by one of degree
$r+1$
. Recent work [Reference Wooley21] shows that the missing equation of degree r in this last result can be replaced by one of degree
![]() $r-d$
, provided that d is not too large. Meanwhile, when the exponents
$r-d$
, provided that d is not too large. Meanwhile, when the exponents
![]() $k_j$
satisfy (1.4), results falling just short of paucity have been obtained in general for systems of the shape
$k_j$
satisfy (1.4), results falling just short of paucity have been obtained in general for systems of the shape
(see [Reference Parsell and Wooley11, Reference Wooley, Pollington and Moran18]). In the special case
![]() $\mathbf k=(1,3,\ldots ,2r-1)$
, Brüdern and Robert [Reference Brüdern and Robert2] have even established the desired paucity result. We should note also that the existence of nondiagonal solutions, often exhibited by remarkable parametric formulae, has long been the subject of investigation, as recorded in Gloden’s book [Reference Gloden4], with notable recent contributions by Choudhry [Reference Choudhry3].
$\mathbf k=(1,3,\ldots ,2r-1)$
, Brüdern and Robert [Reference Brüdern and Robert2] have even established the desired paucity result. We should note also that the existence of nondiagonal solutions, often exhibited by remarkable parametric formulae, has long been the subject of investigation, as recorded in Gloden’s book [Reference Gloden4], with notable recent contributions by Choudhry [Reference Choudhry3].
Taking k large and
![]() $r=k-\lfloor \!\sqrt {2k}\rfloor +1$
, we see that (1.6) constitutes a Diophantine system of r equations in
$r=k-\lfloor \!\sqrt {2k}\rfloor +1$
, we see that (1.6) constitutes a Diophantine system of r equations in
![]() $k=r+\!\!\sqrt {2r}+O(1)$
pairs of variables having a paucity of nondiagonal solutions. Corollary 1.2 therefore exhibits a large class of Diophantine systems in which the barrier described in the previous paragraph is emphatically surmounted. There are two exceptions to the rule noted in that paragraph. First, Salberger and the author [Reference Salberger and Wooley13, Corollary 1.4 and Theorem 5.2] have established the paucity of nondiagonal solutions in situations where the underlying equations have very large degree in terms of the number of variables. Second, work of Bourgain et al. [Reference Bourgain, Garaev, Konyagin and Shparlinski1, Theorem 26] and Heap et al. [Reference Heap, Sahay and Wooley7, Theorem 1.2] examines systems of equations determined by relations of divisor type having the shape
$k=r+\!\!\sqrt {2r}+O(1)$
pairs of variables having a paucity of nondiagonal solutions. Corollary 1.2 therefore exhibits a large class of Diophantine systems in which the barrier described in the previous paragraph is emphatically surmounted. There are two exceptions to the rule noted in that paragraph. First, Salberger and the author [Reference Salberger and Wooley13, Corollary 1.4 and Theorem 5.2] have established the paucity of nondiagonal solutions in situations where the underlying equations have very large degree in terms of the number of variables. Second, work of Bourgain et al. [Reference Bourgain, Garaev, Konyagin and Shparlinski1, Theorem 26] and Heap et al. [Reference Heap, Sahay and Wooley7, Theorem 1.2] examines systems of equations determined by relations of divisor type having the shape
in which
![]() ${\theta }\in {\mathbb C}$
is algebraic of degree d over
${\theta }\in {\mathbb C}$
is algebraic of degree d over
![]() ${\mathbb Q}$
. When
${\mathbb Q}$
. When
![]() $d\le k$
, this relation generates d independent symmetric Diophantine equations, and it is shown that the number of integral solutions of (1.7) with
$d\le k$
, this relation generates d independent symmetric Diophantine equations, and it is shown that the number of integral solutions of (1.7) with
![]() $1\le x_i,y_i\le X$
is asymptotically
$1\le x_i,y_i\le X$
is asymptotically
![]() $T_k(X)+O(X^{k-d+1+\varepsilon })$
. In particular, when
$T_k(X)+O(X^{k-d+1+\varepsilon })$
. In particular, when
![]() $d=2$
, we obtain a pair of simultaneous Diophantine equations in k variables having a paucity of nondiagonal solutions. For example, when
$d=2$
, we obtain a pair of simultaneous Diophantine equations in k variables having a paucity of nondiagonal solutions. For example, when
![]() $k=4$
and
$k=4$
and
![]() ${\theta }=\!\sqrt {-1}$
, we obtain the system
${\theta }=\!\sqrt {-1}$
, we obtain the system
 $$ \begin{align*} \left.{\begin{aligned} x_1x_2x_3x_4-&x_1x_2-x_2x_3-x_3x_4-x_4x_1-x_2x_4-x_1x_3\\ &=y_1y_2y_3y_4-y_1y_2-y_2y_3-y_3y_4-y_4y_1-y_2y_4-y_1y_3\\ x_1x_2x_3+x_2&x_3x_4+x_3x_4x_1+x_4x_1x_2-x_1-x_2-x_3-x_4\\ &=y_1y_2y_3+y_2y_3y_4+y_3y_4y_1+y_4y_1y_2-y_1-y_2-y_3-y_4 \end{aligned}}\right\} \end{align*} $$
$$ \begin{align*} \left.{\begin{aligned} x_1x_2x_3x_4-&x_1x_2-x_2x_3-x_3x_4-x_4x_1-x_2x_4-x_1x_3\\ &=y_1y_2y_3y_4-y_1y_2-y_2y_3-y_3y_4-y_4y_1-y_2y_4-y_1y_3\\ x_1x_2x_3+x_2&x_3x_4+x_3x_4x_1+x_4x_1x_2-x_1-x_2-x_3-x_4\\ &=y_1y_2y_3+y_2y_3y_4+y_3y_4y_1+y_4y_1y_2-y_1-y_2-y_3-y_4 \end{aligned}}\right\} \end{align*} $$
having
![]() $4!X^4+O(X^{3+\varepsilon })$
integral solutions with
$4!X^4+O(X^{3+\varepsilon })$
integral solutions with
![]() $1\le x_i,y_i\le X$
.
$1\le x_i,y_i\le X$
.
We have avoided discussion of systems (1.1) containing the equation
Here, when
![]() $r\ge 2$
, one may parametrise the solutions of (1.8) in the shape
$r\ge 2$
, one may parametrise the solutions of (1.8) in the shape
 $$ \begin{align*} x_1={\alpha}_1{\alpha}_2\cdots {\alpha}_k,\quad x_2&={\beta}_1{\beta}_2\cdots {\beta}_k,\quad \ldots ,\quad x_k={\omega}_1{\omega}_2\cdots {\omega}_k,\\ y_1={\alpha}_1{\beta}_1\cdots {\omega}_1,\quad y_2&={\alpha}_2{\beta}_2\cdots {\omega}_2,\quad \ldots , \quad y_k={\alpha}_k{\beta}_k\cdots {\omega}_k, \end{align*} $$
$$ \begin{align*} x_1={\alpha}_1{\alpha}_2\cdots {\alpha}_k,\quad x_2&={\beta}_1{\beta}_2\cdots {\beta}_k,\quad \ldots ,\quad x_k={\omega}_1{\omega}_2\cdots {\omega}_k,\\ y_1={\alpha}_1{\beta}_1\cdots {\omega}_1,\quad y_2&={\alpha}_2{\beta}_2\cdots {\omega}_2,\quad \ldots , \quad y_k={\alpha}_k{\beta}_k\cdots {\omega}_k, \end{align*} $$
to provide a paucity result by simple elimination. The reader will find all of the ideas necessary to complete this elementary exercise in [Reference Vaughan and Wooley16].
This paper is organised as follows. In Section 2 we derive a multiplicative relation among the variables
![]() ${\mathbf x},{\mathbf y}$
of the system (1.1). This may be applied to obtain Theorem 1.1 and Corollary 1.2. The polynomials
${\mathbf x},{\mathbf y}$
of the system (1.1). This may be applied to obtain Theorem 1.1 and Corollary 1.2. The polynomials
![]() $\varphi _j({\mathbf z})$
that are the subject of Theorem 1.1 are integral linear combinations of the elementary symmetric polynomials
$\varphi _j({\mathbf z})$
that are the subject of Theorem 1.1 are integral linear combinations of the elementary symmetric polynomials
![]() ${\sigma }_1({\mathbf z}),\ldots ,{\sigma }_k({\mathbf z})$
. In Section 3 we examine the extent to which our methods are applicable when the polynomials
${\sigma }_1({\mathbf z}),\ldots ,{\sigma }_k({\mathbf z})$
. In Section 3 we examine the extent to which our methods are applicable when the polynomials
![]() $\varphi _j({\mathbf z})$
are permitted to depend nonlinearly on
$\varphi _j({\mathbf z})$
are permitted to depend nonlinearly on
![]() ${\sigma }_1({\mathbf z}),\ldots ,{\sigma }_k({\mathbf z})$
.
${\sigma }_1({\mathbf z}),\ldots ,{\sigma }_k({\mathbf z})$
.
Our basic parameter is X, a sufficiently large positive number. Whenever
![]() $\varepsilon $
appears in a statement, either implicitly or explicitly, we assert that the statement holds for each
$\varepsilon $
appears in a statement, either implicitly or explicitly, we assert that the statement holds for each
![]() $\varepsilon>0$
. We make frequent use of vector notation in the form
$\varepsilon>0$
. We make frequent use of vector notation in the form
![]() ${\mathbf x}=(x_1,\ldots ,x_k)$
. Here, the dimension k will be evident to the reader from the ambient context.
${\mathbf x}=(x_1,\ldots ,x_k)$
. Here, the dimension k will be evident to the reader from the ambient context.
2 Multiplicative relations from symmetric polynomials
Our initial objective in this section is to obtain a multiplicative relation between the variables underlying the system (1.1). Let
![]() $\varphi _1,\ldots ,\varphi _r$
be polynomials of the shape (1.3), having respective degrees
$\varphi _1,\ldots ,\varphi _r$
be polynomials of the shape (1.3), having respective degrees
![]() $k_1,\ldots ,k_r$
satisfying (1.4). We define the complementary set of exponents
$k_1,\ldots ,k_r$
satisfying (1.4). We define the complementary set of exponents
![]() ${\mathcal R}={\mathcal R}({\boldsymbol \varphi })$
by putting
${\mathcal R}={\mathcal R}({\boldsymbol \varphi })$
by putting
The counting function
![]() $N_k(X;{\boldsymbol \varphi })$
remains unchanged when we replace the polynomials
$N_k(X;{\boldsymbol \varphi })$
remains unchanged when we replace the polynomials
![]() $\varphi _j\ (1\le j\le r)$
by any collection of linearly independent integral linear combinations, and thus we may suppose that these polynomials take the shape
$\varphi _j\ (1\le j\le r)$
by any collection of linearly independent integral linear combinations, and thus we may suppose that these polynomials take the shape
 $$ \begin{align} \varphi_j({\mathbf z})=a_j{\sigma}_{k_j}({\mathbf z})-\sum_{\substack{1\le l<k_j\\ l\in {\mathcal R}}} b_{jl}{\sigma}_l({\mathbf z})\quad (1\le j\le r), \end{align} $$
$$ \begin{align} \varphi_j({\mathbf z})=a_j{\sigma}_{k_j}({\mathbf z})-\sum_{\substack{1\le l<k_j\\ l\in {\mathcal R}}} b_{jl}{\sigma}_l({\mathbf z})\quad (1\le j\le r), \end{align} $$
where
![]() $a_j\in {\mathbb Z}\setminus \{0\}$
and
$a_j\in {\mathbb Z}\setminus \{0\}$
and
![]() $b_{jl}\in {\mathbb Z}$
.
$b_{jl}\in {\mathbb Z}$
.
Given a solution
![]() ${\mathbf x},{\mathbf y}$
of the system (1.1) counted by
${\mathbf x},{\mathbf y}$
of the system (1.1) counted by
![]() $N_k(X;{\boldsymbol \varphi })$
, we define the integers
$N_k(X;{\boldsymbol \varphi })$
, we define the integers
![]() $h_l=h_l({\mathbf x},{\mathbf y})$
for
$h_l=h_l({\mathbf x},{\mathbf y})$
for
![]() $l\in {\mathcal R}$
by putting
$l\in {\mathcal R}$
by putting
Thus, since
![]() $1\le x_i,y_i\le X\ (1\le i\le k)$
, one has
$1\le x_i,y_i\le X\ (1\le i\le k)$
, one has
![]() $|h_l({\mathbf x},{\mathbf y})|\le 2^kX^l\ (l\in {\mathcal R})$
. By making use of relations (2.2) and (2.3), the system (1.1) becomes
$|h_l({\mathbf x},{\mathbf y})|\le 2^kX^l\ (l\in {\mathcal R})$
. By making use of relations (2.2) and (2.3), the system (1.1) becomes
 $$ \begin{align} a_j({\sigma}_{k_j}({\mathbf x})-{\sigma}_{k_j}({\mathbf y})) =\sum_{\substack{1\le l<k_j\\ l\in {\mathcal R}}} b_{jl}h_l\quad (1\le j\le r). \end{align} $$
$$ \begin{align} a_j({\sigma}_{k_j}({\mathbf x})-{\sigma}_{k_j}({\mathbf y})) =\sum_{\substack{1\le l<k_j\\ l\in {\mathcal R}}} b_{jl}h_l\quad (1\le j\le r). \end{align} $$
Then, by wielding (1.2) in combination with (2.3) and (2.4), we obtain
 $$ \begin{align} \prod_{i=1}^k(t+x_i)-\prod_{i=1}^k(t+y_i)&=\sum_{m=0}^kt^{k-m} ({\sigma}_m({\mathbf x})-{\sigma}_m({\mathbf y})) \notag \\ &=\sum_{m\in {\mathcal R}}h_mt^{k-m}+\sum_{j=1}^ra_j^{-1}t^{k-k_j} \sum_{\substack{1\le l<k_j\\ l\in {\mathcal R}}}b_{jl}h_l. \end{align} $$
$$ \begin{align} \prod_{i=1}^k(t+x_i)-\prod_{i=1}^k(t+y_i)&=\sum_{m=0}^kt^{k-m} ({\sigma}_m({\mathbf x})-{\sigma}_m({\mathbf y})) \notag \\ &=\sum_{m\in {\mathcal R}}h_mt^{k-m}+\sum_{j=1}^ra_j^{-1}t^{k-k_j} \sum_{\substack{1\le l<k_j\\ l\in {\mathcal R}}}b_{jl}h_l. \end{align} $$
Put
![]() $A=a_1a_2\cdots a_r$
and
$A=a_1a_2\cdots a_r$
and
![]() $c_j=A/a_j\ (1\le j\le r)$
. Also, define
$c_j=A/a_j\ (1\le j\le r)$
. Also, define
 $$ \begin{align*} \psi_l(t)=At^{k-l}+\sum_{\substack{1\le j\le r\\ k_j>l}}c_jb_{jl}t^{k-k_j}\quad (l\in {\mathcal R}), \end{align*} $$
$$ \begin{align*} \psi_l(t)=At^{k-l}+\sum_{\substack{1\le j\le r\\ k_j>l}}c_jb_{jl}t^{k-k_j}\quad (l\in {\mathcal R}), \end{align*} $$
and then set
Notice here that the polynomial
![]() $\Psi (t;{\mathbf h})$
has integral coefficients and degree at most
$\Psi (t;{\mathbf h})$
has integral coefficients and degree at most
![]() $k-1$
with respect to t. Moreover, it follows from (2.5) that
$k-1$
with respect to t. Moreover, it follows from (2.5) that
 $$ \begin{align} A\bigg( \prod_{i=1}^k(t+x_i)-\prod_{i=1}^k(t+y_i)\bigg) =\Psi(t;{\mathbf h}). \end{align} $$
$$ \begin{align} A\bigg( \prod_{i=1}^k(t+x_i)-\prod_{i=1}^k(t+y_i)\bigg) =\Psi(t;{\mathbf h}). \end{align} $$
We may now record the multiplicative relation employed in our proof of Theorem 1.1. Suppose that
![]() ${\mathbf x},{\mathbf y}$
is an integral solution of the system (1.1), where
${\mathbf x},{\mathbf y}$
is an integral solution of the system (1.1), where
![]() $\varphi _1,\ldots ,\varphi _r$
are symmetric polynomials as described above. Then, with
$\varphi _1,\ldots ,\varphi _r$
are symmetric polynomials as described above. Then, with
we deduce by substituting
![]() $t=-y_j$
into (2.7) that
$t=-y_j$
into (2.7) that
 $$ \begin{align} A\prod_{i=1}^k(x_i-y_j)=\Psi(-y_j;{\mathbf h})\quad (1\le j\le k). \end{align} $$
$$ \begin{align} A\prod_{i=1}^k(x_i-y_j)=\Psi(-y_j;{\mathbf h})\quad (1\le j\le k). \end{align} $$
Proof of Theorem 1.1
Divide the solutions of the system (1.1) with
![]() $1\le x_i,y_i\le X$
into two types. A solution
$1\le x_i,y_i\le X$
into two types. A solution
![]() ${\mathbf x},{\mathbf y}$
will be called potentially diagonal when
${\mathbf x},{\mathbf y}$
will be called potentially diagonal when
![]() $\{x_1,\ldots ,x_k\}=\{y_1,\ldots ,y_k\}$
, and nondiagonal when, for some index j with
$\{x_1,\ldots ,x_k\}=\{y_1,\ldots ,y_k\}$
, and nondiagonal when, for some index j with
![]() $1\le j\le k$
, one has either
$1\le j\le k$
, one has either
![]() $y_j\not \in \{x_1,\ldots ,x_k\}$
or
$y_j\not \in \{x_1,\ldots ,x_k\}$
or
![]() $x_j\not \in \{y_1,\ldots ,y_k\}$
.
$x_j\not \in \{y_1,\ldots ,y_k\}$
.
We first consider potentially diagonal solutions
![]() ${\mathbf x},{\mathbf y}$
. Suppose, if possible, that
${\mathbf x},{\mathbf y}$
. Suppose, if possible, that
![]() ${\mathbf x},{\mathbf y}$
satisfies the condition that the polynomial
${\mathbf x},{\mathbf y}$
satisfies the condition that the polynomial
![]() $\Psi (t;{\mathbf h})$
defined in (2.6) is identically zero as a polynomial in t. Since
$\Psi (t;{\mathbf h})$
defined in (2.6) is identically zero as a polynomial in t. Since
![]() $A\ne 0$
, it follows from (2.7) that
$A\ne 0$
, it follows from (2.7) that
 $$ \begin{align*} \prod_{i=1}^k(t+x_i)=\prod_{i=1}^k(t+y_i). \end{align*} $$
$$ \begin{align*} \prod_{i=1}^k(t+x_i)=\prod_{i=1}^k(t+y_i). \end{align*} $$
The roots of the polynomials on the left- and right-hand sides here must be identical, and so too must be their respective multiplicities. Thus
![]() $(x_1,\ldots ,x_k)$
is a permutation of
$(x_1,\ldots ,x_k)$
is a permutation of
![]() $(y_1,\ldots ,y_k)$
, and it follows that the number of solutions
$(y_1,\ldots ,y_k)$
, and it follows that the number of solutions
![]() ${\mathbf x},{\mathbf y}$
of this type counted by
${\mathbf x},{\mathbf y}$
of this type counted by
![]() $N_k(X;{\boldsymbol \varphi })$
is precisely
$N_k(X;{\boldsymbol \varphi })$
is precisely
![]() $T_k(X)$
.
$T_k(X)$
.
Suppose next that
![]() ${\mathbf x},{\mathbf y}$
is a potentially diagonal solution with
${\mathbf x},{\mathbf y}$
is a potentially diagonal solution with
![]() $\Psi (t;{\mathbf h})$
not identically zero, where
$\Psi (t;{\mathbf h})$
not identically zero, where
![]() ${\mathbf h}$
is defined via (2.3). In this situation, there are distinct integers
${\mathbf h}$
is defined via (2.3). In this situation, there are distinct integers
![]() $w_1,\ldots ,w_s$
, for some integer s with
$w_1,\ldots ,w_s$
, for some integer s with
![]() $1\le s\le k$
, such that
$1\le s\le k$
, such that
Consider any tuple of integers
![]() ${\mathbf h}$
with
${\mathbf h}$
with
![]() $|h_l|\le 2^kX^l\ (l\in {\mathcal R})$
for which the polynomial
$|h_l|\le 2^kX^l\ (l\in {\mathcal R})$
for which the polynomial
![]() $\Psi (t;{\mathbf h})$
is not identically zero. This polynomial has degree at most
$\Psi (t;{\mathbf h})$
is not identically zero. This polynomial has degree at most
![]() $k-1$
, and hence there is an integer
$k-1$
, and hence there is an integer
![]() $\xi $
with
$\xi $
with
![]() $1\le \xi \le k$
for which the integer
$1\le \xi \le k$
for which the integer
![]() ${\Theta }=\Psi (\xi ;{\mathbf h})$
is nonzero. We see from (2.7) that
${\Theta }=\Psi (\xi ;{\mathbf h})$
is nonzero. We see from (2.7) that
![]() $(\xi +w_1)\cdots (\xi +w_s)$
divides
$(\xi +w_1)\cdots (\xi +w_s)$
divides
![]() ${\Theta }$
. Thus, an elementary divisor function estimate (see, for example, [Reference Hardy and Wright6, Theorem 317]) shows the number of possible choices for
${\Theta }$
. Thus, an elementary divisor function estimate (see, for example, [Reference Hardy and Wright6, Theorem 317]) shows the number of possible choices for
![]() $\xi +w_1,\ldots ,\xi +w_s$
to be at most
$\xi +w_1,\ldots ,\xi +w_s$
to be at most
 $$ \begin{align*} \sum_{\substack{d_1,\ldots ,d_s\in \mathbb N\\ d_1\cdots d_s|{\Theta}}}1\le \bigg( \sum_{d|{\Theta}}1\bigg)^s=d(|{\Theta}|)^s\ll |{\Theta}|^\varepsilon. \end{align*} $$
$$ \begin{align*} \sum_{\substack{d_1,\ldots ,d_s\in \mathbb N\\ d_1\cdots d_s|{\Theta}}}1\le \bigg( \sum_{d|{\Theta}}1\bigg)^s=d(|{\Theta}|)^s\ll |{\Theta}|^\varepsilon. \end{align*} $$
Since one has
![]() ${\Theta }=O(X^k)$
, we see that there are at most
${\Theta }=O(X^k)$
, we see that there are at most
![]() $O(X^\varepsilon )$
possible choices for
$O(X^\varepsilon )$
possible choices for
![]() $\xi +w_1,\ldots ,\xi +w_s$
, and hence also for
$\xi +w_1,\ldots ,\xi +w_s$
, and hence also for
![]() $w_1,\ldots ,w_s$
. From here, relation (2.9) implies that, for these fixed choices of
$w_1,\ldots ,w_s$
. From here, relation (2.9) implies that, for these fixed choices of
![]() ${\mathbf h}$
, the number of possible choices for
${\mathbf h}$
, the number of possible choices for
![]() ${\mathbf x}$
and
${\mathbf x}$
and
![]() ${\mathbf y}$
is also
${\mathbf y}$
is also
![]() $O(X^\varepsilon )$
. On recalling (1.5), we discern that the total number of choices for the tuple
$O(X^\varepsilon )$
. On recalling (1.5), we discern that the total number of choices for the tuple
![]() ${\mathbf h}$
with
${\mathbf h}$
with
![]() $|h_l|\le 2^kX^l\ (l\in {\mathcal R})$
is
$|h_l|\le 2^kX^l\ (l\in {\mathcal R})$
is
![]() $O(X^{w({\boldsymbol \varphi })})$
. Let
$O(X^{w({\boldsymbol \varphi })})$
. Let
![]() $T_k^*(X;{\boldsymbol \varphi })$
denote the number of potentially diagonal solutions
$T_k^*(X;{\boldsymbol \varphi })$
denote the number of potentially diagonal solutions
![]() ${\mathbf x},{\mathbf y}$
not counted by
${\mathbf x},{\mathbf y}$
not counted by
![]() $T_k(X)$
. For each of the
$T_k(X)$
. For each of the
![]() $O(X^{w({\boldsymbol \varphi })})$
choices for
$O(X^{w({\boldsymbol \varphi })})$
choices for
![]() ${\mathbf h}$
associated with these solutions, we have shown that there are
${\mathbf h}$
associated with these solutions, we have shown that there are
![]() $O(X^\varepsilon )$
solutions
$O(X^\varepsilon )$
solutions
![]() ${\mathbf x},{\mathbf y}$
, whence
${\mathbf x},{\mathbf y}$
, whence
Finally, suppose that
![]() ${\mathbf x},{\mathbf y}$
is a nondiagonal solution of the system (1.1). By invoking symmetry (twice), we may suppose that
${\mathbf x},{\mathbf y}$
is a nondiagonal solution of the system (1.1). By invoking symmetry (twice), we may suppose that
![]() $y_k\not \in \{x_1,\ldots ,x_k\}$
, whence (2.8) shows the integer
$y_k\not \in \{x_1,\ldots ,x_k\}$
, whence (2.8) shows the integer
![]() ${\Theta } =\Psi (-y_k;{\mathbf h})$
to be nonzero. There are
${\Theta } =\Psi (-y_k;{\mathbf h})$
to be nonzero. There are
![]() $O(X^{w({\boldsymbol \varphi })})$
possible choices for
$O(X^{w({\boldsymbol \varphi })})$
possible choices for
![]() ${\mathbf h}$
and
${\mathbf h}$
and
![]() $O(X)$
possible choices for
$O(X)$
possible choices for
![]() $y_k$
corresponding to this situation. Fixing any one such, and noting that
$y_k$
corresponding to this situation. Fixing any one such, and noting that
![]() ${\Theta }=O(X^k)$
, an elementary divisor function estimate again shows that there are
${\Theta }=O(X^k)$
, an elementary divisor function estimate again shows that there are
![]() $O(X^\varepsilon )$
possible choices for
$O(X^\varepsilon )$
possible choices for
![]() $x_1-y_k,\ldots ,x_k-y_k$
satisfying (2.8). Fix any one such choice for these divisors. Since
$x_1-y_k,\ldots ,x_k-y_k$
satisfying (2.8). Fix any one such choice for these divisors. Since
![]() $y_k$
is already fixed, it follows that
$y_k$
is already fixed, it follows that
![]() $x_1,\ldots ,x_k$
are likewise fixed.
$x_1,\ldots ,x_k$
are likewise fixed.
It remains to determine
![]() $y_1,\ldots ,y_{k-1}$
. Since the tuple
$y_1,\ldots ,y_{k-1}$
. Since the tuple
![]() ${\mathbf h}$
has already been fixed and
${\mathbf h}$
has already been fixed and
![]() $\Psi (t;{\mathbf h})$
has degree at most
$\Psi (t;{\mathbf h})$
has degree at most
![]() $k-1$
with respect to t, the polynomial
$k-1$
with respect to t, the polynomial
 $$ \begin{align*} A\prod_{i=1}^k(x_i-t)-\Psi(-t;{\mathbf h}) \end{align*} $$
$$ \begin{align*} A\prod_{i=1}^k(x_i-t)-\Psi(-t;{\mathbf h}) \end{align*} $$
has degree k with respect to t, and has all of its coefficients already fixed. It therefore follows from (2.8) that there are at most k choices for each of the variables
![]() $y_1,\ldots ,y_{k-1}$
. Let
$y_1,\ldots ,y_{k-1}$
. Let
![]() $T_k^\dagger (X;{\boldsymbol \varphi })$
denote the number of nondiagonal solutions
$T_k^\dagger (X;{\boldsymbol \varphi })$
denote the number of nondiagonal solutions
![]() ${\mathbf x},{\mathbf y}$
counted by
${\mathbf x},{\mathbf y}$
counted by
![]() $N_k(X;{\boldsymbol \varphi })$
. Then we may conclude that
$N_k(X;{\boldsymbol \varphi })$
. Then we may conclude that
On recalling our opening discussion together with the estimates (2.10) and (2.11), we arrive at the upper bound
This delivers the first conclusion of Theorem 1.1. On recalling the definition (1.5) of
![]() $w({\boldsymbol \varphi })$
, it follows that when
$w({\boldsymbol \varphi })$
, it follows that when
![]() $k_1+\cdots +k_r\ge \tfrac {1}{2}k(k-1)+2$
, one has
$k_1+\cdots +k_r\ge \tfrac {1}{2}k(k-1)+2$
, one has
![]() $w({\boldsymbol \varphi })\le k-2$
, and thus the second conclusion of Theorem 1.1 is immediate from (2.12) and the asymptotic formula
$w({\boldsymbol \varphi })\le k-2$
, and thus the second conclusion of Theorem 1.1 is immediate from (2.12) and the asymptotic formula
![]() $T_k(X)=k!X^k+O(X^{k-1})$
.
$T_k(X)=k!X^k+O(X^{k-1})$
.
Proof of Corollary 1.2
Write
 $$ \begin{align*} \varphi_j({\mathbf z})={\sigma}_j(z_1,\ldots ,z_k)+\sum_{l=1}^{k-r}a_{jl}{\sigma}_l(z_1,\ldots ,z_k)\quad (k-r+1\le j\le k). \end{align*} $$
$$ \begin{align*} \varphi_j({\mathbf z})={\sigma}_j(z_1,\ldots ,z_k)+\sum_{l=1}^{k-r}a_{jl}{\sigma}_l(z_1,\ldots ,z_k)\quad (k-r+1\le j\le k). \end{align*} $$
Then we see that the system (1.6) is comprised of symmetric polynomials having degrees
![]() $k-r+1,\ldots ,k$
. For this system, it follows from (1.5) that
$k-r+1,\ldots ,k$
. For this system, it follows from (1.5) that
 $$ \begin{align*} w({\boldsymbol \varphi})=\tfrac{1}{2}k(k+1)-\sum_{j=k-r+1}^k j=\tfrac{1}{2}(k-r)(k-r+1). \end{align*} $$
$$ \begin{align*} w({\boldsymbol \varphi})=\tfrac{1}{2}k(k+1)-\sum_{j=k-r+1}^k j=\tfrac{1}{2}(k-r)(k-r+1). \end{align*} $$
We therefore deduce from Theorem 1.1 that
and so there is a paucity of nondiagonal solutions in the system (1.6) provided that
![]() $(k-r)(k-r+1)<2k-2$
. This completes the proof of the corollary.
$(k-r)(k-r+1)<2k-2$
. This completes the proof of the corollary.
3 Nonlinear variants
The system of Diophantine equations (1.1) underlying Theorem 1.1 and Corollary 1.2 possesses features inherently linear in nature. Indeed, as is evident from the discussion initiating Section 2, we are able to restrict attention to integral linear combinations of elementary symmetric polynomials of the shape (2.2). This is a convenient but not essential simplification, as we now explain.
We first describe the symmetric polynomials presently in our field of view. Recall the exponents
![]() $k_1,\ldots ,k_r$
satisfying (1.4), the complementary set of exponents
$k_1,\ldots ,k_r$
satisfying (1.4), the complementary set of exponents
![]() ${\mathcal R}={\mathcal R}({\boldsymbol \varphi })$
defined in (2.1), and the definition (1.5) of
${\mathcal R}={\mathcal R}({\boldsymbol \varphi })$
defined in (2.1), and the definition (1.5) of
![]() $w({\boldsymbol \varphi })$
. Putting
$w({\boldsymbol \varphi })$
. Putting
![]() $R=\text {card}({\mathcal R})$
, we label the elements of
$R=\text {card}({\mathcal R})$
, we label the elements of
![]() ${\mathcal R}$
so that
${\mathcal R}$
so that
![]() ${\mathcal R}=\{l_1,\ldots ,l_R\}$
. We consider symmetric polynomials in the variables
${\mathcal R}=\{l_1,\ldots ,l_R\}$
. We consider symmetric polynomials in the variables
![]() ${\mathbf z}=(z_1,\ldots ,z_k)$
of the shape
${\mathbf z}=(z_1,\ldots ,z_k)$
of the shape
where
![]() $a_j\in {\mathbb Z}\setminus \{0\}$
and
$a_j\in {\mathbb Z}\setminus \{0\}$
and
![]() ${\Upsilon }_j\in {\mathbb Z}[s_1,\ldots ,s_R]$
.
${\Upsilon }_j\in {\mathbb Z}[s_1,\ldots ,s_R]$
.
Theorem 3.1. Let
![]() $\varphi _1,\ldots ,\varphi _r$
be symmetric polynomials of the shape (3.1) with respective degrees
$\varphi _1,\ldots ,\varphi _r$
be symmetric polynomials of the shape (3.1) with respective degrees
![]() $k_1,\ldots ,k_r$
satisfying (1.4). Then
$k_1,\ldots ,k_r$
satisfying (1.4). Then
In particular, when
![]() $k_1+\cdots +k_r\ge \tfrac {1}{2}k^2+1$
, one has
$k_1+\cdots +k_r\ge \tfrac {1}{2}k^2+1$
, one has
A specialisation again makes for accessible conclusions. Fix the polynomials
![]() ${\Upsilon }_j\in {\mathbb Z}[s_1,\ldots ,s_R]$
for
${\Upsilon }_j\in {\mathbb Z}[s_1,\ldots ,s_R]$
for
![]() $k-r+1\le j\le k$
, and denote by
$k-r+1\le j\le k$
, and denote by
![]() $L_{k,r}(X;{\boldsymbol {\Upsilon }})$
the number of solutions of the simultaneous equations
$L_{k,r}(X;{\boldsymbol {\Upsilon }})$
the number of solutions of the simultaneous equations
in variables
![]() ${\mathbf x}=(x_1,\ldots ,x_k)$
and
${\mathbf x}=(x_1,\ldots ,x_k)$
and
![]() ${\mathbf y}=(y_1,\ldots ,y_k)$
with
${\mathbf y}=(y_1,\ldots ,y_k)$
with
![]() $1\le x_i,y_i\le X$
.
$1\le x_i,y_i\le X$
.
Corollary 3.2. Suppose that
![]() $k,r\in {\mathbb N}$
satisfy
$k,r\in {\mathbb N}$
satisfy
![]() $(k-r)(k-r+1)<k-1$
. Then there is a paucity of nondiagonal solutions in the system (3.2). In particular,
$(k-r)(k-r+1)<k-1$
. Then there is a paucity of nondiagonal solutions in the system (3.2). In particular,
Proof of Theorem 3.1
Our present strategy is very similar to that wrought against Theorem 1.1. Given a solution
![]() ${\mathbf x},{\mathbf y}$
of the system (1.1) counted by
${\mathbf x},{\mathbf y}$
of the system (1.1) counted by
![]() $N_k(X;{\boldsymbol \varphi })$
, define
$N_k(X;{\boldsymbol \varphi })$
, define
![]() $h_m({\mathbf z})={\sigma }_{l_m}({\mathbf z})$
for
$h_m({\mathbf z})={\sigma }_{l_m}({\mathbf z})$
for
![]() ${\mathbf z}\in \{{\mathbf x},{\mathbf y}\}$
and
${\mathbf z}\in \{{\mathbf x},{\mathbf y}\}$
and
![]() $1\le m\le R$
. In view of (3.1), the system (1.1) now becomes
$1\le m\le R$
. In view of (3.1), the system (1.1) now becomes
In the present nonlinear scenario there may be some index j for which the integer on the right-hand side of (3.3) is not equal to
![]() ${\Upsilon }_j({\mathbf h}({\mathbf x})-{\mathbf h}({\mathbf y}))$
. The argument here therefore contains extra complications, with weaker quantitative conclusions than Theorem 1.1.
${\Upsilon }_j({\mathbf h}({\mathbf x})-{\mathbf h}({\mathbf y}))$
. The argument here therefore contains extra complications, with weaker quantitative conclusions than Theorem 1.1.
Put
![]() $A=a_1a_2\cdots a_r$
and
$A=a_1a_2\cdots a_r$
and
![]() $c_j=A/a_j\ (1\le j\le r)$
. Then, by applying the identity (1.2) together with (3.3), we obtain for
$c_j=A/a_j\ (1\le j\le r)$
. Then, by applying the identity (1.2) together with (3.3), we obtain for
![]() $1\le j\le r$
the relation
$1\le j\le r$
the relation
 $$ \begin{align} A\bigg( \prod_{i=1}^k(t+x_i)-\prod_{i=1}^k(t+y_i)\bigg)=\Psi(t;{\mathbf h})-\Psi(t;{\mathbf g}), \end{align} $$
$$ \begin{align} A\bigg( \prod_{i=1}^k(t+x_i)-\prod_{i=1}^k(t+y_i)\bigg)=\Psi(t;{\mathbf h})-\Psi(t;{\mathbf g}), \end{align} $$
where
![]() ${\mathbf h}=(h_1({\mathbf x}),\ldots ,h_R({\mathbf x}))$
,
${\mathbf h}=(h_1({\mathbf x}),\ldots ,h_R({\mathbf x}))$
,
![]() ${\mathbf g}=(h_1({\mathbf y}),\ldots ,h_R({\mathbf y}))$
, and we write
${\mathbf g}=(h_1({\mathbf y}),\ldots ,h_R({\mathbf y}))$
, and we write
 $$ \begin{align*} \Psi(t;{\mathbf e})=A\sum_{m\in {\mathcal R}}e_mt^{k-m}+\sum_{j=1}^rc_jt^{k-k_j}{\Upsilon}_j({\mathbf e}). \end{align*} $$
$$ \begin{align*} \Psi(t;{\mathbf e})=A\sum_{m\in {\mathcal R}}e_mt^{k-m}+\sum_{j=1}^rc_jt^{k-k_j}{\Upsilon}_j({\mathbf e}). \end{align*} $$
If
![]() ${\mathbf x},{\mathbf y}$
is a solution of (1.1) counted by
${\mathbf x},{\mathbf y}$
is a solution of (1.1) counted by
![]() $N_k(X;{\boldsymbol \varphi })$
, then, with
$N_k(X;{\boldsymbol \varphi })$
, then, with
![]() $h_m={\sigma }_{l_m}({\mathbf x})$
and
$h_m={\sigma }_{l_m}({\mathbf x})$
and
![]() $g_m={\sigma }_{l_m}({\mathbf y})$
for
$g_m={\sigma }_{l_m}({\mathbf y})$
for
![]() $1\le m\le R$
, we deduce by setting
$1\le m\le R$
, we deduce by setting
![]() $t=-y_j$
in (3.4) that
$t=-y_j$
in (3.4) that
 $$ \begin{align} A\prod_{i=1}^k(x_i-y_j)=\Psi(-y_j;{\mathbf h})-\Psi(-y_j;{\mathbf g})\quad (1\le j\le k). \end{align} $$
$$ \begin{align} A\prod_{i=1}^k(x_i-y_j)=\Psi(-y_j;{\mathbf h})-\Psi(-y_j;{\mathbf g})\quad (1\le j\le k). \end{align} $$
We now follow the path already trodden in the proof of Theorem 1.1 presented in Section 2. Suppose first that
![]() ${\mathbf x},{\mathbf y}$
is a potentially diagonal solution. When the polynomial
${\mathbf x},{\mathbf y}$
is a potentially diagonal solution. When the polynomial
![]() $\Psi (-t;{\mathbf h})-\Psi (-t;{\mathbf g})$
is identically zero, we find that
$\Psi (-t;{\mathbf h})-\Psi (-t;{\mathbf g})$
is identically zero, we find that
![]() ${\mathbf x},{\mathbf y}$
is counted by
${\mathbf x},{\mathbf y}$
is counted by
![]() $T_k(X)$
. Meanwhile, when instead this polynomial is not identically zero, a divisor function argument shows that for each fixed choice of
$T_k(X)$
. Meanwhile, when instead this polynomial is not identically zero, a divisor function argument shows that for each fixed choice of
![]() ${\mathbf h}$
and
${\mathbf h}$
and
![]() ${\mathbf g}$
, there are
${\mathbf g}$
, there are
![]() $O(X^\varepsilon )$
possible choices for
$O(X^\varepsilon )$
possible choices for
![]() ${\mathbf x}$
and
${\mathbf x}$
and
![]() ${\mathbf y}$
. We have
${\mathbf y}$
. We have
![]() $|h_m({\mathbf x})|\le 2^kX^{l_m}$
and
$|h_m({\mathbf x})|\le 2^kX^{l_m}$
and
![]() $|h_m({\mathbf y})|\le 2^kX^{l_m}$
, so the total number of choices for
$|h_m({\mathbf y})|\le 2^kX^{l_m}$
, so the total number of choices for
![]() $(h_1,\ldots ,h_R)$
and
$(h_1,\ldots ,h_R)$
and
![]() $(g_1,\ldots ,g_R)$
is
$(g_1,\ldots ,g_R)$
is
![]() $O(X^{2w({\boldsymbol \varphi })})$
, where
$O(X^{2w({\boldsymbol \varphi })})$
, where
![]() $w({\boldsymbol \varphi })$
is defined by (1.5). Thus, the total number of potentially diagonal solutions is equal to
$w({\boldsymbol \varphi })$
is defined by (1.5). Thus, the total number of potentially diagonal solutions is equal to
![]() $T_k(X)+O(X^{2w({\boldsymbol \varphi })+\varepsilon })$
.
$T_k(X)+O(X^{2w({\boldsymbol \varphi })+\varepsilon })$
.
Suppose next that
![]() ${\mathbf x},{\mathbf y}$
is a nondiagonal solution of the system (1.1). By symmetry, we may again suppose that
${\mathbf x},{\mathbf y}$
is a nondiagonal solution of the system (1.1). By symmetry, we may again suppose that
![]() $y_k\not \in \{x_1,\ldots ,x_k\}$
, and (3.5) shows that the integer
$y_k\not \in \{x_1,\ldots ,x_k\}$
, and (3.5) shows that the integer
![]() ${\Theta } =\Psi (-y_j;{\mathbf h})-\Psi (-y_j;{\mathbf g})$
is nonzero. There are
${\Theta } =\Psi (-y_j;{\mathbf h})-\Psi (-y_j;{\mathbf g})$
is nonzero. There are
![]() $O(X^{2w({\boldsymbol \varphi })})$
possible choices for
$O(X^{2w({\boldsymbol \varphi })})$
possible choices for
![]() ${\mathbf h}$
and
${\mathbf h}$
and
![]() ${\mathbf g}$
, and
${\mathbf g}$
, and
![]() $O(X)$
possible choices for
$O(X)$
possible choices for
![]() $y_k$
in this scenario. Fix any one such choice and note from (3.5) that
$y_k$
in this scenario. Fix any one such choice and note from (3.5) that
![]() ${\Theta }=O(X^k)$
. An elementary divisor function estimate shows there to be
${\Theta }=O(X^k)$
. An elementary divisor function estimate shows there to be
![]() $O(X^\varepsilon )$
choices for
$O(X^\varepsilon )$
choices for
![]() $x_1-y_k,\ldots ,x_k-y_k$
satisfying (3.5). Fixing any one such choice fixes the integers
$x_1-y_k,\ldots ,x_k-y_k$
satisfying (3.5). Fixing any one such choice fixes the integers
![]() $x_1,\ldots ,x_k$
. An argument essentially identical to that applied in the proof of Theorem 1.1 shows from here that there are
$x_1,\ldots ,x_k$
. An argument essentially identical to that applied in the proof of Theorem 1.1 shows from here that there are
![]() $O(1)$
possible choices for
$O(1)$
possible choices for
![]() $y_1,\ldots ,y_{k-1}$
. Hence, the number of nondiagonal solutions of the system (1.1) is
$y_1,\ldots ,y_{k-1}$
. Hence, the number of nondiagonal solutions of the system (1.1) is
![]() $O(X^{2w({\boldsymbol \varphi })+1+\varepsilon })$
.
$O(X^{2w({\boldsymbol \varphi })+1+\varepsilon })$
.
Combining the two contributions to
![]() $N_k(X;{\boldsymbol \varphi })$
that we have obtained yields
$N_k(X;{\boldsymbol \varphi })$
that we have obtained yields
confirming the first conclusion of Theorem 3.1. The definition (1.5) of
![]() $w({\boldsymbol \varphi })$
, moreover, implies that when
$w({\boldsymbol \varphi })$
, moreover, implies that when
![]() $k_1+\cdots +k_r\ge \tfrac {1}{2}k^2+1$
, one has
$k_1+\cdots +k_r\ge \tfrac {1}{2}k^2+1$
, one has
![]() $2w({\boldsymbol \varphi })\le k-2$
. The second conclusion of Theorem 3.1 therefore follows directly from the first.
$2w({\boldsymbol \varphi })\le k-2$
. The second conclusion of Theorem 3.1 therefore follows directly from the first.
Proof of Corollary 3.2
When
![]() $k-r+1\le j\le k$
, write
$k-r+1\le j\le k$
, write
Then we see from (1.5) that the system (3.2) is comprised of symmetric polynomials with
![]() $w({\boldsymbol \varphi })=\tfrac {1}{2}(k-r)(k-r+1)$
. Theorem 3.1 therefore shows that
$w({\boldsymbol \varphi })=\tfrac {1}{2}(k-r)(k-r+1)$
. Theorem 3.1 therefore shows that
and provided that
![]() $(k-r)(k-r+1)<k-1$
, there is a paucity of nondiagonal solutions in the system (3.2). This completes the proof of the corollary.
$(k-r)(k-r+1)<k-1$
, there is a paucity of nondiagonal solutions in the system (3.2). This completes the proof of the corollary.
Acknowledgement
We thank the referee for useful comments.