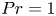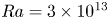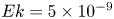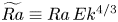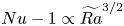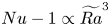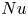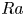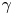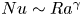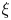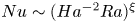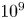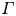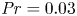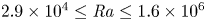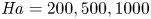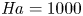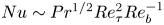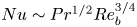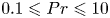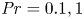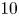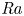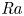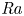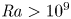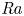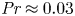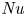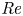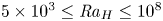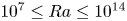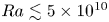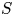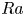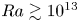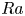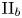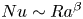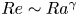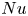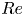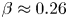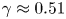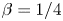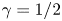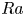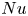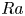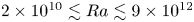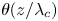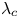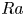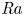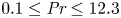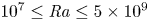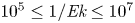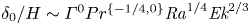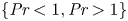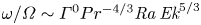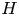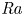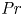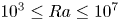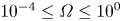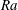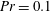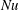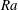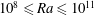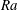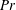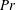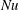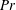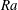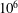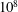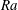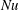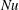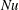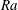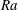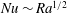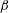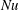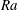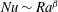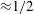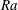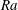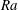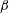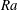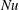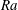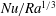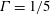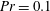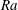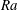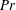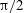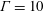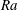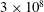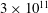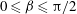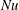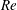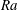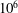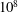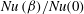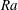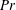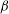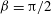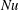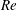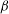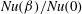29 results
Scaling regimes in rapidly rotating thermal convection at extreme Rayleigh numbers
-
- Journal:
- Journal of Fluid Mechanics / Volume 984 / 10 April 2024
- Published online by Cambridge University Press:
- 04 April 2024, A45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unifying heat transport model for the transition between buoyancy-dominated and Lorentz-force-dominated regimes in quasistatic magnetoconvection
-
- Journal:
- Journal of Fluid Mechanics / Volume 980 / 10 February 2024
- Published online by Cambridge University Press:
- 05 February 2024, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Oscillatory large-scale circulation in liquid-metal thermal convection and its structural unit
-
- Journal:
- Journal of Fluid Mechanics / Volume 977 / 25 December 2023
- Published online by Cambridge University Press:
- 13 December 2023, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wall mode dynamics and transition to chaos in magnetoconvection with a vertical magnetic field
-
- Journal:
- Journal of Fluid Mechanics / Volume 975 / 25 November 2023
- Published online by Cambridge University Press:
- 16 November 2023, R2
-
- Article
- Export citation
Passive scalar transport in Couette flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 943 / 25 July 2022
- Published online by Cambridge University Press:
- 09 June 2022, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flow states and heat transport in Rayleigh–Bénard convection with different sidewall boundary conditions
-
- Journal:
- Journal of Fluid Mechanics / Volume 936 / 10 April 2022
- Published online by Cambridge University Press:
- 18 February 2022, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics and length scales in vertical convection of liquid metals
-
- Journal:
- Journal of Fluid Mechanics / Volume 932 / 10 February 2022
- Published online by Cambridge University Press:
- 02 December 2021, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regime transitions in thermally driven high-Rayleigh number vertical convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 917 / 25 June 2021
- Published online by Cambridge University Press:
- 21 April 2021, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thermal boundary-layer structure in laminar horizontal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 915 / 25 May 2021
- Published online by Cambridge University Press:
- 31 March 2021, R5
-
- Article
- Export citation
Boundary zonal flows in rapidly rotating turbulent thermal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 915 / 25 May 2021
- Published online by Cambridge University Press:
- 17 March 2021, A62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generation of zonal flows in convective systems by travelling thermal waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 913 / 25 April 2021
- Published online by Cambridge University Press:
- 23 February 2021, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tenacious wall states in thermal convection in rapidly rotating containers
-
- Journal:
- Journal of Fluid Mechanics / Volume 898 / 10 September 2020
- Published online by Cambridge University Press:
- 24 June 2020, F1
-
- Article
-
- You have access
- HTML
- Export citation
Classical and symmetrical horizontal convection: detaching plumes and oscillations
-
- Journal:
- Journal of Fluid Mechanics / Volume 892 / 10 June 2020
- Published online by Cambridge University Press:
- 01 April 2020, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The influence of the cell inclination on the heat transport and large-scale circulation in liquid metal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 884 / 10 February 2020
- Published online by Cambridge University Press:
- 09 December 2019, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Natural convection in cylindrical containers with isothermal ring-shaped obstacles
-
- Journal:
- Journal of Fluid Mechanics / Volume 882 / 10 January 2020
- Published online by Cambridge University Press:
- 31 October 2019, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
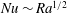 $Nu\sim Ra^{1/2}$ scaling enabled by multiscale wall roughness in Rayleigh–Bénard turbulence
$Nu\sim Ra^{1/2}$ scaling enabled by multiscale wall roughness in Rayleigh–Bénard turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 869 / 25 June 2019
- Published online by Cambridge University Press:
- 23 April 2019, R4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bulk temperature and heat transport in turbulent Rayleigh–Bénard convection of fluids with temperature-dependent properties
-
- Journal:
- Journal of Fluid Mechanics / Volume 851 / 25 September 2018
- Published online by Cambridge University Press:
- 20 July 2018, pp. 374-390
-
- Article
- Export citation
Confined inclined thermal convection in low-Prandtl-number fluids
-
- Journal:
- Journal of Fluid Mechanics / Volume 850 / 10 September 2018
- Published online by Cambridge University Press:
- 10 July 2018, pp. 984-1008
-
- Article
- Export citation
Mean flow structure in horizontal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 812 / 10 February 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 525-540
-
- Article
- Export citation
Thermal convection in inclined cylindrical containers
-
- Journal:
- Journal of Fluid Mechanics / Volume 790 / 10 March 2016
- Published online by Cambridge University Press:
- 11 February 2016, R3
-
- Article
- Export citation