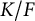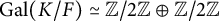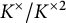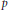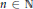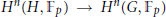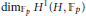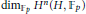20 results
Galois module structure of square power classes for biquadratic extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 804-827
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomological Dimension and Schreier's Formula in Galois Cohomology
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 4 / 01 December 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 588-593
- Print publication:
- 01 December 2007
-
- Article
-
- You have access
- Export citation
GALOIS MODULE STRUCTURE OF pTH-POWER CLASSES OF CYCLIC EXTENSIONS OF DEGREE pn
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 92 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 20 February 2006, pp. 307-341
- Print publication:
- March 2006
-
- Article
- Export citation
Microsatellite variation among divergent populations of stalk-eyed flies, genus Cyrtodiopsis
-
- Journal:
- Genetical Research / Volume 84 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 12 October 2004, pp. 27-40
-
- Article
-
- You have access
- Export citation
2 - Algebraic Numbers, Field Extensions, and Minimal Polynomials
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp 22-38
-
- Chapter
- Export citation
Preface
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp ix-xii
-
- Chapter
- Export citation

Exploratory Galois Theory
-
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004
Appendix: Subgroups of Symmetric Groups
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp 197-200
-
- Chapter
- Export citation
Introduction
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp 1-4
-
- Chapter
- Export citation
6 - Some Classical Topics
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp 152-192
-
- Chapter
- Export citation
Historical Note
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp 193-196
-
- Chapter
- Export citation
1 - Preliminaries
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp 5-21
-
- Chapter
- Export citation
3 - Working with Algebraic Numbers, Field Extensions, and Minimal Polynomials
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp 39-62
-
- Chapter
- Export citation
4 - Multiply Generated Fields
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp 63-102
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp 201-204
-
- Chapter
- Export citation
Index
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp 205-208
-
- Chapter
- Export citation
Contents
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp vii-viii
-
- Chapter
- Export citation
5 - The Galois Correspondence
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp 103-151
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Exploratory Galois Theory
- Published online:
- 06 July 2010
- Print publication:
- 11 October 2004, pp i-vi
-
- Chapter
- Export citation
The long and short of sperm polymorphisms in insects
-
- Journal:
- Biological Reviews / Volume 77 / Issue 2 / May 2002
- Published online by Cambridge University Press:
- 05 June 2002, pp. 153-182
- Print publication:
- May 2002
-
- Article
- Export citation