12 results
Contributors
-
-
- Book:
- The Cambridge Handbook of Communication Disorders
- Published online:
- 05 March 2015
- Print publication:
- 24 October 2013, pp -
-
- Chapter
- Export citation
Bifurcation of positive solutions for a Neumann boundary value problem
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 3 / January 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 324-340
-
- Article
-
- You have access
- Export citation
Conditions for permanence in well-known biological competition models
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 195-223
-
- Article
-
- You have access
- Export citation
Preface
-
- Book:
- Large-Scale Atmosphere-Ocean Dynamics
- Published online:
- 04 February 2010
- Print publication:
- 15 August 2002, pp xi-xii
-
- Chapter
- Export citation
Contents
-
- Book:
- Large-Scale Atmosphere-Ocean Dynamics
- Published online:
- 04 February 2010
- Print publication:
- 15 August 2002, pp vii-viii
-
- Chapter
- Export citation
Contributors
-
- Book:
- Large-Scale Atmosphere-Ocean Dynamics
- Published online:
- 04 February 2010
- Print publication:
- 15 August 2002, pp ix-x
-
- Chapter
- Export citation

Large-Scale Atmosphere-Ocean Dynamics
- Analytical Methods and Numerical Models
-
- Published online:
- 04 February 2010
- Print publication:
- 15 August 2002
Frontmatter
-
- Book:
- Large-Scale Atmosphere-Ocean Dynamics
- Published online:
- 04 February 2010
- Print publication:
- 15 August 2002, pp i-vi
-
- Chapter
- Export citation
Permanence and asymptotic stability in diagonally convex reaction–diffusion systems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 128 / Issue 1 / 1998
- Published online by Cambridge University Press:
- 14 November 2011, pp. 147-172
- Print publication:
- 1998
-
- Article
- Export citation
Some existence, uniqueness and nonuniqueness theorems for solutions of parabolic equations with discontinuous nonlinearities
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 119 / Issue 1-2 / 1991
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1-17
- Print publication:
- 1991
-
- Article
- Export citation
A semilinear elliptic eigenvalue problem, II. The plasma problem
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 87 / Issue 1-2 / 1980
- Published online by Cambridge University Press:
- 14 November 2011, pp. 83-109
- Print publication:
- 1980
-
- Article
- Export citation
A semilinear elliptic eigenvalue problem, I
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 87 / Issue 1-2 / 1980
- Published online by Cambridge University Press:
- 14 November 2011, pp. 65-82
- Print publication:
- 1980
-
- Article
- Export citation



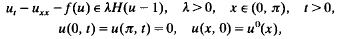
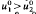 for any
for any 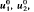 , respectively.
, respectively.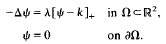

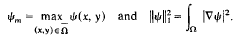
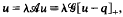 , describes both semilinear elliptic boundary value problems (P) and their natural discretisations (P
, describes both semilinear elliptic boundary value problems (P) and their natural discretisations (P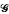 is a positive compact linear operator and [
is a positive compact linear operator and [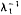 is the first (positive) eigenvalue of
is the first (positive) eigenvalue of 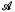 maps a smaller cone
maps a smaller cone 