Article contents
A semilinear elliptic eigenvalue problem, II. The plasma problem
Published online by Cambridge University Press: 14 November 2011
Synopsis
This paper continues the study of the boundary value problem, for (λ, ψ)
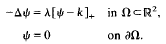
Here δ denotes the Laplacian, k is a given positive constant, and λ1 will denote the first eigenvalue for the Dirichlet problem for −δ on Ω. For λ ≦ λ1, the only solutions are those with ψ = 0. Throughout we will be interested in solutions (λ, ψ) with λ > λ1 and with ψ > 0 in Ω.
In the special case Ω = B(0, R) there is a branch ℱe, of explicit exact solutions which bifurcate from infinity at λ = λ1 and for which the following conclusions are valid, (a) The set Aψ,
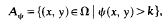
is simply-connected, (b) Along ℱe, ψm → k, ‖ψ‖1 → 0 and the diameter of Aψ tends to zero as λ → ∞, where
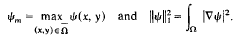
Here it is shown that the above conclusions hold for other choices of Ω, and in particular, for Ω = (−a, a)×(−b, b). (Existence is settled in Part I, and elsewhere.)
The results of numerical and asymptotic calculations when Ω = (−a, a)×(−b, b) are given to illustrate both the above, and some limitations in the conclusions of our analysis.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 87 , Issue 1-2 , 1980 , pp. 83 - 109
- Copyright
- Copyright © Royal Society of Edinburgh 1980
References
- 7
- Cited by




