21 results
On flatness and the Ore condition
-
-
- Book:
- Noncommutative Localization in Algebra and Topology
- Published online:
- 19 October 2009
- Print publication:
- 09 February 2006, pp 1-4
-
- Chapter
- Export citation
A note on Cohn's universal localisation at a semiprime ideal
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 69 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 17 April 2009, pp. 361-367
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
Frontmatter
-
- Book:
- Introductory Lectures on Rings and Modules
- Published online:
- 05 June 2012
- Print publication:
- 22 April 1999, pp i-iv
-
- Chapter
- Export citation
4 - REPRESENTATIONS OF FINITE GROUPS
-
- Book:
- Introductory Lectures on Rings and Modules
- Published online:
- 05 June 2012
- Print publication:
- 22 April 1999, pp 171-206
-
- Chapter
- Export citation
INDEX
-
- Book:
- Introductory Lectures on Rings and Modules
- Published online:
- 05 June 2012
- Print publication:
- 22 April 1999, pp 233-238
-
- Chapter
- Export citation
BIBLIOGRAPHY
-
- Book:
- Introductory Lectures on Rings and Modules
- Published online:
- 05 June 2012
- Print publication:
- 22 April 1999, pp 229-230
-
- Chapter
- Export citation
LIST OF SYMBOLS
-
- Book:
- Introductory Lectures on Rings and Modules
- Published online:
- 05 June 2012
- Print publication:
- 22 April 1999, pp 231-232
-
- Chapter
- Export citation
3 - STRUCTURE OF NONCOMMUTATIVE RINGS
-
- Book:
- Introductory Lectures on Rings and Modules
- Published online:
- 05 June 2012
- Print publication:
- 22 April 1999, pp 137-170
-
- Chapter
- Export citation

Introductory Lectures on Rings and Modules
-
- Published online:
- 05 June 2012
- Print publication:
- 22 April 1999
A - APPENDIX
-
- Book:
- Introductory Lectures on Rings and Modules
- Published online:
- 05 June 2012
- Print publication:
- 22 April 1999, pp 207-228
-
- Chapter
- Export citation
1 - RINGS
-
- Book:
- Introductory Lectures on Rings and Modules
- Published online:
- 05 June 2012
- Print publication:
- 22 April 1999, pp 1-62
-
- Chapter
- Export citation
2 - MODULES
-
- Book:
- Introductory Lectures on Rings and Modules
- Published online:
- 05 June 2012
- Print publication:
- 22 April 1999, pp 63-136
-
- Chapter
- Export citation
Contents
-
- Book:
- Introductory Lectures on Rings and Modules
- Published online:
- 05 June 2012
- Print publication:
- 22 April 1999, pp v-vi
-
- Chapter
- Export citation
Weak ideal invariance and orders in artinian rings: Corrigendum
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 25 / Issue 2 / April 1982
- Published online by Cambridge University Press:
- 17 April 2009, pp. 317-320
- Print publication:
- April 1982
-
- Article
-
- You have access
- Export citation
Weak ideal invariance and orders in Artinian rings
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 23 / Issue 2 / April 1981
- Published online by Cambridge University Press:
- 17 April 2009, pp. 255-264
- Print publication:
- April 1981
-
- Article
-
- You have access
- Export citation
On Localization at an Ideal
-
- Journal:
- Canadian Mathematical Bulletin / Volume 22 / Issue 4 / 01 December 1979
- Published online by Cambridge University Press:
- 20 November 2018, pp. 397-401
- Print publication:
- 01 December 1979
-
- Article
-
- You have access
- Export citation
On Maximal Torsion Radicals, II
-
- Journal:
- Canadian Journal of Mathematics / Volume 27 / Issue 1 / 01 February 1975
- Published online by Cambridge University Press:
- 20 November 2018, pp. 115-120
- Print publication:
- 01 February 1975
-
- Article
-
- You have access
- Export citation
Bicommutators Of Cofaithful, Fully Divisible Modules*: Corrigendum
-
- Journal:
- Canadian Journal of Mathematics / Volume 26 / Issue 1 / February 1974
- Published online by Cambridge University Press:
- 20 November 2018, p. 256
- Print publication:
- February 1974
-
- Article
-
- You have access
- Export citation
On Maximal Torsion Radicals
-
- Journal:
- Canadian Journal of Mathematics / Volume 25 / Issue 4 / August 1973
- Published online by Cambridge University Press:
- 20 November 2018, pp. 712-726
- Print publication:
- August 1973
-
- Article
-
- You have access
- Export citation
Cotorsion radicals and projective modules
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 5 / Issue 2 / October 1971
- Published online by Cambridge University Press:
- 17 April 2009, pp. 241-253
- Print publication:
- October 1971
-
- Article
-
- You have access
- Export citation



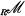 denote the category of unital left
denote the category of unital left 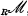 , and showed that if
, and showed that if 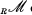 denote the category of unital left
denote the category of unital left 