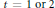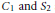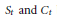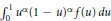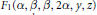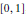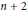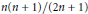14 results
The Bernoulli clock: probabilistic and combinatorial interpretations of the Bernoulli polynomials by circular convolution
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 210-237
-
- Article
- Export citation
A direct approach to the stable distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 261-282
- Print publication:
- July 2016
-
- Article
- Export citation
Concave Majorants of Random Walks and Related Poisson Processes
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 18 August 2011, pp. 651-682
-
- Article
- Export citation
11 - Characterizations of exchangeable partitions and random discrete distributions by deletion properties
-
-
- Book:
- Probability and Mathematical Genetics
- Published online:
- 07 September 2011
- Print publication:
- 15 July 2010, pp 264-298
-
- Chapter
- Export citation
Coloured Loop-Erased Random Walk on the Complete Graph
-
- Journal:
- Combinatorics, Probability and Computing / Volume 17 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 727-740
-
- Article
- Export citation
Analysis of Top To Random Shuffles
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 135-155
-
- Article
- Export citation
Poisson Representation of a Ewens Fragmentation Process
-
- Journal:
- Combinatorics, Probability and Computing / Volume 16 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 819-827
-
- Article
- Export citation
Infinitely Divisible Laws Associated with Hyperbolic Functions
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 2 / 01 April 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 292-330
- Print publication:
- 01 April 2003
-
- Article
-
- You have access
- Export citation
Poisson–Dirichlet and GEM Invariant Distributions for Split-and-Merge Transformations of an Interval Partition
-
- Journal:
- Combinatorics, Probability and Computing / Volume 11 / Issue 5 / September 2002
- Published online by Cambridge University Press:
- 09 October 2002, pp. 501-514
-
- Article
- Export citation
Asymptotics of the Hurwitz Binomial Distribution Related to Mixed Poisson Galton–Watson Trees
-
- Journal:
- Combinatorics, Probability and Computing / Volume 10 / Issue 3 / May 2001
- Published online by Cambridge University Press:
- 25 June 2001, pp. 203-211
-
- Article
- Export citation
Algebraic Evaluations of Some Euler Integrals, Duplication Formulae for Appell's Hypergeometric Function F1, and Brownian Variations
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 5 / 01 October 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-981
- Print publication:
- 01 October 2000
-
- Article
-
- You have access
- Export citation
Random discrete distributions invariant under size-biased permutation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 525-539
- Print publication:
- June 1996
-
- Article
- Export citation
Fluctuation identities for lévy processes and splitting at the maximum
-
- Journal:
- Advances in Applied Probability / Volume 12 / Issue 4 / December 1980
- Published online by Cambridge University Press:
- 01 July 2016, pp. 893-902
- Print publication:
- December 1980
-
- Article
- Export citation
Fluctuation identities for random walk by path decomposition at the maximum
-
- Journal:
- Advances in Applied Probability / Volume 12 / Issue 2 / June 1980
- Published online by Cambridge University Press:
- 01 July 2016, pp. 291-293
- Print publication:
- June 1980
-
- Article
- Export citation



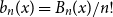
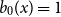
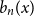
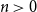
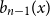

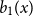
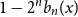
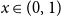

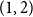
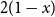
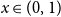
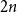
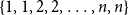
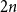
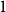
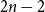
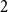
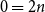
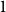
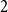

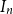
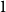
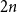

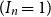
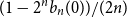
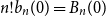

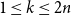
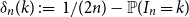
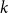
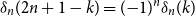
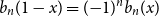
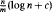 shuffles to get close to random. The formulae lead to new subalgebras in the group algebra of the symmetric group.
shuffles to get close to random. The formulae lead to new subalgebras in the group algebra of the symmetric group.