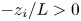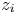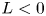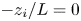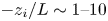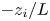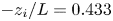As discussed in a recent paper by Brasseur & Wei (1994), scale interactions in fully developed turbulence are of two basic types in the Fourier-spectral view. The cascade of energy from large to small scales is embedded within ‘local-to-non-local’ triadic interactions separated in scale by a decade or less. ‘Distant’ triadic interactions between widely disparate scales transfer negligible energy between the largest and smallest scales, but directly modify the structure of the smallest scales in relationship to the structure of the energy-dominated large scales. Whereas cascading interactions tend to isotropize the small scales as energy moves through spectral shells from low to high wavenumbers, distant interactions redistribute energy within spectral shells in a manner that leads to anisotropic redistributions of small-scale energy and phase in response to anisotropic structure in the large scales. To study the role of long-range interactions in small-scale dynamics, Yeung & Brasseur (1991) carried out a numerical experiment in which the marginally distant triads were purposely stimulated through a coherent narrow-band anisotropic forcing at the large scales readily interpretable in both the Fourier- and physical-space views. It was found that, after one eddy turnover time, the smallest scales rapidly became anisotropic as a direct consequence of the marginally distant triadic group in a manner consistent with the distant triadic equations. Because these asymptotic equations apply in the infinite Reynolds number limit, Yeung & Brasseur argued that the observed long-range effects should be applicable also at high Reynolds numbers.
We continue the analysis of forced simulations in this study, focusing (i) on the detailed three-dimensional restructuring of the small scales as predicted by the asymptotic triadic equations, and (ii) on the relationship between Fourier- and physical-space evolution during forcing. We show that the three-dimensional restructuring of small-scale energy and vorticity in Fourier space from large-scale forcing is predicted in some detail by the distant triadic equations. We find that during forcing the distant interactions alter small-scale structure in two ways: energy is redistributed anisotropically within high-wavenumber spectral shells, and phase correlations are established at the small scales by the distant interactions. In the numerical experiments, the long-range interactions create two pairs of localized volumes of concentrated energy in three-dimensional Fourier space at high wavenumbers in which the Fourier modes are phase coupled. Each pair of locally phase-correlated volumes of Fourier modes separately corresponds to aligned vortex tubes in physical space in two orthogonal directions. We show that the dynamics of distant interactions in creating small-scale anisotropy may be described in physical space by differential advection and distortion of small-scale vorticity by the coherent large-scale energy-containing eddies, producing anisotropic alignment of small-scale vortex tubes.
Scaling arguments indicate a disparity in timescale between distant triadic interactions and energy-cascading local-to-non-local interactions which increases with scale separation. Consequently, the small scales respond to forcing initially through the distant interactions. However, as energy cascades from the large-scale to the small-scale Fourier modes, the stimulated distant interactions become embedded within a sea of local-to-non-local energy cascading interactions which reduce (but do not eliminate) small-scale anisotropy at later times. We find that whereas the small-scale structure is still anisotropic at these later times, the second-order velocity moment tensor is insensitive to this anisotropy. Third-order moments, on the other hand, do detect the anisotropy. We conclude that whereas a single statistical measure of anisotropy can be used to indicate the presence of anisotropy, a null result in that measure does not necessarily imply that the signal is isotropic. The results indicate that non-equilibrium non-stationary turbulence is particularly sensitive to long-range interactions and deviations from local isotropy.