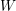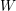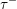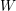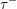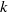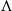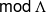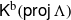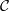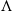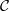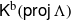30 results
Lattice structure of Weyl groups via representation theory of preprojective algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1269-1305
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
Quotient closed subcategories of quiver representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 15 October 2014, pp. 568-602
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
 $\tau $-tilting theory
$\tau $-tilting theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 3 / March 2014
- Published online by Cambridge University Press:
- 03 December 2013, pp. 415-452
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Acyclic Calabi–Yau categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1332-1348
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
8 - Tilting theory and homologically finite subcategories with applications to quasihereditary algebras
-
-
- Book:
- Handbook of Tilting Theory
- Published online:
- 25 May 2010
- Print publication:
- 04 January 2007, pp 179-214
-
- Chapter
- Export citation
Infinite Dimensional Representations of Canonical Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 1 / 01 February 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 180-224
- Print publication:
- 01 February 2006
-
- Article
-
- You have access
- Export citation
Old and recent work with Maurice
-
-
- Book:
- Representation Theory and Algebraic Geometry
- Published online:
- 06 December 2010
- Print publication:
- 15 May 1997, pp 63-88
-
- Chapter
- Export citation
V - Almost split sequences
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp 136-190
-
- Chapter
- Export citation
VII - The Auslander–Reiten-quiver
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp 224-256
-
- Chapter
- Export citation
Open problems
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp 411-412
-
- Chapter
- Export citation
Relevant conference proceedings
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp 421-422
-
- Chapter
- Export citation

Representation Theory of Artin Algebras
-
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995
Conjectures
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp 409-410
-
- Chapter
- Export citation
I - Artin rings
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp 1-25
-
- Chapter
- Export citation
Introduction
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp xi-xiv
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp 413-420
-
- Chapter
- Export citation
VIII - Hereditary algebras
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp 257-312
-
- Chapter
- Export citation
Notation
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp 406-408
-
- Chapter
- Export citation
IV - The transpose and the dual
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp 100-135
-
- Chapter
- Export citation
Index
-
- Book:
- Representation Theory of Artin Algebras
- Published online:
- 11 May 2010
- Print publication:
- 12 January 1995, pp 423-425
-
- Chapter
- Export citation