The primary aim of this study was to evaluate the effect of auditory feedback in a VR system planned for clinical use and to address the different factors that should be taken into account in building a bimodal virtual environment (VE). We conducted an experiment in which we assessed spatial performances in agoraphobic patients and normal subjects comparing two kinds of VEs, visual alone (Vis) and auditory–visual (AVis), during separate sessions. Subjects were equipped with a head-mounted display coupled with an electromagnetic sensor system and immersed in a virtual town. Their task was to locate different landmarks and become familiar with the town. In the AVis condition subjects were equipped with the head-mounted display and headphones, which delivered a soundscape updated in real-time according to their movement in the virtual town. While general performances remained comparable across the conditions, the reported feeling of immersion was more compelling in the AVis environment. However, patients exhibited more cybersickness symptoms in this condition. The result of this study points to the multisensory integration deficit of agoraphobic patients and underline the need for further research on multimodal VR systems for clinical use.

The aim of the present study is to examine the relationship between cigarette smoking and personality patterns in the general population, taking into account the possible influence of nicotine dependence. We used a stratified random sample of 1,081 adults from the general population (519 smokers and 562 non-smokers) in the region of Galicia (Spain). Personality patterns were assessed with the Millon Clinical Multiaxial Inventory-III (MCMI-III). The results indicated that nicotine-dependent smokers had a higher probability of obtaining a PREV > 75 in the histrionic and antisocial personality patterns and non-nicotine-dependent smokers are more likely to present a PREV > 75 in paranoid personality pattern than non-smokers. On the contrary, non-smokers are more likely to have a PREV > 75 on the compulsive personality scale. Our findings suggest that there are different personality patterns according to smoking status (smoker/non-smoker) and according to the presence of nicotine dependence. We concluded that it is necessary to identify the personality characteristics of smokers, since these characteristics could be key variables in increased risk of being a smoker and of difficulties for quitting smoking.

In this paper we consider horseshoes with homoclinic tangencies inside the limit set. For a class of such maps, we prove the existence of a unique equilibrium state μt, associated to the (non-continuous) potential −tlog Ju. We also prove that the Hausdorff dimension of the limit set, in any open piece of unstable manifold, is the unique number t0 such that the pressure of μt0 is zero. To deal with the discontinuity of the jacobian, we introduce a countable Markov partition adapted to the dynamics, and work with the first return map defined in a rectangle of it.

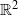We consider C2 Hénon-like families of diffeomorphisms of and study the boundary of the region of parameter values for which the non-wandering set is uniformly hyperbolic. Assuming sufficient dissipativity, we show that the loss of hyperbolicity is caused by a first homoclinic or heteroclinic tangency and that uniform hyperbolicity estimates hold uniformly in the parameter up to the bifurcation parameter and even, to some extent, at the bifurcation parameter.

El propósito primario de este estudio era evaluar el efecto de la retroalimentación auditiva en un sistema de realidad virtual (RV) planeado para el uso clínico y estudiar los diferentes factores que se deben tener en cuenta al construir un entorno virtual (EV) bimodal. Realizamos un experimento en el que evaluamos el desempeño espacial en pacientes con agorafobia y sujetos normales comparando dos clases de EV: visual solo (Vis) y auditivo-visual (AVis), durante sesiones separadas. Se equipó a los sujetos con un visualizador montado en la cabeza acoplado a un sistema sensor electromagnético e inmerso en una ciudad virtual. Su tarea era localizar diferentes mojones y familiarizarse con la ciudad. En la condición AVis, se equipó a los sujetos con el visualizador montado en la cabeza y auriculares, que proporcionaban un paisaje sonoro actualizado en tiempo real según su movimiento en la ciudad virtual. Aunque el desempeño general era comparable a través de las condiciones, la sensación comunicada por los sujetos de estar inmerso en el ambiente era más convincente en el entorno AVis. Sin embargo, los pacientes mostraron más síntomas de mareo de simulación en esta condición. El resultado de este estudio apunta al déficit de integración multisensorial en los pacientes con agorafobia y subrayan la necesidad de más investigaciones sobre los sistemas de RV multimodal para su uso clínico.