60 results
The Abstract Group G3,7,16: A Correction
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 13 / Issue 2 / December 1962
- Published online by Cambridge University Press:
- 20 January 2009, p. 188
-
- Article
-
- You have access
- Export citation
Surprising relationships among unitary reflection groups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 27 / Issue 2 / June 1984
- Published online by Cambridge University Press:
- 20 January 2009, pp. 185-194
-
- Article
-
- You have access
- Export citation
The Abstract Group G3, 7, 16
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 13 / Issue 1 / June 1962
- Published online by Cambridge University Press:
- 20 January 2009, pp. 47-61
-
- Article
-
- You have access
- Export citation
A practical method for enumerating cosets of a finite abstract group
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 5 / Issue 1 / October 1936
- Published online by Cambridge University Press:
- 20 January 2009, pp. 26-34
-
- Article
-
- You have access
- Export citation
XIII - AREA
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 241-251
-
- Chapter
- Export citation
XIV - EUCLIDEAN MODELS
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 252-266
-
- Chapter
- Export citation
VI - ELLIPTIC GEOMETRY IN TWO DIMENSIONS
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 109-127
-
- Chapter
- Export citation
Contents
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp xiii-xviii
-
- Chapter
- Export citation
XII - THE USE OF A GENERAL TRIANGLE OF REFERENCE
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 224-240
-
- Chapter
- Export citation
XV - CONCLUDING REMARKS
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 267-298
-
- Chapter
- Export citation
X - HYPERBOLIC GEOMETRY IN TWO DIMENSIONS
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 199-212
-
- Chapter
- Export citation
APPENDIX: ANGLES AND ARCS IN THE HYPERBOLIC PLANE
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 299-316
-
- Chapter
- Export citation
I - THE HISTORICAL DEVELOPMENT OF NON-EUCLIDEAN GEOMETRY
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 1-15
-
- Chapter
- Export citation
IX - EUCLIDEAN AND HYPERBOLIC GEOMETRY
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 179-198
-
- Chapter
- Export citation
IV - HOMOGENEOUS COORDINATES
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 71-94
-
- Chapter
- Export citation
VII - ELLIPTIC GEOMETRY IN THREE DIMENSIONS
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 128-156
-
- Chapter
- Export citation
VIII - DESCRIPTIVE GEOMETRY
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 157-178
-
- Chapter
- Export citation
XI - CIRCLES AND TRIANGLES
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 213-223
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp i-viii
-
- Chapter
- Export citation
II - REAL PROJECTIVE GEOMETRY: FOUNDATIONS
-
- Book:
- Non-Euclidean Geometry
- Published by:
- Mathematical Association of America
- Published online:
- 05 September 2014
- Print publication:
- 01 June 1998, pp 16-47
-
- Chapter
- Export citation



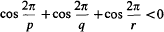
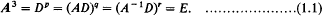
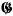 , that is, a set of relations
, that is, a set of relations