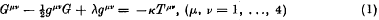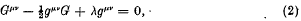15 results
Scale covariant Lagrangians and spaces reciprocal to static Einstein spaces
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 3 / January 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 338-344
-
- Article
-
- You have access
- Export citation
On a Set of Conform-Invariant Equations of the Gravitational Field
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 10 / Issue 1 / January 1953
- Published online by Cambridge University Press:
- 20 January 2009, pp. 16-20
-
- Article
-
- You have access
- Export citation
On Eddington's higher order equations of the gravitational field
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 8 / Issue 2 / October 1948
- Published online by Cambridge University Press:
- 20 January 2009, pp. 89-94
-
- Article
-
- You have access
- Export citation
The Thermodynamics of Fluid Systems. By L. C. WOODS. Clarendon Press (Oxford University Press), 1975. 359 pp. £15.00.
-
- Journal:
- Journal of Fluid Mechanics / Volume 83 / Issue 1 / 1 November 1977
- Published online by Cambridge University Press:
- 12 April 2006, pp. 207-208
-
- Article
- Export citation
Remark on the theorem of Carathéodory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 76 / Issue 3 / November 1974
- Published online by Cambridge University Press:
- 24 October 2008, pp. 529-530
- Print publication:
- November 1974
-
- Article
- Export citation
Quadratic Langrangians and static gravitational fields
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 74 / Issue 1 / July 1973
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-148
- Print publication:
- July 1973
-
- Article
- Export citation
On functionally constant invariants of the Riemann tensor
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 68 / Issue 1 / July 1970
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-185
- Print publication:
- July 1970
-
- Article
- Export citation
ε- and γ-formalisms in the calculus of 4-spinors
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 67 / Issue 1 / January 1970
- Published online by Cambridge University Press:
- 24 October 2008, pp. 123-126
- Print publication:
- January 1970
-
- Article
- Export citation
The relativistic incompressible sphere
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 8 / Issue 1 / February 1968
- Published online by Cambridge University Press:
- 09 April 2009, pp. 6-16
- Print publication:
- February 1968
-
- Article
-
- You have access
- Export citation
On Rotor calculus, I
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 402-423
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
On Rotor calculus, II
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 6 / Issue 4 / November 1966
- Published online by Cambridge University Press:
- 09 April 2009, pp. 424-448
- Print publication:
- November 1966
-
- Article
-
- You have access
- Export citation
Remark on the defining relation of the σ-symbols
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 5 / Issue 3 / August 1965
- Published online by Cambridge University Press:
- 09 April 2009, pp. 393-395
- Print publication:
- August 1965
-
- Article
-
- You have access
- Export citation
On certain identities involving basic spinors and curvature spinors
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 2 / Issue 3 / February 1962
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-379
- Print publication:
- February 1962
-
- Article
-
- You have access
- Export citation
Non-linear Lagrangians and Palatine's device
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 56 / Issue 4 / October 1960
- Published online by Cambridge University Press:
- 24 October 2008, pp. 396-400
- Print publication:
- October 1960
-
- Article
- Export citation
On the trace of the energy-momentum tensor of fields associated with particles of zero rest mass
-
- Journal:
- Journal of the Australian Mathematical Society (1959) / Volume 1 / Issue 1 / August 1959
- Published online by Cambridge University Press:
- 09 April 2009, pp. 99-105
- Print publication:
- August 1959
-
- Article
-
- You have access
- Export citation





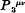 is a linear combination of
is a linear combination of 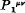 and
and 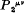 , i.e. of the Hamiltonian derivatives of
, i.e. of the Hamiltonian derivatives of