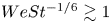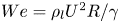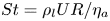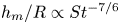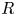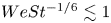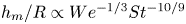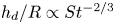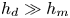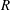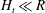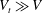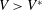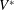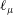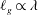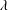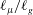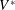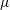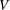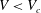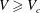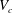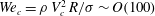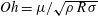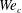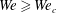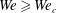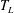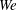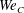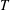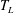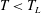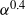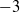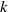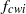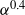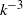12 results
The initial impact of drops cushioned by an air or vapour layer with applications to the dynamic Leidenfrost regime
-
- Journal:
- Journal of Fluid Mechanics / Volume 941 / 25 June 2022
- Published online by Cambridge University Press:
- 25 April 2022, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inclined impact of drops
-
- Journal:
- Journal of Fluid Mechanics / Volume 897 / 25 August 2020
- Published online by Cambridge University Press:
- 10 June 2020, A12
-
- Article
- Export citation
A note on the aerodynamic splashing of droplets
-
- Journal:
- Journal of Fluid Mechanics / Volume 871 / 25 July 2019
- Published online by Cambridge University Press:
- 24 May 2019, R3
-
- Article
- Export citation
Splashing of droplets impacting superhydrophobic substrates
-
- Journal:
- Journal of Fluid Mechanics / Volume 870 / 10 July 2019
- Published online by Cambridge University Press:
- 07 May 2019, pp. 175-188
-
- Article
- Export citation
A theory on the spreading of impacting droplets
-
- Journal:
- Journal of Fluid Mechanics / Volume 866 / 10 May 2019
- Published online by Cambridge University Press:
- 05 March 2019, pp. 298-315
-
- Article
- Export citation
Maximum drop radius and critical Weber number for splashing in the dynamical Leidenfrost regime
-
- Journal:
- Journal of Fluid Mechanics / Volume 803 / 25 September 2016
- Published online by Cambridge University Press:
- 30 August 2016, pp. 516-527
-
- Article
- Export citation
Phase diagram for droplet impact on superheated surfaces
-
- Journal:
- Journal of Fluid Mechanics / Volume 779 / 25 September 2015
- Published online by Cambridge University Press:
- 21 August 2015, R3
-
- Article
- Export citation
The diameters and velocities of the droplets ejected after splashing
-
- Journal:
- Journal of Fluid Mechanics / Volume 772 / 10 June 2015
- Published online by Cambridge University Press:
- 07 May 2015, pp. 630-648
-
- Article
- Export citation
A model of bubble-induced turbulence based on large-scale wake interactions
-
- Journal:
- Journal of Fluid Mechanics / Volume 719 / 25 March 2013
- Published online by Cambridge University Press:
- 19 February 2013, pp. 362-387
-
- Article
- Export citation
Whipping instability characterization of an electrified visco-capillary jet
-
- Journal:
- Journal of Fluid Mechanics / Volume 671 / 25 March 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 226-253
-
- Article
- Export citation
Experimental Characterization of the Whipping Instability of Charged Microjets in Liquid Baths
-
- Journal:
- MRS Online Proceedings Library Archive / Volume 1272 / 2010
- Published online by Cambridge University Press:
- 01 February 2011, 1272-KK05-01
- Print publication:
- 2010
-
- Article
- Export citation
Experimental characterization of the agitation generated by bubbles rising at high Reynolds number
-
- Journal:
- Journal of Fluid Mechanics / Volume 643 / 25 January 2010
- Published online by Cambridge University Press:
- 23 December 2009, pp. 509-539
-
- Article
- Export citation