17 results
One-Relator Groups: An Overview
-
-
- Book:
- Groups St Andrews 2017 in Birmingham
- Published online:
- 15 April 2019
- Print publication:
- 11 April 2019, pp 119-157
-
- Chapter
- Export citation
Something for nothing: some consequences of the solution of the Tarski problems
-
-
- Book:
- Groups St Andrews 2013
- Published online:
- 05 September 2015
- Print publication:
- 22 October 2015, pp 242-270
-
- Chapter
- Export citation
Discriminating groups: a comprehensive overview
-
-
- Book:
- Groups St Andrews 2009 in Bath
- Published online:
- 05 July 2011
- Print publication:
- 16 June 2011, pp 395-414
-
- Chapter
- Export citation
Surface groups within Baumslag doubles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 91-97
-
- Article
-
- You have access
- Export citation
The isomorphism problem for a class of para-free groups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 40 / Issue 3 / October 1997
- Published online by Cambridge University Press:
- 20 January 2009, pp. 541-549
-
- Article
-
- You have access
- Export citation
Minimal generating systems of a subgroup of SL(2, ℂ)
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 31 / Issue 2 / June 1988
- Published online by Cambridge University Press:
- 20 January 2009, pp. 261-265
-
- Article
-
- You have access
- Export citation
Spectral rigidity and discreteness of 2233-groups
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 145-180
- Print publication:
- January 2008
-
- Article
- Export citation
On surface groups: motivating examples in combinatorial group theory
-
-
- Book:
- Groups St Andrews 2005
- Published online:
- 07 May 2010
- Print publication:
- 04 January 2007, pp 96-129
-
- Chapter
- Export citation
Finite generalized tetrahedron groups with a cubic relator
-
-
- Book:
- Groups St Andrews 2001 in Oxford
- Published online:
- 15 December 2009
- Print publication:
- 06 November 2003, pp 455-486
-
- Chapter
- Export citation
Elementary theory of groups
-
-
- Book:
- Groups St Andrews 2001 in Oxford
- Published online:
- 11 January 2010
- Print publication:
- 06 November 2003, pp 197-231
-
- Chapter
- Export citation
Looking Backward, Looking Forward: MLA Members Speak
-
- Journal:
- PMLA / Publications of the Modern Language Association of America / Volume 115 / Issue 7 / December 2000
- Published online by Cambridge University Press:
- 23 October 2020, pp. 1986-2078
- Print publication:
- December 2000
-
- Article
- Export citation
4 - On certain finite generalized tetrahedron groups
-
-
- Book:
- Computational and Geometric Aspects of Modern Algebra
- Published online:
- 06 July 2010
- Print publication:
- 15 June 2000, pp 54-65
-
- Chapter
- Export citation
A property of subgroups of free groups
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 43 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 17 April 2009, pp. 269-272
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
12 - Generalizing algebraic properties of Fuchsian groups
-
-
- Book:
- Groups St Andrews 1989
- Published online:
- 05 April 2013
- Print publication:
- 21 March 1991, pp 124-147
-
- Chapter
- Export citation
Powers of Genus two in Free Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 3 / 01 September 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 342-344
- Print publication:
- 01 September 1990
-
- Article
-
- You have access
- Export citation
Automorphisms of Fuchsian Groups and their Lifts to Free Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 41 / Issue 1 / 01 February 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 123-131
- Print publication:
- 01 February 1989
-
- Article
-
- You have access
- Export citation
19 - Applications of Nielsen's reduction method to the solution of combinatorial problems in group theory: a survey
-
-
- Book:
- Homological Group Theory
- Published online:
- 05 April 2013
- Print publication:
- 27 December 1979, pp 339-358
-
- Chapter
- Export citation



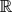 ) generated by four elliptic elements α, β, γ, δ of respective orders 2, 2, 3, 3, satisfying αβγδ = 1. We give a parametrization and a fundamental domain in the parameter space of such groups. Furthermore we construct an algorithm that decides whether or not a given group is discrete and which moves the discrete groups into the fundamental domain. Our main result is that any two discrete such groups are isospectral if and only if they are conjugate in (2,
) generated by four elliptic elements α, β, γ, δ of respective orders 2, 2, 3, 3, satisfying αβγδ = 1. We give a parametrization and a fundamental domain in the parameter space of such groups. Furthermore we construct an algorithm that decides whether or not a given group is discrete and which moves the discrete groups into the fundamental domain. Our main result is that any two discrete such groups are isospectral if and only if they are conjugate in (2, 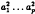 , or that
, or that