15 results
Generalized Bomber and Fighter Problems: Offline Optimal Allocation of a Discrete Asset
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 403-418
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
The Noisy Secretary Problem and Some Results on Extreme Concomitant Variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 821-837
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
The fighter problem: optimal allocation of a discrete commodity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 121-130
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
On optimal allocation of a continuous resource using an iterative approach and total positivity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 795-815
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
The secretary problem of minimizing the expected rank: a simple suboptimal approach with generalizations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1041-1058
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Beat the Mean: Sequential Selection by Better Than Average Rules
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 244-259
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Two-choice optimal stopping
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1116-1147
- Print publication:
- December 2004
-
- Article
- Export citation
Simple ratio prophet inequalities for a mortal with multiple choices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1084-1091
- Print publication:
- December 2000
-
- Article
- Export citation
An unexpected connection between branching processes and optimal stopping
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 613-626
- Print publication:
- September 2000
-
- Article
- Export citation
Optimal multivariate stopping rules
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 693-706
- Print publication:
- September 1998
-
- Article
- Export citation
The secretary problem: minimizing the expected rank with I.I.D. random variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 828-852
- Print publication:
- September 1996
-
- Article
- Export citation
Simple approximations to the expected waiting time for a cluster of any given size, for point processes
-
- Journal:
- Advances in Applied Probability / Volume 15 / Issue 1 / March 1983
- Published online by Cambridge University Press:
- 01 July 2016, pp. 21-38
- Print publication:
- March 1983
-
- Article
- Export citation
Necessary and sufficient conditions for recurrence and transience of Markov chains, in terms of inequalities
-
- Journal:
- Journal of Applied Probability / Volume 15 / Issue 4 / December 1978
- Published online by Cambridge University Press:
- 14 July 2016, pp. 848-851
- Print publication:
- December 1978
-
- Article
- Export citation
Algebraic characterization of infinite Markov chains where movement to the right is limited to one step
-
- Journal:
- Journal of Applied Probability / Volume 14 / Issue 4 / December 1977
- Published online by Cambridge University Press:
- 14 July 2016, pp. 740-747
- Print publication:
- December 1977
-
- Article
- Export citation
Asymptotic distribution for the coupon — collector's and sampling-tagging problems, when tagging affects catchability
-
- Journal:
- Journal of Applied Probability / Volume 12 / Issue 3 / September 1975
- Published online by Cambridge University Press:
- 14 July 2016, pp. 625-628
- Print publication:
- September 1975
-
- Article
- Export citation



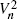 equal the expectation of the smaller of the two values chosen by the statistician when proceeding optimally. We obtain the asymptotic behaviour of the sequence
equal the expectation of the smaller of the two values chosen by the statistician when proceeding optimally. We obtain the asymptotic behaviour of the sequence 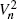 for a large class of
for a large class of 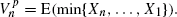 , as well as with the ‘prophet value’ sequence
, as well as with the ‘prophet value’ sequence 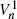
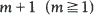 points cluster within an interval of length at most
points cluster within an interval of length at most 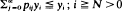 in which
in which 