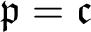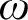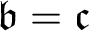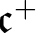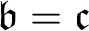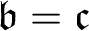1 Introduction
In [Reference Starosolski10], M. E. Rudin proved that, under CH, for each P-point p there exists a P-point q strictly RK-greater than p. A. Blass showed the same [Reference Blass1] assuming that
![]() $\mathfrak {p}=\mathfrak {c}$
;Footnote
1
moreover, he proved that if
$\mathfrak {p}=\mathfrak {c}$
;Footnote
1
moreover, he proved that if
![]() $\mathfrak {p}=\mathfrak {c}$
, then each RK-increasing
$\mathfrak {p}=\mathfrak {c}$
, then each RK-increasing
![]() $\omega $
-sequence of P-points is upper bounded by a P-point, and there exists an order-embedding of the real line into the class of P-points with respect to the RK-ordering. Since then, the RK-ordering of P-points has been thoroughly investigated; however, most of the obtained results were proved under
$\omega $
-sequence of P-points is upper bounded by a P-point, and there exists an order-embedding of the real line into the class of P-points with respect to the RK-ordering. Since then, the RK-ordering of P-points has been thoroughly investigated; however, most of the obtained results were proved under
![]() $MA_{\sigma -\mathrm { centr}}$
, or stronger assumptions,Footnote
2
usually with complicated proofs and using sophisticated techniques. We prove the results mentioned above under
$MA_{\sigma -\mathrm { centr}}$
, or stronger assumptions,Footnote
2
usually with complicated proofs and using sophisticated techniques. We prove the results mentioned above under
![]() $\mathfrak {b}= \mathfrak {c}$
. Perhaps more importantly, we present a method of proof that turns out be effective in the study of P-points under
$\mathfrak {b}= \mathfrak {c}$
. Perhaps more importantly, we present a method of proof that turns out be effective in the study of P-points under
![]() $\mathfrak {b}= \mathfrak {c}$
. The ideas used in the present paper were originally presented in an unpublished paper [Reference Starosolski12], where the RK-ordering concerned the ultrafilters in the classes of the so-called P-hierarchy, the first class of which coincides with that of P-points. The method is based on the use of contours and quasi-subbases, which enables us to employ surprisingly concise arguments, in contrast with the approaches of some other papers on similar topics.
$\mathfrak {b}= \mathfrak {c}$
. The ideas used in the present paper were originally presented in an unpublished paper [Reference Starosolski12], where the RK-ordering concerned the ultrafilters in the classes of the so-called P-hierarchy, the first class of which coincides with that of P-points. The method is based on the use of contours and quasi-subbases, which enables us to employ surprisingly concise arguments, in contrast with the approaches of some other papers on similar topics.
After a scrutiny of mechanisms underlying our proofs, we introduce an apparently new cardinal invariant
![]() $\mathfrak {q}$
, the use of which enables us to weaken the set-theoretic assumptions of most of our results. Finally, we show that
$\mathfrak {q}$
, the use of which enables us to weaken the set-theoretic assumptions of most of our results. Finally, we show that
![]() $\mathfrak {q}$
is an instance of a general method of constructing useful variants of cardinal invariants.
$\mathfrak {q}$
is an instance of a general method of constructing useful variants of cardinal invariants.
In a recent paper, D. Raghavan and S. Shelah [Reference Raghavan and Verner8] proved (under
![]() $\mathfrak {p}=\mathfrak {c}$
) that there is an order-embedding of
$\mathfrak {p}=\mathfrak {c}$
) that there is an order-embedding of
![]() ${ \mathcal {P}}(\omega )/\mathrm {fin\,}$
into the set of P-points ordered by
${ \mathcal {P}}(\omega )/\mathrm {fin\,}$
into the set of P-points ordered by
![]() $\geq _{RK}$
, and gave a short review of earlier results concerning embeddings of different orders into the class of P-points.
$\geq _{RK}$
, and gave a short review of earlier results concerning embeddings of different orders into the class of P-points.
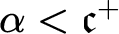
A. Blass also asked [Reference Blass1, Question 4] which ordinals can be embedded in the set of P-points, and pointed out that such an ordinal cannot be greater than
![]() $\mathfrak {c}^{+}$
. We show that under
$\mathfrak {c}^{+}$
. We show that under
![]() $\mathfrak {b}=\mathfrak {c}$
each ordinal less than
$\mathfrak {b}=\mathfrak {c}$
each ordinal less than
![]() $\mathfrak {c}^{+}$
is order-embeddable into P-points. A recent paper by B. Kuzeljević and D. Raghavan [Reference Mathias6] answers the question of the embedding of ordinals into P-points under MA.
$\mathfrak {c}^{+}$
is order-embeddable into P-points. A recent paper by B. Kuzeljević and D. Raghavan [Reference Mathias6] answers the question of the embedding of ordinals into P-points under MA.
2 Tools
A free ultrafilter u is a P-point if and only if, for each partition
![]() $(V_{n})_{n<\omega }$
of
$(V_{n})_{n<\omega }$
of
![]() $\omega $
, there exists a set
$\omega $
, there exists a set
![]() $U\in u$
such that either
$U\in u$
such that either
![]() $U\subset V_{n}$
for some
$U\subset V_{n}$
for some
![]() $n<\omega $
or else
$n<\omega $
or else
![]() $U\cap V_{n}$
is finite for all
$U\cap V_{n}$
is finite for all
![]() $n<\omega $
. A filter
$n<\omega $
. A filter
![]() $\mathcal {F}$
is said to be Rudin–Keisler greater (RK-greater) than a filter
$\mathcal {F}$
is said to be Rudin–Keisler greater (RK-greater) than a filter
![]() $\mathcal {G}$
(written as
$\mathcal {G}$
(written as
![]() $\mathcal {F} \geq _{RK} \mathcal {G}$
) if there exists a map h such that
$\mathcal {F} \geq _{RK} \mathcal {G}$
) if there exists a map h such that
![]() $G \in \mathcal {G}$
if and only if
$G \in \mathcal {G}$
if and only if
![]() $h^{-1}(G)\in \mathcal {F}$
. Let
$h^{-1}(G)\in \mathcal {F}$
. Let
be a partition of a subset of
![]() $\omega $
into infinite sets. A filter
$\omega $
into infinite sets. A filter
![]() $ \mathcal {K}$
is called a contour if there exists a partition
$ \mathcal {K}$
is called a contour if there exists a partition
![]() $ \mathcal {W}$
such that
$ \mathcal {W}$
such that
![]() $K\in \mathcal {K}$
if and only if there is a cofinite set
$K\in \mathcal {K}$
if and only if there is a cofinite set
![]() $ I\subset \omega $
such that
$ I\subset \omega $
such that
![]() $K\cap W_{n}$
is cofinite on
$K\cap W_{n}$
is cofinite on
![]() $W_{n}$
for each
$W_{n}$
for each
![]() $ n\in I$
. We call
$ n\in I$
. We call
![]() $\mathcal {K}$
a contour of
$\mathcal {K}$
a contour of
![]() $\mathcal {W}$
, and denote
$\mathcal {W}$
, and denote
![]() $ \mathcal {K}=\int \mathcal {W}$
.Footnote
3
$ \mathcal {K}=\int \mathcal {W}$
.Footnote
3
A fundamental property used in the present paper is the following reformulation of [Reference Starosolski11, Proposition 2.1].
Proposition 2.1. A free ultrafilter is a P-point if and only if it does not include a contour.
As usual,
![]() $\mathfrak {c}$
denotes the cardinality of the continuum. If
$\mathfrak {c}$
denotes the cardinality of the continuum. If
![]() $f,g\in {{}^{\omega }\omega }$
, then we say that f dominates g (and write
$f,g\in {{}^{\omega }\omega }$
, then we say that f dominates g (and write
![]() $f\geq ^{\ast }g$
) if
$f\geq ^{\ast }g$
) if
![]() $f(n)\leq g(n)$
for almost all
$f(n)\leq g(n)$
for almost all
![]() $n<\omega $
. We say that a family
$n<\omega $
. We say that a family
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() ${{}^{\omega }\omega }$
functions is unbounded if there is no
${{}^{\omega }\omega }$
functions is unbounded if there is no
![]() $g\in {{}^{\omega }\omega }$
that dominates all functions
$g\in {{}^{\omega }\omega }$
that dominates all functions
![]() $f\in \mathcal {F}$
. The minimal cardinality of an unbounded family is the bounding number
$f\in \mathcal {F}$
. The minimal cardinality of an unbounded family is the bounding number
![]() $\mathfrak {b}$
. We also say that a family
$\mathfrak {b}$
. We also say that a family
![]() $\mathcal {F}\subset {{}^{\omega }\omega }$
is dominating if, for each
$\mathcal {F}\subset {{}^{\omega }\omega }$
is dominating if, for each
![]() $g\in {{}^{\omega }\omega }$
, there is some
$g\in {{}^{\omega }\omega }$
, there is some
![]() $f\in \mathcal {F}$
that dominates g. The dominating number
$f\in \mathcal {F}$
that dominates g. The dominating number
![]() $\mathfrak {d} $
is the minimal cardinality of a dominating family. The pseudointersection number
$\mathfrak {d} $
is the minimal cardinality of a dominating family. The pseudointersection number
![]() $\mathfrak {p}$
is the minimal cardinality of a free filter without pseudointersection, which is a set almost included in each element of the filter. Finally, the ultrafilter number
$\mathfrak {p}$
is the minimal cardinality of a free filter without pseudointersection, which is a set almost included in each element of the filter. Finally, the ultrafilter number
![]() $\mathfrak {u }$
is the minimal cardinality of a base of a free ultrafilter. It is well known that
$\mathfrak {u }$
is the minimal cardinality of a base of a free ultrafilter. It is well known that
![]() $\mathfrak {b}\leq \mathfrak {d}\leq \mathfrak {c}$
, and
$\mathfrak {b}\leq \mathfrak {d}\leq \mathfrak {c}$
, and
![]() $\mathfrak {p }\leq \mathfrak {b}\leq \mathfrak {u}\leq \mathfrak {c}$
, and that there are models for which
$\mathfrak {p }\leq \mathfrak {b}\leq \mathfrak {u}\leq \mathfrak {c}$
, and that there are models for which
![]() $\mathfrak {p}<\mathfrak {b}$
(see, for example, [Reference Kuzeljević and Raghavan5]).
$\mathfrak {p}<\mathfrak {b}$
(see, for example, [Reference Kuzeljević and Raghavan5]).
We say that a family
![]() $\mathcal {A}$
is centered (has fip) if the intersection of any finite subfamily is nonempty; a family
$\mathcal {A}$
is centered (has fip) if the intersection of any finite subfamily is nonempty; a family
![]() $\mathcal {A}$
is strongly centered (has sfip) if the intersection of any finite subfamily is infinite. If
$\mathcal {A}$
is strongly centered (has sfip) if the intersection of any finite subfamily is infinite. If
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are families of sets, then we say that
$\mathcal {B}$
are families of sets, then we say that
![]() $ \mathcal {A}$
and
$ \mathcal {A}$
and
![]() $\mathcal {B}$
are compatible if
$\mathcal {B}$
are compatible if
![]() $\mathcal {A} \cup \mathcal {B}$
is centered. If
$\mathcal {A} \cup \mathcal {B}$
is centered. If
![]() $\mathcal {A} = \{A\}$
we say that A is compatible with
$\mathcal {A} = \{A\}$
we say that A is compatible with
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
If a family
![]() $\mathcal {A}$
is centered, then we denote by
$\mathcal {A}$
is centered, then we denote by
![]() $\langle \mathcal {A}\rangle $
the filter generated by
$\langle \mathcal {A}\rangle $
the filter generated by
![]() $\mathcal {A}$
. Let A be an infinite subset of
$\mathcal {A}$
. Let A be an infinite subset of
![]() $\omega $
. A filter
$\omega $
. A filter
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\omega $
is said to be cofinite on A whenever
$\omega $
is said to be cofinite on A whenever
![]() $U\in \mathcal {F}$
if and only if
$U\in \mathcal {F}$
if and only if
![]() $ A\setminus U$
is finite. A filter
$ A\setminus U$
is finite. A filter
![]() $\mathcal {F}$
is said to be cofinite if it is cofinite on some
$\mathcal {F}$
is said to be cofinite if it is cofinite on some
![]() $A \subset \omega $
. It is well-known that a filter is free on A if and only if it includes the cofinite filter of A.
$A \subset \omega $
. It is well-known that a filter is free on A if and only if it includes the cofinite filter of A.
2.1 A relation between sets and functions
Let
![]() $\mathcal {W}$
be a partition (1). For each
$\mathcal {W}$
be a partition (1). For each
![]() $n<\omega $
, let
$n<\omega $
, let
 $\left ( w_{k}^{n}\right ) _{k<\omega }$
be an increasing sequence such that
$\left ( w_{k}^{n}\right ) _{k<\omega }$
be an increasing sequence such that
For each
![]() $f\in {{}^{\omega }\omega }$
and
$f\in {{}^{\omega }\omega }$
and
![]() $m<\omega $
, let
$m<\omega $
, let
If
![]() $F\in \int \mathcal {W}$
, then, by definition, there exists the least
$F\in \int \mathcal {W}$
, then, by definition, there exists the least
![]() $ n_{F}<\omega $
such that
$ n_{F}<\omega $
such that
![]() $W_{n}\setminus F$
is finite for each
$W_{n}\setminus F$
is finite for each
![]() $n\geq n_{F}$
. Now, for each
$n\geq n_{F}$
. Now, for each
![]() $n\geq n_{F}$
, there exists a minimal
$n\geq n_{F}$
, there exists a minimal
![]() $k_{n}<\omega $
such that
$k_{n}<\omega $
such that
![]() $w_{k}^{n}\in F$
for each
$w_{k}^{n}\in F$
for each
![]() $k\geq k_{n}$
. Let
$k\geq k_{n}$
. Let
![]() ${f f}_{F}$
denote the set of those functions f for which
${f f}_{F}$
denote the set of those functions f for which
Then
![]() $E_{\mathcal {W}}\left ( f,n_{F}\right ) $
is the same for each
$E_{\mathcal {W}}\left ( f,n_{F}\right ) $
is the same for each
![]() $f\in {f f}_{F}$
, and it is the largest set of the form (2) included in F. Sure enough,
$f\in {f f}_{F}$
, and it is the largest set of the form (2) included in F. Sure enough,
![]() $E_{\mathcal {W} }\left ( f_{F},n_{F}\right ) \in \int \mathcal {W}$
.
$E_{\mathcal {W} }\left ( f_{F},n_{F}\right ) \in \int \mathcal {W}$
.
Conversely, for every function
![]() $f\in {{}^{\omega }\omega }$
, we define a family
$f\in {{}^{\omega }\omega }$
, we define a family
![]() $\mathcal {W}_{f}$
of subsets of
$\mathcal {W}_{f}$
of subsets of
![]() $\omega $
as follows:
$\omega $
as follows:
![]() $F\in \mathcal {W }_{f}$
if there is
$F\in \mathcal {W }_{f}$
if there is
![]() $n_{F}<\omega $
such that
$n_{F}<\omega $
such that
![]() $F=E_{\mathcal {W}} \left ( f_{F},n_{F}\right ) $
. Therefore, we can state the following.
$F=E_{\mathcal {W}} \left ( f_{F},n_{F}\right ) $
. Therefore, we can state the following.
Proposition 2.2. The family
 $\bigcup _{f\in {{}^{\omega }\omega }}\mathcal {W}_{f}$
is a base of
$\bigcup _{f\in {{}^{\omega }\omega }}\mathcal {W}_{f}$
is a base of
![]() $\int \mathcal {W}$
.
$\int \mathcal {W}$
.
2.2 Quasi-subbases
We say that a family
![]() $\mathcal {A}$
is finer than
$\mathcal {A}$
is finer than
![]() $\mathcal {B}$
if
$\mathcal {B}$
if
![]() $\langle \mathcal {B}\rangle \subset \langle \mathcal {A} \rangle $
. Moreover,
$\langle \mathcal {B}\rangle \subset \langle \mathcal {A} \rangle $
. Moreover,
![]() $\mathcal {A}$
is called a quasi-subbase of (a filter)
$\mathcal {A}$
is called a quasi-subbase of (a filter)
![]() $\mathcal {F}$
if there exists a countable family
$\mathcal {F}$
if there exists a countable family
![]() $\mathcal {C}$
such that
$\mathcal {C}$
such that
![]() $\langle \mathcal {A}\cup \mathcal {C}\rangle =\mathcal {F}$
. Accordingly,
$\langle \mathcal {A}\cup \mathcal {C}\rangle =\mathcal {F}$
. Accordingly,
![]() $\mathcal {A}$
is quasi-finer than
$\mathcal {A}$
is quasi-finer than
![]() $\mathcal {B}$
if there exists a countable family
$\mathcal {B}$
if there exists a countable family
![]() $\mathcal {C}$
such that
$\mathcal {C}$
such that
![]() $\mathcal {A} \cup \mathcal {C}$
is centered and
$\mathcal {A} \cup \mathcal {C}$
is centered and
![]() $ \mathcal {B} \subset \langle \mathcal {A}\cup \mathcal {C}\rangle $
. Finally we say that a family is a
$ \mathcal {B} \subset \langle \mathcal {A}\cup \mathcal {C}\rangle $
. Finally we say that a family is a
![]() $P^+$
-family if it is quasi-finer than no contour.
$P^+$
-family if it is quasi-finer than no contour.
If
![]() $\mathcal {W}$
is a partition (1), then for each
$\mathcal {W}$
is a partition (1), then for each
![]() $ i<\omega $
, let
$ i<\omega $
, let
 $$ \begin{align*} {\widetilde{W}_{i}=}\bigcup_{n\geq i}W_{n}\text{ and }\widetilde{\mathcal{W}} =\{{\widetilde{W}_{i}}:i<\omega \}. \end{align*} $$
$$ \begin{align*} {\widetilde{W}_{i}=}\bigcup_{n\geq i}W_{n}\text{ and }\widetilde{\mathcal{W}} =\{{\widetilde{W}_{i}}:i<\omega \}. \end{align*} $$
Proposition 2.3. Let
![]() $\mathcal {W}$
be a partition and let
$\mathcal {W}$
be a partition and let
![]() $\mathcal {A}$
be a centered family. Then the following are equivalent
$\mathcal {A}$
be a centered family. Then the following are equivalent
![]() $:$
$:$
![]() $(1) \mathcal {A}$
is quasi-finer than
$(1) \mathcal {A}$
is quasi-finer than
![]() $\int \mathcal {W}$
,
$\int \mathcal {W}$
,
![]() $(2)$
there exists a set D such that
$(2)$
there exists a set D such that
 $\mathcal {A}\cup \widetilde {\mathcal {W}} \cup \{D\}$
is centered, and
$\mathcal {A}\cup \widetilde {\mathcal {W}} \cup \{D\}$
is centered, and
 $\int {\mathcal {W}}\subset \langle \mathcal {A}\cup \widetilde {\mathcal {W}}\cup \{D\}\rangle $
.
$\int {\mathcal {W}}\subset \langle \mathcal {A}\cup \widetilde {\mathcal {W}}\cup \{D\}\rangle $
.
Proof. The implication
![]() $2\Rightarrow 1$
is evident. We will show
$2\Rightarrow 1$
is evident. We will show
![]() $1\Rightarrow 2$
. Suppose the contrary, and let
$1\Rightarrow 2$
. Suppose the contrary, and let
![]() $\mathcal {B}$
be a countable family of sets such that
$\mathcal {B}$
be a countable family of sets such that
![]() $\int \mathcal {W}\subset \langle \mathcal {A}\cup \mathcal {B }\rangle $
. Taking finite intersections
$\int \mathcal {W}\subset \langle \mathcal {A}\cup \mathcal {B }\rangle $
. Taking finite intersections
 $\bigcap _{i\leq n}B_{i}$
instead of
$\bigcap _{i\leq n}B_{i}$
instead of
![]() $ B_{n},$
we obtain a decreasing sequence so that, without loss of generality, we can assume that
$ B_{n},$
we obtain a decreasing sequence so that, without loss of generality, we can assume that
![]() $\mathcal {B}=\{B_{n}\}_{n<\omega }$
is decreasing. Since (2) is false, for each n there exists
$\mathcal {B}=\{B_{n}\}_{n<\omega }$
is decreasing. Since (2) is false, for each n there exists
![]() $A_{n}\in \int \mathcal {W}$
such that
$A_{n}\in \int \mathcal {W}$
such that
 $ A_{n}\not \in \langle \mathcal {A}\cup \widetilde {\mathcal {W}}\cup \{B_{n}\}\rangle $
.
$ A_{n}\not \in \langle \mathcal {A}\cup \widetilde {\mathcal {W}}\cup \{B_{n}\}\rangle $
.
Without loss of generality, for each n there is
![]() $k(n)\geq n$
such that
$k(n)\geq n$
such that
![]() $ A_{n}\cap W_{i}$
is empty for all
$ A_{n}\cap W_{i}$
is empty for all
![]() $i<k(n)$
and
$i<k(n)$
and
![]() $W_{i}\setminus A_{n}$
is finite for all
$W_{i}\setminus A_{n}$
is finite for all
![]() $i\geq k(n)$
. Define
$i\geq k(n)$
. Define
 $A_{\infty }=\bigcup _{i<\omega }\left ( \bigcap _{\{n:k(n)\leq i\}}A_{n}\cap W_{i}\right ) $
and note that
$A_{\infty }=\bigcup _{i<\omega }\left ( \bigcap _{\{n:k(n)\leq i\}}A_{n}\cap W_{i}\right ) $
and note that
![]() $A_{\infty }\in \int \mathcal {W}$
.
$A_{\infty }\in \int \mathcal {W}$
.
We will show that
 $A_{\infty }\not \in \langle \mathcal {A}\cup \mathcal {B} \cup \widetilde {\mathcal {W}}\rangle \supset \langle \mathcal {A}\cup \mathcal { B}\rangle $
. For this purpose, it suffices to show that
$A_{\infty }\not \in \langle \mathcal {A}\cup \mathcal {B} \cup \widetilde {\mathcal {W}}\rangle \supset \langle \mathcal {A}\cup \mathcal { B}\rangle $
. For this purpose, it suffices to show that
 $A_{\infty }\not \in \langle \mathcal {A}\cup \widetilde {\mathcal {W}}\cup \{B_{n}\}\rangle $
for each
$A_{\infty }\not \in \langle \mathcal {A}\cup \widetilde {\mathcal {W}}\cup \{B_{n}\}\rangle $
for each
![]() $n<\omega $
. Indeed, note that
$n<\omega $
. Indeed, note that
 $A_{\infty }\subset A_{n}\cup \widetilde { W}_{k(n)}^{c}$
for each
$A_{\infty }\subset A_{n}\cup \widetilde { W}_{k(n)}^{c}$
for each
![]() $n<\omega $
. From
$n<\omega $
. From
 $(A_{n}\cup \widetilde {W} _{k(n)}^{c})\cap \widetilde {W}_{k(n)}\subset A_{n}\not \in \langle \mathcal {A} \cup \widetilde {\mathcal {W}}\cup \{B_{n}\}\rangle $
, we infer that
$(A_{n}\cup \widetilde {W} _{k(n)}^{c})\cap \widetilde {W}_{k(n)}\subset A_{n}\not \in \langle \mathcal {A} \cup \widetilde {\mathcal {W}}\cup \{B_{n}\}\rangle $
, we infer that
 $ (A_{n}\cup \widetilde {W}_{k(n)}^{c})\not \in \langle \mathcal {A}\cup \widetilde {\mathcal {W}}\cup \{B_{n}\}\rangle $
, and so
$ (A_{n}\cup \widetilde {W}_{k(n)}^{c})\not \in \langle \mathcal {A}\cup \widetilde {\mathcal {W}}\cup \{B_{n}\}\rangle $
, and so
 $A_{\infty }\not \in \langle \mathcal {A}\cup \widetilde {\mathcal {W}}\cup \{B_{n}\}\rangle $
.⊣
$A_{\infty }\not \in \langle \mathcal {A}\cup \widetilde {\mathcal {W}}\cup \{B_{n}\}\rangle $
.⊣
Remark 2.4. Let
![]() $\mathcal {A}$
be finer than
$\mathcal {A}$
be finer than
![]() $\int \mathcal {W}$
. Then there exists a partition
$\int \mathcal {W}$
. Then there exists a partition
![]() $\mathcal {V}$
such that
$\mathcal {V}$
such that
 $\int \mathcal {V}\subset \langle \mathcal {A}\cup \widetilde {\mathcal {V}}\rangle $
.
$\int \mathcal {V}\subset \langle \mathcal {A}\cup \widetilde {\mathcal {V}}\rangle $
.
Proof. Take
![]() $V_i$
to be the i-th infinite
$V_i$
to be the i-th infinite
![]() $W_j \cap D$
, with D from Proposition 2.3(2).
$W_j \cap D$
, with D from Proposition 2.3(2).
Theorem 2.5. Let
![]() $(\mathcal {A}_{\alpha })_{\alpha <\beta <\mathfrak {b}}$
be an increasing sequence of
$(\mathcal {A}_{\alpha })_{\alpha <\beta <\mathfrak {b}}$
be an increasing sequence of
![]() $P^+$
-families. Then,
$P^+$
-families. Then,
 $\bigcup _{\alpha <\beta }\mathcal {A} _{\alpha }$
is a
$\bigcup _{\alpha <\beta }\mathcal {A} _{\alpha }$
is a
![]() $P^+$
-family.
$P^+$
-family.
Proof. By way of contradiction,
![]() $\{\mathcal {A}_{\alpha }\}_{\alpha <\beta < \mathfrak {b}}$
be as in the assumptions, and let
$\{\mathcal {A}_{\alpha }\}_{\alpha <\beta < \mathfrak {b}}$
be as in the assumptions, and let
![]() $\int \mathcal {W}$
be a contour and
$\int \mathcal {W}$
be a contour and
![]() $\mathcal {B}$
be a countable family of sets such that
$\mathcal {B}$
be a countable family of sets such that
![]() $\int \mathcal {W}\subset \langle \mathcal {A}\cup \mathcal {B}\rangle $
. By Proposition 2.3 and Remark 2.4, without loss of generality, we may assume that
$\int \mathcal {W}\subset \langle \mathcal {A}\cup \mathcal {B}\rangle $
. By Proposition 2.3 and Remark 2.4, without loss of generality, we may assume that
 $\mathcal {B}=\{B_{n}\}_{n<\omega }=\widetilde {\mathcal {W}} $
is decreasing. Let
$\mathcal {B}=\{B_{n}\}_{n<\omega }=\widetilde {\mathcal {W}} $
is decreasing. Let
![]() $\mathcal {C}_{\alpha }=\langle \mathcal {A_{\alpha }} \cup \mathcal {B}\rangle $
. Clearly
$\mathcal {C}_{\alpha }=\langle \mathcal {A_{\alpha }} \cup \mathcal {B}\rangle $
. Clearly
![]() $\mathcal {C}_{\alpha }$
does not include
$\mathcal {C}_{\alpha }$
does not include
![]() $\int \mathcal {W}$
for each
$\int \mathcal {W}$
for each
![]() $\alpha <\beta $
. Thus, for each
$\alpha <\beta $
. Thus, for each
![]() $\alpha <\beta $
, there exists a set
$\alpha <\beta $
, there exists a set
![]() $D_{\alpha }\in \int \mathcal {W}$
such that
$D_{\alpha }\in \int \mathcal {W}$
such that
![]() $D_{\alpha }\not \in \mathcal {C}_{\alpha }$
. Let
$D_{\alpha }\not \in \mathcal {C}_{\alpha }$
. Let
![]() $g_{\alpha }\in {f\hspace {-0.45em}f} _{D_{\alpha }}$
for each
$g_{\alpha }\in {f\hspace {-0.45em}f} _{D_{\alpha }}$
for each
![]() $\alpha <\beta $
. As
$\alpha <\beta $
. As
![]() $\beta <\mathfrak {b}$
, the family
$\beta <\mathfrak {b}$
, the family
![]() $\{g_{\alpha }\}_{\alpha <\beta }$
is bounded by some function g. Let
$\{g_{\alpha }\}_{\alpha <\beta }$
is bounded by some function g. Let
![]() $G\in \mathcal {W}_{g}$
. We will show that
$G\in \mathcal {W}_{g}$
. We will show that
 $G\not \in \bigcup _{\alpha <\beta }\mathcal {C}_{\alpha }$
, hence
$G\not \in \bigcup _{\alpha <\beta }\mathcal {C}_{\alpha }$
, hence
![]() $G\not \in \mathcal {C}_{\alpha }$
for each
$G\not \in \mathcal {C}_{\alpha }$
for each
![]() $\alpha <\beta $
. Suppose not, and let
$\alpha <\beta $
. Suppose not, and let
![]() $\alpha _{0}$
be a witness. By construction, there exists
$\alpha _{0}$
be a witness. By construction, there exists
![]() $n_{0}<\omega $
such that
$n_{0}<\omega $
such that
![]() $G\subset B_{n_{0}}^{c}\cup D_{\alpha _{0}}$
. As
$G\subset B_{n_{0}}^{c}\cup D_{\alpha _{0}}$
. As
 $(D_{\alpha _{0}}\cup B_{n_{0}}^{c})\cap B_{n_{0}}\subset D_{\alpha _{0}}\not \in \mathcal {C} _{\alpha _{0}}$
, it follows that
$(D_{\alpha _{0}}\cup B_{n_{0}}^{c})\cap B_{n_{0}}\subset D_{\alpha _{0}}\not \in \mathcal {C} _{\alpha _{0}}$
, it follows that
![]() $D_{\alpha _{0}}\cup B_{n_{0}}^{c}\not \in \mathcal {C}_{\alpha _{0}}$
, and so
$D_{\alpha _{0}}\cup B_{n_{0}}^{c}\not \in \mathcal {C}_{\alpha _{0}}$
, and so
![]() $G\not \in \mathcal {C}_{\alpha _{0}}$
.⊣
$G\not \in \mathcal {C}_{\alpha _{0}}$
.⊣
The anonymous referee noticed that Corollary 2.6 easily follows from [Reference Raghavan and Shelah7, Proposition 2.28] by A. R. D. Mathias by argument pointed out in Mathias’ proof. One can also prove Corollary 2.6 inductively using Theorem 2.5 and Proposition 2.1.
Corollary 2.6 [Reference Raghavan and Shelah7]
 $(\mathfrak {b}=\mathfrak {c})$
$(\mathfrak {b}=\mathfrak {c})$
If
![]() $\mathcal {A}$
is a strongly centered
$\mathcal {A}$
is a strongly centered
![]() $P^+$
-family of subsets of
$P^+$
-family of subsets of
![]() $\omega $
, then there exists a P-point p such that
$\omega $
, then there exists a P-point p such that
![]() $\mathcal {A}\subset p$
.
$\mathcal {A}\subset p$
.
Let us recall a well-known theorem (see, for example, [Reference Blass1, Corollary 1]).
Theorem 2.7. Let u be an ultrafilter. If
![]() $f(u)=_{RK}u$
, then there exists
$f(u)=_{RK}u$
, then there exists
![]() $U\in u$
such that f is one-to-one on U.
$U\in u$
such that f is one-to-one on U.
3 Applications: RK-ordering of P-points
M. E. Rudin [Reference Starosolski10] proved that, under CH, for each P-point p there exists a P-point q strictly RK-greater than p. Some years later, A. Blass [Reference Blass1, Theorem 6] proved this theorem under
![]() $\mathfrak {p}=\mathfrak {c}$
.
$\mathfrak {p}=\mathfrak {c}$
.
The referee also noticed that Theorem 3.1 is easily derivable from [Reference Raghavan and Shelah7, Proposition 2.28] by A. R. D. Mathias combined with [Reference Blass1, Theorem 6] by A. Blass. Nevertheless we present our original proof because its methods will be used in the sequel.
Theorem 3.1.
![]() $(\mathfrak {b}=\mathfrak {c})$
.Footnote
4
If p is a P-point, then there exists a P-point q that is strictly Rudin–Keisler greater than p.
$(\mathfrak {b}=\mathfrak {c})$
.Footnote
4
If p is a P-point, then there exists a P-point q that is strictly Rudin–Keisler greater than p.
Proof. Let
![]() $f\in {{}^{\omega }\omega }$
be a finite-to-one function such that
$f\in {{}^{\omega }\omega }$
be a finite-to-one function such that
 $$ \begin{align*} \limsup\nolimits_{n\in P}\mathrm{card\,}(f^{-1}(n))=\infty \end{align*} $$
$$ \begin{align*} \limsup\nolimits_{n\in P}\mathrm{card\,}(f^{-1}(n))=\infty \end{align*} $$
holds for all
![]() $P\in p$
. We define a family
$P\in p$
. We define a family
![]() $\mathcal {A}$
as follows:
$\mathcal {A}$
as follows:
![]() $A\in \mathcal {A}$
if and only if there exist
$A\in \mathcal {A}$
if and only if there exist
![]() $i<\omega $
and
$i<\omega $
and
![]() $P\in p$
such that
$P\in p$
such that
![]() $\mathrm { card\,}(f^{-1}(n)\setminus A)<i$
for each
$\mathrm { card\,}(f^{-1}(n)\setminus A)<i$
for each
![]() $n\in P$
. Then, Theorem 2.7 ensures that the ultrafilters we are building are strictly RK-greater than
$n\in P$
. Then, Theorem 2.7 ensures that the ultrafilters we are building are strictly RK-greater than
![]() $p $
.
$p $
.
We claim that
 $\left \{ f^{-1}(p)\right \} \cup \mathcal {A}$
is a
$\left \{ f^{-1}(p)\right \} \cup \mathcal {A}$
is a
![]() $P^+$
-family. Suppose not, and take a witness
$P^+$
-family. Suppose not, and take a witness
![]() $\int \mathcal { W}$
. From Remark 2.4, without loss of generality, we may assume that
$\int \mathcal { W}$
. From Remark 2.4, without loss of generality, we may assume that
 $\int {\mathcal {W}}\subset \langle f^{-1}(p)\cup \mathcal {A}\cup \widetilde {\mathcal {W}}\rangle $
. Consider two cases:
$\int {\mathcal {W}}\subset \langle f^{-1}(p)\cup \mathcal {A}\cup \widetilde {\mathcal {W}}\rangle $
. Consider two cases:
Case 1: There exists a sequence
![]() $(B_{n})_{n<\omega }$
and a strictly increasing
$(B_{n})_{n<\omega }$
and a strictly increasing
![]() $k\in {{}^{\omega }\omega }$
such that
$k\in {{}^{\omega }\omega }$
such that
![]() $B_{n}\subset W_{k(n)}$
,
$B_{n}\subset W_{k(n)}$
,
![]() $ f(B_{n})\not \in p$
, and B is compatible with
$ f(B_{n})\not \in p$
, and B is compatible with
 $f^{-1}(p)\cup \mathcal {A} \cup \widetilde { \mathcal {W}}$
, where
$f^{-1}(p)\cup \mathcal {A} \cup \widetilde { \mathcal {W}}$
, where
![]() $B=\bigcup _{n<\omega }B_{n}$
. Take a sequence
$B=\bigcup _{n<\omega }B_{n}$
. Take a sequence
 $ (f(\bigcup _{i\leq n}B_{n}))_{n<\omega }$
. This is an increasing sequence, and it is clear that
$ (f(\bigcup _{i\leq n}B_{n}))_{n<\omega }$
. This is an increasing sequence, and it is clear that
 $\bigcup _{n<\omega }f(\bigcup _{i\leq n}B_{n})=f(B)\in p$
. Make a partition of
$\bigcup _{n<\omega }f(\bigcup _{i\leq n}B_{n})=f(B)\in p$
. Make a partition of
![]() $f(B)$
by taking
$f(B)$
by taking
 $f(\bigcup _{n\leq i+1}B_{n})\setminus f(\bigcup _{n\leq i}B_{n})$
for
$f(\bigcup _{n\leq i+1}B_{n})\setminus f(\bigcup _{n\leq i}B_{n})$
for
![]() $i<\omega $
. As p is a P-point, there exists some
$i<\omega $
. As p is a P-point, there exists some
![]() $P\in p$
such that
$P\in p$
such that
 $P\cap (f(\bigcup _{n\leq i+1}B_{n})\setminus f(\bigcup _{n\leq i}B_{n}))$
is finite for all
$P\cap (f(\bigcup _{n\leq i+1}B_{n})\setminus f(\bigcup _{n\leq i}B_{n}))$
is finite for all
![]() $i<\omega $
, and thus
$i<\omega $
, and thus
![]() $ f^{-1}(P)\cap B_{n}$
is finite for all
$ f^{-1}(P)\cap B_{n}$
is finite for all
![]() $i<\omega $
. Therefore,
$i<\omega $
. Therefore,
![]() $ f^{-1}(P)\cap W_{i}\cap B$
is finite, and thus
$ f^{-1}(P)\cap W_{i}\cap B$
is finite, and thus
![]() $(f^{-1}(P)\cap B)^{c}\in \int \mathcal {W}$
, which means that
$(f^{-1}(P)\cap B)^{c}\in \int \mathcal {W}$
, which means that
![]() $\int {\mathcal {W}}$
is not compatible with
$\int {\mathcal {W}}$
is not compatible with
![]() $\langle f^{-1}(p)\cup \{B\}\rangle $
.
$\langle f^{-1}(p)\cup \{B\}\rangle $
.
Case 2: Otherwise without loss of generality
![]() $f(W_{i})\in p$
for each
$f(W_{i})\in p$
for each
![]() $ i<\omega $
, since we are not in Case 1. Define sets
$ i<\omega $
, since we are not in Case 1. Define sets
![]() $V_{1}=W_{1}$
,
$V_{1}=W_{1}$
,
 $ V_{i}=W_{j}\cap f^{-1}(\bigcap _{k<i}f(W_{k}))$
, and note that
$ V_{i}=W_{j}\cap f^{-1}(\bigcap _{k<i}f(W_{k}))$
, and note that
 $ \bigcup _{i<\omega }V_{i}\in \langle \mathcal {A}\cup f^{-1}(p)\rangle $
since we are not in Case 1. Then,
$ \bigcup _{i<\omega }V_{i}\in \langle \mathcal {A}\cup f^{-1}(p)\rangle $
since we are not in Case 1. Then,
![]() $(f(V_{i}))_{i<\omega }$
is a decreasing sequence, and because f is finite-to-one,
$(f(V_{i}))_{i<\omega }$
is a decreasing sequence, and because f is finite-to-one,
![]() $(f(V_{i})\setminus f(V_{i+1}))_{i<\omega }$
is a partition of
$(f(V_{i})\setminus f(V_{i+1}))_{i<\omega }$
is a partition of
![]() $f(V_{1})\in p$
. As p is a P-point, there exists
$f(V_{1})\in p$
. As p is a P-point, there exists
![]() $P\in p$
such that
$P\in p$
such that
![]() $P_{i}=(f(V_{i})\setminus f(V_{i+1}))\cap P$
is finite for each
$P_{i}=(f(V_{i})\setminus f(V_{i+1}))\cap P$
is finite for each
![]() $i<\omega $
. Let
$i<\omega $
. Let
![]() $g:\omega \rightarrow \omega $
be defined by
$g:\omega \rightarrow \omega $
be defined by
 $g(i)=E\left ( \frac {i+1}{2}\right ) $
, where
$g(i)=E\left ( \frac {i+1}{2}\right ) $
, where
![]() $E\left ( x\right ) $
stands for the integer part of x. Let
$E\left ( x\right ) $
stands for the integer part of x. Let
 $$ \begin{align*} R=\bigcup\nolimits_{i<\omega }(f^{-1}(P_{i})\cap \bigcup\nolimits_{j\in \lbrack g(i),...,i]}V_{i}). \end{align*} $$
$$ \begin{align*} R=\bigcup\nolimits_{i<\omega }(f^{-1}(P_{i})\cap \bigcup\nolimits_{j\in \lbrack g(i),...,i]}V_{i}). \end{align*} $$
Note that
![]() $R\cap V_{i}$
is finite for each
$R\cap V_{i}$
is finite for each
![]() $i<\omega $
, and that
$i<\omega $
, and that
 $$ \begin{align*} \limsup\nolimits_{n\in \tilde{P}}\mathrm{card\,}(f^{-1}(n)\cap R)=\infty \end{align*} $$
$$ \begin{align*} \limsup\nolimits_{n\in \tilde{P}}\mathrm{card\,}(f^{-1}(n)\cap R)=\infty \end{align*} $$
for all
![]() $\tilde {P}\in p$
and
$\tilde {P}\in p$
and
![]() $\tilde {P}\subset P$
. Thus,
$\tilde {P}\subset P$
. Thus,
 $R^{c}\not \in \langle \mathcal {A}\cup f^{-1}(p)\cup \widetilde {\mathcal {W}}\rangle $
, although
$R^{c}\not \in \langle \mathcal {A}\cup f^{-1}(p)\cup \widetilde {\mathcal {W}}\rangle $
, although
![]() $R^{c}\in \int \mathcal {W}$
, which completes Case 2.
$R^{c}\in \int \mathcal {W}$
, which completes Case 2.
To complete the proof of the theorem use Corollary 2.6.⊣
The following two, probably known, facts will be needed for Theorem 3.4 that extends, under CH, Theorem 3.1.
Fact 3.2. Let
![]() $\mathcal {A}$
be a centered family of subsets of
$\mathcal {A}$
be a centered family of subsets of
![]() $\omega $
such that
$\omega $
such that
![]() $\mathcal {A} \cup \{F\}$
is not an ultrafilter subbase for any F compatible with
$\mathcal {A} \cup \{F\}$
is not an ultrafilter subbase for any F compatible with
![]() $ \mathcal {A}$
. Let
$ \mathcal {A}$
. Let
![]() $\mathcal {F}$
be a countable family compatible with
$\mathcal {F}$
be a countable family compatible with
![]() $\mathcal {A}$
. Then
$\mathcal {A}$
. Then
![]() $\mathcal {A} \cup \mathcal {F}$
is not an ultrafilter subbase.
$\mathcal {A} \cup \mathcal {F}$
is not an ultrafilter subbase.
Proof. Without loss of generality, we may assume that
![]() $(F_{n})_{n<\omega }$
is a decreasing sequence of sets, such that
$(F_{n})_{n<\omega }$
is a decreasing sequence of sets, such that
![]() $F_{n+1}\not \in \langle \mathcal {A} \cup \{F_{n}\}\rangle $
. Put
$F_{n+1}\not \in \langle \mathcal {A} \cup \{F_{n}\}\rangle $
. Put
![]() $B_{n}=F_{n}\setminus F_{n+1}$
and define
$B_{n}=F_{n}\setminus F_{n+1}$
and define
 $ B^1=\bigcup _{n<\omega }B_{2n}$
,
$ B^1=\bigcup _{n<\omega }B_{2n}$
,
 $B^2=\bigcup _{n<\omega }B_{2n+1}$
. Clearly at least one of sets
$B^2=\bigcup _{n<\omega }B_{2n+1}$
. Clearly at least one of sets
![]() $B^1$
,
$B^1$
,
![]() $B^2$
interact
$B^2$
interact
![]() $\mathcal {A}$
—say
$\mathcal {A}$
—say
![]() $B_1$
does. If
$B_1$
does. If
![]() $B^1\not \in \langle \mathcal {A}\cup \mathcal {F}\rangle $
then we are done. Suppose that
$B^1\not \in \langle \mathcal {A}\cup \mathcal {F}\rangle $
then we are done. Suppose that
![]() $B^1\in \langle \mathcal {A}\cup \mathcal {F}\rangle $
, and denote by
$B^1\in \langle \mathcal {A}\cup \mathcal {F}\rangle $
, and denote by
![]() $n_{0}$
, the minimal
$n_{0}$
, the minimal
![]() $n<\omega $
that
$n<\omega $
that
![]() $B^1\in \langle \mathcal {A} \cup \{F_{n}\}\rangle $
. But
$B^1\in \langle \mathcal {A} \cup \{F_{n}\}\rangle $
. But
 $F_{n_{0}+1}\cap B^1=F_{n_{0}+2}\cap B^1$
and so
$F_{n_{0}+1}\cap B^1=F_{n_{0}+2}\cap B^1$
and so
![]() $F_{n_{0}+2}\in \langle \mathcal {A}\cup \mathcal {F}_{n_{0}+1}\rangle $
, which is a contradiction.⊣
$F_{n_{0}+2}\in \langle \mathcal {A}\cup \mathcal {F}_{n_{0}+1}\rangle $
, which is a contradiction.⊣
Fact 3.3. Let
![]() $\mathcal {Y},\mathcal {Z}$
be centered families of subsets of
$\mathcal {Y},\mathcal {Z}$
be centered families of subsets of
![]() $ \omega $
, which are not ultrafilter subbases. If
$ \omega $
, which are not ultrafilter subbases. If
![]() $h\in {{}^{\omega }\omega }$
, then there exist sets Y and Z such that Y is compatible with
$h\in {{}^{\omega }\omega }$
, then there exist sets Y and Z such that Y is compatible with
![]() $\mathcal {Y}$
,
$\mathcal {Y}$
,
![]() $ Z$
is compatible with
$ Z$
is compatible with
![]() $\mathcal {Z}$
, and
$\mathcal {Z}$
, and
![]() $h(Z)$
is not compatible with Y.
$h(Z)$
is not compatible with Y.
Proof. Take any O such that O and
![]() $O^c$
are compatible with
$O^c$
are compatible with
![]() $ \mathcal {Y}$
.
$ \mathcal {Y}$
.
If
![]() $h^{-1}(O)$
is not compatible with
$h^{-1}(O)$
is not compatible with
![]() $ \mathcal {Z}$
then
$ \mathcal {Z}$
then
![]() $Y=O$
,
$Y=O$
,
![]() $Z=(h^{-1}(O))^c$
;
$Z=(h^{-1}(O))^c$
;
if
![]() $h^{-1}(O^c)$
is not compatible with
$h^{-1}(O^c)$
is not compatible with
![]() $ \mathcal {Z}$
then
$ \mathcal {Z}$
then
![]() $Y=O^c$
,
$Y=O^c$
,
![]() $Z=h^{-1}(O)$
;
$Z=h^{-1}(O)$
;
if
![]() $h^{-1}(O) $
is compatible with
$h^{-1}(O) $
is compatible with
![]() $ \mathcal {Z}$
and
$ \mathcal {Z}$
and
![]() $h^{-1}(O^c) $
is compatible with
$h^{-1}(O^c) $
is compatible with
![]() $ \mathcal {Z}$
then
$ \mathcal {Z}$
then
![]() $Y=O$
,
$Y=O$
,
![]() $Z=(h^{-1}(O))^c$
.⊣
$Z=(h^{-1}(O))^c$
.⊣
Theorem 3.4 (CH)
If p is a P-point, then there exists a set
![]() $\mathfrak {U}$
of cardinality
$\mathfrak {U}$
of cardinality
![]() $ \mathfrak {c}$
of Rudin–Keisler incomparable P-points with
$ \mathfrak {c}$
of Rudin–Keisler incomparable P-points with
![]() $u>_{RK} p$
for each
$u>_{RK} p$
for each
![]() $u\in \mathfrak {U}$
.
$u\in \mathfrak {U}$
.
Proof. First repeat the proof of Theorem 3.1 except for the last line. Then continue as follows.
We arrange all contours in a sequence
![]() $(\int {\mathcal {W}}_{\alpha })_{\alpha < \mathfrak {b}}$
and
$(\int {\mathcal {W}}_{\alpha })_{\alpha < \mathfrak {b}}$
and
![]() ${{}^{\omega }\omega }$
in a sequence
${{}^{\omega }\omega }$
in a sequence
![]() $(f_{\beta })_{\beta < \mathfrak {b}}$
. We will build a family
$(f_{\beta })_{\beta < \mathfrak {b}}$
. We will build a family
 $\{({\mathcal {F}}_{\alpha }^{\beta })_{\alpha <\mathfrak {b}}\}_{\beta <\mathfrak {b}}$
of increasing
$\{({\mathcal {F}}_{\alpha }^{\beta })_{\alpha <\mathfrak {b}}\}_{\beta <\mathfrak {b}}$
of increasing
![]() $\mathfrak {b }$
-sequences
$\mathfrak {b }$
-sequences
 $({\mathcal {F}}_{\alpha }^{\beta })_{\alpha <\mathfrak {b}}$
of filters such that:
$({\mathcal {F}}_{\alpha }^{\beta })_{\alpha <\mathfrak {b}}$
of filters such that:
-
1) Each
 ${\mathcal {F}}_{\alpha }^{\beta }$
is generated by
${\mathcal {F}}_{\alpha }^{\beta }$
is generated by
 $\mathcal {A}$
together with some family of sets of cardinality
$\mathcal {A}$
together with some family of sets of cardinality
 $<\mathfrak {b}$
;
$<\mathfrak {b}$
; -
2)
 ${\mathcal {F}}^\beta _0 = \mathcal {A}$
for each
${\mathcal {F}}^\beta _0 = \mathcal {A}$
for each
 $\beta <\mathfrak {b}$
;
$\beta <\mathfrak {b}$
; -
3) For each
 $\alpha ,\beta <\mathfrak {b}$
, there exists
$\alpha ,\beta <\mathfrak {b}$
, there exists
 $F\in {\mathcal {F}} _{\alpha +1}^{\beta }$
such that
$F\in {\mathcal {F}} _{\alpha +1}^{\beta }$
such that
 $F^{c}\in \int {\mathcal {W}}_{\alpha }$
;
$F^{c}\in \int {\mathcal {W}}_{\alpha }$
; -
4) For every limit
 $\alpha $
and for each
$\alpha $
and for each
 $\beta $
, let
$\beta $
, let
 ${\mathcal {F}} _{\alpha }^{\beta }=\bigcup _{\gamma <\alpha }{\mathcal {F}}_{\gamma }^{\beta } $
;
${\mathcal {F}} _{\alpha }^{\beta }=\bigcup _{\gamma <\alpha }{\mathcal {F}}_{\gamma }^{\beta } $
; -
5) For each
 $\alpha ,\gamma <\alpha ,\beta _{1}$
,
$\alpha ,\gamma <\alpha ,\beta _{1}$
,
 $\beta _{2}<\alpha ,$
there exists a set
$\beta _{2}<\alpha ,$
there exists a set
 $F\in {\mathcal {F}}_{\alpha +1}^{\beta _{1}}$
such that
$F\in {\mathcal {F}}_{\alpha +1}^{\beta _{1}}$
such that
 $ (f_{\gamma }(F))^{c}\in {\mathcal {F}}_{\alpha +1}^{\beta _{2}}$
.
$ (f_{\gamma }(F))^{c}\in {\mathcal {F}}_{\alpha +1}^{\beta _{2}}$
.
The existence of such families follows by a standard induction with sub-inductions using Theorem 2.5 and Fact 3.3 for Condition 5. It follows from the proof of Fact 3.2 that
![]() ${\mathcal {F}} _{\alpha }^{\beta }$
is not an ultrafilter subbase for each
${\mathcal {F}} _{\alpha }^{\beta }$
is not an ultrafilter subbase for each
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. It suffices now to take for each
$\beta $
. It suffices now to take for each
![]() $\beta <\mathfrak {c}$
, any ultrafilter extending
$\beta <\mathfrak {c}$
, any ultrafilter extending
 $\bigcup _{\beta <\mathfrak {c}}{\mathcal {F}}_{\alpha }^{\beta }$
and note that, by Proposition 2.1, it is a P-point.⊣
$\bigcup _{\beta <\mathfrak {c}}{\mathcal {F}}_{\alpha }^{\beta }$
and note that, by Proposition 2.1, it is a P-point.⊣
A. Blass [Reference Blass1, Theorem 7] also proved that, under
![]() $\mathfrak {p}= \mathfrak {c}$
, each RK-increasing sequence of P-points is upper bounded by a P-point. By
$\mathfrak {p}= \mathfrak {c}$
, each RK-increasing sequence of P-points is upper bounded by a P-point. By
![]() $\mathrm {Level\,}_n(T)$
we denote level n in the tree T.
$\mathrm {Level\,}_n(T)$
we denote level n in the tree T.
Theorem 3.5
 $(\mathfrak {b}=\mathfrak {c})$
$(\mathfrak {b}=\mathfrak {c})$
If
![]() $(p_{n})_{n<\omega }$
is an RK-increasing sequence of P-points, then there exists a P-point u such that
$(p_{n})_{n<\omega }$
is an RK-increasing sequence of P-points, then there exists a P-point u such that
![]() $u>_{RK}p_{n}$
for each
$u>_{RK}p_{n}$
for each
![]() $n<\omega $
.
$n<\omega $
.
Proof. For each
![]() $n<\omega $
we let
$n<\omega $
we let
![]() $f_{n}$
to be a finite-to-one function that witnesses
$f_{n}$
to be a finite-to-one function that witnesses
![]() $ p_{n+1}>_{RK}p_{n}$
. Consider a sequence
$ p_{n+1}>_{RK}p_{n}$
. Consider a sequence
![]() $(T_n)_{n<\omega }$
of disjoint trees such that for each
$(T_n)_{n<\omega }$
of disjoint trees such that for each
![]() $n<\omega $
$n<\omega $
-
1) the root of
 $T_n$
is equal to
$T_n$
is equal to
 $n\in \omega $
;
$n\in \omega $
; -
2)
 $\mathrm {Level\,}_m(T_n) = \{f_m^{-1}(k): k\in \mathrm {Level\,}_{m-1}(T_n)\}$
for
$\mathrm {Level\,}_m(T_n) = \{f_m^{-1}(k): k\in \mathrm {Level\,}_{m-1}(T_n)\}$
for
 $1\leq m\leq n$
;
$1\leq m\leq n$
; -
3)
 $\mathrm {Level\,}_m(T_n)=\emptyset $
for
$\mathrm {Level\,}_m(T_n)=\emptyset $
for
 $m>n$
.
$m>n$
.
Since
![]() $L_\infty =\bigcup _{n<\omega }\mathrm {max\,} T_n$
is countably infinite we treat it as
$L_\infty =\bigcup _{n<\omega }\mathrm {max\,} T_n$
is countably infinite we treat it as
![]() $\omega $
as well as
$\omega $
as well as
![]() $L_m=\bigcup _{n<\omega }\mathrm {Level\,} _m(T_n)$
. Let
$L_m=\bigcup _{n<\omega }\mathrm {Level\,} _m(T_n)$
. Let
![]() $g_m: L_\infty \setminus \bigcup _{k<m}L_k \to L_m$
be a function defined by order of the trees
$g_m: L_\infty \setminus \bigcup _{k<m}L_k \to L_m$
be a function defined by order of the trees
![]() $T_n$
.
$T_n$
.
On
![]() $L_\infty $
we define a family of sets:
$L_\infty $
we define a family of sets:
 $\mathcal {B}=\bigcup _{n<\omega } g_m^{-1}(p_m)$
.
$\mathcal {B}=\bigcup _{n<\omega } g_m^{-1}(p_m)$
.
To conclude it suffices, by Corollary 2.6, to show that
![]() $\mathcal {B} $
is a
$\mathcal {B} $
is a
![]() $P^+$
-family, thus by Theorem 2.5 it suffices to prove that
$P^+$
-family, thus by Theorem 2.5 it suffices to prove that
![]() $g_{m}^{-1}(p_{m})$
is a
$g_{m}^{-1}(p_{m})$
is a
![]() $P^+$
-family, for any m. But this is an easier version of the fact which we established in the proof of Theorem 3.1.⊣
$P^+$
-family, for any m. But this is an easier version of the fact which we established in the proof of Theorem 3.1.⊣
In [Reference Blass1], A. Blass asked (Question 4) which ordinals could be embedded in the set of P-points, noticing that such an ordinal could not be greater than
![]() $\mathfrak {c}^+$
. The question was also considered by D. Raghavan and S. Shelah in [Reference Raghavan and Verner8] and answered, under MA, by B. Kuzeljević and D. Raghavan in a recent paper [Reference Mathias6].
$\mathfrak {c}^+$
. The question was also considered by D. Raghavan and S. Shelah in [Reference Raghavan and Verner8] and answered, under MA, by B. Kuzeljević and D. Raghavan in a recent paper [Reference Mathias6].
We prove that, under
![]() $\mathfrak {b}=\mathfrak {c}$
, there is an order embedding of each ordinal less than
$\mathfrak {b}=\mathfrak {c}$
, there is an order embedding of each ordinal less than
![]() $\mathfrak {c}^{+}$
into P-points. To this end, we need some (probably known) facts associated with the following definition: we say that a subset A of
$\mathfrak {c}^{+}$
into P-points. To this end, we need some (probably known) facts associated with the following definition: we say that a subset A of
![]() ${{}^{\omega }\omega }$
is sparse if
${{}^{\omega }\omega }$
is sparse if
![]() $\mathrm {lim\,}_{n<\omega }\left \vert f(n)-g(n)\right \vert =\infty $
for each
$\mathrm {lim\,}_{n<\omega }\left \vert f(n)-g(n)\right \vert =\infty $
for each
![]() $f,g\in A$
such that
$f,g\in A$
such that
![]() $f\not =g$
.
$f\not =g$
.
Fact 3.6. There exists a strictly
![]() $<^{\ast }$
-increasing sparse sequence
$<^{\ast }$
-increasing sparse sequence
![]() $ \mathcal {F}=(f_{\alpha })_{\alpha <\mathfrak {b}}\subset {{}^{\omega }\omega }$
of nondecreasing functions such that
$ \mathcal {F}=(f_{\alpha })_{\alpha <\mathfrak {b}}\subset {{}^{\omega }\omega }$
of nondecreasing functions such that
![]() $f_{\alpha }\left ( n\right ) \leq n$
for each
$f_{\alpha }\left ( n\right ) \leq n$
for each
![]() $n<\omega $
and
$n<\omega $
and
![]() $\alpha <\mathfrak {b}$
.
$\alpha <\mathfrak {b}$
.
Proof. First, we build, from the definition of
![]() $\mathfrak {b}$
, an
$\mathfrak {b}$
, an
![]() $<^{\ast }$
-increasing sparse sequence
$<^{\ast }$
-increasing sparse sequence
![]() $(g_{\alpha })_{\alpha <\mathfrak {b}}\subset { ^{\omega }\omega }$
of nondecreasing functions that fulfill the following condition: if
$(g_{\alpha })_{\alpha <\mathfrak {b}}\subset { ^{\omega }\omega }$
of nondecreasing functions that fulfill the following condition: if
![]() $\alpha <\beta <\mathfrak {b}$
, then
$\alpha <\beta <\mathfrak {b}$
, then
![]() $g_{\alpha }(n)>g_{\beta }(2n)+n$
for almost all
$g_{\alpha }(n)>g_{\beta }(2n)+n$
for almost all
![]() $n<\omega $
. Then a
$n<\omega $
. Then a
![]() $\mathfrak {b}$
-sequence
$\mathfrak {b}$
-sequence
![]() $(f_\alpha )_{\alpha <\mathfrak {b}}$
defined by
$(f_\alpha )_{\alpha <\mathfrak {b}}$
defined by
![]() $ f_\alpha (m)=m - \mathrm {max\,}\{n: g_\alpha (n)<m\}$
is as desired.⊣
$ f_\alpha (m)=m - \mathrm {max\,}\{n: g_\alpha (n)<m\}$
is as desired.⊣
Fact 3.7. If an ordinal number
![]() $\alpha $
can be sparsely embedded in
$\alpha $
can be sparsely embedded in
![]() ${{}^{\omega }\omega }$
, under identity, as nondecreasing functions, then
${{}^{\omega }\omega }$
, under identity, as nondecreasing functions, then
![]() $\alpha $
can be sparsely embedded in
$\alpha $
can be sparsely embedded in
![]() ${{}^{\omega }\omega }$
, under any function f that converges to
${{}^{\omega }\omega }$
, under any function f that converges to
![]() $\infty $
.
$\infty $
.
Proof. Let
![]() $h<f$
be a nondecreasing function such that
$h<f$
be a nondecreasing function such that
![]() $h(n+1)-h(n)\leq 1$
. Let
$h(n+1)-h(n)\leq 1$
. Let
![]() $ (g_\beta )_{\beta <\alpha }$
be an embedding of
$ (g_\beta )_{\beta <\alpha }$
be an embedding of
![]() $\alpha $
. Define
$\alpha $
. Define
![]() $ (f_\beta )_{\beta <\alpha }$
by:
$ (f_\beta )_{\beta <\alpha }$
by:
![]() $f(\alpha )(k)=g_\alpha (n)$
if and only if
$f(\alpha )(k)=g_\alpha (n)$
if and only if
![]() $h(k)=n$
.⊣
$h(k)=n$
.⊣
Fact 3.8. If an ordinal number
![]() $\alpha $
can be sparsely embedded in
$\alpha $
can be sparsely embedded in
![]() ${ ^{\omega }\omega }$
as nondecreasing functions that are less than any function
${ ^{\omega }\omega }$
as nondecreasing functions that are less than any function
![]() $f\in {{}^{\omega }\omega }$
, then
$f\in {{}^{\omega }\omega }$
, then
![]() $\alpha $
can be sparsely embedded as nondecreasing functions between any sparse pair of functions
$\alpha $
can be sparsely embedded as nondecreasing functions between any sparse pair of functions
![]() $g<^{\ast }h\in {{}^{\omega }\omega }$
.
$g<^{\ast }h\in {{}^{\omega }\omega }$
.
Proof. Without loss of generality, we assume f to be nondecreasing. Let
![]() $(f_{\beta })_{\beta <\alpha }$
be an embedding of
$(f_{\beta })_{\beta <\alpha }$
be an embedding of
![]() $\alpha $
under f. Clearly, it suffices to prove that there is an embedding under s defined by
$\alpha $
under f. Clearly, it suffices to prove that there is an embedding under s defined by
![]() $s(n)=h(n)-g(n)$
if
$s(n)=h(n)-g(n)$
if
![]() $ h(n)\geq g(n)$
and
$ h(n)\geq g(n)$
and
![]() $s(n)=0$
otherwise.
$s(n)=0$
otherwise.
Define a sequence
![]() $(k(n))_{n<\omega }$
by
$(k(n))_{n<\omega }$
by
![]() $k(0)=\mathrm {min\,}\{m:s(i)\geq f(0)$
for all
$k(0)=\mathrm {min\,}\{m:s(i)\geq f(0)$
for all
![]() $i\geq m\}$
,
$i\geq m\}$
,
![]() $k(n+1)=\mathrm {min\,}\{m:m>k(n)\text { }\&\text { } s(i)\geq f(n+1)$
for all
$k(n+1)=\mathrm {min\,}\{m:m>k(n)\text { }\&\text { } s(i)\geq f(n+1)$
for all
![]() $i\geq m\}$
. Finally define
$i\geq m\}$
. Finally define
![]() $g_\alpha $
as follows:
$g_\alpha $
as follows:
![]() $g_\alpha (n)=f_\alpha (m)$
if and only if
$g_\alpha (n)=f_\alpha (m)$
if and only if
![]() $k(n) \leq m < k(n+1)$
.⊣
$k(n) \leq m < k(n+1)$
.⊣
Fact 3.9. For each
![]() $\gamma <\mathfrak {b^{+}}$
, there exists a strictly
$\gamma <\mathfrak {b^{+}}$
, there exists a strictly
![]() $ <^{\ast }$
-increasing sparse sequence
$ <^{\ast }$
-increasing sparse sequence
![]() $\mathcal {F}=(f_{\alpha })_{\alpha <\gamma }\subset {{}^{\omega }\omega }$
of nondecreasing functions.
$\mathcal {F}=(f_{\alpha })_{\alpha <\gamma }\subset {{}^{\omega }\omega }$
of nondecreasing functions.
Proof. Facts 3.6 and 3.8 clearly imply that the first ordinal number which cannot be embedded as a sparse sequence in
![]() ${{}^{\omega }\omega } $
under
${{}^{\omega }\omega } $
under
![]() $\mathrm {id\,}_{\omega }$
is equal to
$\mathrm {id\,}_{\omega }$
is equal to
![]() $\alpha $
or to
$\alpha $
or to
![]() $\alpha +1$
where
$\alpha +1$
where
![]() $\alpha $
is a limit number. Facts 3.6 and 3.8 also imply that the set of ordinals less than
$\alpha $
is a limit number. Facts 3.6 and 3.8 also imply that the set of ordinals less than
![]() $\alpha $
is closed under
$\alpha $
is closed under
![]() $ \mathfrak {b}$
sums.
$ \mathfrak {b}$
sums.
Indeed, let
![]() $\beta $
be the minimal ordinal number
$\beta $
be the minimal ordinal number
![]() $< \mathfrak {b}^+$
that may not be embedded under identity as an
$< \mathfrak {b}^+$
that may not be embedded under identity as an
![]() $<^*$
-increasing sparse sequence. Clearly
$<^*$
-increasing sparse sequence. Clearly
![]() $\mathrm {cof\, }(\beta ) \leq \mathfrak {b}$
. Take an increasing sequence
$\mathrm {cof\, }(\beta ) \leq \mathfrak {b}$
. Take an increasing sequence
![]() $(\alpha _\delta )_{ \delta < \mathrm {cof\,} \beta }$
that converges to
$(\alpha _\delta )_{ \delta < \mathrm {cof\,} \beta }$
that converges to
![]() $\beta $
. Clearly for each
$\beta $
. Clearly for each
![]() $ \alpha < \beta $
there is
$ \alpha < \beta $
there is
 $(g^\alpha _\eta )_{\eta <\alpha }$
—an embedding of
$(g^\alpha _\eta )_{\eta <\alpha }$
—an embedding of
![]() $ \alpha $
into
$ \alpha $
into
![]() ${^\omega \omega }$
as a sparse sequence under identity. By Fact 3.8 for each
${^\omega \omega }$
as a sparse sequence under identity. By Fact 3.8 for each
![]() $\alpha < \beta $
there is an
$\alpha < \beta $
there is an
![]() $<^*$
-increasing sparse sequence of
$<^*$
-increasing sparse sequence of
 $(f^\alpha _\eta )_{\eta <\alpha }$
such that
$(f^\alpha _\eta )_{\eta <\alpha }$
such that
![]() $f_\alpha <^* f^\alpha _\eta <^* f_{\alpha +1}$
(for
$f_\alpha <^* f^\alpha _\eta <^* f_{\alpha +1}$
(for
![]() $f_\alpha $
,
$f_\alpha $
,
![]() $f_{\alpha +1}$
from the proof of Fact 3.6). Now
$f_{\alpha +1}$
from the proof of Fact 3.6). Now
 $(f^\alpha _\eta )_{\alpha <\mathrm {cof\,} (\beta ), \eta <\alpha }$
with lexicographic order is a required embedding of
$(f^\alpha _\eta )_{\alpha <\mathrm {cof\,} (\beta ), \eta <\alpha }$
with lexicographic order is a required embedding of
![]() $ \beta $
.
$ \beta $
.
Thus, this number is not less than
![]() $\mathfrak {b}^{+}$
.⊣
$\mathfrak {b}^{+}$
.⊣
Theorem 3.10
 $(\mathfrak {b}=\mathfrak {c})$
$(\mathfrak {b}=\mathfrak {c})$
For each
![]() $\gamma <\mathfrak {b^{+}}$
, for each P-point p there exists an RK-increasing sequence
$\gamma <\mathfrak {b^{+}}$
, for each P-point p there exists an RK-increasing sequence
![]() $\{p_{\alpha }:\alpha <\gamma \}$
of P-points such that
$\{p_{\alpha }:\alpha <\gamma \}$
of P-points such that
![]() $p_{0}=p$
.
$p_{0}=p$
.
Proof. Note that
![]() $\mathrm {cof\,}(\gamma )\leq \mathfrak {b}$
. Consider a set of pairwise disjoint trees
$\mathrm {cof\,}(\gamma )\leq \mathfrak {b}$
. Consider a set of pairwise disjoint trees
![]() $T_{n}$
such that each
$T_{n}$
such that each
![]() $T_{n}$
has a minimal element, each element of
$T_{n}$
has a minimal element, each element of
![]() $T_{n}$
has exactly n immediate successors, and each branch has the highest
$T_{n}$
has exactly n immediate successors, and each branch has the highest
![]() $\omega $
.
$\omega $
.
Let
![]() $\{f_{\alpha }\}_{\alpha <\gamma }\subset {{}^{\omega }\omega }$
be a sparse, strictly
$\{f_{\alpha }\}_{\alpha <\gamma }\subset {{}^{\omega }\omega }$
be a sparse, strictly
![]() $<^{\ast }$
-increasing sequence, the existence of which is demonstrated by Fact 3.9. For each
$<^{\ast }$
-increasing sequence, the existence of which is demonstrated by Fact 3.9. For each
![]() $\alpha <\gamma $
, define
$\alpha <\gamma $
, define
 $$ \begin{align*} X_{\alpha }=\bigcup\nolimits_{n<\omega }\mathrm{Level\,}_{f_{\alpha }(n)}T_{n}. \end{align*} $$
$$ \begin{align*} X_{\alpha }=\bigcup\nolimits_{n<\omega }\mathrm{Level\,}_{f_{\alpha }(n)}T_{n}. \end{align*} $$
For each
![]() $\alpha <\beta \leq \gamma $
, define
$\alpha <\beta \leq \gamma $
, define
 $$ \begin{align*} f_{\alpha }^{\beta }:\bigcup\nolimits_{\{n<\omega: f_{\alpha }(n)<f_{\beta }(n)\}}\mathrm{Level\,}_{f_{\beta }(n)}T_{n}\rightarrow \bigcup\nolimits_{\{n<\omega: f_{\alpha }(n)<f_{\beta }(n)\}}\mathrm{Level\,} _{f_{\alpha }(n)}T_{n} \end{align*} $$
$$ \begin{align*} f_{\alpha }^{\beta }:\bigcup\nolimits_{\{n<\omega: f_{\alpha }(n)<f_{\beta }(n)\}}\mathrm{Level\,}_{f_{\beta }(n)}T_{n}\rightarrow \bigcup\nolimits_{\{n<\omega: f_{\alpha }(n)<f_{\beta }(n)\}}\mathrm{Level\,} _{f_{\alpha }(n)}T_{n} \end{align*} $$
that agrees with the order of trees
![]() $T_{n}$
for
$T_{n}$
for
![]() $n<\omega $
such that
$n<\omega $
such that
![]() $ f_{\alpha }(n)<f_{\beta }(n)$
. Note that
$ f_{\alpha }(n)<f_{\beta }(n)$
. Note that
 $\mathrm {dom\,}f_{\alpha }^{\beta }$
is cofinite on
$\mathrm {dom\,}f_{\alpha }^{\beta }$
is cofinite on
![]() $X_{\beta }$
for each
$X_{\beta }$
for each
![]() $\alpha <\beta $
.
$\alpha <\beta $
.
Let
![]() $p=p_{0}$
be a P-point on
$p=p_{0}$
be a P-point on
![]() $X_{0}=\bigcup _{n<\omega }\mathrm {Level\,} _{0}T_{n}$
. We proceed by recursively building a filter
$X_{0}=\bigcup _{n<\omega }\mathrm {Level\,} _{0}T_{n}$
. We proceed by recursively building a filter
![]() $p_{\beta }$
on
$p_{\beta }$
on
![]() $ X_{\beta }$
. Suppose that
$ X_{\beta }$
. Suppose that
![]() $p_{\alpha }$
are already defined for
$p_{\alpha }$
are already defined for
![]() $\alpha <\beta $
. If
$\alpha <\beta $
. If
![]() $\beta $
is a successor, then it suffice to repeat a proof of Theorem 3.1 for
$\beta $
is a successor, then it suffice to repeat a proof of Theorem 3.1 for
![]() $P_{\beta -1}$
and
$P_{\beta -1}$
and
 $f^{\beta }_{\beta -1}$
.
$f^{\beta }_{\beta -1}$
.
So suppose that
![]() $\beta $
is limit. Let
$\beta $
is limit. Let
![]() $R\subset \beta $
be cofinite with
$R\subset \beta $
be cofinite with
![]() $ \beta $
and of order type less than or equal to
$ \beta $
and of order type less than or equal to
![]() $\mathfrak {b}$
. Define a family
$\mathfrak {b}$
. Define a family
 $$ \begin{align*} \mathcal{C}=\bigcup_{\alpha \in R }\{(f_{\alpha }^{\beta })^{-1}(p_{\alpha }) \}, \end{align*} $$
$$ \begin{align*} \mathcal{C}=\bigcup_{\alpha \in R }\{(f_{\alpha }^{\beta })^{-1}(p_{\alpha }) \}, \end{align*} $$
which is obviously strongly centered.
Clearly each filter that extends
![]() $\mathcal {C}$
is
$\mathcal {C}$
is
![]() $RK$
-greater than each
$RK$
-greater than each
![]() $ p_{\alpha }$
for
$ p_{\alpha }$
for
![]() $\alpha <\beta $
. But we need a P-point extension. Thus, by Corollary 2.6 it suffices to prove that
$\alpha <\beta $
. But we need a P-point extension. Thus, by Corollary 2.6 it suffices to prove that
![]() $\mathcal {C}$
is a
$\mathcal {C}$
is a
![]() $P^+$
-family. Thus, by Theorem 2.5 it suffices to prove that
$P^+$
-family. Thus, by Theorem 2.5 it suffices to prove that
 $\bigcup _{\gamma \in R,\gamma \leq \alpha }\{(f_{\gamma }^{\beta })^{-1}(p_{\gamma })\}\subset (f_{\alpha }^{\beta })^{-1}(p_{\alpha })$
is a
$\bigcup _{\gamma \in R,\gamma \leq \alpha }\{(f_{\gamma }^{\beta })^{-1}(p_{\gamma })\}\subset (f_{\alpha }^{\beta })^{-1}(p_{\alpha })$
is a
![]() $P^+$
-family, for each
$P^+$
-family, for each
![]() $\alpha \in R$
. But it is (an easier version of) what we did in the proof of Theorem 3.1.⊣
$\alpha \in R$
. But it is (an easier version of) what we did in the proof of Theorem 3.1.⊣
By Theorems 3.5 and 3.10 the following natural question arises:
Question 3.11. What is the least ordinal
![]() $\alpha $
such that there exists an unbounded embedding of
$\alpha $
such that there exists an unbounded embedding of
![]() $\alpha $
into the set of P-points?Footnote
5
$\alpha $
into the set of P-points?Footnote
5
A. Blass [Reference Blass1, Theorem 8] also proved that, under
![]() $\mathfrak {p}= \mathfrak {c}$
, there is an order-embedding of the real line into the set of P-points. We will prove the same fact, but under
$\mathfrak {p}= \mathfrak {c}$
, there is an order-embedding of the real line into the set of P-points. We will prove the same fact, but under
![]() $\mathfrak {b}=\mathfrak {c}$
. Our proof is based on the original idea of set X defined by A. Blass. Therefore, we quote the beginning of his proof, and then use our machinery.
$\mathfrak {b}=\mathfrak {c}$
. Our proof is based on the original idea of set X defined by A. Blass. Therefore, we quote the beginning of his proof, and then use our machinery.
Theorem 3.12
 $(\mathfrak {b}=\mathfrak {c})$
$(\mathfrak {b}=\mathfrak {c})$
There exists an order-embedding of the real line into the set of P-points.
Proof. ———————— (beginning of quotation) ————————
Let X be a set of all functions
![]() $x: \mathbb {Q} \to \omega $
such that
$x: \mathbb {Q} \to \omega $
such that
![]() $ x(r)=0$
for all but finitely many
$ x(r)=0$
for all but finitely many
![]() $r\in \mathbb {Q}$
; here
$r\in \mathbb {Q}$
; here
![]() $\mathbb {Q}$
is the set of rational numbers. As X is denumerable, we may identify it with
$\mathbb {Q}$
is the set of rational numbers. As X is denumerable, we may identify it with
![]() $ \omega $
via some bijection. For each
$ \omega $
via some bijection. For each
![]() $\xi \in \mathbb {R}$
, we define
$\xi \in \mathbb {R}$
, we define
![]() $h_\xi : X \to X$
by
$h_\xi : X \to X$
by
 $$ \begin{align*} h_{\xi }(x)(r)=\left\{ \begin{array}{c} x(r)\text{ if }r<\xi , \\ 0\text{ if }r\geq \xi. \end{array} \right. \end{align*} $$
$$ \begin{align*} h_{\xi }(x)(r)=\left\{ \begin{array}{c} x(r)\text{ if }r<\xi , \\ 0\text{ if }r\geq \xi. \end{array} \right. \end{align*} $$
Clearly, if
![]() $\xi < \eta $
, then
$\xi < \eta $
, then
![]() $h_\xi \circ h_\eta = h_\eta \circ h_\xi = h_\xi $
. The embedding of
$h_\xi \circ h_\eta = h_\eta \circ h_\xi = h_\xi $
. The embedding of
![]() $\mathbb {R}$
into P-points will be defined by
$\mathbb {R}$
into P-points will be defined by
![]() $\xi \to D_\xi = h_\xi (D)$
for a certain ultrafilter D on X. If
$\xi \to D_\xi = h_\xi (D)$
for a certain ultrafilter D on X. If
![]() $\xi < \eta $
, then
$\xi < \eta $
, then
![]() $D_{\xi }=h_{\xi }(D)=h_{\xi }\circ h_{\eta }(D)=h_{\xi }(D_{\eta })\leq D_{\eta }$
.
$D_{\xi }=h_{\xi }(D)=h_{\xi }\circ h_{\eta }(D)=h_{\xi }(D_{\eta })\leq D_{\eta }$
.
We wish to choose D in such a way that
(a)
![]() $D_\xi \not \cong D_\eta $
(therefore,
$D_\xi \not \cong D_\eta $
(therefore,
![]() $D_\xi < D_\eta $
when
$D_\xi < D_\eta $
when
![]() $\xi < \eta $
), and
$\xi < \eta $
), and
(b)
![]() $D_\xi $
is a P-point.
$D_\xi $
is a P-point.
Observe that it will be sufficient to choose D such that
(a’)
![]() $D_\xi \not \cong D_\eta $
when
$D_\xi \not \cong D_\eta $
when
![]() $\xi < \eta $
and both
$\xi < \eta $
and both
![]() $\xi $
and
$\xi $
and
![]() $\eta $
are rational, and
$\eta $
are rational, and
(b’) D is a P-point.
Indeed, (a’) implies (a) because
![]() $\mathbb {Q}$
is dense in
$\mathbb {Q}$
is dense in
![]() $\mathbb {R}$
. If (a) holds, then
$\mathbb {R}$
. If (a) holds, then
![]() $D_{\xi -1} < D_\xi $
, so
$D_{\xi -1} < D_\xi $
, so
![]() $D_\xi $
is a nonprincipal ultrafilter
$D_\xi $
is a nonprincipal ultrafilter
![]() $\leq D$
; hence (b’) implies condition (b).
$\leq D$
; hence (b’) implies condition (b).
Condition (a’) means that, for all
![]() $\xi <\eta \in \mathbb {Q}$
and all
$\xi <\eta \in \mathbb {Q}$
and all
![]() $ g:X\rightarrow X$
,
$ g:X\rightarrow X$
,
![]() $D_{\eta }\not =g(D_{\xi })=gh_{\xi }(D_{\eta })$
. By Theorem 2.7, this is equivalent to
$D_{\eta }\not =g(D_{\xi })=gh_{\xi }(D_{\eta })$
. By Theorem 2.7, this is equivalent to
![]() $\{x:gh_{\xi }(x)=x\}\not \in D_{\eta }$
, or by our definition of
$\{x:gh_{\xi }(x)=x\}\not \in D_{\eta }$
, or by our definition of
![]() $D_{\eta }$
,
$D_{\eta }$
,
 $$ \begin{align} \{x:gh_{\xi }(x)=h_{\eta }(x)\}=h_{\eta }^{-1}\{x:gh_{\xi }(x)=x\}\not\in D. \end{align} $$
$$ \begin{align} \{x:gh_{\xi }(x)=h_{\eta }(x)\}=h_{\eta }^{-1}\{x:gh_{\xi }(x)=x\}\not\in D. \end{align} $$
We now proceed to construct a P-point D satisfying (a’’) for all
![]() $\xi <\eta \in \mathbb {Q}$
and for all
$\xi <\eta \in \mathbb {Q}$
and for all
![]() $g:X\rightarrow X$
; this will suffice to establish the theorem.
$g:X\rightarrow X$
; this will suffice to establish the theorem.
————————– (end of quotation) —————————–
List all pairs
![]() $(\xi , \eta )$
,
$(\xi , \eta )$
,
![]() $\xi < \eta \in \mathbb {Q}$
in the sequence
$\xi < \eta \in \mathbb {Q}$
in the sequence
![]() $ (\xi _i, \eta _i)_{i<\omega }$
. For each
$ (\xi _i, \eta _i)_{i<\omega }$
. For each
![]() $g\in {{}^{X}X}$
,
$g\in {{}^{X}X}$
,
![]() $\xi <\eta \in \mathbb { Q}$
, define
$\xi <\eta \in \mathbb { Q}$
, define
![]() ${A}_{g,\xi ,\eta }=\{x\in X:gh_{\xi }(x)\not =h_{\eta }(x)\}$
,
${A}_{g,\xi ,\eta }=\{x\in X:gh_{\xi }(x)\not =h_{\eta }(x)\}$
,
![]() $ \mathcal {A}_{i}=\mathcal {A}_{\xi _{i},\eta _{i}}=\{{A}_{g,\xi _{i},\eta _{i}}:g\in {{}^{X}X}\}$
, and
$ \mathcal {A}_{i}=\mathcal {A}_{\xi _{i},\eta _{i}}=\{{A}_{g,\xi _{i},\eta _{i}}:g\in {{}^{X}X}\}$
, and
![]() $\mathcal {A}=\bigcup _{i<\omega }\mathcal {A}_{i}$
. Clearly,
$\mathcal {A}=\bigcup _{i<\omega }\mathcal {A}_{i}$
. Clearly,
![]() $\mathcal {A}$
is strongly centered.
$\mathcal {A}$
is strongly centered.
We claim that
![]() $\mathcal {A}$
is a
$\mathcal {A}$
is a
![]() $P^+$
-family.
$P^+$
-family.
Indeed, by Theorem 2.5, it suffices to prove that for each
![]() $n<\omega $
,
$n<\omega $
,
![]() $\bigcup _{i<n}\mathcal {A}_{i}$
is a
$\bigcup _{i<n}\mathcal {A}_{i}$
is a
![]() $P^+$
-family. Suppose not and take (by Remark 2.4) the witnesses
$P^+$
-family. Suppose not and take (by Remark 2.4) the witnesses
![]() $i_{0}$
and
$i_{0}$
and
![]() $ \int \mathcal {W}$
such that
$ \int \mathcal {W}$
such that
 $\int {\mathcal {W}}\subset \langle \bigcup _{i<i_{0}}\mathcal {A}_{i}\cup \widetilde {\mathcal {W}}\rangle $
. For each
$\int {\mathcal {W}}\subset \langle \bigcup _{i<i_{0}}\mathcal {A}_{i}\cup \widetilde {\mathcal {W}}\rangle $
. For each
![]() $n<\omega $
, consider the condition
$n<\omega $
, consider the condition
![]() $(S_{n})$
:
$(S_{n})$
:
 $$ \begin{align*} \exists x_{n}:\forall i<i_{0}:\left( x_{n}\in h_{\xi _{i}}({\widetilde{W}_{1} })\text{ }\&\text{ }\mathrm{card\,}(h_{\eta _{i}}(h_{\xi _{i}}^{-1}(x_{n}))\cap h_{\eta _{i}}({\widetilde{W}_{n}}))>n\right). \end{align*} $$
$$ \begin{align*} \exists x_{n}:\forall i<i_{0}:\left( x_{n}\in h_{\xi _{i}}({\widetilde{W}_{1} })\text{ }\&\text{ }\mathrm{card\,}(h_{\eta _{i}}(h_{\xi _{i}}^{-1}(x_{n}))\cap h_{\eta _{i}}({\widetilde{W}_{n}}))>n\right). \end{align*} $$
Case 1:
![]() $S_{n}$
is fulfilled for all
$S_{n}$
is fulfilled for all
![]() $n<\omega $
. Then, for each
$n<\omega $
. Then, for each
![]() $n<\omega $
,
$n<\omega $
,
![]() $j<n$
, choose
$j<n$
, choose
![]() $x_{n}^{j}\in \widetilde {W}_{n}$
such that
$x_{n}^{j}\in \widetilde {W}_{n}$
such that
 $h_{\xi _i }(x_{n}^{j})=x_{n}$
and
$h_{\xi _i }(x_{n}^{j})=x_{n}$
and
 $h_{\eta _{i}}(x_{n}^{j_{0}})\not =h_{\eta _{i}}(x_{n}^{j_{1}})$
for
$h_{\eta _{i}}(x_{n}^{j_{0}})\not =h_{\eta _{i}}(x_{n}^{j_{1}})$
for
![]() $j_{0}\not =j_{1}$
. Define
$j_{0}\not =j_{1}$
. Define
 ${E}=\bigcup _{n<\omega }\bigcup _{j\leq n}\{x_{n}^{j}\}$
. Clearly
${E}=\bigcup _{n<\omega }\bigcup _{j\leq n}\{x_{n}^{j}\}$
. Clearly
![]() ${E}^{c}\in \int {\mathcal {W}}$
, but
${E}^{c}\in \int {\mathcal {W}}$
, but
 ${E}\not \subset \bigcup _{i<i_{0}}\bigcup _{g\in \mathcal {G}}({A}_{g,\xi _{i},\eta _{i}})\cup \bigcup _{l<m}W_{l}$
for any choice of finite family
${E}\not \subset \bigcup _{i<i_{0}}\bigcup _{g\in \mathcal {G}}({A}_{g,\xi _{i},\eta _{i}})\cup \bigcup _{l<m}W_{l}$
for any choice of finite family
![]() $ \mathcal {G}\subset {{}^{X}X}$
and for any
$ \mathcal {G}\subset {{}^{X}X}$
and for any
![]() $m<\omega $
.
$m<\omega $
.
Case 2:
![]() $S_{n}$
is not fulfilled for some
$S_{n}$
is not fulfilled for some
![]() $n_{0}<\omega $
. Then, there exist functions
$n_{0}<\omega $
. Then, there exist functions
![]() $\{g_{n,i}\}_{n\leq n_{0},i<i_{0}}\subset {{}^{X}X}$
such that
$\{g_{n,i}\}_{n\leq n_{0},i<i_{0}}\subset {{}^{X}X}$
such that
 $ \widetilde {W}_{1}\subset \bigcup _{n\leq n_{0}}\bigcup _{i<i_{0}}({A} _{g_{n,i},\xi _{i},\eta _{i}})\cup \bigcup _{n\leq n_{0}}W_{n}$
, i.e.,
$ \widetilde {W}_{1}\subset \bigcup _{n\leq n_{0}}\bigcup _{i<i_{0}}({A} _{g_{n,i},\xi _{i},\eta _{i}})\cup \bigcup _{n\leq n_{0}}W_{n}$
, i.e.,
 $\int \mathcal {W}\lnot\ \text{is not compatible with}\ \langle \bigcup _{i<i_{0}}\mathcal {A}_{i}\cup \widetilde { \mathcal {W}}\rangle $
.
$\int \mathcal {W}\lnot\ \text{is not compatible with}\ \langle \bigcup _{i<i_{0}}\mathcal {A}_{i}\cup \widetilde { \mathcal {W}}\rangle $
.
Corollary 2.6 completes the proof.⊣
The long line is defined as
![]() $\mathbb {L} = \omega _1 \times (0,1]$
ordered lexicographically. If
$\mathbb {L} = \omega _1 \times (0,1]$
ordered lexicographically. If
![]() $f:Y \to \omega $
, then the support of f is defined as
$f:Y \to \omega $
, then the support of f is defined as
Lemma 3.13
 $(\mathfrak {b}=\mathfrak {c})$
$(\mathfrak {b}=\mathfrak {c})$
For each P-point p, there exists an order-embedding of the real line into the set of P-points above p.
Proof. We will combine ideas form proofs of Theorems 3.1 and 3.12 with some new arguments.
Again, let X be a set of all functions
![]() $x: \mathbb {Q} \to \omega $
such that
$x: \mathbb {Q} \to \omega $
such that
![]() $x(r)=0$
for all but finitely many
$x(r)=0$
for all but finitely many
![]() $r\in \mathbb {Q}$
. Since X is infinitely countable, we treat it as
$r\in \mathbb {Q}$
. Since X is infinitely countable, we treat it as
![]() $\omega $
.
$\omega $
.
Let p be a P-point on X such that for each
![]() $q\in \mathbb {Q}$
and for each
$q\in \mathbb {Q}$
and for each
![]() $ P\in p$
there exists
$ P\in p$
there exists
![]() $x \in P$
such that
$x \in P$
such that
![]() $\mathrm {max\,} \mathrm {supp\,}(x)< q$
. Let
$\mathrm {max\,} \mathrm {supp\,}(x)< q$
. Let
![]() $f\in {{}^{X}X }$
be a finite-to-one function such that
$f\in {{}^{X}X }$
be a finite-to-one function such that
 $ \limsup \nolimits _{x\in P}\mathrm {card\,}(f^{-1}(x))=\infty $
for all
$ \limsup \nolimits _{x\in P}\mathrm {card\,}(f^{-1}(x))=\infty $
for all
![]() $P\in p$
and that
$P\in p$
and that
![]() $\mathrm {max\,} \mathrm {supp\,} x < \mathrm {max\,} \mathrm {supp\,} f(x)$
. Again, we define a family
$\mathrm {max\,} \mathrm {supp\,} x < \mathrm {max\,} \mathrm {supp\,} f(x)$
. Again, we define a family
![]() $\mathcal {A}$
as follows:
$\mathcal {A}$
as follows:
![]() $A\in \mathcal {A}$
if and only if there exist
$A\in \mathcal {A}$
if and only if there exist
![]() $i<\omega $
and
$i<\omega $
and
![]() $P\in p$
such that
$P\in p$
such that
![]() $\mathrm {card\,} (f^{-1}(x)\setminus A)\leq i$
for each
$\mathrm {card\,} (f^{-1}(x)\setminus A)\leq i$
for each
![]() $x\in P$
. For each
$x\in P$
. For each
![]() $\xi \in \mathbb {R} $
, we again define functions
$\xi \in \mathbb {R} $
, we again define functions
![]() $h_\xi : X \to X$
by
$h_\xi : X \to X$
by
 $$ \begin{align*} h_{\xi }(x)(r)=\left\{ \begin{array}{c} x(r)\text{ if }r<\xi , \\ 0\text{ if }r\geq \xi. \end{array} \right. \end{align*} $$
$$ \begin{align*} h_{\xi }(x)(r)=\left\{ \begin{array}{c} x(r)\text{ if }r<\xi , \\ 0\text{ if }r\geq \xi. \end{array} \right. \end{align*} $$
List all rational numbers in
![]() $\omega $
-sequence
$\omega $
-sequence
![]() $\mathbb {Q}=(q_i)_{i<\omega }$
. Let
$\mathbb {Q}=(q_i)_{i<\omega }$
. Let
 $\mathcal {B}_i=h^{-1}_{q_i}(\mathcal {A} \cup f^{-1}(p))$
and let
$\mathcal {B}_i=h^{-1}_{q_i}(\mathcal {A} \cup f^{-1}(p))$
and let
![]() $ \mathcal {B} = \bigcup _{i<\omega } \mathcal {B}_i$
.
$ \mathcal {B} = \bigcup _{i<\omega } \mathcal {B}_i$
.
Our aim is to prove that
![]() $\mathcal {B}$
can be extended to such a P-point Q that
$\mathcal {B}$
can be extended to such a P-point Q that
![]() $h_\xi (Q) \not = h_\eta (Q)$
for each
$h_\xi (Q) \not = h_\eta (Q)$
for each
![]() $\xi \not = \eta \in \mathbb {Q}$
(and thus for each
$\xi \not = \eta \in \mathbb {Q}$
(and thus for each
![]() $\xi \not = \eta \in \mathbb {R}$
). (4)
$\xi \not = \eta \in \mathbb {R}$
). (4)
To this end, we add to
![]() $\mathcal {B}$
a family
$\mathcal {B}$
a family
![]() $\mathcal {C}$
defined as follows: list all pairs
$\mathcal {C}$
defined as follows: list all pairs
![]() $(\xi , \eta )$
,
$(\xi , \eta )$
,
![]() $\xi < \eta \in \mathbb {Q}$
in the sequence
$\xi < \eta \in \mathbb {Q}$
in the sequence
![]() $(\xi _i, \eta _i)_{i<\omega }$
. For each
$(\xi _i, \eta _i)_{i<\omega }$
. For each
![]() $g\in {{}^{X}X}$
,
$g\in {{}^{X}X}$
,
![]() $\xi <\eta \in \mathbb {Q}$
, define
$\xi <\eta \in \mathbb {Q}$
, define
![]() ${C}_{g,\xi ,\eta }=\{x\in X:gh_{\xi }(x)\not =h_{\eta }(x)\}$
,
${C}_{g,\xi ,\eta }=\{x\in X:gh_{\xi }(x)\not =h_{\eta }(x)\}$
,
![]() $\mathcal {C}_{i}=\mathcal {C}_{\xi _{i},\eta _{i}}=\{{C}_{g,\xi _{i},\eta _{i}}:g\in {{}^{X}X}\}$
, and
$\mathcal {C}_{i}=\mathcal {C}_{\xi _{i},\eta _{i}}=\{{C}_{g,\xi _{i},\eta _{i}}:g\in {{}^{X}X}\}$
, and
![]() $\mathcal {C} =\bigcup _{i<\omega }\mathcal {C}_{i}$
.
$\mathcal {C} =\bigcup _{i<\omega }\mathcal {C}_{i}$
.
Thus to prove (4), it suffices by Corollary 2.6 to prove that
![]() $ \mathcal {B}\cup \mathcal {C}$
is a
$ \mathcal {B}\cup \mathcal {C}$
is a
![]() $P^+$
-family. Thus, by Theorem 2.5, in order to prove (4), it suffices to prove that:
$P^+$
-family. Thus, by Theorem 2.5, in order to prove (4), it suffices to prove that:
![]() $\mathcal {D}_{i}$
is a
$\mathcal {D}_{i}$
is a
![]() $P^+$
-family for
$P^+$
-family for
![]() $\mathcal {D}_{i}$
defined for
$\mathcal {D}_{i}$
defined for
![]() $i<\omega $
as follows:
$i<\omega $
as follows:
 $$\begin{align*}\mathcal{D}_{i}=\bigcup_{j\leq i}\mathcal{B}_{i}\cup \bigcup_{j\leq i} \mathcal{C}_{i}.\tag{5} \end{align*}$$
$$\begin{align*}\mathcal{D}_{i}=\bigcup_{j\leq i}\mathcal{B}_{i}\cup \bigcup_{j\leq i} \mathcal{C}_{i}.\tag{5} \end{align*}$$
First, to prove it, we notice that
![]() $\mathcal {D}_i$
is strongly centered. Indeed, define
$\mathcal {D}_i$
is strongly centered. Indeed, define
![]() $ q_m = \mathrm {min\,} \{q_j: j \leq i\}$
,
$ q_m = \mathrm {min\,} \{q_j: j \leq i\}$
,
![]() $q_M = \mathrm {max\,} \{q_j: j \leq i\}$
, and
$q_M = \mathrm {max\,} \{q_j: j \leq i\}$
, and
![]() $\xi _m=\mathrm {min\,}\{\xi _j: j\leq i\} $
and note that
$\xi _m=\mathrm {min\,}\{\xi _j: j\leq i\} $
and note that
 $ h^{-1}_{q_M}(x) \subset h^{-1}_{q_j}(x)$
for each
$ h^{-1}_{q_M}(x) \subset h^{-1}_{q_j}(x)$
for each
![]() $j \leq i$
and for each x such that
$j \leq i$
and for each x such that
![]() $\mathrm {max\,}\mathrm {supp\,}(x) < \mathrm {min\,}\{ q_m, \xi _m \}$
. It is easy to see that
$\mathrm {max\,}\mathrm {supp\,}(x) < \mathrm {min\,}\{ q_m, \xi _m \}$
. It is easy to see that
 $h^{-1}_{q_M}(x) \cup \bigcup _{j\leq i}\mathcal {C} _i $
is strongly centered, hence
$h^{-1}_{q_M}(x) \cup \bigcup _{j\leq i}\mathcal {C} _i $
is strongly centered, hence
![]() $\mathcal {D}_i$
is strongly centered.
$\mathcal {D}_i$
is strongly centered.
Fix i, and suppose that (5) does not hold. So take a witness
![]() $\int \mathcal {W}$
. From Remark 2.4, without loss of generality, we may assume that
$\int \mathcal {W}$
. From Remark 2.4, without loss of generality, we may assume that
 $ \int {\mathcal {W}}\subset \langle \mathcal {D}_{i}\cup \widetilde {\mathcal {W}} \rangle $
.
$ \int {\mathcal {W}}\subset \langle \mathcal {D}_{i}\cup \widetilde {\mathcal {W}} \rangle $
.
Let
![]() $A_W \in \mathcal {A}$
,
$A_W \in \mathcal {A}$
,
![]() $P_W\in p$
,
$P_W\in p$
,
![]() $n_W\in \omega $
,
$n_W\in \omega $
,
![]() $C_n^W \in \mathcal {C }$
for
$C_n^W \in \mathcal {C }$
for
![]() $n\leq n_W$
, and
$n\leq n_W$
, and
![]() $l_W \in \omega $
. Define
$l_W \in \omega $
. Define
 $$ \begin{align*} W^*(A_W, P_W, C_1^W, \ldots , C_{n_W}^W, \widetilde{W_{l_W}}) = \bigcap_{n\leq n_W} C_n^W \cap \bigcap_{j \leq i} h^{-1}_{\xi_j} (A_W \cap P_W) \cap \widetilde{W_{l_W}}. \end{align*} $$
$$ \begin{align*} W^*(A_W, P_W, C_1^W, \ldots , C_{n_W}^W, \widetilde{W_{l_W}}) = \bigcap_{n\leq n_W} C_n^W \cap \bigcap_{j \leq i} h^{-1}_{\xi_j} (A_W \cap P_W) \cap \widetilde{W_{l_W}}. \end{align*} $$
Define
![]() $W \in \mathcal {W}^-$
if and only if
$W \in \mathcal {W}^-$
if and only if
![]() $W \in \int \mathcal {W}$
and W is co-finite or empty on each
$W \in \int \mathcal {W}$
and W is co-finite or empty on each
![]() $W_i$
. We will say that a set
$W_i$
. We will say that a set
![]() $W\in \mathcal {W}$
is
$W\in \mathcal {W}$
is
![]() $\mathit {attainable}$
(by
$\mathit {attainable}$
(by
![]() $(n_A, P_W, n_W, l_W)$
) if there exist
$(n_A, P_W, n_W, l_W)$
) if there exist
![]() $A_W \in \mathcal {A}_{n_A}$
,
$A_W \in \mathcal {A}_{n_A}$
,
 $\{C_k^W \in \bigcup _{j \leq i} \mathcal {C}_j: k \leq n_W\}$
such that the condition
$\{C_k^W \in \bigcup _{j \leq i} \mathcal {C}_j: k \leq n_W\}$
such that the condition
 $W^*(A_W, P_W, C_1^W, \ldots , C_{n_W}^W, \widetilde {W_{l_W} }) \subset W$
is satisfied. The complement (to
$W^*(A_W, P_W, C_1^W, \ldots , C_{n_W}^W, \widetilde {W_{l_W} }) \subset W$
is satisfied. The complement (to
![]() $\widetilde {W_1}$
) of the attainable set is called removable and sometimes we indicate which variables, sets, functions.
$\widetilde {W_1}$
) of the attainable set is called removable and sometimes we indicate which variables, sets, functions.
Since
![]() $\int \mathcal {W} \subset \langle \mathcal {D}_i \rangle $
, thus each set
$\int \mathcal {W} \subset \langle \mathcal {D}_i \rangle $
, thus each set
![]() $W \in \mathcal {W}^-$
is attainable.
$W \in \mathcal {W}^-$
is attainable.
Consider a sequence of possibilities:
-
1) l cannot be fixed, i.e., for each
 $l\in \omega $
there exists
$l\in \omega $
there exists
 $W \in { \mathcal {W}^-}$
such that W is not removable by any
$W \in { \mathcal {W}^-}$
such that W is not removable by any
 $(n_A, P_W, n_W, l)$
;
$(n_A, P_W, n_W, l)$
; -
2) l can be fixed, but
 $n_A$
cannot, i.e., for each
$n_A$
cannot, i.e., for each
 $W\in \mathcal {W}^-$
, W is attainable by some
$W\in \mathcal {W}^-$
, W is attainable by some
 $(n^A_W, P_W, n^C_W, l)$
, but for each
$(n^A_W, P_W, n^C_W, l)$
, but for each
 $n_A$
there exists
$n_A$
there exists
 $W^{\prime }\in {\mathcal {W}^-}$
such that
$W^{\prime }\in {\mathcal {W}^-}$
such that
 $W^{\prime }$
is not attainable by any
$W^{\prime }$
is not attainable by any
 $(n^A, P_{W^{\prime }}, n^C_{W^{\prime }}, l)$
;
$(n^A, P_{W^{\prime }}, n^C_{W^{\prime }}, l)$
; -
3) l and
 $n^A$
can be fixed, but
$n^A$
can be fixed, but
 $n_C$
cannot;
$n_C$
cannot; -
4) l,
 $n^A$
and
$n^A$
and
 $n^C$
can be fixed, but P cannot;
$n^C$
can be fixed, but P cannot; -
5) l,
 $n^A$
,
$n^A$
,
 $n^C$
, and P can be fixed.
$n^C$
, and P can be fixed.
Note that each set
![]() $W \in \mathcal {W}^-$
is attainable if and only if an alternative of cases 1) to 5) holds.
$W \in \mathcal {W}^-$
is attainable if and only if an alternative of cases 1) to 5) holds.
In case 1) for each l, let
![]() $W_l\subset \widetilde { {W}_l}$
and
$W_l\subset \widetilde { {W}_l}$
and
![]() $W_l \in \mathcal {W}^-$
be a witness that l may not be fixed. Note that
$W_l \in \mathcal {W}^-$
be a witness that l may not be fixed. Note that
![]() $\bigcup _{l<\omega }W_l \in \mathcal {W}^-$
and that
$\bigcup _{l<\omega }W_l \in \mathcal {W}^-$
and that
![]() $\bigcup _{l<\omega }W_l$
may not be removed by any
$\bigcup _{l<\omega }W_l$
may not be removed by any
 $(n^A_W, P_W, n^C_W, l_W)$
.
$(n^A_W, P_W, n^C_W, l_W)$
.
In case 2) we proceed like in case 1). Note that if
![]() $l^{\prime }\geq l$
and
$l^{\prime }\geq l$
and
![]() ${ n^A}^{\prime }$
and a set
${ n^A}^{\prime }$
and a set
![]() $W \in \mathcal {W}^-$
is not removable by any
$W \in \mathcal {W}^-$
is not removable by any
 $({ n^A}^{\prime }, P_W, n^C_W, l^{\prime })$
then the set W is also not removable by any
$({ n^A}^{\prime }, P_W, n^C_W, l^{\prime })$
then the set W is also not removable by any
 $(n^A, P_W, n^C_W, l)$
. Thus it suffices to consider cases when
$(n^A, P_W, n^C_W, l)$
. Thus it suffices to consider cases when
![]() $l=n^A$
. For each l, let
$l=n^A$
. For each l, let
![]() $W_l\subset \widetilde { {W}_l}$
and
$W_l\subset \widetilde { {W}_l}$
and
![]() $W_l \in \mathcal {W}^-$
be a witness that l and
$W_l \in \mathcal {W}^-$
be a witness that l and
![]() $n^A=l$
may not be fixed. Again note that
$n^A=l$
may not be fixed. Again note that
![]() $\bigcup _{l<\omega }W_l \in \mathcal {W}^-$
and that
$\bigcup _{l<\omega }W_l \in \mathcal {W}^-$
and that
![]() $\bigcup _{l<\omega }W_l$
may not be removed by any
$\bigcup _{l<\omega }W_l$
may not be removed by any
 $(n^A_W, P_W, n^C_W, l_W)$
.
$(n^A_W, P_W, n^C_W, l_W)$
.
In case 3) we proceed just like in case 2), not using that
![]() $n^A$
is fixed.
$n^A$
is fixed.
In case 4) for
![]() $k<\omega $
, let
$k<\omega $
, let
![]() $X_k$
be the set of those
$X_k$
be the set of those
![]() $x\in X$
that for all
$x\in X$
that for all
![]() $U\subset f^{-1}(x)$
such that
$U\subset f^{-1}(x)$
such that
![]() $\mathrm {card\,}(f^{-1}(x) \setminus U) \leq n^A$
, for all partitions of a set
$\mathrm {card\,}(f^{-1}(x) \setminus U) \leq n^A$
, for all partitions of a set
 $\bigcup _{j=1}^i(\xi _j^{-1}(X) \cap \widetilde {(W_k)})$
on the sets
$\bigcup _{j=1}^i(\xi _j^{-1}(X) \cap \widetilde {(W_k)})$
on the sets
![]() $X_{m,n}$
, for
$X_{m,n}$
, for
![]() $m<n\leq i$
, there exist
$m<n\leq i$
, there exist
![]() $ m_0, n_0$
such that
$ m_0, n_0$
such that
![]() $m_0<n_0\leq i$
and there exist
$m_0<n_0\leq i$
and there exist
![]() $x_1, \ldots , x_{n^C+1} \in X_{m_0,n_0}$
that for
$x_1, \ldots , x_{n^C+1} \in X_{m_0,n_0}$
that for
![]() $\xi _{(min)}=\mathrm {min\,}\{\xi _{m_0}, \xi _{n_0}\} $
,
$\xi _{(min)}=\mathrm {min\,}\{\xi _{m_0}, \xi _{n_0}\} $
,
![]() $\xi _{(max)}=\mathrm {max\,}\{\xi _{m_0}, \xi _{n_0}\}$
there is
$\xi _{(max)}=\mathrm {max\,}\{\xi _{m_0}, \xi _{n_0}\}$
there is
![]() $\xi _{(min)}(x_r)=\xi _{(min)}(x_j)$
for
$\xi _{(min)}(x_r)=\xi _{(min)}(x_j)$
for
![]() $r,j \leq n^C+1$
and
$r,j \leq n^C+1$
and
![]() $ \xi _{(max)}(x_r)\not =\xi _{(max)}(x_j)$
for
$ \xi _{(max)}(x_r)\not =\xi _{(max)}(x_j)$
for
![]() $r,j \leq n^C+1$
,
$r,j \leq n^C+1$
,
![]() $r\not = j$
.
$r\not = j$
.
Clearly,
![]() $(X_{k})$
is a decreasing sequence. If there exists k such that
$(X_{k})$
is a decreasing sequence. If there exists k such that
![]() $ X_{k}\not \in p$
then putting
$ X_{k}\not \in p$
then putting
![]() $l=k$
there exists a set
$l=k$
there exists a set
![]() $P=(X_{k})^{c}$
such that all
$P=(X_{k})^{c}$
such that all
![]() $W\in \mathcal {W}^{-}$
may be attained by
$W\in \mathcal {W}^{-}$
may be attained by
![]() $(n^{A},P,n^{C},l)$
so we would be in case 5), so, without loss of generality,
$(n^{A},P,n^{C},l)$
so we would be in case 5), so, without loss of generality,
![]() $X_{k}\in P$
for each
$X_{k}\in P$
for each
![]() $ k<\omega $
.
$ k<\omega $
.
Thus take a partition of X by
![]() $(X_k\setminus X_{k+1})$
. Since p is a P-point, and since
$(X_k\setminus X_{k+1})$
. Since p is a P-point, and since
![]() $X_k\in p$
thus there exists
$X_k\in p$
thus there exists
![]() $P_0\in p$
such that
$P_0\in p$
such that
![]() $ P_k=P_0\cap (X_k \setminus X_{k+1})$
is finite for all
$ P_k=P_0\cap (X_k \setminus X_{k+1})$
is finite for all
![]() $k<\omega $
. For each
$k<\omega $
. For each
![]() $ x\in P_k$
there exists a finite(!) set
$ x\in P_k$
there exists a finite(!) set
 $K_{k,x}\subset \widetilde {(W_k)} \cap \bigcup _{j\leq i}h^{-1}_{\xi _i}$
that may not be removed by
$K_{k,x}\subset \widetilde {(W_k)} \cap \bigcup _{j\leq i}h^{-1}_{\xi _i}$
that may not be removed by
![]() $ (n^A,X,n^C,k)$
. (The proof that
$ (n^A,X,n^C,k)$
. (The proof that
![]() $K_{k,x}$
may be chosen finite is analogical, but easier, to that of case 5)). Take
$K_{k,x}$
may be chosen finite is analogical, but easier, to that of case 5)). Take
 $ K=\bigcup _{k<\omega , x\in P_k}K_{k,x}$
and notice that
$ K=\bigcup _{k<\omega , x\in P_k}K_{k,x}$
and notice that
 $\widetilde {(W_1)} \setminus K \in \mathcal {W}^-$
and that
$\widetilde {(W_1)} \setminus K \in \mathcal {W}^-$
and that
 $\widetilde {(W_1)}\setminus K$
is not removable by
$\widetilde {(W_1)}\setminus K$
is not removable by
![]() $(n^A, P, n^C, l)$
for any
$(n^A, P, n^C, l)$
for any
![]() $P\in p$
.
$P\in p$
.
In case 5) arrange
 $\bigcup _{j \leq i} h^{-1}_{\xi _j} (P) \cap \widetilde { W_{l}}$
into a sequence
$\bigcup _{j \leq i} h^{-1}_{\xi _j} (P) \cap \widetilde { W_{l}}$
into a sequence
![]() $(x_k)_{k<\omega }$
. Let
$(x_k)_{k<\omega }$
. Let
 $R(x) = {\binom {{\mathrm { card\,}(f^{-1}(x))} }{{\mathrm {card\,}(f^{-1}(x)) - n^C}}}$
, where
$R(x) = {\binom {{\mathrm { card\,}(f^{-1}(x))} }{{\mathrm {card\,}(f^{-1}(x)) - n^C}}}$
, where
![]() $\binom {{n } }{{k}}$
denotes a binomial coefficient, and let
$\binom {{n } }{{k}}$
denotes a binomial coefficient, and let
![]() $(A_{x,r})_{r \leq R}$
be a sequence of all subsets of
$(A_{x,r})_{r \leq R}$
be a sequence of all subsets of
![]() $f^{-1}(x)$
of cardinality equal to
$f^{-1}(x)$
of cardinality equal to
![]() $\mathrm { card\,}(f^{-1}(x) - n^C)$
. Consider a tree T, where the root is
$\mathrm { card\,}(f^{-1}(x) - n^C)$
. Consider a tree T, where the root is
![]() $\emptyset $
and on a level k the nodes are pairs of natural numbers
$\emptyset $
and on a level k the nodes are pairs of natural numbers
![]() $j,r$
such that
$j,r$
such that
![]() $ j\leq i$
and
$ j\leq i$
and
![]() $r\leq R(f(x_k))$
and, for each branch
$r\leq R(f(x_k))$
and, for each branch
![]() $\tilde {T}$
of T,
$\tilde {T}$
of T,
![]() $ \pi _2(\tilde {T}(k_1))=\pi _2(\tilde {T}(k_2))$
if
$ \pi _2(\tilde {T}(k_1))=\pi _2(\tilde {T}(k_2))$
if
![]() $f(x_{k_1})=f(x_{k_2})$
, where
$f(x_{k_1})=f(x_{k_2})$
, where
![]() $\tilde {T}(k)$
is an element of level k of a branch
$\tilde {T}(k)$
is an element of level k of a branch
![]() $\tilde {T}$
and
$\tilde {T}$
and
![]() $ \pi _2$
is a projection on the second coordinate. We see j as a choice to which class
$ \pi _2$
is a projection on the second coordinate. We see j as a choice to which class
![]() $\mathcal {C}_j$
does a set
$\mathcal {C}_j$
does a set
 $C_{(.)}^{(.)}$
belongs and we see r as a choice of one of sets
$C_{(.)}^{(.)}$
belongs and we see r as a choice of one of sets
![]() $A_{f(x),r}$
that
$A_{f(x),r}$
that
 $C_{(.)}^{(.)}$
together with
$C_{(.)}^{(.)}$
together with
![]() $ A_{f(x),r}$
removes
$ A_{f(x),r}$
removes
![]() $x_k$
.
$x_k$
.
Clearly, the complements of all finite sets belong to
![]() $\int \mathcal {W}$
, so each finite set is removable. (6)
$\int \mathcal {W}$
, so each finite set is removable. (6)
The maximal element of the branch
![]() $\tilde {T}$
has no successors if and only if there is
$\tilde {T}$
has no successors if and only if there is
![]() $j \leq i$
such that there is no n sets in
$j \leq i$
such that there is no n sets in
![]() $\mathcal {C}_j$
that remove all
$\mathcal {C}_j$
that remove all
![]() $ x_t$
such that
$ x_t$
such that
![]() $\tilde {T}(k)=j$
and
$\tilde {T}(k)=j$
and
 $f(x_k)\in A_{f(x_k), \pi _2(\tilde {T} (k))}$
. It implies that the set
$f(x_k)\in A_{f(x_k), \pi _2(\tilde {T} (k))}$
. It implies that the set
 $\{x_k: \tilde {T}(k)=j, f(x_k)\in A_{f(x_k), \pi _2(\tilde {T}(k))}\}$
contains more than n different elements, say
$\{x_k: \tilde {T}(k)=j, f(x_k)\in A_{f(x_k), \pi _2(\tilde {T}(k))}\}$
contains more than n different elements, say
![]() $x^1, \ldots , x^{n+1}$
, such that
$x^1, \ldots , x^{n+1}$
, such that
 $h_{\xi _j}(x_{s_1}) = h_{\xi _j}(x_{s_2})$
and
$h_{\xi _j}(x_{s_1}) = h_{\xi _j}(x_{s_2})$
and
 $h_{\eta _j}(x_{s_1}) \not = h_{\eta _j}(x_{s_2})$
for
$h_{\eta _j}(x_{s_1}) \not = h_{\eta _j}(x_{s_2})$
for
![]() $ s_1\not = s_2$
,
$ s_1\not = s_2$
,
![]() $s_1, s_2 \in \{1, \ldots , n+1\}$
.
$s_1, s_2 \in \{1, \ldots , n+1\}$
.
By K
![]() $\ddot {\mathrm {o}}$
nig Lemma if all branches are finite, then the height of the tree T is finite, and so there are irremovable finite sets in contrary to (6). Thus there is infinite branch and the whole set
$\ddot {\mathrm {o}}$
nig Lemma if all branches are finite, then the height of the tree T is finite, and so there are irremovable finite sets in contrary to (6). Thus there is infinite branch and the whole set
 $\bigcap _{j \leq i} h^{-1}_{\xi _i} (P) \cap \widetilde {W_{l}}$
is removable.⊣
$\bigcap _{j \leq i} h^{-1}_{\xi _i} (P) \cap \widetilde {W_{l}}$
is removable.⊣
As an immediate consequence of Lemma 3.13 (with the use of Theorem 3.5) we have the following:
Theorem 3.14.
![]() $(\mathfrak {b}=\mathfrak {c})$
. For each P-point p, there exists an order embedding of the long line into the set of P-points above p.
$(\mathfrak {b}=\mathfrak {c})$
. For each P-point p, there exists an order embedding of the long line into the set of P-points above p.
Remark 3.15. Note that there is a potential chance to improve Theorem 3.14 in the virtue of Question 3.11, i.e., if, in some model, for each
![]() $\alpha < \kappa $
(for some cardinal invariant
$\alpha < \kappa $
(for some cardinal invariant
![]() $\kappa $
) each RK-increasing
$\kappa $
) each RK-increasing
![]() $\alpha $
-sequence of P-points is upper bounded by a P-point, then (in that model) if
$\alpha $
-sequence of P-points is upper bounded by a P-point, then (in that model) if
![]() $\mathfrak {b}=\mathfrak {c}$
, then, above each P-point, there is an order embedding of a
$\mathfrak {b}=\mathfrak {c}$
, then, above each P-point, there is an order embedding of a
![]() $\kappa $
-long-line into the set of P-points.
$\kappa $
-long-line into the set of P-points.
4 Cardinal
 $\mathfrak {q}$
$\mathfrak {q}$
An inspection of our proofs indicates a possibility of refinement of most results with the aid of an, a priori, new cardinal invariant. We define
![]() $\mathfrak {q}$
to be the minimal cardinality of families
$\mathfrak {q}$
to be the minimal cardinality of families
![]() $\mathcal { B}$
, for which there exists a family
$\mathcal { B}$
, for which there exists a family
![]() $\mathcal {A}$
such that
$\mathcal {A}$
such that
![]() $\langle \mathcal {A}\cup \mathcal {B}\rangle $
includes a contour, and
$\langle \mathcal {A}\cup \mathcal {B}\rangle $
includes a contour, and
![]() $\langle \mathcal {A}\cup \mathcal {C}\rangle $
includes no contour for every countable family
$\langle \mathcal {A}\cup \mathcal {C}\rangle $
includes no contour for every countable family
![]() $\mathcal {C}$
.Footnote
6
$\mathcal {C}$
.Footnote
6
If
![]() $\mathbb {P}$
is a collection of families such that
$\mathbb {P}$
is a collection of families such that
![]() $\mathcal {P}\in \mathbb {P}$
whenever
$\mathcal {P}\in \mathbb {P}$
whenever
![]() $\langle \mathcal {P}\rangle $
includes a contour, then
$\langle \mathcal {P}\rangle $
includes a contour, then
![]() $ \mathfrak {q}$
fulfills
$ \mathfrak {q}$
fulfills
 $$ \begin{align*} \mathfrak{q}=\mathrm{min\,}\{\mathrm{card\,}(\mathcal{B}):\underset{\mathcal{ A}}{\exists }\;\mathcal{A}\cup \mathcal{B}\in \mathbb{P}\wedge \underset{ \mathcal{C}}{\forall }\left( \mathrm{card\,}(\mathcal{C})\leq \aleph _{0}\Longrightarrow \mathcal{A}\cup \mathcal{C}\notin \mathbb{P}\right) \}. \end{align*} $$
$$ \begin{align*} \mathfrak{q}=\mathrm{min\,}\{\mathrm{card\,}(\mathcal{B}):\underset{\mathcal{ A}}{\exists }\;\mathcal{A}\cup \mathcal{B}\in \mathbb{P}\wedge \underset{ \mathcal{C}}{\forall }\left( \mathrm{card\,}(\mathcal{C})\leq \aleph _{0}\Longrightarrow \mathcal{A}\cup \mathcal{C}\notin \mathbb{P}\right) \}. \end{align*} $$
Each contour has a base of cardinality
![]() $\mathfrak {d}$
, which, by the way, is the minimal cardinality of bases of contours [Reference van Douwen, Kunen and Vaughan13, Theorem 5.2]. Therefore, taking into account Theorem 2.5, we have
$\mathfrak {d}$
, which, by the way, is the minimal cardinality of bases of contours [Reference van Douwen, Kunen and Vaughan13, Theorem 5.2]. Therefore, taking into account Theorem 2.5, we have
Theorem 4.1.
 $\mathfrak {b}\leq \mathrm {cof\,}(\mathfrak {q}) \leq \mathfrak {q}\leq \mathfrak {d}$
$\mathfrak {b}\leq \mathrm {cof\,}(\mathfrak {q}) \leq \mathfrak {q}\leq \mathfrak {d}$
Using the cardinal
![]() $\mathfrak {q}$
, we are in a position to formulate stronger versions, if
$\mathfrak {q}$
, we are in a position to formulate stronger versions, if
![]() $\mathfrak {b}<\mathfrak {q}$
is consistent, of several of our theorems with almost unchanged proofs. Indeed, by the proof of Theorem 3.1 we get the following theorem:
$\mathfrak {b}<\mathfrak {q}$
is consistent, of several of our theorems with almost unchanged proofs. Indeed, by the proof of Theorem 3.1 we get the following theorem:
Theorem 4.2
 $(\mathfrak {q}=\mathfrak {c})$
$(\mathfrak {q}=\mathfrak {c})$
For each P-point p there exists a P-point q strictly RK-greater than p.
By the proof of Theorem 3.5, we have
Theorem 4.3
 $(\mathfrak {q}=\mathfrak {c})$
$(\mathfrak {q}=\mathfrak {c})$
If
![]() $(p_{n})_{n<\omega }$
is an RK-increasing sequence of P-points, then there exists a P-point u such that
$(p_{n})_{n<\omega }$
is an RK-increasing sequence of P-points, then there exists a P-point u such that
![]() $ u>_{RK}p_{n} $
for each
$ u>_{RK}p_{n} $
for each
![]() $n<\omega $
.
$n<\omega $
.
By the proof of Theorem 3.10, we get
Theorem 4.4
 $(\mathfrak {q}=\mathfrak {c})$
$(\mathfrak {q}=\mathfrak {c})$
For each P-point p, for each
![]() $\alpha < \mathfrak {b}^+$
, there exists an order embedding of
$\alpha < \mathfrak {b}^+$
, there exists an order embedding of
![]() $\alpha $
into P-points above p.
$\alpha $
into P-points above p.
By the proof of Theorem 3.12, we obtain
Theorem 4.5
 $(\mathfrak {q}=\mathfrak {c})$
$(\mathfrak {q}=\mathfrak {c})$
Above each P-point, there exists an order-embedding of the real line in the set of P-points.
By the proof of Theorem 3.14, we have
Theorem 4.6
 $(\mathfrak {q}=\mathfrak {c})$
$(\mathfrak {q}=\mathfrak {c})$
Above each P-point, there exists an order embedding of the long line into the set of P-points.
A relative importance of the facts formulated above depends on answers to the following quest.
Question 4.7. Is
![]() $\mathfrak {q}$
equal to any already defined cardinal invariant? Is
$\mathfrak {q}$
equal to any already defined cardinal invariant? Is
![]() $ \mathfrak {b}<\mathfrak {q}$
consistent? Is
$ \mathfrak {b}<\mathfrak {q}$
consistent? Is
![]() $\mathfrak {q}<\mathfrak {d}$
consistent?
$\mathfrak {q}<\mathfrak {d}$
consistent?
5 Variants of invariants
The cardinal
![]() $\mathfrak {q}$
can be seen as an instance of cardinal invariants, which can possibly be defined in order to refine certain types of theorems, by scrutinizing the mechanisms underlying their proofs. In our approach, such cardinals represent “distances” between certain classes of objects. They carry some obvious questions about their relation to the usual cardinal invariants, and in particular to those that they are supposed to replace in potentially refined arguments.
$\mathfrak {q}$
can be seen as an instance of cardinal invariants, which can possibly be defined in order to refine certain types of theorems, by scrutinizing the mechanisms underlying their proofs. In our approach, such cardinals represent “distances” between certain classes of objects. They carry some obvious questions about their relation to the usual cardinal invariants, and in particular to those that they are supposed to replace in potentially refined arguments.
Let
![]() $\mathbb {S}$
and
$\mathbb {S}$
and
![]() $\mathbb {T}$
be collections of families (of sets or functions, or possibly other objects) such that for each
$\mathbb {T}$
be collections of families (of sets or functions, or possibly other objects) such that for each
![]() $\mathcal {S}\in \mathbb {S}$
there exists
$\mathcal {S}\in \mathbb {S}$
there exists
![]() $\mathcal {T}\in \mathbb {T}$
such that
$\mathcal {T}\in \mathbb {T}$
such that
![]() $\mathcal {S}\subset \mathcal {T}$
. For each
$\mathcal {S}\subset \mathcal {T}$
. For each
![]() $\mathcal {S} \in \mathbb {S}$
, we define
$\mathcal {S} \in \mathbb {S}$
, we define
Let
![]() $\mathfrak {D}(\mathbb {S},\mathbb {T})=\{\mathfrak {dist}(\mathcal {S}, \mathbb {T}):\mathcal {S}\in \mathbb {S}\}$
. As a set of cardinal numbers,
$\mathfrak {D}(\mathbb {S},\mathbb {T})=\{\mathfrak {dist}(\mathcal {S}, \mathbb {T}):\mathcal {S}\in \mathbb {S}\}$
. As a set of cardinal numbers,
![]() $ \mathfrak {D}(\mathbb {S},\mathbb {T})$
is well ordered, hence we can define
$ \mathfrak {D}(\mathbb {S},\mathbb {T})$
is well ordered, hence we can define
![]() $ \mathfrak {dist}_{\beta }(\mathbb {S},\mathbb {T})$
to be the
$ \mathfrak {dist}_{\beta }(\mathbb {S},\mathbb {T})$
to be the
![]() $\beta $
-th element of
$\beta $
-th element of
![]() $\mathfrak {D}(\mathbb {S},\mathbb {T})$
.Footnote
7
Moreover, if
$\mathfrak {D}(\mathbb {S},\mathbb {T})$
.Footnote
7
Moreover, if
![]() $\alpha $
is a limit ordinal, and the cardinals
$\alpha $
is a limit ordinal, and the cardinals
![]() $\mathfrak {dist}_{\beta }(\mathbb {S}, \mathbb {T})$
are defined for all
$\mathfrak {dist}_{\beta }(\mathbb {S}, \mathbb {T})$
are defined for all
![]() $\beta <\alpha $
, then
$\beta <\alpha $
, then
 $\mathfrak {dist} _{<\alpha }(\mathbb {S},\mathbb {T}) = \mathrm {sup\,}_{\beta <\alpha }\mathfrak { dist}_{\beta }(\mathbb {S},\mathbb {T})$
.
$\mathfrak {dist} _{<\alpha }(\mathbb {S},\mathbb {T}) = \mathrm {sup\,}_{\beta <\alpha }\mathfrak { dist}_{\beta }(\mathbb {S},\mathbb {T})$
.
In particular, if
![]() $\mathbb {S}$
denotes the collection of compatible with a contour families of subsets of
$\mathbb {S}$
denotes the collection of compatible with a contour families of subsets of
![]() $\omega $
, and
$\omega $
, and
![]() $\mathbb {T}$
stands for the collection of families including a subbases of a contour, then we write
$\mathbb {T}$
stands for the collection of families including a subbases of a contour, then we write
![]() $\mathfrak {q}_{\alpha }=\mathfrak {dist}_{\alpha }(\mathbb {S}, \mathbb {T})$
. In order to show that
$\mathfrak {q}_{\alpha }=\mathfrak {dist}_{\alpha }(\mathbb {S}, \mathbb {T})$
. In order to show that
![]() $\left ( \mathfrak {q}_{\alpha }\right ) _{\alpha }$
are variants of
$\left ( \mathfrak {q}_{\alpha }\right ) _{\alpha }$
are variants of
![]() $\mathfrak {q}$
, we need the following Alternative Theorem [Reference Dolecki and Starosolski4, Theorem 3.1]. A relation
$\mathfrak {q}$
, we need the following Alternative Theorem [Reference Dolecki and Starosolski4, Theorem 3.1]. A relation
![]() $A\subset \left \{ \left ( n,k\right ) :n<\omega ,k<\omega \right \} $
is called transversal if A is infinite, and
$A\subset \left \{ \left ( n,k\right ) :n<\omega ,k<\omega \right \} $
is called transversal if A is infinite, and
![]() $\left \{ l:\left ( n,l\right ) \in A\right \} $
and
$\left \{ l:\left ( n,l\right ) \in A\right \} $
and
![]() $\left \{ m:\left ( m,k\right ) \in A\right \} $
are at most singletons for each
$\left \{ m:\left ( m,k\right ) \in A\right \} $
are at most singletons for each
![]() $n,k<\omega .$
⊣
$n,k<\omega .$
⊣
Theorem 5.1. Let
![]() $\left ( \mathcal {F}_{n}\right ) _{n}$
and
$\left ( \mathcal {F}_{n}\right ) _{n}$
and
![]() $\left ( \mathcal { G}_{k}\right ) _{k}$
be sequences of filters on a set X, and let
$\left ( \mathcal { G}_{k}\right ) _{k}$
be sequences of filters on a set X, and let
 $$ \begin{align*} \mathcal{F}:=\bigcup\nolimits_{m<\omega }\bigcap\nolimits_{n>m}\mathcal{F} _{n},\text{ and }\mathcal{G}:=\bigcup\nolimits_{m<\omega }\bigcap\nolimits_{k>m}\mathcal{G}_{k}. \end{align*} $$
$$ \begin{align*} \mathcal{F}:=\bigcup\nolimits_{m<\omega }\bigcap\nolimits_{n>m}\mathcal{F} _{n},\text{ and }\mathcal{G}:=\bigcup\nolimits_{m<\omega }\bigcap\nolimits_{k>m}\mathcal{G}_{k}. \end{align*} $$
If
![]() $\mathcal {F}$
is compatible with
$\mathcal {F}$
is compatible with
![]() $\mathcal {G}$
, then the following alternative holds
$\mathcal {G}$
, then the following alternative holds
![]() $:$
$:$
![]() $ \mathcal {F}_{n}$
is compatible with
$ \mathcal {F}_{n}$
is compatible with
![]() $\mathcal {G}_{k}$
for a transversal set of
$\mathcal {G}_{k}$
for a transversal set of
![]() $\left ( n,k\right ) $
, or
$\left ( n,k\right ) $
, or
![]() $\mathcal {F}$
is compatible with
$\mathcal {F}$
is compatible with
![]() $\mathcal {G}_{k}$
for infinitely many
$\mathcal {G}_{k}$
for infinitely many
![]() $k,$
or
$k,$
or
![]() $ \mathcal {F}_{n}$
is compatible with
$ \mathcal {F}_{n}$
is compatible with
![]() $\mathcal {G}$
for infinitely many
$\mathcal {G}$
for infinitely many
![]() $n.$
$n.$
Proposition 5.2.
![]() $\mathfrak {q}_{0}=0$
,
$\mathfrak {q}_{0}=0$
,
![]() $\mathfrak {q}_{1}=1$
,
$\mathfrak {q}_{1}=1$
,
![]() $\mathfrak {q}_{2}=\aleph _{0}$
,
$\mathfrak {q}_{2}=\aleph _{0}$
,
![]() $ \mathfrak {q}_{3}=\mathfrak {q}$
, and
$ \mathfrak {q}_{3}=\mathfrak {q}$
, and
![]() $\mathfrak {q}_\alpha \leq \mathfrak {d}$
for all
$\mathfrak {q}_\alpha \leq \mathfrak {d}$
for all
![]() $\alpha $
.
$\alpha $
.
Proof. By taking
![]() $\mathcal {S}\in \mathbb {T}$
and
$\mathcal {S}\in \mathbb {T}$
and
![]() $\mathcal {B}=\emptyset ,$
we infer that
$\mathcal {B}=\emptyset ,$
we infer that
![]() $\mathfrak {q}_{0}=0$
.
$\mathfrak {q}_{0}=0$
.
To see that
![]() $\mathfrak {q}_{1}=1,$
let A, B be disjoint countably infinite sets. Let
$\mathfrak {q}_{1}=1,$
let A, B be disjoint countably infinite sets. Let
![]() $\mathcal {S}_{A}$
be a contour on A and let
$\mathcal {S}_{A}$
be a contour on A and let
![]() $\mathcal {S} _{B}$
be a cofinite filter on B. Define a filter
$\mathcal {S} _{B}$
be a cofinite filter on B. Define a filter
![]() $\mathcal {S}$
on
$\mathcal {S}$
on
![]() $A\cup B$
by
$A\cup B$
by
![]() $S\in \mathcal {S}$
if and only if
$S\in \mathcal {S}$
if and only if
![]() $S\cap A\in \mathcal {S}_{A}$
and
$S\cap A\in \mathcal {S}_{A}$
and
![]() $S\cap B\in \mathcal {S}_{B}$
. Clearly
$S\cap B\in \mathcal {S}_{B}$
. Clearly
![]() $\mathcal {S}$
is not finer than a contour (since is RK-smaller than a cofinite filter
$\mathcal {S}$
is not finer than a contour (since is RK-smaller than a cofinite filter
![]() $\mathcal {S}_{B}$
), and
$\mathcal {S}_{B}$
), and
![]() $\mathcal {S} \cup \{A\}$
is a subbase of a contour.
$\mathcal {S} \cup \{A\}$
is a subbase of a contour.
Clearly,
![]() $\mathfrak {q}_{2}$
cannot be finite. To see that
$\mathfrak {q}_{2}$
cannot be finite. To see that
![]() $\mathfrak {q} _{2}=\aleph _{0},$
let
$\mathfrak {q} _{2}=\aleph _{0},$
let
![]() $\mathcal {W}=(W_{n})_{n<\omega }$
be a partition of
$\mathcal {W}=(W_{n})_{n<\omega }$
be a partition of
![]() $ \omega $
into infinite sets. We define a family
$ \omega $
into infinite sets. We define a family
![]() $\mathcal {S}$
so that
$\mathcal {S}$
so that
![]() $S\in \mathcal {S}$
if and only if S is cofinite on each
$S\in \mathcal {S}$
if and only if S is cofinite on each
![]() $W_{n}$
. Suppose that there is a partition
$W_{n}$
. Suppose that there is a partition
![]() $\mathcal {V}=(V_{n})_{n<\omega }$
such that
$\mathcal {V}=(V_{n})_{n<\omega }$
such that
![]() $\int {\mathcal {V}} \subset \langle \mathcal {S}\cup S_{0}\rangle $
for some set
$\int {\mathcal {V}} \subset \langle \mathcal {S}\cup S_{0}\rangle $
for some set
![]() $S_{0}$
such that
$S_{0}$
such that
![]() $\mathcal {S}\cup S_{0}$
is strongly centered. Let
$\mathcal {S}\cup S_{0}$
is strongly centered. Let
![]() $N_{fin}=\{n<\omega : \mathrm {card\,}(W_{n}\cap S_{0})<\omega \}$
and
$N_{fin}=\{n<\omega : \mathrm {card\,}(W_{n}\cap S_{0})<\omega \}$
and
![]() $N_{\mathrm {\infty }}=\omega \setminus N_{fin}$
. Define
$N_{\mathrm {\infty }}=\omega \setminus N_{fin}$
. Define
 $S_{fin}=S_{0}\cap \bigcup _{n\in N_{fin}}W_{n}$
and
$S_{fin}=S_{0}\cap \bigcup _{n\in N_{fin}}W_{n}$
and
![]() $S_{\infty }=S_{0}\cap \bigcup _{n\in N_{\infty }}W_{n}$
. Since
$S_{\infty }=S_{0}\cap \bigcup _{n\in N_{\infty }}W_{n}$
. Since
 $S_{fin}^{c}\in \mathcal {S }$
, without loss of generality, we can assume that
$S_{fin}^{c}\in \mathcal {S }$
, without loss of generality, we can assume that
![]() $S_{0}=S_{\infty }$
and so without loss of generality we can assume that
$S_{0}=S_{\infty }$
and so without loss of generality we can assume that
![]() $S_{0}=\omega $
.
$S_{0}=\omega $
.
Note also that
![]() $\bigcup _{n<\omega }V_{n}\cap W_{i}$
is infinite for infinitely many i, and so
$\bigcup _{n<\omega }V_{n}\cap W_{i}$
is infinite for infinitely many i, and so
![]() $\int \mathcal{W}$
is compatible with
$\int \mathcal{W}$
is compatible with
![]() $\int \mathcal{V}$
. Thus we meet the assumptions of Theorem 5.1, and in each of the three cases there exist
$\int \mathcal{V}$
. Thus we meet the assumptions of Theorem 5.1, and in each of the three cases there exist
![]() $i,j<\omega $
such that
$i,j<\omega $
such that
![]() $V_{i}\cap W_{j}$
is infinite. But
$V_{i}\cap W_{j}$
is infinite. But
![]() $ \omega \setminus V_{i}\in \int \mathcal {V}$
and thus
$ \omega \setminus V_{i}\in \int \mathcal {V}$
and thus
![]() $\omega \setminus (V_{i}\cap W_{j})\in \mathcal {S}$
, contrary to the definition of
$\omega \setminus (V_{i}\cap W_{j})\in \mathcal {S}$
, contrary to the definition of
![]() $\mathcal {S} $
. On the other hand, by adding
$\mathcal {S} $
. On the other hand, by adding
![]() $\widetilde {\mathcal {W}}$
to
$\widetilde {\mathcal {W}}$
to
![]() $\mathcal {S}$
, we obtain a subbase of
$\mathcal {S}$
, we obtain a subbase of
![]() $\int \mathcal {W}.$
$\int \mathcal {W}.$
That
![]() $\mathfrak {q}_{3}=\mathfrak {q}$
follows directly from the definition of
$\mathfrak {q}_{3}=\mathfrak {q}$
follows directly from the definition of
![]() $\mathfrak {q}$
.
$\mathfrak {q}$
.
Finally,
![]() $\mathfrak {q}_{\alpha }\leq \mathfrak {d}$
since each contour has a base of cardinality
$\mathfrak {q}_{\alpha }\leq \mathfrak {d}$
since each contour has a base of cardinality
![]() $\mathfrak {d}$
, as we have shown in [Reference van Douwen, Kunen and Vaughan13, Theorem 5.2].
$\mathfrak {d}$
, as we have shown in [Reference van Douwen, Kunen and Vaughan13, Theorem 5.2].
If
![]() $\mathbb {S}$
is the collection of strongly centered families, but
$\mathbb {S}$
is the collection of strongly centered families, but
![]() $ \mathbb {T}$
is the collection of free ultrafilter subbases, then, taking
$ \mathbb {T}$
is the collection of free ultrafilter subbases, then, taking
![]() $\mathcal {S}$
as an empty family, clearly
$\mathcal {S}$
as an empty family, clearly
![]() $\mathfrak {dist}(\mathcal {S}, \mathbb {T})=u$
and so
$\mathfrak {dist}(\mathcal {S}, \mathbb {T})=u$
and so
![]() $\mathfrak {dist}_{\alpha }(\mathbb {S},\mathbb {T})=\mathfrak {u}$
for some
$\mathfrak {dist}_{\alpha }(\mathbb {S},\mathbb {T})=\mathfrak {u}$
for some
![]() $ \alpha $
, thus we obtain variants of
$ \alpha $
, thus we obtain variants of
![]() $\mathfrak {u}$
. By Fact 3.2,
$\mathfrak {u}$
. By Fact 3.2,
Fact 5.3.
![]() $\mathfrak {u}_0=0$
,
$\mathfrak {u}_0=0$
,
![]() $\mathfrak {u}_1=1$
,
$\mathfrak {u}_1=1$
,
![]() $\mathfrak {u}_2 \geq \aleph _1$
.
$\mathfrak {u}_2 \geq \aleph _1$
.
By the proof of Theorem 3.4, we obtain:
Theorem 5.4
 $(\mathfrak {q}=\mathfrak {u}_{2}=\mathfrak {c})$
$(\mathfrak {q}=\mathfrak {u}_{2}=\mathfrak {c})$
If p is a P-point, then there is a set
![]() $\mathfrak {U}$
of Rudin–Keisler incomparable P-points such that
$\mathfrak {U}$
of Rudin–Keisler incomparable P-points such that
![]() $\mathrm {card\,}\mathfrak {U}=\mathfrak {c}$
and
$\mathrm {card\,}\mathfrak {U}=\mathfrak {c}$
and
![]() $u>_{RK}p$
for each
$u>_{RK}p$
for each
![]() $u\in \mathfrak {U}$
.
$u\in \mathfrak {U}$
.
A similar approach can be carried out for all other cardinal invariants. Its usefulness, however, depends on the way these cardinals are used in specific arguments.
Acknowledgments
The author is grateful to Professor Szymon Dolecki for inspiring talks during the preparation of this paper, to the late Professor Józef Burzyk for a detailed perusing and pointing out some inaccuracies in the previous version of the paper and to the anonymous referee for a valuable pieces of information.