1 Introduction
Small organisms swimming at very low Reynolds numbers, for example spermatozoa in cervical mucus, cannot propel themselves by utilising the inertia of the surrounding fluid; time-reversible kinematics result in zero net displacement for the small body. G. I. Taylor’s pioneering study presented the first model of zero-Reynolds-number swimming where time-reversal symmetry is broken by the wave direction (Taylor Reference Taylor1951). This model was formulated as the far-field Stokes flow produced by a swimming motion given by a small amplitude sinusoidal wave, and the mean rate of working was calculated as a measure of the energetic cost of swimming. Our recent study (Cupples, Dyson & Smith Reference Cupples, Dyson and Smith2017) adapted Taylor’s model to account for fibre-reinforced media, similar in nature to the glycofilament structure of cervical mucus, through the transversely isotropic constitutive equations of Ericksen (Reference Ericksen1960); we now detail a correction and further analysis, which in particular shows the importance of fibre orientation for both passive and active fluid cases.
Our previous paper (Cupples et al. Reference Cupples, Dyson and Smith2017) consisted of calculating the mean swimming velocity and energy dissipation of an infinite waving sheet in a transversely isotropic fluid in two dimensions, extending the classical Taylor’s swimming sheet model to include anisotropic effects and active rheology. A surprising conclusion was that fibre orientation only affected swimming velocity in the active case. However a recent study by Shi & Powers (Reference Shi and Powers2017) investigated microscopic propulsion in nematic liquid crystals and found that in a common limit (passive, zero elasticity, zero shear viscosity and small extensional viscosity) the models disagreed, with their study finding an angle dependence in swimming speed. Here we find that this discrepancy is due to missed terms in the solution of the governing equation in Cupples et al. (Reference Cupples, Dyson and Smith2017). These terms are relevant to both the passive and active cases, and qualitatively change the conclusions.
The analysis involves a perturbation expansion in the small parameter
![]() $\unicode[STIX]{x1D700}=k^{\ast }b^{\ast }$
, where
$\unicode[STIX]{x1D700}=k^{\ast }b^{\ast }$
, where
![]() $b^{\ast }$
is the amplitude and
$b^{\ast }$
is the amplitude and
![]() $k^{\ast }$
the wavenumber. The leading-order solution at
$k^{\ast }$
the wavenumber. The leading-order solution at
![]() $O(\unicode[STIX]{x1D700})$
is unchanged from Cupples et al. (Reference Cupples, Dyson and Smith2017), and we here discuss a correction to the
$O(\unicode[STIX]{x1D700})$
is unchanged from Cupples et al. (Reference Cupples, Dyson and Smith2017), and we here discuss a correction to the
![]() $O(\unicode[STIX]{x1D700}^{2})$
solution which determines the swimming velocity. First the passive transversely isotropic fluid case is discussed (
$O(\unicode[STIX]{x1D700}^{2})$
solution which determines the swimming velocity. First the passive transversely isotropic fluid case is discussed (
![]() $\unicode[STIX]{x1D707}_{1}=0$
) in § 2, which is shown to be consistent with Shi & Powers (Reference Shi and Powers2017) in a common limit; the mean swimming velocity is recalculated and presented for a wide range of anisotropic extensional and shear viscosities in § 2.2. After this, a solution to the active case is considered in § 3, where a spatially averaged swimming velocity is calculated and discussed.
$\unicode[STIX]{x1D707}_{1}=0$
) in § 2, which is shown to be consistent with Shi & Powers (Reference Shi and Powers2017) in a common limit; the mean swimming velocity is recalculated and presented for a wide range of anisotropic extensional and shear viscosities in § 2.2. After this, a solution to the active case is considered in § 3, where a spatially averaged swimming velocity is calculated and discussed.
1.1 Equation formulation
The full system of equations is derived from the dimensionless Navier–Stokes equations, at zero Reynolds number, along with Ericksen’s (Reference Ericksen1960) constitutive equation for a transversely isotropic fluid (equations (2.1)–(2.3) in Cupples et al.
Reference Cupples, Dyson and Smith2017). A streamfunction
![]() $\unicode[STIX]{x1D713}$
, satisfying incompressibility, and an equation governing the perturbation to the fibre orientation
$\unicode[STIX]{x1D713}$
, satisfying incompressibility, and an equation governing the perturbation to the fibre orientation
![]() $\unicode[STIX]{x1D703}$
around a uniform initial fibre angle
$\unicode[STIX]{x1D703}$
around a uniform initial fibre angle
![]() $\unicode[STIX]{x1D719}$
(equation (2.5) in Cupples et al.
Reference Cupples, Dyson and Smith2017), complete the model. At
$\unicode[STIX]{x1D719}$
(equation (2.5) in Cupples et al.
Reference Cupples, Dyson and Smith2017), complete the model. At
![]() $O(\unicode[STIX]{x1D700}^{2})$
the system of partial differential equations is
$O(\unicode[STIX]{x1D700}^{2})$
the system of partial differential equations is
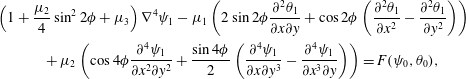 $$\begin{eqnarray}\displaystyle & \displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)\unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D713}_{1}-\unicode[STIX]{x1D707}_{1}\left(2\sin 2\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{1}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}+\cos 2\unicode[STIX]{x1D719}\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{1}}{\unicode[STIX]{x2202}x^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{1}}{\unicode[STIX]{x2202}y^{2}}\right)\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \quad +\,\unicode[STIX]{x1D707}_{2}\left(\cos 4\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x^{2}\unicode[STIX]{x2202}y^{2}}+\frac{\sin 4\unicode[STIX]{x1D719}}{2}\left(\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y^{3}}-\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x^{3}\unicode[STIX]{x2202}y}\right)\right)=F(\unicode[STIX]{x1D713}_{0},\unicode[STIX]{x1D703}_{0}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)\unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D713}_{1}-\unicode[STIX]{x1D707}_{1}\left(2\sin 2\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{1}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}+\cos 2\unicode[STIX]{x1D719}\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{1}}{\unicode[STIX]{x2202}x^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{1}}{\unicode[STIX]{x2202}y^{2}}\right)\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \quad +\,\unicode[STIX]{x1D707}_{2}\left(\cos 4\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x^{2}\unicode[STIX]{x2202}y^{2}}+\frac{\sin 4\unicode[STIX]{x1D719}}{2}\left(\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y^{3}}-\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x^{3}\unicode[STIX]{x2202}y}\right)\right)=F(\unicode[STIX]{x1D713}_{0},\unicode[STIX]{x1D703}_{0}), & \displaystyle\end{eqnarray}$$
where
![]() $F$
and
$F$
and
![]() $G$
are known functions of the
$G$
are known functions of the
![]() $O(\unicode[STIX]{x1D700})$
solutions and are given in appendix A. This is stated in full in Cupples et al. (Reference Cupples, Dyson and Smith2017, equation (C 1) of appendix C). These functions involve terms proportional to
$O(\unicode[STIX]{x1D700})$
solutions and are given in appendix A. This is stated in full in Cupples et al. (Reference Cupples, Dyson and Smith2017, equation (C 1) of appendix C). These functions involve terms proportional to
![]() $\cos ^{2}(x-t)$
,
$\cos ^{2}(x-t)$
,
![]() $\sin ^{2}(x-t)$
and
$\sin ^{2}(x-t)$
and
![]() $\sin (x-t)\cos (x-t)$
with coefficients in terms of the anisotropic parameters.
$\sin (x-t)\cos (x-t)$
with coefficients in terms of the anisotropic parameters.
In § 2 we take
![]() $\unicode[STIX]{x1D707}_{1}=0$
, which we refer to as the ‘passive fluid’ case, and solve the resulting system to determine the mean swimming velocity. The steps in this calculation are elucidated in more detail in order to highlight how to correct the solution. In § 3 we reconsider the active case for non-zero
$\unicode[STIX]{x1D707}_{1}=0$
, which we refer to as the ‘passive fluid’ case, and solve the resulting system to determine the mean swimming velocity. The steps in this calculation are elucidated in more detail in order to highlight how to correct the solution. In § 3 we reconsider the active case for non-zero
![]() $\unicode[STIX]{x1D707}_{1}$
.
$\unicode[STIX]{x1D707}_{1}$
.
2 Mean swimming velocity in a passive fluid
For a passive fluid, i.e. when
![]() $\unicode[STIX]{x1D707}_{1}=0$
, the system of equations at
$\unicode[STIX]{x1D707}_{1}=0$
, the system of equations at
![]() $O(\unicode[STIX]{x1D700}^{2})$
, equations (1.1) and (1.2), become
$O(\unicode[STIX]{x1D700}^{2})$
, equations (1.1) and (1.2), become
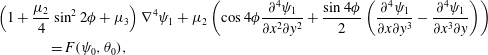 $$\begin{eqnarray}\displaystyle & \displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)\unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D713}_{1}+\unicode[STIX]{x1D707}_{2}\left(\cos 4\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x^{2}\unicode[STIX]{x2202}y^{2}}+\frac{\sin 4\unicode[STIX]{x1D719}}{2}\left(\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y^{3}}-\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x^{3}\unicode[STIX]{x2202}y}\right)\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle =F(\unicode[STIX]{x1D713}_{0},\unicode[STIX]{x1D703}_{0}),\hspace{227.62204pt} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)\unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D713}_{1}+\unicode[STIX]{x1D707}_{2}\left(\cos 4\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x^{2}\unicode[STIX]{x2202}y^{2}}+\frac{\sin 4\unicode[STIX]{x1D719}}{2}\left(\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y^{3}}-\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x^{3}\unicode[STIX]{x2202}y}\right)\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle =F(\unicode[STIX]{x1D713}_{0},\unicode[STIX]{x1D703}_{0}),\hspace{227.62204pt} & \displaystyle\end{eqnarray}$$
along with boundary conditions (given as (3.31)–(3.32) in Cupples et al. Reference Cupples, Dyson and Smith2017)
Upon substitution of
![]() $\unicode[STIX]{x1D713}_{0}$
and
$\unicode[STIX]{x1D713}_{0}$
and
![]() $\unicode[STIX]{x1D703}_{0}$
into (A 1) and (A 2), the inhomogeneous terms (when
$\unicode[STIX]{x1D703}_{0}$
into (A 1) and (A 2), the inhomogeneous terms (when
![]() $\unicode[STIX]{x1D707}_{1}=0$
) take the form
$\unicode[STIX]{x1D707}_{1}=0$
) take the form
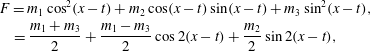 $$\begin{eqnarray}\displaystyle & \displaystyle F=m_{1}\cos ^{2}(x-t)+m_{2}\cos (x-t)\sin (x-t)+m_{3}\sin ^{2}(x-t), & \displaystyle \nonumber\\ \displaystyle & \displaystyle =\frac{m_{1}+m_{3}}{2}+\frac{m_{1}-m_{3}}{2}\cos 2(x-t)+\frac{m_{2}}{2}\sin 2(x-t),\quad \;\;\; & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F=m_{1}\cos ^{2}(x-t)+m_{2}\cos (x-t)\sin (x-t)+m_{3}\sin ^{2}(x-t), & \displaystyle \nonumber\\ \displaystyle & \displaystyle =\frac{m_{1}+m_{3}}{2}+\frac{m_{1}-m_{3}}{2}\cos 2(x-t)+\frac{m_{2}}{2}\sin 2(x-t),\quad \;\;\; & \displaystyle\end{eqnarray}$$
where
![]() $m_{j}=\sum _{k=1}^{10}M_{j}^{(k)}\exp (\unicode[STIX]{x1D6FE}_{k}y)$
and
$m_{j}=\sum _{k=1}^{10}M_{j}^{(k)}\exp (\unicode[STIX]{x1D6FE}_{k}y)$
and
![]() $n_{j}=\sum _{k=1}^{10}N_{j}^{(k)}\exp (\unicode[STIX]{x1D6FE}_{k}y)$
for
$n_{j}=\sum _{k=1}^{10}N_{j}^{(k)}\exp (\unicode[STIX]{x1D6FE}_{k}y)$
for
![]() $j=1,2,3$
. There are ten possibilities for
$j=1,2,3$
. There are ten possibilities for
![]() $\unicode[STIX]{x1D6FE}_{k}$
, resulting from combinations of
$\unicode[STIX]{x1D6FE}_{k}$
, resulting from combinations of
![]() $\unicode[STIX]{x1D713}_{0}$
and
$\unicode[STIX]{x1D713}_{0}$
and
![]() $\unicode[STIX]{x1D703}_{0}$
, which are
$\unicode[STIX]{x1D703}_{0}$
, which are
where
![]() $\unicode[STIX]{x1D706}_{j}$
are determined as part of the leading-order solution. Since all
$\unicode[STIX]{x1D706}_{j}$
are determined as part of the leading-order solution. Since all
![]() $\unicode[STIX]{x1D706}_{j}$
have negative real part, to satisfy the far-field condition at leading order, the real part of these exponentials will always be negative. By setting
$\unicode[STIX]{x1D706}_{j}$
have negative real part, to satisfy the far-field condition at leading order, the real part of these exponentials will always be negative. By setting
![]() $\unicode[STIX]{x1D707}_{1}=0$
the governing equations (2.1) and (2.2) decouple; since we are interested in the mean swimming velocity we focus on the solution to (2.1) only.
$\unicode[STIX]{x1D707}_{1}=0$
the governing equations (2.1) and (2.2) decouple; since we are interested in the mean swimming velocity we focus on the solution to (2.1) only.
2.1 Corrected solution
The first step we take is to note that
![]() $x$
and
$x$
and
![]() $t$
only appear together as
$t$
only appear together as
![]() $x-t$
and so we make the substitution
$x-t$
and so we make the substitution
![]() $z=x-t$
; in what follows we will be precise regarding which variable we are averaging over as the active case is not
$z=x-t$
; in what follows we will be precise regarding which variable we are averaging over as the active case is not
![]() $t$
-periodic in general.
$t$
-periodic in general.
Equation (2.1) becomes
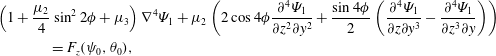 $$\begin{eqnarray}\displaystyle & \displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)\unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D6F9}_{1}+\unicode[STIX]{x1D707}_{2}\left(2\cos 4\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D6F9}_{1}}{\unicode[STIX]{x2202}z^{2}\unicode[STIX]{x2202}y^{2}}+{\displaystyle \frac{\sin 4\unicode[STIX]{x1D719}}{2}}\left(\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D6F9}_{1}}{\unicode[STIX]{x2202}z\unicode[STIX]{x2202}y^{3}}-\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D6F9}_{1}}{\unicode[STIX]{x2202}z^{3}\unicode[STIX]{x2202}y}\right)\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle =F_{z}(\unicode[STIX]{x1D713}_{0},\unicode[STIX]{x1D703}_{0}),\hspace{227.62204pt} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)\unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D6F9}_{1}+\unicode[STIX]{x1D707}_{2}\left(2\cos 4\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D6F9}_{1}}{\unicode[STIX]{x2202}z^{2}\unicode[STIX]{x2202}y^{2}}+{\displaystyle \frac{\sin 4\unicode[STIX]{x1D719}}{2}}\left(\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D6F9}_{1}}{\unicode[STIX]{x2202}z\unicode[STIX]{x2202}y^{3}}-\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D6F9}_{1}}{\unicode[STIX]{x2202}z^{3}\unicode[STIX]{x2202}y}\right)\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle =F_{z}(\unicode[STIX]{x1D713}_{0},\unicode[STIX]{x1D703}_{0}),\hspace{227.62204pt} & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6F9}_{1}(z,y)=\unicode[STIX]{x1D713}_{1}(x-t,y)$
and
$\unicode[STIX]{x1D6F9}_{1}(z,y)=\unicode[STIX]{x1D713}_{1}(x-t,y)$
and
![]() $F_{z}$
is
$F_{z}$
is
and the boundary conditions, equations (2.3) and (2.4), are
The periodic nature of the swimming sheet means
![]() $\unicode[STIX]{x1D6F9}_{1}$
is also periodic in
$\unicode[STIX]{x1D6F9}_{1}$
is also periodic in
![]() $z$
and so, upon taking the
$z$
and so, upon taking the
![]() $z$
-average of the system (2.8)–(2.11), the
$z$
-average of the system (2.8)–(2.11), the
![]() $z$
derivatives disappear and the system becomes
$z$
derivatives disappear and the system becomes
where
![]() $\overline{\,\cdot \,}^{z}\equiv (1/2\unicode[STIX]{x03C0})\int _{-\unicode[STIX]{x03C0}}^{\unicode[STIX]{x03C0}}\cdot \,\text{d}z$
.
$\overline{\,\cdot \,}^{z}\equiv (1/2\unicode[STIX]{x03C0})\int _{-\unicode[STIX]{x03C0}}^{\unicode[STIX]{x03C0}}\cdot \,\text{d}z$
.
At this stage in Cupples et al. (Reference Cupples, Dyson and Smith2017) an incorrect ansatz was assumed which neglected inhomogeneous terms. Hence we alter this ansatz to correctly determine the first-order streamfunction
![]() $\unicode[STIX]{x1D6F9}_{1}$
and thus the swimming velocity. Consider a complementary solution to the homogeneous problem and a particular integral satisfying the inhomogeneous portion; i.e.
$\unicode[STIX]{x1D6F9}_{1}$
and thus the swimming velocity. Consider a complementary solution to the homogeneous problem and a particular integral satisfying the inhomogeneous portion; i.e.
For the homogeneous problem we have
with general solution
![]() $\overline{\unicode[STIX]{x1D6F9}}_{C}^{z}(y)=A_{3}y^{3}+A_{2}y^{2}+A_{1}y+A_{0}$
, where
$\overline{\unicode[STIX]{x1D6F9}}_{C}^{z}(y)=A_{3}y^{3}+A_{2}y^{2}+A_{1}y+A_{0}$
, where
![]() $^{\prime }\equiv \text{d}/\text{d}y$
.
$^{\prime }\equiv \text{d}/\text{d}y$
.
The inhomogeneous problem is
hence assume
![]() $\overline{\unicode[STIX]{x1D6F9}}_{P}^{z}(y)$
takes the form
$\overline{\unicode[STIX]{x1D6F9}}_{P}^{z}(y)$
takes the form
where
![]() $P^{(k)}$
are constants to be determined. Substituting this form into (2.17) and rearranging for constants
$P^{(k)}$
are constants to be determined. Substituting this form into (2.17) and rearranging for constants
![]() $P^{(k)}$
, we find
$P^{(k)}$
, we find
for each
![]() $k$
and where
$k$
and where
![]() $M^{(k)}=(M_{1}^{(k)}+M_{3}^{(k)})/2$
. Combining these two solutions,
$M^{(k)}=(M_{1}^{(k)}+M_{3}^{(k)})/2$
. Combining these two solutions,
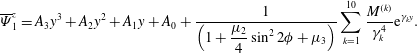 $$\begin{eqnarray}\overline{\unicode[STIX]{x1D6F9}}_{1}^{z}=A_{3}y^{3}+A_{2}y^{2}+A_{1}y+A_{0}+\frac{1}{\displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{4}}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}.\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D6F9}}_{1}^{z}=A_{3}y^{3}+A_{2}y^{2}+A_{1}y+A_{0}+\frac{1}{\displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{4}}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}.\end{eqnarray}$$
The boundary conditions are used to determine the constants in (2.20); for the velocity to be bounded we require
![]() $A_{3}=A_{2}=0$
and for the
$A_{3}=A_{2}=0$
and for the
![]() $z$
-averaged problem the boundary condition (2.3) becomes
$z$
-averaged problem the boundary condition (2.3) becomes
which yields
and
![]() $A_{0}$
can be set to zero without loss of generality. Hence the full solution is
$A_{0}$
can be set to zero without loss of generality. Hence the full solution is
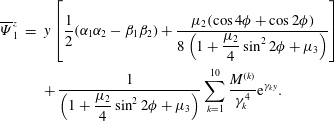 $$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D6F9}}_{1}^{z} & = & \displaystyle y\left[\frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2})+\frac{\unicode[STIX]{x1D707}_{2}(\cos 4\unicode[STIX]{x1D719}+\cos 2\unicode[STIX]{x1D719})}{\displaystyle 8\left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)}\mathop{\sum }_{k=1}^{10}{\displaystyle \frac{M^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{4}}}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D6F9}}_{1}^{z} & = & \displaystyle y\left[\frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2})+\frac{\unicode[STIX]{x1D707}_{2}(\cos 4\unicode[STIX]{x1D719}+\cos 2\unicode[STIX]{x1D719})}{\displaystyle 8\left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{\displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)}\mathop{\sum }_{k=1}^{10}{\displaystyle \frac{M^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{4}}}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}.\end{eqnarray}$$
Due to the periodicity of the problem, the time and
![]() $z$
-averages are identical, i.e.
$z$
-averages are identical, i.e.
![]() $\overline{U}^{z}=\overline{U}^{t}$
. In the far field the mean swimming velocity is thus
$\overline{U}^{z}=\overline{U}^{t}$
. In the far field the mean swimming velocity is thus
where
![]() $\overline{\,\cdot \,}^{t}\equiv (1/2\unicode[STIX]{x03C0})\int _{0}^{2\unicode[STIX]{x03C0}}\cdot \,\text{d}t$
.
$\overline{\,\cdot \,}^{t}\equiv (1/2\unicode[STIX]{x03C0})\int _{0}^{2\unicode[STIX]{x03C0}}\cdot \,\text{d}t$
.
The second term in this solution was not included in our previous analysis. In comparison, the solution presented by Shi & Powers is
Equations (2.24) and (2.25) agree in the limit
![]() $\unicode[STIX]{x1D707}_{2}\rightarrow 0$
and
$\unicode[STIX]{x1D707}_{2}\rightarrow 0$
and
![]() $\unicode[STIX]{x1D707}_{3}=0$
, modulo a factor of two introduced in the analysis by Shi & Powers (which can be absorbed into
$\unicode[STIX]{x1D707}_{3}=0$
, modulo a factor of two introduced in the analysis by Shi & Powers (which can be absorbed into
![]() $\unicode[STIX]{x1D707}_{2}$
).
$\unicode[STIX]{x1D707}_{2}$
).
2.2 Results
We present the new results for a range of parameter values and compare them with those produced by Shi & Powers.
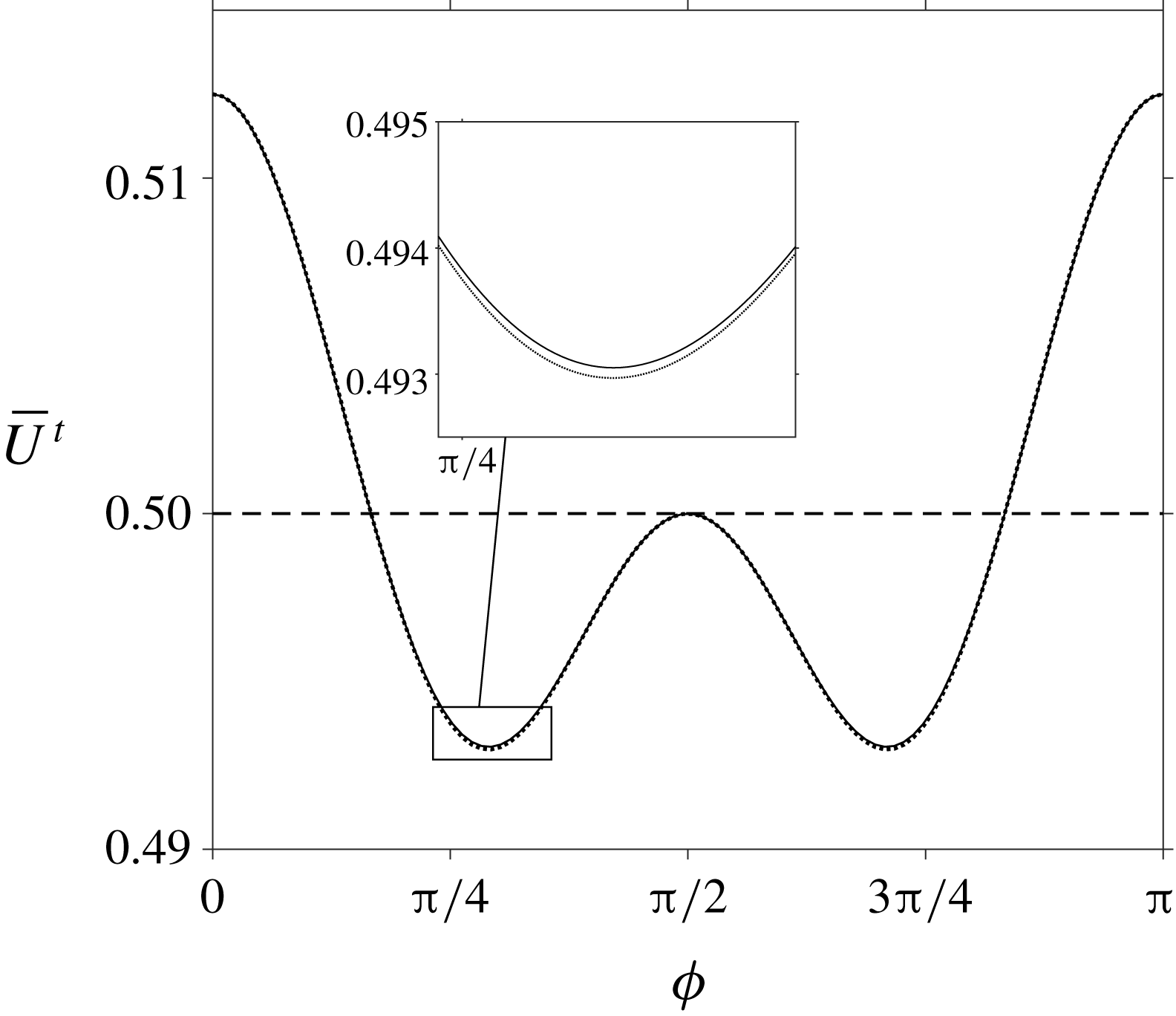
Figure 1. Mean swimming velocity comparison for passive transversely isotropic media where
![]() $\unicode[STIX]{x1D707}_{2}=0.05$
and
$\unicode[STIX]{x1D707}_{2}=0.05$
and
![]() $\unicode[STIX]{x1D707}_{3}=0$
. Three different results are compared: the incorrect calculation from Cupples et al. (Reference Cupples, Dyson and Smith2017) (dashed line), the corrected calculation (solid line) and the solution provided by Shi & Powers (Reference Shi and Powers2017) (dotted line). A magnified view of the first minimum in this figure has been included.
$\unicode[STIX]{x1D707}_{3}=0$
. Three different results are compared: the incorrect calculation from Cupples et al. (Reference Cupples, Dyson and Smith2017) (dashed line), the corrected calculation (solid line) and the solution provided by Shi & Powers (Reference Shi and Powers2017) (dotted line). A magnified view of the first minimum in this figure has been included.
Firstly we make a direct comparison with the work by Shi & Powers in figure 1; our original calculation,
![]() $\overline{U}^{t}=(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2})/2$
(equation (3.36) in Cupples et al.
Reference Cupples, Dyson and Smith2017) is plotted as the dashed line, the corrected solution is the solid line and the Shi & Powers result is shown by the dotted line. In addition to
$\overline{U}^{t}=(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2})/2$
(equation (3.36) in Cupples et al.
Reference Cupples, Dyson and Smith2017) is plotted as the dashed line, the corrected solution is the solid line and the Shi & Powers result is shown by the dotted line. In addition to
![]() $\unicode[STIX]{x1D707}_{1}=0$
, the anisotropic shear viscosity
$\unicode[STIX]{x1D707}_{1}=0$
, the anisotropic shear viscosity
![]() $\unicode[STIX]{x1D707}_{3}$
is set to zero and
$\unicode[STIX]{x1D707}_{3}$
is set to zero and
![]() $\unicode[STIX]{x1D707}_{2}=0.05$
. It is immediately seen that the inclusion of the extra term has altered the mean swimming velocity and introduced a dependence on the initial orientation angle
$\unicode[STIX]{x1D707}_{2}=0.05$
. It is immediately seen that the inclusion of the extra term has altered the mean swimming velocity and introduced a dependence on the initial orientation angle
![]() $\unicode[STIX]{x1D719}$
. Aside from the minimum values of the mean swimming velocity, the corrected solution agrees well with the work from Shi & Powers; this small difference is due to the
$\unicode[STIX]{x1D719}$
. Aside from the minimum values of the mean swimming velocity, the corrected solution agrees well with the work from Shi & Powers; this small difference is due to the
![]() $1/(1+\unicode[STIX]{x1D707}_{2}\sin ^{2}2\unicode[STIX]{x1D719}/4+\unicode[STIX]{x1D707}_{3})$
multiplying the second term in (2.24), as can be seen in the magnified view in figure 1.
$1/(1+\unicode[STIX]{x1D707}_{2}\sin ^{2}2\unicode[STIX]{x1D719}/4+\unicode[STIX]{x1D707}_{3})$
multiplying the second term in (2.24), as can be seen in the magnified view in figure 1.
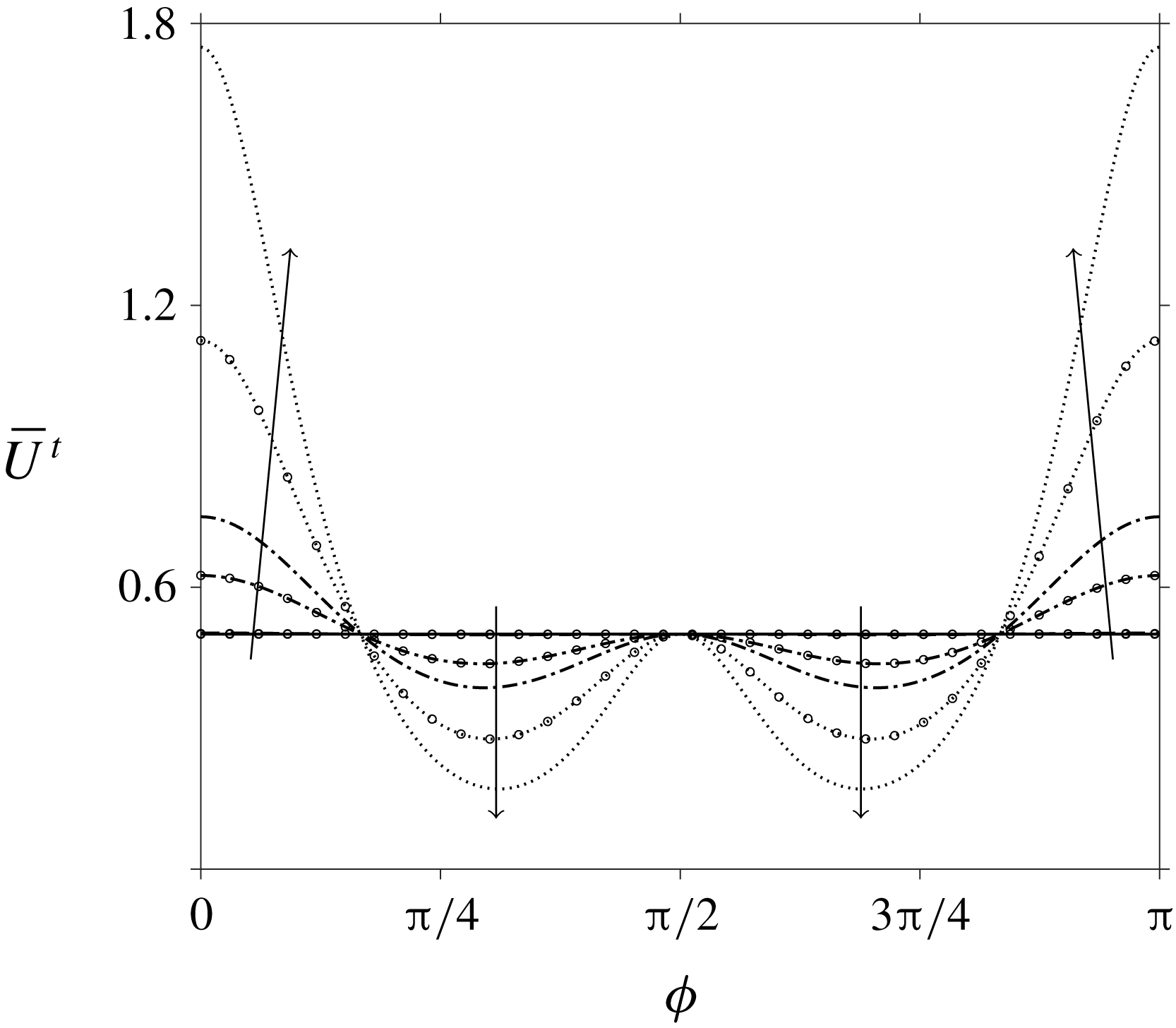
Figure 2. Corrected mean swimming velocity for small
![]() $\unicode[STIX]{x1D707}_{2}$
and
$\unicode[STIX]{x1D707}_{2}$
and
![]() $\unicode[STIX]{x1D707}_{3}$
. Four
$\unicode[STIX]{x1D707}_{3}$
. Four
![]() $\unicode[STIX]{x1D707}_{2}$
values are chosen,
$\unicode[STIX]{x1D707}_{2}$
values are chosen,
![]() $\unicode[STIX]{x1D707}_{2}=0$
(solid lines),
$\unicode[STIX]{x1D707}_{2}=0$
(solid lines),
![]() $\unicode[STIX]{x1D707}_{2}=0.01$
(dashed lines),
$\unicode[STIX]{x1D707}_{2}=0.01$
(dashed lines),
![]() $\unicode[STIX]{x1D707}_{2}=1$
(dot-dashed lines) and
$\unicode[STIX]{x1D707}_{2}=1$
(dot-dashed lines) and
![]() $\unicode[STIX]{x1D707}_{2}=5$
(dotted lines). Two
$\unicode[STIX]{x1D707}_{2}=5$
(dotted lines). Two
![]() $\unicode[STIX]{x1D707}_{3}$
values are selected,
$\unicode[STIX]{x1D707}_{3}$
values are selected,
![]() $\unicode[STIX]{x1D707}_{3}=0$
and
$\unicode[STIX]{x1D707}_{3}=0$
and
![]() $\unicode[STIX]{x1D707}_{3}=1$
(circle markers).
$\unicode[STIX]{x1D707}_{3}=1$
(circle markers).
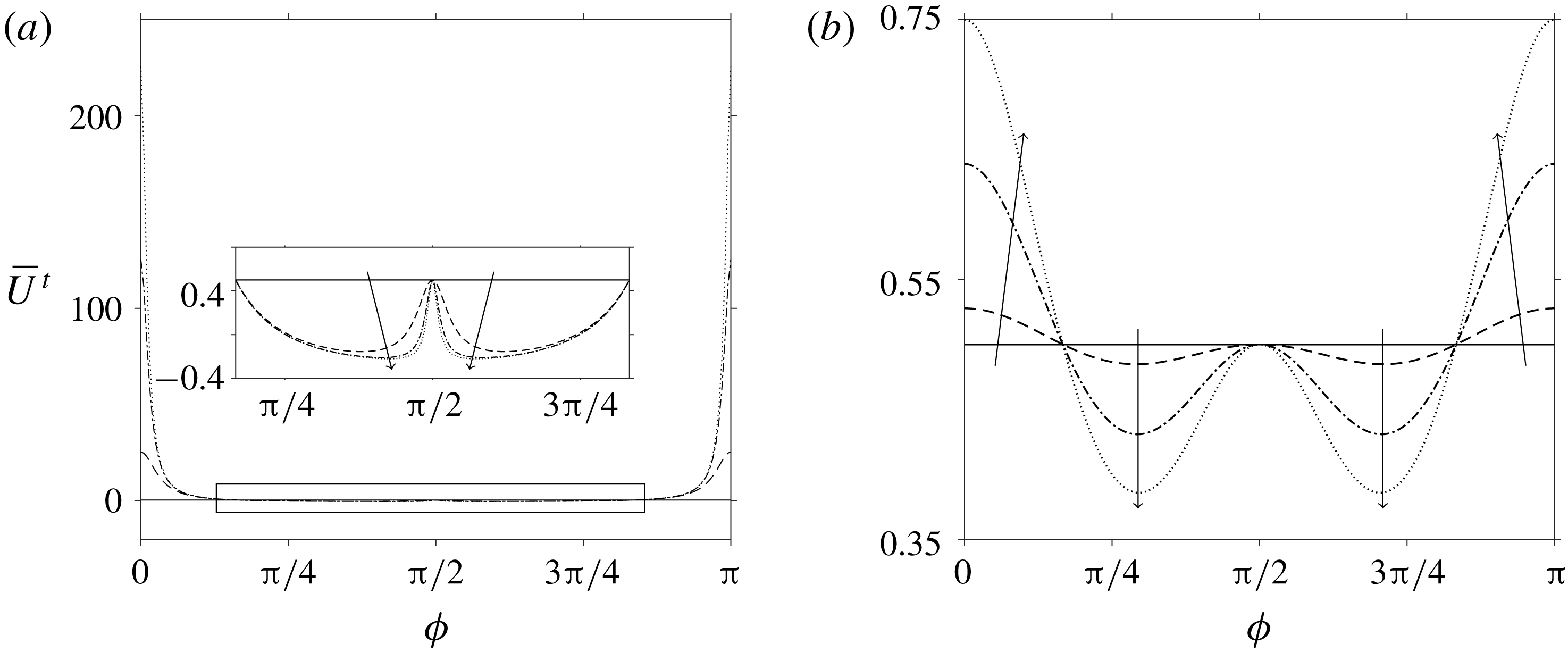
Figure 3. Corrected mean swimming velocity for large
![]() $\unicode[STIX]{x1D707}_{2}$
. (a)
$\unicode[STIX]{x1D707}_{2}$
. (a)
![]() $\unicode[STIX]{x1D707}_{3}=0$
and (b)
$\unicode[STIX]{x1D707}_{3}=0$
and (b)
![]() $\unicode[STIX]{x1D707}_{3}=900$
. Four choices for
$\unicode[STIX]{x1D707}_{3}=900$
. Four choices for
![]() $\unicode[STIX]{x1D707}_{2}$
are compared:
$\unicode[STIX]{x1D707}_{2}$
are compared:
![]() $\unicode[STIX]{x1D707}_{2}=0$
(solid lines),
$\unicode[STIX]{x1D707}_{2}=0$
(solid lines),
![]() $\unicode[STIX]{x1D707}_{2}=100$
(dashed lines),
$\unicode[STIX]{x1D707}_{2}=100$
(dashed lines),
![]() $\unicode[STIX]{x1D707}_{2}=500$
(dot-dashed lines) and
$\unicode[STIX]{x1D707}_{2}=500$
(dot-dashed lines) and
![]() $\unicode[STIX]{x1D707}_{2}=900$
(dotted lines). Panel (a) contains a magnified view of the middle section of the results.
$\unicode[STIX]{x1D707}_{2}=900$
(dotted lines). Panel (a) contains a magnified view of the middle section of the results.
Next we consider a larger range of
![]() $\unicode[STIX]{x1D707}_{2}$
and
$\unicode[STIX]{x1D707}_{2}$
and
![]() $\unicode[STIX]{x1D707}_{3}$
and compare the mean swimming velocity. First consider small
$\unicode[STIX]{x1D707}_{3}$
and compare the mean swimming velocity. First consider small
![]() $\unicode[STIX]{x1D707}_{2}$
and
$\unicode[STIX]{x1D707}_{2}$
and
![]() $\unicode[STIX]{x1D707}_{3}$
(figure 2). Increasing
$\unicode[STIX]{x1D707}_{3}$
(figure 2). Increasing
![]() $\unicode[STIX]{x1D707}_{2}$
dominates the impact of the initial orientation angle on the mean swimming velocity, and the anisotropic shear viscosity works to collapse the results back towards the Newtonian value; when both parameters are zero we return to the Newtonian solution as expected. For very small
$\unicode[STIX]{x1D707}_{2}$
dominates the impact of the initial orientation angle on the mean swimming velocity, and the anisotropic shear viscosity works to collapse the results back towards the Newtonian value; when both parameters are zero we return to the Newtonian solution as expected. For very small
![]() $\unicode[STIX]{x1D707}_{2}$
(dashed lines which are not seen) the variation from the Newtonian solution is very small.
$\unicode[STIX]{x1D707}_{2}$
(dashed lines which are not seen) the variation from the Newtonian solution is very small.
Finally we investigate the impact when both
![]() $\unicode[STIX]{x1D707}_{2}$
and
$\unicode[STIX]{x1D707}_{2}$
and
![]() $\unicode[STIX]{x1D707}_{3}$
may take on large values. Here we have separated the results into two cases: when
$\unicode[STIX]{x1D707}_{3}$
may take on large values. Here we have separated the results into two cases: when
![]() $\unicode[STIX]{x1D707}_{3}=0$
(figure 3
a) and when
$\unicode[STIX]{x1D707}_{3}=0$
(figure 3
a) and when
![]() $\unicode[STIX]{x1D707}_{3}=900$
(figure 3
b). When
$\unicode[STIX]{x1D707}_{3}=900$
(figure 3
b). When
![]() $\unicode[STIX]{x1D707}_{3}=0$
, the mean swimming velocity takes on large values near
$\unicode[STIX]{x1D707}_{3}=0$
, the mean swimming velocity takes on large values near
![]() $\unicode[STIX]{x1D719}=0$
and
$\unicode[STIX]{x1D719}=0$
and
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$
; these sharp peaks are consistent with the results in Cupples et al. (Reference Cupples, Dyson and Smith2017) occurring when one parameter was much larger than the others. Away from these regions, the mean swimming velocity takes on values similar to those presented in figures 1 and 2. When both parameters are large (figure 3
b), the mean swimming velocity reduces in comparison to figure 3(a). The shape of the
$\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$
; these sharp peaks are consistent with the results in Cupples et al. (Reference Cupples, Dyson and Smith2017) occurring when one parameter was much larger than the others. Away from these regions, the mean swimming velocity takes on values similar to those presented in figures 1 and 2. When both parameters are large (figure 3
b), the mean swimming velocity reduces in comparison to figure 3(a). The shape of the
![]() $\unicode[STIX]{x1D719}$
–
$\unicode[STIX]{x1D719}$
–
![]() $\overline{U}^{t}$
curve is similar as the anisotropic parameters are varied, only the magnitude changes.
$\overline{U}^{t}$
curve is similar as the anisotropic parameters are varied, only the magnitude changes.
3 Mean swimming velocity in active media
Next consider active transversely isotropic media, where
![]() $\unicode[STIX]{x1D707}_{1}\neq 0$
. The equations governing the flow and orientation are given by (1.1) and (1.2) respectively. Due to the time derivatives that force the evolution of orientation (equation (1.2)) we can no longer seek a solution depending on
$\unicode[STIX]{x1D707}_{1}\neq 0$
. The equations governing the flow and orientation are given by (1.1) and (1.2) respectively. Due to the time derivatives that force the evolution of orientation (equation (1.2)) we can no longer seek a solution depending on
![]() $z=x-t$
and instead look at an
$z=x-t$
and instead look at an
![]() $x$
-average of the coupled system.
$x$
-average of the coupled system.
3.1 Corrected solution
Based on the geometry of the problem,
![]() $\unicode[STIX]{x1D713}_{1}$
and
$\unicode[STIX]{x1D713}_{1}$
and
![]() $\unicode[STIX]{x1D703}_{1}$
will be periodic in
$\unicode[STIX]{x1D703}_{1}$
will be periodic in
![]() $x$
. Hence, an
$x$
. Hence, an
![]() $x$
-average is taken,
$x$
-average is taken,
where
![]() $\overline{\,\cdot \,}^{x}\equiv (1/2\unicode[STIX]{x03C0})\int _{0}^{2\unicode[STIX]{x03C0}}\cdot \,\text{d}x$
. Equation (3.1) can be directly integrated twice with respect to
$\overline{\,\cdot \,}^{x}\equiv (1/2\unicode[STIX]{x03C0})\int _{0}^{2\unicode[STIX]{x03C0}}\cdot \,\text{d}x$
. Equation (3.1) can be directly integrated twice with respect to
![]() $y$
,
$y$
,
and substituted into (3.2) to give
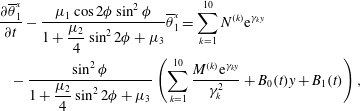 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}_{1}^{x}}{\unicode[STIX]{x2202}t}-\frac{\unicode[STIX]{x1D707}_{1}\cos 2\unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D719}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\overline{\unicode[STIX]{x1D703}}_{1}^{x}=\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\sin ^{2}\unicode[STIX]{x1D719}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\left(\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}+B_{0}(t)y+B_{1}(t)\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}_{1}^{x}}{\unicode[STIX]{x2202}t}-\frac{\unicode[STIX]{x1D707}_{1}\cos 2\unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D719}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\overline{\unicode[STIX]{x1D703}}_{1}^{x}=\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\sin ^{2}\unicode[STIX]{x1D719}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\left(\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}+B_{0}(t)y+B_{1}(t)\right),\end{eqnarray}$$
where
![]() $B_{0}(t)$
and
$B_{0}(t)$
and
![]() $B_{1}(t)$
are functions of time to be determined. To simplify the following calculations, the functions are written in the form
$B_{1}(t)$
are functions of time to be determined. To simplify the following calculations, the functions are written in the form
![]() $B_{0}(t)={\dot{F}}_{0}(t)\exp (\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t)$
and
$B_{0}(t)={\dot{F}}_{0}(t)\exp (\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t)$
and
![]() $B_{1}(t)={\dot{F}}_{1}(t)\exp (\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t)$
, where the dot notation represents a time derivative,
$B_{1}(t)={\dot{F}}_{1}(t)\exp (\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t)$
, where the dot notation represents a time derivative,
![]() $F_{0}(t)$
and
$F_{0}(t)$
and
![]() $F_{1}(t)$
are functions of time to be determined and
$F_{1}(t)$
are functions of time to be determined and
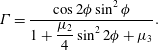 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}=\frac{\cos 2\unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D719}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}=\frac{\cos 2\unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D719}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}.\end{eqnarray}$$
Then, equation (3.4) can be solved via an integrating factor to give
where
and
![]() $c(y)$
is a function to be determined. The full solution is detailed in appendix B. Since the fibres have initial orientation
$c(y)$
is a function to be determined. The full solution is detailed in appendix B. Since the fibres have initial orientation
![]() $\unicode[STIX]{x1D719}$
, the initial condition for the angle is
$\unicode[STIX]{x1D719}$
, the initial condition for the angle is
![]() $\overline{\unicode[STIX]{x1D703}}_{1}^{x}(x,y,0)=0$
and so
$\overline{\unicode[STIX]{x1D703}}_{1}^{x}(x,y,0)=0$
and so
where
![]() $F_{j}^{0}=F_{j}(0)$
. The solution is thus
$F_{j}^{0}=F_{j}(0)$
. The solution is thus
for
![]() $B_{2}(t)=F_{0}(t)-F_{0}^{0}$
,
$B_{2}(t)=F_{0}(t)-F_{0}^{0}$
,
![]() $B_{3}(t)=F_{1}(t)-F_{1}^{0}$
.
$B_{3}(t)=F_{1}(t)-F_{1}^{0}$
.
The form for
![]() $\overline{\unicode[STIX]{x1D703}}_{1}^{x}$
can now be substituted back into (3.3),
$\overline{\unicode[STIX]{x1D703}}_{1}^{x}$
can now be substituted back into (3.3),
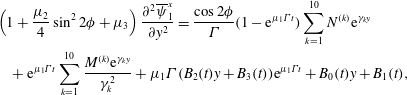 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)\frac{\unicode[STIX]{x2202}^{2}\overline{\unicode[STIX]{x1D713}}_{1}^{x}}{\unicode[STIX]{x2202}y^{2}}=\frac{\cos 2\unicode[STIX]{x1D719}}{\unicode[STIX]{x1D6E4}}(1-\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t})\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}(B_{2}(t)y+B_{3}(t))\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}+B_{0}(t)y+B_{1}(t),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)\frac{\unicode[STIX]{x2202}^{2}\overline{\unicode[STIX]{x1D713}}_{1}^{x}}{\unicode[STIX]{x2202}y^{2}}=\frac{\cos 2\unicode[STIX]{x1D719}}{\unicode[STIX]{x1D6E4}}(1-\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t})\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}(B_{2}(t)y+B_{3}(t))\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}+B_{0}(t)y+B_{1}(t),\end{eqnarray}$$
which can then be directly integrated with respect to
![]() $y$
to obtain
$y$
to obtain
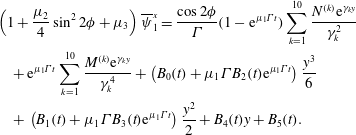 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)\overline{\unicode[STIX]{x1D713}}_{1}^{x}=\frac{\cos 2\unicode[STIX]{x1D719}}{\unicode[STIX]{x1D6E4}}(1-\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t})\mathop{\sum }_{k=1}^{10}\frac{N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{4}}+\left(B_{0}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{2}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\right)\frac{y^{3}}{6}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left(B_{1}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{3}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\right)\frac{y^{2}}{2}+B_{4}(t)y+B_{5}(t).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}\right)\overline{\unicode[STIX]{x1D713}}_{1}^{x}=\frac{\cos 2\unicode[STIX]{x1D719}}{\unicode[STIX]{x1D6E4}}(1-\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t})\mathop{\sum }_{k=1}^{10}\frac{N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{4}}+\left(B_{0}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{2}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\right)\frac{y^{3}}{6}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left(B_{1}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{3}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\right)\frac{y^{2}}{2}+B_{4}(t)y+B_{5}(t).\end{eqnarray}$$
To determine the functions of integration, reconsider the boundary condition
and note that since the velocity must remain bounded in the far field we require
![]() $B_{0}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{2}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}=0$
and
$B_{0}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{2}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}=0$
and
![]() $B_{1}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{3}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}=0$
. It can be shown that this is equivalent to
$B_{1}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{3}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}=0$
. It can be shown that this is equivalent to
![]() $B_{0}(t)=B_{1}(t)=B_{2}(t)=B_{3}(t)=0$
(see appendix C). Since
$B_{0}(t)=B_{1}(t)=B_{2}(t)=B_{3}(t)=0$
(see appendix C). Since
![]() $B_{5}$
has no impact on the velocity it can, without loss of generality, be set to zero. The final function
$B_{5}$
has no impact on the velocity it can, without loss of generality, be set to zero. The final function
![]() $B_{4}(t)$
is determined from (3.12) as
$B_{4}(t)$
is determined from (3.12) as
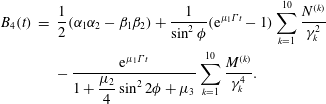 $$\begin{eqnarray}\displaystyle B_{4}(t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2})+\frac{1}{\sin ^{2}\unicode[STIX]{x1D719}}(\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}-1)\mathop{\sum }_{k=1}^{10}\frac{N^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{2}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{4}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B_{4}(t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2})+\frac{1}{\sin ^{2}\unicode[STIX]{x1D719}}(\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}-1)\mathop{\sum }_{k=1}^{10}\frac{N^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{2}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{4}}.\end{eqnarray}$$
Hence, the solutions
![]() $\overline{\unicode[STIX]{x1D713}}_{1}^{x}$
and
$\overline{\unicode[STIX]{x1D713}}_{1}^{x}$
and
![]() $\overline{\unicode[STIX]{x1D703}}_{1}^{x}$
are given by
$\overline{\unicode[STIX]{x1D703}}_{1}^{x}$
are given by
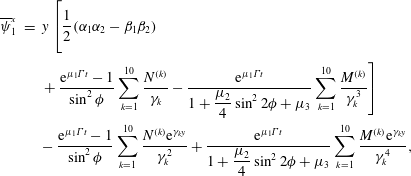 $$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D713}}_{1}^{x} & = & \displaystyle y\left[\frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}-1}{\sin ^{2}\unicode[STIX]{x1D719}}\mathop{\sum }_{k=1}^{10}\frac{N^{(k)}}{\unicode[STIX]{x1D6FE}_{k}}-\frac{\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{3}}\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}-1}{\sin ^{2}\unicode[STIX]{x1D719}}\mathop{\sum }_{k=1}^{10}\frac{N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}+\frac{\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{4}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D713}}_{1}^{x} & = & \displaystyle y\left[\frac{1}{2}(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}-1}{\sin ^{2}\unicode[STIX]{x1D719}}\mathop{\sum }_{k=1}^{10}\frac{N^{(k)}}{\unicode[STIX]{x1D6FE}_{k}}-\frac{\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{3}}\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}-1}{\sin ^{2}\unicode[STIX]{x1D719}}\mathop{\sum }_{k=1}^{10}\frac{N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}+\frac{\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{4}},\end{eqnarray}$$
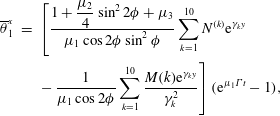 $$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D703}}_{1}^{x} & = & \displaystyle \left[\frac{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}{\unicode[STIX]{x1D707}_{1}\cos 2\unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D719}}\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\frac{1}{\unicode[STIX]{x1D707}_{1}\cos 2\unicode[STIX]{x1D719}}\mathop{\sum }_{k=1}^{10}\frac{M(k)\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}\right](\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}-1),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D703}}_{1}^{x} & = & \displaystyle \left[\frac{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}{\unicode[STIX]{x1D707}_{1}\cos 2\unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D719}}\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\frac{1}{\unicode[STIX]{x1D707}_{1}\cos 2\unicode[STIX]{x1D719}}\mathop{\sum }_{k=1}^{10}\frac{M(k)\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}\right](\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}-1),\end{eqnarray}$$
where the swimming velocity is given at far field as
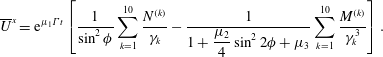 $$\begin{eqnarray}\overline{U}^{x}=\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\left[\frac{1}{\sin ^{2}\unicode[STIX]{x1D719}}\mathop{\sum }_{k=1}^{10}\frac{N^{(k)}}{\unicode[STIX]{x1D6FE}_{k}}-\frac{1}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{3}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\overline{U}^{x}=\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\left[\frac{1}{\sin ^{2}\unicode[STIX]{x1D719}}\mathop{\sum }_{k=1}^{10}\frac{N^{(k)}}{\unicode[STIX]{x1D6FE}_{k}}-\frac{1}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}}{\unicode[STIX]{x1D6FE}_{k}^{3}}\right].\end{eqnarray}$$
3.2 Comments
Equation (3.16) will be valid only when
![]() $\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}\leqslant 0$
or for very short time scales. The sign of
$\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}\leqslant 0$
or for very short time scales. The sign of
![]() $\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}$
is determined by
$\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}$
is determined by
![]() $\unicode[STIX]{x1D707}_{1}\cos 2\unicode[STIX]{x1D719}$
; for ‘puller’ type behaviour, where
$\unicode[STIX]{x1D707}_{1}\cos 2\unicode[STIX]{x1D719}$
; for ‘puller’ type behaviour, where
![]() $\unicode[STIX]{x1D707}_{1}$
is positive, the solution is valid only for
$\unicode[STIX]{x1D707}_{1}$
is positive, the solution is valid only for
![]() $\unicode[STIX]{x03C0}/4\leqslant \unicode[STIX]{x1D719}\leqslant 3\unicode[STIX]{x03C0}/4$
and these exponential terms decay with time. This however leads to a steady-state swimming velocity
$\unicode[STIX]{x03C0}/4\leqslant \unicode[STIX]{x1D719}\leqslant 3\unicode[STIX]{x03C0}/4$
and these exponential terms decay with time. This however leads to a steady-state swimming velocity
![]() $\overline{U}^{x}=0$
and so the active properties of the fluid halt any propulsion. For ‘pusher’ type behaviour, where
$\overline{U}^{x}=0$
and so the active properties of the fluid halt any propulsion. For ‘pusher’ type behaviour, where
![]() $\unicode[STIX]{x1D707}_{1}$
is negative, this validity is for
$\unicode[STIX]{x1D707}_{1}$
is negative, this validity is for
![]() $0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x03C0}/4$
and the same result for the swimming velocity is obtained.
$0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x03C0}/4$
and the same result for the swimming velocity is obtained.
Outside this region, the solution for
![]() $\overline{\unicode[STIX]{x1D703}}_{1}^{x}$
and further the swimming velocity
$\overline{\unicode[STIX]{x1D703}}_{1}^{x}$
and further the swimming velocity
![]() $\overline{U}^{x}$
grow exponentially and hence will not be valid in the perturbation expansion currently considered. To fully understand microscopic propulsion in active transversely isotropic media, it will be necessary to consider a numerical solution to the full swimming problem.
$\overline{U}^{x}$
grow exponentially and hence will not be valid in the perturbation expansion currently considered. To fully understand microscopic propulsion in active transversely isotropic media, it will be necessary to consider a numerical solution to the full swimming problem.
4 Discussion
New results arising from correction of an error in Cupples et al. (Reference Cupples, Dyson and Smith2017) have been described, prompted by Shi & Powers (Reference Shi and Powers2017) who investigated propulsion in nematic liquid crystals and discovered a discrepancy between the two models in a common limit. The corrected swimming velocity was calculated for a passive fluid, from which it was found that the extra terms introduce a dependence of the mean swimming velocity on the initial orientation angle. By setting
![]() $\unicode[STIX]{x1D707}_{2}$
to be small and
$\unicode[STIX]{x1D707}_{2}$
to be small and
![]() $\unicode[STIX]{x1D707}_{3}=0$
our corrected result agrees with Shi & Powers (Reference Shi and Powers2017) in the common limit.
$\unicode[STIX]{x1D707}_{3}=0$
our corrected result agrees with Shi & Powers (Reference Shi and Powers2017) in the common limit.
The corrected swimming velocity was then compared for a range of
![]() $\unicode[STIX]{x1D707}_{2}$
and
$\unicode[STIX]{x1D707}_{2}$
and
![]() $\unicode[STIX]{x1D707}_{3}$
. The effects of the initial orientation angle on
$\unicode[STIX]{x1D707}_{3}$
. The effects of the initial orientation angle on
![]() $\overline{U}^{t}$
were increased by increasing the anisotropic extensional viscosity and larger anisotropic shear viscosities reduce the effect of the initial orientation angle. Further, when one parameter is large and the other small, rapid changes in the swimming velocity and a reversal in the swimming direction (i.e. negative swimming velocity) were seen; a result seen consistent with the mean rate of working found in Cupples et al. (Reference Cupples, Dyson and Smith2017).
$\overline{U}^{t}$
were increased by increasing the anisotropic extensional viscosity and larger anisotropic shear viscosities reduce the effect of the initial orientation angle. Further, when one parameter is large and the other small, rapid changes in the swimming velocity and a reversal in the swimming direction (i.e. negative swimming velocity) were seen; a result seen consistent with the mean rate of working found in Cupples et al. (Reference Cupples, Dyson and Smith2017).
Finally a solution for the swimming velocity in active media (
![]() $\unicode[STIX]{x1D707}_{1}\neq 0$
) was sought. Periodicity in
$\unicode[STIX]{x1D707}_{1}\neq 0$
) was sought. Periodicity in
![]() $x$
was imposed for the streamfunction and evolution of orientation angle due to the problem geometry; this observation simplified the calculations required. The coupled equations were solved to determine the first-order evolution of orientation and the swimming velocity. The swimming velocity varied exponentially in time, with the sign of the exponent dependent on
$x$
was imposed for the streamfunction and evolution of orientation angle due to the problem geometry; this observation simplified the calculations required. The coupled equations were solved to determine the first-order evolution of orientation and the swimming velocity. The swimming velocity varied exponentially in time, with the sign of the exponent dependent on
![]() $\unicode[STIX]{x1D707}_{1}$
and the initial orientation angle. Thus the expansion is valid only for very short time periods, or for specific
$\unicode[STIX]{x1D707}_{1}$
and the initial orientation angle. Thus the expansion is valid only for very short time periods, or for specific
![]() $\unicode[STIX]{x1D707}_{1}$
and initial orientation angles where the exponent is negative; in these cases the active properties appear to halt propulsion. Setting
$\unicode[STIX]{x1D707}_{1}$
and initial orientation angles where the exponent is negative; in these cases the active properties appear to halt propulsion. Setting
![]() $\unicode[STIX]{x1D707}_{1}=0$
returned the result for the passive case. A topic of significant interest for future work is to investigate a fully numerical solution to the swimming problem in active transversely isotropic media.
$\unicode[STIX]{x1D707}_{1}=0$
returned the result for the passive case. A topic of significant interest for future work is to investigate a fully numerical solution to the swimming problem in active transversely isotropic media.
Acknowledgements
This work was supported by a Biotechnology and Biological Sciences Research Council (BBSRC) Industrial CASE Studentship (BB/L015587/1). The authors acknowledge Professors J. Shi and T. R. Powers for identifying the discrepancy between our respective papers.
Appendix A. Inhomogeneous terms in
 $O(\unicode[STIX]{x1D700}^{2})$
governing equations
$O(\unicode[STIX]{x1D700}^{2})$
governing equations
The right-hand side of (1.1) and (1.2) are
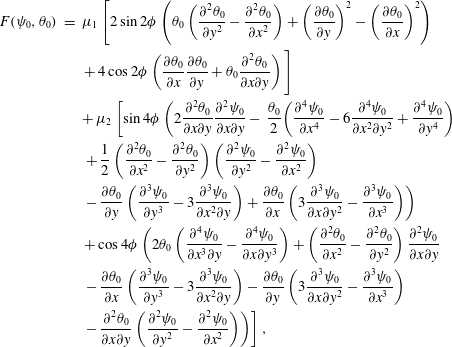 $$\begin{eqnarray}\displaystyle F(\unicode[STIX]{x1D713}_{0},\unicode[STIX]{x1D703}_{0}) & = & \displaystyle \unicode[STIX]{x1D707}_{1}\left[2\sin 2\unicode[STIX]{x1D719}\left(\unicode[STIX]{x1D703}_{0}\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x^{2}}\right)+\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y}\right)^{2}-\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x}\right)^{2}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,4\cos 2\unicode[STIX]{x1D719}\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y}+\unicode[STIX]{x1D703}_{0}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D707}_{2}\left[\sin 4\unicode[STIX]{x1D719}\left(2\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}-\,\frac{\unicode[STIX]{x1D703}_{0}}{2}\!\left(\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{4}}-6\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{2}\unicode[STIX]{x2202}y^{2}}+\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{4}}\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.+\,\frac{1}{2}\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y^{2}}\right)\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{2}}\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.-\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y}\left(\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{3}}-3\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{2}\unicode[STIX]{x2202}y}\right)+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x}\left(3\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{3}}\right)\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\cos 4\unicode[STIX]{x1D719}\left(2\unicode[STIX]{x1D703}_{0}\left(\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{3}\unicode[STIX]{x2202}y}-\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y^{3}}\right)+\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y^{2}}\right)\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.-\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x}\left(\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{3}}-3\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{2}\unicode[STIX]{x2202}y}\right)-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y}\left(3\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{3}}\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.-\,\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{2}}\right)\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(\unicode[STIX]{x1D713}_{0},\unicode[STIX]{x1D703}_{0}) & = & \displaystyle \unicode[STIX]{x1D707}_{1}\left[2\sin 2\unicode[STIX]{x1D719}\left(\unicode[STIX]{x1D703}_{0}\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x^{2}}\right)+\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y}\right)^{2}-\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x}\right)^{2}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,4\cos 2\unicode[STIX]{x1D719}\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y}+\unicode[STIX]{x1D703}_{0}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D707}_{2}\left[\sin 4\unicode[STIX]{x1D719}\left(2\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}-\,\frac{\unicode[STIX]{x1D703}_{0}}{2}\!\left(\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{4}}-6\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{2}\unicode[STIX]{x2202}y^{2}}+\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{4}}\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.+\,\frac{1}{2}\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y^{2}}\right)\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{2}}\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.-\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y}\left(\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{3}}-3\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{2}\unicode[STIX]{x2202}y}\right)+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x}\left(3\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{3}}\right)\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\cos 4\unicode[STIX]{x1D719}\left(2\unicode[STIX]{x1D703}_{0}\left(\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{3}\unicode[STIX]{x2202}y}-\frac{\unicode[STIX]{x2202}^{4}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y^{3}}\right)+\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y^{2}}\right)\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.-\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x}\left(\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{3}}-3\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{2}\unicode[STIX]{x2202}y}\right)-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y}\left(3\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{3}}\right)\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.-\,\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x^{2}}\right)\right)\right],\end{eqnarray}$$
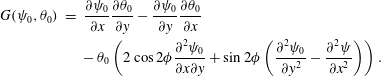 $$\begin{eqnarray}\displaystyle G(\unicode[STIX]{x1D713}_{0},\unicode[STIX]{x1D703}_{0}) & = & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x}\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D703}_{0}\left(2\cos 2\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}+\sin 2\unicode[STIX]{x1D719}\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}x^{2}}\right)\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G(\unicode[STIX]{x1D713}_{0},\unicode[STIX]{x1D703}_{0}) & = & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}y}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{0}}{\unicode[STIX]{x2202}x}\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D703}_{0}\left(2\cos 2\unicode[STIX]{x1D719}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}y}+\sin 2\unicode[STIX]{x1D719}\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{0}}{\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}x^{2}}\right)\right).\end{eqnarray}$$
Appendix B. Evolution of orientation in an active suspension
To determine the swimming velocity and evolution of orientation from system (3.1)–(3.2), firstly (3.1) is integrated twice (equation (3.3)) and substituted into (3.2) resulting in (3.4),
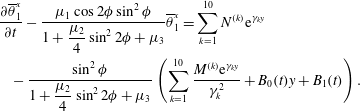 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}_{1}^{x}}{\unicode[STIX]{x2202}t}-\frac{\unicode[STIX]{x1D707}_{1}\cos 2\unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D719}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\overline{\unicode[STIX]{x1D703}}_{1}^{x}=\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\sin ^{2}\unicode[STIX]{x1D719}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\left(\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}+B_{0}(t)y+B_{1}(t)\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}_{1}^{x}}{\unicode[STIX]{x2202}t}-\frac{\unicode[STIX]{x1D707}_{1}\cos 2\unicode[STIX]{x1D719}\sin ^{2}\unicode[STIX]{x1D719}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\overline{\unicode[STIX]{x1D703}}_{1}^{x}=\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\sin ^{2}\unicode[STIX]{x1D719}}{\displaystyle 1+\frac{\unicode[STIX]{x1D707}_{2}}{4}\sin ^{2}2\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{3}}\left(\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}+B_{0}(t)y+B_{1}(t)\right).\end{eqnarray}$$
We set
![]() $B_{0}(t)=F_{0}^{\prime }(t)\exp (\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t)$
and
$B_{0}(t)=F_{0}^{\prime }(t)\exp (\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t)$
and
![]() $B_{1}(t)=F_{1}^{\prime }(t)\exp (\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t)$
, where
$B_{1}(t)=F_{1}^{\prime }(t)\exp (\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t)$
, where
![]() $\unicode[STIX]{x1D6E4}$
is given by (3.5), to simplify the following calculations.
$\unicode[STIX]{x1D6E4}$
is given by (3.5), to simplify the following calculations.
Introduce an integrating factor such that
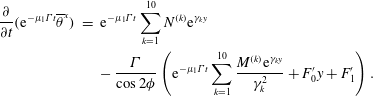 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(\text{e}^{-\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\overline{\unicode[STIX]{x1D703}}^{x}) & = & \displaystyle \text{e}^{-\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D6E4}}{\cos 2\unicode[STIX]{x1D719}}\left(\text{e}^{-\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}+F_{0}^{\prime }y+F_{1}^{\prime }\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(\text{e}^{-\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\overline{\unicode[STIX]{x1D703}}^{x}) & = & \displaystyle \text{e}^{-\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D6E4}}{\cos 2\unicode[STIX]{x1D719}}\left(\text{e}^{-\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}+F_{0}^{\prime }y+F_{1}^{\prime }\right).\end{eqnarray}$$
Next integrate with respect to
![]() $t$
and rearrange to give
$t$
and rearrange to give
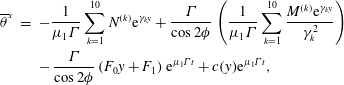 $$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D703}}^{x} & = & \displaystyle -\frac{1}{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}}\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}+\frac{\unicode[STIX]{x1D6E4}}{ cos2\unicode[STIX]{x1D719}}\left(\frac{1}{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D6E4}}{\cos 2\unicode[STIX]{x1D719}}\left(F_{0}y+F_{1}\right)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}+c(y)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D703}}^{x} & = & \displaystyle -\frac{1}{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}}\mathop{\sum }_{k=1}^{10}N^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}+\frac{\unicode[STIX]{x1D6E4}}{ cos2\unicode[STIX]{x1D719}}\left(\frac{1}{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}}\mathop{\sum }_{k=1}^{10}\frac{M^{(k)}\text{e}^{\unicode[STIX]{x1D6FE}_{k}y}}{\unicode[STIX]{x1D6FE}_{k}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D6E4}}{\cos 2\unicode[STIX]{x1D719}}\left(F_{0}y+F_{1}\right)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}+c(y)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t},\end{eqnarray}$$
which is simplified to
for function
![]() $c(y)$
determined via boundary condition (3.12) in § 3.1.
$c(y)$
determined via boundary condition (3.12) in § 3.1.
Appendix C. Finding constants of integration
From (3.12) we require
![]() $B_{0}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{2}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}=0$
, and
$B_{0}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{2}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}=0$
, and
![]() $B_{1}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{3}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}=0$
. We here show that this is equivalent to
$B_{1}(t)+\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}B_{3}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}=0$
. We here show that this is equivalent to
![]() $B_{0}(t)=B_{1}(t)=B_{2}(t)=B_{3}(t)=0$
.
$B_{0}(t)=B_{1}(t)=B_{2}(t)=B_{3}(t)=0$
.
Recall the forms
![]() $B_{0}(t)={\dot{F}}_{0}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}$
and
$B_{0}(t)={\dot{F}}_{0}(t)\text{e}^{\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6E4}t}$
and
![]() $B_{2}(t)=F_{0}(t)-F_{0}^{0}$
, and similarly for
$B_{2}(t)=F_{0}(t)-F_{0}^{0}$
, and similarly for
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{3}$
respectively. Substituting this form into the expressions satisfying the far-field condition we have
$B_{3}$
respectively. Substituting this form into the expressions satisfying the far-field condition we have
Since both equations have the same form, we illustrate the solution for (C 1) only; rearrange and integrate with respect to
![]() $t$
to obtain
$t$
to obtain
for some constant
![]() $D$
. As
$D$
. As
![]() $F_{0}(0)=F_{0}^{0}$
, we find
$F_{0}(0)=F_{0}^{0}$
, we find
![]() $D=0$
and hence
$D=0$
and hence
![]() $F_{0}$
is constant in time; this then enforces
$F_{0}$
is constant in time; this then enforces
![]() $B_{0}(t)=B_{2}(t)=0$
.
$B_{0}(t)=B_{2}(t)=0$
.








