1. Introduction
Modern climatology faces the question of whether anthropogenically induced climate change is already observable in climatic variables. Because the climate system can be regarded as non-linear (Reference HoughtonHoughton and others, 2001), traditional linear statistical models cannot describe the full complexity of its behaviour, and thus fail to answer this question. Non-linear neural network models (NNMs) provide a statistical solution to this problem.
NNMs originated in the study of the cognitive abilities of biological brain functions, i.e. how the brain processes information and how it learns (Reference AdrianAdrian, 1926; Reference RosenblattRosenblatt, 1958; Reference Grossberg and GrossbergGrossberg, 1982). A comprehensive overview of the wide range of applications of NNMs to time-series analysis is summarized in Anderson and Rosenfeld (1986) and Reference Rumelhart, Hinton, Williams, Rumelhart and McClellandRumelhart and McClelland (1986).
As an analogue to biological brains, a typical NNM consists of a yet to be defined number of simple processing units. The task of a (supervised learning) NNM is to ‘learn’ certain features of the data, which consist of input variables and desired output responses, using a training subset. After the training process, these features are interpolated on an unknown validation subset, on which the performance of the NNM can be determined. Internal parameters of the network architecture are adjusted according to a specific learning rule so that the network ideally captures all intrinsic data features.
What distinguishes NNM from traditional statistical methods is its non-linear character, due to a non-linear mapping function. This mapping function is commonly chosen out of the class of sigmoid functions, because it has been shown experimentally by Reference AdrianAdrian (1926) that biological neurons respond to a stimulus in a sigmoidal fashion, i.e. no output until a certain threshold is exceeded, followed by a nearly linear input–output relation and saturation from a certain input level onward.
Conventional studies of climate change are based either on physical climate models (e.g. general circulation models (GCMs) with a high computing and CPU time demand), or on statistical models such as multiple linear regression (MLR) models, which allow only a limited exploration of the state of the climate system. There is a wide variety of models for studying the behaviour of the climate system that can be ordered by increasing complexity (e.g. radiative–convective models, energy-balance models). The MLR and GCM approaches represent the extremes of this model hierarchy. Nevertheless, NNM represents a quite simple non-linear method for gaining insight into the behaviour of the climate system.
The non-linear NNM combines the advantages of physically motivated (possibly non-linear) climate models, with high complexity, and linear statistical models, with a low CPU time demand. Two recent climatological applications of NNM have been the detection and attribution of anthropogenic climate change (Reference Walter and Schönwiese.Walter and Schönwiese, 2002, 2003), and forecasting tropical Pacific sea surface temperatures in the El Niño region (Reference Wu and Hsieh.Wu and Hsieh, 2003). For a general overview of climatological applications of neural networks, see Reference Hsieh and TangHsieh and Tang (1998) or Reference WalterWalter (2001).
In this paper, we simulate and reconstruct a proxy for annual mass balance of Grosse Aletschgletscher, Switzerland, using a back-propagation network (Reference Rumelhart and McClellandRumelhart and others, 1986). This is the first time that a neural network approach has been used in this glaciological context to simulate and reconstruct glacier mass balance.
The mass balance of glaciers varies with changing climate, and many studies and measurements have been carried out to investigate this connection (e.g. Reference Oerlemans and ReichertOerlemans and Reichert, 2000, and references therein). To relate annual glacier mass balance to meteorological data, a suitable combination of climate data is required. In many studies, (summer) temperature and (winter) precipitation are assumed to be the best predictors for this objective (Reference Oerlemans and ReichertOerlemans and Reichert, 2000). Because mass balance is a complex function dependent on climate, time and other factors, it may be well suited to non-linear approaches. In fact, nonlinear functions in the glacier–climate system have been found in several recent studies (e.g. Reference Braithwaite and RaperBraithwaite and Raper, 2002; Reference Lie, Dahl and NesjeLie and others, 2003). The aim of this study is to use an easy non-linear model, driven only by a combination of temperature and precipitation data.
In section 2 we provide an overview of the data used in this study and the concept behind the BPN. In section 3 we discuss how the BPN can be used to simulate a proxy for annual glacier mass balance by suitable selection of monthly instrumental data (temperature, precipitation) for the 20th century. As well as simulating glacier mass balance, this work aims to reconstruct a longer-term mass-balance series. Applying the BPN technique, we propose to use multi-proxy seasonal reconstructions of temperature (Reference Luterbacher, Dietrich, Xoplaki, Grosjean and WannerLuterbacher and others, 2004) and precipitation (Reference Pauling, Luterbacher, Casty and WannerPauling and others, in press) to calculate a new annual mass-balance series back to AD 1500. In section 4 the performance of the BPN is discussed, questions are presented and further investigations are proposed.
2. Data and Methods
2.1. Instrumental data of the 20th century
Figure 1 shows the topography and the locations of the meteorological stations within the greater region of Aletschgletscher, the largest stream of ice in the Alps, lying in the Bernese Alps of south-central Switzerland. Aletschgletscher is divided into main (Grosse Aletschgletscher), middle and upper parts. The main glacier (46º30′ N, 8º2′ E) is 24.7 km long and covers an area of 86.76 km2. Its head is at 4160ma.s.l., the glacier terminates at 1556ma.s.l. and its average height is about 3140 m (Reference Haeberli, Hoelzle, Suter and FrauenfelderHaeberli and others, 1998). The exposure of Grosse Aletschgletscher is to the southeast (accumulation area) and to the south (ablation area). As shown in Figure 1a, the ice stream consists of three large firn fields: the Aletschfirn, the Jungfraufirn and the Ewigschnee-feldfirn. In 1994, depth soundings made by means of radio echolot (radar) located the glacier bed at depths of 600– 700 m in the Konkordia region (VAW/SANW, 1881–2002, Nos. 115/116 (1999)).

Fig. 1. (a) Map showing Aletschgletscher with its main branches and tributaries. (b) The Aletsch region (area with dashed outline) and the meteorological stations used as forcing or reference data in this study. Also shown is the grid range (area with solid outline) over which seasonal averages were calculated.
The study site which borders on the upper Valais (Rhone valley) is characterized by a generally temperate humid climate. It is more subcontinental than that of the northern Alpine region, which is more suboceanic (Reference Van der Knaap and van Leeuwen.Van der Knaap and Van Leeuwen, 2003). Reference Frei and Schär.Frei and Schär (1998) point out that the dry inner Alpine conditions of the Valais contrast with the wet anomalies along the Alpine rims, especially in the north of the Aletsch region. Because the Valais has a complex topography, like the whole Alpine region, marked vertical temperature gradients are found over short distances. Furthermore, the major west–east orientation of the Valais, occasionally across the main airflow direction, can cause mesoscale meteorological phenomena like the föhn (Reference Schüepp, Bouët and BiderSchüepp and others, 1978).
The fluctuations in length of Grosse Aletschgletscher have been carefully reconstructed on the basis of documents, archaeological field studies and precise dendrochronological dating. In the last 500 years, a very small advance around 1500 is dated by both dendrochronology and archaeology. Dendrochronological analysis allows an exact reconstruction of the marked advance, leading to a maximum glacier extent from 1670 to 1680. Pictures and texts document fluctuations during the 18th and 19th centuries, especially the final advance to the last Little Ice Age maximum extent around 1856. From 1892 to the present, the continuously decreasing tongue has been precisely measured every year (VAW/SANW, 1881–2002; Reference Holzhauser and Zumbühl.Holzhauser and Zumbühl, 1999; Reference Haeberli and HolzhauserHaeberli and Holzhauser, 2003).
As a continuation of the mass-balance studies of the 1950s (Reference KasserKasser, 1954, Reference Kasser1967), Reference Aellen and FunkAellen and Funk (1990) estimated an average yearly net balance for the period 1931–87 from a simple hydrological model, calculating daily to annual water-storage variations in the basin of the Massa river. Based on water-flux measurements of the Massa river, a tributary of the Rhone river which issues from Grosse Aletschgletscher, and precipitation data from the surrounding area, a proxy for annual mass balances can be calculated (Reference PatersonPaterson, 1994). Later, in order to correct systematic errors in these calculations (under- or overestimations of areal precipitation), the data were revised by a linear regression approach. Besides the uncorrected data series from Reference Aellen and FunkAellen and Funk (1990), information from direct glaciological mass-balance measurements on Grosse Aletschgletscher and a reference mass-balance series (average of Grosse Aletschgletscher (uncorrected), Limmeren and Plattalvagletscher) were incorporated into the linear model to determine a corrected proxy for annual mass balances (Reference Müller-Lemans, Funk, Aellen and KappenbergerMüller-Lemans and others, 1995).
As a control of the Aletsch data, variations of total volume, surface area and mean thickness were determined for the years 1926/27, 1957, 1980 and 1999, using geodetic methods (terrestrial or aerial surveys). There is clear agreement between the Aletsch cumulative mass balance and these geodetic measurements (Reference Vincent, Kappenberger, Valla, Bauder, Funk and Le Meur.Vincent and others, 2004). An annual check is also provided by the average net balances computed from a stake network observed on Grosse Aletschgletscher from 1950 to 1986 (Reference AellenAellen, 1995). Finally, new data made it possible to expand the mass-balance data to the 1919–99 period with the model approach presented here.
It should be noted that this proxy for annual balances of Grosse Aletschgletscher comes from a hydrological model and not directly from field measurements. So the resulting series is probably not as reliable as direct measurements, even though the data have been checked against independent geodetic measurements (Reference Vincent, Kappenberger, Valla, Bauder, Funk and Le Meur.Vincent and others, 2004). Nevertheless, this proxy will serve as target function in our neural network modelling approach.
The forcing data, monthly temperature and precipitation series from the surroundings of Grosse Aletschgletscher were provided by MeteoSwiss (online database of MeteoSwiss). The data are homogenized, i.e. they are adjusted for nonclimatic factors like changes in station location or changes in observation practices (Reference Begert, Seiz, Schlegel, Musa, Baudraz and MoeschBegert and others, 2003). Table 1 represents all climate series used in this study. In agreement with Reference Schüepp, Bouët and BiderSchüepp and others (1978), we found a lack of long climatic time series in this region of the Swiss Alps.
Table 1. Principal meteorological stations used in this study (data from the online database of MeteoSwiss)

As the Alpine precipitation field shows large spatio-temporal variability, there is a strong need for long-term precipitation data close to a glacier in order to relate climatic conditions to glacier activities. The precipitation series (Fiesch, Kippel) were selected according to the study by Reference Aellen and FunkAellen and Funk (1990). But instead of the precipitation series for Grindelwald applied there, which is missing values for the period 1903–10, we chose the highly correlated (r = 0.92) nearby precipitation series for Lauterbrunnen. Furthermore, the Sion and Meiringen data were used as temperature datasets. With this data selection, we climatically represent both the inner Alpine dry valley of the upper Valais and the wetter northern part of the Bernese Alps. However, these data series serve as potential model inputs for the BPN.
To complete the precipitation series of Fiesch and Kippel for the missing periods 1992–2003 and 1974–2003, a method derived from the homogenization process at MeteoSwiss was used (Reference Begert, Seiz, Schlegel, Musa, Baudraz and MoeschBegert and others, 2003). Based on a highly correlated reference series, nearby precipitation series were reduced to the level of the series with missing values. For this, average ratios between all precipitation series and the reference series were calculated for the overlapping periods. Based on the proportion of these average ratios, it is possible to determine reduction factors for the nearby precipitation stations (personal communication from T. Schlegel, 2004).
The Fiesch precipitation data series (PFiesch) was completed as follows:
-
1. The highly correlated (r = 0.92) precipitation series from Brig was used as reference series.
-
2. The two nearby precipitation stations, Ernen (PErnen; 1.3 km from Fiesch) and Fieschertal (PFieschertal; 2.2 km from Fiesch), were then reduced to the level of Fiesch.
-
3. For the missing time period 1992–98,
(1)
-
4. For the missing time period 1999–2003,
(2)
where q Fiesch, q Ernen and q Fieschertal are the average ratios between the Fiesch, Ernen and Fieschertal precipitation series and the Brig reference series for the overlapping measured period.
In an analogous procedure, the Kippel data series (PKippel) was completed using the Leukerbad reference series (r = 0.90) and the nearby Ried precipitation series (PRied; 3.1 km from Kippel) as a reduction series.
For the missing time period 1974–2003,
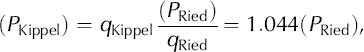
where q Kippel and q Ried are the average ratios between the Kippel and Ried precipitation series and the Leukerbad reference series for the overlapping measured period.
2.2. Multi-proxy reconstructions of temperature and precipitation back to 1500
In the absence of widespread instrumental data, we must rely upon indirect lines of evidence to provide information about climate variability over the past several centuries. To determine annual or higher-resolution climate variations, however, high-resolution ‘proxy’ climate indicators such as ice cores and tree-ring measurements, combined with the scant available documentary or instrumental evidence available in prior centuries, are required (e.g. Reference MannMann, 2002; Reference Jones and MannJones and Mann, 2004; Reference Luterbacher, Dietrich, Xoplaki, Grosjean and WannerLuterbacher and others, 2004).
In this study, two new gridded (0.5° × 0.5° resolution) multi-proxy reconstructions of seasonal temperature (Luter-bacher and others, 2004) and precipitation fields (Reference Pauling, Luterbacher, Casty and WannerPauling and others, in press) from 1500 to 2000 for European land areas were used. The temperature reconstruction is based on a dataset that includes instrumental data series, reconstructed sea-ice and temperature indices, and proxy temperature reconstructions from ice cores and tree rings (see Reference Luterbacher, Dietrich, Xoplaki, Grosjean and WannerLuterbacher and others, 2004, for a detailed description of the method and the data used). Like the temperature reconstructions, the precipitation estimates were based on a combination of instrumental series, documentary indices (precipitation) and natural proxies (tree rings, corals, ice cores). As these reconstructions share no common predictors, they can be compared in terms of climate dynamics or temporal stability of the precipitation–temperature relationship. The temperature reconstructions end in 2004, the precipitation reconstructions in 2000. As a consequence, we studied the period mentioned above (1500–2000).
As input data for the model, a seasonal average of both temperature and precipitation sums was calculated over the area 46–47° N, 7–8.5° E, comprising xy gridpoints (see Fig. 1b for the grid range). This grid extent covers the entire Aletsch region and clearly reflects its climatic conditions, presented in section 2.1. The seasonal averages generally show higher correlations with the observed precipitation (Fiesch, Kippel, Lauterbrunnen) and temperature measurements (Sion, Meiringen) for the overlapping 1900–2000 period than nearby single gridpoints. The correlation coefficients range from 0.87 (June–August;Meiringen) to 0.95 (March–May; Sion) for temperature, and from 0.61 (June–August;Fiesch) to 0.77 (December–February; Kippel) for precipitation. The generally lower correlation coefficients for precipitation probably reflect the greater difficulty in reconstructing and/or representing precipitation fields in mountainous regions due to their large spatio-temporal variability. As with all models, the output of a BPN depends on the quality of the input data, and possible uncertainties in the precipitation data will significantly reduce the accuracy of the trained neural networks. Related to this issue, Reference Klein and RossinKlein and Rossin (1999) found that errors in training data affect neural network models more severely than linear regression models.
2.3. Back-propagation neural networks as modelling tools
Neural networks use non-linear functions and a large number of processing units to reduce the risk of model mismatch errors. Instead of matching the architecture of the model to a problem, a model is used that can describe almost anything, and careful training of the model is used to constrain it to describe the data.
In this study, the standard NNM, the Back-Propagation Network (BPN), was applied (Reference Rumelhart and McClellandRumelhart and others, 1986). This network architecture is based on a supervised learning algorithm to find the minimum of a cost function. Unlike a simulated annealing schedule (Reference Metropolis, Rosenbluth, Rosenbluth, Teller and TellerMetropolis and others, 1953), the BPN does not guarantee that the global minimum of this cost function will be reached, though it is very likely that a minimum good enough to reproduce responses in the data can be found. This approach also bears a certain risk of overfitting, so the data have to be separated into a training and a validation subset (calibration/verification in reconstruction exercises). The ‘learning’ process of the network is performed on the training subset only, whereas the validation subset serves as an independent reference for the simulation quality. This technique is called cross-validation (Reference StoneStone, 1974; Reference MichaelsonMichaelson, 1987). When applying NNM to a non-stationary time series, as in this approach, the choice of the training subset must ensure that the entire amplitude range of all forcing mechanisms considered is covered; otherwise the algorithm will fail if confronted with an extreme value during the validation process, and such an extreme value never occurred in the learning period. The training must be carried out using a representative data subset. Therefore the training data cannot be chosen continuously out of all data available but must be chosen so that all the amplitudes are covered. We used 75% of all data for training, and the remaining 25% for validation (Reference Walter and Scho¨nwiese.Walter and Schönwiese, 2003).
A typical NNM consists of three layers: input, processing and output layers. Figure 2 shows a simplified neural network. Although the units of the processing layer are sometimes called ‘hidden units’, their weights, activation and all other internal parameters are easily accessible from the outside.

Fig. 2. An example of a simplified three-layer k-j-1 BPN architecture. Also shown is the concept behind the back-propagation training algorithm (arrows).
The input to an NNM is a vector of elements (xk ), where the index k stands for the number of input units in the network. In our study, k = 12 indicates the major short-term climatic influences on the mass balance of Aletschgletscher in the 20th century. For the long-term reconstructions of annual glacier mass balance since 1500, we chose k = 2 (see section 3 for the selection of the input variables). These inputs are weighted with weights wjk , where j represents the number of processing units, to give the inputs to the processing units
Using too few/many processing units can lead to under-fitting/overfitting problems. That is, the simulation results are highly sensitive to the number of processing units and learning parameters chosen. The best number of processing units can be determined by repeated simulations with increasing numbers of processing units, i.e. j = 1,2, ..., n, and by observing the performance of these different network architectures on the validation sample. Multiple versions of the BPN must be tried to obtain robust results. Typically, the validation error decreases with increasing numbers of processing units until the network has too many degrees of freedom, i.e. too many processing units. After that, the validation error increases and the model with the optimal number of processing units, i.e. the model configuration with the lowest validation error, must be chosen for the final simulations.
For the 20th century we used 12 input units as forcings. In addition, there are 6 processing units in one processing layer and 1 output unit as a target function. This neural network architecture is abbreviated as 12–6-1. For long-term simulations back to 1500, a 2–2-1 architecture was applied.
After weighting and summation of the inputs, the nonlinear aspects of the BPN were encountered first, as the results were passed to non-linear activation functions in each processing unit. These functions produced the output of the processing layer

To retain the original analogy between NNM and learning mechanisms in the brain (Reference AdrianAdrian, 1926; Reference Amit and RosenfeldAmit, 1989), the activation functions are commonly chosen from the class of sigmoid functions, which also will keep the model response bounded. We have chosen
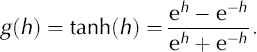
The outputs of the processing units are fed to the output layer where they are again weighted
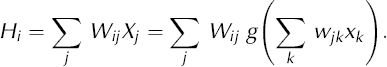
The use of a second activation function will finally produce the output of the network
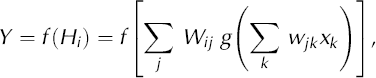
where f is the output activation function, Xk are the chosen input variables, wik are the weights from the k input units to the i processing units, and Wii are the weights from the processing units to the output unit. As an output activation function we apply the identity function f(x) = x, so that Equation (7) is the complete BPN function.
This model is very general. However, it has been shown that ‘with one layer and an arbitrary continuous sigmoidal function, this model can approximate any continuous function, provided that no constraints are placed on the number of units or the size of the weights’ (Reference CybenkoCybenko, 1989).
2.4. The back-propagation architecture
The purpose of training an NNM is to find a set of coefficients that reduces the error between the model outputs and the given test data y(xk). This is usually done by adjusting the weights Wii and wik to minimize the least-squares error

where n is the length of the time series. One way to adjust these weights, and thus to reduce χ2, is gradient descent. The update step in the output weights can be found by differentiating

defining
The so-called learning constant γ, given in Equation (10), is a scale factor which controls how big the update step is, and g’ is the derivation of the sigmoidal activation function used, here tanh(x). The choice of 7 is crucial because 7 determines the step width of the gradient descent algorithm. If 7 is too small, the algorithm might get stuck in steep canyons of the x 1 hypersurface. If it is too large, the algorithm might just jump over minima.
The update in the input weights can be found using the chain rule

defining
The deltas for the input layer are found in terms of the deltas for the output layer by running them backwards through the network’s Wij’s. Thus, the errors between model output and observations are propagated backwards through the weights of the output and the processing layer, and these errors are used to adjust the weights throughout the network. Training a network by gradient descent and feeding the errors backwards through the network is called error back-propagation.
As mentioned above, this network architecture risks being stuck in local minima on the x1 hypersurface. To reduce this risk, an enhanced version of standard back-propagation with a momentum term α was used. The momentum term introduces the old weight change as a parameter for computing the new weight change. This avoids the oscillation problems common with the standard back-propagation algorithm when the error hypersurface has a very narrow minimum area. The new weight change is computed by

The term α, a number between 0 and 1, is the so-called momentum parameter, and ∆w(t — 1) the weight change in the time-step t - 1. The effect of these enhancements is that flat spots of the error hypersurface are traversed relatively rapidly with a few large steps, while the step size is decreased as the hypersurface gets rougher. This adaption of the step size increases learning speed significantly.
One obvious problem concerning BPN is that Equation (14) contains two parameters, 7 and a, whose optimum values will typically vary from one iteration to the next. We might therefore seek some procedure for setting these automatically as part of the training algorithm. One approach for doing this is the Polak-Ribiere variant of the conjugate gradient descent. Conjugate gradient is a method of accelerating gradient descent in which the learning rate 7 and the momentum parameter α are determined in each iteration. In ordinary gradient descent, one uses the gradient to find the steepest downhill direction, then moves along that line to the minimum in that direction. With conjugate gradient, a search is made along the conjugate gradient direction to determine the step size, which minimizes the error function along that line. The momentum term α is calculated by the Polak-Ribiere formula, since this controls the search direction, while the learning rate 7 is determined by the golden section method for line minimization (Reference Press, Teukolsky, Vetterling and FlanneryPress and others, 1992; Reference BishopBishop, 1995). For an excellent overview of the conjugate gradient descent method, see the unpublished draft by J.R. Shewchuk (http://www.cs.cmu.edu/~quake-papers/painless-conjugate-gradient.ps). It should be noted that for many applications the Polak-Ribiere method gives slightly better results than other conjugate gradient methods or even the conventional gradient descent approach (Reference Press, Teukolsky, Vetterling and FlanneryPress and others, 1992; Reference BishopBishop, 1995; Reference Dao and VemuriDao and Vemuri, 2002).
A second uncertainty in the BPN simulation is related to the fact that the minimum, found from the algorithm, is dependent on the initial starting point on the x1 hypersurface. Since the BPN represents a non-linear mapping function, slightly different initial conditions can lead to large differences in the simulation results. To eliminate this kind of uncertainty, the BPN was driven 30 times, each time only varying the initial starting point for the conjugate gradient algorithm on the x 1 hypersurface.
3. Results
3.1. Mass balance in the 20th century
One of the most important factors in determining the success of a practical application of neural networks is the form of pre-processing applied to the data. In the simplest case, preprocessing may take the form of a linear transformation of the input and output data (see the z-transformation below). More complex pre-processing may also involve reduction of the dimensionality of the input data. The fact that such dimensionality reduction can improve performance may at first appear somewhat paradoxical, since it will decrease the information content of the input data in most cases (Reference BishopBishop, 1995). Some of these techniques, such as genetic algorithms, are highly heuristic, while other methods such as principal components analysis make assumptions as to the linearity of relationships between the input data items. Finally, an exhaustive search of optimal input configurations is highly effective but computationally intensive. With the 60 input variables used in this study (five datasets with monthly resolution, each) there are 160 ≈ 1018 possible subsets to consider.
In the present study, we therefore used the stepwise multiple linear regression approach to extract the potential influences on the mass balance of Grosse Aletschgletscher. Although there is an assumption of linearity behind this method, Reference Addison, McGarry, Wermter, MacIntyre. and HamzaAddison and others (2004) show that the use of stepwise multiple linear regression could perform comparably to, if not better than, most other reduction methods. Stepwise multiple linear regression examines variables incorporated in the model at every stage of the regression. A variable that may have been the best choice to enter the model at an early stage may later be non-significant because of the relationships between it and other variables now in the regression. Once a variable is proven to be nonsignificant, it is removed from the model. This process continues until no more variables can be accepted and no more can be rejected (Von Reference Storch and ZwiersStorch and Zwiers, 1999).
We performed a stepwise multiple linear regression with the monthly averages of temperature and precipitation as independent variables and the proxy of annual mass balance of Grosse Aletschgletscher as an output dataset (dependent). As model inputs for the BPN, we found the following subset of 12 independent variables (>99% confidence level): Meiringen (August, September), Sion (June, July), Fiesch (January, May, July, November) and Kippel (February, July, October, December).
Changes in glacier mass balance can be viewed as a direct, undelayed reaction of a glacier to climatic variations (Reference Reichert, Bengtsson and OerlemansReichert and others, 2001; Reference Nesje and DahlNesje and Dahl, 2003). Furthermore, glacier mass is determined by taking into account the accumulation of snow, mostly in winter, and warm-season ablation, and thus shows an immediate response to climate variability and site meteorological conditions. Therefore, it is not surprising that ‘summer’ (June– September) temperature and ‘winter’ (October–February) precipitation turn out to be highly correlated with the annual glacier mass balance. The high correlations of May and July precipitation could indicate that the mass balance also responds to effects of spring and summer precipitation. Furthermore, it seems that there is no (linear) relationship between the mass-balance series of Grosse Aletschgletscher and the Lauterbrunnen precipitation series.
In contrast to the proxy-based reconstruction back to 1500 (see section 3.2), we use monthly data for a reconstruction of the 20th-century mass balance. In this way a choice of potential climatic driving factors is more differentiated and probably leads to better model performance.
Before feeding the BPN, the data are standardized to 1919–99 mean and standard deviation (z-transformation) so that temperature and precipitation are in comparable units (for robust NNM performance). After fitting the BPN with the conjugate gradient descent method, the full model was used to reconstruct a proxy of annual mass balance from the forcing data when no output data were available. In a final step, the data were rescaled by the inverse z-transformation.
Figure 3 is the composite made up of the annual glacier mass balance for the 1919–99 training/validation period, presented in section 2.1, and BPN predictions for those years when estimations are missing (1900–18, 2000–03). An error envelope (95% confidence interval) based on the rms errors in predictions appears around each section of BPN prediction (Reference Mann and JonesMann and Jones, 2003; Reference Reusch and AlleyReusch and Alley, 2004). The simulation and the reconstruction are the average outputs of 30 model runs to reduce the effect of falling into local minima (see section 2.4).

Fig. 3. Results of the BPN simulation and reconstruction (solid curve). Also shown is the proxy of annual glacier mass balance (thick curve) for the 1919–99 period and the output of the stepwise multiple linear regression (dotted curve). Confidence intervals derived from rms errors appear as grey envelopes around predictions.
The simulation quality over the 1919–99 training/validation period amounts to 97.3% of explained variance, while the stepwise multiple linear regression model driven by the same input data ends with an explained variance of 86.3%. Reference Chen and FunkChen and Funk (1990) applied a similar multiple linear regression approach to reconstruct the mass balance of Rhonegletscher. They used mean annual precipitation and mean summer temperature of nearby stations as model inputs. So our stepwise multiple linear regression model represents a refinement of their approach with higher-resolution data.
To ensure that the neural network has captured most relevant mechanisms, the residuals of the simulations must be tested. This is usually done by testing for Gaussian distribution of the residuals. In the case of a non-linear neural network, the residuals undergo non-linear transformations during the training of the network. Therefore the residuals do not have to be Gaussian-distributed even if the model captures all relevant mechanisms and the residuals are in fact (white) noise. An alternative statistical method for testing residuals of this kind is the autocorrelation function. If the residuals are indeed white noise, i.e. uncorrelated at all lags, the autocorrelation function should have no structure (Von Reference Storch and ZwiersStorch and Zwiers, 1999; Reference Walter and Schönwiese.Walter and Schönwiese, 2002).
The autocorrelation coefficient of our simulations shows no significant deflection from zero (95% confidence level); therefore the BPN captured all relevant mechanisms and the remaining residuals can be treated as white noise.
The BPN used here can simulate a proxy of annual glacier mass balance for the 20th century. While the stepwise multiple linear regression approach often under-or overestimates the extremes of the mass-balance function, the trained BPN is better able to learn the intrinsic data features. A small number of NN misfits were found. Furthermore, it is possible to reconstruct missing mass-balance data. For the 2000–03 period we estimated a cumulative mass balance of about –2.2 m (Fig. 3), consistent with several studies and measurements that show persistent melting of Alpine glaciers during the last two decades (BUWAL, BWG, MeteoSchweiz, 2004; Reference Vincent, Kappenberger, Valla, Bauder, Funk and Le Meur.Vincent and others, 2004). The beginning of the 20th century is characterized by a short period of negative mass balances (minimum around 1905) followed by a relative maximum in 1910. In 1911, a strongly negative mass balance was found, after which a period with mainly positive mass balances can be detected (maximum around 1914). Again, this is in good agreement with other mass-balance reconstructions of Alpine glaciers, such as Hintereisferner (Reference NicolussiNicolussi, 1994; Reference Kuhn, Schlosser and SpanKuhn and others, 1997).
3.2. Proxy-based reconstructions of mass balance back to 1500
To reconstruct annual glacier mass balance back to 1500, we used the same method described in section 3.1 but with different inputs. We focused attention on a longer-term reconstruction of mass balance. Because our data were not available in monthly resolution back to 1500, we used seasonal averages. After a stepwise multiple linear regression with the seasonal averages, calculated from gridded datasets, as independent variables and with annual glacier mass balance as output dataset (dependent), the potential climate influences were chosen. Significant datasets (>99% confidence level) were winter (December– February) precipitation and summer (June–August) temperature. As presented in section 3.1, the input data were standardized before training.
Figure 4 shows the simulation (1919–99) and the reconstruction (1500–1918) of the annual glacier mass balance, with an error envelope (grey shaded) around each section of BPN predictions based on its rms errors (95% confidence interval). Also given are a 30 year low-pass filtered time series for the BPN simulation and reconstruction of yearly mass balance (thick line), and the output of the stepwise multiple linear regression (solid line). Figure 5 represents the cumulative glacier mass-balance changes back to 1500, also with an error envelope (95% confidence interval). A positive slope in Figure 5 is the result of years with positive mass balance, indicating a mass gain, and the opposite for a negative slope.

Fig. 4. Results of the BPN simulation and reconstruction (solid curve) of yearly mass balance. Confidence intervals derived from rms errors appear as grey envelopes around predictions. Also shown is the proxy of annual glacier mass balance for the 1919–99 period. The smoothed thick curve represents the 30 year low-pass filtered time series of the results of the BPN simulation and reconstruction. The smoothed solid curve is the 30 year low-pass filtered output of the stepwise multiple linear regression model.

Fig. 5. Cumulative mass-balance changes in Grosse Aletsch-gletscher for the 1500–1999 period (1919 = 0). The thick curve represents the mass changes observed (1919–99); the solid curve is the result of the BPN simulation and reconstruction. Also shown is an error envelope (grey shading) around the predictions of cumulative mass balance. The dashed curve shows the length fluctuations of nearby Unter Grindelwaldgletscher, 1535–1983.
Again, the BPN was trained by the conjugate gradient descent method to simulate the mass balance over the 1919–99 training/validation period. The model was then used to reconstruct annual mass changes since 1500 by averaging 30 different BPN runs that started from different points in the space of possible weights. In this case, the simulation skill amounts to 60.8% of explained variance, while the stepwise multiple linear regression approach driven by the same input data accounts for 54.8% of explained variance. Again, the autocorrelation coefficient function indicates no significant deflection from zero (95% confidence level).
A comparison of the reconstructed cumulative mass balance of Grosse Aletschgletscher and the statistics of front positions of nearby Unter Grindelwaldgletscher (e.g. Reference Zumbühl, Messerli and PfisterZumbühl and others, 1983; Reference Holzhauser, Zumbühl., Weingartner and SpreaficoHolzhauser and Zumbühl, 2003), provided in Figure 5, shows correlation coefficients of r = 0.89 for the overlapping 1535–1983 period and r = 0.69 for the 1535–1918 reconstruction period.
Figures 4 and 5 show significant trends in glacier mass-balance fluctuations over the past five centuries.
Around the mid-16th century, Grosse Aletschgletscher showed generally negative mass balances, with a consequent minimum in cumulative mass balance at this time. As shown in Figures 6 and 7 (Reference Luterbacher, Dietrich, Xoplaki, Grosjean and WannerLuterbacher and others, 2004; Reference Pauling, Luterbacher, Casty and WannerPauling and others, in press), this coincides with an extended period of higher summer temperatures. This period ends when winter precipitation increases.

Fig. 6. Winter (December-February) precipitation anomaly for the 1500–1999 period (solid curve) over the grid range used in this study (after Reference Pauling, Luterbacher, Casty and WannerPauling and others, in press). Also shown is the 30 year low-pass filtered time series of the winter precipitation model input (thick curve). The time series is z-standardized relative to the 1919–99 calibration average.

Fig. 7. Summer (June–August) temperature anomaly for the 1500– 1999 period (solid curve) over the grid range used in this study (after Reference Luterbacher, Dietrich, Xoplaki, Grosjean and WannerLuterbacher and others, 2004). Also shown is the 30 year low-pass filtered time series of the summer temperature model input (thick curve). The time series is z-standardized relative to the 1919–99 calibration average.
The maximum mass balances around 1600 are connected with low summer temperatures and average winter precipitation. These conditions led to low ablation rates and an extended period of increasing mass balance.
During the next century (~1610–1710), mass balance remained static and showed a slight negative trend. Summer temperature and winter precipitation are also found to stagnate. Cumulative mass balance shows a broad plateau in the 17th century, with two relative minima in the mid-17th century and at the beginning of the 18th century.
From around 1710, decreasing summer temperatures and very high winter precipitation caused a phase of uniform positive mass balance with a mass gain. The later stagnancy of glacier mass balance is represented by a nearly constant cumulative mass balance. This period of maximal cumulative mass balance coincides with a minimum in glacier length (Reference Haeberli and HolzhauserHaeberli and Holzhauser, 2003).
From 1770 to 1810, low winter accumulation potential and high summer ablation potential overlap, producing conditions favourable for negative mass balances and a resulting continuous mass loss, with a minimum of cumulative mass balance around 1810. The 1856 glacial maximum was likely produced by 40–50 years of cool summers without anomalous positive winter precipitation, identifiable as two short periods of positive mass balance. After 1856, higher summer temperatures and low winter precipitation caused an extended ablation-dominated mode with an enormous mass loss until the beginning of the 20th century. From then until the 1920s, retreat rates slowed substantially, and a small mass gain was determined. Low summer temperatures coupled with increasing winter precipitation coincided with an increasing (positive) mass balance. Note that for this time a little stagnancy in length was documented for Grosse Aletschgletscher (VAW/SANW, 1881–2002; Reference Zumbühl and HolzhauserZumbühl and Holzhauser, 1988). The mid-1950s mass loss was characterized by high summer temperatures, while the subsequent positive mass balances in the 1980s can be explained by lower summer temperatures and high winter precipitation.
The evidence presented here suggests that maxima in the mass balance of Grosse Aletschgletscher are predominantly caused by cold summers, often coupled with high winter precipitation. This is in good agreement with Reference Oerlemans and ReichertOerlemans and Reichert (2000) who show that summer temperature is the important factor in drier (inner Alpine) climates. Negative mass balance is mainly driven by high summer temperature. There is probably a weaker dependence on low winter precipitation, which can be influential under strong enough forcing. This longer-term model was driven by a very small number of forcing factors, so spring and fall conditions, and the effects of summer precipitation, are not taken into account.
4. Conclusions and Outlook
For the first time, an NNM has been used to reconstruct the mass balance of Grosse Aletschgletscher. Two new gridded datasets of temperature and precipitation were applied to the NNM as potential driving factors of the glacier system. This was a unique opportunity to bring these two aspects, a new method and two new datasets, together.
The results of this study show that the NNM approach is a useful tool for quantifying Grosse Aletschgletscher’s mass-balance changes in a non-linear way. In fact, the reconstructed mass balance is the result of a combination of several climatic input variables (precipitation and temperature) that vary in their composition and input importance. It can be shown how the mass balance reacts to changes in local to regional temperature and precipitation. We observed maximum mass balances for Grosse Aletschgletscher around 1600, 1730, 1815/45 and 1920. Minima in glacier mass balance were found in the 1540s, 1790s, 1870s and 1950s.
Furthermore, we confirm that summer temperature is an important driving factor for variations in mass balance. Thus the results presented here suggest that neural network models capture the appropriate dependence on the relevant inputs that likely affect a glacier system. We also conclude that the climate–mass-balance relation of Grosse Aletschgletscher consists of a significant non-linear part.
In our approach we used only temperature and precipitation data as inputs for the BPN. It would be interesting to see whether other data (e.g. North Atlantic Oscillation, solar irradiance or tree rings) could improve the quality of the model. In the absence of widespread mass-balance data that can be used as training sets, the possibility of using the present approach to model glacier length variations should be further investigated.
Acknowledgements
This study was supported by the following institutions: Stiftung Marchese Francesco Medici del Vascello, and the Swiss National Science Foundation, through its National Centre of Competence in Research on Climate (NCCR Climate), project PALVAREX. The authors are grateful to MeteoSwiss, J. Luterbacher and A. Pauling for providing instrumental and multi-proxy reconstructions of temperature and precipitation. Thanks also go to A. Bauder for providing data from Grosse Aletschgletscher and for helpful advice. The detailed comments and fruitful suggestions of H. Wanner, D.B. Reusch, an anonymous reviewer and the Scientific Editor, R.A. Bindschadler, helped to improve this paper.














