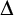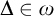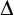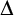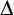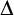1 Introduction
In this paper, we consider locally checkable labeling problems (LCLs) on regular trees. We will use the following formulation of such LCLs from [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky4]. Colorings in this formulation are on so-called “half edges,” and we will need a nonstandard formalization of the notion of a graph to fully accommodate these. Fix
![]() $\Delta \geq 2$
.
$\Delta \geq 2$
.
Definition 1.1. A
![]() $\Delta $
-regular graph G with vertex set X and edge set E is a subset
$\Delta $
-regular graph G with vertex set X and edge set E is a subset
![]() $G \subset X \times E$
such that for each
$G \subset X \times E$
such that for each
![]() $x \in X$
, there are exactly
$x \in X$
, there are exactly
![]() $\Delta \ e \in E$
with
$\Delta \ e \in E$
with
![]() $(x,e) \in G$
, for each
$(x,e) \in G$
, for each
![]() $e \in E$
, the number of
$e \in E$
, the number of
![]() $x \in X$
with
$x \in X$
with
![]() $(x,e) \in G$
is either 1 or 2, and for each
$(x,e) \in G$
is either 1 or 2, and for each
![]() $x \neq y$
in X, there is at most 1
$x \neq y$
in X, there is at most 1
![]() $e \in E$
with
$e \in E$
with
![]() $(x,e),(y,e) \in G$
.
$(x,e),(y,e) \in G$
.
An element
![]() $(x,e)\ G$
is called a half edge incident to x, x an endpoint of e, and e incident to x. If a given edge e has two endpoints, say
$(x,e)\ G$
is called a half edge incident to x, x an endpoint of e, and e incident to x. If a given edge e has two endpoints, say
![]() $x,y \in X$
, we call it a true edge, and say x and y are adjacent and that y is a neighbor of x. In this case we may also identify the half edge
$x,y \in X$
, we call it a true edge, and say x and y are adjacent and that y is a neighbor of x. In this case we may also identify the half edge
![]() $(x,e)$
with the ordered pair
$(x,e)$
with the ordered pair
![]() $(x,y)$
. We will also call the half edges
$(x,y)$
. We will also call the half edges
![]() $(x,e)$
and
$(x,e)$
and
![]() $(y,e)$
the half edges comprising e. Otherwise we call e a virtual edge and
$(y,e)$
the half edges comprising e. Otherwise we call e a virtual edge and
![]() $(x,e)$
a virtual half edge.
$(x,e)$
a virtual half edge.
If x is a vertex of G, the degree of x, denoted
![]() $\deg (x)$
, is the number of neighbors of x. Call G truly
$\deg (x)$
, is the number of neighbors of x. Call G truly
![]() $\Delta $
-regular if the degree of each vertex is
$\Delta $
-regular if the degree of each vertex is
![]() $\Delta $
. This is equivalent to G having no virtual edges.
$\Delta $
. This is equivalent to G having no virtual edges.
We use the definition of adjacency for vertices above to port standard graph theoretic terminology into this model, e.g., path, path distance, cycle, and connected component. We call a graph G acyclic or a forest if it has no cycles. We call a set of vertices G-invariant if it is a union of G-connected components. We use
![]() $B(-,r)$
to denote the radius r (w.r.t. path distance) neighborhood of a vertex or set of vertices.
$B(-,r)$
to denote the radius r (w.r.t. path distance) neighborhood of a vertex or set of vertices.
Observe also that if our G is truly
![]() $\Delta $
-regular, the adjacency relation gives a
$\Delta $
-regular, the adjacency relation gives a
![]() $\Delta $
-regular graph on X in the traditional sense, call it
$\Delta $
-regular graph on X in the traditional sense, call it
![]() $\overline {G}$
. In this case the identification in paragraph 2 of the above definition actually gives a bijection between G and
$\overline {G}$
. In this case the identification in paragraph 2 of the above definition actually gives a bijection between G and
![]() $\overline {G}$
where half edges in G go to ordered edges in
$\overline {G}$
where half edges in G go to ordered edges in
![]() $\overline {G}$
. We can thus identify G and
$\overline {G}$
. We can thus identify G and
![]() $\overline {G}$
in this case.
$\overline {G}$
in this case.
We can now describe our LCLs:
Definition 1.2. An LCL on
![]() $\Delta $
-regular graphs
$\Delta $
-regular graphs
![]() $\Pi $
is a triple
$\Pi $
is a triple
![]() $(\Sigma ,\mathcal {V},\mathcal {E})$
, where
$(\Sigma ,\mathcal {V},\mathcal {E})$
, where
![]() $\Sigma $
is a finite set, and
$\Sigma $
is a finite set, and
![]() $\mathcal {V}$
and
$\mathcal {V}$
and
![]() $\mathcal {E}$
are sets of size
$\mathcal {E}$
are sets of size
![]() $\Delta $
and
$\Delta $
and
![]() $2$
, respectively, multisets of labels from
$2$
, respectively, multisets of labels from
![]() $\Sigma $
.
$\Sigma $
.
Let G be a
![]() $\Delta $
-regular graph and
$\Delta $
-regular graph and
![]() $c:G \rightarrow \Sigma $
. (That is, c is a labeling of the half edges of G.)
$c:G \rightarrow \Sigma $
. (That is, c is a labeling of the half edges of G.)
-
• If e is a true edge of G, write
 $c(e)$
to denote the size 2 multiset
$c(e)$
to denote the size 2 multiset
 $\{c(x,e),c(y,e)\}$
, where x and y are the endpoints of e.
$\{c(x,e),c(y,e)\}$
, where x and y are the endpoints of e. -
• If x is a vertex of G, write
 $c(x)$
to denote the size
$c(x)$
to denote the size
 $\Delta $
multiset of colors given to the half edges meeting x.
$\Delta $
multiset of colors given to the half edges meeting x.
We say c is a
![]() $\Pi $
-coloring of G if for each true edge e of G,
$\Pi $
-coloring of G if for each true edge e of G,
![]() $c(e) \in \mathcal {E}$
, and for each vertex x of G,
$c(e) \in \mathcal {E}$
, and for each vertex x of G,
![]() $c(x) \in \mathcal {V}$
.
$c(x) \in \mathcal {V}$
.
Much exciting recent work has found connections between the study of LCLs in various settings. For example, in the LOCAL model [Reference Linial7], one imagines vertices as processors and edges as communication channels, where each processor must decide on labels for its incident half edges based on a small amount of communication with its neighbors so that the result of all these decisions amounts to a
![]() $\Pi $
-coloring for a given
$\Pi $
-coloring for a given
![]() $\Pi $
. In the descriptive setting, the vertex and edge sets are Polish spaces, G is a descriptive-set-theoretically “nice” relation on them (e.g., Borel), and one looks for
$\Pi $
. In the descriptive setting, the vertex and edge sets are Polish spaces, G is a descriptive-set-theoretically “nice” relation on them (e.g., Borel), and one looks for
![]() $\Pi $
-colorings which are similarly “nice.” The systematic study of connections between these two settings was introduced in [Reference Bernshteyn3]. A starting point for this paper is the work in [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky4, Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky5], which carried out a much more complete study of connections between these settings and others in the special case where G is acyclic.
$\Pi $
-colorings which are similarly “nice.” The systematic study of connections between these two settings was introduced in [Reference Bernshteyn3]. A starting point for this paper is the work in [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky4, Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky5], which carried out a much more complete study of connections between these settings and others in the special case where G is acyclic.
Less explored are connections between these fields and the computable setting, where one is given a graph which is in some sense computable, and looks for similarly computable
![]() $\Pi $
-colorings. Work of Qian and Weilacher [Reference Qian and Weilacher9] established some parallels between certain parts of this setting and of the descriptive setting, but failed to find any direct relationship. The main results of this paper show that such direct relationships do exist if one again restricts to the special case of acyclic graphs.
$\Pi $
-colorings. Work of Qian and Weilacher [Reference Qian and Weilacher9] established some parallels between certain parts of this setting and of the descriptive setting, but failed to find any direct relationship. The main results of this paper show that such direct relationships do exist if one again restricts to the special case of acyclic graphs.
We now formally describe some of the settings which were described informally above. In (3) below and throughout the paper,
![]() $\text {HF}$
denotes the set of hereditarily finite sets, which we use as our domain for discussing computability. Note that the definitions below make sense for general classes of graphs, but in this paper we are chiefly concerned with complexity classes for acyclic graphs.
$\text {HF}$
denotes the set of hereditarily finite sets, which we use as our domain for discussing computability. Note that the definitions below make sense for general classes of graphs, but in this paper we are chiefly concerned with complexity classes for acyclic graphs.
Definition 1.3. Let
![]() $\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
be an LCL on
$\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
be an LCL on
![]() $\Delta $
-regular graphs.
$\Delta $
-regular graphs.
-
(1) We call a truly
 $\Delta $
-regular graph G Borel if its vertex set X is a Polish space and the associated
$\Delta $
-regular graph G Borel if its vertex set X is a Polish space and the associated
 $\overline {G}$
(see the comment after Definition 1.1) is Borel in
$\overline {G}$
(see the comment after Definition 1.1) is Borel in
 $X \times X$
. We call a coloring
$X \times X$
. We call a coloring
 $c:G \rightarrow \Sigma $
Borel if it is Borel as function on
$c:G \rightarrow \Sigma $
Borel if it is Borel as function on
 $\overline {G} \subset X \times X$
. We say
$\overline {G} \subset X \times X$
. We say
 $\Pi $
is in the class BAIRE if every acyclic such G admits a Borel
$\Pi $
is in the class BAIRE if every acyclic such G admits a Borel
 $\Pi $
-coloring off a G-invariant meager Borel subset of vertices. I.e., there is a G-invariant comeager Borel set
$\Pi $
-coloring off a G-invariant meager Borel subset of vertices. I.e., there is a G-invariant comeager Borel set
 $C \subset X$
such that the graph identified with
$C \subset X$
such that the graph identified with
 $\overline {G} \cap (C \times C)$
admits a Borel
$\overline {G} \cap (C \times C)$
admits a Borel
 $\Pi $
-coloring.
$\Pi $
-coloring. -
(2) [Reference Bernshteyn2, Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky5] We call a Borel
 $\Delta $
-regular graph G as in (1) continuous if X is zero-dimensional and for any clopen
$\Delta $
-regular graph G as in (1) continuous if X is zero-dimensional and for any clopen
 $U \subset X$
, the set of neighbors of elements of U is clopen. We call a coloring
$U \subset X$
, the set of neighbors of elements of U is clopen. We call a coloring
 $c: G \rightarrow \Sigma $
continuous if it continuous as a function on
$c: G \rightarrow \Sigma $
continuous if it continuous as a function on
 $\overline {G} \subset X \times X$
with the subspace topology. We say
$\overline {G} \subset X \times X$
with the subspace topology. We say
 $\Pi $
is in the class CONTINUOUS if every acyclic such G admits a continuous
$\Pi $
is in the class CONTINUOUS if every acyclic such G admits a continuous
 $\Pi $
-coloring.
$\Pi $
-coloring. -
(3) We call a
 $\Delta $
-regular graph G computable if its vertex and edge sets X and E are computable subsets of
$\Delta $
-regular graph G computable if its vertex and edge sets X and E are computable subsets of
 $\text {HF}$
and G is a computable subset of
$\text {HF}$
and G is a computable subset of
 $X \times E$
. We call a coloring
$X \times E$
. We call a coloring
 $c : G \rightarrow \Sigma $
computable if it is computable as a function (we may of course assume
$c : G \rightarrow \Sigma $
computable if it is computable as a function (we may of course assume
 $\Sigma \subset \text {HF}$
). We say
$\Sigma \subset \text {HF}$
). We say
 $\Pi $
is in the class COMPUTABLE if every computable acyclic
$\Pi $
is in the class COMPUTABLE if every computable acyclic
 $\Delta $
-regular graph admits a computable
$\Delta $
-regular graph admits a computable
 $\Pi $
-coloring.
$\Pi $
-coloring. -
(4) We call a computable
 $\Delta $
-regular graph G as in (3) highly computable if the degree function
$\Delta $
-regular graph G as in (3) highly computable if the degree function
 $\deg :X \rightarrow \omega $
is computable. Since there are
$\deg :X \rightarrow \omega $
is computable. Since there are
 $\Delta $
edges incident to each
$\Delta $
edges incident to each
 $x \in X$
and
$x \in X$
and
 $\deg (x)$
is the number of true such edges, this is equivalent to the set of true edges being computable. In particular, truly
$\deg (x)$
is the number of true such edges, this is equivalent to the set of true edges being computable. In particular, truly
 $\Delta $
-regular computable graphs are highly computable. We say
$\Delta $
-regular computable graphs are highly computable. We say
 $\Pi $
is in the class HCOMP if every highly computable acyclic
$\Pi $
is in the class HCOMP if every highly computable acyclic
 $\Delta $
-regular graph admits a computable
$\Delta $
-regular graph admits a computable
 $\Pi $
-coloring.
$\Pi $
-coloring.
We can now state our results. In [Reference Qian and Weilacher9], Qian and Weilacher ask whether, for a general nice class of graphs, LCLs solvable in the highly computable setting are always solvable Baire-measurably. Our first result confirms this for regular forests.
Theorem 1.4.
![]() $\mathrm {BAIRE} = \mathrm {HCOMP}$
.
$\mathrm {BAIRE} = \mathrm {HCOMP}$
.
Our second result concerns the class COMPUTABLE. This class does not strongly parallel any in the descriptive or LOCAL settings; the inability in computable but not highly computable graphs to effectively quantify over the neighbors of a vertex, a process which is trivial in these other settings, severely restricts the problems one can make headway on. Still, the class does contain nontrivial problems such as
![]() $(\Delta +1)$
-proper vertex coloring [Reference Schmerl10], making it meaningful to establish the following one-sided implication:
$(\Delta +1)$
-proper vertex coloring [Reference Schmerl10], making it meaningful to establish the following one-sided implication:
Theorem 1.5.
![]() $\mathrm {COMPUTABLE} \subset \mathrm {CONTINUOUS}$
, but the reverse inclusion does not hold. Moreover, if an LCL on
$\mathrm {COMPUTABLE} \subset \mathrm {CONTINUOUS}$
, but the reverse inclusion does not hold. Moreover, if an LCL on
![]() $\Delta $
-regular graphs is in COMPUTABLE, it can be solved continuously on any
$\Delta $
-regular graphs is in COMPUTABLE, it can be solved continuously on any
![]() $\Delta $
-regular continuous graph, and computably on any
$\Delta $
-regular continuous graph, and computably on any
![]() $\Delta $
-regular computable graph.
$\Delta $
-regular computable graph.
It should be noted that, by the equivalences shown in [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky4, Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky5] between our descriptive set theoretic classes of interest and various classes from other settings (such as the LOCAL model), Theorems 1.4 and 1.5 also provide connections between these other settings and computable combinatorics. For example, an LCL is in HCOMP if and only if it can be solved by a deterministic LOCAL algorithm on trees in time
![]() $O(\log (n))$
, and if an LCL is in COMPUTABLE, it can be solved by a deterministic LOCAL algorithm on trees in time
$O(\log (n))$
, and if an LCL is in COMPUTABLE, it can be solved by a deterministic LOCAL algorithm on trees in time
![]() $O(\log ^*(n))$
.
$O(\log ^*(n))$
.
2 Highly computable forests
In this section we prove Theorem 1.4. Key to the equality is the following combinatorial condition:
Definition 2.1.
-
• Let
 $l \in \omega $
. A
$l \in \omega $
. A
 $\Delta $
-regular path of length l is a
$\Delta $
-regular path of length l is a
 $\Delta $
-regular tree with
$\Delta $
-regular tree with
 $l+1$
vertices, say
$l+1$
vertices, say
 $x_0,\ldots ,x_l$
, with
$x_0,\ldots ,x_l$
, with
 $x_i$
and
$x_i$
and
 $x_{i+1}$
adjacent for each
$x_{i+1}$
adjacent for each
 $i < l$
, and all other edges being virtual.
$i < l$
, and all other edges being virtual.
 $x_0$
and
$x_0$
and
 $x_l$
are called the endpoints of the path.
$x_l$
are called the endpoints of the path. -
• Let
 $\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
be an LCL on
$\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
be an LCL on
 $\Delta $
-regular graphs. Let
$\Delta $
-regular graphs. Let
 $l \geq 1$
. Let
$l \geq 1$
. Let
 $\mathcal {V}' \subset \mathcal {V}$
. We say
$\mathcal {V}' \subset \mathcal {V}$
. We say
 $\mathcal {V}'$
is l-full if whenever P is a
$\mathcal {V}'$
is l-full if whenever P is a
 $\Delta $
-regular path of length at least l and the half edges incident to its endpoints, say x and y, are precolored so that
$\Delta $
-regular path of length at least l and the half edges incident to its endpoints, say x and y, are precolored so that
 $c(x),c(y) \in \mathcal {V}'$
, this can be extended to a
$c(x),c(y) \in \mathcal {V}'$
, this can be extended to a
 $\Pi $
-coloring of P so that
$\Pi $
-coloring of P so that
 $c(z) \in \mathcal {V}'$
for every vertex z of P. We say
$c(z) \in \mathcal {V}'$
for every vertex z of P. We say
 $\Pi $
is l-full if it admits some nonempty such
$\Pi $
is l-full if it admits some nonempty such
 $\mathcal {V}'$
. We say
$\mathcal {V}'$
. We say
 $\Pi $
is full if it is l-full for some l.
$\Pi $
is full if it is l-full for some l.
Recall the second bullet point in Definition 1.2 for the meaning of
![]() $c(x)$
when x is a vertex. The fullness condition is due to Anton Bernshteyn, who also has shown [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky4] that an LCL on
$c(x)$
when x is a vertex. The fullness condition is due to Anton Bernshteyn, who also has shown [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky4] that an LCL on
![]() $\Delta $
-regular graphs is in BAIRE if and only if it is full. It thus suffices for us to prove:
$\Delta $
-regular graphs is in BAIRE if and only if it is full. It thus suffices for us to prove:
Theorem 2.2. An LCL on
![]() $\Delta $
-regular graphs is in
$\Delta $
-regular graphs is in
![]() $\mathrm {HCOMP} $
if and only if it is full.
$\mathrm {HCOMP} $
if and only if it is full.
The proof in [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky4] of the reverse direction of Bernshteyn’s result uses a construction called a toast:
Definition 2.3. Let G be a
![]() $\Delta $
-regular graph and
$\Delta $
-regular graph and
![]() $l \in \omega $
. An l-toast for G is a collection
$l \in \omega $
. An l-toast for G is a collection
![]() $\mathcal {C}$
of nonempty finite G-connected sets of vertices (called pieces) such that:
$\mathcal {C}$
of nonempty finite G-connected sets of vertices (called pieces) such that:
-
(1) For distinct
 $C,D \in \mathcal {C}$
, either
$C,D \in \mathcal {C}$
, either
 $B(C,l) \subset D$
,
$B(C,l) \subset D$
,
 $B(D,l) \subset C$
, or the path distance from C to D is greater than l.
$B(D,l) \subset C$
, or the path distance from C to D is greater than l. -
(2) If vertices
 $x,y$
are in the same G-component, there is some
$x,y$
are in the same G-component, there is some
 $C \in \mathcal {C}$
containing both of them.
$C \in \mathcal {C}$
containing both of them.
If G is a computable graph, it makes sense to ask that a toast for G be computable. In [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky4, Proposition 6.4], a straightforward algorithm is presented which uses a
![]() $(2l+2)$
-toast for a
$(2l+2)$
-toast for a
![]() $\Delta $
-regular forest, say T, to produce a
$\Delta $
-regular forest, say T, to produce a
![]() $\Pi $
-coloring of T given that
$\Pi $
-coloring of T given that
![]() $\Pi $
is l-full. One can easily see that this will produce a computable
$\Pi $
is l-full. One can easily see that this will produce a computable
![]() $\Pi $
-coloring if the input toast is computable, so it suffices for our reverse direction to prove the following, whose origins seem to be in [Reference Bean1, Theorem 3].
$\Pi $
-coloring if the input toast is computable, so it suffices for our reverse direction to prove the following, whose origins seem to be in [Reference Bean1, Theorem 3].
Theorem 2.4. Let G be a highly computable
![]() $\Delta $
-regular graph. G admits a computable l-toast for every
$\Delta $
-regular graph. G admits a computable l-toast for every
![]() $l \in \omega $
.
$l \in \omega $
.
Proof Fix l. WLOG the vertex set of G, say X, is a subset of
![]() $\omega $
. We will construct our toast recursively in
$\omega $
. We will construct our toast recursively in
![]() $\omega $
-stages. At each stage, we will have only finitely many pieces in our toast.
$\omega $
-stages. At each stage, we will have only finitely many pieces in our toast.
At stage n, if
![]() $n \not \in X$
, we do nothing. If
$n \not \in X$
, we do nothing. If
![]() $n \in X$
, we check our finitely many pieces to see if any contains
$n \in X$
, we check our finitely many pieces to see if any contains
![]() $B(n,1)$
. If so, we do nothing.
$B(n,1)$
. If so, we do nothing.
If not, we find the least
![]() $r> 0$
such that
$r> 0$
such that
![]() $B(n,r)$
can be added to our toast without violating (1). This exists since our toast so far is finite (so, in fact, there is a tail of r’s which will work) and it can be determined effectively since G is highly computable, which means we can computably output the finite graph
$B(n,r)$
can be added to our toast without violating (1). This exists since our toast so far is finite (so, in fact, there is a tail of r’s which will work) and it can be determined effectively since G is highly computable, which means we can computably output the finite graph
![]() $G \upharpoonright B(n,r)$
given n and r. We then add
$G \upharpoonright B(n,r)$
given n and r. We then add
![]() $B(n,r)$
to our toast.
$B(n,r)$
to our toast.
Call the resulting set of finite connected sets of vertices
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
![]() $\mathcal {C}$
is computable since at stage n, if we add a new set to
$\mathcal {C}$
is computable since at stage n, if we add a new set to
![]() $\mathcal {C}$
, that set contains the vertex n. Thus, to test whether a given finite set C is in
$\mathcal {C}$
, that set contains the vertex n. Thus, to test whether a given finite set C is in
![]() $\mathcal {C}$
, we only need to run our algorithm until stage
$\mathcal {C}$
, we only need to run our algorithm until stage
![]() $\max (C)$
. (1) is satisfied since we made sure it was satisfied when adding each new piece. For each
$\max (C)$
. (1) is satisfied since we made sure it was satisfied when adding each new piece. For each
![]() $n \in X$
, at stage n we made sure there was a piece of toast containing
$n \in X$
, at stage n we made sure there was a piece of toast containing
![]() $B(n,1)$
. This implies (2) by induction on the path distance between x and y: If z is a neighbor of y and we have a piece of toast C containing x and z and a piece of toast D containing
$B(n,1)$
. This implies (2) by induction on the path distance between x and y: If z is a neighbor of y and we have a piece of toast C containing x and z and a piece of toast D containing
![]() $B(y,1)$
, then
$B(y,1)$
, then
![]() $C \cap D \neq \emptyset $
, so one must contain the other, and then the larger one contains x and y.
$C \cap D \neq \emptyset $
, so one must contain the other, and then the larger one contains x and y.
We now prove by contrapositive the forward direction of Theorem 2.2. The following proof is inspired by [Reference Manaster and Rosenstein8], which used a similar argument to construct, for a given
![]() $k \geq 2$
, a computable truly k-regular computably bipartite graph with no computable perfect matching:
$k \geq 2$
, a computable truly k-regular computably bipartite graph with no computable perfect matching:
Proposition 2.5. If an LCL on
![]() $\Delta $
-regular graphs
$\Delta $
-regular graphs
![]() $\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
is not full, there is a computable truly
$\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
is not full, there is a computable truly
![]() $\Delta $
-regular forest (thus highly computable) with no computable
$\Delta $
-regular forest (thus highly computable) with no computable
![]() $\Pi $
-coloring.
$\Pi $
-coloring.
Proof If
![]() $\Pi $
is not full, then for every nonempty
$\Pi $
is not full, then for every nonempty
![]() $\mathcal {V}' \subset \mathcal {V}$
and
$\mathcal {V}' \subset \mathcal {V}$
and
![]() $l' \geq 1$
, there are
$l' \geq 1$
, there are
![]() $l \geq l'$
, multisets, say
$l \geq l'$
, multisets, say
![]() $a,b \in \mathcal {V}'$
, and labels, say
$a,b \in \mathcal {V}'$
, and labels, say
![]() $\alpha , \beta \in \Sigma $
appearing in a and b respectively such that the following holds: Let P be a
$\alpha , \beta \in \Sigma $
appearing in a and b respectively such that the following holds: Let P be a
![]() $\Delta $
-regular path of length l, say with vertices
$\Delta $
-regular path of length l, say with vertices
![]() $x_0,\ldots ,x_l$
in order. Label the half edges incident to
$x_0,\ldots ,x_l$
in order. Label the half edges incident to
![]() $x_0$
such that
$x_0$
such that
![]() $c(x_0) = a$
and
$c(x_0) = a$
and
![]() $c(x_0,x_1) = \alpha $
, and likewise for
$c(x_0,x_1) = \alpha $
, and likewise for
![]() $x_l, b, x_{l-1}$
and
$x_l, b, x_{l-1}$
and
![]() $\beta $
respectively. Then if this labeling is extended to a
$\beta $
respectively. Then if this labeling is extended to a
![]() $\Pi $
-coloring c of P, some vertex
$\Pi $
-coloring c of P, some vertex
![]() $x_i$
has
$x_i$
has
![]() $c(x_i) \not \in \mathcal {V}'$
. Note that if
$c(x_i) \not \in \mathcal {V}'$
. Note that if
![]() $\mathcal {V}' = \mathcal {V}$
, this means there is no such extension.
$\mathcal {V}' = \mathcal {V}$
, this means there is no such extension.
Since
![]() $\Sigma $
is finite, we can say instead that for all nonempty
$\Sigma $
is finite, we can say instead that for all nonempty
![]() $\mathcal {V}' \subset \mathcal {V}$
, there exists
$\mathcal {V}' \subset \mathcal {V}$
, there exists
![]() $a,b \in \mathcal {V}'$
and
$a,b \in \mathcal {V}'$
and
![]() $\alpha ,\beta \in \Sigma $
which have this property for infinitely many l. Fix choices of such
$\alpha ,\beta \in \Sigma $
which have this property for infinitely many l. Fix choices of such
![]() $a,b,\alpha $
, and
$a,b,\alpha $
, and
![]() $\beta $
for each
$\beta $
for each
![]() $\mathcal {V}'$
, and call them bad for
$\mathcal {V}'$
, and call them bad for
![]() $\mathcal {V}'$
. Also call the infinite set of l witnessing this badness the set of bad l for
$\mathcal {V}'$
. Also call the infinite set of l witnessing this badness the set of bad l for
![]() $\mathcal {V}'$
. Note that determining whether a given l is bad for a given
$\mathcal {V}'$
. Note that determining whether a given l is bad for a given
![]() $\mathcal {V}'$
is computable: It can be done by checking all possible colorings of a
$\mathcal {V}'$
is computable: It can be done by checking all possible colorings of a
![]() $\Delta $
-regular path of length l with labels from
$\Delta $
-regular path of length l with labels from
![]() $\Sigma $
, of which there are only finitely many.
$\Sigma $
, of which there are only finitely many.
Fix
![]() $X,E \subset \text {HF}$
disjoint infinite computable sets, and a computable well order of
$X,E \subset \text {HF}$
disjoint infinite computable sets, and a computable well order of
![]() $\text {HF}$
of type
$\text {HF}$
of type
![]() $\omega $
. X and E will be our vertex and edge sets respectively. Fix an effective enumeration
$\omega $
. X and E will be our vertex and edge sets respectively. Fix an effective enumeration
![]() $\{\phi _t \mid t \in \omega \}$
of the set of partial recursive functions
$\{\phi _t \mid t \in \omega \}$
of the set of partial recursive functions
![]() $X \times E \rightarrow \Sigma $
. (These are candidates for computable colorings of the half edges of our graph.) Fix also an effective enumeration
$X \times E \rightarrow \Sigma $
. (These are candidates for computable colorings of the half edges of our graph.) Fix also an effective enumeration
![]() $\{t_n \mid n \in \omega \}$
of
$\{t_n \mid n \in \omega \}$
of
![]() $\omega $
which lists each natural number infinitely many times. We are about to describe a recursive construction of
$\omega $
which lists each natural number infinitely many times. We are about to describe a recursive construction of
![]() $\Delta $
-regular forests
$\Delta $
-regular forests
![]() $\emptyset = T_0 \subset T_1 \subset \cdots $
with vertex sets contained in X. The vertex set for each
$\emptyset = T_0 \subset T_1 \subset \cdots $
with vertex sets contained in X. The vertex set for each
![]() $T_n$
will be finite. It will happen that in our construction every
$T_n$
will be finite. It will happen that in our construction every
![]() $x \in X$
will eventually become a vertex and be made to have degree
$x \in X$
will eventually become a vertex and be made to have degree
![]() $\Delta $
. The limit
$\Delta $
. The limit
![]() $T = \bigcup _n T_n$
will then be a computable truly
$T = \bigcup _n T_n$
will then be a computable truly
![]() $\Delta $
-regular forest. Our construction will be designed so that T does not admit a computable
$\Delta $
-regular forest. Our construction will be designed so that T does not admit a computable
![]() $\Pi $
-coloring.
$\Pi $
-coloring.
Alongside T, we will recursively build a T-invariant total computable function
![]() $C:X \rightarrow \omega $
. The idea is that the vertices in
$C:X \rightarrow \omega $
. The idea is that the vertices in
![]() $C^{-1}(t)$
will be responsible for ensuring that
$C^{-1}(t)$
will be responsible for ensuring that
![]() $\phi _t$
is not a
$\phi _t$
is not a
![]() $\Pi $
-coloring of T. At stage n, the vertices on which C has been defined will be exactly those in the vertex set of
$\Pi $
-coloring of T. At stage n, the vertices on which C has been defined will be exactly those in the vertex set of
![]() $T_n$
.
$T_n$
.
At a typical stage in the construction, we will take currently unused (not in the vertex set of our current finite tree) vertices, define C on them, and give them
![]() $\Delta $
incident half edges. We will refer to these as “new vertices,” and always choose the least (according to our previously fixed order of
$\Delta $
incident half edges. We will refer to these as “new vertices,” and always choose the least (according to our previously fixed order of
![]() $\text {HF}$
) available. For example, if x has degree 0 in
$\text {HF}$
) available. For example, if x has degree 0 in
![]() $T_n$
, and in the definition of
$T_n$
, and in the definition of
![]() $T_{n+1}$
we say “add
$T_{n+1}$
we say “add
![]() $\Delta $
new vertices as neighbors to x,” it means: let
$\Delta $
new vertices as neighbors to x,” it means: let
![]() $y_0,\ldots ,y_{\Delta -1}$
be the least elements of X not in the vertex set of
$y_0,\ldots ,y_{\Delta -1}$
be the least elements of X not in the vertex set of
![]() $T_n$
, let
$T_n$
, let
![]() $e_0,\ldots ,e_{\Delta -1}$
be the virtual edges incident to x in
$e_0,\ldots ,e_{\Delta -1}$
be the virtual edges incident to x in
![]() $T_n$
, and add the half edges
$T_n$
, and add the half edges
![]() $(y_i,e_i)$
to
$(y_i,e_i)$
to
![]() $T_{n+1}$
for
$T_{n+1}$
for
![]() $i < \Delta -1$
. The exact same treatment will be given to edges. For example, in the previous example, we would probably want to finish by saying “add
$i < \Delta -1$
. The exact same treatment will be given to edges. For example, in the previous example, we would probably want to finish by saying “add
![]() $\Delta -1$
new virtual edges incident to each
$\Delta -1$
new virtual edges incident to each
![]() $y_i$
” to maintain
$y_i$
” to maintain
![]() $\Delta $
-regularity. This would mean: let
$\Delta $
-regularity. This would mean: let
![]() $f_{i,j}$
for
$f_{i,j}$
for
![]() $i < \Delta $
,
$i < \Delta $
,
![]() $j < \Delta - 1$
be the least elements of E not in the edge set of
$j < \Delta - 1$
be the least elements of E not in the edge set of
![]() $T_n$
, and add the half edges
$T_n$
, and add the half edges
![]() $(y_i,f_{i,j})$
to
$(y_i,f_{i,j})$
to
![]() $T_{n+1}$
for each
$T_{n+1}$
for each
![]() $i,j$
.
$i,j$
.
In both steps of the previous example, our language leaves some ambiguity about exactly which new vertices/edges are connected to which old edges/vertices. The exact decision here will never matter (except of course in that it should be made in a computable way).
If the stage of our construction is n, C will always be defined to be
![]() $t_n$
on new vertices. Thus, our construction will essentially build
$t_n$
on new vertices. Thus, our construction will essentially build
![]() $\omega $
forests in parallel, one for each t. Let us fix t, and describe the
$\omega $
forests in parallel, one for each t. Let us fix t, and describe the
![]() $\omega $
steps in the construction of the t-th forest, i.e.,
$\omega $
steps in the construction of the t-th forest, i.e.,
![]() $T \upharpoonright C^{-1}(t)$
.
$T \upharpoonright C^{-1}(t)$
.
Fix a very large
![]() $N_0\gg |\Sigma |$
to be determined later, independent of t. In the 0-th stage of the construction, place
$N_0\gg |\Sigma |$
to be determined later, independent of t. In the 0-th stage of the construction, place
![]() $N_0$
new vertices, say
$N_0$
new vertices, say
![]() $x_0,\ldots ,x_{N_0-1}$
, in
$x_0,\ldots ,x_{N_0-1}$
, in
![]() $C^{-1}(t)$
. Also give each
$C^{-1}(t)$
. Also give each
![]() $x_i \ \Delta $
new virtual incident edges. This is shown in Figure 1.
$x_i \ \Delta $
new virtual incident edges. This is shown in Figure 1.

Figure 1 Stage 0 of the construction for a fixed t for
![]() $\Delta = 3$
.
$\Delta = 3$
.
We also initialize several variables: Set
![]() $\mathcal {V}' = \emptyset $
and
$\mathcal {V}' = \emptyset $
and
![]() $N = N_0$
. Also, for each
$N = N_0$
. Also, for each
![]() $i < N$
, let
$i < N$
, let
![]() $P_i$
be the
$P_i$
be the
![]() $\Delta $
-regular path of length 0 whose unique vertex is
$\Delta $
-regular path of length 0 whose unique vertex is
![]() $x_i$
.
$x_i$
.
At the start of an arbitrary successor stage, say
![]() $m+1$
, suppose we have some
$m+1$
, suppose we have some
![]() $\mathcal {V}' \subset \Sigma $
and
$\mathcal {V}' \subset \Sigma $
and
![]() $N \in \omega $
very large. Suppose also that we have
$N \in \omega $
very large. Suppose also that we have
![]() $\Delta $
-regular paths
$\Delta $
-regular paths
![]() $P_i$
for
$P_i$
for
![]() $i < N$
and vertices
$i < N$
and vertices
![]() $y_i^c$
for
$y_i^c$
for
![]() $i < N$
and
$i < N$
and
![]() $c \in \mathcal {V}'$
such that:
$c \in \mathcal {V}'$
such that:
-
(1) The
 $P_i$
’s and
$P_i$
’s and
 $y_i^c$
’s all lie in distinct
$y_i^c$
’s all lie in distinct
 $C^{-1}(t)$
-components.
$C^{-1}(t)$
-components. -
(2) For each i, if
 $\phi _t$
restricted to the half edges meeting
$\phi _t$
restricted to the half edges meeting
 $P_i$
is a
$P_i$
is a
 $\Pi $
-coloring of
$\Pi $
-coloring of
 $P_i$
, there must be some vertex x of
$P_i$
, there must be some vertex x of
 $P_i$
with
$P_i$
with
 $\phi _t(x) \not \in \mathcal {V}'$
.
$\phi _t(x) \not \in \mathcal {V}'$
. -
(3)
 $\phi _t(y_i^c) = c$
for each i and c.
$\phi _t(y_i^c) = c$
for each i and c.
Note that this is all satisfied after stage 0.
We start our successor stage by running the Turing machine computing
![]() $\phi _t$
for m steps on all of the half edges meeting all of the
$\phi _t$
for m steps on all of the half edges meeting all of the
![]() $P_i$
’s.
$P_i$
’s.
If
![]() $\phi _t$
fails to converge in
$\phi _t$
fails to converge in
![]() $\leq m$
steps on one of these inputs, or if it converges on all of them but the result fails to be a
$\leq m$
steps on one of these inputs, or if it converges on all of them but the result fails to be a
![]() $\Pi $
-coloring of some
$\Pi $
-coloring of some
![]() $P_i$
, we do what is shown in Figure 2: For each virtual edge e with unique endpoint in
$P_i$
, we do what is shown in Figure 2: For each virtual edge e with unique endpoint in
![]() $C^{-1}(t)$
, we make e true by adding a new vertex, say x, as its other endpoint, then to maintain
$C^{-1}(t)$
, we make e true by adding a new vertex, say x, as its other endpoint, then to maintain
![]() $\Delta $
-regularity we add
$\Delta $
-regularity we add
![]() $\Delta -1$
new edges as virtual edges incident to this x. We call this the “uninteresting case.”
$\Delta -1$
new edges as virtual edges incident to this x. We call this the “uninteresting case.”

Figure 2 The “uninteresting case” for a step of the construction for a fixed t, for
![]() $\Delta = 3$
.
$\Delta = 3$
.
The “interesting case” is of course if
![]() $\phi _t$
does converge on all these inputs in
$\phi _t$
does converge on all these inputs in
![]() $\leq m$
steps, and the result is a
$\leq m$
steps, and the result is a
![]() $\Pi $
-coloring for each
$\Pi $
-coloring for each
![]() $P_i$
. In this case, by condition (2) above, there is a vertex in each
$P_i$
. In this case, by condition (2) above, there is a vertex in each
![]() $P_i$
, say
$P_i$
, say
![]() $z_i$
, with
$z_i$
, with
![]() $\phi _t(z_i) \not \in \mathcal {V}'$
. Let
$\phi _t(z_i) \not \in \mathcal {V}'$
. Let
![]() $d \in \mathcal {V} \setminus \mathcal {V}'$
such that
$d \in \mathcal {V} \setminus \mathcal {V}'$
such that
![]() $\phi _t(z_i) = d$
for at least
$\phi _t(z_i) = d$
for at least
![]() $N/|\mathcal {V}| \ i$
’s. Update
$N/|\mathcal {V}| \ i$
’s. Update
![]() $\mathcal {V}'$
to
$\mathcal {V}'$
to
![]() $\mathcal {V}' \cup \{d\}$
.
$\mathcal {V}' \cup \{d\}$
.
Now
![]() $\mathcal {V}'$
is nonempty, so let
$\mathcal {V}'$
is nonempty, so let
![]() $a,b \in \mathcal {V}'$
with
$a,b \in \mathcal {V}'$
with
![]() $\alpha \in a$
and
$\alpha \in a$
and
![]() $\beta \in b$
be bad for
$\beta \in b$
be bad for
![]() $\mathcal {V}'$
. Between the
$\mathcal {V}'$
. Between the
![]() $z_i$
’s and the
$z_i$
’s and the
![]() $y_i^c$
’s, and using condition (1) above, we can choose degree
$y_i^c$
’s, and using condition (1) above, we can choose degree
![]() $\Delta $
vertices
$\Delta $
vertices
![]() $v_i$
and
$v_i$
and
![]() $w_i$
for
$w_i$
for
![]() $i < M := N/(2|\mathcal {V}|)$
such that
$i < M := N/(2|\mathcal {V}|)$
such that
![]() $\phi _t(v_i) = a$
for each i,
$\phi _t(v_i) = a$
for each i,
![]() $\phi _t(w_i) = b$
for each i, and all
$\phi _t(w_i) = b$
for each i, and all
![]() $2M$
of these vertices lie in distinct
$2M$
of these vertices lie in distinct
![]() $C^{-1}(t)$
-components. (The factor of
$C^{-1}(t)$
-components. (The factor of
![]() $1/2$
is needed for the case
$1/2$
is needed for the case
![]() $a = b$
.)
$a = b$
.)
Now for each
![]() $i < M / 2$
, pick
$i < M / 2$
, pick
![]() $e_i$
and
$e_i$
and
![]() $f_i$
virtual edges meeting the components of
$f_i$
virtual edges meeting the components of
![]() $v_i$
and
$v_i$
and
![]() $w_i$
respectively such that if e is the first edge in the path from
$w_i$
respectively such that if e is the first edge in the path from
![]() $v_i$
to
$v_i$
to
![]() $e_i$
, then
$e_i$
, then
![]() $\phi _t(v_i,e) = \alpha $
, and likewise for
$\phi _t(v_i,e) = \alpha $
, and likewise for
![]() $w_i$
,
$w_i$
,
![]() $f_i$
, and
$f_i$
, and
![]() $\beta $
. Note that these exist since our components are finite
$\beta $
. Note that these exist since our components are finite
![]() $\Delta $
-regular trees. As shown in in the first step in Figure 3, join
$\Delta $
-regular trees. As shown in in the first step in Figure 3, join
![]() $e_i$
and
$e_i$
and
![]() $f_i$
with a path of new vertices so that the resulting path between
$f_i$
with a path of new vertices so that the resulting path between
![]() $v_i$
and
$v_i$
and
![]() $w_i$
has a total length which is bad for
$w_i$
has a total length which is bad for
![]() $\mathcal {V}'$
. (Recall that this is possible as there are arbitrarily long bad lengths, and that determining if a length is bad is computable.) Call this new path
$\mathcal {V}'$
. (Recall that this is possible as there are arbitrarily long bad lengths, and that determining if a length is bad is computable.) Call this new path
![]() $P_i$
. Also, as shown in the second step in Figure 3, add
$P_i$
. Also, as shown in the second step in Figure 3, add
![]() $\Delta -2$
new virtual incident edges to the newly added vertices in
$\Delta -2$
new virtual incident edges to the newly added vertices in
![]() $P_i$
to maintain
$P_i$
to maintain
![]() $\Delta $
-regularity. Condition (2) is satisfied for each
$\Delta $
-regularity. Condition (2) is satisfied for each
![]() $P_i$
by definition of bad.
$P_i$
by definition of bad.

Figure 3 The “interesting case” for a step of the construction for a fixed t. The top and bottom of the image represent the before and after states respectively. The dashed line encloses one of the new paths,
![]() $P_i$
.
$P_i$
.
We can now finish this stage of the construction with the updated value of N being
![]() $M/2$
. We still need to define the new
$M/2$
. We still need to define the new
![]() $y_i^c$
’s. Use the unused
$y_i^c$
’s. Use the unused
![]() $v_i$
’s and
$v_i$
’s and
![]() $w_i$
’s for
$w_i$
’s for
![]() $c \in \{a,b\}$
. For
$c \in \{a,b\}$
. For
![]() $c \not \in \{a,b\}$
, use the first
$c \not \in \{a,b\}$
, use the first
![]() $M/2 \ z_i$
’s with
$M/2 \ z_i$
’s with
![]() $\phi _t(z_i) = d$
if
$\phi _t(z_i) = d$
if
![]() $c = d$
, and the first
$c = d$
, and the first
![]() $M/2 \ y_i^{c}$
’s from the previous stage of the construction if
$M/2 \ y_i^{c}$
’s from the previous stage of the construction if
![]() $c \neq d$
(i.e., if c was in the previous
$c \neq d$
(i.e., if c was in the previous
![]() $\mathcal {V}'$
.) (1) is clear by construction.
$\mathcal {V}'$
.) (1) is clear by construction.
Thus the description of the construction is complete. We can also see now that the correct value of
![]() $N_0$
to take was
$N_0$
to take was
![]() $N_0> (4|\mathcal {V}|)^{|\mathcal {V}|}$
, since the value of N was divided by
$N_0> (4|\mathcal {V}|)^{|\mathcal {V}|}$
, since the value of N was divided by
![]() $4|\mathcal {V}|$
each time the interesting case occurred, and it cannot occur more than
$4|\mathcal {V}|$
each time the interesting case occurred, and it cannot occur more than
![]() $|\mathcal {V}|$
times for a fixed t (Since
$|\mathcal {V}|$
times for a fixed t (Since
![]() $|\mathcal {V}'|$
increases by one each time it does).
$|\mathcal {V}'|$
increases by one each time it does).
Claim 2.6.
T is a computable truly
![]() $\Delta $
-regular forest.
$\Delta $
-regular forest.
Proof At each stage in the construction, we either added new trees as components, added new degree 1 neighbors to vertices, or joined pairs of components along a single path. Thus the components at each stage were trees, and so the limit T must be acyclic.
For each fixed t, the interesting case could only have occurred finitely many times as noted before the claim. Thus each vertex, once added to
![]() $C^{-1}(t)$
, must have eventually experienced the uninteresting case, at which point it would be made degree
$C^{-1}(t)$
, must have eventually experienced the uninteresting case, at which point it would be made degree
![]() $\Delta $
by construction. Since we added new vertices at the first stage for each t, and we always take these to be the least available, each
$\Delta $
by construction. Since we added new vertices at the first stage for each t, and we always take these to be the least available, each
![]() $x \in X$
is eventually added to some
$x \in X$
is eventually added to some
![]() $C^{-1}(t)$
, and subsequently made to have degree
$C^{-1}(t)$
, and subsequently made to have degree
![]() $\Delta $
. Thus T is truly
$\Delta $
. Thus T is truly
![]() $\Delta $
-regular and its vertex set is X, which was chosen to be computable. Similarly the edge set of T is E, also chosen to be computable.
$\Delta $
-regular and its vertex set is X, which was chosen to be computable. Similarly the edge set of T is E, also chosen to be computable.
Finally, T is clearly computable: The construction of the
![]() $T_n$
’s was clearly recursive, so to check whether a given
$T_n$
’s was clearly recursive, so to check whether a given
![]() $(x,e) \in X \times E$
is in T, we can run the construction until x is added to the vertex set, at which point it gets
$(x,e) \in X \times E$
is in T, we can run the construction until x is added to the vertex set, at which point it gets
![]() $\Delta $
incident edges, and we can check if any of these is e.
$\Delta $
incident edges, and we can check if any of these is e.
Claim 2.7.
T has no computable
![]() $\Pi $
-coloring.
$\Pi $
-coloring.
Proof Suppose
![]() $\phi _t$
is a
$\phi _t$
is a
![]() $\Pi $
-coloring of T, and consider our construction for this fixed value of t. In between each interesting case stage of our construction, we have finitely many
$\Pi $
-coloring of T, and consider our construction for this fixed value of t. In between each interesting case stage of our construction, we have finitely many
![]() $\Delta $
-regular paths
$\Delta $
-regular paths
![]() $P_i$
, and are waiting for
$P_i$
, and are waiting for
![]() $\phi _t$
to converge to a
$\phi _t$
to converge to a
![]() $\Pi $
-coloring of them. Since
$\Pi $
-coloring of them. Since
![]() $\phi _t$
is in fact a
$\phi _t$
is in fact a
![]() $\Pi $
-coloring of T, we are always guaranteed that this will eventually happen. That is, the interesting case will occur unboundedly many times for this t, but as noted before Claim 2.6, it can only occur
$\Pi $
-coloring of T, we are always guaranteed that this will eventually happen. That is, the interesting case will occur unboundedly many times for this t, but as noted before Claim 2.6, it can only occur
![]() $|\mathcal {V}| < \omega $
times.
$|\mathcal {V}| < \omega $
times.
Thus T is as desired.
3 Computable forests
In this section we prove Theorem 1.5. As in the previous section, the key is to find a combinatorial condition characterizing our class.

Figure 4 An illustration of Definition 3.1 with
![]() $\Delta = 5$
and
$\Delta = 5$
and
![]() $k = 3$
. True edges are divided with slashes to show the two half edges comprising them. The left-hand figure is given, and the right-hand figure is the needed extension. The
$k = 3$
. True edges are divided with slashes to show the two half edges comprising them. The left-hand figure is given, and the right-hand figure is the needed extension. The
![]() $\alpha $
’s are colors from
$\alpha $
’s are colors from
![]() $\Sigma '$
, whereas the
$\Sigma '$
, whereas the
![]() $\beta $
’s can be any elements of
$\beta $
’s can be any elements of
![]() $\Sigma $
. Definition 3.1 also technically asks for colors for the other half edges incident to the
$\Sigma $
. Definition 3.1 also technically asks for colors for the other half edges incident to the
![]() $y_i$
’s, but these do not turn out to be relevant and so are not drawn.
$y_i$
’s, but these do not turn out to be relevant and so are not drawn.
Definition 3.1. Let
![]() $\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
be an LCL on
$\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
be an LCL on
![]() $\Delta $
-regular graphs. Let
$\Delta $
-regular graphs. Let
![]() $\Sigma ' \subset \Sigma $
. We say
$\Sigma ' \subset \Sigma $
. We say
![]() $\Sigma '$
is greedy if the following holds: Let
$\Sigma '$
is greedy if the following holds: Let
![]() $k \in \{0,\ldots ,\Delta \}$
, and consider the
$k \in \{0,\ldots ,\Delta \}$
, and consider the
![]() $\Delta $
-regular tree H with vertices x and
$\Delta $
-regular tree H with vertices x and
![]() $y_i$
for
$y_i$
for
![]() $i < k$
with x and
$i < k$
with x and
![]() $y_i$
adjacent for each i and all other edges being virtual. Precolor each half edge
$y_i$
adjacent for each i and all other edges being virtual. Precolor each half edge
![]() $(y_i,x)$
with a label from
$(y_i,x)$
with a label from
![]() $\Sigma '$
. Then this can be extended to a
$\Sigma '$
. Then this can be extended to a
![]() $\Pi $
-coloring of H such that
$\Pi $
-coloring of H such that
![]() $c(x,e) \in \Sigma '$
for each virtual edge e incident to x. (See Figure 4.) We say
$c(x,e) \in \Sigma '$
for each virtual edge e incident to x. (See Figure 4.) We say
![]() $\Pi $
is greedy if it admits some greedy
$\Pi $
is greedy if it admits some greedy
![]() $\Sigma '$
.
$\Sigma '$
.
In analogy with Theorem 2.2, we prove:
Theorem 3.2. An LCL on
![]() $\Delta $
-regular graphs is in
$\Delta $
-regular graphs is in
![]() $\mathrm {COMPUTABLE}$
if and only if it is greedy.
$\mathrm {COMPUTABLE}$
if and only if it is greedy.
We start with the reverse direction. Actually, to prove the final claim of Theorem 1.5, we deal with the stronger statement where our graph need not be acyclic:
Proposition 3.3. Let
![]() $\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
be an LCL on
$\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
be an LCL on
![]() $\Delta $
-regular graphs, and assume
$\Delta $
-regular graphs, and assume
![]() $\Pi $
is greedy. Then any computable
$\Pi $
is greedy. Then any computable
![]() $\Delta $
-regular graph admits a computable
$\Delta $
-regular graph admits a computable
![]() $\Pi $
-coloring.
$\Pi $
-coloring.
Proof Let G be such a graph, say with vertex and edge sets X and E respectively. WLOG
![]() $X \subset \omega $
. Let
$X \subset \omega $
. Let
![]() $\Sigma ' \subset \Sigma $
be greedy. We will recursively define our coloring c in
$\Sigma ' \subset \Sigma $
be greedy. We will recursively define our coloring c in
![]() $\omega $
stages. At stage
$\omega $
stages. At stage
![]() $n \in \omega $
, we will color exactly the half edges incident to n if
$n \in \omega $
, we will color exactly the half edges incident to n if
![]() $n \in X$
, and do nothing otherwise. We will maintain that if
$n \in X$
, and do nothing otherwise. We will maintain that if
![]() $e \in E$
is such that exactly one of the half edges comprising e has been colored so far, then it gets a color from
$e \in E$
is such that exactly one of the half edges comprising e has been colored so far, then it gets a color from
![]() $\Sigma '$
.
$\Sigma '$
.
We now describe stage n if
![]() $n \in X$
: Let
$n \in X$
: Let
![]() $y_i$
for
$y_i$
for
![]() $i < k$
be the neighbors of n less than n. Then by inductive hypothesis,
$i < k$
be the neighbors of n less than n. Then by inductive hypothesis,
![]() $c(y_i,n) \in \Sigma '$
for each i, and the
$c(y_i,n) \in \Sigma '$
for each i, and the
![]() $\Delta -k$
other incident edges to x, say
$\Delta -k$
other incident edges to x, say
![]() $e_j$
for
$e_j$
for
![]() $j < \Delta - k$
, not having a
$j < \Delta - k$
, not having a
![]() $y_i$
as their other endpoint have not been touched. Thus, by the definition of greedy, we may color the half edges incident to x so that
$y_i$
as their other endpoint have not been touched. Thus, by the definition of greedy, we may color the half edges incident to x so that
![]() $c(x,e_j) \in \Sigma '$
for each j, thus maintaining our inductive hypothesis.
$c(x,e_j) \in \Sigma '$
for each j, thus maintaining our inductive hypothesis.
As is apparent from this proof, if an LCL on
![]() $\Delta $
-regular graphs is greedy, it can be solved using a “greedy” algorithm. Such algorithms our typically easy to carry out in other combinatorial settings, making the analogue of Proposition 3.3 easy to prove in these settings. For example (giving another of the parts of Theorem 1.5):
$\Delta $
-regular graphs is greedy, it can be solved using a “greedy” algorithm. Such algorithms our typically easy to carry out in other combinatorial settings, making the analogue of Proposition 3.3 easy to prove in these settings. For example (giving another of the parts of Theorem 1.5):
Proposition 3.4. Let
![]() $\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
be an LCL on
$\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
be an LCL on
![]() $\Delta $
-regular graphs, and assume
$\Delta $
-regular graphs, and assume
![]() $\Pi $
is greedy. Then any continuous
$\Pi $
is greedy. Then any continuous
![]() $\Delta $
-regular graph admits a computable
$\Delta $
-regular graph admits a computable
![]() $\Pi $
-coloring.
$\Pi $
-coloring.
Proof Let G be such a graph, say with vertex set X. By [Reference Bernshteyn2], there is a continuous proper coloring
![]() $d:X \rightarrow \omega $
. We can then repeat the construction of the previous proposition, except that at stage
$d:X \rightarrow \omega $
. We can then repeat the construction of the previous proposition, except that at stage
![]() $n \in \omega $
we color the half edges incident to all vertices in
$n \in \omega $
we color the half edges incident to all vertices in
![]() $d^{-1}(n)$
. This works because each
$d^{-1}(n)$
. This works because each
![]() $d^{-1}(n)$
is independent, and the result is continuous since d and G are. (See, for example, Theorem 3.2 in [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky5].)
$d^{-1}(n)$
is independent, and the result is continuous since d and G are. (See, for example, Theorem 3.2 in [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky5].)
We now turn to the forward direction of Theorem 3.2. Again we prove the contrapositive:
Proposition 3.5. If an LCL on
![]() $\Delta $
-regular graphs
$\Delta $
-regular graphs
![]() $\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
is not greedy, there is a computable
$\Pi = (\Sigma ,\mathcal {V},\mathcal {E})$
is not greedy, there is a computable
![]() $\Delta $
-regular tree with no computable
$\Delta $
-regular tree with no computable
![]() $\Pi $
-coloring.
$\Pi $
-coloring.
Proof Our construction will closely follow that in the proof of Proposition 2.5. Fix
![]() $X,E$
, and the
$X,E$
, and the
![]() $\phi _t$
’s as before. Once again, we will be recursively constructing a sequence of
$\phi _t$
’s as before. Once again, we will be recursively constructing a sequence of
![]() $\Delta $
-regular forests with finite vertex sets, but really building a sequence of
$\Delta $
-regular forests with finite vertex sets, but really building a sequence of
![]() $\omega $
forests in parallel as kept track of by a recursively defined function
$\omega $
forests in parallel as kept track of by a recursively defined function
![]() $C:X \rightarrow \omega $
. We will use the term “new” for added vertices and edges in the same way. Call the forest we are building T.
$C:X \rightarrow \omega $
. We will use the term “new” for added vertices and edges in the same way. Call the forest we are building T.
Since
![]() $\Pi $
is not greedy, for every
$\Pi $
is not greedy, for every
![]() $\Sigma ' \subset \Sigma $
, there are a
$\Sigma ' \subset \Sigma $
, there are a
![]() $k \in \{0,\ldots ,\Delta \}$
and a sequence
$k \in \{0,\ldots ,\Delta \}$
and a sequence
![]() $\alpha _0,\ldots ,\alpha _{k-1}$
from
$\alpha _0,\ldots ,\alpha _{k-1}$
from
![]() $\Sigma '$
witnessing that
$\Sigma '$
witnessing that
![]() $\Sigma '$
is not greedy. That is, such that in the situation of Definition 3.1, if this k is used and each half edge
$\Sigma '$
is not greedy. That is, such that in the situation of Definition 3.1, if this k is used and each half edge
![]() $(y_i,x)$
is given the color
$(y_i,x)$
is given the color
![]() $\alpha _i$
, then if this is extended to a
$\alpha _i$
, then if this is extended to a
![]() $\Pi $
-coloring of H, there is some virtual half edge
$\Pi $
-coloring of H, there is some virtual half edge
![]() $(x,e)$
such that
$(x,e)$
such that
![]() $c(x,e) \not \in \Sigma '$
. Fix choices of such k and
$c(x,e) \not \in \Sigma '$
. Fix choices of such k and
![]() $(\alpha _i)_{i < k}$
for each
$(\alpha _i)_{i < k}$
for each
![]() $\Sigma '$
and call them bad for
$\Sigma '$
and call them bad for
![]() $\Sigma '$
.
$\Sigma '$
.
Again, let us fix
![]() $t \in \omega $
and describe the
$t \in \omega $
and describe the
![]() $\omega $
steps in the construction of
$\omega $
steps in the construction of
![]() $T \upharpoonright C^{-1}(t)$
.
$T \upharpoonright C^{-1}(t)$
.
The 0-th stage will be similar: Fix a very large
![]() $N_0\gg |\Sigma |$
to be determined later, independent of t. In the 0-th stage, place
$N_0\gg |\Sigma |$
to be determined later, independent of t. In the 0-th stage, place
![]() $N_0$
new vertices, say
$N_0$
new vertices, say
![]() $w_0,\ldots ,w_{N_0-1}$
, in
$w_0,\ldots ,w_{N_0-1}$
, in
![]() $C^{-1}(t)$
, and give each
$C^{-1}(t)$
, and give each
![]() $\Delta $
new virtual incident edges.
$\Delta $
new virtual incident edges.
We also initialize several variables: Set
![]() $\Sigma ' = \emptyset $
and
$\Sigma ' = \emptyset $
and
![]() $N = N_0$
. Also set
$N = N_0$
. Also set
![]() $x_i = w_i$
for each
$x_i = w_i$
for each
![]() $i < N$
.
$i < N$
.
At the start of an arbitrary successor stage, say
![]() $m+1$
, suppose we have some
$m+1$
, suppose we have some
![]() $\Sigma ' \subset \Sigma $
,
$\Sigma ' \subset \Sigma $
,
![]() $N \in \omega $
very large, and vertices
$N \in \omega $
very large, and vertices
![]() $x_i$
for
$x_i$
for
![]() $i < N$
and virtual half edges
$i < N$
and virtual half edges
![]() $(y_i^{\alpha },e_i^{\alpha })$
for
$(y_i^{\alpha },e_i^{\alpha })$
for
![]() $i < N$
and
$i < N$
and
![]() $\alpha \in \Sigma '$
such that:
$\alpha \in \Sigma '$
such that:
-
(1) The
 $x_i$
’s and
$x_i$
’s and
 $y_i^{\alpha }$
’s all lie in distinct
$y_i^{\alpha }$
’s all lie in distinct
 $C^{-1}(t)$
-components.
$C^{-1}(t)$
-components. -
(2) For each i, if
 $\phi _t$
restricted to half edges meeting
$\phi _t$
restricted to half edges meeting
 $B(x_i,1)$
gives a
$B(x_i,1)$
gives a
 $\Pi $
-coloring, there must be some virtual edge e incident to x with
$\Pi $
-coloring, there must be some virtual edge e incident to x with
 $\phi _t(x,e) \not \in \Sigma '$
.
$\phi _t(x,e) \not \in \Sigma '$
. -
(3) For each i and
 $\alpha $
,
$\alpha $
,
 $\phi _t(y_i^{\alpha },e_i^{\alpha }) = \alpha $
.
$\phi _t(y_i^{\alpha },e_i^{\alpha }) = \alpha $
.
Note that this is all satisfied after stage 0.
We start our successor stage by running the Turing machine computing
![]() $\phi _t$
for m steps on all the half edges meeting each
$\phi _t$
for m steps on all the half edges meeting each
![]() $B(x_i,1)$
. (Note that we can compute
$B(x_i,1)$
. (Note that we can compute
![]() $B(x_i,1)$
since our vertex set so far is finite.)
$B(x_i,1)$
since our vertex set so far is finite.)
If
![]() $\phi _t$
fails to converge in
$\phi _t$
fails to converge in
![]() $\leq m$
steps on one of these inputs, or if it converges on all of them but the result fails to be a
$\leq m$
steps on one of these inputs, or if it converges on all of them but the result fails to be a
![]() $\Pi $
-coloring of some
$\Pi $
-coloring of some
![]() $B(x_i,1)$
, we do nothing. We call this the “uninteresting case.”
$B(x_i,1)$
, we do nothing. We call this the “uninteresting case.”
The “interesting case” is of course if
![]() $\phi _t$
does converge on all these inputs in
$\phi _t$
does converge on all these inputs in
![]() $\leq m$
steps, and the result is a
$\leq m$
steps, and the result is a
![]() $\Pi $
-coloring for each
$\Pi $
-coloring for each
![]() $B(x_i,1)$
. In this case by condition (2) above, there is a virtual edge
$B(x_i,1)$
. In this case by condition (2) above, there is a virtual edge
![]() $f_i$
for each
$f_i$
for each
![]() $i < N$
meeting
$i < N$
meeting
![]() $x_i$
with
$x_i$
with
![]() $\phi _t(x_i,f_i) \not \in \Sigma '$
. Let
$\phi _t(x_i,f_i) \not \in \Sigma '$
. Let
![]() $\beta \in \Sigma \setminus \Sigma '$
such that
$\beta \in \Sigma \setminus \Sigma '$
such that
![]() $\phi _t(x_i,f_i) = \beta $
for at least
$\phi _t(x_i,f_i) = \beta $
for at least
![]() $N/|\Sigma | \ i$
’s. Update
$N/|\Sigma | \ i$
’s. Update
![]() $\Sigma '$
to
$\Sigma '$
to
![]() $\Sigma ' \cup \{\beta \}$
.
$\Sigma ' \cup \{\beta \}$
.
Let k and
![]() $\alpha _0,\ldots ,\alpha _{k-1} \in \Sigma '$
be bad for
$\alpha _0,\ldots ,\alpha _{k-1} \in \Sigma '$
be bad for
![]() $\Sigma '$
. Between the
$\Sigma '$
. Between the
![]() $(x_i,f_i)$
’s and the
$(x_i,f_i)$
’s and the
![]() $(y_i^{\alpha },e_i^{\alpha })$
’s, and using condition (1) above, we can chose virtual half edges
$(y_i^{\alpha },e_i^{\alpha })$
’s, and using condition (1) above, we can chose virtual half edges
![]() $(z_i^j,g_i^j)$
for
$(z_i^j,g_i^j)$
for
![]() $i < M := N / (\Delta |\Sigma |)$
such that the
$i < M := N / (\Delta |\Sigma |)$
such that the
![]() $z_i^j$
’s all lie in distinct
$z_i^j$
’s all lie in distinct
![]() $C^{-1}(t)$
-components and
$C^{-1}(t)$
-components and
![]() $\phi _t(z_i^j,g_i^j) = \alpha _j$
for each
$\phi _t(z_i^j,g_i^j) = \alpha _j$
for each
![]() $j < k$
.
$j < k$
.
Now for each
![]() $i < M/2$
, let
$i < M/2$
, let
![]() $v_i$
be a new vertex and add it as an endpoint to
$v_i$
be a new vertex and add it as an endpoint to
![]() $g_i^j$
for each j, making all these edges true. Then, to maintain
$g_i^j$
for each j, making all these edges true. Then, to maintain
![]() $\Delta $
-regularity, add
$\Delta $
-regularity, add
![]() $\Delta -k$
new virtual incident edges to
$\Delta -k$
new virtual incident edges to
![]() $v_i$
. This is shown in Figure 5.
$v_i$
. This is shown in Figure 5.

Figure 5 The “interesting case” for a step of the construction for a fixed t with
![]() $\Delta = 3$
. The top and bottom images represent the before and after states respectively.
$\Delta = 3$
. The top and bottom images represent the before and after states respectively.
We can now finish this stage of the construction with the updated value of N being
![]() $M/2$
. First set
$M/2$
. First set
![]() $x_i = v_i$
for each i. Condition(2) is then satisfied by definition of bad. We now define the
$x_i = v_i$
for each i. Condition(2) is then satisfied by definition of bad. We now define the
![]() $(y_i^{\alpha },e_i^{\alpha })$
’s. If
$(y_i^{\alpha },e_i^{\alpha })$
’s. If
![]() $\alpha = \alpha _j$
for some j, we can use the unused
$\alpha = \alpha _j$
for some j, we can use the unused
![]() $(z_i^j,g_i^j)$
’s. Else, if
$(z_i^j,g_i^j)$
’s. Else, if
![]() $\alpha = \beta $
we can use the first
$\alpha = \beta $
we can use the first
![]() $M/2 \ (x_i,f_i)$
’s, and if not, the first
$M/2 \ (x_i,f_i)$
’s, and if not, the first
![]() $M/2 \ (y_i^{\alpha },e_i^{\alpha })$
’s from the previous stage of the construction.
$M/2 \ (y_i^{\alpha },e_i^{\alpha })$
’s from the previous stage of the construction.
Thus the description of the construction is complete. As in the proof of Proposition 2.5, it will be significant that the interesting case cannot occur more than
![]() $|\Sigma |$
times for a fixed t (since
$|\Sigma |$
times for a fixed t (since
![]() $|\Sigma '|$
increases by one each time it does). As in that proof, the first application of this is that it tells us what to pick for
$|\Sigma '|$
increases by one each time it does). As in that proof, the first application of this is that it tells us what to pick for
![]() $N_0$
: We can take
$N_0$
: We can take
![]() $N_0> (2\Delta |\Sigma |)^{|\Sigma |}$
, since
$N_0> (2\Delta |\Sigma |)^{|\Sigma |}$
, since
![]() $2\Delta |\Sigma |$
is by how much the value of N was divided each time the interesting case occurred.
$2\Delta |\Sigma |$
is by how much the value of N was divided each time the interesting case occurred.
Claim 3.6.
T is a computable
![]() $\Delta $
-regular forest.
$\Delta $
-regular forest.
Proof At each stage in the construction, we either added new trees as components, did nothing, or joined separate components at a single new vertex. Thus T is acyclic.
T has vertex and edge set X and E for the same reason as in the proof of Proposition 2.5. Also, since we maintain
![]() $\Delta $
-regularity at each stage in the construction, to check if a pair
$\Delta $
-regularity at each stage in the construction, to check if a pair
![]() $(x,e) \in X \times E$
is in T, we can run the construction until x is added as a vertex, and then check if e is one of its incident edges. Thus T is computable.
$(x,e) \in X \times E$
is in T, we can run the construction until x is added as a vertex, and then check if e is one of its incident edges. Thus T is computable.
Claim 3.7.
T admits no computable
![]() $\Pi $
-coloring.
$\Pi $
-coloring.
We end this paper by showing that the inclusion in Theorem 1.5 is strict as promised. Actually by results from [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky5, Reference Chang, Kopelowitz and Pettie6], there is a sense in which being solvable by a greedy algorithm characterizes the class CONTINUOUS as well: An LCL
![]() $\Pi $
is in CONTINUOUS if and only if there is some
$\Pi $
is in CONTINUOUS if and only if there is some
![]() $l \in \omega $
such that
$l \in \omega $
such that
![]() $\Pi $
can be solved on
$\Pi $
can be solved on
![]() $\Delta $
-regular forests by first finding a proper coloring of the distance l graph (in which two vertices are adjacent if their distance in the original graph is at most l), then applying some constant-time local algorithm with that coloring as an input. It is easy to find proper colorings greedily, hence our statement.
$\Delta $
-regular forests by first finding a proper coloring of the distance l graph (in which two vertices are adjacent if their distance in the original graph is at most l), then applying some constant-time local algorithm with that coloring as an input. It is easy to find proper colorings greedily, hence our statement.
As in the proof of Proposition 3.4, it is also easy to find proper colorings continuously. This is true even for the distance l graph, hence the reverse direction in the result mentioned in the previous paragraph. However, in the computable setting, there is a big difference between
![]() $l = 1$
and
$l = 1$
and
![]() $l> 1$
; if a graph is computable but not highly computable, we cannot effectively determine which pairs of vertices have distance l from each other if
$l> 1$
; if a graph is computable but not highly computable, we cannot effectively determine which pairs of vertices have distance l from each other if
![]() $l> 1$
. This difference will be key to our upcoming example.
$l> 1$
. This difference will be key to our upcoming example.
Our example will be a so-called “homomorphism problem.” This means that it encodes the problem of finding a homomorphism to a fixed finite graph. We use the same formalization of this as in [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky4]:
Definition 3.8. Let H be a finite graph (in the usual sense) with vertex set V.
![]() $\Pi _H$
is the LCL on
$\Pi _H$
is the LCL on
![]() $\Delta $
-regular graphs
$\Delta $
-regular graphs
![]() $(V,\mathcal {V},\mathcal {E})$
, where
$(V,\mathcal {V},\mathcal {E})$
, where
![]() $\mathcal {V}$
is the set of multisets whose
$\mathcal {V}$
is the set of multisets whose
![]() $\Delta $
-elements are all the same, and
$\Delta $
-elements are all the same, and
![]() $\mathcal {E}$
is the set of pairs
$\mathcal {E}$
is the set of pairs
![]() $\{v,w\}$
with v and w adjacent in H.
$\{v,w\}$
with v and w adjacent in H.
For example,
![]() $\Pi _{K_k}$
is the problem of proper k-coloring. We start with a characterization of which homomorphism problems are greedy which may be interesting in its own right. For example, by Theorem 3.2 and the previous remark about
$\Pi _{K_k}$
is the problem of proper k-coloring. We start with a characterization of which homomorphism problems are greedy which may be interesting in its own right. For example, by Theorem 3.2 and the previous remark about
![]() $\Pi _{K_k}$
, it generalizes the observation of Schmerl [Reference Schmerl10] that every computable maximum degree
$\Pi _{K_k}$
, it generalizes the observation of Schmerl [Reference Schmerl10] that every computable maximum degree
![]() $\Delta $
-graph is computable (
$\Delta $
-graph is computable (
![]() $\Delta +1$
)-colorable, but that there are such graphs which are not computably
$\Delta +1$
)-colorable, but that there are such graphs which are not computably
![]() $\Delta $
-colorable.
$\Delta $
-colorable.
Lemma 3.9. Let H be a finite graph in the usual sense.
![]() $\Pi _H$
is greedy if and only if H contains a
$\Pi _H$
is greedy if and only if H contains a
![]() $(\Delta +1)$
-clique.
$(\Delta +1)$
-clique.
Proof If
![]() $\Sigma '$
is a size
$\Sigma '$
is a size
![]() $\Delta +1$
set of vertices on which H induces a clique, then this set clearly witnesses that
$\Delta +1$
set of vertices on which H induces a clique, then this set clearly witnesses that
![]() $\Pi _H$
is greedy.
$\Pi _H$
is greedy.
On the other hand, suppose
![]() $\Sigma '$
is a set of vertices witnessing that
$\Sigma '$
is a set of vertices witnessing that
![]() $\Pi _H$
is greedy. We will produce inductively a sequence
$\Pi _H$
is greedy. We will produce inductively a sequence
![]() $v_0,\ldots ,v_{\Delta }$
on which H induces a clique, maintaining inductively that
$v_0,\ldots ,v_{\Delta }$
on which H induces a clique, maintaining inductively that
![]() $v_i \in \Sigma '$
for
$v_i \in \Sigma '$
for
![]() $i < \Delta $
.
$i < \Delta $
.
We use the notation of Definition 3.1. Let
![]() $k \leq \Delta $
and suppose we have
$k \leq \Delta $
and suppose we have
![]() $v_i \in \Sigma '$
for
$v_i \in \Sigma '$
for
![]() $i < k$
, all pairwise adjacent. Apply the definition with this value of k and
$i < k$
, all pairwise adjacent. Apply the definition with this value of k and
![]() $c(y_i,x) = v_i$
for all i. We get an extension to the half edges incident to x in which, by definition of
$c(y_i,x) = v_i$
for all i. We get an extension to the half edges incident to x in which, by definition of
![]() $\Pi _H$
, all these half edges must get the same label, call it
$\Pi _H$
, all these half edges must get the same label, call it
![]() $v_k$
, and
$v_k$
, and
![]() $v_k$
must be adjacent to each previous
$v_k$
must be adjacent to each previous
![]() $v_i$
. Furthermore, if
$v_i$
. Furthermore, if
![]() $k < \Delta $
, x has some incident virtual edge, and so
$k < \Delta $
, x has some incident virtual edge, and so
![]() $v_k$
must be in
$v_k$
must be in
![]() $\Sigma '$
, maintaining our inductive hypothesis.
$\Sigma '$
, maintaining our inductive hypothesis.
It now suffices to produce a finite graph H with no
![]() $(\Delta +1)$
-clique but with
$(\Delta +1)$
-clique but with
![]() $\Pi _H \in \text {CONTINUOUS}$
. We will do this by induction on
$\Pi _H \in \text {CONTINUOUS}$
. We will do this by induction on
![]() $\Delta $
, and thus call the graph
$\Delta $
, and thus call the graph
![]() $H_\Delta $
.
$H_\Delta $
.
The base case
![]() $H_2$
will be a 5 cycle, say with vertices
$H_2$
will be a 5 cycle, say with vertices
![]() $v_0,\ldots ,v_4$
, with
$v_0,\ldots ,v_4$
, with
![]() $v_i$
and
$v_i$
and
![]() $v_j$
adjacent if and only if i and j differ by one mod 5.
$v_j$
adjacent if and only if i and j differ by one mod 5.
Given
![]() $H_\Delta $
, we define
$H_\Delta $
, we define
![]() $H_{\Delta +1}$
by introducing a new vertex, call it
$H_{\Delta +1}$
by introducing a new vertex, call it
![]() $w_{\Delta +1}$
, which is adjacent to each vertex of
$w_{\Delta +1}$
, which is adjacent to each vertex of
![]() $H_\Delta $
.
$H_\Delta $
.
Claim 3.10. For each
![]() $\Delta $
,
$\Delta $
,
![]() $H_\Delta $
does not contain a
$H_\Delta $
does not contain a
![]() $(\Delta +1)$
-clique.
$(\Delta +1)$
-clique.
Proof We proceed by induction on
![]() $\Delta $
.
$\Delta $
.
![]() $H_2$
, a 5 cycle, does not contain a triangle. Suppose we know that
$H_2$
, a 5 cycle, does not contain a triangle. Suppose we know that
![]() $H_\Delta $
contains no
$H_\Delta $
contains no
![]() $(\Delta +1)$
-clique, and suppose to the contrary that
$(\Delta +1)$
-clique, and suppose to the contrary that
![]() $H_{\Delta +1}$
contains a
$H_{\Delta +1}$
contains a
![]() $(\Delta +2)$
-clique K. Then since
$(\Delta +2)$
-clique K. Then since
![]() $H_{\Delta +1}$
has only one new vertex compared to
$H_{\Delta +1}$
has only one new vertex compared to
![]() $H_\Delta $
, the restriction of K to
$H_\Delta $
, the restriction of K to
![]() $H_\Delta $
must give either a
$H_\Delta $
must give either a
![]() $(\Delta +1)$
or
$(\Delta +1)$
or
![]() $(\Delta +2)$
clique depending on whether
$(\Delta +2)$
clique depending on whether
![]() $w_{\Delta +1} \in K$
. In either case this contradicts the inductive hypothesis.
$w_{\Delta +1} \in K$
. In either case this contradicts the inductive hypothesis.
Claim 3.11. For each
![]() $\Delta $
,
$\Delta $
,
![]() $H_\Delta \in \mathrm {CONTINUOUS}$
(for
$H_\Delta \in \mathrm {CONTINUOUS}$
(for
![]() $\Delta $
-regular forests).
$\Delta $
-regular forests).
Proof For this proof we abandon talk of half edges and switch to the usual notion of a graph. We prove by induction on
![]() $\Delta $
that every continuous forest with maximum degree
$\Delta $
that every continuous forest with maximum degree
![]() $\leq \Delta $
admits a continuous homomorphism to
$\leq \Delta $
admits a continuous homomorphism to
![]() $H_\Delta $
.
$H_\Delta $
.
For the base case, let G be a continuous forest on a Polish space X with maximum degree 2. By [Reference Bernshteyn2], we can find a clopen maximal 4-discrete set A. Let
![]() $G'$
be the continuous graph
$G'$
be the continuous graph
![]() $G \upharpoonright (X \setminus A)$
. Also by [Reference Bernshteyn2], let
$G \upharpoonright (X \setminus A)$
. Also by [Reference Bernshteyn2], let
![]() $d:(X \setminus A) \rightarrow \omega $
be a continuous coloring such that each
$d:(X \setminus A) \rightarrow \omega $
be a continuous coloring such that each
![]() $d^{-1}(n)$
is 7-discrete. Note that each
$d^{-1}(n)$
is 7-discrete. Note that each
![]() $G'$
-component is a path of length at most 7, and so d labels the vertices of each component with unique labels.
$G'$
-component is a path of length at most 7, and so d labels the vertices of each component with unique labels.
We now define our continuous homomorphism, call it c. Set
![]() $c(x) = v_0$
for
$c(x) = v_0$
for
![]() $x \in A$
. Now consider a
$x \in A$
. Now consider a
![]() $G'$
-component, call it P. P is a path of length at most 7. The endpoints are possibly G-adjacent to points in A, and if both are so, the length of P is at least 3. Observe then that we can always extend c to P while keeping it a homomorphism to
$G'$
-component, call it P. P is a path of length at most 7. The endpoints are possibly G-adjacent to points in A, and if both are so, the length of P is at least 3. Observe then that we can always extend c to P while keeping it a homomorphism to
![]() $H_2$
: This is trivial if we are not in the case where both endpoints of P are adjacent to a point in A, and if we are in that case, we can alternate between
$H_2$
: This is trivial if we are not in the case where both endpoints of P are adjacent to a point in A, and if we are in that case, we can alternate between
![]() $v_0$
and
$v_0$
and
![]() $v_1$
along P if the length of P is even, or circle the 5-cycle
$v_1$
along P if the length of P is even, or circle the 5-cycle
![]() $H_2$
once then do this alternation if the length is odd. (Note that P is long enough to allow this.) Furthermore, since
$H_2$
once then do this alternation if the length is odd. (Note that P is long enough to allow this.) Furthermore, since
![]() $d \upharpoonright P$
is injective, we can do this in a constructive way using d to break symmetry. That is, we can extend c to a homomorphism
$d \upharpoonright P$
is injective, we can do this in a constructive way using d to break symmetry. That is, we can extend c to a homomorphism
![]() $G \upharpoonright H_2$
in such a way that the value of c at a point x depends only on the values of d and the indicator function
$G \upharpoonright H_2$
in such a way that the value of c at a point x depends only on the values of d and the indicator function
![]() $\chi _A$
of A on
$\chi _A$
of A on
![]() $B(x,N)$
for some large constant N. It follows from this and the continuity of d and
$B(x,N)$
for some large constant N. It follows from this and the continuity of d and
![]() $\chi _A$
that c is continuous. (See, for example, Theorem 3.2 in [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky5].)
$\chi _A$
that c is continuous. (See, for example, Theorem 3.2 in [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and Vidnyánszky5].)
The inductive step is now easy. Suppose we have this result for some
![]() $\Delta \geq 2$
, and let G be a continuous forest on a Polish space X with maximum degree
$\Delta \geq 2$
, and let G be a continuous forest on a Polish space X with maximum degree
![]() $\leq \Delta +1$
. We will define a continuous homomorphism c to
$\leq \Delta +1$
. We will define a continuous homomorphism c to
![]() $H_{\Delta +1}$
. By [Reference Bernshteyn2] again, we may define c be
$H_{\Delta +1}$
. By [Reference Bernshteyn2] again, we may define c be
![]() $w_{\Delta +1}$
on a clopen maximal independent set. Let
$w_{\Delta +1}$
on a clopen maximal independent set. Let
![]() $G' = G \upharpoonright (X \setminus c^{-1}(w_{\Delta +1}))$
. This is a continuous graph with maximum degree
$G' = G \upharpoonright (X \setminus c^{-1}(w_{\Delta +1}))$
. This is a continuous graph with maximum degree
![]() $\leq \Delta $
by maximality of
$\leq \Delta $
by maximality of
![]() $c^{-1}(w_{\Delta +1})$
. Thus by inductive hypothesis there is a continuous homomorphism
$c^{-1}(w_{\Delta +1})$
. Thus by inductive hypothesis there is a continuous homomorphism
![]() $c':G' \upharpoonright H_\Delta $
. Since
$c':G' \upharpoonright H_\Delta $
. Since
![]() $w_{\Delta +1}$
is adjacent to every vertex in
$w_{\Delta +1}$
is adjacent to every vertex in
![]() $H_\Delta $
, we can just extend c to all of X by setting
$H_\Delta $
, we can just extend c to all of X by setting
![]() $c \upharpoonright (X \setminus A) = c'$
.
$c \upharpoonright (X \setminus A) = c'$
.
Acknowledgements
Thanks to the American Institute of Mathematics for hosting the workshop at which much of this research was conducted, as well as to the organizers of that workshop, Clinton Conley, Stephen Jackson, Andrew Marks, and Slawomir Solecki. Thanks also to Jan Grebík for suggesting that Theorem 1.4 ought to be true, and encouraging me to write up the proof of it.