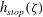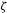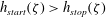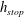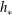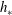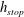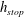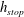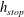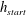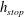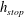1 Introduction
Many phenomena that are observed in shallow dry granular flows, such as phase transitions between fluid-like and solid-like regions (Daerr & Douady Reference Daerr and Douady1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002), self-channelization and levee formation (Félix & Thomas Reference Félix and Thomas2004; Mangeney et al.
Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007; Rocha, Johnson & Gray Reference Rocha, Johnson and Gray2019) as well as erosion–deposition waves (Daerr & Douady Reference Daerr and Douady1999; Clément et al.
Reference Clément, Malloggi, Andreotti and Aranson2007; Börzsönyi, Halsey & Ecke Reference Börzsönyi, Halsey and Ecke2008; Takagi, McElwaine & Huppert Reference Takagi, McElwaine and Huppert2011; Edwards & Gray Reference Edwards and Gray2015; McArdell Reference McArdell2016; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017; Russell et al.
Reference Russell, Johnson, Edwards, Viroulet, Rocha and Gray2019) arise due to frictional hysteresis. At the heart of this is the empirical observation (Daerr & Douady Reference Daerr and Douady1999; Pouliquen Reference Pouliquen1999a
) that on a rough bed, inclined at an angle
![]() $\unicode[STIX]{x1D701}$
to the horizontal, a steady uniform flow of grains will leave behind a deposit of thickness
$\unicode[STIX]{x1D701}$
to the horizontal, a steady uniform flow of grains will leave behind a deposit of thickness
![]() $h=h_{stop}(\unicode[STIX]{x1D701})$
when the inflow is closed off, but a uniform layer of thickness
$h=h_{stop}(\unicode[STIX]{x1D701})$
when the inflow is closed off, but a uniform layer of thickness
![]() $h$
will not start to flow again until the angle of the chute is increased to
$h$
will not start to flow again until the angle of the chute is increased to
![]() $\unicode[STIX]{x1D701}_{start}(h)$
. The inverse of
$\unicode[STIX]{x1D701}_{start}(h)$
. The inverse of
![]() $\unicode[STIX]{x1D701}_{start}(h)$
defines the maximum thickness
$\unicode[STIX]{x1D701}_{start}(h)$
defines the maximum thickness
![]() $h_{start}(\unicode[STIX]{x1D701})$
that a deposit can reach before it will spontaneously flow on a slope inclined at an angle
$h_{start}(\unicode[STIX]{x1D701})$
that a deposit can reach before it will spontaneously flow on a slope inclined at an angle
![]() $\unicode[STIX]{x1D701}$
. A similar inverse function
$\unicode[STIX]{x1D701}$
. A similar inverse function
![]() $\unicode[STIX]{x1D701}_{stop}(h)$
also exists for
$\unicode[STIX]{x1D701}_{stop}(h)$
also exists for
![]() $h_{stop}(\unicode[STIX]{x1D701})$
.
$h_{stop}(\unicode[STIX]{x1D701})$
.
The thickness
![]() $h_{stop}$
can be measured by slowly closing off a steady supply of particles and measuring the deposit depth at a given inclination angle. This gives a point on the
$h_{stop}$
can be measured by slowly closing off a steady supply of particles and measuring the deposit depth at a given inclination angle. This gives a point on the
![]() $h_{stop}(\unicode[STIX]{x1D701})$
curve as shown in figure 1(a). For this value of the thickness
$h_{stop}(\unicode[STIX]{x1D701})$
curve as shown in figure 1(a). For this value of the thickness
![]() $h$
the starting angle
$h$
the starting angle
![]() $\unicode[STIX]{x1D701}_{start}(h)$
can be determined by gently increasing the angle of the slope and noting the point of failure. The grains then flow for a short period before coming to rest again and determining a new point on the
$\unicode[STIX]{x1D701}_{start}(h)$
can be determined by gently increasing the angle of the slope and noting the point of failure. The grains then flow for a short period before coming to rest again and determining a new point on the
![]() $h_{stop}(\unicode[STIX]{x1D701})$
curve. By repeating this process several times the functional form of the curves can be identified. Both Daerr & Douady (Reference Daerr and Douady1999) and Pouliquen (Reference Pouliquen1999a
) proposed that that the tangent of the inverse function
$h_{stop}(\unicode[STIX]{x1D701})$
curve. By repeating this process several times the functional form of the curves can be identified. Both Daerr & Douady (Reference Daerr and Douady1999) and Pouliquen (Reference Pouliquen1999a
) proposed that that the tangent of the inverse function
![]() $\unicode[STIX]{x1D701}_{stop}(h)$
was an exponentially decaying function of thickness
$\unicode[STIX]{x1D701}_{stop}(h)$
was an exponentially decaying function of thickness
![]() $h$
. However, Pouliquen & Forterre (Reference Pouliquen and Forterre2002) suggested a reciprocal fit, which has now been widely adopted.
$h$
. However, Pouliquen & Forterre (Reference Pouliquen and Forterre2002) suggested a reciprocal fit, which has now been widely adopted.

Figure 1. (a) Diagram showing that the slope inclination
![]() $\unicode[STIX]{x1D701}$
must be increased (right arrows) before a granular layer of thickness
$\unicode[STIX]{x1D701}$
must be increased (right arrows) before a granular layer of thickness
![]() $h_{start}$
(green line) spontaneously collapses (down arrows) to leave a thinner layer
$h_{start}$
(green line) spontaneously collapses (down arrows) to leave a thinner layer
![]() $h_{stop}$
(red line) at the steeper angle. The minimum thickness
$h_{stop}$
(red line) at the steeper angle. The minimum thickness
![]() $h_{\ast }$
(orange line) for which a steady-uniform flow is possible lies between
$h_{\ast }$
(orange line) for which a steady-uniform flow is possible lies between
![]() $h_{start}$
and
$h_{start}$
and
![]() $h_{stop}$
. (b) The variation of the friction coefficient
$h_{stop}$
. (b) The variation of the friction coefficient
![]() $\unicode[STIX]{x1D707}$
(black line) with the Froude number
$\unicode[STIX]{x1D707}$
(black line) with the Froude number
![]() $Fr$
for constant flow thickness
$Fr$
for constant flow thickness
![]() $h$
in the dynamic (
$h$
in the dynamic (
![]() $Fr>\unicode[STIX]{x1D6FD}_{\ast }$
), multivalued static (
$Fr>\unicode[STIX]{x1D6FD}_{\ast }$
), multivalued static (
![]() $Fr=0$
) and intermediate (
$Fr=0$
) and intermediate (
![]() $0<Fr\leqslant \unicode[STIX]{x1D6FD}_{\ast }$
) flow regimes. The vertical dashed line shows the transition between the monotonically increasing dynamic and monotonically decreasing intermediate regimes at
$0<Fr\leqslant \unicode[STIX]{x1D6FD}_{\ast }$
) flow regimes. The vertical dashed line shows the transition between the monotonically increasing dynamic and monotonically decreasing intermediate regimes at
![]() $Fr=\unicode[STIX]{x1D6FD}_{\ast }$
.
$Fr=\unicode[STIX]{x1D6FD}_{\ast }$
.
As well as making measurements of the
![]() $h_{stop}$
curve, Pouliquen (Reference Pouliquen1999a
) found a remarkable linear scaling law between the Froude number
$h_{stop}$
curve, Pouliquen (Reference Pouliquen1999a
) found a remarkable linear scaling law between the Froude number
![]() $Fr$
and the ratio of the flow thickness
$Fr$
and the ratio of the flow thickness
![]() $h$
to the deposit thickness
$h$
to the deposit thickness
![]() $h_{stop}$
, i.e.
$h_{stop}$
, i.e.
![]() $Fr=\unicode[STIX]{x1D6FD}h/h_{stop}$
. This empirical flow rule collapsed the experimental data for a wide range of inclination angles and flow depths and allowed Pouliquen (Reference Pouliquen1999a
) to infer an effective basal friction law for the flowing grains. The dynamic friction is an increasing function of
$Fr=\unicode[STIX]{x1D6FD}h/h_{stop}$
. This empirical flow rule collapsed the experimental data for a wide range of inclination angles and flow depths and allowed Pouliquen (Reference Pouliquen1999a
) to infer an effective basal friction law for the flowing grains. The dynamic friction is an increasing function of
![]() $Fr/h$
and allows the steady-uniform flow velocity to be calculated for any inclination angle and flow depth. This insight proved to be critical to the development of the
$Fr/h$
and allows the steady-uniform flow velocity to be calculated for any inclination angle and flow depth. This insight proved to be critical to the development of the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (GDR-MiDi 2004; Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2005, Reference Jop, Forterre and Pouliquen2006), which has dramatically advanced our understanding of granular flows.
$\unicode[STIX]{x1D707}(I)$
-rheology (GDR-MiDi 2004; Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2005, Reference Jop, Forterre and Pouliquen2006), which has dramatically advanced our understanding of granular flows.
Pouliquen & Forterre (Reference Pouliquen and Forterre2002) combined Pouliquen’s (Reference Pouliquen1999a
) dynamic friction law for the flowing grains with a friction law for static grains. The two regimes are shown in figure 1(b). When the Froude number is equal to zero there are a range of static states, and the maximum static friction
![]() $\unicode[STIX]{x1D707}_{start}$
can be derived from a knowledge of the
$\unicode[STIX]{x1D707}_{start}$
can be derived from a knowledge of the
![]() $h_{start}(\unicode[STIX]{x1D701})$
curve (Daerr & Douady Reference Daerr and Douady1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002). The dynamic friction can only be measured above a threshold Froude number
$h_{start}(\unicode[STIX]{x1D701})$
curve (Daerr & Douady Reference Daerr and Douady1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002). The dynamic friction can only be measured above a threshold Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
at which the minimum dynamic friction occurs. Pouliquen & Forterre (Reference Pouliquen and Forterre2002) took the Froude number
$\unicode[STIX]{x1D6FD}_{\ast }$
at which the minimum dynamic friction occurs. Pouliquen & Forterre (Reference Pouliquen and Forterre2002) took the Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
of the minimum steady-uniform flow to be equal to the constant
$\unicode[STIX]{x1D6FD}_{\ast }$
of the minimum steady-uniform flow to be equal to the constant
![]() $\unicode[STIX]{x1D6FD}$
in the linear flow rule scaling, but that is not necessarily the case. The minimum dynamic friction is typically lower than the maximum static friction at
$\unicode[STIX]{x1D6FD}$
in the linear flow rule scaling, but that is not necessarily the case. The minimum dynamic friction is typically lower than the maximum static friction at
![]() $Fr=0$
and very little is known about the friction in the intermediate regime for
$Fr=0$
and very little is known about the friction in the intermediate regime for
![]() $Fr\in [0,\unicode[STIX]{x1D6FD}_{\ast }]$
. In the absence of experimental data, Pouliquen & Forterre (Reference Pouliquen and Forterre2002) suggested that one might simply interpolate between the static and dynamic curves with a decreasing function of the Froude number. Rather than using the linear interpolation shown in figure 1(b), Pouliquen & Forterre (Reference Pouliquen and Forterre2002) used a power law with a very small exponent, which is highly sensitive to the numerical implementation, as will be discussed in § 6.1.
$Fr\in [0,\unicode[STIX]{x1D6FD}_{\ast }]$
. In the absence of experimental data, Pouliquen & Forterre (Reference Pouliquen and Forterre2002) suggested that one might simply interpolate between the static and dynamic curves with a decreasing function of the Froude number. Rather than using the linear interpolation shown in figure 1(b), Pouliquen & Forterre (Reference Pouliquen and Forterre2002) used a power law with a very small exponent, which is highly sensitive to the numerical implementation, as will be discussed in § 6.1.
For flows of angular particles, Forterre & Pouliquen (Reference Forterre and Pouliquen2003) found a similar relation to spherical particles between the steady uniform Froude number and the ratio of the flow thickness
![]() $h$
to
$h$
to
![]() $h_{stop}$
except that there was a constant negative offset
$h_{stop}$
except that there was a constant negative offset
![]() $\unicode[STIX]{x1D6E4}$
. This offset can be problematic when trying to implement non-monotonic friction laws with static, dynamic and intermediate regimes. For instance, a simple generalization in the manner of Pouliquen & Forterre (Reference Pouliquen and Forterre2002) for angular particles can lead to flows being constrained entirely to the dynamic regime. This motivated Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to introduce a transition between the dynamic and intermediate flow regimes at a Froude number
$\unicode[STIX]{x1D6E4}$
. This offset can be problematic when trying to implement non-monotonic friction laws with static, dynamic and intermediate regimes. For instance, a simple generalization in the manner of Pouliquen & Forterre (Reference Pouliquen and Forterre2002) for angular particles can lead to flows being constrained entirely to the dynamic regime. This motivated Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to introduce a transition between the dynamic and intermediate flow regimes at a Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }>\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
and at a corresponding thickness
$\unicode[STIX]{x1D6FD}_{\ast }>\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
and at a corresponding thickness
![]() $h_{\ast }\in [h_{stop},h_{start}]$
, for steady uniform flows. This is consistent with the steady-uniform flow data of Pouliquen (Reference Pouliquen1999a
), where the minimum observed thickness of a steady uniform flow is somewhat greater than
$h_{\ast }\in [h_{stop},h_{start}]$
, for steady uniform flows. This is consistent with the steady-uniform flow data of Pouliquen (Reference Pouliquen1999a
), where the minimum observed thickness of a steady uniform flow is somewhat greater than
![]() $h_{stop}$
itself. A key distinguishing feature of Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law is therefore that there are three important thicknesses, namely
$h_{stop}$
itself. A key distinguishing feature of Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law is therefore that there are three important thicknesses, namely
![]() $h_{stop}$
,
$h_{stop}$
,
![]() $h_{start}$
and the thickness
$h_{start}$
and the thickness
![]() $h_{\ast }$
at which the friction law switches between the monotonically decreasing intermediate and monotonically increasing dynamic regimes, and below which steady uniform flows are not possible.
$h_{\ast }$
at which the friction law switches between the monotonically decreasing intermediate and monotonically increasing dynamic regimes, and below which steady uniform flows are not possible.
Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) showed that their non-monotonic friction law was capable of quantitatively modelling the release of a finite mass of grains on an erodible layer of the same grains. In order to do this, the friction law was incorporated into a depth-averaged avalanche model that included viscous terms (Gray & Edwards Reference Gray and Edwards2014; Baker, Barker & Gray Reference Baker, Barker and Gray2016a
) that were derived from the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (Jop et al.
Reference Jop, Forterre and Pouliquen2006). In particular, Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) were able to capture key morphological features such as levees, troughs and elevated channels, during the growth, decay and steady propagation of erosion–deposition waves. Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) chose to transition between intermediate and dynamic friction regimes at a thickness
$\unicode[STIX]{x1D707}(I)$
-rheology (Jop et al.
Reference Jop, Forterre and Pouliquen2006). In particular, Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) were able to capture key morphological features such as levees, troughs and elevated channels, during the growth, decay and steady propagation of erosion–deposition waves. Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) chose to transition between intermediate and dynamic friction regimes at a thickness
![]() $h_{\ast }=(1-a)h_{stop}+ah_{start}$
that lay in between
$h_{\ast }=(1-a)h_{stop}+ah_{start}$
that lay in between
![]() $h_{stop}$
and
$h_{stop}$
and
![]() $h_{start}$
(where the constant parameter
$h_{start}$
(where the constant parameter
![]() $a\in [0,1]$
). This implies that
$a\in [0,1]$
). This implies that
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
is a function of the inclination angle and is therefore only defined for
$\unicode[STIX]{x1D6FD}_{\ast }$
is a function of the inclination angle and is therefore only defined for
![]() $\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{2}]$
, where
$\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{2}]$
, where
![]() $h_{start}$
is defined. Here, instead, it is proposed that
$h_{start}$
is defined. Here, instead, it is proposed that
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
is a constant for all inclination angles, which implies that the transition thickness is a constant multiple
$\unicode[STIX]{x1D6FD}_{\ast }$
is a constant for all inclination angles, which implies that the transition thickness is a constant multiple
![]() $\unicode[STIX]{x1D6EC}>1$
of
$\unicode[STIX]{x1D6EC}>1$
of
![]() $h_{stop}$
, i.e.
$h_{stop}$
, i.e.
![]() $h_{\ast }=\unicode[STIX]{x1D6EC}h_{stop}<h_{start}$
. This has the major advantage that the modified friction law proposed here is well defined for all angles.
$h_{\ast }=\unicode[STIX]{x1D6EC}h_{stop}<h_{start}$
. This has the major advantage that the modified friction law proposed here is well defined for all angles.
Table 1. Material properties for the flows of carborundum on a bed of glass beads, measured by Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017).

Figure 2. Space–time
![]() $(x,t)$
plot showing the trajectories of 280–350
$(x,t)$
plot showing the trajectories of 280–350
![]() $\unicode[STIX]{x03BC}\text{m}$
diameter carborundum particles as they are deposited by a steady-uniform flow of thickness
$\unicode[STIX]{x03BC}\text{m}$
diameter carborundum particles as they are deposited by a steady-uniform flow of thickness
![]() $h(x=0,t)\approx h_{start}(36.3^{\circ })+0.5~\text{mm}=2.4$
mm on a rough slope made of 750–1000
$h(x=0,t)\approx h_{start}(36.3^{\circ })+0.5~\text{mm}=2.4$
mm on a rough slope made of 750–1000
![]() $\unicode[STIX]{x03BC}\text{m}$
diameter spherical glass beads and inclined at
$\unicode[STIX]{x03BC}\text{m}$
diameter spherical glass beads and inclined at
![]() $\unicode[STIX]{x1D701}=36.3^{\circ }$
. The depth-averaged frictional properties of the bed and the particles are summarized in table 1. A high-speed camera is used to capture still images of the flow from above in a region between
$\unicode[STIX]{x1D701}=36.3^{\circ }$
. The depth-averaged frictional properties of the bed and the particles are summarized in table 1. A high-speed camera is used to capture still images of the flow from above in a region between
![]() $x=50$
and 86 cm downslope and the middle column of successive images are laid out horizontally to create the plot. All the trajectories have a distinctive curved shape as they decelerate from steady-uniform flow and stop, whereas the static material produces a series of vertical parallel lines. The point at which particles begin to rapidly decelerate (dotted white line) and the transition between static and moving grains (dashed white line) have the same constant slope. This together with the similarity of the particle trajectories implies that a steadily travelling deposition wave brings the grains to rest.
$x=50$
and 86 cm downslope and the middle column of successive images are laid out horizontally to create the plot. All the trajectories have a distinctive curved shape as they decelerate from steady-uniform flow and stop, whereas the static material produces a series of vertical parallel lines. The point at which particles begin to rapidly decelerate (dotted white line) and the transition between static and moving grains (dashed white line) have the same constant slope. This together with the similarity of the particle trajectories implies that a steadily travelling deposition wave brings the grains to rest.

Figure 3. Measured downslope thickness profile for 280–350
![]() $\unicode[STIX]{x03BC}\text{m}$
diameter carborundum particles on a rough slope made of 750–1000
$\unicode[STIX]{x03BC}\text{m}$
diameter carborundum particles on a rough slope made of 750–1000
![]() $\unicode[STIX]{x03BC}\text{m}$
diameter spherical glass beads inclined at
$\unicode[STIX]{x03BC}\text{m}$
diameter spherical glass beads inclined at
![]() $\unicode[STIX]{x1D701}=36.3^{\circ }$
. The frictional properties of the bed and the particles are summarized in table 1. A steady-uniform flow of thickness
$\unicode[STIX]{x1D701}=36.3^{\circ }$
. The frictional properties of the bed and the particles are summarized in table 1. A steady-uniform flow of thickness
![]() $\simeq 2.4$
mm, which is 0.5 mm greater than the theoretical value of
$\simeq 2.4$
mm, which is 0.5 mm greater than the theoretical value of
![]() $h_{start}$
(solid green line), is brought to rest by closing the supply of particles. This produces a steadily travelling deposition wave that moves downstream. A laser profile sensor is used to record the data at a frequency of 100 Hz for 10 s between 53 cm and 65 cm downslope. Under the assumption that the deposition occurs as a travelling wave, the profiles are translated by the known wavespeed to produce downslope thickness data (grey markers). This is then averaged in time to produce a mean downslope profile (solid black line). For comparison the dashed black line shows a numerical simulation of the same problem, which is described in § 4.2. The deposit depths of the simulation and the data are in good agreement with the theoretical value of
$h_{start}$
(solid green line), is brought to rest by closing the supply of particles. This produces a steadily travelling deposition wave that moves downstream. A laser profile sensor is used to record the data at a frequency of 100 Hz for 10 s between 53 cm and 65 cm downslope. Under the assumption that the deposition occurs as a travelling wave, the profiles are translated by the known wavespeed to produce downslope thickness data (grey markers). This is then averaged in time to produce a mean downslope profile (solid black line). For comparison the dashed black line shows a numerical simulation of the same problem, which is described in § 4.2. The deposit depths of the simulation and the data are in good agreement with the theoretical value of
![]() $h_{stop}$
(solid red line). The amplitude and length of the wave are also in good quantitative agreement, although there are some qualitative differences in its overall shape. The orange line represents the minimum thickness
$h_{stop}$
(solid red line). The amplitude and length of the wave are also in good quantitative agreement, although there are some qualitative differences in its overall shape. The orange line represents the minimum thickness
![]() $h_{\ast }$
of a steady-uniform flow.
$h_{\ast }$
of a steady-uniform flow.
As well as proposing an important modification to the friction law, this paper considers in detail how the friction brings grains to rest to leave a deposit of thickness
![]() $h_{stop}$
. The same experimental set-up as Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) is used here. It consists of a rough inclined plane, which has a monolayer of 750–1000
$h_{stop}$
. The same experimental set-up as Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) is used here. It consists of a rough inclined plane, which has a monolayer of 750–1000
![]() $\unicode[STIX]{x03BC}\text{m}$
diameter spherical glass beads attached to it with double-sided sticky tape (to produce no-slip at the base), and 280–350
$\unicode[STIX]{x03BC}\text{m}$
diameter spherical glass beads attached to it with double-sided sticky tape (to produce no-slip at the base), and 280–350
![]() $\unicode[STIX]{x03BC}\text{m}$
diameter carborundum particles, whose depth-averaged effective frictional properties are summarized in table 1. Firstly, a steady-uniform flow of thickness
$\unicode[STIX]{x03BC}\text{m}$
diameter carborundum particles, whose depth-averaged effective frictional properties are summarized in table 1. Firstly, a steady-uniform flow of thickness
![]() $h(x=0,t)\approx h_{start}(36.3^{\circ })+0.5~\text{mm}=2.4$
mm is formed by allowing carborundum particles to flow at constant rate out of a hopper at the top of the plane inclined at an angle of
$h(x=0,t)\approx h_{start}(36.3^{\circ })+0.5~\text{mm}=2.4$
mm is formed by allowing carborundum particles to flow at constant rate out of a hopper at the top of the plane inclined at an angle of
![]() $\unicode[STIX]{x1D701}=36.3^{\circ }$
to the horizontal. Once the hopper has emptied, the steady-uniform flow comes to rest and leaves a thinner deposit of near constant thickness
$\unicode[STIX]{x1D701}=36.3^{\circ }$
to the horizontal. Once the hopper has emptied, the steady-uniform flow comes to rest and leaves a thinner deposit of near constant thickness
![]() $h_{stop}$
. A high-speed camera (Teledyne DALSA Genie Nano M1940) is used to capture still images of the flow from above in a region between 50 and 86 cm downslope from the hopper. The space–time plot, shown in figure 2, is constructed by extracting the middle row from each successive image and laying them out horizontally to give increasing time
$h_{stop}$
. A high-speed camera (Teledyne DALSA Genie Nano M1940) is used to capture still images of the flow from above in a region between 50 and 86 cm downslope from the hopper. The space–time plot, shown in figure 2, is constructed by extracting the middle row from each successive image and laying them out horizontally to give increasing time
![]() $t$
moving down the ordinate. Vertical lines indicate stationary grains, since there is no movement downslope with changing time, and non-vertical lines represent moving particles. The surface velocity of the moving particles in the steady uniform flow region is measured to be 0.23 m s
$t$
moving down the ordinate. Vertical lines indicate stationary grains, since there is no movement downslope with changing time, and non-vertical lines represent moving particles. The surface velocity of the moving particles in the steady uniform flow region is measured to be 0.23 m s
![]() $^{-1}$
and adjacent particle trajectories all have a very similar shape. It is evident that the boundary between moving and stationary grains at the rear of the flow propagates downslope at a slightly faster constant speed of 0.24 m s
$^{-1}$
and adjacent particle trajectories all have a very similar shape. It is evident that the boundary between moving and stationary grains at the rear of the flow propagates downslope at a slightly faster constant speed of 0.24 m s
![]() $^{-1}$
. These observations indicate that the newly deposited
$^{-1}$
. These observations indicate that the newly deposited
![]() $h_{stop}$
layer is formed by a steadily travelling deposition wave. This is an important physical observation, which helps to constrain the functional form of the friction law, and suggests that the theory should admit travelling-wave solutions.
$h_{stop}$
layer is formed by a steadily travelling deposition wave. This is an important physical observation, which helps to constrain the functional form of the friction law, and suggests that the theory should admit travelling-wave solutions.
In addition, a Micro-Epsilon scanCONTROL 2950-100 laser profile sensor is used to acquire thickness data at 1200 points between 53 cm and 65 cm downslope of the gate and at the cross-slope centre of the plane. The laser line measures the distance of the bulk flow particles away from the sensor at a frequency of 100 Hz for 10 s and to an accuracy of
![]() $\pm$
0.2 mm (approximately a grain diameter) by laser triangulation. Also measuring the distance between the sensor and the bed before it is coated with the static layer of carborundum particles allows the thickness profile
$\pm$
0.2 mm (approximately a grain diameter) by laser triangulation. Also measuring the distance between the sensor and the bed before it is coated with the static layer of carborundum particles allows the thickness profile
![]() $h$
of the avalanche in the
$h$
of the avalanche in the
![]() $z$
-direction to be calculated along the laser line. Adjacent measurements are shifted in downslope position according to the wavespeed measured from the space–time plot to give an average thickness profile in time passing through the midpoint of the laser line. This is then converted back to a downslope profile with the appropriate transformation. The data are plotted in figure 3 and are compared to a numerical simulation, which will be described in greater detail in § 4.2. The deposit depths in the experiment and the simulation are in good agreement with one another and with
$z$
-direction to be calculated along the laser line. Adjacent measurements are shifted in downslope position according to the wavespeed measured from the space–time plot to give an average thickness profile in time passing through the midpoint of the laser line. This is then converted back to a downslope profile with the appropriate transformation. The data are plotted in figure 3 and are compared to a numerical simulation, which will be described in greater detail in § 4.2. The deposit depths in the experiment and the simulation are in good agreement with one another and with
![]() $h_{stop}$
, whilst the general shapes of the flow thickness profiles are also qualitatively comparable. Furthermore, the measured downslope length of the varying thickness region between the uniform and deposit layers is approximately equal to that of the numerics. This implies that the wavespeed obtained from the space–time plot, which is used to transform the time-dependent laser data into a downslope thickness profile, is in good agreement with the theoretical value.
$h_{stop}$
, whilst the general shapes of the flow thickness profiles are also qualitatively comparable. Furthermore, the measured downslope length of the varying thickness region between the uniform and deposit layers is approximately equal to that of the numerics. This implies that the wavespeed obtained from the space–time plot, which is used to transform the time-dependent laser data into a downslope thickness profile, is in good agreement with the theoretical value.
The paper is arranged as follows. The depth-averaged model is introduced in § 2 and the modifications to the friction law (which ensure that it is valid at all angles) are described in detail in §§ 3.2 and 3.3. Numerical simulations of the deposition process for a wide range of angles and initial flow thicknesses are performed in § 4. These simulations confirm the experimental observations of § 1, which show that a travelling wave forms as the particles are deposited. An exact inviscid solution for this wave is derived in § 5, which explicitly shows that a steady-uniform flow of thickness
![]() $h_{\ast }$
produces a deposit that is close to
$h_{\ast }$
produces a deposit that is close to
![]() $h_{stop}$
for all inclination angles. Finally the pathologies of earlier formulations of the friction law are discussed in § 6 before concluding in § 7.
$h_{stop}$
for all inclination angles. Finally the pathologies of earlier formulations of the friction law are discussed in § 6 before concluding in § 7.
2 Depth-averaged avalanche model with viscous dissipation
The avalanches are assumed to take place on a plane that is inclined at an angle
![]() $\unicode[STIX]{x1D701}$
to the horizontal and a coordinate system
$\unicode[STIX]{x1D701}$
to the horizontal and a coordinate system
![]() $Oxz$
is defined with the
$Oxz$
is defined with the
![]() $x$
-axis pointing down the chute and the
$x$
-axis pointing down the chute and the
![]() $z$
-axis being the upward pointing normal. The granular material is treated as either being moving, or static, through its entire depth, which is consistent with the measurements of
$z$
-axis being the upward pointing normal. The granular material is treated as either being moving, or static, through its entire depth, which is consistent with the measurements of
![]() $h_{stop}$
and
$h_{stop}$
and
![]() $h_{start}$
that were used to determine the effective basal friction law (Pouliquen & Forterre Reference Pouliquen and Forterre2002; Edwards & Gray Reference Edwards and Gray2015). The problem is modelled using a system of one-dimensional viscous avalanche equations for the thickness
$h_{start}$
that were used to determine the effective basal friction law (Pouliquen & Forterre Reference Pouliquen and Forterre2002; Edwards & Gray Reference Edwards and Gray2015). The problem is modelled using a system of one-dimensional viscous avalanche equations for the thickness
![]() $h(x,t)$
and the depth-averaged downslope velocity
$h(x,t)$
and the depth-averaged downslope velocity
![]() $\bar{u}(x,t)$
, which result from Gray & Edwards’ (Reference Gray and Edwards2014) depth-averaged
$\bar{u}(x,t)$
, which result from Gray & Edwards’ (Reference Gray and Edwards2014) depth-averaged
![]() $\unicode[STIX]{x1D707}(I)$
–rheology. The depth-averaged mass and momentum balance equations in this representation are
$\unicode[STIX]{x1D707}(I)$
–rheology. The depth-averaged mass and momentum balance equations in this representation are
where
![]() $g$
is the constant of gravitational acceleration and
$g$
is the constant of gravitational acceleration and
![]() $\unicode[STIX]{x1D712}=\overline{u^{2}}/\bar{u}^{2}$
is the shape factor. The
$\unicode[STIX]{x1D712}=\overline{u^{2}}/\bar{u}^{2}$
is the shape factor. The
![]() $\unicode[STIX]{x1D707}(I)$
-rheology implies that for steady-uniform flow a Bagnold velocity profile develops (see e.g. GDR-MiDi 2004; Gray & Edwards Reference Gray and Edwards2014) and the resulting shape factor
$\unicode[STIX]{x1D707}(I)$
-rheology implies that for steady-uniform flow a Bagnold velocity profile develops (see e.g. GDR-MiDi 2004; Gray & Edwards Reference Gray and Edwards2014) and the resulting shape factor
![]() $\unicode[STIX]{x1D712}=5/4$
. For thin flows close to
$\unicode[STIX]{x1D712}=5/4$
. For thin flows close to
![]() $h_{stop}$
weakly exponential profiles develop (Kamrin & Henann Reference Kamrin and Henann2015) and surface velocity measurements in § 4.2 suggest that
$h_{stop}$
weakly exponential profiles develop (Kamrin & Henann Reference Kamrin and Henann2015) and surface velocity measurements in § 4.2 suggest that
![]() $\unicode[STIX]{x1D712}\approx 1.16$
for the experiments performed here. Non-unity values of the shape factor (Lagrée et al.
Reference Lagrée, Saingier, Deboeuf, Staron and Popinet2017) change the characteristic structure of the inviscid equations, and cause problems when handling grain-free regions (Hogg & Pritchard Reference Hogg and Pritchard2004), so virtually all avalanche models (e.g. Grigorian, Eglit & Iakimov Reference Grigorian, Eglit and Iakimov1967; Savage & Hutter Reference Savage and Hutter1989; Gray, Wieland & Hutter Reference Gray, Wieland and Hutter1999; Pouliquen Reference Pouliquen1999b
; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Gray, Tai & Noelle Reference Gray, Tai and Noelle2003) assume, as in this paper, that
$\unicode[STIX]{x1D712}\approx 1.16$
for the experiments performed here. Non-unity values of the shape factor (Lagrée et al.
Reference Lagrée, Saingier, Deboeuf, Staron and Popinet2017) change the characteristic structure of the inviscid equations, and cause problems when handling grain-free regions (Hogg & Pritchard Reference Hogg and Pritchard2004), so virtually all avalanche models (e.g. Grigorian, Eglit & Iakimov Reference Grigorian, Eglit and Iakimov1967; Savage & Hutter Reference Savage and Hutter1989; Gray, Wieland & Hutter Reference Gray, Wieland and Hutter1999; Pouliquen Reference Pouliquen1999b
; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Gray, Tai & Noelle Reference Gray, Tai and Noelle2003) assume, as in this paper, that
![]() $\unicode[STIX]{x1D712}=1$
. The slow flows studied here are insensitive to this approximation, since the magnitude of the momentum transport term in (2.2) is small compared to the pressure gradient and source terms (see equations (5.10)–(5.12) of Viroulet et al.
Reference Viroulet, Baker, Edwards, Johnson, Gjaltema, Clavel and Gray2017).
$\unicode[STIX]{x1D712}=1$
. The slow flows studied here are insensitive to this approximation, since the magnitude of the momentum transport term in (2.2) is small compared to the pressure gradient and source terms (see equations (5.10)–(5.12) of Viroulet et al.
Reference Viroulet, Baker, Edwards, Johnson, Gjaltema, Clavel and Gray2017).
In the source terms on the right-hand side of (2.2) the non-dimensional net acceleration
consists of the downslope component of gravity and the effective basal friction
![]() $\unicode[STIX]{x1D707}$
that opposes the direction of motion. For all problems in this paper
$\unicode[STIX]{x1D707}$
that opposes the direction of motion. For all problems in this paper
![]() $\bar{u}\geqslant 0$
and hence
$\bar{u}\geqslant 0$
and hence
![]() $\bar{u}/|\bar{u}|=1$
.
$\bar{u}/|\bar{u}|=1$
.
Gray & Edwards (Reference Gray and Edwards2014) showed that to leading order the inviscid avalanche equations emerge naturally from depth averaging the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (GDR-MiDi 2004; Jop et al.
Reference Jop, Forterre and Pouliquen2006) with the basal friction given by the dynamic basal friction law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002). The depth-averaged
$\unicode[STIX]{x1D707}(I)$
-rheology (GDR-MiDi 2004; Jop et al.
Reference Jop, Forterre and Pouliquen2006) with the basal friction given by the dynamic basal friction law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002). The depth-averaged
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (Gray & Edwards Reference Gray and Edwards2014; Baker et al.
Reference Baker, Barker and Gray2016a
), used here, differs from the standard inviscid equations by the inclusion of an in-plane deviatoric stress, which gives rise to a depth-averaged viscous-like term in the momentum balance (2.2). The coefficient
$\unicode[STIX]{x1D707}(I)$
-rheology (Gray & Edwards Reference Gray and Edwards2014; Baker et al.
Reference Baker, Barker and Gray2016a
), used here, differs from the standard inviscid equations by the inclusion of an in-plane deviatoric stress, which gives rise to a depth-averaged viscous-like term in the momentum balance (2.2). The coefficient
![]() $\unicode[STIX]{x1D708}$
in the effective viscosity
$\unicode[STIX]{x1D708}$
in the effective viscosity
![]() $\unicode[STIX]{x1D708}h^{1/2}/2$
is explicitly derived in the depth-integration process and is given by
$\unicode[STIX]{x1D708}h^{1/2}/2$
is explicitly derived in the depth-integration process and is given by
Table 2. Critical layer thicknesses and coefficients
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D701})$
in the depth-averaged viscosity
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D701})$
in the depth-averaged viscosity
![]() $\unicode[STIX]{x1D708}h^{1/2}/2$
for various different slope angles with the material properties for carborundum in table 1.
$\unicode[STIX]{x1D708}h^{1/2}/2$
for various different slope angles with the material properties for carborundum in table 1.

where the parameters
![]() $\mathscr{L}$
,
$\mathscr{L}$
,
![]() $\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FD}$
,
![]() $\unicode[STIX]{x1D701}_{1}$
and
$\unicode[STIX]{x1D701}_{1}$
and
![]() $\unicode[STIX]{x1D701}_{2}$
are determined by Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) basal friction law described below. Values of these parameters measured by Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) are summarized in table 1 and the associated values of
$\unicode[STIX]{x1D701}_{2}$
are determined by Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) basal friction law described below. Values of these parameters measured by Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) are summarized in table 1 and the associated values of
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D701})$
are given in table 2 for various slope angles. Although small in magnitude, strong evidence for these viscous terms is provided by the fact that, unlike the inviscid avalanche model, they (i) predict a downslope velocity profile that varies across a channel with rough sidewalls (Baker et al.
Reference Baker, Barker and Gray2016a
), (ii) allow the experimental cutoff frequency of roll waves to be matched without fitting parameters (Forterre Reference Forterre2006; Gray & Edwards Reference Gray and Edwards2014), (iii) determine the width and height of self-channelized monodisperse flows (Rocha et al.
Reference Rocha, Johnson and Gray2019) and (iv) regularize depth-averaged models of segregation-induced fingering (Pouliquen, Delour & Savage Reference Pouliquen, Delour and Savage1997; Pouliquen & Vallance Reference Pouliquen and Vallance1999; Woodhouse et al.
Reference Woodhouse, Thornton, Johnson, Kokelaar and Gray2012; Baker, Johnson & Gray Reference Baker, Johnson and Gray2016b
). It should be noted, however, that the viscous theory is only well posed for slope inclinations in the range where the friction law, from which it is derived, is defined i.e. for
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D701})$
are given in table 2 for various slope angles. Although small in magnitude, strong evidence for these viscous terms is provided by the fact that, unlike the inviscid avalanche model, they (i) predict a downslope velocity profile that varies across a channel with rough sidewalls (Baker et al.
Reference Baker, Barker and Gray2016a
), (ii) allow the experimental cutoff frequency of roll waves to be matched without fitting parameters (Forterre Reference Forterre2006; Gray & Edwards Reference Gray and Edwards2014), (iii) determine the width and height of self-channelized monodisperse flows (Rocha et al.
Reference Rocha, Johnson and Gray2019) and (iv) regularize depth-averaged models of segregation-induced fingering (Pouliquen, Delour & Savage Reference Pouliquen, Delour and Savage1997; Pouliquen & Vallance Reference Pouliquen and Vallance1999; Woodhouse et al.
Reference Woodhouse, Thornton, Johnson, Kokelaar and Gray2012; Baker, Johnson & Gray Reference Baker, Johnson and Gray2016b
). It should be noted, however, that the viscous theory is only well posed for slope inclinations in the range where the friction law, from which it is derived, is defined i.e. for
![]() $\unicode[STIX]{x1D701}\in (\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})$
. Outside of this range some form of regularization is required, i.e. the negative viscosity for
$\unicode[STIX]{x1D701}\in (\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})$
. Outside of this range some form of regularization is required, i.e. the negative viscosity for
![]() $\unicode[STIX]{x1D701}\notin (\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})$
must be prevented (see Gray & Edwards Reference Gray and Edwards2014). Also note that Gray & Edwards’ (Reference Gray and Edwards2014) derivation of the viscous term in (2.2) implicitly assumes that the friction coefficient is always given by Pouliquen’s (Reference Pouliquen1999a
) dynamic law. In principle, the form of the viscous term should change when the friction law is in the intermediate regime. However, it is not obvious how to achieve this, since there is no longer a stable steady-uniform flow solution to determine the velocity and pressure profiles in the depth-integration process. For simplicity, it is therefore assumed, as in Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017), that the simple viscous-term in (2.2) applies over all regimes.
$\unicode[STIX]{x1D701}\notin (\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})$
must be prevented (see Gray & Edwards Reference Gray and Edwards2014). Also note that Gray & Edwards’ (Reference Gray and Edwards2014) derivation of the viscous term in (2.2) implicitly assumes that the friction coefficient is always given by Pouliquen’s (Reference Pouliquen1999a
) dynamic law. In principle, the form of the viscous term should change when the friction law is in the intermediate regime. However, it is not obvious how to achieve this, since there is no longer a stable steady-uniform flow solution to determine the velocity and pressure profiles in the depth-integration process. For simplicity, it is therefore assumed, as in Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017), that the simple viscous-term in (2.2) applies over all regimes.
3 A non-monotonic friction law for hysteresis
3.1 Basic definitions of
 $h_{stop}$
,
$h_{stop}$
,
 $h_{start}$
and the empirical flow rule
$h_{start}$
and the empirical flow rule
Pouliquen (Reference Pouliquen1999a
) performed experiments with spherical glass beads on rough beds and measured the deposit thickness
![]() $h_{stop}(\unicode[STIX]{x1D701})$
left by a steady-uniform flow as a function of the inclination angle
$h_{stop}(\unicode[STIX]{x1D701})$
left by a steady-uniform flow as a function of the inclination angle
![]() $\unicode[STIX]{x1D701}$
. The inverse function of this deposit thickness
$\unicode[STIX]{x1D701}$
. The inverse function of this deposit thickness
![]() $\unicode[STIX]{x1D701}_{stop}(h)$
was found to have the following empirical fit, given here in Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) reciprocal form,
$\unicode[STIX]{x1D701}_{stop}(h)$
was found to have the following empirical fit, given here in Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) reciprocal form,
where
![]() $\unicode[STIX]{x1D701}_{1}$
is the slope inclination below which a layer of any thickness comes to rest and
$\unicode[STIX]{x1D701}_{1}$
is the slope inclination below which a layer of any thickness comes to rest and
![]() $\unicode[STIX]{x1D701}_{2}$
is the angle above which it is not possible for a uniform layer of grains to remain static on the slope. The parameter
$\unicode[STIX]{x1D701}_{2}$
is the angle above which it is not possible for a uniform layer of grains to remain static on the slope. The parameter
![]() $\mathscr{L}$
(having the dimensions of a length) is the characteristic flow depth over which a transition between the angles
$\mathscr{L}$
(having the dimensions of a length) is the characteristic flow depth over which a transition between the angles
![]() $\unicode[STIX]{x1D701}_{1}$
and
$\unicode[STIX]{x1D701}_{1}$
and
![]() $\unicode[STIX]{x1D701}_{2}$
occurs and, as such, it is dependent on the properties of the grains and on the bed roughness. It follows that for
$\unicode[STIX]{x1D701}_{2}$
occurs and, as such, it is dependent on the properties of the grains and on the bed roughness. It follows that for
![]() $\unicode[STIX]{x1D701}\in (\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})$
the deposit layer thickness may be written as
$\unicode[STIX]{x1D701}\in (\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})$
the deposit layer thickness may be written as
Experimental measurements of the flow thickness
![]() $h$
and the depth-averaged velocity
$h$
and the depth-averaged velocity
![]() $\bar{u}$
have been found to collapse (Pouliquen Reference Pouliquen1999a
; Forterre & Pouliquen Reference Forterre and Pouliquen2003; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017) for an empirical flow rule of the form
$\bar{u}$
have been found to collapse (Pouliquen Reference Pouliquen1999a
; Forterre & Pouliquen Reference Forterre and Pouliquen2003; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017) for an empirical flow rule of the form
which relates the Froude number,
to the flow height and the deposit depth
![]() $h_{stop}$
. The constant of proportionality
$h_{stop}$
. The constant of proportionality
![]() $\unicode[STIX]{x1D6FD}$
and the offset
$\unicode[STIX]{x1D6FD}$
and the offset
![]() $\unicode[STIX]{x1D6E4}$
have been measured as
$\unicode[STIX]{x1D6E4}$
have been measured as
![]() $\unicode[STIX]{x1D6FD}=0.136/\sqrt{\cos \unicode[STIX]{x1D701}}$
with
$\unicode[STIX]{x1D6FD}=0.136/\sqrt{\cos \unicode[STIX]{x1D701}}$
with
![]() $\unicode[STIX]{x1D6E4}=0$
for flows of spherical glass beads on a rough bed of the same material (Pouliquen Reference Pouliquen1999a
),
$\unicode[STIX]{x1D6E4}=0$
for flows of spherical glass beads on a rough bed of the same material (Pouliquen Reference Pouliquen1999a
),
![]() $\unicode[STIX]{x1D6FD}=0.65/\sqrt{\cos \unicode[STIX]{x1D701}}$
with
$\unicode[STIX]{x1D6FD}=0.65/\sqrt{\cos \unicode[STIX]{x1D701}}$
with
![]() $\unicode[STIX]{x1D6E4}=0.77/\sqrt{\cos \unicode[STIX]{x1D701}}$
for flows of sand on a rough bed of the same material (Forterre & Pouliquen Reference Forterre and Pouliquen2003) and
$\unicode[STIX]{x1D6E4}=0.77/\sqrt{\cos \unicode[STIX]{x1D701}}$
for flows of sand on a rough bed of the same material (Forterre & Pouliquen Reference Forterre and Pouliquen2003) and
![]() $\unicode[STIX]{x1D6FD}=0.63$
with
$\unicode[STIX]{x1D6FD}=0.63$
with
![]() $\unicode[STIX]{x1D6E4}=0.40$
for flows of carborundum on a rough bed of spherical glass beads (Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017). Note that the alternative definition of the Froude number
$\unicode[STIX]{x1D6E4}=0.40$
for flows of carborundum on a rough bed of spherical glass beads (Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017). Note that the alternative definition of the Froude number
![]() $\hat{Fr}=|\bar{u}|/\sqrt{gh}$
by Pouliquen (Reference Pouliquen1999a
) and Forterre & Pouliquen (Reference Forterre and Pouliquen2003) gives rise to the apparent angle dependence in
$\hat{Fr}=|\bar{u}|/\sqrt{gh}$
by Pouliquen (Reference Pouliquen1999a
) and Forterre & Pouliquen (Reference Forterre and Pouliquen2003) gives rise to the apparent angle dependence in
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6E4}$
, but this is a small correction and they should be thought of as constants. Using (3.3) to substitute for
$\unicode[STIX]{x1D6E4}$
, but this is a small correction and they should be thought of as constants. Using (3.3) to substitute for
![]() $h_{stop}(\unicode[STIX]{x1D701})$
in (3.2) and the fact that
$h_{stop}(\unicode[STIX]{x1D701})$
in (3.2) and the fact that
![]() $\unicode[STIX]{x1D707}=\tan \unicode[STIX]{x1D701}$
for steady uniform flows, Pouliquen (Reference Pouliquen1999a
) determined an empirical dynamic friction law for flows on rough beds provided that the Froude number
$\unicode[STIX]{x1D707}=\tan \unicode[STIX]{x1D701}$
for steady uniform flows, Pouliquen (Reference Pouliquen1999a
) determined an empirical dynamic friction law for flows on rough beds provided that the Froude number
![]() $Fr>\unicode[STIX]{x1D6FD}$
, which is the value that they assumed was the minimum steady uniform Froude number, i.e.
$Fr>\unicode[STIX]{x1D6FD}$
, which is the value that they assumed was the minimum steady uniform Froude number, i.e.
![]() $\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}$
.
Pouliquen & Forterre (Reference Pouliquen and Forterre2002) combined this dynamic rough bed friction law with Daerr & Douady’s (Reference Daerr and Douady1999) concept that once the grains were stopped (i.e.
![]() $Fr=0$
) flow could not spontaneously start again until the inclination angle was increased past a critical value,
$Fr=0$
) flow could not spontaneously start again until the inclination angle was increased past a critical value,
![]() $\unicode[STIX]{x1D701}_{start}(h)$
. This was similarly found to have an empirical fit of the form
$\unicode[STIX]{x1D701}_{start}(h)$
. This was similarly found to have an empirical fit of the form
where the third critical angle,
![]() $\unicode[STIX]{x1D701}_{3}$
, is the minimum angle at which it is possible for a layer of any thickness to accelerate from stationary and is the asymptote for large
$\unicode[STIX]{x1D701}_{3}$
, is the minimum angle at which it is possible for a layer of any thickness to accelerate from stationary and is the asymptote for large
![]() $h$
of the curve
$h$
of the curve
![]() $\unicode[STIX]{x1D701}_{start}(h)$
. The inverse function of this curve gives the thickness of a flow that is initiated at the critical slope angle as
$\unicode[STIX]{x1D701}_{start}(h)$
. The inverse function of this curve gives the thickness of a flow that is initiated at the critical slope angle as
This slope angle-dependent critical flow thickness is infinite at
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}_{3}$
and is undefined for
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}_{3}$
and is undefined for
![]() $\unicode[STIX]{x1D701}<\unicode[STIX]{x1D701}_{3}$
. For angles
$\unicode[STIX]{x1D701}<\unicode[STIX]{x1D701}_{3}$
. For angles
![]() $\unicode[STIX]{x1D701}\leqslant \unicode[STIX]{x1D701}_{3}$
a static uniform layer of any thickness will therefore remain stationary unless it is disturbed.
$\unicode[STIX]{x1D701}\leqslant \unicode[STIX]{x1D701}_{3}$
a static uniform layer of any thickness will therefore remain stationary unless it is disturbed.
In the intermediate regime
![]() $Fr\in [0,\unicode[STIX]{x1D6FD}]$
there was no further experimental information and Pouliquen & Forterre (Reference Pouliquen and Forterre2002) suggested a Froude number dependent power law interpolation between the minimum dynamic and maximum static friction. Since the maximum static friction was higher than the minimum dynamic friction, the intermediate friction was a monotonically decreasing function of
$Fr\in [0,\unicode[STIX]{x1D6FD}]$
there was no further experimental information and Pouliquen & Forterre (Reference Pouliquen and Forterre2002) suggested a Froude number dependent power law interpolation between the minimum dynamic and maximum static friction. Since the maximum static friction was higher than the minimum dynamic friction, the intermediate friction was a monotonically decreasing function of
![]() $Fr$
. Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) definition of a multivalued static friction, monotonically decreasing intermediate friction and monotonically increasing dynamic friction, as shown in figure 1(b), provide the essential ingredients for frictional hysteresis.
$Fr$
. Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) definition of a multivalued static friction, monotonically decreasing intermediate friction and monotonically increasing dynamic friction, as shown in figure 1(b), provide the essential ingredients for frictional hysteresis.
3.2 The transition thickness
 $h_{\ast }$
and Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law
$h_{\ast }$
and Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law
One assumption underlying Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) friction law is that the slowest steady-uniform flow, with Froude number
![]() $\unicode[STIX]{x1D6FD}$
, has the same thickness as the resulting deposit
$\unicode[STIX]{x1D6FD}$
, has the same thickness as the resulting deposit
![]() $h_{stop}$
. However, as shown in the erosion–deposition wave simulations of Edwards & Gray (Reference Edwards and Gray2015) (see their figure 15) in which
$h_{stop}$
. However, as shown in the erosion–deposition wave simulations of Edwards & Gray (Reference Edwards and Gray2015) (see their figure 15) in which
![]() $\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}$
, the resulting flow actually comes to rest to form a deposit that is thinner than
$\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}$
, the resulting flow actually comes to rest to form a deposit that is thinner than
![]() $h_{stop}$
. As a consequence of this, and other deficiencies that are described in greater detail in § 6, Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) introduced the idea that the minimum thickness for a steady-uniform flow
$h_{stop}$
. As a consequence of this, and other deficiencies that are described in greater detail in § 6, Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) introduced the idea that the minimum thickness for a steady-uniform flow
![]() $h_{\ast }$
was greater than
$h_{\ast }$
was greater than
![]() $h_{stop}$
and that it occurred at Froude number
$h_{stop}$
and that it occurred at Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }>\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
. This is consistent with Pouliquen’s (Reference Pouliquen1999a
) empirical flow rule, since all the steady-uniform flows are measured for
$\unicode[STIX]{x1D6FD}_{\ast }>\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
. This is consistent with Pouliquen’s (Reference Pouliquen1999a
) empirical flow rule, since all the steady-uniform flows are measured for
![]() $h>h_{stop}$
and
$h>h_{stop}$
and
![]() $Fr>\unicode[STIX]{x1D6FD}$
. Both Forterre & Pouliquen (Reference Forterre and Pouliquen2003) and Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) also only observed steady-uniform flows that had Froude numbers significantly greater than
$Fr>\unicode[STIX]{x1D6FD}$
. Both Forterre & Pouliquen (Reference Forterre and Pouliquen2003) and Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) also only observed steady-uniform flows that had Froude numbers significantly greater than
![]() $\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
in their experiments with angular sand and carborundum particles.
$\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
in their experiments with angular sand and carborundum particles.
Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) assumed that
![]() $h_{\ast }(\unicode[STIX]{x1D701})$
occurred at a linear combination of
$h_{\ast }(\unicode[STIX]{x1D701})$
occurred at a linear combination of
![]() $h_{stop}(\unicode[STIX]{x1D701})$
and
$h_{stop}(\unicode[STIX]{x1D701})$
and
![]() $h_{start}(\unicode[STIX]{x1D701})$
and, hence, by the flow rule (3.3) the transition Froude number
$h_{start}(\unicode[STIX]{x1D701})$
and, hence, by the flow rule (3.3) the transition Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
varied with the inclination angle. This approach allowed Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to model the formation of eroded troughs, lateral levees and elevated channels for mono-disperse flows of carborundum on an erodible bed. While this was a reasonable first approximation, one consequence of this definition, which was not immediately apparent at the time, was that if
$\unicode[STIX]{x1D6FD}_{\ast }$
varied with the inclination angle. This approach allowed Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to model the formation of eroded troughs, lateral levees and elevated channels for mono-disperse flows of carborundum on an erodible bed. While this was a reasonable first approximation, one consequence of this definition, which was not immediately apparent at the time, was that if
![]() $\unicode[STIX]{x1D701}<\unicode[STIX]{x1D701}_{3}$
then
$\unicode[STIX]{x1D701}<\unicode[STIX]{x1D701}_{3}$
then
![]() $h_{start}$
was undefined and hence the transition thickness
$h_{start}$
was undefined and hence the transition thickness
![]() $h_{\ast }$
and
$h_{\ast }$
and
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
were also undefined. Furthermore, variation in
$\unicode[STIX]{x1D6FD}_{\ast }$
were also undefined. Furthermore, variation in
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
with inclination leads to deposit layers that are significantly thicker than
$\unicode[STIX]{x1D6FD}_{\ast }$
with inclination leads to deposit layers that are significantly thicker than
![]() $h_{stop}$
being produced for shallow slope angles, as will be shown in § 6. Predictions of deposit layer depth are, however, still in good agreement with
$h_{stop}$
being produced for shallow slope angles, as will be shown in § 6. Predictions of deposit layer depth are, however, still in good agreement with
![]() $h_{stop}$
on steeper inclinations, which explains why Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) were able to qualitatively match simulations with experiments in the small range of slope angles
$h_{stop}$
on steeper inclinations, which explains why Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) were able to qualitatively match simulations with experiments in the small range of slope angles
![]() $34.0^{\circ }\leqslant \unicode[STIX]{x1D701}\leqslant 35.2^{\circ }$
that they investigated. This paper therefore introduces a relatively minor, but important, modification that the transition is instead assumed to occur at a fixed Froude number
$34.0^{\circ }\leqslant \unicode[STIX]{x1D701}\leqslant 35.2^{\circ }$
that they investigated. This paper therefore introduces a relatively minor, but important, modification that the transition is instead assumed to occur at a fixed Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
for all slope angles, which means that the friction law is now valid for all inclinations. The flow rule (3.3) then implies that the minimum steady-uniform flow thickness
$\unicode[STIX]{x1D6FD}_{\ast }$
for all slope angles, which means that the friction law is now valid for all inclinations. The flow rule (3.3) then implies that the minimum steady-uniform flow thickness
![]() $h_{\ast }(\unicode[STIX]{x1D701})$
is a constant multiple of
$h_{\ast }(\unicode[STIX]{x1D701})$
is a constant multiple of
![]() $h_{stop}(\unicode[STIX]{x1D701})$
$h_{stop}(\unicode[STIX]{x1D701})$
which has the advantage that it is defined for all slope angles in the range
![]() $\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]$
. The variation of
$\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]$
. The variation of
![]() $h_{\ast }(\unicode[STIX]{x1D701})$
with the inclination is shown in figure 1(a). To ensure that
$h_{\ast }(\unicode[STIX]{x1D701})$
with the inclination is shown in figure 1(a). To ensure that
![]() $h_{\ast }(\unicode[STIX]{x1D701})>h_{stop}(\unicode[STIX]{x1D701})$
, the transition Froude number
$h_{\ast }(\unicode[STIX]{x1D701})>h_{stop}(\unicode[STIX]{x1D701})$
, the transition Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }>\max (\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4},0)$
. This condition ensures that
$\unicode[STIX]{x1D6FD}_{\ast }>\max (\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4},0)$
. This condition ensures that
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
is strictly positive, and hence that the frictional transitions are well defined, even if
$\unicode[STIX]{x1D6FD}_{\ast }$
is strictly positive, and hence that the frictional transitions are well defined, even if
![]() $\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}<0$
as in the case of sand. A further constraint on the transition thickness is that
$\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}<0$
as in the case of sand. A further constraint on the transition thickness is that
![]() $h_{\ast }(\unicode[STIX]{x1D701})<h_{start}(\unicode[STIX]{x1D701})$
for all inclinations, which using (3.7) implies that
$h_{\ast }(\unicode[STIX]{x1D701})<h_{start}(\unicode[STIX]{x1D701})$
for all inclinations, which using (3.7) implies that
The right-hand side of (3.8) has a minimum at
![]() $\unicode[STIX]{x1D701}=\tan ^{-1}((\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D707}_{3})/2)$
, where
$\unicode[STIX]{x1D701}=\tan ^{-1}((\unicode[STIX]{x1D707}_{2}+\unicode[STIX]{x1D707}_{3})/2)$
, where
![]() $\unicode[STIX]{x1D707}_{i}=\tan \unicode[STIX]{x1D701}_{i}$
for
$\unicode[STIX]{x1D707}_{i}=\tan \unicode[STIX]{x1D701}_{i}$
for
![]() $i=1,2,3$
. It follows that the transition thickness
$i=1,2,3$
. It follows that the transition thickness
![]() $h_{\ast }<h_{start}$
for all angles provided
$h_{\ast }<h_{start}$
for all angles provided
This has a value of
![]() $\unicode[STIX]{x1D6FD}_{\ast }^{max}=0.47$
for the material properties in table 1, which is equal (to two decimal places) to the value of
$\unicode[STIX]{x1D6FD}_{\ast }^{max}=0.47$
for the material properties in table 1, which is equal (to two decimal places) to the value of
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
that was chosen by Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to match deposit layer depths
$\unicode[STIX]{x1D6FD}_{\ast }$
that was chosen by Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to match deposit layer depths
![]() $h_{deposit}(35.2^{\circ })\approx h_{stop}(35.2^{\circ })$
for carborundum particles on a rough bed of glass beads. In fact, in § 4 it is explicitly shown, by performing direct numerical computations, that a single value of
$h_{deposit}(35.2^{\circ })\approx h_{stop}(35.2^{\circ })$
for carborundum particles on a rough bed of glass beads. In fact, in § 4 it is explicitly shown, by performing direct numerical computations, that a single value of
![]() $\unicode[STIX]{x1D6FD}_{\ast }=0.466$
gives the correct experimental deposit layer depth
$\unicode[STIX]{x1D6FD}_{\ast }=0.466$
gives the correct experimental deposit layer depth
![]() $h_{stop}(\unicode[STIX]{x1D701})$
for all inclination angles. It is also in approximate agreement with the minimum observed Froude number for steady-uniform flows in Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) flow rule experiments. However, for other materials and slope roughnesses
$h_{stop}(\unicode[STIX]{x1D701})$
for all inclination angles. It is also in approximate agreement with the minimum observed Froude number for steady-uniform flows in Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) flow rule experiments. However, for other materials and slope roughnesses
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
may not be equal to
$\unicode[STIX]{x1D6FD}_{\ast }$
may not be equal to
![]() $\unicode[STIX]{x1D6FD}_{\ast }^{max}$
and should rather be inferred directly from the flow rule experiments. As such,
$\unicode[STIX]{x1D6FD}_{\ast }^{max}$
and should rather be inferred directly from the flow rule experiments. As such,
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
may be considered as another intrinsic rheological property, whereas
$\unicode[STIX]{x1D6FD}_{\ast }$
may be considered as another intrinsic rheological property, whereas
![]() $h_{stop}$
(and therefore
$h_{stop}$
(and therefore
![]() $h_{\ast }$
too) is an emerging property.
$h_{\ast }$
too) is an emerging property.
3.3 The modified friction law
The modified friction coefficient in the dynamic
![]() $(Fr\geqslant \unicode[STIX]{x1D6FD}_{\ast })$
, intermediate
$(Fr\geqslant \unicode[STIX]{x1D6FD}_{\ast })$
, intermediate
![]() $(0<Fr\leqslant \unicode[STIX]{x1D6FD}_{\ast })$
and static
$(0<Fr\leqslant \unicode[STIX]{x1D6FD}_{\ast })$
and static
![]() $(Fr=0)$
regimes with a constant
$(Fr=0)$
regimes with a constant
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
is therefore
$\unicode[STIX]{x1D6FD}_{\ast }$
is therefore
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}=\left({\displaystyle \frac{Fr}{\unicode[STIX]{x1D6FD}_{\ast }}}\right)^{\unicode[STIX]{x1D705}}\left(\unicode[STIX]{x1D707}_{1}+{\displaystyle \frac{\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}}{1+h\unicode[STIX]{x1D6FD}/(\mathscr{L}(\unicode[STIX]{x1D6FD}_{\ast }+\unicode[STIX]{x1D6E4}))}}-\unicode[STIX]{x1D707}_{3}-{\displaystyle \frac{\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}}{1+h/\mathscr{L}}}\right) & & \displaystyle \nonumber\\ \displaystyle \qquad +\,\unicode[STIX]{x1D707}_{3}+{\displaystyle \frac{\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}}{1+h/\mathscr{L}}}, & 0<Fr\leqslant \unicode[STIX]{x1D6FD}_{\ast }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}=\left({\displaystyle \frac{Fr}{\unicode[STIX]{x1D6FD}_{\ast }}}\right)^{\unicode[STIX]{x1D705}}\left(\unicode[STIX]{x1D707}_{1}+{\displaystyle \frac{\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}}{1+h\unicode[STIX]{x1D6FD}/(\mathscr{L}(\unicode[STIX]{x1D6FD}_{\ast }+\unicode[STIX]{x1D6E4}))}}-\unicode[STIX]{x1D707}_{3}-{\displaystyle \frac{\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}}{1+h/\mathscr{L}}}\right) & & \displaystyle \nonumber\\ \displaystyle \qquad +\,\unicode[STIX]{x1D707}_{3}+{\displaystyle \frac{\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}}{1+h/\mathscr{L}}}, & 0<Fr\leqslant \unicode[STIX]{x1D6FD}_{\ast }, & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D705}$
is the interpolation power in the intermediate regime. Values of the friction angles
$\unicode[STIX]{x1D705}$
is the interpolation power in the intermediate regime. Values of the friction angles
![]() $\unicode[STIX]{x1D701}_{i}=\tan ^{-1}\unicode[STIX]{x1D707}_{i}$
,
$\unicode[STIX]{x1D701}_{i}=\tan ^{-1}\unicode[STIX]{x1D707}_{i}$
,
![]() $i=1,2,3$
and the flow rule parameters
$i=1,2,3$
and the flow rule parameters
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\mathscr{L}$
measured by Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) together with
$\mathscr{L}$
measured by Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) together with
![]() $\unicode[STIX]{x1D705}$
are given in table 1. This law reduces to the Pouliquen & Forterre (Reference Pouliquen and Forterre2002) friction coefficient for glass beads when
$\unicode[STIX]{x1D705}$
are given in table 1. This law reduces to the Pouliquen & Forterre (Reference Pouliquen and Forterre2002) friction coefficient for glass beads when
![]() $\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6E4}=0$
. The key difference to Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) law is that
$\unicode[STIX]{x1D6E4}=0$
. The key difference to Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) law is that
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
is now constant, rather than being a function of the slope angle, i.e.
$\unicode[STIX]{x1D6FD}_{\ast }$
is now constant, rather than being a function of the slope angle, i.e.
![]() $\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D6FD}h_{\ast }(\unicode[STIX]{x1D701})/h_{stop}(\unicode[STIX]{x1D701})-\unicode[STIX]{x1D6E4}$
, where
$\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D6FD}h_{\ast }(\unicode[STIX]{x1D701})/h_{stop}(\unicode[STIX]{x1D701})-\unicode[STIX]{x1D6E4}$
, where
![]() $h_{\ast }(\unicode[STIX]{x1D701})=(1-a)h_{stop}(\unicode[STIX]{x1D701})+ah_{start}(\unicode[STIX]{x1D701})$
and
$h_{\ast }(\unicode[STIX]{x1D701})=(1-a)h_{stop}(\unicode[STIX]{x1D701})+ah_{start}(\unicode[STIX]{x1D701})$
and
![]() $a$
is a constant. This immediately implies that the friction law (3.10)–(3.12) is valid for all inclinations, not just where both
$a$
is a constant. This immediately implies that the friction law (3.10)–(3.12) is valid for all inclinations, not just where both
![]() $h_{stop}$
and
$h_{stop}$
and
![]() $h_{start}$
exist, i.e. the range
$h_{start}$
exist, i.e. the range
![]() $[\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{2}]$
. This small change therefore represents a significant extension of the range of validity of the theory.
$[\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{2}]$
. This small change therefore represents a significant extension of the range of validity of the theory.
It is important to note that in the static regime (3.12) the friction can take a maximum value of
![]() $\unicode[STIX]{x1D707}_{start}=\unicode[STIX]{x1D707}_{3}+(\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1})/(1+h/\mathscr{L})$
, but any state in which the grains can be held static by a lesser friction is also permissible, as shown in figure 1(b). A general two-dimensional static momentum balance implies that the friction must precisely match the gravitational force pulling the grains downslope as well as any pressure gradients that may be driving them in other directions. As a result
$\unicode[STIX]{x1D707}_{start}=\unicode[STIX]{x1D707}_{3}+(\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1})/(1+h/\mathscr{L})$
, but any state in which the grains can be held static by a lesser friction is also permissible, as shown in figure 1(b). A general two-dimensional static momentum balance implies that the friction must precisely match the gravitational force pulling the grains downslope as well as any pressure gradients that may be driving them in other directions. As a result
![]() $\unicode[STIX]{x1D707}=|\text{tan}\,\unicode[STIX]{x1D701}\boldsymbol{i}-\unicode[STIX]{x1D735}h|$
, where
$\unicode[STIX]{x1D707}=|\text{tan}\,\unicode[STIX]{x1D701}\boldsymbol{i}-\unicode[STIX]{x1D735}h|$
, where
![]() $\boldsymbol{i}$
is the unit vector in the downslope direction and
$\boldsymbol{i}$
is the unit vector in the downslope direction and
![]() $\unicode[STIX]{x1D735}h$
is the gradient of the thickness. This force also needs to be oriented to oppose the net forces in the static momentum balance.
$\unicode[STIX]{x1D735}h$
is the gradient of the thickness. This force also needs to be oriented to oppose the net forces in the static momentum balance.
3.4 Motion of a uniform depth layer
The properties of the friction law (3.10)–(3.12) can be neatly summarized by considering its effect in the case of a uniform flow of constant thickness
![]() $h$
. For this situation the momentum balance (2.2) reduces to
$h$
. For this situation the momentum balance (2.2) reduces to
where the non-dimensional net acceleration
![]() $S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}$
determines whether the flow accelerates (
$S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}$
determines whether the flow accelerates (
![]() $S>0$
), decelerates (
$S>0$
), decelerates (
![]() $S<0$
) or moves at constant speed
$S<0$
) or moves at constant speed
![]() $S=0$
. This can be visualized by plotting the zero contour of the non-dimensional net acceleration
$S=0$
. This can be visualized by plotting the zero contour of the non-dimensional net acceleration
![]() $S$
as a function of the Froude number
$S$
as a function of the Froude number
![]() $Fr$
and the thickness
$Fr$
and the thickness
![]() $h$
as shown in figure 4. In the blue shaded region
$h$
as shown in figure 4. In the blue shaded region
![]() $S$
is positive and the flow is accelerated, which is indicated by arrows pointing to the right, while in the white region the flow is decelerated and the arrows point to the left. On the thick black line between the two domains
$S$
is positive and the flow is accelerated, which is indicated by arrows pointing to the right, while in the white region the flow is decelerated and the arrows point to the left. On the thick black line between the two domains
![]() $S$
is equal to zero and the flow will move at constant speed. It follows that all flows whose thickness is below
$S$
is equal to zero and the flow will move at constant speed. It follows that all flows whose thickness is below
![]() $h_{\ast }$
are decelerated towards the static state, while flows whose thickness is above
$h_{\ast }$
are decelerated towards the static state, while flows whose thickness is above
![]() $h_{start}$
are either accelerated, or decelerated, towards steady-uniform flow. In the hysteretic regime between
$h_{start}$
are either accelerated, or decelerated, towards steady-uniform flow. In the hysteretic regime between
![]() $h_{\ast }$
and
$h_{\ast }$
and
![]() $h_{start}$
initially static layers of grains are stable to small perturbations, because of the decelerative region immediately adjacent to the
$h_{start}$
initially static layers of grains are stable to small perturbations, because of the decelerative region immediately adjacent to the
![]() $h$
axis. The interpolation parameter
$h$
axis. The interpolation parameter
![]() $\unicode[STIX]{x1D705}$
, between the static and dynamic friction regimes, controls the necessary magnitude of finite sized disturbances (represented by an instantaneous Froude number) that are needed to destabilize a static layer of grains. Pouliquen & Forterre (Reference Pouliquen and Forterre2002) chose a value of
$\unicode[STIX]{x1D705}$
, between the static and dynamic friction regimes, controls the necessary magnitude of finite sized disturbances (represented by an instantaneous Froude number) that are needed to destabilize a static layer of grains. Pouliquen & Forterre (Reference Pouliquen and Forterre2002) chose a value of
![]() $\unicode[STIX]{x1D705}=10^{-3}$
, which led to unphysically high sensitivity and under-resolution of the friction law (discussed in § 6.1). The stability of static layers to finite perturbations is better described by order-unity values of
$\unicode[STIX]{x1D705}=10^{-3}$
, which led to unphysically high sensitivity and under-resolution of the friction law (discussed in § 6.1). The stability of static layers to finite perturbations is better described by order-unity values of
![]() $\unicode[STIX]{x1D705}$
that give a roughly linearly decreasing zero contour in figure 4 between
$\unicode[STIX]{x1D705}$
that give a roughly linearly decreasing zero contour in figure 4 between
![]() $Fr=0$
and
$Fr=0$
and
![]() $Fr=\unicode[STIX]{x1D6FD}_{\ast }$
, which forms an upper boundary to an approximately triangular decelerating region between
$Fr=\unicode[STIX]{x1D6FD}_{\ast }$
, which forms an upper boundary to an approximately triangular decelerating region between
![]() $h_{\ast }$
and
$h_{\ast }$
and
![]() $h_{start}$
. Since this region is much wider at the bottom than at the top it is much easier to destabilize material whose thickness is closer to
$h_{start}$
. Since this region is much wider at the bottom than at the top it is much easier to destabilize material whose thickness is closer to
![]() $h_{start}$
than
$h_{start}$
than
![]() $h_{\ast }$
. Once material in this region has been mobilized, however, it will accelerate/decelerate towards steady-uniform flow. A contour plot of the non-dimensional net acceleration
$h_{\ast }$
. Once material in this region has been mobilized, however, it will accelerate/decelerate towards steady-uniform flow. A contour plot of the non-dimensional net acceleration
![]() $S$
, such as in figure 4, therefore provides a useful way of visualizing the hysteretic behaviour of the friction law.
$S$
, such as in figure 4, therefore provides a useful way of visualizing the hysteretic behaviour of the friction law.

Figure 4. The zero contour of the non-dimensional net acceleration
![]() $S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}$
(solid black line) as a function of the Froude number and the flow thickness for the material properties of carborundum. Flows accelerate when
$S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}$
(solid black line) as a function of the Froude number and the flow thickness for the material properties of carborundum. Flows accelerate when
![]() $S>0$
(blue region and right arrows) and decelerate for
$S>0$
(blue region and right arrows) and decelerate for
![]() $S<0$
(white region and left arrows). The solid vertical black line at
$S<0$
(white region and left arrows). The solid vertical black line at
![]() $Fr=0$
shows the multivaluedness of the friction coefficient for stationary material. The region of positive net acceleration reaches
$Fr=0$
shows the multivaluedness of the friction coefficient for stationary material. The region of positive net acceleration reaches
![]() $h=h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange line) at
$h=h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange line) at
![]() $Fr=\unicode[STIX]{x1D6FD}_{\ast }$
(dashed black line), where
$Fr=\unicode[STIX]{x1D6FD}_{\ast }$
(dashed black line), where
![]() $h_{\ast }(\unicode[STIX]{x1D701})$
is a constant multiple (3.7) of
$h_{\ast }(\unicode[STIX]{x1D701})$
is a constant multiple (3.7) of
![]() $h_{stop}(\unicode[STIX]{x1D701})$
(solid red line), and approaches
$h_{stop}(\unicode[STIX]{x1D701})$
(solid red line), and approaches
![]() $h=h_{start}(\unicode[STIX]{x1D701})$
(solid green line) for small Froude numbers. Note the interpolation parameter
$h=h_{start}(\unicode[STIX]{x1D701})$
(solid green line) for small Froude numbers. Note the interpolation parameter
![]() $\unicode[STIX]{x1D705}=1$
produces an approximately linearly decreasing
$\unicode[STIX]{x1D705}=1$
produces an approximately linearly decreasing
![]() $S=0$
contour between
$S=0$
contour between
![]() $Fr=0$
and
$Fr=0$
and
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
. The material properties are given in table 1 and the slope angle-dependent properties in table 2.
$\unicode[STIX]{x1D6FD}_{\ast }$
. The material properties are given in table 1 and the slope angle-dependent properties in table 2.
Note that the qualitative picture in figure 4 is the same for Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction coefficient, in the reduced region of parameter space
![]() $\unicode[STIX]{x1D701}\in (\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{2})$
for which their law is valid, although it will be shown in § 6 to produce deposit layers that are much thicker than
$\unicode[STIX]{x1D701}\in (\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{2})$
for which their law is valid, although it will be shown in § 6 to produce deposit layers that are much thicker than
![]() $h_{stop}$
on shallow inclinations.
$h_{stop}$
on shallow inclinations.
4 Numerical simulations of the deposition process
The governing equations (2.1)–(2.4) together with the modified friction law (3.10)–(3.12) are now solved numerically to investigate how particles are deposited to form a layer of thickness
![]() $h_{stop}$
.
$h_{stop}$
.
4.1 Numerical method
High-resolution shock capturing numerical methods (e.g. Nessyahu & Tadmor Reference Nessyahu and Tadmor1990) are required to solve the standard depth-averaged avalanche equations (e.g. Gray et al.
Reference Gray, Tai and Noelle2003), which are a system of hyperbolic equations. The inclusion of the depth-averaged
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (Gray & Edwards Reference Gray and Edwards2014; Baker et al.
Reference Baker, Barker and Gray2016a
) changes this system into a set of (advection dominated) convection–diffusion equations. Therefore the closely related semi-discrete high-resolution non-oscillatory central schemes of Kurganov & Tadmor (Reference Kurganov and Tadmor2000) are used to solve the equations here. The time stepping is handled with a second-order Runge–Kutta method limited by upper bounds of both a Courant–Friedrichs–Lewy (CFL) number of 0.125 and a maximum step size of
$\unicode[STIX]{x1D707}(I)$
-rheology (Gray & Edwards Reference Gray and Edwards2014; Baker et al.
Reference Baker, Barker and Gray2016a
) changes this system into a set of (advection dominated) convection–diffusion equations. Therefore the closely related semi-discrete high-resolution non-oscillatory central schemes of Kurganov & Tadmor (Reference Kurganov and Tadmor2000) are used to solve the equations here. The time stepping is handled with a second-order Runge–Kutta method limited by upper bounds of both a Courant–Friedrichs–Lewy (CFL) number of 0.125 and a maximum step size of
![]() $10^{-4}$
s (as used by Edwards & Gray Reference Edwards and Gray2015; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017), which helps with the extra constraints on the stable time step beyond the CFL condition due to the source and, in particular, viscous terms. The one-dimensional numerical domain spans
$10^{-4}$
s (as used by Edwards & Gray Reference Edwards and Gray2015; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017), which helps with the extra constraints on the stable time step beyond the CFL condition due to the source and, in particular, viscous terms. The one-dimensional numerical domain spans
![]() $x\in [0,2]$
m and is discretized linearly over 2000 grid points. At the upstream boundary,
$x\in [0,2]$
m and is discretized linearly over 2000 grid points. At the upstream boundary,
![]() $x=0$
, there is no advective or diffusive flux, which is implemented by setting
$x=0$
, there is no advective or diffusive flux, which is implemented by setting
![]() $m=0$
and
$m=0$
and
![]() $\text{d}m/\text{d}x=0$
there. There is free outflow at the downstream boundary
$\text{d}m/\text{d}x=0$
there. There is free outflow at the downstream boundary
![]() $x=2$
m, which is imposed via a linear extrapolation of the values of
$x=2$
m, which is imposed via a linear extrapolation of the values of
![]() $h$
and
$h$
and
![]() $m$
from the final two columns of interior cells. In order to solve the system, the depth-averaged equations (2.1)–(2.3) are written in conservative vector form as
$m$
from the final two columns of interior cells. In order to solve the system, the depth-averaged equations (2.1)–(2.3) are written in conservative vector form as
where
![]() $\boldsymbol{w}=(h,m)^{\text{T}}$
is the vector of conserved variables
$\boldsymbol{w}=(h,m)^{\text{T}}$
is the vector of conserved variables
![]() $h$
and
$h$
and
![]() $m=h\bar{u}$
. The resulting convection flux function
$m=h\bar{u}$
. The resulting convection flux function
![]() $\boldsymbol{f}$
, source term vector
$\boldsymbol{f}$
, source term vector
![]() $\boldsymbol{S}$
and diffusive flux function
$\boldsymbol{S}$
and diffusive flux function
![]() $\boldsymbol{Q}$
are
$\boldsymbol{Q}$
are
 $$\begin{eqnarray}\displaystyle \boldsymbol{f}=\left(\begin{array}{@{}c@{}}m\\ {\displaystyle \frac{m^{2}}{h}}+{\displaystyle \frac{h^{2}}{2}}g\cos \unicode[STIX]{x1D701}\end{array}\right),\quad \boldsymbol{S}=hg\cos \unicode[STIX]{x1D701}\left(\begin{array}{@{}c@{}}0\\ \tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}\end{array}\right),\quad \boldsymbol{Q}=\unicode[STIX]{x1D708}h^{1/2}\left(\begin{array}{@{}c@{}}0\\ {\displaystyle \frac{\unicode[STIX]{x2202}m}{\unicode[STIX]{x2202}x}}-{\displaystyle \frac{m}{h}}{\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}}\end{array}\right), & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{f}=\left(\begin{array}{@{}c@{}}m\\ {\displaystyle \frac{m^{2}}{h}}+{\displaystyle \frac{h^{2}}{2}}g\cos \unicode[STIX]{x1D701}\end{array}\right),\quad \boldsymbol{S}=hg\cos \unicode[STIX]{x1D701}\left(\begin{array}{@{}c@{}}0\\ \tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}\end{array}\right),\quad \boldsymbol{Q}=\unicode[STIX]{x1D708}h^{1/2}\left(\begin{array}{@{}c@{}}0\\ {\displaystyle \frac{\unicode[STIX]{x2202}m}{\unicode[STIX]{x2202}x}}-{\displaystyle \frac{m}{h}}{\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}}\end{array}\right), & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
respectively. The friction
![]() $\unicode[STIX]{x1D707}$
in the source term vector
$\unicode[STIX]{x1D707}$
in the source term vector
![]() $\boldsymbol{S}$
is given by (3.10)–(3.12) with the material parameter values given in table 1.
$\boldsymbol{S}$
is given by (3.10)–(3.12) with the material parameter values given in table 1.

Figure 5. The flow thickness
![]() $h$
and downslope velocity
$h$
and downslope velocity
![]() $u(x,z,t)$
at a sequence of time steps (a–d) for a slope inclined at
$u(x,z,t)$
at a sequence of time steps (a–d) for a slope inclined at
![]() $\unicode[STIX]{x1D701}=36.3^{\circ }$
and with an initially uniform static layer of initial thickness
$\unicode[STIX]{x1D701}=36.3^{\circ }$
and with an initially uniform static layer of initial thickness
![]() $h(x,0)=2.4$
mm, which is
$h(x,0)=2.4$
mm, which is
![]() $0.5$
mm greater than
$0.5$
mm greater than
![]() $h_{start}(36.3^{\circ })$
(solid green line). The filled region shows the thickness and the contour scale within it denotes the velocity, which is reconstructed from the depth-averaged downslope velocity
$h_{start}(36.3^{\circ })$
(solid green line). The filled region shows the thickness and the contour scale within it denotes the velocity, which is reconstructed from the depth-averaged downslope velocity
![]() $\bar{u}(x,t)$
by assuming an exponential profile (4.3) through the avalanche depth. There is no further inflow at
$\bar{u}(x,t)$
by assuming an exponential profile (4.3) through the avalanche depth. There is no further inflow at
![]() $x=0$
, but there is free outflow at the downstream boundary. A travelling wave at the rear of the steady-uniform flow region (dash-dotted black line) passes through the material at a constant wavespeed that is greater than the surface velocity. This is followed by a slightly slower travelling deposition wave (between the dashed black line and the dotted black line) that connects the static deposit and the transition thickness
$x=0$
, but there is free outflow at the downstream boundary. A travelling wave at the rear of the steady-uniform flow region (dash-dotted black line) passes through the material at a constant wavespeed that is greater than the surface velocity. This is followed by a slightly slower travelling deposition wave (between the dashed black line and the dotted black line) that connects the static deposit and the transition thickness
![]() $h_{\ast }$
(solid orange line). These waves catch up with surface particles, which are shown with light blue circular markers, and they are deposited on the surface of the final deposit layer that has a thickness of approximately
$h_{\ast }$
(solid orange line). These waves catch up with surface particles, which are shown with light blue circular markers, and they are deposited on the surface of the final deposit layer that has a thickness of approximately
![]() $h_{stop}$
(solid red line). The material properties are given in table 1 and there is a movie of the simulation in the online supplementary material (movie 1).
$h_{stop}$
(solid red line). The material properties are given in table 1 and there is a movie of the simulation in the online supplementary material (movie 1).
4.2 Simulating the formation of an
 $h_{stop}$
layer
$h_{stop}$
layer
A numerical simulation of the formation of an
![]() $h_{stop}$
layer on a slope of
$h_{stop}$
layer on a slope of
![]() $36.3^{\circ }$
and with a static initial layer thickness
$36.3^{\circ }$
and with a static initial layer thickness
![]() $h(x,0)=h_{start}(36.3^{\circ })+0.5$
mm
$h(x,0)=h_{start}(36.3^{\circ })+0.5$
mm
![]() $=2.4$
mm, which matches the experiment of § 1, is shown in figure 5. When the simulation commences this layer accelerates towards steady-uniform flow and at its trailing edge a non-uniform flow develops. The two-dimensional downslope velocity field is reconstructed from the depth-averaged velocity
$=2.4$
mm, which matches the experiment of § 1, is shown in figure 5. When the simulation commences this layer accelerates towards steady-uniform flow and at its trailing edge a non-uniform flow develops. The two-dimensional downslope velocity field is reconstructed from the depth-averaged velocity
![]() $\bar{u}(x,t)$
by assuming an exponential velocity profile (Wiederseiner et al.
Reference Wiederseiner, Andreini, Epely-Chauvin, Moser, Monnereau, Gray and Ancey2011; Kamrin & Henann Reference Kamrin and Henann2015),
$\bar{u}(x,t)$
by assuming an exponential velocity profile (Wiederseiner et al.
Reference Wiederseiner, Andreini, Epely-Chauvin, Moser, Monnereau, Gray and Ancey2011; Kamrin & Henann Reference Kamrin and Henann2015),
where the constant
![]() $\unicode[STIX]{x1D706}=1.4$
is chosen to match surface velocities. As the flow accelerates, a small pile of material is formed near the inflow due to frictional hysteresis, but by 40–50 cm downstream a uniform deposit is left behind, whose thickness
$\unicode[STIX]{x1D706}=1.4$
is chosen to match surface velocities. As the flow accelerates, a small pile of material is formed near the inflow due to frictional hysteresis, but by 40–50 cm downstream a uniform deposit is left behind, whose thickness
![]() $h_{deposit}(36.3^{\circ })\approx h_{stop}(36.3^{\circ })$
. Indeed, Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) chose the transition Froude number
$h_{deposit}(36.3^{\circ })\approx h_{stop}(36.3^{\circ })$
. Indeed, Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) chose the transition Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }=0.466$
precisely because it produced the correct deposit layer thickness in the range of inclinations that they studied.
$\unicode[STIX]{x1D6FD}_{\ast }=0.466$
precisely because it produced the correct deposit layer thickness in the range of inclinations that they studied.
The thick steady-uniform flow and the thinner static deposit are connected by two travelling waves, as shown by the diagonal lines in figure 5. The first travelling wave marks the rear of the region of steady-uniform flow and moves slightly quicker than the second wave, which rapidly deposits material and connects the minimum steady-uniform flow thickness
![]() $h_{\ast }$
with the final deposit. In between the two waves is a slowly expanding region, within which the grains slow down and the flow thins from the steady-uniform value to
$h_{\ast }$
with the final deposit. In between the two waves is a slowly expanding region, within which the grains slow down and the flow thins from the steady-uniform value to
![]() $h_{\ast }$
. The speed of the second wave is calculated to be
$h_{\ast }$
. The speed of the second wave is calculated to be
![]() $0.22$
m s
$0.22$
m s
![]() $^{-1}$
, which is in good agreement with the experimentally measured value of
$^{-1}$
, which is in good agreement with the experimentally measured value of
![]() $0.24$
m s
$0.24$
m s
![]() $^{-1}$
in § 1, for the same steady-uniform flow thickness and slope angle. Both travelling waves actually move faster than any of the grains, so a typical surface particle (shown in figure 5 by light blue markers) will initially accelerate and then travel downslope at constant speed, until it is caught up first by the steady-uniform flow wave and then by the rapid deposition wave. As the first wave passes by, the flow thins and the particles slow down, before the second travelling wave quickly brings the grains to rest on the surface of the
$^{-1}$
in § 1, for the same steady-uniform flow thickness and slope angle. Both travelling waves actually move faster than any of the grains, so a typical surface particle (shown in figure 5 by light blue markers) will initially accelerate and then travel downslope at constant speed, until it is caught up first by the steady-uniform flow wave and then by the rapid deposition wave. As the first wave passes by, the flow thins and the particles slow down, before the second travelling wave quickly brings the grains to rest on the surface of the
![]() $h_{stop}$
deposit. An animation of the process is available in the online supplementary material (https://doi.org/10.1017/jfm.2019.517).
$h_{stop}$
deposit. An animation of the process is available in the online supplementary material (https://doi.org/10.1017/jfm.2019.517).

Figure 6. Space–time
![]() $(x,t)$
plot showing the surface velocity
$(x,t)$
plot showing the surface velocity
![]() $u(x,h,t)$
for a flow at
$u(x,h,t)$
for a flow at
![]() $\unicode[STIX]{x1D701}=36.3^{\circ }$
and with an initial stationary layer of thickness
$\unicode[STIX]{x1D701}=36.3^{\circ }$
and with an initial stationary layer of thickness
![]() $h(x,0)=h_{start}(36.3^{\circ })+0.5~\text{mm}=2.4$
mm. Individual surface particles are tracked (light blue lines) to visualize the particle trajectories through the travelling wave at the back of the steady-uniform region (dash-dotted black line), the slowly expanding region and the subsequent travelling deposition wave (between the black dotted and dashed lines). The vertical lines indicate stationary material and diagonal lines represent moving grains. The first travelling wave moves slightly faster than the second travelling wave, which rapidly deposits the grains once they have been slowed down in the expanding region (between the dotted and dash-dotted black lines). The material properties are given in table 1.
$h(x,0)=h_{start}(36.3^{\circ })+0.5~\text{mm}=2.4$
mm. Individual surface particles are tracked (light blue lines) to visualize the particle trajectories through the travelling wave at the back of the steady-uniform region (dash-dotted black line), the slowly expanding region and the subsequent travelling deposition wave (between the black dotted and dashed lines). The vertical lines indicate stationary material and diagonal lines represent moving grains. The first travelling wave moves slightly faster than the second travelling wave, which rapidly deposits the grains once they have been slowed down in the expanding region (between the dotted and dash-dotted black lines). The material properties are given in table 1.
The downslope surface velocity can also be visualized as a space–time plot as shown in figure 6. Since the surface velocity contours are separated at the friction transition thickness into regions of two slightly different gradients, this gives further support to the observation that the deposition process occurs by way of two travelling waves that move downslope at slightly different constant speeds and are connected by a slowly expanding region. A series of surface particle trajectories are also plotted on top of the contours in figure 6 and these all have the same shape. In the region of steady-uniform flow they propagate downslope with a constant surface velocity of
![]() $0.22$
m s
$0.22$
m s
![]() $^{-1}$
, but as the deposition wave approaches with a slightly faster speed they slow down and stop to form vertical parallel lines. This agrees well with the experimental observations from the space–time plot in figure 2.
$^{-1}$
, but as the deposition wave approaches with a slightly faster speed they slow down and stop to form vertical parallel lines. This agrees well with the experimental observations from the space–time plot in figure 2.
Setting
![]() $\unicode[STIX]{x1D712}=1$
in the momentum balance (2.2), which is equivalent to an exponential velocity profile (4.3) with
$\unicode[STIX]{x1D712}=1$
in the momentum balance (2.2), which is equivalent to an exponential velocity profile (4.3) with
![]() $\unicode[STIX]{x1D706}\rightarrow 0$
, results in a surface velocity of
$\unicode[STIX]{x1D706}\rightarrow 0$
, results in a surface velocity of
![]() $0.12$
m s
$0.12$
m s
![]() $^{-1}$
that is equal to the depth-averaged steady-uniform flow velocity. Choosing
$^{-1}$
that is equal to the depth-averaged steady-uniform flow velocity. Choosing
![]() $\unicode[STIX]{x1D712}\approx 1.16$
produces a velocity reconstruction that is in better agreement with the experimentally measured surface velocity.
$\unicode[STIX]{x1D712}\approx 1.16$
produces a velocity reconstruction that is in better agreement with the experimentally measured surface velocity.
4.3 Deposit layer depths at different inclination angles

Figure 7. A series of numerical simulations showing the evolving flow thickness starting from
![]() $h(x,0)=h_{\ast }(\unicode[STIX]{x1D701})$
(dashed black line) at slope angles (a)
$h(x,0)=h_{\ast }(\unicode[STIX]{x1D701})$
(dashed black line) at slope angles (a)
![]() $\unicode[STIX]{x1D701}=31.9^{\circ }$
, (b)
$\unicode[STIX]{x1D701}=31.9^{\circ }$
, (b)
![]() $\unicode[STIX]{x1D701}=34.1^{\circ }$
, (c)
$\unicode[STIX]{x1D701}=34.1^{\circ }$
, (c)
![]() $\unicode[STIX]{x1D701}=36.3^{\circ }$
, (d)
$\unicode[STIX]{x1D701}=36.3^{\circ }$
, (d)
![]() $\unicode[STIX]{x1D701}=38.5^{\circ }$
and (e)
$\unicode[STIX]{x1D701}=38.5^{\circ }$
and (e)
![]() $\unicode[STIX]{x1D701}=40.7^{\circ }$
. In each panel the flow thickness is shown at one second intervals by light blue lines and the blue shading increases in intensity with increasing time. The initial layer depths are equal to the thickness of the friction law transition
$\unicode[STIX]{x1D701}=40.7^{\circ }$
. In each panel the flow thickness is shown at one second intervals by light blue lines and the blue shading increases in intensity with increasing time. The initial layer depths are equal to the thickness of the friction law transition
![]() $h_{\ast }$
(solid orange lines), which are less than
$h_{\ast }$
(solid orange lines), which are less than
![]() $h_{start}(\unicode[STIX]{x1D701})$
(solid green lines). An initial momentum
$h_{start}(\unicode[STIX]{x1D701})$
(solid green lines). An initial momentum
![]() $m(x,0)=h_{\ast }\bar{u}_{\ast }$
is therefore imposed in order to start the flow, where
$m(x,0)=h_{\ast }\bar{u}_{\ast }$
is therefore imposed in order to start the flow, where
![]() $\bar{u}_{\ast }=\bar{u}_{\infty }$
is given by the steady-uniform flow velocity relation (4.4). As the deposition wave travels through the system all the flows eventually leave a deposit that is close to
$\bar{u}_{\ast }=\bar{u}_{\infty }$
is given by the steady-uniform flow velocity relation (4.4). As the deposition wave travels through the system all the flows eventually leave a deposit that is close to
![]() $h_{stop}(\unicode[STIX]{x1D701})$
(solid red lines). The material properties are given in table 1 and the slope angle-dependent properties in table 2. Movies of the full simulations are available in the online supplementary material (movies 2–6).
$h_{stop}(\unicode[STIX]{x1D701})$
(solid red lines). The material properties are given in table 1 and the slope angle-dependent properties in table 2. Movies of the full simulations are available in the online supplementary material (movies 2–6).

Figure 8. A series of numerical simulations showing the evolving flow thickness starting from
![]() $h(x,0)=h_{start}(\unicode[STIX]{x1D701})+0.1~\text{mm}$
(dashed black line) at slope angles (a)
$h(x,0)=h_{start}(\unicode[STIX]{x1D701})+0.1~\text{mm}$
(dashed black line) at slope angles (a)
![]() $\unicode[STIX]{x1D701}=33.0^{\circ }$
, (b)
$\unicode[STIX]{x1D701}=33.0^{\circ }$
, (b)
![]() $\unicode[STIX]{x1D701}=35.2^{\circ }$
, (c)
$\unicode[STIX]{x1D701}=35.2^{\circ }$
, (c)
![]() $\unicode[STIX]{x1D701}=37.4^{\circ }$
, (d)
$\unicode[STIX]{x1D701}=37.4^{\circ }$
, (d)
![]() $\unicode[STIX]{x1D701}=39.6^{\circ }$
and (e)
$\unicode[STIX]{x1D701}=39.6^{\circ }$
and (e)
![]() $\unicode[STIX]{x1D701}=41.8^{\circ }$
. In each panel the flow thickness is shown at one second intervals by light blue lines and the blue shading increases in intensity with increasing time. All of the initially static layers have a thickness
$\unicode[STIX]{x1D701}=41.8^{\circ }$
. In each panel the flow thickness is shown at one second intervals by light blue lines and the blue shading increases in intensity with increasing time. All of the initially static layers have a thickness
![]() $h>h_{start}(\unicode[STIX]{x1D701})$
(solid green lines) and so they gain momentum. As the deposition wave travels through the system all the flows eventually leave a deposit that is close to
$h>h_{start}(\unicode[STIX]{x1D701})$
(solid green lines) and so they gain momentum. As the deposition wave travels through the system all the flows eventually leave a deposit that is close to
![]() $h_{stop}(\unicode[STIX]{x1D701})$
(solid red lines). The friction law has a transition thickness
$h_{stop}(\unicode[STIX]{x1D701})$
(solid red lines). The friction law has a transition thickness
![]() $h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange lines). The material properties are given in table 1 and the slope angle-dependent properties in table 2. Movies of the full simulations are available in the online supplementary material (movies 7–11).
$h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange lines). The material properties are given in table 1 and the slope angle-dependent properties in table 2. Movies of the full simulations are available in the online supplementary material (movies 7–11).
The friction law (3.10)–(3.12) does not just produce the correct deposit depth at one inclination angle and static layer thickness, but it does so for various initial conditions in the entire range of angles at which
![]() $h_{stop}$
layers form with carborundum particles. Figure 7 shows a series of simulations at inclinations ranging from
$h_{stop}$
layers form with carborundum particles. Figure 7 shows a series of simulations at inclinations ranging from
![]() $31.9^{\circ }$
to
$31.9^{\circ }$
to
![]() $40.7^{\circ }$
that start with a static layer of thickness
$40.7^{\circ }$
that start with a static layer of thickness
![]() $h(x,0)=h_{\ast }(\unicode[STIX]{x1D701})$
. Since the initial thicknesses are less than
$h(x,0)=h_{\ast }(\unicode[STIX]{x1D701})$
. Since the initial thicknesses are less than
![]() $h_{start}$
, an initial momentum
$h_{start}$
, an initial momentum
![]() $m(x,0)=h(x,0)\bar{u}(x,0)$
must be imposed to initiate a flow. The initial velocity is set to
$m(x,0)=h(x,0)\bar{u}(x,0)$
must be imposed to initiate a flow. The initial velocity is set to
![]() $\bar{u}(x,0)=\bar{u}_{\infty }$
, where in general, for a flow of uniform thickness
$\bar{u}(x,0)=\bar{u}_{\infty }$
, where in general, for a flow of uniform thickness
![]() $h(x,0)=h_{\infty }$
, the dynamic friction regime (3.10) implies that the steady uniform velocity is
$h(x,0)=h_{\infty }$
, the dynamic friction regime (3.10) implies that the steady uniform velocity is
Each plot in figure 7 shows a time sequence of the free surface at one second intervals, so the complete evolution of the formation of the deposit can be visualized by a shading that increases in intensity with increasing time. All the simulations show the rapid development of a travelling wave that directly connects the friction transition at
![]() $h=h_{\ast }$
to a deposit depth that is very close to
$h=h_{\ast }$
to a deposit depth that is very close to
![]() $h_{stop}$
, as shown in figure 7.
$h_{stop}$
, as shown in figure 7.
Figure 8 shows a series of simulations at inclinations ranging from
![]() $33.0$
to
$33.0$
to
![]() $41.8^{\circ }$
that start with a static layer
$41.8^{\circ }$
that start with a static layer
![]() $h(x,0)=h_{start}(\unicode[STIX]{x1D701})+0.1$
mm, which therefore flows spontaneously. All of these flows leave a uniform thickness deposit by about 30–50 cm downstream that is very close to the correct experimental
$h(x,0)=h_{start}(\unicode[STIX]{x1D701})+0.1$
mm, which therefore flows spontaneously. All of these flows leave a uniform thickness deposit by about 30–50 cm downstream that is very close to the correct experimental
![]() $h_{stop}$
value, as shown in figure 9. Indeed, the mean deviation of
$h_{stop}$
value, as shown in figure 9. Indeed, the mean deviation of
![]() $h_{deposit}$
from
$h_{deposit}$
from
![]() $h_{stop}$
for all simulations is less than
$h_{stop}$
for all simulations is less than
![]() $3\,\%$
, whilst the maximum is less than
$3\,\%$
, whilst the maximum is less than
![]() $5\,\%$
. At low inclination angles (figure 8
b) there are clearly two travelling waves that are separated by an expanding region, but as the inclination increases (figure 8
c–e) the first and second waves move at almost the same speed, so the deposition wave as a whole looks like the back of the erosion–deposition waves observed by Edwards & Gray (Reference Edwards and Gray2015). It is also evident from figure 8 that the time taken to reach a steady travelling wave state, as well as the speed of the wave, both decrease with increasing slope angle. The travelling waves will be studied in more detail in § 5.
$5\,\%$
. At low inclination angles (figure 8
b) there are clearly two travelling waves that are separated by an expanding region, but as the inclination increases (figure 8
c–e) the first and second waves move at almost the same speed, so the deposition wave as a whole looks like the back of the erosion–deposition waves observed by Edwards & Gray (Reference Edwards and Gray2015). It is also evident from figure 8 that the time taken to reach a steady travelling wave state, as well as the speed of the wave, both decrease with increasing slope angle. The travelling waves will be studied in more detail in § 5.

Figure 9. The deposit thickness (orange squares) left by simulations starting from initial thickness
![]() $h(x,0)=h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange line), as shown in figure 7, and the deposit thickness (green squares) left by simulations starting from
$h(x,0)=h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange line), as shown in figure 7, and the deposit thickness (green squares) left by simulations starting from
![]() $h(x,0)=h_{start}(\unicode[STIX]{x1D701})$
(solid green line), as shown in figure 8. All the deposit thicknesses are in good agreement with
$h(x,0)=h_{start}(\unicode[STIX]{x1D701})$
(solid green line), as shown in figure 8. All the deposit thicknesses are in good agreement with
![]() $h_{stop}(\unicode[STIX]{x1D701})$
(solid red line). Simulations on a slope inclined at
$h_{stop}(\unicode[STIX]{x1D701})$
(solid red line). Simulations on a slope inclined at
![]() $\unicode[STIX]{x1D701}=36.3^{\circ }$
with various initial thicknesses (black circles) greater than
$\unicode[STIX]{x1D701}=36.3^{\circ }$
with various initial thicknesses (black circles) greater than
![]() $h_{start}(36.3^{\circ })$
also all collapse (downward arrow) to leave deposits (black squares) close
$h_{start}(36.3^{\circ })$
also all collapse (downward arrow) to leave deposits (black squares) close
![]() $h_{stop}(36.3^{\circ })$
and are in good agreement with one another. An example of one of these simulations, for
$h_{stop}(36.3^{\circ })$
and are in good agreement with one another. An example of one of these simulations, for
![]() $h(x,0)=h_{start}(36.3^{\circ })+0.5$
mm, is shown in figure 5. The material properties are given in table 1 and the various slope angle-dependent properties for the initially uniform layer simulations in table 2.
$h(x,0)=h_{start}(36.3^{\circ })+0.5$
mm, is shown in figure 5. The material properties are given in table 1 and the various slope angle-dependent properties for the initially uniform layer simulations in table 2.
An investigation into how the deposit depth is affected by changing the thickness of the initial layers is also crucial to our understanding of the deposition process. It has already been shown that the numerical deposits closely agree with the experimental value of
![]() $h_{stop}$
for both
$h_{stop}$
for both
![]() $h(x,0)=h_{\ast }(\unicode[STIX]{x1D701})$
and
$h(x,0)=h_{\ast }(\unicode[STIX]{x1D701})$
and
![]() $h(x,0)=h_{start}(\unicode[STIX]{x1D701})+0.1$
mm for the whole range of valid inclinations. Figure 9 also shows the results of a series of simulations with different initial layer thicknesses on a fixed slope inclination of
$h(x,0)=h_{start}(\unicode[STIX]{x1D701})+0.1$
mm for the whole range of valid inclinations. Figure 9 also shows the results of a series of simulations with different initial layer thicknesses on a fixed slope inclination of
![]() $\unicode[STIX]{x1D701}=36.3^{\circ }$
. All of these simulations, of which figure 5 is one example, produce a deposit depth that is within
$\unicode[STIX]{x1D701}=36.3^{\circ }$
. All of these simulations, of which figure 5 is one example, produce a deposit depth that is within
![]() $3\,\%$
of the correct experimental value for
$3\,\%$
of the correct experimental value for
![]() $h_{stop}(36.3^{\circ })$
. This strongly suggests that, at least for a system of carborundum particles on a bed of glass beads, a universal
$h_{stop}(36.3^{\circ })$
. This strongly suggests that, at least for a system of carborundum particles on a bed of glass beads, a universal
![]() $h_{stop}$
layer thickness develops due to the combination of two travelling waves that move at slightly different speeds and are connected by a slowly expanding region between them. The empirical deposit depth
$h_{stop}$
layer thickness develops due to the combination of two travelling waves that move at slightly different speeds and are connected by a slowly expanding region between them. The empirical deposit depth
![]() $h_{stop}$
is therefore insensitive to the initial conditions, since thick initial layers are able to connect to the top of a travelling deposition wave at
$h_{stop}$
is therefore insensitive to the initial conditions, since thick initial layers are able to connect to the top of a travelling deposition wave at
![]() $h_{\ast }$
, which then leaves the correct deposit thickness. Such solutions may not always exist for other granular materials, hence the form of the travelling deposition waves suggest that, in general, the most robust method of recovering the experimental deposit depth is by way of a steady-uniform flow at the minimum possible thickness
$h_{\ast }$
, which then leaves the correct deposit thickness. Such solutions may not always exist for other granular materials, hence the form of the travelling deposition waves suggest that, in general, the most robust method of recovering the experimental deposit depth is by way of a steady-uniform flow at the minimum possible thickness
![]() $h_{\ast }$
.
$h_{\ast }$
.
Changing the shape factor from
![]() $\unicode[STIX]{x1D712}=1$
, as used here, to
$\unicode[STIX]{x1D712}=1$
, as used here, to
![]() $\unicode[STIX]{x1D712}=1.16$
that results from the exponential velocity profile (4.3) with
$\unicode[STIX]{x1D712}=1.16$
that results from the exponential velocity profile (4.3) with
![]() $\unicode[STIX]{x1D706}=1.4$
, has little effect on the deposit depth, despite changing the reconstructed surface velocity. For typical parameters, the thickness of the layer that is deposited is still within
$\unicode[STIX]{x1D706}=1.4$
, has little effect on the deposit depth, despite changing the reconstructed surface velocity. For typical parameters, the thickness of the layer that is deposited is still within
![]() $2\,\%$
of the experimental value of
$2\,\%$
of the experimental value of
![]() $h_{stop}$
when calculated with
$h_{stop}$
when calculated with
![]() $\unicode[STIX]{x1D712}=1.16$
.
$\unicode[STIX]{x1D712}=1.16$
.
4.4 Simulation of the experimental procedure to measure
 $h_{stop}$
and
$h_{stop}$
and
 $h_{start}$
$h_{start}$
The experimental procedure for determining the
![]() $h_{stop}(\unicode[STIX]{x1D701})$
and
$h_{stop}(\unicode[STIX]{x1D701})$
and
![]() $h_{start}(\unicode[STIX]{x1D701})$
functions, which was discussed in the introduction and sketched in figure 1(a), is now simulated numerically to further test the modified friction law proposed here. The simulation starts at a shallow angle
$h_{start}(\unicode[STIX]{x1D701})$
functions, which was discussed in the introduction and sketched in figure 1(a), is now simulated numerically to further test the modified friction law proposed here. The simulation starts at a shallow angle
![]() $\unicode[STIX]{x1D701}=32.5^{\circ }$
. This is below
$\unicode[STIX]{x1D701}=32.5^{\circ }$
. This is below
![]() $\unicode[STIX]{x1D701}_{3}$
, where
$\unicode[STIX]{x1D701}_{3}$
, where
![]() $h_{start}$
is undefined, and where there is no thickness above which a static layer can spontaneously start to flow downslope. However, with the definition of
$h_{start}$
is undefined, and where there is no thickness above which a static layer can spontaneously start to flow downslope. However, with the definition of
![]() $h_{\ast }$
as a multiple of
$h_{\ast }$
as a multiple of
![]() $h_{stop}$
proposed in (3.7) it is still possible to have steady-uniform flows in the range
$h_{stop}$
proposed in (3.7) it is still possible to have steady-uniform flows in the range
![]() $[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{3}]$
provided there is a sufficient initial perturbation. The simulation is therefore started with a layer of thickness
$[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{3}]$
provided there is a sufficient initial perturbation. The simulation is therefore started with a layer of thickness
![]() $h(x,0)=h_{\ast }(32.5^{\circ })=8.1$
mm that is given the corresponding minimum steady-uniform flow velocity that is possible at that inclination, according to (4.4) with
$h(x,0)=h_{\ast }(32.5^{\circ })=8.1$
mm that is given the corresponding minimum steady-uniform flow velocity that is possible at that inclination, according to (4.4) with
![]() $h_{\infty }=h(x,0)$
. It is important to note that the modified friction law (3.10)–(3.12) with constant
$h_{\infty }=h(x,0)$
. It is important to note that the modified friction law (3.10)–(3.12) with constant
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
is crucial, since it allows
$\unicode[STIX]{x1D6FD}_{\ast }$
is crucial, since it allows
![]() $h_{\ast }$
to be defined for all slope angles
$h_{\ast }$
to be defined for all slope angles
![]() $\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]$
. In the case of Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law with non-constant
$\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]$
. In the case of Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law with non-constant
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
, the minimum steady-uniform flow thickness
$\unicode[STIX]{x1D6FD}_{\ast }$
, the minimum steady-uniform flow thickness
![]() $h_{\ast }(\unicode[STIX]{x1D701})$
is not defined for
$h_{\ast }(\unicode[STIX]{x1D701})$
is not defined for
![]() $\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{3}]$
, since
$\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{3}]$
, since
![]() $h_{start}$
is undefined, and the model therefore fails to predict the initial collapse.
$h_{start}$
is undefined, and the model therefore fails to predict the initial collapse.
Since there is no further mass supply at the inflow, a deposition wave forms at the trailing edge of the steady-uniform flow and a deposit that is close to
![]() $h_{stop}(32.5^{\circ })$
is left on the chute. This static numerical deposit is then used as the initial condition for the next flow. To induce it, the chute inclination is increased progressively in
$h_{stop}(32.5^{\circ })$
is left on the chute. This static numerical deposit is then used as the initial condition for the next flow. To induce it, the chute inclination is increased progressively in
![]() $0.1^{\circ }$
increments until the entire layer, ignoring small movements in the thicker transient regions, gains momentum and collapses again to leave an even thinner deposit at a steeper slope angle. The process is repeated for the collapse of an entire static layer at five different inclination angles to produce a staircase of numerically predicted
$0.1^{\circ }$
increments until the entire layer, ignoring small movements in the thicker transient regions, gains momentum and collapses again to leave an even thinner deposit at a steeper slope angle. The process is repeated for the collapse of an entire static layer at five different inclination angles to produce a staircase of numerically predicted
![]() $h_{stop}$
and
$h_{stop}$
and
![]() $h_{start}$
values, shown in figure 10. The angle at which the layer collapses and the theoretical value of
$h_{start}$
values, shown in figure 10. The angle at which the layer collapses and the theoretical value of
![]() $h_{start}(\unicode[STIX]{x1D701})$
are in good agreement for each collapse. Furthermore, the mean deposit thickness
$h_{start}(\unicode[STIX]{x1D701})$
are in good agreement for each collapse. Furthermore, the mean deposit thickness
![]() $h_{deposit}$
, taken between 1 m and 2 m downslope at the end of the simulations when all of the material has come to rest, is also shown in figure 10 to be approximately equal to
$h_{deposit}$
, taken between 1 m and 2 m downslope at the end of the simulations when all of the material has come to rest, is also shown in figure 10 to be approximately equal to
![]() $h_{stop}(\unicode[STIX]{x1D701})$
for each of the slope angles. This is the first time that anyone has successfully been able to model this complex experimental procedure and it is remarkable that the modified friction law, with an intermediate/dynamic transition at a fixed value of
$h_{stop}(\unicode[STIX]{x1D701})$
for each of the slope angles. This is the first time that anyone has successfully been able to model this complex experimental procedure and it is remarkable that the modified friction law, with an intermediate/dynamic transition at a fixed value of
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
, is able to predict it so accurately. In § 6 it will be shown that all existing non-monotonic friction laws are unable to predict this behaviour, because either they (i) produce the incorrect deposit layer depth or (ii) are unable to hold grains static on the chute as the inclination is increased towards
$\unicode[STIX]{x1D6FD}_{\ast }$
, is able to predict it so accurately. In § 6 it will be shown that all existing non-monotonic friction laws are unable to predict this behaviour, because either they (i) produce the incorrect deposit layer depth or (ii) are unable to hold grains static on the chute as the inclination is increased towards
![]() $\unicode[STIX]{x1D701}_{start}$
.
$\unicode[STIX]{x1D701}_{start}$
.

Figure 10. Numerical simulation of the experimental procedure to determine the
![]() $h_{stop}$
(black squares) and
$h_{stop}$
(black squares) and
![]() $h_{start}$
(black circles) curves for the material properties of carborundum. The first simulation requires perturbing a uniform layer of thickness
$h_{start}$
(black circles) curves for the material properties of carborundum. The first simulation requires perturbing a uniform layer of thickness
![]() $h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange line), since no layer is thick enough to flow spontaneously for shallow inclinations
$h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange line), since no layer is thick enough to flow spontaneously for shallow inclinations
![]() $\unicode[STIX]{x1D701}<\unicode[STIX]{x1D701}_{3}$
. Imposing a steady-uniform flow causes this entire layer to collapse and leave a thinner deposit (leftmost downward arrow). The slope is then progressively inclined in
$\unicode[STIX]{x1D701}<\unicode[STIX]{x1D701}_{3}$
. Imposing a steady-uniform flow causes this entire layer to collapse and leave a thinner deposit (leftmost downward arrow). The slope is then progressively inclined in
![]() $0.1^{\circ }$
increments until this static layer spontaneously begins to flow (rightward arrows). The inclination angle at which the collapse occurs is found to be in good agreement with
$0.1^{\circ }$
increments until this static layer spontaneously begins to flow (rightward arrows). The inclination angle at which the collapse occurs is found to be in good agreement with
![]() $h_{start}(\unicode[STIX]{x1D701})$
(solid green line). Each successive flow leaves an increasingly thinner deposit (downward arrows), whose thickness is in good agreement with
$h_{start}(\unicode[STIX]{x1D701})$
(solid green line). Each successive flow leaves an increasingly thinner deposit (downward arrows), whose thickness is in good agreement with
![]() $h_{stop}(\unicode[STIX]{x1D701})$
(solid red line). The material properties are given in table 1 and the various slope angle-dependent properties for the initially uniform layer simulations in table 2.
$h_{stop}(\unicode[STIX]{x1D701})$
(solid red line). The material properties are given in table 1 and the various slope angle-dependent properties for the initially uniform layer simulations in table 2.
5 Inviscid travelling deposition waves
The experiments in figure 2 and the numerical simulations in figures 5–8 strongly suggest that two travelling waves are responsible for the deposit of an
![]() $h_{stop}$
layer. The first travelling wave marks the back of the steady-uniform flow region, while the second develops at the tail of the flow and connects the minimum steady-uniform flow thickness
$h_{stop}$
layer. The first travelling wave marks the back of the steady-uniform flow region, while the second develops at the tail of the flow and connects the minimum steady-uniform flow thickness
![]() $h_{\ast }$
to the final deposit depth. To study this wave in greater detail, the inviscid (
$h_{\ast }$
to the final deposit depth. To study this wave in greater detail, the inviscid (
![]() $\unicode[STIX]{x1D708}=0$
) depth-averaged mass and momentum equations (2.1)–(2.2) are now transformed to a frame moving downslope with speed
$\unicode[STIX]{x1D708}=0$
) depth-averaged mass and momentum equations (2.1)–(2.2) are now transformed to a frame moving downslope with speed
![]() $u_{w}$
, by making the coordinate transformation
$u_{w}$
, by making the coordinate transformation
![]() $\unicode[STIX]{x1D70F}=t$
and
$\unicode[STIX]{x1D70F}=t$
and
![]() $\unicode[STIX]{x1D709}=x-u_{w}t$
, to give
$\unicode[STIX]{x1D709}=x-u_{w}t$
, to give
respectively, where
![]() $S$
is defined in (2.3). Assuming a steady solution in the moving frame the system reduces to a pair of ordinary differential equations (ODEs),
$S$
is defined in (2.3). Assuming a steady solution in the moving frame the system reduces to a pair of ordinary differential equations (ODEs),
Integrating the mass balance ODE (5.3) subject to the condition that the depth-averaged velocity is zero in a stationary deposit of as yet unknown constant thickness
![]() $h_{0}$
, implies that the depth-averaged velocity is a function of the frame speed and the flow thickness
$h_{0}$
, implies that the depth-averaged velocity is a function of the frame speed and the flow thickness
Substituting the depth-averaged velocity (5.5) into the momentum balance (5.4) reduces the problem to a single ODE for the flow thickness
The ODE (5.6) is singular at a critical thickness
![]() $h_{c}$
where the denominator is zero. This allows the unknown deposit thickness
$h_{c}$
where the denominator is zero. This allows the unknown deposit thickness
![]() $h_{0}$
to be expressed in terms of
$h_{0}$
to be expressed in terms of
![]() $h_{c}$
as
$h_{c}$
as
and hence the ODE (5.6) may be written as
which can be solved numerically for a given value of
![]() $h_{c}$
.
$h_{c}$
.
It is possible to construct a range of travelling-wave solutions with different structures that connect a static deposit layer of thickness
![]() $h_{0}$
to a steady-uniform flow of thickness
$h_{0}$
to a steady-uniform flow of thickness
![]() $h_{\infty }$
. However, the numerical solutions in figures 5–8 suggest that the travelling waves do not directly connect
$h_{\infty }$
. However, the numerical solutions in figures 5–8 suggest that the travelling waves do not directly connect
![]() $h_{0}$
to
$h_{0}$
to
![]() $h_{\infty }$
, but that there is a time-dependent expansion zone for
$h_{\infty }$
, but that there is a time-dependent expansion zone for
![]() $h>h_{\ast }$
. This paper therefore focuses on how the minimal steady-uniform flow of thickness
$h>h_{\ast }$
. This paper therefore focuses on how the minimal steady-uniform flow of thickness
![]() $h_{\ast }$
connects to a deposit of thickness
$h_{\ast }$
connects to a deposit of thickness
![]() $h_{0}$
, i.e. it is assumed that
$h_{0}$
, i.e. it is assumed that
![]() $h_{\infty }=h_{\ast }$
. This implies that the steady-uniform part of the solution lies at
$h_{\infty }=h_{\ast }$
. This implies that the steady-uniform part of the solution lies at
![]() $(\unicode[STIX]{x1D6FD}_{\ast },h_{\ast })$
in figure 4, at the transition between the intermediate and dynamic regimes and where the non-dimensional net acceleration
$(\unicode[STIX]{x1D6FD}_{\ast },h_{\ast })$
in figure 4, at the transition between the intermediate and dynamic regimes and where the non-dimensional net acceleration
![]() $S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}=0$
. If
$S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}=0$
. If
![]() $h_{\ast }$
is a regular point then the ODE (5.8) would imply that the solution had zero gradient. However, it is anticipated from the numerical simulations in figure 7 that, in the absence of viscosity, the solutions will have a finite gradient and hence that
$h_{\ast }$
is a regular point then the ODE (5.8) would imply that the solution had zero gradient. However, it is anticipated from the numerical simulations in figure 7 that, in the absence of viscosity, the solutions will have a finite gradient and hence that
![]() $h_{\ast }$
must lie at a critical point.
$h_{\ast }$
must lie at a critical point.

Figure 11. Exact travelling-wave solution (solid black line) for the flow thickness
![]() $h$
as a function of
$h$
as a function of
![]() $x=\unicode[STIX]{x1D709}+u_{w}t$
with
$x=\unicode[STIX]{x1D709}+u_{w}t$
with
![]() $t=4.0$
s, as well as a comparison with numerical solutions both with and without viscosity (solid and dashed blue lines respectively). The slope angle
$t=4.0$
s, as well as a comparison with numerical solutions both with and without viscosity (solid and dashed blue lines respectively). The slope angle
![]() $\unicode[STIX]{x1D701}=36.3^{\circ }$
and the steady-uniform flow thickness
$\unicode[STIX]{x1D701}=36.3^{\circ }$
and the steady-uniform flow thickness
![]() $h_{\infty }=1.6$
mm is equal to
$h_{\infty }=1.6$
mm is equal to
![]() $h_{\ast }(36.3^{\circ })$
(solid orange line). The travelling deposition wave connects the steady-uniform flow to the deposit layer, which is approximately equal to
$h_{\ast }(36.3^{\circ })$
(solid orange line). The travelling deposition wave connects the steady-uniform flow to the deposit layer, which is approximately equal to
![]() $h_{stop}(36.3^{\circ })$
(solid red line). Since
$h_{stop}(36.3^{\circ })$
(solid red line). Since
![]() $h_{\ast }$
is less than
$h_{\ast }$
is less than
![]() $h_{start}(36.3^{\circ })$
(solid green line) the initial layer is assumed to be moving with the steady-uniform flow velocity (4.4) in the simulations. The viscosity slightly increases the deposit depth, and hence the speed of the wave. The material properties are given in table 1 and the slope angle-dependent properties in table 2.
$h_{start}(36.3^{\circ })$
(solid green line) the initial layer is assumed to be moving with the steady-uniform flow velocity (4.4) in the simulations. The viscosity slightly increases the deposit depth, and hence the speed of the wave. The material properties are given in table 1 and the slope angle-dependent properties in table 2.

Figure 12. Deposit thickness
![]() $h_{0}$
(solid black line) as a function of the slope angle
$h_{0}$
(solid black line) as a function of the slope angle
![]() $\unicode[STIX]{x1D701}$
, given exactly by (5.10), for a steady-uniform flow thickness
$\unicode[STIX]{x1D701}$
, given exactly by (5.10), for a steady-uniform flow thickness
![]() $h_{\infty }(\unicode[STIX]{x1D701})$
(dashed black line) that is equal to
$h_{\infty }(\unicode[STIX]{x1D701})$
(dashed black line) that is equal to
![]() $h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange line). The deposit thickness is in quantitative agreement with
$h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange line). The deposit thickness is in quantitative agreement with
![]() $h_{stop}(\unicode[STIX]{x1D701})$
(solid red line) for all angles, although the values are slightly under-predicted due to the lack of viscosity. The thickness above which material flows spontaneously is
$h_{stop}(\unicode[STIX]{x1D701})$
(solid red line) for all angles, although the values are slightly under-predicted due to the lack of viscosity. The thickness above which material flows spontaneously is
![]() $h_{start}(\unicode[STIX]{x1D701})$
(solid green line).
$h_{start}(\unicode[STIX]{x1D701})$
(solid green line).
Assuming that the critical point
![]() $h_{c}=h_{\ast }$
, it follows from equations (5.5) and (5.7) that the speed of the wave
$h_{c}=h_{\ast }$
, it follows from equations (5.5) and (5.7) that the speed of the wave
where
![]() $\bar{u}_{\ast }=\bar{u}_{\infty }(h_{\ast })$
is defined by (4.4). The speed of the wave (5.9) is therefore equal to the maximum characteristic wavespeed in the system. The wave is faster than the speed of the surface particles, for the exponential velocity profile assumed in (4.3), which implies that all the grains are caught up by the wave and deposited. The deposit depth
$\bar{u}_{\ast }=\bar{u}_{\infty }(h_{\ast })$
is defined by (4.4). The speed of the wave (5.9) is therefore equal to the maximum characteristic wavespeed in the system. The wave is faster than the speed of the surface particles, for the exponential velocity profile assumed in (4.3), which implies that all the grains are caught up by the wave and deposited. The deposit depth
![]() $h_{0}$
can be found by substituting (4.4) and (5.9) into (5.7) to give
$h_{0}$
can be found by substituting (4.4) and (5.9) into (5.7) to give
Since
![]() $h_{0}$
is known explicitly the ODE (5.8) is solved by integrating forwards from
$h_{0}$
is known explicitly the ODE (5.8) is solved by integrating forwards from
![]() $h=h_{0}$
at
$h=h_{0}$
at
![]() $\unicode[STIX]{x1D709}=0$
until the steady uniform flow is reached. The solution for
$\unicode[STIX]{x1D709}=0$
until the steady uniform flow is reached. The solution for
![]() $\unicode[STIX]{x1D701}=36.3^{\circ }$
and
$\unicode[STIX]{x1D701}=36.3^{\circ }$
and
![]() $h_{\infty }=h_{\ast }(36.3^{\circ })=1.6$
mm is shown in figure 11. It is in very close agreement with an inviscid solution (
$h_{\infty }=h_{\ast }(36.3^{\circ })=1.6$
mm is shown in figure 11. It is in very close agreement with an inviscid solution (
![]() $\unicode[STIX]{x1D708}=0$
) calculated with the numerical method described in § 4.1. The inclusion of the depth-averaged viscous terms in (2.2) acts to smooth out the wave, making the deposit depth slightly thicker and therefore in better agreement with the experimental value
$\unicode[STIX]{x1D708}=0$
) calculated with the numerical method described in § 4.1. The inclusion of the depth-averaged viscous terms in (2.2) acts to smooth out the wave, making the deposit depth slightly thicker and therefore in better agreement with the experimental value
![]() $h_{stop}$
, and as shown in figure 11.
$h_{stop}$
, and as shown in figure 11.
The deposit depth
![]() $h_{0}$
as a function of inclination angle (5.10) is plotted in figure 12. For a steady-uniform flow thickness
$h_{0}$
as a function of inclination angle (5.10) is plotted in figure 12. For a steady-uniform flow thickness
![]() $h_{\ast }$
the deposit depth agrees to within
$h_{\ast }$
the deposit depth agrees to within
![]() $6\,\%$
of
$6\,\%$
of
![]() $h_{stop}$
for all slope angles, where the consistent under-prediction of the deposit thickness is accounted for by the lack of viscosity. The fact that the travelling-wave solution produces a deposit depth that is so close to
$h_{stop}$
for all slope angles, where the consistent under-prediction of the deposit thickness is accounted for by the lack of viscosity. The fact that the travelling-wave solution produces a deposit depth that is so close to
![]() $h_{stop}$
, for all inclination angles, suggests that the angle dependence of
$h_{stop}$
, for all inclination angles, suggests that the angle dependence of
![]() $h_{\ast }(\unicode[STIX]{x1D701})$
, given by (3.7), is correct. Since (3.7) is derived from the empirical flow law (3.3) assuming that the transition Froude number
$h_{\ast }(\unicode[STIX]{x1D701})$
, given by (3.7), is correct. Since (3.7) is derived from the empirical flow law (3.3) assuming that the transition Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
is constant, this strongly suggests that the modified friction law (3.10)–(3.12) with constant
$\unicode[STIX]{x1D6FD}_{\ast }$
is constant, this strongly suggests that the modified friction law (3.10)–(3.12) with constant
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
is a good approximation.
$\unicode[STIX]{x1D6FD}_{\ast }$
is a good approximation.
6 Comparison with existing friction laws
To understand the motivation behind the non-monotonic friction law (3.10)–(3.12) it is useful to understand some of the pathologies that are present in earlier formulations. These can be seen by considering plots of the non-dimensional net acceleration
![]() $S(Fr,h)$
as well as simple numerical simulations of (i) an initially stationary layer with a thickness just above
$S(Fr,h)$
as well as simple numerical simulations of (i) an initially stationary layer with a thickness just above
![]() $h_{start}$
, which should accelerate away leaving behind a deposit layer close to
$h_{start}$
, which should accelerate away leaving behind a deposit layer close to
![]() $h_{stop}$
and (ii) an initially static deposit with a thickness slightly less than
$h_{stop}$
and (ii) an initially static deposit with a thickness slightly less than
![]() $h_{start}$
, which should remain static.
$h_{start}$
, which should remain static.
6.1 Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) friction coefficient for glass beads
The non-monotonic friction law (3.10)–(3.12) reduces to the extended law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002) for flows of spherical glass beads when the constant transition Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}=0.136/\sqrt{\cos \unicode[STIX]{x1D701}}$
and the offset
$\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}=0.136/\sqrt{\cos \unicode[STIX]{x1D701}}$
and the offset
![]() $\unicode[STIX]{x1D6E4}=0$
. This implies that the minimum steady-uniform Froude number is equal to
$\unicode[STIX]{x1D6E4}=0$
. This implies that the minimum steady-uniform Froude number is equal to
![]() $\unicode[STIX]{x1D6FD}$
, which is lower than that observed by Pouliquen (Reference Pouliquen1999a
) for most systems, and results in a minimum steady-uniform flow thickness
$\unicode[STIX]{x1D6FD}$
, which is lower than that observed by Pouliquen (Reference Pouliquen1999a
) for most systems, and results in a minimum steady-uniform flow thickness
![]() $h_{\ast }=h_{stop}$
. The non-dimensional net acceleration
$h_{\ast }=h_{stop}$
. The non-dimensional net acceleration
![]() $S(Fr,h)$
, with the material parameters for glass beads (table 3
a), is shown in figure 13 to display some notable differences to the modified friction law proposed here. Most significantly, Pouliquen & Forterre (Reference Pouliquen and Forterre2002) chose the power
$S(Fr,h)$
, with the material parameters for glass beads (table 3
a), is shown in figure 13 to display some notable differences to the modified friction law proposed here. Most significantly, Pouliquen & Forterre (Reference Pouliquen and Forterre2002) chose the power
![]() $\unicode[STIX]{x1D705}=10^{-3}$
in the interpolation between the static and dynamic regimes. This extremely small value of
$\unicode[STIX]{x1D705}=10^{-3}$
in the interpolation between the static and dynamic regimes. This extremely small value of
![]() $\unicode[STIX]{x1D705}$
was chosen to give a rapid decrease of the friction coefficient concentrated near to
$\unicode[STIX]{x1D705}$
was chosen to give a rapid decrease of the friction coefficient concentrated near to
![]() $Fr=0$
and then an almost constant friction until the dynamic regime took over. In practice, however, the value of
$Fr=0$
and then an almost constant friction until the dynamic regime took over. In practice, however, the value of
![]() $\unicode[STIX]{x1D705}$
is so small that the friction law starts at the maximum static friction at
$\unicode[STIX]{x1D705}$
is so small that the friction law starts at the maximum static friction at
![]() $Fr=0$
, but at the nearest non-zero positive number that can be represented by machine precision (which is around
$Fr=0$
, but at the nearest non-zero positive number that can be represented by machine precision (which is around
![]() $10^{-324}$
) immediately drops down to a low value of
$10^{-324}$
) immediately drops down to a low value of
![]() $\unicode[STIX]{x1D707}$
as shown in figure 13(b). As a result the triangular decelerating region that should lie adjacent to the
$\unicode[STIX]{x1D707}$
as shown in figure 13(b). As a result the triangular decelerating region that should lie adjacent to the
![]() $h$
-axis between
$h$
-axis between
![]() $h\in [h_{stop},h_{start}]$
is partially lost in finite precision calculations. This may explain why Pouliquen & Forterre (Reference Pouliquen and Forterre2002) found that their simulations of a finite mass release on an erodible layer ran out considerably further than in experiments.
$h\in [h_{stop},h_{start}]$
is partially lost in finite precision calculations. This may explain why Pouliquen & Forterre (Reference Pouliquen and Forterre2002) found that their simulations of a finite mass release on an erodible layer ran out considerably further than in experiments.

Figure 13. Zero contours of the non-dimensional net acceleration
![]() $S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}$
(solid black lines) with the material properties for glass beads (table 3
a) against the Froude number and flow thickness on (a) a linear and (b) a semi-log scale. In the blue shaded region (with right pointing arrows)
$S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}$
(solid black lines) with the material properties for glass beads (table 3
a) against the Froude number and flow thickness on (a) a linear and (b) a semi-log scale. In the blue shaded region (with right pointing arrows)
![]() $S>0$
and flows accelerate, while in the white region (with left pointing arrows)
$S>0$
and flows accelerate, while in the white region (with left pointing arrows)
![]() $S<0$
and flows decelerate. The solid vertical black line at
$S<0$
and flows decelerate. The solid vertical black line at
![]() $Fr=0$
in panel (a) shows the multivalued friction coefficient for stationary material. The transition between the intermediate and dynamic friction regimes occurs at
$Fr=0$
in panel (a) shows the multivalued friction coefficient for stationary material. The transition between the intermediate and dynamic friction regimes occurs at
![]() $Fr=\unicode[STIX]{x1D6FD}$
(dashed lines), whilst the
$Fr=\unicode[STIX]{x1D6FD}$
(dashed lines), whilst the
![]() $h_{stop}$
and
$h_{stop}$
and
![]() $h_{start}$
thicknesses are shown by the red and green lines, respectively. Note that in panel (b) the range of Froude numbers extends down to the minimum representable non-zero positive number on a typical computer.
$h_{start}$
thicknesses are shown by the red and green lines, respectively. Note that in panel (b) the range of Froude numbers extends down to the minimum representable non-zero positive number on a typical computer.
The high sensitivity of Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) friction law is also unphysical, since it is known from their own experiments that in practice the deposit layers can be inclined up to
![]() $\unicode[STIX]{x1D701}_{start}$
(which may be several degrees higher than
$\unicode[STIX]{x1D701}_{start}$
(which may be several degrees higher than
![]() $\unicode[STIX]{x1D701}_{stop}$
) before a flow is triggered. Static layers are therefore relatively stable to small disturbances. A larger value of
$\unicode[STIX]{x1D701}_{stop}$
) before a flow is triggered. Static layers are therefore relatively stable to small disturbances. A larger value of
![]() $\unicode[STIX]{x1D705}$
may therefore be chosen to give a greater stability to layers in the intermediate frictional regime, which is why Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) set
$\unicode[STIX]{x1D705}$
may therefore be chosen to give a greater stability to layers in the intermediate frictional regime, which is why Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) set
![]() $\unicode[STIX]{x1D705}=1$
. Whilst this overcomes the problem of hysteresis in stationary layers, the non-zero offset
$\unicode[STIX]{x1D705}=1$
. Whilst this overcomes the problem of hysteresis in stationary layers, the non-zero offset
![]() $\unicode[STIX]{x1D6E4}$
in the empirical flow rule for more angular granular materials such as sand and carborundum causes further problems.
$\unicode[STIX]{x1D6E4}$
in the empirical flow rule for more angular granular materials such as sand and carborundum causes further problems.
Table 3. Material properties for (a) glass beads on a bed of the same material, measured by Pouliquen & Forterre (Reference Pouliquen and Forterre2002) and (b) sand on a bed of the same material, measured by Forterre & Pouliquen (Reference Forterre and Pouliquen2003).

6.2 A friction law based on the empirical flow rule for sand
In an investigation into the long-surface-wave instability of granular materials, Forterre & Pouliquen (Reference Forterre and Pouliquen2003) performed experiments using a flow of 800
![]() $\unicode[STIX]{x03BC}\text{m}$
diameter sand on a rough bed of the same particles. They measured a constant of proportionality
$\unicode[STIX]{x03BC}\text{m}$
diameter sand on a rough bed of the same particles. They measured a constant of proportionality
![]() $\unicode[STIX]{x1D6FD}=0.65/\sqrt{\cos \unicode[STIX]{x1D701}}$
an offset
$\unicode[STIX]{x1D6FD}=0.65/\sqrt{\cos \unicode[STIX]{x1D701}}$
an offset
![]() $\unicode[STIX]{x1D6E4}=0.77/\sqrt{\cos \unicode[STIX]{x1D701}}$
in the empirical flow rule. The friction angles and flow rule parameters measured by Forterre & Pouliquen (Reference Forterre and Pouliquen2003) for sand, along with an estimate
$\unicode[STIX]{x1D6E4}=0.77/\sqrt{\cos \unicode[STIX]{x1D701}}$
in the empirical flow rule. The friction angles and flow rule parameters measured by Forterre & Pouliquen (Reference Forterre and Pouliquen2003) for sand, along with an estimate
![]() $\unicode[STIX]{x1D701}_{3}=\unicode[STIX]{x1D701}_{1}+3^{\circ }$
are given in table 3(b). The offset
$\unicode[STIX]{x1D701}_{3}=\unicode[STIX]{x1D701}_{1}+3^{\circ }$
are given in table 3(b). The offset
![]() $\unicode[STIX]{x1D6E4}$
in the flow rule alters the dynamic friction coefficient and the transition point to the intermediate regime, which now occurs at a Froude number
$\unicode[STIX]{x1D6E4}$
in the flow rule alters the dynamic friction coefficient and the transition point to the intermediate regime, which now occurs at a Froude number
![]() $\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
. This would suggest, by following the same argument as Pouliquen & Forterre (Reference Pouliquen and Forterre2002), that the friction coefficient might naively be written as
$\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
. This would suggest, by following the same argument as Pouliquen & Forterre (Reference Pouliquen and Forterre2002), that the friction coefficient might naively be written as

Figure 14. Zero contours of the non-dimensional net acceleration
![]() $S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}$
(solid black lines) against the Froude number and flow thickness with the material properties of (a) sand (table 3
b), for which
$S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}$
(solid black lines) against the Froude number and flow thickness with the material properties of (a) sand (table 3
b), for which
![]() $\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D6E4}$
, and (b) carborundum (table 1), for which
$\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D6E4}$
, and (b) carborundum (table 1), for which
![]() $\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}>0$
. Flows accelerate when
$\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}>0$
. Flows accelerate when
![]() $S>0$
(blue region and right arrows) and decelerate for
$S>0$
(blue region and right arrows) and decelerate for
![]() $S<0$
(white region and left arrows). The solid vertical black line at
$S<0$
(white region and left arrows). The solid vertical black line at
![]() $Fr=0$
in panel (b) shows the multivaluedness of the friction coefficient for stationary material. The transition between dynamic and intermediate regimes occurs at
$Fr=0$
in panel (b) shows the multivaluedness of the friction coefficient for stationary material. The transition between dynamic and intermediate regimes occurs at
![]() $Fr=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
, which is negative for sand, implying that all flows are dynamic and even initially static (
$Fr=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
, which is negative for sand, implying that all flows are dynamic and even initially static (
![]() $Fr=0$
) flows of thickness
$Fr=0$
) flows of thickness
![]() $h>h_{steady}(0)>h_{stop}(\unicode[STIX]{x1D701})$
(solid red lines) will accelerate, including those with thickness
$h>h_{steady}(0)>h_{stop}(\unicode[STIX]{x1D701})$
(solid red lines) will accelerate, including those with thickness
![]() $h<h_{start}(\unicode[STIX]{x1D701})$
(solid green lines). For carborundum with
$h<h_{start}(\unicode[STIX]{x1D701})$
(solid green lines). For carborundum with
![]() $\unicode[STIX]{x1D6FD}>\unicode[STIX]{x1D6E4}$
the transition Froude number
$\unicode[STIX]{x1D6FD}>\unicode[STIX]{x1D6E4}$
the transition Froude number
![]() $Fr=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
(dashed black line) is positive so the friction regimes are all well defined. The slope angle-dependent properties for (a) sand and (b) carborundum are given in tables 4(b) and 2 respectively.
$Fr=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
(dashed black line) is positive so the friction regimes are all well defined. The slope angle-dependent properties for (a) sand and (b) carborundum are given in tables 4(b) and 2 respectively.
With the parameters for sand,
![]() $\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}<0$
, and hence all flows are always in the dynamic regime. This is shown in figure 14(a), by plotting the zero contour of the non-dimensional net acceleration
$\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}<0$
, and hence all flows are always in the dynamic regime. This is shown in figure 14(a), by plotting the zero contour of the non-dimensional net acceleration
![]() $S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}$
with the material properties for sand. Since only the dynamic regime is active, an explicit formula for the zero contour
$S=\tan \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}$
with the material properties for sand. Since only the dynamic regime is active, an explicit formula for the zero contour
![]() $h_{steady}$
can be derived by equating (2.3) to zero for the dynamic friction coefficient (6.1) and simplifying with (3.2) to give
$h_{steady}$
can be derived by equating (2.3) to zero for the dynamic friction coefficient (6.1) and simplifying with (3.2) to give
which is linear in the Froude number. For
![]() $h>h_{steady}$
all flows are accelerative and for
$h>h_{steady}$
all flows are accelerative and for
![]() $h<h_{steady}$
all flows are decelerative. As a result, all constant thickness flows will either accelerate towards steady-uniform flow or decelerate towards zero velocity. However, the friction in the static state is not properly defined, so there is an issue here too. All of these problems arise directly from
$h<h_{steady}$
all flows are decelerative. As a result, all constant thickness flows will either accelerate towards steady-uniform flow or decelerate towards zero velocity. However, the friction in the static state is not properly defined, so there is an issue here too. All of these problems arise directly from
![]() $\unicode[STIX]{x1D6E4}$
being greater than
$\unicode[STIX]{x1D6E4}$
being greater than
![]() $\unicode[STIX]{x1D6FD}$
for the parameters for sand, which is a different problem to that of Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) law with
$\unicode[STIX]{x1D6FD}$
for the parameters for sand, which is a different problem to that of Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) law with
![]() $\unicode[STIX]{x1D705}=10^{-3}$
.
$\unicode[STIX]{x1D705}=10^{-3}$
.
Returning to the material properties for carborundum (given in table 1), for which
![]() $\unicode[STIX]{x1D6FD}>\unicode[STIX]{x1D6E4}$
, the dynamic, intermediate and static regimes are still properly defined in (6.1)–(6.3) if
$\unicode[STIX]{x1D6FD}>\unicode[STIX]{x1D6E4}$
, the dynamic, intermediate and static regimes are still properly defined in (6.1)–(6.3) if
![]() $\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
. The
$\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
. The
![]() $S=0$
contour for the carborundum parameters is plotted against Froude number and flow thickness in figure 14(b). It has many of the desired properties for a hysteretic friction law, with (i) acceleration for
$S=0$
contour for the carborundum parameters is plotted against Froude number and flow thickness in figure 14(b). It has many of the desired properties for a hysteretic friction law, with (i) acceleration for
![]() $h>h_{start}$
, (ii) deceleration below
$h>h_{start}$
, (ii) deceleration below
![]() $h_{stop}$
and (iii) a triangular region of deceleration between
$h_{stop}$
and (iii) a triangular region of deceleration between
![]() $[h_{stop},h_{start}]$
adjacent to the
$[h_{stop},h_{start}]$
adjacent to the
![]() $h$
-axis. As
$h$
-axis. As
![]() $h$
approaches
$h$
approaches
![]() $h_{start}$
from below this triangular region becomes progressively smaller, implying that static grains are more likely to mobilized by a disturbance. However, Edwards & Gray (Reference Edwards and Gray2015) and Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) found that numerical simulations of a depositional steady-uniform flow using the material properties of carborundum and a transition Froude number
$h_{start}$
from below this triangular region becomes progressively smaller, implying that static grains are more likely to mobilized by a disturbance. However, Edwards & Gray (Reference Edwards and Gray2015) and Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) found that numerical simulations of a depositional steady-uniform flow using the material properties of carborundum and a transition Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
did not leave a deposit layer with the correct thickness, i.e.
$\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
did not leave a deposit layer with the correct thickness, i.e.
![]() $h_{deposit}(\unicode[STIX]{x1D701})\neq h_{stop}(\unicode[STIX]{x1D701})$
, as will be demonstrated in § 6.4.
$h_{deposit}(\unicode[STIX]{x1D701})\neq h_{stop}(\unicode[STIX]{x1D701})$
, as will be demonstrated in § 6.4.
6.3 Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law for angular materials
The non-monotonic friction law with constant
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
presented here (3.10)–(3.12) reverts back to Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) original formulation if the transition thickness is assumed to lie between the
$\unicode[STIX]{x1D6FD}_{\ast }$
presented here (3.10)–(3.12) reverts back to Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) original formulation if the transition thickness is assumed to lie between the
![]() $h_{stop}$
and
$h_{stop}$
and
![]() $h_{start}$
curves according to
$h_{start}$
curves according to
![]() $h_{\ast }(\unicode[STIX]{x1D701})=(1-a)h_{stop}(\unicode[STIX]{x1D701})+ah_{start}(\unicode[STIX]{x1D701})$
. The flow rule (3.3) then implies that the corresponding transition Froude number varies with the inclination angle like
$h_{\ast }(\unicode[STIX]{x1D701})=(1-a)h_{stop}(\unicode[STIX]{x1D701})+ah_{start}(\unicode[STIX]{x1D701})$
. The flow rule (3.3) then implies that the corresponding transition Froude number varies with the inclination angle like
Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) chose
![]() $a=0.5$
to give
$a=0.5$
to give
![]() $\unicode[STIX]{x1D6FD}_{\ast }(35.2^{\circ })=0.473$
in order to produce the correct deposit layer depth at that angle. It is no surprise that this approach was successful in the small range of angles
$\unicode[STIX]{x1D6FD}_{\ast }(35.2^{\circ })=0.473$
in order to produce the correct deposit layer depth at that angle. It is no surprise that this approach was successful in the small range of angles
![]() $34.0^{\circ }\leqslant \unicode[STIX]{x1D701}\leqslant 35.2^{\circ }$
that they investigated, since it is close to the constant value of
$34.0^{\circ }\leqslant \unicode[STIX]{x1D701}\leqslant 35.2^{\circ }$
that they investigated, since it is close to the constant value of
![]() $\unicode[STIX]{x1D6FD}_{\ast }=0.466$
imposed here, which results in deposit layers close to
$\unicode[STIX]{x1D6FD}_{\ast }=0.466$
imposed here, which results in deposit layers close to
![]() $h_{stop}$
for all permitted inclinations
$h_{stop}$
for all permitted inclinations
![]() $\unicode[STIX]{x1D701}\in (\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})$
. However, a slope angle-dependent transition Froude number (6.5) results in deposit layers that are increasingly thicker than
$\unicode[STIX]{x1D701}\in (\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2})$
. However, a slope angle-dependent transition Froude number (6.5) results in deposit layers that are increasingly thicker than
![]() $h_{stop}$
as the inclination is reduced towards
$h_{stop}$
as the inclination is reduced towards
![]() $\unicode[STIX]{x1D701}_{3}$
, as will be demonstrated in § 6.4. Furthermore, the transition thickness
$\unicode[STIX]{x1D701}_{3}$
, as will be demonstrated in § 6.4. Furthermore, the transition thickness
![]() $h_{\ast }(\unicode[STIX]{x1D701})$
and hence
$h_{\ast }(\unicode[STIX]{x1D701})$
and hence
![]() $\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})$
become undefined for
$\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})$
become undefined for
![]() $\unicode[STIX]{x1D701}<\unicode[STIX]{x1D701}_{3}$
in this formulation, since
$\unicode[STIX]{x1D701}<\unicode[STIX]{x1D701}_{3}$
in this formulation, since
![]() $h_{start}$
is undefined there. Zero contours of the non-dimensional net acceleration
$h_{start}$
is undefined there. Zero contours of the non-dimensional net acceleration
![]() $S$
do appear qualitatively the same for Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law as they did for the modified version, shown in figure 4. However, that only holds if
$S$
do appear qualitatively the same for Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law as they did for the modified version, shown in figure 4. However, that only holds if
![]() $\unicode[STIX]{x1D701}\in (\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{2})$
and not for extremely shallow slope angles
$\unicode[STIX]{x1D701}\in (\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{2})$
and not for extremely shallow slope angles
![]() $\unicode[STIX]{x1D701}<\unicode[STIX]{x1D701}_{3}$
, which is a crucial flaw that was not immediately apparent.
$\unicode[STIX]{x1D701}<\unicode[STIX]{x1D701}_{3}$
, which is a crucial flaw that was not immediately apparent.
Table 4. Slope angle-dependent critical layer thicknesses and coefficients
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D701})$
in the depth-averaged viscosity
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D701})$
in the depth-averaged viscosity
![]() $\unicode[STIX]{x1D708}h^{1/2}/2$
for flows of (a) glass beads and (b) sand on a bed of the same material. The material properties for each are given in the respective rows of table 3.
$\unicode[STIX]{x1D708}h^{1/2}/2$
for flows of (a) glass beads and (b) sand on a bed of the same material. The material properties for each are given in the respective rows of table 3.

6.4 Numerical simulations with an initial stationary layer thicker than
 $h_{start}(\unicode[STIX]{x1D701})$
$h_{start}(\unicode[STIX]{x1D701})$
Numerical simulations are first carried out for an initially static layer of constant thickness
![]() $h(x,0)=h_{start}(\unicode[STIX]{x1D701})+0.1$
mm, with no further inflow at
$h(x,0)=h_{start}(\unicode[STIX]{x1D701})+0.1$
mm, with no further inflow at
![]() $x=0$
. With these initial and boundary conditions the constant thickness section should accelerate towards a steady-uniform flow and a deposition wave should develop at its trailing edge to leave a deposit of thickness
$x=0$
. With these initial and boundary conditions the constant thickness section should accelerate towards a steady-uniform flow and a deposition wave should develop at its trailing edge to leave a deposit of thickness
![]() $h_{stop}$
, as was the case in the simulations shown in figure 5 for carborundum with the friction law (3.10)–(3.12). Five different cases are considered here, that are shown in figure 15. In each case the constant thickness sections do accelerate towards a steady-uniform flow and a static deposit is left on the chute.
$h_{stop}$
, as was the case in the simulations shown in figure 5 for carborundum with the friction law (3.10)–(3.12). Five different cases are considered here, that are shown in figure 15. In each case the constant thickness sections do accelerate towards a steady-uniform flow and a static deposit is left on the chute.
For glass beads with
![]() $\unicode[STIX]{x1D705}=10^{-3}$
(figure 15
a), the flow leaves a deposit layer
$\unicode[STIX]{x1D705}=10^{-3}$
(figure 15
a), the flow leaves a deposit layer
![]() $h_{deposit}(23.0^{\circ })\approx h_{stop}(23.0^{\circ })$
, which is the physically correct thickness that the empirical law is derived from. However, this is simply because the extremely small value of
$h_{deposit}(23.0^{\circ })\approx h_{stop}(23.0^{\circ })$
, which is the physically correct thickness that the empirical law is derived from. However, this is simply because the extremely small value of
![]() $\unicode[STIX]{x1D705}$
means that the friction law cannot bring to rest any material that is thicker than
$\unicode[STIX]{x1D705}$
means that the friction law cannot bring to rest any material that is thicker than
![]() $h_{stop}$
. Setting
$h_{stop}$
. Setting
![]() $\unicode[STIX]{x1D705}=1$
(figure 15
b), which is required to capture the hysteretic behaviour, deposits a layer of physically incorrect thickness
$\unicode[STIX]{x1D705}=1$
(figure 15
b), which is required to capture the hysteretic behaviour, deposits a layer of physically incorrect thickness
![]() $h_{deposit}(23.0^{\circ })>h_{stop}(23.0^{\circ })$
. In the case of sand (figure 15
c) a deposit layer
$h_{deposit}(23.0^{\circ })>h_{stop}(23.0^{\circ })$
. In the case of sand (figure 15
c) a deposit layer
![]() $h_{deposit}(35.0^{\circ })\approx h_{steady}(0)$
given by (6.4) is produced. This is because the friction law is always in the dynamic regime. Since
$h_{deposit}(35.0^{\circ })\approx h_{steady}(0)$
given by (6.4) is produced. This is because the friction law is always in the dynamic regime. Since
![]() $h_{deposit}(35.0^{\circ })\neq h_{stop}(35.0^{\circ })$
the friction law for sand is also physically incorrect and, moreover, the deposit is not completely stationary. The simulation with the parameters for carborundum (figure 15
d) and the friction law (6.1)–(6.3) also leaves an incorrect deposit thickness
$h_{deposit}(35.0^{\circ })\neq h_{stop}(35.0^{\circ })$
the friction law for sand is also physically incorrect and, moreover, the deposit is not completely stationary. The simulation with the parameters for carborundum (figure 15
d) and the friction law (6.1)–(6.3) also leaves an incorrect deposit thickness
![]() $h_{deposit}(35.2^{\circ })<h_{stop}(35.2^{\circ })$
, which was one of the main motivations for Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to introduce a frictional transition at a greater Froude number. Finally, Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law, with a slope angle-dependent transition Froude number
$h_{deposit}(35.2^{\circ })<h_{stop}(35.2^{\circ })$
, which was one of the main motivations for Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to introduce a frictional transition at a greater Froude number. Finally, Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law, with a slope angle-dependent transition Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }(33.0^{\circ })=2.05$
, is shown in figure 15(e) to produce a deposit layer that is approximately
$\unicode[STIX]{x1D6FD}_{\ast }(33.0^{\circ })=2.05$
, is shown in figure 15(e) to produce a deposit layer that is approximately
![]() $50\,\%$
deeper than
$50\,\%$
deeper than
![]() $h_{stop}(33.0^{\circ })$
. In fact, simulations with this friction law on a wide range of slope angles reveal that the deposit depths become increasingly thicker than
$h_{stop}(33.0^{\circ })$
. In fact, simulations with this friction law on a wide range of slope angles reveal that the deposit depths become increasingly thicker than
![]() $h_{stop}$
when the slope angle is reduced, as shown in figure 16. Furthermore, simulations are not possible at all for angles
$h_{stop}$
when the slope angle is reduced, as shown in figure 16. Furthermore, simulations are not possible at all for angles
![]() $\unicode[STIX]{x1D701}\leqslant \unicode[STIX]{x1D701}_{3}$
since
$\unicode[STIX]{x1D701}\leqslant \unicode[STIX]{x1D701}_{3}$
since
![]() $h_{start}$
and therefore
$h_{start}$
and therefore
![]() $h_{\ast }$
become undefined there.
$h_{\ast }$
become undefined there.

Figure 15. Flow thickness
![]() $h$
is shown at one second intervals by light blue lines and the blue shading increases in intensity with increasing time for numerical simulations using the material properties of (a) glass beads with
$h$
is shown at one second intervals by light blue lines and the blue shading increases in intensity with increasing time for numerical simulations using the material properties of (a) glass beads with
![]() $\unicode[STIX]{x1D705}=10^{-3}$
, (b) glass beads with
$\unicode[STIX]{x1D705}=10^{-3}$
, (b) glass beads with
![]() $\unicode[STIX]{x1D705}=1$
, (c) sand, (d) carborundum with
$\unicode[STIX]{x1D705}=1$
, (c) sand, (d) carborundum with
![]() $\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
and (e) carborundum with
$\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
and (e) carborundum with
![]() $\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})=2.05>\unicode[STIX]{x1D6FD}$
, i.e. Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law that has a transition thickness
$\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})=2.05>\unicode[STIX]{x1D6FD}$
, i.e. Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law that has a transition thickness
![]() $h_{\ast }(\unicode[STIX]{x1D701})=(h_{stop}+h_{start})/2$
(solid orange line). The initial conditions (dashed black lines) are stationary layers of thickness
$h_{\ast }(\unicode[STIX]{x1D701})=(h_{stop}+h_{start})/2$
(solid orange line). The initial conditions (dashed black lines) are stationary layers of thickness
![]() $h(x,0)=h_{start}(\unicode[STIX]{x1D701})+0.1$
mm. All of the initial layers are of thickness
$h(x,0)=h_{start}(\unicode[STIX]{x1D701})+0.1$
mm. All of the initial layers are of thickness
![]() $h>h_{start}(\unicode[STIX]{x1D701})$
(solid green lines) and should gain momentum before leaving a deposit of thickness
$h>h_{start}(\unicode[STIX]{x1D701})$
(solid green lines) and should gain momentum before leaving a deposit of thickness
![]() $h_{stop}(\unicode[STIX]{x1D701})$
(solid red lines). The material properties are given in tables 1 and 3, whilst the slope angle-dependent properties in tables 2 and 4. Movies of the full simulations are available in the online supplementary material (movies 12–16).
$h_{stop}(\unicode[STIX]{x1D701})$
(solid red lines). The material properties are given in tables 1 and 3, whilst the slope angle-dependent properties in tables 2 and 4. Movies of the full simulations are available in the online supplementary material (movies 12–16).

Figure 16. For the friction law of Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017), the deposit thickness (orange squares) left by simulations with
![]() $h(x,t)=h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange line) and the deposit thickness (green squares) left by simulations with
$h(x,t)=h_{\ast }(\unicode[STIX]{x1D701})$
(solid orange line) and the deposit thickness (green squares) left by simulations with
![]() $h(x,t)=h_{start}(\unicode[STIX]{x1D701})$
(solid green line), e.g. that of figure 15(e), are shown to deviate increasingly from
$h(x,t)=h_{start}(\unicode[STIX]{x1D701})$
(solid green line), e.g. that of figure 15(e), are shown to deviate increasingly from
![]() $h_{stop}(\unicode[STIX]{x1D701})$
(solid red line) as the slope angle is reduced. Furthermore, for inclinations
$h_{stop}(\unicode[STIX]{x1D701})$
(solid red line) as the slope angle is reduced. Furthermore, for inclinations
![]() $\unicode[STIX]{x1D701}\leqslant \unicode[STIX]{x1D701}_{3}$
(shaded area) the friction law is undefined and simulations are not possible at all in this region, whereas they are now permitted by the modified friction law presented in § 3.3. The material properties are given in table 1, except for
$\unicode[STIX]{x1D701}\leqslant \unicode[STIX]{x1D701}_{3}$
(shaded area) the friction law is undefined and simulations are not possible at all in this region, whereas they are now permitted by the modified friction law presented in § 3.3. The material properties are given in table 1, except for
![]() $\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})$
which varies with slope angle (equation 3.9 of Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017).
$\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})$
which varies with slope angle (equation 3.9 of Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017).
It is therefore only the modified friction law (3.10)–(3.12) with constant
![]() $\unicode[STIX]{x1D6FD}_{\ast }=0.466$
that is able to accurately match
$\unicode[STIX]{x1D6FD}_{\ast }=0.466$
that is able to accurately match
![]() $h_{stop}$
whilst also capturing the hysteretic behaviour, as has been demonstrated in § 4. Indeed, the modified friction law does not just produce the correct experimental
$h_{stop}$
whilst also capturing the hysteretic behaviour, as has been demonstrated in § 4. Indeed, the modified friction law does not just produce the correct experimental
![]() $h_{stop}$
deposit thickness, but it does so over the complete range of inclinations where deposit layers are expected to form. This includes, in particular, angles
$h_{stop}$
deposit thickness, but it does so over the complete range of inclinations where deposit layers are expected to form. This includes, in particular, angles
![]() $\unicode[STIX]{x1D701}_{1}<\unicode[STIX]{x1D701}\leqslant \unicode[STIX]{x1D701}_{3}$
, which are not permissible for Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) original formulation.
$\unicode[STIX]{x1D701}_{1}<\unicode[STIX]{x1D701}\leqslant \unicode[STIX]{x1D701}_{3}$
, which are not permissible for Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) original formulation.

Figure 17. Flow thickness
![]() $h$
is shown at one second intervals by light blue lines and the blue shading increases in intensity with increasing time for numerical simulations using the material properties of (a) glass beads with
$h$
is shown at one second intervals by light blue lines and the blue shading increases in intensity with increasing time for numerical simulations using the material properties of (a) glass beads with
![]() $\unicode[STIX]{x1D705}=10^{-3}$
, (b) glass beads with
$\unicode[STIX]{x1D705}=10^{-3}$
, (b) glass beads with
![]() $\unicode[STIX]{x1D705}=1$
, (c) sand, (d) carborundum with
$\unicode[STIX]{x1D705}=1$
, (c) sand, (d) carborundum with
![]() $\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
and (e) carborundum with
$\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
and (e) carborundum with
![]() $\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})=2.05>\unicode[STIX]{x1D6FD}$
, i.e. Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law that has a transition thickness
$\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})=2.05>\unicode[STIX]{x1D6FD}$
, i.e. Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law that has a transition thickness
![]() $h_{\ast }(\unicode[STIX]{x1D701})=(h_{stop}+h_{start})/2$
(solid orange line). The initial conditions (dashed black lines) are stationary layers of thickness
$h_{\ast }(\unicode[STIX]{x1D701})=(h_{stop}+h_{start})/2$
(solid orange line). The initial conditions (dashed black lines) are stationary layers of thickness
![]() $h(x,0)=h_{start}(\unicode[STIX]{x1D701})-0.1$
mm. All of the initial layers are of thickness
$h(x,0)=h_{start}(\unicode[STIX]{x1D701})-0.1$
mm. All of the initial layers are of thickness
![]() $h<h_{start}(\unicode[STIX]{x1D701})$
(solid green lines) and should remain static. The solid red line denotes
$h<h_{start}(\unicode[STIX]{x1D701})$
(solid green lines) and should remain static. The solid red line denotes
![]() $h_{stop}$
. The material properties are given in tables 1 and 3, whilst the slope angle-dependent properties in tables 2 and 4. Movies of the full simulations are available in the online supplementary material (movies 17–21).
$h_{stop}$
. The material properties are given in tables 1 and 3, whilst the slope angle-dependent properties in tables 2 and 4. Movies of the full simulations are available in the online supplementary material (movies 17–21).
6.5 Numerical simulations with an initial stationary layer thinner than
 $h_{start}(\unicode[STIX]{x1D701})$
$h_{start}(\unicode[STIX]{x1D701})$
As a final and perhaps most basic check on the friction law, an initial layer of thickness
![]() $h(x,0)=h_{start}(\unicode[STIX]{x1D701})-0.1$
mm is now considered. Since the static layer is thinner than
$h(x,0)=h_{start}(\unicode[STIX]{x1D701})-0.1$
mm is now considered. Since the static layer is thinner than
![]() $h_{start}$
is should remain static. The results are plotted in figure 17. For the case of glass beads with
$h_{start}$
is should remain static. The results are plotted in figure 17. For the case of glass beads with
![]() $\unicode[STIX]{x1D705}=10^{-3}$
(in figure 17
a) any disturbance will result in the friction jumping from the static value at
$\unicode[STIX]{x1D705}=10^{-3}$
(in figure 17
a) any disturbance will result in the friction jumping from the static value at
![]() $Fr=0$
to a much lower value at the next non-zero number that can be represented on the computer as shown in § 6.1 and figure 13. As a result, the static layer flows down the chute and leaves a deposit close to
$Fr=0$
to a much lower value at the next non-zero number that can be represented on the computer as shown in § 6.1 and figure 13. As a result, the static layer flows down the chute and leaves a deposit close to
![]() $h_{stop}$
, instead of remaining stationary. Choosing
$h_{stop}$
, instead of remaining stationary. Choosing
![]() $\unicode[STIX]{x1D705}=1$
(figure 17
b) is sufficient to keep the material at rest. The results for sand (figure 17
c), which has an offset
$\unicode[STIX]{x1D705}=1$
(figure 17
b) is sufficient to keep the material at rest. The results for sand (figure 17
c), which has an offset
![]() $\unicode[STIX]{x1D6E4}>\unicode[STIX]{x1D6FD}$
, also highlights a problem. This time the layer flows down the plane because the dynamic regime is always active, as shown in figure 14(a). When
$\unicode[STIX]{x1D6E4}>\unicode[STIX]{x1D6FD}$
, also highlights a problem. This time the layer flows down the plane because the dynamic regime is always active, as shown in figure 14(a). When
![]() $\unicode[STIX]{x1D6E4}<\unicode[STIX]{x1D6FD}$
for carborundum, however, the intermediate and static regimes exist in the friction law (6.1)–(6.3) and the initial layer remains static as shown in figure 17(d). Finally, Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law (figure 17
e) also ensures that flows of thickness
$\unicode[STIX]{x1D6E4}<\unicode[STIX]{x1D6FD}$
for carborundum, however, the intermediate and static regimes exist in the friction law (6.1)–(6.3) and the initial layer remains static as shown in figure 17(d). Finally, Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) friction law (figure 17
e) also ensures that flows of thickness
![]() $h<h_{start}(\unicode[STIX]{x1D701})$
are not accelerated and therefore remain stationary in simulations, as required.
$h<h_{start}(\unicode[STIX]{x1D701})$
are not accelerated and therefore remain stationary in simulations, as required.
In all of the cases where the friction law correctly captures the initially static layer (figure 17
b,d,e) the simulations in § 6.4 produce incorrect deposit layer depths (figure 15
b,d,e). Hence only the modified frictional law (3.10)–(3.12) is able to capture the hysteretic behaviour and leave deposits that are approximately equal to the experimental value of
![]() $h_{stop}$
for the entire range of slope angles.
$h_{stop}$
for the entire range of slope angles.
7 Conclusions
Frictional hysteresis plays a crucial role in a variety of granular flows in which static and flowing regions coexist. In its simplest form it is responsible for the formation of a static deposit of thickness
![]() $h_{stop}(\unicode[STIX]{x1D701})$
on a slope of angle
$h_{stop}(\unicode[STIX]{x1D701})$
on a slope of angle
![]() $\unicode[STIX]{x1D701}$
to the horizontal, when the mass supply onto the chute is closed off. Moreover, this layer does not spontaneously start to flow again until the thickness is increased to
$\unicode[STIX]{x1D701}$
to the horizontal, when the mass supply onto the chute is closed off. Moreover, this layer does not spontaneously start to flow again until the thickness is increased to
![]() $h_{start}(\unicode[STIX]{x1D701})>h_{stop}(\unicode[STIX]{x1D701})$
or the slope is increased to a higher angle
$h_{start}(\unicode[STIX]{x1D701})>h_{stop}(\unicode[STIX]{x1D701})$
or the slope is increased to a higher angle
![]() $\unicode[STIX]{x1D701}_{start}>\unicode[STIX]{x1D701}$
. The same physics is crucial for a wide range of phenomena from retrogressive slope failures (Daerr & Douady Reference Daerr and Douady1999; Russell et al.
Reference Russell, Johnson, Edwards, Viroulet, Rocha and Gray2019) to self-channelization and levee formation (Félix & Thomas Reference Félix and Thomas2004; Mangeney et al.
Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007; Rocha et al.
Reference Rocha, Johnson and Gray2019) as well as erosion–deposition waves (Daerr & Douady Reference Daerr and Douady1999; Clément et al.
Reference Clément, Malloggi, Andreotti and Aranson2007; Börzsönyi et al.
Reference Börzsönyi, Halsey and Ecke2008; Takagi et al.
Reference Takagi, McElwaine and Huppert2011; Edwards & Gray Reference Edwards and Gray2015; McArdell Reference McArdell2016; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017).
$\unicode[STIX]{x1D701}_{start}>\unicode[STIX]{x1D701}$
. The same physics is crucial for a wide range of phenomena from retrogressive slope failures (Daerr & Douady Reference Daerr and Douady1999; Russell et al.
Reference Russell, Johnson, Edwards, Viroulet, Rocha and Gray2019) to self-channelization and levee formation (Félix & Thomas Reference Félix and Thomas2004; Mangeney et al.
Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007; Rocha et al.
Reference Rocha, Johnson and Gray2019) as well as erosion–deposition waves (Daerr & Douady Reference Daerr and Douady1999; Clément et al.
Reference Clément, Malloggi, Andreotti and Aranson2007; Börzsönyi et al.
Reference Börzsönyi, Halsey and Ecke2008; Takagi et al.
Reference Takagi, McElwaine and Huppert2011; Edwards & Gray Reference Edwards and Gray2015; McArdell Reference McArdell2016; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017).
In depth-averaged theories for granular flow the hysteresis is modelled by a non-monotonic friction law (Pouliquen & Forterre Reference Pouliquen and Forterre2002; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017) that has a monotonically increasing dynamic friction as a function of
![]() $Fr/h$
, a multivalued static friction at
$Fr/h$
, a multivalued static friction at
![]() $Fr=0$
and a monotonically decreasing intermediate friction connecting them, as sketched in figure 1(b). Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) introduced the idea that the transition between the intermediate and dynamic regimes occurred at Froude number
$Fr=0$
and a monotonically decreasing intermediate friction connecting them, as sketched in figure 1(b). Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) introduced the idea that the transition between the intermediate and dynamic regimes occurred at Froude number
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
, so that a flow at the minimum steady-uniform flow thickness
$\unicode[STIX]{x1D6FD}_{\ast }$
, so that a flow at the minimum steady-uniform flow thickness
![]() $h_{\ast }\in [h_{stop},h_{start}]$
would produce the correct deposit depth
$h_{\ast }\in [h_{stop},h_{start}]$
would produce the correct deposit depth
![]() $h_{stop}$
in the small range of slope angles that they investigated. In this paper, a modification to Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) law is proposed, which extends its definition to all inclination angles. The key idea is to make
$h_{stop}$
in the small range of slope angles that they investigated. In this paper, a modification to Edwards et al.’s (Reference Edwards, Viroulet, Kokelaar and Gray2017) law is proposed, which extends its definition to all inclination angles. The key idea is to make
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
a constant, rather than a function of the inclination angle as in Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017). As a result the minimum steady-uniform flow thickness
$\unicode[STIX]{x1D6FD}_{\ast }$
a constant, rather than a function of the inclination angle as in Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017). As a result the minimum steady-uniform flow thickness
![]() $h_{\ast }$
is a constant multiple of
$h_{\ast }$
is a constant multiple of
![]() $h_{stop}$
as shown in (3.7).
$h_{stop}$
as shown in (3.7).
Numerical simulations of the full system of governing equations (2.1)–(2.4) and the friction law (3.10)–(3.12) using the material parameters for carborundum particles on a bed of glass beads (table 1 and figures 5–8) demonstrate that this model is able to predict the correct deposit thickness for the complete range of inclination angles for which
![]() $h_{stop}$
layers form. Indeed, it is even possible to accurately simulate the staircase procedure, by which the
$h_{stop}$
layers form. Indeed, it is even possible to accurately simulate the staircase procedure, by which the
![]() $h_{stop}$
and
$h_{stop}$
and
![]() $h_{start}$
curves are determined experimentally, as shown in figure 10.
$h_{start}$
curves are determined experimentally, as shown in figure 10.
One of the most striking features of the numerical solutions is that two travelling waves are responsible for the deposition of a layer whose thickness lies close to
![]() $h_{stop}$
. The first travelling wave marks the trailing edge of the region of steady-uniform flow, while the second wave rapidly deposits the grains once their thickness falls below
$h_{stop}$
. The first travelling wave marks the trailing edge of the region of steady-uniform flow, while the second wave rapidly deposits the grains once their thickness falls below
![]() $h_{\ast }$
. The second wave travels slightly slower than the first wave, as shown in figures 5 and 6, so there is a slowly expanding region between the two. Both waves travel more quickly than all the particles in the system. In particular, as the waves catch up with the surface particles in figure 5 they slow down and then stop on the surface of the deposited
$h_{\ast }$
. The second wave travels slightly slower than the first wave, as shown in figures 5 and 6, so there is a slowly expanding region between the two. Both waves travel more quickly than all the particles in the system. In particular, as the waves catch up with the surface particles in figure 5 they slow down and then stop on the surface of the deposited
![]() $h_{stop}$
layer. This can be visualized as a space–time plot as shown in figure 6, which is in quantitative agreement with the experimental space–time plot in figure 2.
$h_{stop}$
layer. This can be visualized as a space–time plot as shown in figure 6, which is in quantitative agreement with the experimental space–time plot in figure 2.
An inviscid exact solution is constructed for the case of a minimal steady-uniform flow of thickness
![]() $h_{\ast }$
in § 5. In this case the steady-uniform flow connects directly to the deposit through a travelling wave as shown in figure 11. An explicit expression is obtained for the deposit depth (5.10) that lies very close to
$h_{\ast }$
in § 5. In this case the steady-uniform flow connects directly to the deposit through a travelling wave as shown in figure 11. An explicit expression is obtained for the deposit depth (5.10) that lies very close to
![]() $h_{stop}$
for the complete range of angles that deposits form (figure 12), which provides strong evidence that choosing
$h_{stop}$
for the complete range of angles that deposits form (figure 12), which provides strong evidence that choosing
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
to be constant is the correct assumption in the friction law.
$\unicode[STIX]{x1D6FD}_{\ast }$
to be constant is the correct assumption in the friction law.
The numerical simulations and exact solutions demonstrate that the friction (3.10)–(3.12) has all of the physical properties that one would want a hysteretic friction law to have, namely (i) material that is thicker than
![]() $h_{start}$
will accelerate/decelerate towards steady-uniform flow, (ii) material below
$h_{start}$
will accelerate/decelerate towards steady-uniform flow, (ii) material below
![]() $h_{\ast }$
will decelerate and stop, (iii) material in the range
$h_{\ast }$
will decelerate and stop, (iii) material in the range
![]() $[h_{\ast },h_{start}]$
is metastable, in the sense that static grains will remain static unless they are subjected to a sufficiently large perturbation and (iv) steady-uniform flows with a thickness close to
$[h_{\ast },h_{start}]$
is metastable, in the sense that static grains will remain static unless they are subjected to a sufficiently large perturbation and (iv) steady-uniform flows with a thickness close to
![]() $h_{\ast }$
will produce a deposit thickness that is approximately equal to
$h_{\ast }$
will produce a deposit thickness that is approximately equal to
![]() $h_{stop}$
. The first three of these properties can be neatly summarized in a contour plot of the non-dimensional acceleration in figure 4, which divides the
$h_{stop}$
. The first three of these properties can be neatly summarized in a contour plot of the non-dimensional acceleration in figure 4, which divides the
![]() $(Fr,h)$
-space up into accelerative and decelerative regions for a uniform layer of granular material.
$(Fr,h)$
-space up into accelerative and decelerative regions for a uniform layer of granular material.
In § 6 the non-monotonic friction law (3.10)–(3.12) is compared to the original formulation of Pouliquen & Forterre (Reference Pouliquen and Forterre2002) as well as the friction laws for angular particles, of Forterre & Pouliquen (Reference Forterre and Pouliquen2003) and Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017), to demonstrate some of their pathologies. For instance, if the interpolation power
![]() $\unicode[STIX]{x1D705}$
is chosen to be
$\unicode[STIX]{x1D705}$
is chosen to be
![]() $10^{-3}$
, as in Pouliquen & Forterre (Reference Pouliquen and Forterre2002), the hysteretic friction law is only partially represented in numerical computations (see figure 13) and a uniform thickness static layer below
$10^{-3}$
, as in Pouliquen & Forterre (Reference Pouliquen and Forterre2002), the hysteretic friction law is only partially represented in numerical computations (see figure 13) and a uniform thickness static layer below
![]() $h_{start}$
can flow down the chute, as shown in figure 17(a), when it should remain stable. In addition, when the empirical flow rule for angular particles is generalized to hysteretic flows in the same way as Pouliquen & Forterre (Reference Pouliquen and Forterre2002), it leads to intermediate-dynamic friction transitions at Froude number
$h_{start}$
can flow down the chute, as shown in figure 17(a), when it should remain stable. In addition, when the empirical flow rule for angular particles is generalized to hysteretic flows in the same way as Pouliquen & Forterre (Reference Pouliquen and Forterre2002), it leads to intermediate-dynamic friction transitions at Froude number
![]() $\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
, which is negative for sand. As a result, grains can also flow off the chute when they should remain stationary. When the same law is applied to carborundum particles the frictional transitions are well defined, but numerical simulations of a static layer that is slightly thicker than
$\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
, which is negative for sand. As a result, grains can also flow off the chute when they should remain stationary. When the same law is applied to carborundum particles the frictional transitions are well defined, but numerical simulations of a static layer that is slightly thicker than
![]() $h_{start}$
produce a deposit that is significantly thinner than
$h_{start}$
produce a deposit that is significantly thinner than
![]() $h_{stop}$
, as shown in figure 15(d). Indeed, it is this observation that originally motivated Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to introduce a frictional transition at
$h_{stop}$
, as shown in figure 15(d). Indeed, it is this observation that originally motivated Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to introduce a frictional transition at
![]() $Fr=\unicode[STIX]{x1D6FD}_{\ast }>\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
and
$Fr=\unicode[STIX]{x1D6FD}_{\ast }>\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
and
![]() $h_{\ast }\in [h_{stop},h_{start}]$
.
$h_{\ast }\in [h_{stop},h_{start}]$
.
There is significant potential to apply the friction law (3.10)–(3.12) to geophysical flows such as snow slab avalanches, where there is a clearly defined layer of erodible material on top of the underlying topography. Incorporation of new snow into such flows is a long standing problem and most models (Bouchaud et al. Reference Bouchaud, Cates, Prakash and Edwards1994; Douady, Andreotti & Daerr Reference Douady, Andreotti and Daerr1999; Gray Reference Gray2001; Doyle et al. Reference Doyle, Huppert, Lube, Mader and Sparks2007; Bouchut et al. Reference Bouchut, Fernández-Nieto, Mangeney and Lagreé2008; Tai & Kuo Reference Tai and Kuo2008; Gray & Ancey Reference Gray and Ancey2009; Iverson Reference Iverson2012; Tai & Kuo Reference Tai and Kuo2012; Capart, Hung & Stark Reference Capart, Hung and Stark2015) assume that this happens by basal entrainment. In our approach the material is either static or flowing through its entire depth, and there are evolving regions of flow and no flow, which are governed by the effective basal friction law (3.10)–(3.12). This harks back to some of the very earliest snow avalanche models (Briukhanov et al. Reference Briukhanov, Grigorian, Miagkov, Plam, Shurova, Eglit and Yakimov1967; Grigorian et al. Reference Grigorian, Eglit and Iakimov1967; Eglit & Demidov Reference Eglit and Demidov2005), which coupled shallow-water-like equations within the flowing avalanche to a static layer of entrainable snow ahead of the flow using jump conditions. There is growing evidence from field experiments (Sovilla, Sommavilla & Tomaselli Reference Sovilla, Sommavilla and Tomaselli2001; Sovilla & Bartelt Reference Sovilla and Bartelt2002; Sovilla, Burlando & Bartelt Reference Sovilla, Burlando and Bartelt2006) that incorporation by frontal ploughing is much more significant than basal entrainment, which would support our approach.
The non-monotonic friction law also raises questions about the rheology more generally, since the basal friction law (Pouliquen Reference Pouliquen1999a
; Pouliquen & Forterre Reference Pouliquen and Forterre2002) was key to the development of the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology for granular flows (GDR-MiDi 2004; Jop et al.
Reference Jop, Forterre and Pouliquen2005, Reference Jop, Forterre and Pouliquen2006). One might therefore envisage that one could modify the monotonically increasing dependence of the
$\unicode[STIX]{x1D707}(I)$
-rheology for granular flows (GDR-MiDi 2004; Jop et al.
Reference Jop, Forterre and Pouliquen2005, Reference Jop, Forterre and Pouliquen2006). One might therefore envisage that one could modify the monotonically increasing dependence of the
![]() $\unicode[STIX]{x1D707}(I)$
-curve on the inertial number
$\unicode[STIX]{x1D707}(I)$
-curve on the inertial number
![]() $I$
, to include a monotonically decreasing section at small
$I$
, to include a monotonically decreasing section at small
![]() $I$
to model frictional hysteresis. Unfortunately, Barker et al. (Reference Barker, Schaeffer, Bohórquez and Gray2015) showed that a decreasing section of the
$I$
to model frictional hysteresis. Unfortunately, Barker et al. (Reference Barker, Schaeffer, Bohórquez and Gray2015) showed that a decreasing section of the
![]() $\unicode[STIX]{x1D707}(I)$
curve is always ill posed, in the sense that the growth rate of shortwaves tends to infinity in the high wavenumber limit. Indeed the standard monotonically increasing
$\unicode[STIX]{x1D707}(I)$
curve is always ill posed, in the sense that the growth rate of shortwaves tends to infinity in the high wavenumber limit. Indeed the standard monotonically increasing
![]() $\unicode[STIX]{x1D707}(I)$
-rheology is also ill-posed at small inertial numbers, although it is possible to cure ill posedness by forcing the
$\unicode[STIX]{x1D707}(I)$
-rheology is also ill-posed at small inertial numbers, although it is possible to cure ill posedness by forcing the
![]() $\unicode[STIX]{x1D707}(I)$
-curve to pass through the origin and thereby include a creep state (Barker & Gray Reference Barker and Gray2017). This is, however, diametrically opposed to the form of the friction that seems necessary to model erosion–deposition phenomena (Edwards & Gray Reference Edwards and Gray2015; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017) and one might imagine that another form of rheology, such as the compressible
$\unicode[STIX]{x1D707}(I)$
-curve to pass through the origin and thereby include a creep state (Barker & Gray Reference Barker and Gray2017). This is, however, diametrically opposed to the form of the friction that seems necessary to model erosion–deposition phenomena (Edwards & Gray Reference Edwards and Gray2015; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017) and one might imagine that another form of rheology, such as the compressible
![]() $I$
-dependent rheology (CIDR) of Barker et al. (Reference Barker, Schaeffer, Shearer and Gray2017) or a non-local rheology (Bouzid et al.
Reference Bouzid, Trulsson, Claudin, Clément and Andreotti2013; Kamrin & Henann Reference Kamrin and Henann2015; DeGiuli & Wyart Reference DeGiuli and Wyart2017; Lee & Yang Reference Lee and Yang2017) is needed to model slow flows close to or below yield.
$I$
-dependent rheology (CIDR) of Barker et al. (Reference Barker, Schaeffer, Shearer and Gray2017) or a non-local rheology (Bouzid et al.
Reference Bouzid, Trulsson, Claudin, Clément and Andreotti2013; Kamrin & Henann Reference Kamrin and Henann2015; DeGiuli & Wyart Reference DeGiuli and Wyart2017; Lee & Yang Reference Lee and Yang2017) is needed to model slow flows close to or below yield.
Acknowledgements
This research was supported by NERC grants NE/E003206/1 and NE/K003011/1 as well as EPSRC grants EP/I019189/1, EP/K00428X/1 and EP/M022447/1. J.M.N.T.G. is a Royal Society Wolfson Research Merit Award holder (WM150058) and an EPSRC Established Career Fellow (EP/M022447/1). The authors would like to thank F. M. Rocha for many enlightening discussions.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.517.