Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-27T03:33:02.129Z Has data issue: false hasContentIssue false
  • English
  • Français

WHAT MODEL COMPANIONSHIP CAN SAY ABOUT THE CONTINUUM PROBLEM

Part of: Set theory General and miscellaneous specific topics Model theory Philosophical aspects of logic and foundations

Published online by Cambridge University Press:  25 April 2023

GIORGIO VENTURI Open the ORCID record for GIORGIO VENTURI [Opens in a new window]  and
MATTEO VIALE
GIORGIO VENTURI
Affiliation:
DEPARTMENT OF CIVILISATIONS AND FORMS OF KNOWLEDGE UNIVERSITÀ DI PISA VIA PASQUALE PAOLI, 15 56126 PISA, ITALY E-mail: gio.venturi@gmail.com
MATTEO VIALE
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF TURIN VIA CARLO ALBERTO, 10, TURIN 10124, ITALY E-mail: matteo.viale@unito.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We present recent results on the model companions of set theory, placing them in the context of a current debate in the philosophy of mathematics. We start by describing the dependence of the notion of model companionship on the signature, and then we analyze this dependence in the specific case of set theory. We argue that the most natural model companions of set theory describe (as the signature in which we axiomatize set theory varies) theories of 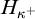$H_{\kappa ^+}$, as 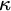$\kappa $ ranges among the infinite cardinals. We also single out 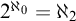$2^{\aleph _0}=\aleph _2$ as the unique solution of the continuum problem which can (and does) belong to some model companion of set theory (enriched with large cardinal axioms). While doing so we bring to light that set theory enriched by large cardinal axioms in the range of supercompactness has as its model companion (with respect to its first order axiomatization in certain natural signatures) the theory of 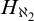$H_{\aleph _2}$ as given by a strong form of Woodin’s axiom $(*)$ (which holds assuming 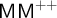$\mathsf {MM}^{++}$). Finally this model-theoretic approach to set-theoretic validities is explained and justified in terms of a form of maximality inspired by Hilbert’s axiom of completeness.

Keywords

set theorycontinuum hypothesismodel companionmaximalitylarge cardinalsphilosophy of mathematics

MSC classification

Primary: 03E35: Consistency and independence results 03E50: Continuum hypothesis and Martin's axiom 03E57: Generic absoluteness and forcing axioms 03C10: Quantifier elimination, model completeness and related topics 03C25: Model-theoretic forcing 00A30: Philosophy of mathematics 03A05: Philosophical and critical
Type
Research Article
Information
The Review of Symbolic Logic , First View , pp. 1 - 40
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Antos, C., Barton, N., & Friedman, S.-D. (2021). Universism and extensions of V. Review of Symbolic Logic, 14(1), 112–154.CrossRefGoogle Scholar
Arrigoni, T., & Friedman, S.-D. (2013). The hyperuniverse program. Bulletin of Symbolic Logic, 19(1), 77–96.CrossRefGoogle Scholar
Asperó, D., & Schindler, R. (2021). Martin’s maximum ${}^{++}$ implies Woodin’s axiom $\left(\ast \right)$ . Annals of Mathematics. Second Series, 193(3), 793–835.CrossRefGoogle Scholar
Asperó, D., & Viale, M. (2022). Incompatible bounded category forcing axioms. Journal of Mathematical Logic, 22(2), Paper no. 2250006, 76 pages.CrossRefGoogle Scholar
Audrito, G., & Viale, M. (2017). Absoluteness via resurrection. Journal of Mathematical Logic, 17(2), 1750005, 36 pages.CrossRefGoogle Scholar
Bagaria, J. (2000). Bounded forcing axioms as principles of generic absoluteness. Archive for Mathematical Logic, 39(6), 393–401.CrossRefGoogle Scholar
Bagaria, J. (2005). Natural axioms of set theory and the continuum problem. In Hájek, P., Valdés-Villanueva, L., and Westertåhl, D., editors. Proceedings of the 12th International Congress of Logic, Methodology, and Philosophy of Science. London: King’s College London Publications, pp. 43–64.Google Scholar
Baldwin, J. T. (2018). Model Theory and the Philosophy of Mathematical Practice. Formalization without Foundationalism. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Barton, N., Ternullo, C., & Venturi, G. (2020). On forms of justification in set theory. Australasian Journal of Logic, 17(4), 158–200.CrossRefGoogle Scholar
Bernays, P. (1935). Sur le platonisme dans les mathématiques. L’Enseignement Mathematique, 34, 52–69.Google Scholar
Boolos, G. (1971). The iterative conception of set. Journal of Philosophy, 68(8), 215–231.CrossRefGoogle Scholar
Caicedo, A. E., & Veličković, B. (2006). The bounded proper forcing axiom and well orderings of the reals. Mathematical Research Letters, 13(2–3), 393–408.CrossRefGoogle Scholar
Chen Chang, C., & Keisler, H. J. (1990). Model Theory (third edition). Studies in Logic and the Foundations of Mathematics, Vol. 73. Amsterdam: North-Holland.Google Scholar
Cohen, P. (2002). The discovery of forcing. Rocky Mountain Journal of Mathematics, 32(4), 1071–1100.CrossRefGoogle Scholar
Franks, C. (2009). The Autonomy of Mathematical Knowledge: Hilbert’s Program Revisited. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Gitman, V., Hamkins, J. D., & Johnstone, T. A. (2016). What is the theory ZFC without power set? Mathematical Logic Quarterly, 62(4-5), 391–406.CrossRefGoogle Scholar
Gödel, K. (1947). What is Cantor’s continuum problem? American Mathematical Monthly, 54, 515–525; errata, 55, 151.CrossRefGoogle Scholar
Hamkins, J. D. (2003). A simple maximality principle. Journal of Symbolic Logic, 68(2), 527–550.CrossRefGoogle Scholar
Hamkins, J. D. (2012). The set-theoretic multiverse. Review of Symbolic Logic, 5, 416–449.CrossRefGoogle Scholar
Hamkins, J. D., & Johnstone, T. A. (2014). Resurrection axioms and uplifting cardinals. Archive for Mathematical Logic, 53(3–4), 463–485.CrossRefGoogle Scholar
Incurvati, L. (2017). Maximality principles in set theory. Philosophia Mathematica, 25(2), 159–193.Google Scholar
Jech, T. (2003). Set Theory (The third millennium edition, revised and expanded). Springer Monographs in Mathematics. Berlin: Springer.Google Scholar
Koellner, P. (2006). On the question of absolute undecidability. Philosophia Mathematica, 14(2), 153–188.CrossRefGoogle Scholar
Koellner, P. (2010). Independence and large cardinals. In Stanford Encyclopedia of Philosophy.Google Scholar
Kunen, K. (1980). Set Theory: An introduction to Independence Proofs. Studies in Logic and the Foundations of Mathematics, Vol. 102. Amsterdam: North-Holland.Google Scholar
Larson, P. B. (2010). Forcing over models of determinacy. In Foreman, M. and Kanamori A., editors. Handbook of Set Theory. Dordrecht: Springer, pp. 2121–2177.CrossRefGoogle Scholar
(2013). The potential hierarchy of sets. Review of Symbolic Logic, 6(2), 205–228.CrossRefGoogle Scholar
, & Shapiro, S. (2019). Actual and potential infinity. Noûs, 53(1), 160–191.Google Scholar
Maddy, P. (1997). Naturalism in Mathematics. Oxford: Oxford University Press.Google Scholar
Maddy, P. (2007). Second Philosophy: A Naturalistic Method. Oxford: Oxford University Press.CrossRefGoogle Scholar
McGee, V. (1992). Two problems with tarski’s theory of consequence. Proceedings of the Aristotelian Society, 92(1), 273–292.CrossRefGoogle Scholar
Moore, J. T. (2005). Set mapping reflection. Journal of Mathematical Logic, 5(1), 87–97.CrossRefGoogle Scholar
Moore, J. T. (2017). What makes the continuum ${\aleph}_2$ . Contemporary Mathematics, 690, 259–287.CrossRefGoogle Scholar
Tent, K., & Ziegler, M. (2012). A Course in Model Theory. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Todorcevic, S. (2002). Generic absoluteness and the continuum. Mathematical Research Letters, 9(4), 465–471.CrossRefGoogle Scholar
Venturi, G. (2019). Genericity and arbitrariness. Logique et Analyse, 248, 435–452.Google Scholar
Venturi, G. (2020). Infinite forcing and the generic multiverse. Studia Logica, 108(2), 277–290.CrossRefGoogle Scholar
Venturi, G., & Viale, M. (2023). Second order arithmetic as the model companion of set theory. Archive for Mathematical Logic, 62(1–2), 29–53.CrossRefGoogle Scholar
Viale, M. (2016). Category forcings, $M{M}^{+++}$ , and generic absoluteness for the theory of strong forcing axioms. Journal of the American Mathematical Society, 29(3), 675–728.CrossRefGoogle Scholar
Viale, M. (2016) Martin’s maximum revisited. Archive for Mathematical Logic, 55(1–2), 295–317.CrossRefGoogle Scholar
Viale, M. (2021). Absolute model companionship, forcibility, and the continuum problem. Preprint, arXiv:2109.02285.Google Scholar
Viale, M. (2023). Strong forcing axioms and the continuum problem [after Asperó, Schindler], Exposé 1201. In Séminaire Bourbaki . Volume 2022/2023. Exposés 1197–1211. Paris: Société Mathématique de France (SMF).Google Scholar
Viale, M. (2023). Notes on model completeness, model companionship, Kaiser hulls. Available on author’s webpage.Google Scholar
Woodin, W. H. (2001). The continuum hypothesis. II. Notices of the American Mathematical Society, 48(7), 681–690.Google Scholar
Woodin, W. H. (2001). The continuum hypothesis. Part I. Notices of the American Mathematical Society, 48(6), 567–576.Google Scholar
Woodin, W. H. (2005). The continuum hypothesis. In Cori, R., Razborov, A., Todorcevic, S., and Wood, C., editors. Logic Colloquium 2000. Lecture Notes in Logic, Vol. 19. Urbana, IL: Association for Symbolic Logic, pp. 143–197.Google Scholar
Woodin, W. H. (2010). The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal (revised edition). De Gruyter Series in Logic and its Applications, Vol. 1. Berlin: Walter de Gruyter.CrossRefGoogle Scholar