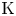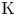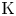1. Introduction
Algebraic $\operatorname K$![]() -theory is one of the most prominent tools for building bridges between differential topology and number theory, ever since Quillen defined it for rings $R$
-theory is one of the most prominent tools for building bridges between differential topology and number theory, ever since Quillen defined it for rings $R$![]() . One of the simplest useful features that is immediate from his many descriptions is that $\operatorname K$
. One of the simplest useful features that is immediate from his many descriptions is that $\operatorname K$![]() -spaces of rings in fact only depend on the categories of finitely generated projective modules and, more drastically, they are well-known to only depend on the perfect derived $\infty$
-spaces of rings in fact only depend on the categories of finitely generated projective modules and, more drastically, they are well-known to only depend on the perfect derived $\infty$![]() -categories. This perspective was strongly advertised by Thomasson in his work on Zariski descent and makes it natural to consider algebraic $\operatorname K$
-categories. This perspective was strongly advertised by Thomasson in his work on Zariski descent and makes it natural to consider algebraic $\operatorname K$![]() -theory as a functor on the $\infty$
-theory as a functor on the $\infty$![]() -category of stable $\infty$
-category of stable $\infty$![]() -categories. That set-up also allows one to express most other important examples in a simple fashion: For example, the algebraic $\operatorname K$
-categories. That set-up also allows one to express most other important examples in a simple fashion: For example, the algebraic $\operatorname K$![]() -theory of scheme $X$
-theory of scheme $X$![]() and Waldhausen's $\mathrm {A}$
and Waldhausen's $\mathrm {A}$![]() -theory of spaces/animae $B$
-theory of spaces/animae $B$![]() are recovered by considering the categories of perfect complexes of quasi-coherent sheaves on $X$
are recovered by considering the categories of perfect complexes of quasi-coherent sheaves on $X$![]() and of compact spectra over $B$
and of compact spectra over $B$![]() . Among the many existing categorical set-ups for $\operatorname K$
. Among the many existing categorical set-ups for $\operatorname K$![]() -theory, it furthermore has the advantage of not relying on extra structure on the categories under consideration.
-theory, it furthermore has the advantage of not relying on extra structure on the categories under consideration.
While most of the fundamental theorems of $\operatorname K$![]() -theory have been transported into this setting (Quillen's dévissage being the notable exception), there is to the best of our knowledge no account that stays within the language of stable $\infty$
-theory have been transported into this setting (Quillen's dévissage being the notable exception), there is to the best of our knowledge no account that stays within the language of stable $\infty$![]() -categories avoiding recourse to exact or Waldhausen categories. The first goal of the present note is to give such an account in particular of the localisation theorem, i.e. the fact that the $\operatorname K$
-categories avoiding recourse to exact or Waldhausen categories. The first goal of the present note is to give such an account in particular of the localisation theorem, i.e. the fact that the $\operatorname K$![]() -space functor $\operatorname {\mathcal {K}} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$
-space functor $\operatorname {\mathcal {K}} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() takes Verdier sequences to fibre sequences. Formally, such a result first appeared in the work of Blumberg, Gepner and Tabuada on the universal property of $\mathcal {K}$
takes Verdier sequences to fibre sequences. Formally, such a result first appeared in the work of Blumberg, Gepner and Tabuada on the universal property of $\mathcal {K}$![]() , i.e. that it is the initial functor with this property that furthermore takes values in ${\mathrm {E}_\infty }$
, i.e. that it is the initial functor with this property that furthermore takes values in ${\mathrm {E}_\infty }$![]() -groups and is equipped with a transformation from the core functor $\mathrm {Cr} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$
-groups and is equipped with a transformation from the core functor $\mathrm {Cr} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() . We give a somewhat minimalistic treatment of this result as well, in particular avoiding all mention of non-commutative motives. We also do not assume the input categories idempotent complete, which allows us to provide an account of the cofinality theorem.
. We give a somewhat minimalistic treatment of this result as well, in particular avoiding all mention of non-commutative motives. We also do not assume the input categories idempotent complete, which allows us to provide an account of the cofinality theorem.
All of these results rest on a version of Waldhausen's additivity theorem which identifies
via the source and target functors $s,t \colon \operatorname {Ar}(\mathcal {C}) \to \mathcal {C}$![]() ; here $\operatorname {Ar}(\mathcal {C}) = \operatorname {Fun}([1],\mathcal {C})$
; here $\operatorname {Ar}(\mathcal {C}) = \operatorname {Fun}([1],\mathcal {C})$![]() is the arrow category of $\mathcal {C}$
is the arrow category of $\mathcal {C}$![]() . We start our tour by providing a new direct proof of this fact that is heavily inspired by work of the first and third authors on hermitian $\operatorname K$
. We start our tour by providing a new direct proof of this fact that is heavily inspired by work of the first and third authors on hermitian $\operatorname K$![]() -theory and specifically Ranicki's algebraic Thom construction.
-theory and specifically Ranicki's algebraic Thom construction.
On account of the occasion, shall take the remainder of this introduction to explain the connection. To this end, we recall that in his quest to give an algebraic description of the (topological) surgery sequence, Ranicki introduced quadratic and symmetric Poincaré chain complexes (building on earlier work of Mishchenko): These consist of a perfect chain complex $C$![]() and a $\left \{\textrm {quadratic} \atop \textrm {symmetric bilinear}\right.$
and a $\left \{\textrm {quadratic} \atop \textrm {symmetric bilinear}\right.$![]() form $q$
form $q$![]() on $C$
on $C$![]() , i.e. an element $q$
, i.e. an element $q$![]() of
of

such that the associated polarisation $q_\sharp \colon C[d] \rightarrow \mathbb {R}\operatorname {Hom}_R(C,R)$![]() is an equivalence. Here $d$
is an equivalence. Here $d$![]() is said to be the dimension of $(C,q)$
is said to be the dimension of $(C,q)$![]() . Especially for $d=0$
. Especially for $d=0$![]() , Poincaré forms can be thought of as derived generalisations of $\left \{\textrm {quadratic} \atop \textrm {symmetric}\right.$
, Poincaré forms can be thought of as derived generalisations of $\left \{\textrm {quadratic} \atop \textrm {symmetric}\right.$![]() unimodular forms. In particular, Poincaré complexes permit a notion of Lagrangians, namely maps $f \colon L \rightarrow C$
unimodular forms. In particular, Poincaré complexes permit a notion of Lagrangians, namely maps $f \colon L \rightarrow C$![]() together with a null-homotopy $\eta \colon f^*q \sim 0$
together with a null-homotopy $\eta \colon f^*q \sim 0$![]() , such that the induced sequence
, such that the induced sequence
is a fibre sequence and $\eta$![]() provides the null-homotopy of the composite. As the starting point for his theory of algebraic surgery, Ranicki then proves the remarkable fact that the anima of Poincaré objects of dimension $d$
provides the null-homotopy of the composite. As the starting point for his theory of algebraic surgery, Ranicki then proves the remarkable fact that the anima of Poincaré objects of dimension $d$![]() equipped with a Lagrangian is equivalent to the anima $\Big\{\begin{smallmatrix}{\mathrm {Fm}({\mathcal {D}}^\mathrm {p}(R),\left({\rm {\unicode{x03D9}}}^\mathrm{q}\right)^{[-d-1]}) }\\ {\mathrm {Fm}({\mathcal{D}}^\mathrm {p}(R),\left({\rm {\unicode{x03D9}}}^\mathrm {s}\right)^{[-d-1]})}\end{smallmatrix}$
equipped with a Lagrangian is equivalent to the anima $\Big\{\begin{smallmatrix}{\mathrm {Fm}({\mathcal {D}}^\mathrm {p}(R),\left({\rm {\unicode{x03D9}}}^\mathrm{q}\right)^{[-d-1]}) }\\ {\mathrm {Fm}({\mathcal{D}}^\mathrm {p}(R),\left({\rm {\unicode{x03D9}}}^\mathrm {s}\right)^{[-d-1]})}\end{smallmatrix}$![]() of chain complexes equipped with a $\left \{\textrm {quadratic} \atop \textrm {symmetric}\right.$
of chain complexes equipped with a $\left \{\textrm {quadratic} \atop \textrm {symmetric}\right.$![]() form of dimension $d+1$
form of dimension $d+1$![]() . On underlying objects, the process takes such a $d$
. On underlying objects, the process takes such a $d$![]() -dimensional Poincaré object $(C,q)$
-dimensional Poincaré object $(C,q)$![]() with Lagrangian $L$
with Lagrangian $L$![]() to the fibre of $L \rightarrow C$
to the fibre of $L \rightarrow C$![]() , and the point is that both $L$
, and the point is that both $L$![]() and $C$
and $C$![]() can be reconstructed from the induced form on the fibre.
can be reconstructed from the induced form on the fibre.
Now Ranicki interpreted Lagrangians in the sense above as an algebraic incarnation of null-bordisms, owing to the fact that for $M$![]() an oriented, compact $d$
an oriented, compact $d$![]() -dimensional manifold, $\mathrm {C}^*(M)$
-dimensional manifold, $\mathrm {C}^*(M)$![]() carries a canonical $d$
carries a canonical $d$![]() -dimensional symmetric Poincaré structure, and if $\partial W = M$
-dimensional symmetric Poincaré structure, and if $\partial W = M$![]() then $\mathrm C^*(W) \rightarrow \mathrm C^*(M)$
then $\mathrm C^*(W) \rightarrow \mathrm C^*(M)$![]() is a Lagrangian. Taking one's cue from Lefschetz duality, one arrives at a notion of algebraic cobordism between two Poincaré objects such that the associated cobordism group is precisely Ranicki's (homotopy) $\left \{\textrm {quadratic} \atop \textrm {symmetric}\right.$
is a Lagrangian. Taking one's cue from Lefschetz duality, one arrives at a notion of algebraic cobordism between two Poincaré objects such that the associated cobordism group is precisely Ranicki's (homotopy) $\left \{\textrm {quadratic} \atop \textrm {symmetric}\right.$![]() Witt- (or ${\rm L}$
Witt- (or ${\rm L}$![]() -) group $\left \{{\rm L} _d^\mathrm {q}(R) \atop {\rm L} _d^\mathrm {s}(R)\right.$
-) group $\left \{{\rm L} _d^\mathrm {q}(R) \atop {\rm L} _d^\mathrm {s}(R)\right.$![]() . In the foundations of hermitian $\operatorname K$
. In the foundations of hermitian $\operatorname K$![]() -theory, one upgrades these cobordism groups to cobordism categories $\Big\{\begin{smallmatrix}\mathrm {Cob}({\mathcal{D}}^\mathrm{p}(R),\left({\rm {\unicode{x03D9}}}^\mathrm {q}\right)^{[-d]}) \\ \mathrm{Cob}({\mathcal{D}}^\mathrm{p}(R),\left({\rm {\unicode{x03D9}}}^\mathrm {s}\right)^{[-d]})\end{smallmatrix}$
-theory, one upgrades these cobordism groups to cobordism categories $\Big\{\begin{smallmatrix}\mathrm {Cob}({\mathcal{D}}^\mathrm{p}(R),\left({\rm {\unicode{x03D9}}}^\mathrm {q}\right)^{[-d]}) \\ \mathrm{Cob}({\mathcal{D}}^\mathrm{p}(R),\left({\rm {\unicode{x03D9}}}^\mathrm {s}\right)^{[-d]})\end{smallmatrix}$![]() . Then as an application of Ranicki's Thom construction, one finds
. Then as an application of Ranicki's Thom construction, one finds

where $\mathrm {He}$![]() denotes the category of forms so that $\mathrm {Fm} \simeq \mathrm {Cr}\mathrm {He}$
denotes the category of forms so that $\mathrm {Fm} \simeq \mathrm {Cr}\mathrm {He}$![]() , and by a simple cofinality argument (i.e. the higher categorical extension of Quillen's theorem A)
, and by a simple cofinality argument (i.e. the higher categorical extension of Quillen's theorem A)

where $\operatorname {Span}(\mathcal {C})$![]() denotes the category of spans in $\mathcal {C}$
denotes the category of spans in $\mathcal {C}$![]() (whenever $\mathcal {C}$
(whenever $\mathcal {C}$![]() admits pullbacks).
admits pullbacks).
In the present note, we will follow Quillen and adopt an appropriate version of span categories as the definition of algebraic $\operatorname K$![]() -spaces, more precisely we shall use $\operatorname {\mathcal {K}}(\mathcal {C}) = \Omega |\operatorname {Span}(\mathcal {C})|$
-spaces, more precisely we shall use $\operatorname {\mathcal {K}}(\mathcal {C}) = \Omega |\operatorname {Span}(\mathcal {C})|$![]() as our definition (though in the stable context it is particularly easy to see that this agrees with an implementation in terms of Segal's $\mathrm S$
as our definition (though in the stable context it is particularly easy to see that this agrees with an implementation in terms of Segal's $\mathrm S$![]() -construction). The additivity theorem therefore takes the form
-construction). The additivity theorem therefore takes the form
Treating the left-hand side as a simplistic analogue of $\mathrm {Cob}^\partial ({\mathcal {D}}^\mathrm {p}(R),{\rm {\unicode{x03D8}}} ^\mathrm {s})$![]() leads one looking for a similar replacement for $\operatorname {Span}(\mathrm {He}(\mathcal {C},({\rm {\unicode{x03D8}}} ^\mathrm {s})^{[-1]}))$
leads one looking for a similar replacement for $\operatorname {Span}(\mathrm {He}(\mathcal {C},({\rm {\unicode{x03D8}}} ^\mathrm {s})^{[-1]}))$![]() . To this end, note that there is a canonical map
. To this end, note that there is a canonical map

where $\operatorname {TwAr^{r}}$![]() denotes the twisted arrow category. One might therefore guess that
denotes the twisted arrow category. One might therefore guess that
for every stable $\mathcal {C}$![]() and we will show that this is indeed true by a rather simple argument. From here, it is then again a cofinality argument to get to the additivity theorem.
and we will show that this is indeed true by a rather simple argument. From here, it is then again a cofinality argument to get to the additivity theorem.
Notation
All categories are tacitly assumed to be $\infty$![]() -categories. $\mathrm {Cat}_\infty ^\mathrm {st}$
-categories. $\mathrm {Cat}_\infty ^\mathrm {st}$![]() denotes the category of stable categories and exact functors; $\mathrm {Sp}$
denotes the category of stable categories and exact functors; $\mathrm {Sp}$![]() and $\mathrm {An}$
and $\mathrm {An}$![]() denote the categories of spectra and of $\infty$
denote the categories of spectra and of $\infty$![]() -groupoids (a.k.a. spaces or animae), and
-groupoids (a.k.a. spaces or animae), and
denote the groupoid-core, the space- and the spectrum-valued $\operatorname K$![]() -theory functors.
-theory functors.
2. Localisation properties of functors on $\mathrm {Cat}_\infty ^\mathrm {st}$
In the present section, we briefly recall various notions of additive and localising functors, and give a brief discussion of their relation, in particular establishing a higher categorical version of Waldhausen's localisation criterion. We will assume the reader is familiar with Verdier sequences, that is sequences that are simultaneously fibre and cofibre sequences in $\mathrm {Cat}_\infty ^\mathrm {st}$![]() , and refer to [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, Appendix A] for a thorough discussion. Let us recall explicitly that a split Verdier sequence, i.e. a Verdier sequence in which both the inclusion and the projection admit both adjoints, is the same thing as a stable recollement or a semi-orthogonal decomposition into stable subcategories, see [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, § A.2].
, and refer to [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, Appendix A] for a thorough discussion. Let us recall explicitly that a split Verdier sequence, i.e. a Verdier sequence in which both the inclusion and the projection admit both adjoints, is the same thing as a stable recollement or a semi-orthogonal decomposition into stable subcategories, see [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, § A.2].
For $\mathcal {C}$![]() stable, we let $\operatorname {Seq}(\mathcal {C})$
stable, we let $\operatorname {Seq}(\mathcal {C})$![]() denote the category of bifibre sequences in $\mathcal {C}$
denote the category of bifibre sequences in $\mathcal {C}$![]() , i.e. the full subcategory of $\operatorname {Fun}([1] \times [1],\mathcal {C})$
, i.e. the full subcategory of $\operatorname {Fun}([1] \times [1],\mathcal {C})$![]() consisting of cartesian squares with lower left corner $0$
consisting of cartesian squares with lower left corner $0$![]() . For example via
. For example via

it is equivalent to $\operatorname {Ar}(\mathcal {C}) = \operatorname {Fun}([1],\mathcal {C})$![]() , and we shall frequently make this identification implicitly.
, and we shall frequently make this identification implicitly.
We very briefly recall some fundamental terminology concerning Verdier sequences: A square

of stable categories and exact functors is a Verdier square if it is cartesian and both vertical maps are Verdier projections (i.e. localisations). It is called left or right split if both vertical maps are left or right split Verdier projections, respectively (i.e. right or left Bousfield localisations, note the order reversal). Finally, it is called a Karoubi square if it becomes cartesian in the localisation of $\mathrm {Cat}_\infty ^\mathrm {st}$![]() at the Karoubi-equivalences (i.e. dense inclusions), and its vertical maps are Karoubi projections, i.e. Verdier projections onto dense subcategories of $\mathcal {D}$
at the Karoubi-equivalences (i.e. dense inclusions), and its vertical maps are Karoubi projections, i.e. Verdier projections onto dense subcategories of $\mathcal {D}$![]() and $\mathcal {D}'$
and $\mathcal {D}'$![]() , respectively.
, respectively.
Definition 2.1 Let $\mathcal {E}$![]() be a category with finite limits. Then we call a functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$
be a category with finite limits. Then we call a functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$![]() with $F(0) \simeq \, \ast$
with $F(0) \simeq \, \ast$![]()
(i) extension splitting if the combined fibre–cofibre map $(\operatorname {fib},\operatorname {cof}) \colon \operatorname {Seq}(\mathcal {C}) \rightarrow \mathcal {C}^2$
 induces an equivalence
\[ F(\operatorname{Seq}(\mathcal{C})) \longrightarrow F(\mathcal{C})^2 \]for every $\mathcal {C} \in \mathrm {Cat}_\infty ^\mathrm {st}$
induces an equivalence
\[ F(\operatorname{Seq}(\mathcal{C})) \longrightarrow F(\mathcal{C})^2 \]for every $\mathcal {C} \in \mathrm {Cat}_\infty ^\mathrm {st}$
 ,
,
(ii) additive if $F$
 takes every split Verdier square to a cartesian square in $\mathcal {E}$
takes every split Verdier square to a cartesian square in $\mathcal {E}$ ,
,(iii) Verdier-localising if $F$
 takes every Verdier square to a cartesian square in $\mathcal {E}$
takes every Verdier square to a cartesian square in $\mathcal {E}$ , and finally
, and finally(iv) Karoubi-localising if $F$
 takes every Karoubi square to a cartesian square in $\mathcal {E}$
takes every Karoubi square to a cartesian square in $\mathcal {E}$ .
.
From the discussion above, it is hopefully obvious that the second, third and fourth conditions are successively stronger. We also record:
Observation 2.2 All four types of functors above preserve pairwise products and moreover any group-like additive functor splits extensions.
Since $\mathrm {Cat}_\infty ^\mathrm {st}$![]() is semi-additive it follows that any product preserving functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$
is semi-additive it follows that any product preserving functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$![]() uniquely lifts to $\operatorname {Mon}_{\mathrm {E}_\infty }(\mathcal {E})$
uniquely lifts to $\operatorname {Mon}_{\mathrm {E}_\infty }(\mathcal {E})$![]() , and we call $F$
, and we call $F$![]() group-like if it happens to take values in $\operatorname {Grp}_{\mathrm {E}_\infty }(\mathcal {E})$
group-like if it happens to take values in $\operatorname {Grp}_{\mathrm {E}_\infty }(\mathcal {E})$![]() . The groupoid-core functor $\mathrm {Cr} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$
. The groupoid-core functor $\mathrm {Cr} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() is an example of a non-group-like Verdier-localising functor, and in particular shows that general additive functors do not split extensions.
is an example of a non-group-like Verdier-localising functor, and in particular shows that general additive functors do not split extensions.
Proof. For the preservation of products for additive functors, simply note that

is a split Verdier square. To see that extension splitting functors preserve products, note that the map from their definition factors as
The composite being an equivalence implies that $F(\operatorname {Seq}(\mathcal {C})) \longrightarrow \mathcal {F}(\mathcal {C}^2)$![]() admits a retraction, and it also admits a section induced by the functor $\mathcal {C}^2 \rightarrow \operatorname {Seq}(\mathcal {C})$
admits a retraction, and it also admits a section induced by the functor $\mathcal {C}^2 \rightarrow \operatorname {Seq}(\mathcal {C})$![]() taking $(x,y)$
taking $(x,y)$![]() to the split fibre sequence $x \rightarrow x \oplus y \rightarrow y$
to the split fibre sequence $x \rightarrow x \oplus y \rightarrow y$![]() . Thus, the first map in the above composition is an equivalence, and so is the second. But generally, the map $F(\mathcal {C} \oplus D) \rightarrow F(\mathcal {C}) \times F(\mathcal {D})$
. Thus, the first map in the above composition is an equivalence, and so is the second. But generally, the map $F(\mathcal {C} \oplus D) \rightarrow F(\mathcal {C}) \times F(\mathcal {D})$![]() is a retract of $F((\mathcal {C} \oplus \mathcal {D}) \oplus (\mathcal {C} \oplus \mathcal {D})) \rightarrow F(\mathcal {C} \oplus \mathcal {D}) \times F(\mathcal {C} \oplus \mathcal {D})$
is a retract of $F((\mathcal {C} \oplus \mathcal {D}) \oplus (\mathcal {C} \oplus \mathcal {D})) \rightarrow F(\mathcal {C} \oplus \mathcal {D}) \times F(\mathcal {C} \oplus \mathcal {D})$![]() , which we have just shown is an equivalence.
, which we have just shown is an equivalence.
The second claim follows from

being a split Verdier square together with the splitting lemma (in the category of ${\mathrm {E}_\infty }$![]() -groups in $\mathcal {E}$
-groups in $\mathcal {E}$![]() ); the splitting lemma itself is a direct consequence for example of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, Lemma 1.5.12].
); the splitting lemma itself is a direct consequence for example of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, Lemma 1.5.12].
We shall now discuss the relation between the four notions above more closely.
Additive vs extension-splitting functors
We start with an observation from [Reference Barwick, Glasman, Mathew and Nikolaus2].
Definition 2.3 Let $\mathrm {KK^{\mathrm {st}}}$![]() denote the ordinary category with objects stable categories and $\operatorname {Hom}_\mathrm {KK^{\mathrm {st}}}(\mathcal {C},\mathcal {D}) = \operatorname K_0(\operatorname {Fun^{ex}}(\mathcal {C},\mathcal {D}))$
denote the ordinary category with objects stable categories and $\operatorname {Hom}_\mathrm {KK^{\mathrm {st}}}(\mathcal {C},\mathcal {D}) = \operatorname K_0(\operatorname {Fun^{ex}}(\mathcal {C},\mathcal {D}))$![]() and composition induced by functor composition.
and composition induced by functor composition.
Recall that $\operatorname K_0(\mathcal {C})$![]() is defined as the quotient of the monoid $\pi _0(\mathrm {Cr} \mathcal {C})$
is defined as the quotient of the monoid $\pi _0(\mathrm {Cr} \mathcal {C})$![]() (under direct sum) by the congruence relation generated by $x + z \sim y$
(under direct sum) by the congruence relation generated by $x + z \sim y$![]() for every bifibre sequence $x \rightarrow y \rightarrow z$
for every bifibre sequence $x \rightarrow y \rightarrow z$![]() in $\mathcal {C}$
in $\mathcal {C}$![]() .
.
The natural transformation
gives a functor $\mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {KK^{\mathrm {st}}}$![]() and we call an exact functor $\mathcal {C} \rightarrow \mathcal {D}$
and we call an exact functor $\mathcal {C} \rightarrow \mathcal {D}$![]() a universal $\operatorname K$
a universal $\operatorname K$![]() -equivalence if it maps to an isomorphism in $\mathrm {KK^{\mathrm {st}}}$
-equivalence if it maps to an isomorphism in $\mathrm {KK^{\mathrm {st}}}$![]() .
.
For example, if
is a left split Verdier sequence where $g$![]() and $q$
and $q$![]() denote the left adjoints of $f$
denote the left adjoints of $f$![]() and $p$
and $p$![]() , respectively, then the functor
, respectively, then the functor
is a universal $\operatorname K$![]() -equivalence: The inverse functor is $f + q \colon \mathcal {C} \oplus \mathcal {E} \rightarrow \mathcal {D}$
-equivalence: The inverse functor is $f + q \colon \mathcal {C} \oplus \mathcal {E} \rightarrow \mathcal {D}$![]() , with the composition $\mathcal {C} \oplus \mathcal {E} \rightarrow \mathcal {C} \oplus \mathcal {E}$
, with the composition $\mathcal {C} \oplus \mathcal {E} \rightarrow \mathcal {C} \oplus \mathcal {E}$![]() the identity already in $\mathrm {Cat}_\infty ^\mathrm {st}$
the identity already in $\mathrm {Cat}_\infty ^\mathrm {st}$![]() , and the other composite contained in a fibre sequence
, and the other composite contained in a fibre sequence
see the discussion preceeding [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, Lemma A.2.11], so
in $\operatorname K_0\operatorname {Fun^{ex}}(\mathcal {D},\mathcal {D})$![]() . The analogous claim for right split Verdier sequences holds as well.
. The analogous claim for right split Verdier sequences holds as well.
Proposition 2.4 For a functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$![]() with $F(0) \simeq \, \ast$
with $F(0) \simeq \, \ast$![]() the following are equivalent:
the following are equivalent:
(i) $F$
 inverts universal $\operatorname K$
inverts universal $\operatorname K$ -equivalences and preserves pairwise products,
-equivalences and preserves pairwise products,(ii) $F$
 is extension splitting, and
is extension splitting, and(iii) $F$
 is additive and group-like.
is additive and group-like.
The proof builds on the following classical observation of Waldhausen. We denote the functors extracting the first, second and third entry of a fibre sequence by $\operatorname {fib}, m, \operatorname {cof} \colon \operatorname {Seq}(\mathcal {C})\to \mathcal {C}$![]() .
.
Lemma 2.5 If $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$![]() is extension splitting then there is a canonical equivalence between $m_*$
is extension splitting then there is a canonical equivalence between $m_*$![]() and
and
In particular, any extension splitting functor is group-like with the inversion map of $F(\mathcal {C})$![]() induced by the shift functor $(-)^{[1]} \colon \mathcal {C} \rightarrow \mathcal {C}$
induced by the shift functor $(-)^{[1]} \colon \mathcal {C} \rightarrow \mathcal {C}$![]() . Furthermore, a product preserving functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$
. Furthermore, a product preserving functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$![]() with $F(0) \simeq 0$
with $F(0) \simeq 0$![]() is extension splitting if and only if $F$
is extension splitting if and only if $F$![]() takes
takes
to an equivalence for every $\mathcal {C} \in \mathrm {Cat}_\infty ^\mathrm {st}$![]() .
.
Proof. Simply note that the two functors
have equivalent evaluations at the first and third spots. Consequently, the latter one induces the identity on $F(\operatorname {Seq}(\mathcal {C}))$![]() by assumption. But post-composing with the evaluation at the middle term gives $\operatorname {fib}_* + \operatorname {cof}_*$
by assumption. But post-composing with the evaluation at the middle term gives $\operatorname {fib}_* + \operatorname {cof}_*$![]() (since $\mathcal {F}$
(since $\mathcal {F}$![]() preserves products by 2.2
). The final item of the first claim follows from the natural bifibre sequence $x \rightarrow 0 \rightarrow x^{[1]}$
preserves products by 2.2
). The final item of the first claim follows from the natural bifibre sequence $x \rightarrow 0 \rightarrow x^{[1]}$![]() .
.
For the second part, consider the equivalence

which tells us that $(\operatorname {cof},\operatorname {fib}^{[1]})_* \colon F\operatorname {Seq}(\mathcal {C}) \rightarrow F(\mathcal {C}^2) \simeq F(\mathcal {C})^2$![]() is an equivalence. Now pre-compose with the shifting equivalence in the second factor.
is an equivalence. Now pre-compose with the shifting equivalence in the second factor.
Proof of proposition 2.4 The implication (i) $\Rightarrow$![]() (ii) is immediate from the example preceding the statement. Conversely, being extension splitting implies that the functor
(ii) is immediate from the example preceding the statement. Conversely, being extension splitting implies that the functor
factors over $\mathrm {KK^{\mathrm {st}}}$![]() (which immediately implies (i)): We have to check that for a bifibre sequence $f \rightarrow g \rightarrow h$
(which immediately implies (i)): We have to check that for a bifibre sequence $f \rightarrow g \rightarrow h$![]() of exact functors $\mathcal {C} \rightarrow \mathcal {D}$
of exact functors $\mathcal {C} \rightarrow \mathcal {D}$![]() , say, we have $[f_*] + [h_*] = [g_*]$
, say, we have $[f_*] + [h_*] = [g_*]$![]() in $\pi _0\operatorname {Hom}_\mathcal {E}(F(\mathcal {C}),F(\mathcal {D}))$
in $\pi _0\operatorname {Hom}_\mathcal {E}(F(\mathcal {C}),F(\mathcal {D}))$![]() . But $f,g$
. But $f,g$![]() and $h$
and $h$![]() define a map $\mathcal {C} \rightarrow \operatorname {Seq}(\mathcal {D})$
define a map $\mathcal {C} \rightarrow \operatorname {Seq}(\mathcal {D})$![]() whence the claim follows from the previous lemma.
whence the claim follows from the previous lemma.
That (iii) implies (ii) is part of 2.2, and for the final implication, the previous lemma takes care of $F$![]() being group-like, while the example preceding the statement implies additivity.
being group-like, while the example preceding the statement implies additivity.
Remark 2.6 The analogous statement in the situation of Poincaré categories from [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle4–Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle6], instead of merely stable ones, is not true. The analogue of an extension splitting functor is a functor $F \colon \mathrm {Cat}^{\mathrm p}_\infty \rightarrow \mathcal {E}$![]() that equates metabolic and hyperbolic Poincaré categories in the sense that the canonical upgrade $\operatorname {Met}(\mathcal {C},{\rm {\unicode{x03D8}}} ) \rightarrow \operatorname {Hyp}(\mathcal {C})$
that equates metabolic and hyperbolic Poincaré categories in the sense that the canonical upgrade $\operatorname {Met}(\mathcal {C},{\rm {\unicode{x03D8}}} ) \rightarrow \operatorname {Hyp}(\mathcal {C})$![]() of the functor $(s,\operatorname {cof}) \colon \operatorname {Ar}(\mathcal {C}) \rightarrow \mathcal {C}^2$
of the functor $(s,\operatorname {cof}) \colon \operatorname {Ar}(\mathcal {C}) \rightarrow \mathcal {C}^2$![]() to a Poincaré functor induces an equivalence for every Poincaré category $(\mathcal {C},{\rm {\unicode{x03D8}}} )$
to a Poincaré functor induces an equivalence for every Poincaré category $(\mathcal {C},{\rm {\unicode{x03D8}}} )$![]() . It is not difficult to see that such a functor inverts universal $\operatorname {GW}$
. It is not difficult to see that such a functor inverts universal $\operatorname {GW}$![]() -equivalences (defined using the Poincaré refinement of $\operatorname {Fun^{ex}}(\mathcal {C},\mathcal {D})$
-equivalences (defined using the Poincaré refinement of $\operatorname {Fun^{ex}}(\mathcal {C},\mathcal {D})$![]() from [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle4, § 6.2]).
from [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle4, § 6.2]).
By an argument of Schlichting, a product preserving functor with this property satisfies the isotropy decomposition principle of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, § 3.2] (i.e. [Reference Ranicki16, Proposition 6.7 (2)] suffices as input to run the argument from [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5]), but it need not be additive in the sense of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, § 1.5] even if $\mathcal {E}$![]() is the category of spectra; a counterexample is the composition $\mathrm H\operatorname {GW}_0 \colon \mathrm {Cat}^{\mathrm p}_\infty \rightarrow \mathcal {A}\mathrm {b} \rightarrow {\mathrm {Sp}}$
is the category of spectra; a counterexample is the composition $\mathrm H\operatorname {GW}_0 \colon \mathrm {Cat}^{\mathrm p}_\infty \rightarrow \mathcal {A}\mathrm {b} \rightarrow {\mathrm {Sp}}$![]() . By contrast, 2.4 or a direct check implies that $\mathrm H\operatorname K_0 \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow {\mathrm {Sp}}$
. By contrast, 2.4 or a direct check implies that $\mathrm H\operatorname K_0 \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow {\mathrm {Sp}}$![]() is additive (as are all $\mathrm H\operatorname K_i$
is additive (as are all $\mathrm H\operatorname K_i$![]() ).
).
The reason for this difference is that the adjoints in a split Poincaré–Verdier sequence are not themselves Poincaré functors.
Additive vs Verdier-localising functors
The relation between additive and Verdier-localising functors is encapsulated by the following result, whose essence appears in Waldhausen's work as the fibration theorem [Reference Waldhausen19, § 1.6]. For a stable subcategory $\mathcal {A} \subseteq \mathcal {B}$![]() let $\operatorname {Fun}^\mathcal {A}(I,\mathcal {B})$
let $\operatorname {Fun}^\mathcal {A}(I,\mathcal {B})$![]() denote the full subcategory of $\operatorname {Fun}(I,\mathcal {B})$
denote the full subcategory of $\operatorname {Fun}(I,\mathcal {B})$![]() , spanned by those diagrams which take each map in $I$
, spanned by those diagrams which take each map in $I$![]() to an equivalence modulo $\mathcal {A}$
to an equivalence modulo $\mathcal {A}$![]() (i.e. a map in $\mathcal {B}$
(i.e. a map in $\mathcal {B}$![]() whose cofibre lies in $\mathcal {A}$
whose cofibre lies in $\mathcal {A}$![]() ). It is easily checked to be a stable subcategory of $\operatorname {Fun}(I,\mathcal {B})$
). It is easily checked to be a stable subcategory of $\operatorname {Fun}(I,\mathcal {B})$![]() .
.
Theorem 2.7 (Waldhausen)
Given a Verdier sequence $\mathcal {A} \rightarrow \mathcal {B} \rightarrow \mathcal {B}/\mathcal {A}$![]() the canonical maps $\mathrm {const} \colon \mathcal {B} \rightarrow \operatorname {Fun}^\mathcal {A}([n],\mathcal {B})$
the canonical maps $\mathrm {const} \colon \mathcal {B} \rightarrow \operatorname {Fun}^\mathcal {A}([n],\mathcal {B})$![]() induce a bifibre sequence
induce a bifibre sequence
of ${\mathrm {E}_\infty }$![]() -groups, whenever $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$
-groups, whenever $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() is group-like and additive; here $F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))$
is group-like and additive; here $F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))$![]() is regarded as a simplicial ${\mathrm {E}_\infty }$
is regarded as a simplicial ${\mathrm {E}_\infty }$![]() -group and the vertical bars denote its colimit.
-group and the vertical bars denote its colimit.
To see the implications of this statement, recall that sifted colimits in $\operatorname {Grp}_{\mathrm {E}_\infty }(\mathrm {An})$![]() are preserved by the forgetful functor to $\mathrm {An}$
are preserved by the forgetful functor to $\mathrm {An}$![]() so the final term is simply the geometric realisation of the simplicial anima $F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))$
so the final term is simply the geometric realisation of the simplicial anima $F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))$![]() . Furthermore, for $M \rightarrow N \rightarrow K$
. Furthermore, for $M \rightarrow N \rightarrow K$![]() (with chosen null homotopy of the composite) being a bifibre sequence in $\operatorname {Grp}_{\mathrm {E}_\infty }(\mathrm {An})$
(with chosen null homotopy of the composite) being a bifibre sequence in $\operatorname {Grp}_{\mathrm {E}_\infty }(\mathrm {An})$![]() is equivalent to the underlying sequence of anima being a fibre sequence (over the unit of $K$
is equivalent to the underlying sequence of anima being a fibre sequence (over the unit of $K$![]() ) and the map $\pi _0N \rightarrow \pi _0K$
) and the map $\pi _0N \rightarrow \pi _0K$![]() being surjective.
being surjective.
Proof. Denote by $\mathrm {dec} \colon \operatorname {Fun}(\Delta ^\mathrm {op},\mathcal {C}) \rightarrow \operatorname {Fun}(\Delta ^\mathrm {op},\mathcal {C})$![]() the décalage functor induced by $[0] * - \colon \Delta \rightarrow \Delta$
the décalage functor induced by $[0] * - \colon \Delta \rightarrow \Delta$![]() . Per construction, the inclusions $[n] \rightarrow [0]*[n] = [1+n]$
. Per construction, the inclusions $[n] \rightarrow [0]*[n] = [1+n]$![]() and $[0] \rightarrow [0]*[n] = [1+n]$
and $[0] \rightarrow [0]*[n] = [1+n]$![]() induce natural transformations $\mathrm {dec} \Rightarrow \mathrm {id}$
induce natural transformations $\mathrm {dec} \Rightarrow \mathrm {id}$![]() and $\mathrm {dec} \Rightarrow \mathrm {ev}_0$
and $\mathrm {dec} \Rightarrow \mathrm {ev}_0$![]() . Recall also that $\mathrm {dec}(X)$
. Recall also that $\mathrm {dec}(X)$![]() is always a split-simplicial object over $X_0$
is always a split-simplicial object over $X_0$![]() using the latter maps and the lowest degeneracies $s_0$
using the latter maps and the lowest degeneracies $s_0$![]() of $X$
of $X$![]() (which do not feature in the simplicial structure of $\mathrm {dec}(X)$
(which do not feature in the simplicial structure of $\mathrm {dec}(X)$![]() ); in particular, $X_0$
); in particular, $X_0$![]() is a colimit of $\mathrm {dec}(X)$
is a colimit of $\mathrm {dec}(X)$![]() by [Reference Lurie12, Lemma 6.1.3.16].
by [Reference Lurie12, Lemma 6.1.3.16].
Now consider the map $d_0 \colon \operatorname {Fun}^\mathcal {A}([1+n],\mathcal {B}) \rightarrow \operatorname {Fun}^\mathcal {A}([n],\mathcal {B})$![]() . It is easily checked to be a right split Verdier projection with kernel $\mathcal {A}$
. It is easily checked to be a right split Verdier projection with kernel $\mathcal {A}$![]() , the requisite fully faithful right adjoint given by
, the requisite fully faithful right adjoint given by
It follows that $\mathrm {dec} F \colon \operatorname {Fun}^\mathcal {A}([-],\mathcal {B}) \rightarrow F\operatorname {Fun}^\mathcal {A}([-],\mathcal {B})$![]() is equifibred, i.e. that
is equifibred, i.e. that

is cartesian for every $f \colon [m] \rightarrow [n]$![]() in $\Delta$
in $\Delta$![]() : A square of ${\mathrm {E}_\infty }$
: A square of ${\mathrm {E}_\infty }$![]() -groups with right vertical map $\pi _0$
-groups with right vertical map $\pi _0$![]() -surjective (in the case at hand even split surjective) is cartesian if and only if the induced map on vertical fibres over $0$
-surjective (in the case at hand even split surjective) is cartesian if and only if the induced map on vertical fibres over $0$![]() is an equivalence. But this map identifies with the identity of $F(\mathcal {A})$
is an equivalence. But this map identifies with the identity of $F(\mathcal {A})$![]() by 2.4 and the analysis above. Note also that prior to applying $F$
by 2.4 and the analysis above. Note also that prior to applying $F$![]() , the square above is not necessarily cartesian (e.g. for $f=d_0$
, the square above is not necessarily cartesian (e.g. for $f=d_0$![]() ), and in particular not a (right split) Verdier square.
), and in particular not a (right split) Verdier square.
It now follows from the equifibrancy lemma of Segal and Rezk, see e.g. [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, Lemma 3.3.14] for a treatment in the present language, that

is cartesian, or in other words that
is a fibre sequence. To finally see that it is also a cofibre sequence, note that the right-hand map is (per construction) simply the inclusion of the $0$![]() -simplices into the realisation which induces a surjection on $\pi _0$
-simplices into the realisation which induces a surjection on $\pi _0$![]() for every simplicial anima.
for every simplicial anima.
Remark 2.8 We will give another proof employing the relative $\operatorname {Q}$![]() -construction in the final section, which passes to the Poincaré setting (though we will not pursue that here).
-construction in the final section, which passes to the Poincaré setting (though we will not pursue that here).
Per construction, the projection $\operatorname {Fun}^\mathcal {A}([n],\mathcal {B}) \rightarrow \operatorname {Fun}([n],\mathcal {B}/\mathcal {A})$![]() takes values in the subcategory spanned by those functors taking all maps in $[n]$
takes values in the subcategory spanned by those functors taking all maps in $[n]$![]() to equivalences in $\mathcal {B}/\mathcal {A}$
to equivalences in $\mathcal {B}/\mathcal {A}$![]() . Since $|[n]| \simeq \, \ast$
. Since $|[n]| \simeq \, \ast$![]() these span the essential image of the fully faithful functor $\mathrm {const} \colon \mathcal {B}/\mathcal {A} \rightarrow \operatorname {Fun}([n],\mathcal {B}/\mathcal {A})$
these span the essential image of the fully faithful functor $\mathrm {const} \colon \mathcal {B}/\mathcal {A} \rightarrow \operatorname {Fun}([n],\mathcal {B}/\mathcal {A})$![]() , so we obtain a map
, so we obtain a map
for every functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {A}$![]() . In particular:
. In particular:
Corollary 2.9 A grouplike additive functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() is Verdier-localising if and only if:
is Verdier-localising if and only if:
(i) the canonical map $|F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))| \longrightarrow F(\mathcal {B}/\mathcal {A})$
 constructed above is an inclusion of path components for every Verdier sequence $\mathcal {A} \rightarrow \mathcal {B} \rightarrow \mathcal {B}/\mathcal {A}$
constructed above is an inclusion of path components for every Verdier sequence $\mathcal {A} \rightarrow \mathcal {B} \rightarrow \mathcal {B}/\mathcal {A}$ , and
, and(ii) for every Verdier square
we have \[ \mathrm{im}(\pi_0F(\mathcal{B}) \rightarrow \pi_0F(\mathcal{B}/\mathcal{A})) = f^{{-}1}\mathrm{im}(\pi_0F(\mathcal{B}') \rightarrow \pi_0F(\mathcal{B}'/\mathcal{A})) . \]
\[ \mathrm{im}(\pi_0F(\mathcal{B}) \rightarrow \pi_0F(\mathcal{B}/\mathcal{A})) = f^{{-}1}\mathrm{im}(\pi_0F(\mathcal{B}') \rightarrow \pi_0F(\mathcal{B}'/\mathcal{A})) . \]
For example, $|F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))| \rightarrow F(\mathcal {B}/\mathcal {A})$![]() is an equivalence for every Verdier sequence if and only if $F$
is an equivalence for every Verdier sequence if and only if $F$![]() is Verdier-localising and $\pi _0F (\mathcal {B}) \rightarrow \pi _0 F(\mathcal {B}/\mathcal {A})$
is Verdier-localising and $\pi _0F (\mathcal {B}) \rightarrow \pi _0 F(\mathcal {B}/\mathcal {A})$![]() is surjective for all Verdier sequences (since $\pi _0 F\mathcal {B} \rightarrow \pi _0|\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))|$
is surjective for all Verdier sequences (since $\pi _0 F\mathcal {B} \rightarrow \pi _0|\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))|$![]() is always surjective). We also obtain:
is always surjective). We also obtain:
Corollary 2.10 An additive functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {Sp}$![]() is Verdier-localising if and only if the canonical map $|F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))| \longrightarrow F(\mathcal {B}/\mathcal {A})$
is Verdier-localising if and only if the canonical map $|F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))| \longrightarrow F(\mathcal {B}/\mathcal {A})$![]() constructed above is an equivalence for every Verdier sequence $\mathcal {A} \rightarrow \mathcal {B} \rightarrow \mathcal {B}/\mathcal {A}$
constructed above is an equivalence for every Verdier sequence $\mathcal {A} \rightarrow \mathcal {B} \rightarrow \mathcal {B}/\mathcal {A}$![]() .
.
Proof. From 2.7 it follows immediately that for additive $F$![]() the cofibre of $F(\mathcal {A}) \rightarrow F(\mathcal {B})$
the cofibre of $F(\mathcal {A}) \rightarrow F(\mathcal {B})$![]() is given by the spectrification of $(|\Omega ^\infty F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))|, |\Omega ^{\infty -1}F(\operatorname {Fun}^\mathcal {A}([-], \mathcal {B}))|, \dots )$
is given by the spectrification of $(|\Omega ^\infty F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))|, |\Omega ^{\infty -1}F(\operatorname {Fun}^\mathcal {A}([-], \mathcal {B}))|, \dots )$![]() . But this is also a formula for the colimit of $F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))$
. But this is also a formula for the colimit of $F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))$![]() , so we learn that
, so we learn that
is a bifibre sequence. It follows immediately that $F$![]() takes Verdier sequences to fibre sequences if and only $|F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))| \longrightarrow F(\mathcal {B}/\mathcal {A})$
takes Verdier sequences to fibre sequences if and only $|F(\operatorname {Fun}^\mathcal {A}([-],\mathcal {B}))| \longrightarrow F(\mathcal {B}/\mathcal {A})$![]() is an equivalence for all $\mathcal {A} \to \mathcal {B}$
is an equivalence for all $\mathcal {A} \to \mathcal {B}$![]() . But for stable targets, this suffices by the following observation.
. But for stable targets, this suffices by the following observation.
Lemma 2.11 If $\mathcal {E}$![]() is stable, then a functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$
is stable, then a functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$![]() with $F(0) \simeq 0$
with $F(0) \simeq 0$![]() is Verdier-localising if and only if it takes Verdier sequences to (bi)fibre sequences.
is Verdier-localising if and only if it takes Verdier sequences to (bi)fibre sequences.
The proof is immediate from the fact that in a stable category a commutative square is cartesian if and only if the induced map on (horizontal, say) fibres is an equivalence.
Verdier-localising vs Karoubi-localising functors
The following is easy to check:
Observation 2.12 A functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$![]() with $F(0) \simeq 0$
with $F(0) \simeq 0$![]() is Karoubi-localising if and only if it is Verdier-localising and inverts Karoubi equivalences.
is Karoubi-localising if and only if it is Verdier-localising and inverts Karoubi equivalences.
It is therefore tempting to construct a Karoubi-localising functor from a Verdier-localising one by forming
(the universal approximation of $F$![]() from the right by a functor inverting Karoubi equivalences). If $F$
from the right by a functor inverting Karoubi equivalences). If $F$![]() is additive then this functor is obviously additive again, but if $F$
is additive then this functor is obviously additive again, but if $F$![]() is Verdier-localising $F \circ (-)^\natural$
is Verdier-localising $F \circ (-)^\natural$![]() need not be so; the standard counterexample being $\mathrm {K} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {Sp}$
need not be so; the standard counterexample being $\mathrm {K} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {Sp}$![]() , the connective $\operatorname K$
, the connective $\operatorname K$![]() -spectrum.
-spectrum.
Lemma 2.13 If $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$![]() is Verdier-localising, then $F \circ (-)^\natural \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$
is Verdier-localising, then $F \circ (-)^\natural \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathcal {E}$![]() is Karoubi-localising if $F$
is Karoubi-localising if $F$![]() takes pullback squares in $\mathrm {Cat}_\infty ^\mathrm {st}$
takes pullback squares in $\mathrm {Cat}_\infty ^\mathrm {st}$![]() , whose vertical legs are dense inclusions, to pullbacks in $\mathcal {E}$
, whose vertical legs are dense inclusions, to pullbacks in $\mathcal {E}$![]() .
.
Proof. Given the previous observation, it suffices to check that $F \circ (-)^\natural$![]() is again Verdier-localising. Given then a Verdier square
is again Verdier-localising. Given then a Verdier square

with common vertical fibre $F$![]() consider the diagram
consider the diagram

Since idempotent completion preserves limits (e.g. by the comments following 3.5) the outer square is still a pullback. Furthermore, the lower vertical maps are dense inclusions (e.g. since their source and target receive compatible dense inclusions from $C = A/F$![]() and $D=B/F$
and $D=B/F$![]() , respectively). It now follows that both squares are in fact pullbacks (in particular, the upper one is a Verdier square): For the lower one, it is clear that the map form $A^\natural /F$
, respectively). It now follows that both squares are in fact pullbacks (in particular, the upper one is a Verdier square): For the lower one, it is clear that the map form $A^\natural /F$![]() to the pullback is fully faithful, and essential surjectivity follows from the essential surjectivity of $B^\natural \rightarrow B^\natural /F$
to the pullback is fully faithful, and essential surjectivity follows from the essential surjectivity of $B^\natural \rightarrow B^\natural /F$![]() and it then formally follows for the upper one.
and it then formally follows for the upper one.
Per assumption, $F$![]() therefore takes both individual squares to pullbacks, and consequently also the outer diagram.
therefore takes both individual squares to pullbacks, and consequently also the outer diagram.
We do not know a similar criterion for the functors $F \circ (-)^\mathrm {min}$![]() , which are again additive whenever $F$
, which are again additive whenever $F$![]() is, but usually lose their localisation properties.
is, but usually lose their localisation properties.
3. A reminder on $\operatorname K$ -spaces via the $\operatorname {Q}$
-spaces via the $\operatorname {Q}$ -construction
-construction
The goal of the present section is to recall the $\operatorname {Q}$![]() -construction, its relation to span categories and $\operatorname K$
-construction, its relation to span categories and $\operatorname K$![]() -theory. Let $\operatorname {TwAr^{r}}(\mathcal {D})$
-theory. Let $\operatorname {TwAr^{r}}(\mathcal {D})$![]() denote the version of the twisted arrow category such that $(s,t) \colon \operatorname {TwAr^{r}}(\mathcal {D}) \rightarrow \mathcal {D} \times \mathcal {D}^\mathrm {op}$
denote the version of the twisted arrow category such that $(s,t) \colon \operatorname {TwAr^{r}}(\mathcal {D}) \rightarrow \mathcal {D} \times \mathcal {D}^\mathrm {op}$![]() is the right fibration classifying $\operatorname {Hom}_\mathcal {D} \colon \mathcal {D}^\mathrm {op} \times \mathcal {D} \rightarrow \mathrm {An}$
is the right fibration classifying $\operatorname {Hom}_\mathcal {D} \colon \mathcal {D}^\mathrm {op} \times \mathcal {D} \rightarrow \mathrm {An}$![]() .
.
Definition 3.1 For a category $\mathcal {C}$![]() with finite limits let $\operatorname {Q}_n(\mathcal {C})$
with finite limits let $\operatorname {Q}_n(\mathcal {C})$![]() be the full subcategory of $\operatorname {Fun}(\operatorname {TwAr^{r}}([n]),\mathcal {D})$
be the full subcategory of $\operatorname {Fun}(\operatorname {TwAr^{r}}([n]),\mathcal {D})$![]() spanned by those diagrams which take every square of the form
spanned by those diagrams which take every square of the form

to a cartesian square in $\mathcal {C}$![]() .
.
One readily checks that these categories assemble into a simplicial subcategory of $\operatorname {Fun}(\operatorname {TwAr^{r}}([-]),\mathcal {D})$![]() , and in total we obtain a functor
, and in total we obtain a functor
which we will refer to as the $\operatorname {Q}$![]() -construction.
-construction.
Proposition 3.2 (Barwick)
For every category $\mathcal {C}$![]() with finite limits, the simplicial category $\operatorname {Q}(\mathcal {C})$
with finite limits, the simplicial category $\operatorname {Q}(\mathcal {C})$![]() is a complete Segal object in $\mathrm {Cat}_\infty$
is a complete Segal object in $\mathrm {Cat}_\infty$![]() (and thus $\mathrm {Cat}_\infty ^\mathrm {lex}$
(and thus $\mathrm {Cat}_\infty ^\mathrm {lex}$![]() ) in the sense that the Segal maps induce equivalences
) in the sense that the Segal maps induce equivalences
and that

is cartesian.
Proof. This exact version is proven in [Reference Haugseng, Hebestreit, Linskens and Nuiten10, § 2].
We can therefore apply any limit preserving functor $\mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$![]() to $\operatorname {Q}(\mathcal {C})$
to $\operatorname {Q}(\mathcal {C})$![]() and obtain a complete Segal space; recall that these are the animae which span the image of the Rezk nerve
and obtain a complete Segal space; recall that these are the animae which span the image of the Rezk nerve
This functor $\operatorname N$![]() is fully faithful and has a left adjoint, the associated category functor, which we will denote by
is fully faithful and has a left adjoint, the associated category functor, which we will denote by
Definition 3.3 For $\mathcal {C}$![]() a category with finite limits we define
a category with finite limits we define
resulting in a functor $\operatorname {Span} \colon \mathrm {Cat}_\infty ^\mathrm {lex} \rightarrow \mathrm {Cat}_\infty$![]() .
.
We shall adopt:
Definition 3.4 For $\mathcal {C}$![]() stable we define its projective class anima or algebraic
$\operatorname K$
stable we define its projective class anima or algebraic
$\operatorname K$![]() -space
as
-space
as
where the loop space is formed with base object $0 \in \mathrm {Cr}(\mathcal {C}) = \mathrm {Cr}(\operatorname {Span}(\mathcal {C}))$![]() .
.
In particular, the functor
induces a map $\mathrm {Cr}(\mathcal {C}) \longrightarrow \operatorname {\mathcal {K}}(\mathcal {C})$![]() natural in the input category $\mathcal {C} \in \mathrm {Cat}_\infty ^\mathrm {st}$
natural in the input category $\mathcal {C} \in \mathrm {Cat}_\infty ^\mathrm {st}$![]() . There results a map
. There results a map
which exhibits the target as the quotient of the source by the congruence relation generated by $b \sim a + c$![]() whenever there is a fibre sequence $a \rightarrow b \rightarrow c$
whenever there is a fibre sequence $a \rightarrow b \rightarrow c$![]() in $\mathcal {C}$
in $\mathcal {C}$![]() ; this is somewhat unpleasant to see directly, but follows for example immediately from the identification of $\operatorname {Q}(\mathcal {C})$
; this is somewhat unpleasant to see directly, but follows for example immediately from the identification of $\operatorname {Q}(\mathcal {C})$![]() with the edgewise subdivision of the $\mathrm S$
with the edgewise subdivision of the $\mathrm S$![]() -construction of $\mathcal {C}$
-construction of $\mathcal {C}$![]() , compare e.g. [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, Appendix B.1]. We will later use the following elementary result of Thomason, see [Reference Thomason18]:
, compare e.g. [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, Appendix B.1]. We will later use the following elementary result of Thomason, see [Reference Thomason18]:
Theorem 3.5 If $\mathcal {A} \rightarrow \mathcal {B}$![]() is a dense inclusion among stable categories (i.e. the functor is fully faithful and every object of $\mathcal {B}$
is a dense inclusion among stable categories (i.e. the functor is fully faithful and every object of $\mathcal {B}$![]() is a retract of one in $\mathcal {A}$
is a retract of one in $\mathcal {A}$![]() ), then the induced map $\operatorname K_0(\mathcal {A}) \rightarrow \operatorname K_0(\mathcal {B})$
), then the induced map $\operatorname K_0(\mathcal {A}) \rightarrow \operatorname K_0(\mathcal {B})$![]() is injective, and sets up a bijective correspondence between dense inclusions into $\mathcal {B}$
is injective, and sets up a bijective correspondence between dense inclusions into $\mathcal {B}$![]() (up to equivalence over $\mathcal {B}$
(up to equivalence over $\mathcal {B}$![]() ) and subgroups of $\operatorname K_0(\mathcal {B})$
) and subgroups of $\operatorname K_0(\mathcal {B})$![]() .
.
In particular, it follows that every stable category $\mathcal {B}$![]() admits a minimal dense stable subcategory, namely $\{b \in \mathcal {B} \mid [b] = 0 \in \operatorname K_0(\mathcal {B})\}$
admits a minimal dense stable subcategory, namely $\{b \in \mathcal {B} \mid [b] = 0 \in \operatorname K_0(\mathcal {B})\}$![]() . We shall denote it by $\mathcal {B}^\mathrm {min}$
. We shall denote it by $\mathcal {B}^\mathrm {min}$![]() and refer to it as the minimalisation of $\mathcal {B}$
and refer to it as the minimalisation of $\mathcal {B}$![]() . In particular, $(-)^\mathrm {min} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {Cat}_\infty ^\mathrm {st}$
. In particular, $(-)^\mathrm {min} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {Cat}_\infty ^\mathrm {st}$![]() is left adjoint to idempotent completion.
is left adjoint to idempotent completion.
4. The additivity theorem
The goal of the present section is to present a short proof of the additivity theorem for $\operatorname K$![]() -spaces. As detailed in the previous section, we adopt $\operatorname {\mathcal {K}}(\mathcal {C}) \simeq \Omega |\operatorname {Span}(\mathcal {C})|$
-spaces. As detailed in the previous section, we adopt $\operatorname {\mathcal {K}}(\mathcal {C}) \simeq \Omega |\operatorname {Span}(\mathcal {C})|$![]() as the definition of these (for $\mathcal {C}$
as the definition of these (for $\mathcal {C}$![]() stable, which is the only case we shall consider). Our goal is therefore to prove:
stable, which is the only case we shall consider). Our goal is therefore to prove:
Theorem 4.1 The source and target projection give an equivalence
for every stable $\mathcal {C}$![]() .
.
From 2.4 we then immediately obtain:
Corollary 4.2 The functor $\operatorname {\mathcal {K}} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() is additive and group-like.
is additive and group-like.
Proof. Given 4.1 and 2.5 note only that $\operatorname {\mathcal {K}}$![]() evidently preserves products, and so lifts uniquely to $\operatorname {Mon}_{\mathrm {E}_\infty }(\mathrm {An})$
evidently preserves products, and so lifts uniquely to $\operatorname {Mon}_{\mathrm {E}_\infty }(\mathrm {An})$![]() (in addition to $\operatorname {Mon}_{\mathrm {E}_1}(\mathrm {An})$
(in addition to $\operatorname {Mon}_{\mathrm {E}_1}(\mathrm {An})$![]() ) since $\mathrm {Cat}_\infty ^\mathrm {st}$
) since $\mathrm {Cat}_\infty ^\mathrm {st}$![]() is semi-additive. Thus, the ${\mathrm {E}_1}$
is semi-additive. Thus, the ${\mathrm {E}_1}$![]() -structure underlying the canonical ${\mathrm {E}_\infty }$
-structure underlying the canonical ${\mathrm {E}_\infty }$![]() -structure is also induced by the loop multiplication and this is group-like.
-structure is also induced by the loop multiplication and this is group-like.
As mentioned in the introduction, the proof of 4.1 is strongly inspired by the algebraic Thom construction of Ranicki. Namely, we will prove the following two results which immediately imply 4.1, since cofinal maps induce equivalences on realisations; see 4.5 for an explanation of the connection to the algebraic Thom construction.
Proposition 4.3 For $\mathcal {C}$![]() stable, there are canonical equivalences $\operatorname {Span}(\mathcal {C}) \simeq \operatorname {Span}(\mathcal {C}^\mathrm {op})$
stable, there are canonical equivalences $\operatorname {Span}(\mathcal {C}) \simeq \operatorname {Span}(\mathcal {C}^\mathrm {op})$![]() and $\operatorname {Span}(\operatorname {Ar}(\mathcal {C})) \simeq \operatorname {Span}(\operatorname {TwAr^{r}}(\mathcal {C}))$
and $\operatorname {Span}(\operatorname {Ar}(\mathcal {C})) \simeq \operatorname {Span}(\operatorname {TwAr^{r}}(\mathcal {C}))$![]() that fit together into a natural commutative square
that fit together into a natural commutative square

It is generally true that if a category $\mathcal {C}$![]() admits pullbacks and pushouts, then $\operatorname {TwAr}(\mathcal {C})$
admits pullbacks and pushouts, then $\operatorname {TwAr}(\mathcal {C})$![]() also has all pullbacks (so that $\operatorname {Span}(\operatorname {TwAr^{r}}(\mathcal {C}))$
also has all pullbacks (so that $\operatorname {Span}(\operatorname {TwAr^{r}}(\mathcal {C}))$![]() is indeed defined): Generally, the total space of a right fibration inherits pullbacks from the base by direct inspection, and this can be applied to $(s,t) \colon \operatorname {TwAr^{r}}(\mathcal {C}) \rightarrow \mathcal {C} \times \mathcal {C}^\mathrm {op}$
is indeed defined): Generally, the total space of a right fibration inherits pullbacks from the base by direct inspection, and this can be applied to $(s,t) \colon \operatorname {TwAr^{r}}(\mathcal {C}) \rightarrow \mathcal {C} \times \mathcal {C}^\mathrm {op}$![]() .
.
Proposition 4.4 If $\mathcal {C}$![]() has finite limits and colimits and a zero object, then
has finite limits and colimits and a zero object, then
is cofinal.
Proof of proposition 4.3 We first review the (well-known) equivalence $\operatorname {Span}(\mathcal {C})\to \operatorname {Span}(\mathcal {C}^\mathrm {op})$![]() for stable $\mathcal {C}$
for stable $\mathcal {C}$![]() . It is the identity on objects, and on morphisms it is given by first completing a span to a bicartesian square and then forgetting the initial vertex:
. It is the identity on objects, and on morphisms it is given by first completing a span to a bicartesian square and then forgetting the initial vertex:

(Here $F_{10}=F_{00}\cup _{F_{01}} F_{11}$![]() .) To define this equivalence on higher cells, denote by $\hat{{\rm Q}}_n(\mathcal {C})\subset \operatorname {Fun}([n]\times [n]^\mathrm {op}, \mathcal {C})$
.) To define this equivalence on higher cells, denote by $\hat{{\rm Q}}_n(\mathcal {C})\subset \operatorname {Fun}([n]\times [n]^\mathrm {op}, \mathcal {C})$![]() the full subcategory of diagrams $F$
the full subcategory of diagrams $F$![]() such that each square
such that each square

is bicartesian. Restriction along the inclusion $\operatorname {TwAr}[n]\to [n]\times [n]^\mathrm {op}$![]() defines an equivalence
defines an equivalence
(to see that this is indeed an equivalence, we note that diagrams on $[n]\times [n]^\mathrm {op}$![]() or on $\operatorname {TwAr}[n]$
or on $\operatorname {TwAr}[n]$![]() lie in $\hat{{\rm Q}}_n(\mathcal {C})$
lie in $\hat{{\rm Q}}_n(\mathcal {C})$![]() or $\operatorname {Q}_n(\mathcal {C})$
or $\operatorname {Q}_n(\mathcal {C})$![]() if and only if they are left Kan extended from the full subcategory $\mathcal {J}_n$
if and only if they are left Kan extended from the full subcategory $\mathcal {J}_n$![]() of pairs $(i,j)$
of pairs $(i,j)$![]() where $i=0$
where $i=0$![]() or $j=n$
or $j=n$![]() , so both categories restrict to $\operatorname {Fun}(\mathcal {J}_n, \mathcal {C})$
, so both categories restrict to $\operatorname {Fun}(\mathcal {J}_n, \mathcal {C})$![]() by an equivalence.)
by an equivalence.)
The duality of $[n]\times [n]^\mathrm {op}$![]() that switches the entries induces an equivalence
that switches the entries induces an equivalence
by pre-composition. This in turn restricts to an equivalence
From this we obtain the desired equivalence $\operatorname {Span}(\mathcal {C})\to \operatorname {Span}(\mathcal {C}^\mathrm {op})$![]() by applying (*) and taking groupoid cores in each simplicial degree, and then passing to the associated categories.
by applying (*) and taking groupoid cores in each simplicial degree, and then passing to the associated categories.
The equivalence $\operatorname {Span}(\operatorname {Ar}(\mathcal {C}))\to \operatorname {Span}(\operatorname {TwAr}(\mathcal {C}))$![]() is essentially obtained by performing the above procedure in the target of the arrows; thus, on morphisms it is given by the rule
is essentially obtained by performing the above procedure in the target of the arrows; thus, on morphisms it is given by the rule

On higher cells, it is obtained from a map of simplicial animae $\hat{{\rm Q}}_n(\operatorname {Ar}(\mathcal {C}))\to \operatorname {Q}_n(\operatorname {TwAr}(\mathcal {C}))$![]() given by (restriction of) the following composite:
given by (restriction of) the following composite:

where the last map is restriction along the embedding
To see that this map of simplicial animae is indeed an equivalence, it suffices to consider the cases $n=0$![]() and $n=1$
and $n=1$![]() by the Segal condition: But for $n=0$
by the Segal condition: But for $n=0$![]() , it is the identity and for $n=1$
, it is the identity and for $n=1$![]() it is given by the rule explained above.
it is given by the rule explained above.
The commutativity of the diagram follows directly from the definition of the equivalences.
Remark 4.5 To explain the connection to Ranicki's algebraic Thom construction, let us briefly recall the latter in the language of Poincaré categories from [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle4], which we shall use freely in the rest of this remark; the relation of this framework to Ranicki's categorical setting from [Reference Ranicki15] is explained in [Reference Hebestreit and Steimle11, 3.2.6 Example].
To every Poincaré category, $(\mathcal {C},{\rm {\unicode{x03D8}}} )$![]() is associated its metabolic category $\operatorname {Met}(\mathcal {C},{\rm {\unicode{x03D8}}} )$
is associated its metabolic category $\operatorname {Met}(\mathcal {C},{\rm {\unicode{x03D8}}} )$![]() , with underlying category $\operatorname {Ar}(\mathcal {C})$
, with underlying category $\operatorname {Ar}(\mathcal {C})$![]() . Translated to this language, Ranicki showed in [Reference Ranicki15, 1.15] that associating to an arrow its fibre induces an equivalence
. Translated to this language, Ranicki showed in [Reference Ranicki15, 1.15] that associating to an arrow its fibre induces an equivalence
where $\mathrm {Pn}$![]() denotes the anima of Poincaré objects, and $\mathrm {He}$
denotes the anima of Poincaré objects, and $\mathrm {He}$![]() the category of hermitian objects; see [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle4, § 2.4] for a treatment in the present generality. The name presumably stems from the fact that for some manifold $M$
the category of hermitian objects; see [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle4, § 2.4] for a treatment in the present generality. The name presumably stems from the fact that for some manifold $M$![]() with boundary, by Atiyah duality the fibre of the metabolic object given by $\mathrm C^*(M) \rightarrow \mathrm C^*(\partial M)$
with boundary, by Atiyah duality the fibre of the metabolic object given by $\mathrm C^*(M) \rightarrow \mathrm C^*(\partial M)$![]() in $\mathcal {C} = {\mathcal {D}}^\mathrm {p}(\mathbb {Z})$
in $\mathcal {C} = {\mathcal {D}}^\mathrm {p}(\mathbb {Z})$![]() is $C_*(\mathrm {Th} \nu _M)$
is $C_*(\mathrm {Th} \nu _M)$![]() , the chains of the Thom spectrum of the stable normal bundle of $M$
, the chains of the Thom spectrum of the stable normal bundle of $M$![]() , up to a shift.
, up to a shift.
Now for any stable category $\mathcal {C}$![]() , there is another Poincaré category $\operatorname {Hyp}(\mathcal {C})$
, there is another Poincaré category $\operatorname {Hyp}(\mathcal {C})$![]() with underlying category $\mathcal {C} \times \mathcal {C}^\mathrm {op}$
with underlying category $\mathcal {C} \times \mathcal {C}^\mathrm {op}$![]() . One has $\mathrm {He}(\operatorname {Hyp}(\mathcal {C})) \simeq \operatorname {TwAr^{r}}(\mathcal {C})$
. One has $\mathrm {He}(\operatorname {Hyp}(\mathcal {C})) \simeq \operatorname {TwAr^{r}}(\mathcal {C})$![]() and $\mathrm {Pn}(\operatorname {Hyp}(\mathcal {C})) \simeq \mathrm {Cr}(\mathcal {C})$
and $\mathrm {Pn}(\operatorname {Hyp}(\mathcal {C})) \simeq \mathrm {Cr}(\mathcal {C})$![]() . Using the hermitian $\operatorname {Q}$
. Using the hermitian $\operatorname {Q}$![]() -construction one can then compute
-construction one can then compute

using various commutation rules and the equivalence $\operatorname {Hyp}(\mathcal {C})^{[-1]} \simeq \operatorname {Hyp}(\mathcal {C})$![]() via $(x,y) \mapsto (x,y^{[-1]})$
via $(x,y) \mapsto (x,y^{[-1]})$![]() : This proves 4.3 and we found the proof given above by unwinding the effect of these equivalences.
: This proves 4.3 and we found the proof given above by unwinding the effect of these equivalences.
In [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5], we used a similar analysis to conclude $\mathrm {Pn}(\operatorname {Q}\operatorname {Met}(\mathcal {C},{\rm {\unicode{x03D8}}} )) \simeq \mathrm {Cr}\operatorname {Q}\mathrm {He}(\mathcal {C},{\rm {\unicode{x03D8}}} )$![]() , where the left-hand side defines the cobordism category $\mathrm {Cob}^\partial (\mathcal {C},{\rm {\unicode{x03D8}}} )$
, where the left-hand side defines the cobordism category $\mathrm {Cob}^\partial (\mathcal {C},{\rm {\unicode{x03D8}}} )$![]() of Poincaré objects with boundary in $(\mathcal {C},{\rm {\unicode{x03D8}}} )$
of Poincaré objects with boundary in $(\mathcal {C},{\rm {\unicode{x03D8}}} )$![]() . We then used an analogue of 4.4 to deduce $|\mathrm {Cob}^\partial (\mathcal {C},{\rm {\unicode{x03D8}}} )| \simeq |\operatorname {Span}(\mathcal {C})|$
. We then used an analogue of 4.4 to deduce $|\mathrm {Cob}^\partial (\mathcal {C},{\rm {\unicode{x03D8}}} )| \simeq |\operatorname {Span}(\mathcal {C})|$![]() , and thus $|\mathrm {Cob}(\operatorname {Met}(\mathcal {C},{\rm {\unicode{x03D8}}} ))| \simeq |\mathrm {Cob}(\operatorname {Hyp}(\mathcal {C}))|$
, and thus $|\mathrm {Cob}(\operatorname {Met}(\mathcal {C},{\rm {\unicode{x03D8}}} ))| \simeq |\mathrm {Cob}(\operatorname {Hyp}(\mathcal {C}))|$![]() , the hermitian analogue of 4.1.
, the hermitian analogue of 4.1.
For the proof of 4.4 we observe:
Lemma 4.6 If $f \colon \mathcal {C} \rightarrow \mathcal {D}$![]() is a left exact right fibration (in particular $\mathcal {C}$
is a left exact right fibration (in particular $\mathcal {C}$![]() and $\mathcal {D}$
and $\mathcal {D}$![]() are assumed to have finite limits) and $x \in \mathcal {D}$
are assumed to have finite limits) and $x \in \mathcal {D}$![]() , then the functor $(f/x)^\mathrm {op} \longrightarrow x/\operatorname {Span}(f)$
, then the functor $(f/x)^\mathrm {op} \longrightarrow x/\operatorname {Span}(f)$![]() that is informally given by
that is informally given by
admits a right adjoint given by
where $\bar y \rightarrow w$![]() is a lift of $\psi$
is a lift of $\psi$![]() .
.
Proof. Unwinding definitions we have to show that

naturally in $(w,f(w) \xrightarrow {\varphi } x)$![]() . The left-hand side, call it $L_\varphi$
. The left-hand side, call it $L_\varphi$![]() , unwinds to be the pullback
, unwinds to be the pullback

where the right vertical map is

But per definition
and similarly for the lower right-hand term, allowing us to rewrite this pullback as

where the right vertical map identifies component-wise as
Switching the order of pullbacks, the fibre of the right-hand map is contractible (since $f$![]() is a right fibration), so this pullback rewrites as
is a right fibration), so this pullback rewrites as

where $\bar y \rightarrow v$![]() is the lift of $\psi$
is the lift of $\psi$![]() to $\mathcal {C}$
to $\mathcal {C}$![]() . Switching the order of pullbacks back this gives
. Switching the order of pullbacks back this gives

where the right-hand vertical map is
But this pullback also describes the right-hand term in the equivalence we have to produce, and the whole procedure above is readily checked to be natural in $(w,\phi \colon f(w) \to x)$![]() .
.
Proof of proposition 4.4 For the cofinality claim, we have to check that $|(c,d)/\operatorname {Span}(s,t)| \simeq \, \ast$![]() for all $(c,d) \in \mathcal {C} \times \mathcal {C}^\mathrm {op}$
for all $(c,d) \in \mathcal {C} \times \mathcal {C}^\mathrm {op}$![]() . But from the lemma we find $|(c,d)/\operatorname {Span}(s,t)| \simeq |(s,t)/(c,d)|$
. But from the lemma we find $|(c,d)/\operatorname {Span}(s,t)| \simeq |(s,t)/(c,d)|$![]() and the category $(s,t)/(c,d)$
and the category $(s,t)/(c,d)$![]() has an initial object: One easily checks that $\mathrm {id} \colon 0 \rightarrow 0$
has an initial object: One easily checks that $\mathrm {id} \colon 0 \rightarrow 0$![]() is initial in $\operatorname {TwAr^{r}}(\mathcal {C})$
is initial in $\operatorname {TwAr^{r}}(\mathcal {C})$![]() , and whenever a functor preserves the initial objects, all its slices inherit these.
, and whenever a functor preserves the initial objects, all its slices inherit these.
5. The universality theorem
The goal of the present section is to give a short and self-contained proof of the universal property of $\mathcal {K} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() , as first established by Blumberg, Gepner and Tabuada in [Reference Blumberg, Gepner and Tabuada3]. A version of the argument for higher Waldhausen categories was given by Barwick [Reference Barwick1], and another proof in the original setting was given in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5]. These sources all prove a more general statement for arbitrary additive functors to $\mathrm {An}$
, as first established by Blumberg, Gepner and Tabuada in [Reference Blumberg, Gepner and Tabuada3]. A version of the argument for higher Waldhausen categories was given by Barwick [Reference Barwick1], and another proof in the original setting was given in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5]. These sources all prove a more general statement for arbitrary additive functors to $\mathrm {An}$![]() (maybe preserving filtered colimits), that gives the universal property when specified to $\mathrm {Cr}$
(maybe preserving filtered colimits), that gives the universal property when specified to $\mathrm {Cr}$![]() . The following rather minimalistic argument below is adapted from [Reference Steimle17], which proves a similar universal property in the setting of (ordinary) Waldhausen categories.
. The following rather minimalistic argument below is adapted from [Reference Steimle17], which proves a similar universal property in the setting of (ordinary) Waldhausen categories.
Theorem 5.1 (Blumberg, Gepner, Tabuada)
The functor $\mathcal {K} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() is the initial group-like additive functor under $\mathrm {Cr} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$
is the initial group-like additive functor under $\mathrm {Cr} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() .
.
Proof. We have to show that restriction along the natural transformation $\mathrm {Cr} \Rightarrow \mathcal {K}$![]() gives an equivalence
gives an equivalence
for every grouplike additive $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() . For a general functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$
. For a general functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() set $G(F) = \Omega |F \operatorname {Q}-|$
set $G(F) = \Omega |F \operatorname {Q}-|$![]() , so that $G(\mathrm {Cr}) \simeq \mathcal {K}$
, so that $G(\mathrm {Cr}) \simeq \mathcal {K}$![]() . The inclusion
. The inclusion
induces a natural transformation $F \rightarrow G(F)$![]() which in turn extends to a natural transformation $\eta \colon \mathrm {id} \Rightarrow G$
which in turn extends to a natural transformation $\eta \colon \mathrm {id} \Rightarrow G$![]() (where $\eta _{\mathrm {Cr}}\colon \mathrm {Cr} \Rightarrow \mathcal {K}$
(where $\eta _{\mathrm {Cr}}\colon \mathrm {Cr} \Rightarrow \mathcal {K}$![]() is of course the transformation considered above). Now consider the commutative diagram
is of course the transformation considered above). Now consider the commutative diagram

the upper square commutes simply because $G$![]() is a functor, and the other three parts are consequences of the naturality of $\eta$
is a functor, and the other three parts are consequences of the naturality of $\eta$![]() . We now claim that the arrows labelled by $\simeq$
. We now claim that the arrows labelled by $\simeq$![]() are equivalences: This is an immediate consequence of the following propositions. A diagram chase then implies that the entire diagram consists of equivalences.
are equivalences: This is an immediate consequence of the following propositions. A diagram chase then implies that the entire diagram consists of equivalences.
Proposition 5.2 The transformation $\eta _F \colon F \rightarrow GF$![]() is an equivalence for every grouplike additive $F$
is an equivalence for every grouplike additive $F$![]() .
.
Proposition 5.3 The two transformations $\eta _{GF}, G\eta _F \colon GF \rightarrow GGF$![]() differ by an automorphism of the target.
differ by an automorphism of the target.
Proposition 5.2 is proven in detail for example in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, Theorem 3.3.4], but in the end the argument again goes back to Quillen and Waldhausen (a version of it is required in the proof that the iterated $\operatorname {Q}$![]() - and $\mathrm {S}$
- and $\mathrm {S}$![]() - constructions define positive $\Omega$
- constructions define positive $\Omega$![]() -spectra). We repeat it for completeness’ sake:
-spectra). We repeat it for completeness’ sake:
Definition 5.4 For $\mathcal {C}$![]() stable we define $\operatorname {Null}(\mathcal {C}) \colon \Delta ^\mathrm {op} \rightarrow \mathrm {Cat}_\infty ^\mathrm {st}$
stable we define $\operatorname {Null}(\mathcal {C}) \colon \Delta ^\mathrm {op} \rightarrow \mathrm {Cat}_\infty ^\mathrm {st}$![]() as $\operatorname {fib}(\mathrm {dec}(\operatorname {Q}(\mathcal {C})) \rightarrow \operatorname {Q}_0(\mathcal {C}))$
as $\operatorname {fib}(\mathrm {dec}(\operatorname {Q}(\mathcal {C})) \rightarrow \operatorname {Q}_0(\mathcal {C}))$![]() , where the fibre is formed over $0 \in \mathcal {C} = \operatorname {Q}_0(\mathcal {C})$
, where the fibre is formed over $0 \in \mathcal {C} = \operatorname {Q}_0(\mathcal {C})$![]() .
.
Here we use the décalage functor $\mathrm {dec}$![]() from the proof of 2.7 where $\mathrm {dec}(\operatorname {Q}(\mathcal {C}))\to \operatorname {Q}_0(\mathcal {C})$
from the proof of 2.7 where $\mathrm {dec}(\operatorname {Q}(\mathcal {C}))\to \operatorname {Q}_0(\mathcal {C})$![]() is induced by the natural transformation $\mathrm {dec}\Rightarrow \mathrm {ev}_0$
is induced by the natural transformation $\mathrm {dec}\Rightarrow \mathrm {ev}_0$![]() . The natural transformation $\mathrm {dec}\rightarrow \mathrm {id}$
. The natural transformation $\mathrm {dec}\rightarrow \mathrm {id}$![]() induces a natural map
induces a natural map
Remark 5.5 It is not difficult to check that $\operatorname {Null}(\mathcal {C})$![]() is again a complete Segal object, and that
is again a complete Segal object, and that
see the discussion in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, § 3.3].
Proof of proposition 5.2 The simplicial object $\operatorname {Null}(\mathcal {C})$![]() is split (over $0$
is split (over $0$![]() ) in the sense of [Reference Lurie12, § 6.1.3], so in particular $|F\operatorname {Null}(\mathcal {C})| \simeq \, \ast$
) in the sense of [Reference Lurie12, § 6.1.3], so in particular $|F\operatorname {Null}(\mathcal {C})| \simeq \, \ast$![]() for every (not necessarily additive) $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$
for every (not necessarily additive) $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() . Further it follows that the natural map
. Further it follows that the natural map
is essentially by definition induced by applying $F$![]() and realisation to the square
and realisation to the square

where the top horizontal map is induced by $\mathcal {C} \rightarrow \operatorname {Null}(\mathcal {C})_0, x \mapsto (0 \leftarrow x \rightarrow 0)$![]() . Thus, we need to show that the square remains cartesian after applying $F$
. Thus, we need to show that the square remains cartesian after applying $F$![]() and realisation. Using the equifibrancy lemma (compare again the proof of 2.7), we can do this by showing that the map of simplicial animae $F\operatorname {Null}(\mathcal {C})\Rightarrow F\operatorname {Q}(\mathcal {C})$
and realisation. Using the equifibrancy lemma (compare again the proof of 2.7), we can do this by showing that the map of simplicial animae $F\operatorname {Null}(\mathcal {C})\Rightarrow F\operatorname {Q}(\mathcal {C})$![]() is equifibred for every group-like additive functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$
is equifibred for every group-like additive functor $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() .
.
It is easy to check from the Segal condition that it suffices to treat the squares

where the vertical maps are one of $d_0,d_1$![]() and $d_2$
and $d_2$![]() . For $d_1$
. For $d_1$![]() and $d_2$
and $d_2$![]() , these squares are split Verdier squares (before applying $F$
, these squares are split Verdier squares (before applying $F$![]() ). For the remaining case, we first note that $d_0$
). For the remaining case, we first note that $d_0$![]() is a split Verdier projection in both vertical maps, so that it suffices to compare vertical fibres over $0$
is a split Verdier projection in both vertical maps, so that it suffices to compare vertical fibres over $0$![]() (since the map $\pi _0F\operatorname {Q}_2(\mathcal {D}) \rightarrow \pi _0F\operatorname {Q}_1(\mathcal {D})$
(since the map $\pi _0F\operatorname {Q}_2(\mathcal {D}) \rightarrow \pi _0F\operatorname {Q}_1(\mathcal {D})$![]() is surjective since it is split by the degeneracy $s_0$
is surjective since it is split by the degeneracy $s_0$![]() ). But on the left, this fibre identifies with $\mathcal {D} \times \mathcal {D}$
). But on the left, this fibre identifies with $\mathcal {D} \times \mathcal {D}$![]() and on the right with $\operatorname {Ar}(\mathcal {D})$
and on the right with $\operatorname {Ar}(\mathcal {D})$![]() , and the functor between them identifies with $(d,d') \mapsto (d' \rightarrow d\oplus d')$
, and the functor between them identifies with $(d,d') \mapsto (d' \rightarrow d\oplus d')$![]() . But this map is clearly a right inverse to $(s,\operatorname {cof}) \colon \operatorname {Ar}(\mathcal {D}) \rightarrow \mathcal {D}^2$
. But this map is clearly a right inverse to $(s,\operatorname {cof}) \colon \operatorname {Ar}(\mathcal {D}) \rightarrow \mathcal {D}^2$![]() , so an equivalence after applying $F$
, so an equivalence after applying $F$![]() by 2.4.
by 2.4.
Proof of proposition 5.3 Unwinding definitions, one finds that the two maps in question
are induced by the maps into the different $\Omega$![]() - and $\operatorname {Q}$
- and $\operatorname {Q}$![]() -terms. In particular, the composites
-terms. In particular, the composites
are exchanged by flipping both the $\Omega$![]() and the $\operatorname {Q}$
and the $\operatorname {Q}$![]() -terms; here the second map is the canonical limit–colimit interchange pulling the right-hand $\Omega$
-terms; here the second map is the canonical limit–colimit interchange pulling the right-hand $\Omega$![]() through the outer realisation. We now claim that this is an equivalence, finishing the proof.
through the outer realisation. We now claim that this is an equivalence, finishing the proof.
To this end, note that for each $k \in \Delta$![]() the sequence
the sequence
(with the appropriate homotopy) is not just a fibre, but also a cofibre sequence of $\mathcal {E}_\infty$![]() -groups: This is equivalent to the assertion that $\pi _0\lvert F \operatorname {Q}\operatorname {Q}_k(\mathcal {C})\rvert = 0$
-groups: This is equivalent to the assertion that $\pi _0\lvert F \operatorname {Q}\operatorname {Q}_k(\mathcal {C})\rvert = 0$![]() and this holds for any stable category $\mathcal {D}$
and this holds for any stable category $\mathcal {D}$![]() in place of $\operatorname {Q}_k(\mathcal {C})$
in place of $\operatorname {Q}_k(\mathcal {C})$![]() : The functor
: The functor
composes to the identity with $d_1 \colon \operatorname {Q}_1(\mathcal {D}) \rightarrow \mathcal {D}$![]() and to $0$
and to $0$![]() with $d_0$
with $d_0$![]() , so the claim is a consequence of $F$
, so the claim is a consequence of $F$![]() being reduced.
being reduced.
But then it follows that also
is a cofibre sequence of ${\mathrm {E}_\infty }$![]() -groups, so in particular a fibre sequence of underlying animae. Looping the resulting equivalence $\lvert \Omega \lvert F \operatorname {Q}^2(\mathcal {C})\rvert \rvert \simeq \Omega \lvert F \operatorname {Q}^2(\mathcal {C})\rvert$
-groups, so in particular a fibre sequence of underlying animae. Looping the resulting equivalence $\lvert \Omega \lvert F \operatorname {Q}^2(\mathcal {C})\rvert \rvert \simeq \Omega \lvert F \operatorname {Q}^2(\mathcal {C})\rvert$![]() once gives the claim.
once gives the claim.
Remark 5.6 The additional input needed for the more general versions of theorem 5.1 proved in [Reference Barwick1, Reference Blumberg, Gepner and Tabuada3] (see [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, § 2.7] for the version in the precise set-up of this paper) is that $GF = \Omega |F\operatorname {Q}-|$![]() is again additive for every additive $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$
is again additive for every additive $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() . With this information, the conclusion is that generally $GF$
. With this information, the conclusion is that generally $GF$![]() is a group completion of $F$
is a group completion of $F$![]() , i.e. it is initial among grouplike additive functors equipped with a transformation from $F$
, i.e. it is initial among grouplike additive functors equipped with a transformation from $F$![]() .
.
While the reader will hopefully agree that the argument we gave for the additivity of $G(\mathrm {Cr}) = \mathcal {K}$![]() in the previous section is simpler than those given in any of the references above, it does not extend beyond this case, essentially because it makes use of the fact that $\mathrm {Cr}$
in the previous section is simpler than those given in any of the references above, it does not extend beyond this case, essentially because it makes use of the fact that $\mathrm {Cr}$![]() is defined on non-stable categories (namely $\operatorname {TwAr}(\mathcal {C})$
is defined on non-stable categories (namely $\operatorname {TwAr}(\mathcal {C})$![]() ).
).
6. The localisation theorem
The goal of this section is to prove:
Theorem 6.1 The algebraic $K$![]() -functor
-functor
is Verdier-localising. The same is true for the spectrum-valued functor obtained from $\operatorname {\mathcal {K}}$![]() by the canonical embedding of ${\mathrm {E}_\infty }$
by the canonical embedding of ${\mathrm {E}_\infty }$![]() -groups into spectra.
-groups into spectra.
To prove this result, we recall from corollary 2.9 that an additive and group-like functor $F\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$![]() is Verdier-localising provided the following condition holds:
is Verdier-localising provided the following condition holds:
(*) For any Verdier sequence $\mathcal {A}\to \mathcal {B}\to \mathcal {C}$
 , the canonical map $\vert F(\operatorname {Fun}^{\mathcal {A}}([-], \mathcal {B}))\vert \to F(\mathcal {C})$
, the canonical map $\vert F(\operatorname {Fun}^{\mathcal {A}}([-], \mathcal {B}))\vert \to F(\mathcal {C})$ is an equivalence.
is an equivalence.
Proposition 6.2 Let $F\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$![]() be an additive, space-valued functor satisfying condition $(\ast )$
be an additive, space-valued functor satisfying condition $(\ast )$![]() . Then also the functor $|F\operatorname {Q}|$
. Then also the functor $|F\operatorname {Q}|$![]() satisfies ($\ast$
satisfies ($\ast$![]() ).
).
In particular, it follows that if $|F\operatorname {Q}|$![]() is again additive, both functors $|F \operatorname {Q}|$
is again additive, both functors $|F \operatorname {Q}|$![]() and $\Omega |F\operatorname {Q}|$
and $\Omega |F\operatorname {Q}|$![]() are Verdier-localising as functors $\mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \operatorname {Grp}_{\mathrm {E}_\infty }(\mathrm {An})$
are Verdier-localising as functors $\mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \operatorname {Grp}_{\mathrm {E}_\infty }(\mathrm {An})$![]() .
.
Remark 6.3 As mentioned previously, it is generally true that $|F\operatorname {Q}|$![]() is additive whenever $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$
is additive whenever $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() is, but we do not prove that in this note (see [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, § 2.7]).
is, but we do not prove that in this note (see [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle5, § 2.7]).
For the proof of 6.2, we use the following result about stable $\infty$![]() -categories:
-categories:
Lemma 6.4 Verdier sequences are stable under applying $(-)^{\mathcal {I}} = \operatorname {Fun}(\mathcal {I}, -)$![]() , for any finite poset $\mathcal {I}$
, for any finite poset $\mathcal {I}$![]() .
.
Proof. Since the cotensor $(-)^{\mathcal {I}}$![]() has a left adjoint, given by the tensor $(-)_{\mathcal {I}}$
has a left adjoint, given by the tensor $(-)_{\mathcal {I}}$![]() , we deduce that $(-)^{\mathcal {I}}$
, we deduce that $(-)^{\mathcal {I}}$![]() preserves limits (for an arbitrary category ${\mathcal {I}}$
preserves limits (for an arbitrary category ${\mathcal {I}}$![]() ). On the other hand, for a finite poset ${\mathcal {I}}$
). On the other hand, for a finite poset ${\mathcal {I}}$![]() , the functor $(-)^{\mathcal {I}}$
, the functor $(-)^{\mathcal {I}}$![]() also has a right adjoint equally given by $(-)_{\mathcal {I}}$
also has a right adjoint equally given by $(-)_{\mathcal {I}}$![]() , see [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle4, Definition 6.5.1 and Lemma 6.5.6], so $(-)^{\mathcal {I}}$
, see [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle4, Definition 6.5.1 and Lemma 6.5.6], so $(-)^{\mathcal {I}}$![]() also preserves colimits.
also preserves colimits.
Remark 6.5 Alternative to using the tensoring construction from [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle4], one may prove the lemma more directly using the formula for mapping spaces in Verdier quotients (we will recall it in 6.9) and that in functor categories from [Reference Gepner, Haugseng and Nikolaus9], namely
This argument goes as follows: For $\mathcal {I}$![]() a finite poset, $\operatorname {TwAr^{r}}(\mathcal {I})$
a finite poset, $\operatorname {TwAr^{r}}(\mathcal {I})$![]() is a finite category, so limits over it commute with filtered colimits in $\mathrm {An}$
is a finite category, so limits over it commute with filtered colimits in $\mathrm {An}$![]() . It then follows easily from 6.9 that the canonical functor
. It then follows easily from 6.9 that the canonical functor
is fully faithful whenever $\mathcal {C}\subseteq \mathcal {D}$![]() is a full stable subcategory. As that formula also implies that any arrow in a Verdier quotient can be lifted with given source, one can inductively show essential surjectivity: Call the length of the longest chain in $\mathcal {I}$
is a full stable subcategory. As that formula also implies that any arrow in a Verdier quotient can be lifted with given source, one can inductively show essential surjectivity: Call the length of the longest chain in $\mathcal {I}$![]() starting at some $i \in \mathcal {I}$
starting at some $i \in \mathcal {I}$![]() the height $h(i)$
the height $h(i)$![]() . Given a functor $F \colon \mathcal {I} \rightarrow \mathcal {D}/\mathcal {C}$
. Given a functor $F \colon \mathcal {I} \rightarrow \mathcal {D}/\mathcal {C}$![]() and a lift $G_k \colon \mathcal {I}_{h \leq k} \rightarrow \mathcal {D}$
and a lift $G_k \colon \mathcal {I}_{h \leq k} \rightarrow \mathcal {D}$![]() to the sub-poset consisting of the elements of height at most $k$
to the sub-poset consisting of the elements of height at most $k$![]() , we can extend $G$
, we can extend $G$![]() to an element $j$
to an element $j$![]() of height $k+1$
of height $k+1$![]() by lifting $\mathop {\mathrm {colim}}_{i < j} F(i) \rightarrow F(j)$
by lifting $\mathop {\mathrm {colim}}_{i < j} F(i) \rightarrow F(j)$![]() with source $\mathop {\mathrm {colim}}_{i< j} G(i)$
with source $\mathop {\mathrm {colim}}_{i< j} G(i)$![]() . Since $I_{d \leq k+1}$
. Since $I_{d \leq k+1}$![]() is obtained from $I_{d \leq k}$
is obtained from $I_{d \leq k}$![]() by glueing on cones over subsets of the form $\{i \in \mathcal {I}\mid i< j\}$
by glueing on cones over subsets of the form $\{i \in \mathcal {I}\mid i< j\}$![]() , any choices of lifts for all $j \in I$
, any choices of lifts for all $j \in I$![]() of height $k+1$
of height $k+1$![]() combine into a functor $G_{k+1}$
combine into a functor $G_{k+1}$![]() as desired.
as desired.
Proof of proposition 6.2 It suffices to show that the relevant map is an equivalence in each simplicial degree of the $\operatorname {Q}$![]() -construction, i.e. that the canonical map
-construction, i.e. that the canonical map
of spaces is an equivalence. By the lemma,
is also a Verdier projection, in view of the equivalence
where $\mathcal {J}_k\subset \operatorname {TwAr}[k]$![]() is the sub-poset
is the sub-poset

Thus, we are reduced to the case $k=0$![]() which holds by assumption.
which holds by assumption.
To prove the first part of 6.1, we are left to show that the groupoid core functor $\mathrm {Cr}\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$![]() satisfies condition $(\ast )$
satisfies condition $(\ast )$![]() . Clearly,
. Clearly,
where $\mathcal {B}_\mathcal {A}$![]() is the category of equivalences modulo $\mathcal {A}$
is the category of equivalences modulo $\mathcal {A}$![]() in $\mathcal {B}$
in $\mathcal {B}$![]() , and $\mathrm {N}$
, and $\mathrm {N}$![]() is the Rezk nerve. Now the canonical map $\vert \mathrm {N} (\mathcal {B}_\mathcal {A})\vert \to |\mathcal {B}_\mathcal {A}|$
is the Rezk nerve. Now the canonical map $\vert \mathrm {N} (\mathcal {B}_\mathcal {A})\vert \to |\mathcal {B}_\mathcal {A}|$![]() is an equivalence, so the claim follows from:
is an equivalence, so the claim follows from:
Proposition 6.6 Let $\mathcal {A}\subseteq \mathcal {B}$![]() be stable subcategory and $\mathcal {B}_\mathcal {A}\subseteq \mathcal {B}$
be stable subcategory and $\mathcal {B}_\mathcal {A}\subseteq \mathcal {B}$![]() the category of equivalences modulo $\mathcal {A}$
the category of equivalences modulo $\mathcal {A}$![]() . Then
. Then
is faithful and even an equivalence if $\mathcal {A}\subseteq \mathcal {B}$![]() is a Verdier inclusion (i.e. closed under retracts).
is a Verdier inclusion (i.e. closed under retracts).
Remark 6.7 Note in particular, that the proposition implies that for dense $\mathcal {C} \subseteq \mathcal {D}$![]() the anima $|\mathcal {D}_\mathcal {C}|$
the anima $|\mathcal {D}_\mathcal {C}|$![]() is discrete and in this case
is discrete and in this case
the former by inspection, the latter by Thomason's theorem 3.5. This observation will yield the cofinality theorem in the next section.
Proposition 6.6 is a special case (namely, $S=\mathcal {B}_\mathcal {A}$![]() ) of the following general computation of cores in (nice enough) localisations:
) of the following general computation of cores in (nice enough) localisations:
Proposition 6.8 Let $S\subset \mathcal {B}$![]() be a subcategory of an $\infty$
be a subcategory of an $\infty$![]() -category $\mathcal {B}$
-category $\mathcal {B}$![]() . Assume that the morphisms of $S$
. Assume that the morphisms of $S$![]() are closed under $2$
are closed under $2$![]() -out-of-$3$
-out-of-$3$![]() and pushouts in $\mathcal {B}$
and pushouts in $\mathcal {B}$![]() . Then, the canonical functor
. Then, the canonical functor
is faithful. Furthermore, the following are equivalent:
(i) $|S|\subseteq \mathrm {Cr} \mathcal {B}[S^{-1}]$
 is fully faithful.
is fully faithful.(ii) The morphisms of $S$
 satisfy $2$
satisfy $2$ -out-of-$6$
-out-of-$6$ in $\mathcal {B}$
in $\mathcal {B}$ .
.(iii) A morphism of $\mathcal {B}$
 lies in $S$
lies in $S$ if and only if its source and target do, and it becomes invertible in $\mathcal {B}[S^{-1}]$
if and only if its source and target do, and it becomes invertible in $\mathcal {B}[S^{-1}]$ .
.
Here closure under pushouts means that the pushouts in $\mathcal {B}$![]() of all morphisms in $S$
of all morphisms in $S$![]() exist and lie in $S$
exist and lie in $S$![]() again. The proof is based on the following formula for mapping spaces in localisations admitting a calculus of fraction, which was established by Nuiten [Reference Nuiten14]. A textbook account is in [Reference Cisinski8, § 7.2].
again. The proof is based on the following formula for mapping spaces in localisations admitting a calculus of fraction, which was established by Nuiten [Reference Nuiten14]. A textbook account is in [Reference Cisinski8, § 7.2].
Theorem 6.9 Let $S\subset \mathcal {B}$![]() be a subcategory of an $\infty$
be a subcategory of an $\infty$![]() -category $\mathcal {B}$
-category $\mathcal {B}$![]() . Assume that the morphisms of $S$
. Assume that the morphisms of $S$![]() contain the equivalences in $\mathcal {C}$
contain the equivalences in $\mathcal {C}$![]() and are closed under pushout in $\mathcal {B}$
and are closed under pushout in $\mathcal {B}$![]() . Then, the canonical map
. Then, the canonical map
is an equivalence, where $S(y)$![]() is the full subcategory of $y/\mathcal {B}$
is the full subcategory of $y/\mathcal {B}$![]() spanned by the maps in $S$
spanned by the maps in $S$![]() .
.
The special case where $\mathcal {B}$![]() is stable and $S = \mathcal {B}_\mathcal {A}$
is stable and $S = \mathcal {B}_\mathcal {A}$![]() (so that $\mathcal {B}[S^{-1}] = \mathcal {B}/\mathcal {A}$
(so that $\mathcal {B}[S^{-1}] = \mathcal {B}/\mathcal {A}$![]() ) was also treated by Nikolaus and Scholze in [Reference Nikolaus and Scholze13, Theorem I.3.3] and enters the basic analysis of Verdier quotients. We include a short proof of the general statement for completeness’ sake.
) was also treated by Nikolaus and Scholze in [Reference Nikolaus and Scholze13, Theorem I.3.3] and enters the basic analysis of Verdier quotients. We include a short proof of the general statement for completeness’ sake.
Proof. Denote by $t_y \colon S(y) \rightarrow \mathcal {B}$![]() the functor taking targets. The proof has three steps, the first two of which in fact work for an arbitrary $S$
the functor taking targets. The proof has three steps, the first two of which in fact work for an arbitrary $S$![]() containing the identities of $\mathcal {C}$
containing the identities of $\mathcal {C}$![]() .
.
Step 1: Whenever the functor
\[ \mathop{\mathrm{colim}}_{(y\to y')\in S(y)} \operatorname{Hom}_{\mathcal{B}}(-,y') \colon \mathcal{B}^\mathrm{op} \rightarrow \mathrm{An} \]inverts $S$
 , it agrees with $\operatorname {Hom}_{\mathcal {B}[S^{-1}]}(-,y) \colon \mathcal {B}^\mathrm {op} \rightarrow \mathrm {An}$
, it agrees with $\operatorname {Hom}_{\mathcal {B}[S^{-1}]}(-,y) \colon \mathcal {B}^\mathrm {op} \rightarrow \mathrm {An}$ .
.
Step 2: We have
\[ \mathop{\mathrm{colim}}_{(y\to y')\in S(y)} \operatorname{Hom}_{\mathcal{B}}(-,y') \simeq (t_y)_! \, \mathrm{const}_\ast{\simeq} \lvert -{/}t_y \rvert \]as functors $\mathcal {B}^\mathrm {op} \rightarrow \mathrm {An}$
 .
.
Step 3: If $S$
 satisfies the assumptions from the statement and $f\colon x \rightarrow x'$
satisfies the assumptions from the statement and $f\colon x \rightarrow x'$ is in $S$
is in $S$ , then $f^* \colon x'/t_y \rightarrow x/t_y$
, then $f^* \colon x'/t_y \rightarrow x/t_y$ admits a left adjoint.
admits a left adjoint.
Since adjunctions give equivalences on realisations, the theorem follows.
Proof of step 1 Denoting by $p \colon \mathcal {B}^\mathrm {op} \rightarrow \mathcal {B}[S^{-1}]^\mathrm {op}$![]() the localisation functor we compute
the localisation functor we compute

as follows. The first equivalence holds because left Kan extension is a left adjoint and thus preserves colimits, and the second one holds because representable functors left Kan extend to representable functors by Yoneda's lemma. For the last equivalence, observe that the functor
inverts all morphisms in $S(y)$![]() by 2-out-of-3 for equivalences in $\mathcal {B}[S^{-1}]$
by 2-out-of-3 for equivalences in $\mathcal {B}[S^{-1}]$![]() , and that $\lvert S(y) \rvert$
, and that $\lvert S(y) \rvert$![]() is contractible since it has $\mathrm {id}_y$
is contractible since it has $\mathrm {id}_y$![]() as an initial object. But if a functor $\mathcal {B}^\mathrm {op} \rightarrow \mathrm {An}$
as an initial object. But if a functor $\mathcal {B}^\mathrm {op} \rightarrow \mathrm {An}$![]() inverts $S$
inverts $S$![]() , then its left Kan extension along $p$
, then its left Kan extension along $p$![]() is simply the induced functor $\mathcal {B}[S^{-1}]^\mathrm {op} \rightarrow \mathrm {An}$
is simply the induced functor $\mathcal {B}[S^{-1}]^\mathrm {op} \rightarrow \mathrm {An}$![]() by inspection of universal properties.
by inspection of universal properties.
Proof of step 2 The right-hand equivalence is a direct consequence of the pointwise formula for Kan extensions:
For the left-hand one, we use
to compute

Proof of step 3 The left adjoint is easily checked to be given by taking an object $x \rightarrow z \leftarrow y$![]() (with left pointing arrow in $S$
(with left pointing arrow in $S$![]() ) to $x' \rightarrow p \leftarrow y$
) to $x' \rightarrow p \leftarrow y$![]() , where
, where

is a pushout; this pushout exists by assumption since $f \colon x \rightarrow x'$![]() is in $S$
is in $S$![]() and similarly the composite $y \rightarrow z \rightarrow p$
and similarly the composite $y \rightarrow z \rightarrow p$![]() is in $S$
is in $S$![]() since $S$
since $S$![]() is closed under pushouts and composition. We leave it to the reader to check the adjunction property.
is closed under pushouts and composition. We leave it to the reader to check the adjunction property.
Remark 6.10 Note in passing that the equivalence
arising from the proof above describes the left-hand side as a certain space of zig-zags
with the left pointing arrow in $S$![]() , as a calculus of fractions is supposed to do.
, as a calculus of fractions is supposed to do.
Proof of proposition 6.8 Applying theorem 6.9 to $S\subset \mathcal {B}$![]() and $S\subset S$
and $S\subset S$![]() (for the latter, noting that pushouts in $S$
(for the latter, noting that pushouts in $S$![]() are computed in the ambient category $\mathcal {B}$
are computed in the ambient category $\mathcal {B}$![]() ), we see that
), we see that
is computed by the formula
Since $S\subset \mathcal {B}$![]() is a subcategory, this is a directed colimit of full inclusions of subspaces, and therefore a full inclusion itself.
is a subcategory, this is a directed colimit of full inclusions of subspaces, and therefore a full inclusion itself.
This shows the first part. For the second part, we first note that all three conditions are conditions on the respective homotopy categories, and that the homotopy categories of the localisations admit a (classical) calculus of fractions as a consequence of theorem 6.9 (cf. [Reference Cisinski8, Corollary 7.2.12]).
We first show the implication (i)$\Rightarrow$![]() (iii): If $f$
(iii): If $f$![]() has source and target in $S$
has source and target in $S$![]() and becomes invertible in $\mathcal {B}[S^{-1}]$
and becomes invertible in $\mathcal {B}[S^{-1}]$![]() , then under (i) it is represented by a zig-zag in $\operatorname {Ho}(S)$
, then under (i) it is represented by a zig-zag in $\operatorname {Ho}(S)$![]() so that, by calculus of fractions and $2$
so that, by calculus of fractions and $2$![]() -out-of-$3$
-out-of-$3$![]() , $f$
, $f$![]() belongs itself to $S$
belongs itself to $S$![]() . The implication (iii)$\Rightarrow$
. The implication (iii)$\Rightarrow$![]() (ii) is trivial, since equivalences satisfy $2$
(ii) is trivial, since equivalences satisfy $2$![]() -out-of-$6$
-out-of-$6$![]() . Finally, assume (ii) holds, and let $f$
. Finally, assume (ii) holds, and let $f$![]() be an invertible morphism in $\mathcal {B}[S^{-1}]$
be an invertible morphism in $\mathcal {B}[S^{-1}]$![]() between objects of $S$
between objects of $S$![]() ; we need to show that it is represented by a zig-zag in $S$
; we need to show that it is represented by a zig-zag in $S$![]() .
.
For this, we may clearly assume that $f$![]() is a morphism in $\mathcal {B}$
is a morphism in $\mathcal {B}$![]() . Applying calculus of fractions again, we see that a morphism $f$
. Applying calculus of fractions again, we see that a morphism $f$![]() of $\mathcal {B}$
of $\mathcal {B}$![]() is split mono in the localisation if and only if, after post-composition with a morphism $g$
is split mono in the localisation if and only if, after post-composition with a morphism $g$![]() of $\mathcal {B}$
of $\mathcal {B}$![]() , it lies in $S$
, it lies in $S$![]() . If $f$
. If $f$![]() is even an equivalence in the localisation, then so is $g$
is even an equivalence in the localisation, then so is $g$![]() , and applying the same argument to $g$
, and applying the same argument to $g$![]() , we find another morphism $h$
, we find another morphism $h$![]() such that $h\circ g\in S$
such that $h\circ g\in S$![]() ; then $f\in S$
; then $f\in S$![]() by $2$
by $2$![]() -out-of-$6$
-out-of-$6$![]() .
.
Proof of theorem 6.1 The groupoid-core functor satisfies $(\ast )$![]() by 6.6 and the discussion preceding it. From 6.2 we conclude that the functor $|\mathrm {Cr} \operatorname {Q}|$
by 6.6 and the discussion preceding it. From 6.2 we conclude that the functor $|\mathrm {Cr} \operatorname {Q}|$![]() also does, so by corollary 2.9, $|\mathrm {Cr} \operatorname {Q}|\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$
also does, so by corollary 2.9, $|\mathrm {Cr} \operatorname {Q}|\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$![]() is Verdier-localising and therefore also $\operatorname {\mathcal {K}}=\Omega |\mathrm {Cr}\operatorname {Q}|$
is Verdier-localising and therefore also $\operatorname {\mathcal {K}}=\Omega |\mathrm {Cr}\operatorname {Q}|$![]() . For the second claim, we recall that a fibre sequence of ${\mathrm {E}_\infty }$
. For the second claim, we recall that a fibre sequence of ${\mathrm {E}_\infty }$![]() -groups gives rise to a fibre sequence of spectra if (and only if) it is surjective on $\pi _0$
-groups gives rise to a fibre sequence of spectra if (and only if) it is surjective on $\pi _0$![]() , but any Verdier projection induces an epimorphism on $\operatorname K_0$
, but any Verdier projection induces an epimorphism on $\operatorname K_0$![]() by the formula for $\operatorname K_0$
by the formula for $\operatorname K_0$![]() (or by noting that $\pi _0 |\mathrm {Cr} \operatorname {Q}(\mathcal {C})|=0$
(or by noting that $\pi _0 |\mathrm {Cr} \operatorname {Q}(\mathcal {C})|=0$![]() for any $\mathcal {C}$
for any $\mathcal {C}$![]() and using that $|\mathrm {Cr} \operatorname {Q}|$
and using that $|\mathrm {Cr} \operatorname {Q}|$![]() is Verdier-localising).
is Verdier-localising).
7. The cofinality theorem
The first goal of this section is to formulate and prove the cofinality theorem for algebraic $K$![]() -theory, and the second, to derive that $\operatorname {\mathcal {K}}$
-theory, and the second, to derive that $\operatorname {\mathcal {K}}$![]() gives rise to a Karoubi-localising functor.
gives rise to a Karoubi-localising functor.
The cofinality theorem follows rather directly from the methods developed for the proof of the fibration theorem. After explaining this, we give a second, independent proof of the cofinality theorem which only uses the universal property of $K$![]() -theory and which is based on the fact that the quotient ${\mathrm {E}_\infty }$
-theory and which is based on the fact that the quotient ${\mathrm {E}_\infty }$![]() -monoid $\mathrm {Cr}(\mathcal {A}^\natural )/\mathrm {Cr}(\mathcal {A})$
-monoid $\mathrm {Cr}(\mathcal {A}^\natural )/\mathrm {Cr}(\mathcal {A})$![]() is group-like and discrete.
is group-like and discrete.
We start by stating the cofinality theorem.
Theorem 7.1 If $\mathcal {A} \rightarrow \mathcal {B}$![]() is a dense inclusion of stable categories, then
is a dense inclusion of stable categories, then
is an isomorphism for $i>0$![]() and there is a short exact sequence
and there is a short exact sequence
The statement at the level of $\operatorname K_0$![]() is of course part of Thomason's theorem 3.5, and we will not give an independent argument for it. One concludes from theorem 7.1 rather easily that the functor $\operatorname {\mathcal {K}} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$
is of course part of Thomason's theorem 3.5, and we will not give an independent argument for it. One concludes from theorem 7.1 rather easily that the functor $\operatorname {\mathcal {K}} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() satisfies the assumptions of 2.13 (see e.g. corollary 7.8 for a generalisation), so we obtain:
satisfies the assumptions of 2.13 (see e.g. corollary 7.8 for a generalisation), so we obtain:
Corollary 7.2 The functor $\operatorname {\mathcal {K}} \circ (-)^\natural \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() is Karoubi-localising.
is Karoubi-localising.
By contrast, the functor $\operatorname {\mathcal {K}} \circ (-)^\mathrm {min}$![]() is not Verdier-localising: The Verdier projection ${\mathcal {D}}^\mathrm {p}(\mathbb {Z}) \rightarrow {\mathcal {D}}^\mathrm {p}(\mathbb {Q})$
is not Verdier-localising: The Verdier projection ${\mathcal {D}}^\mathrm {p}(\mathbb {Z}) \rightarrow {\mathcal {D}}^\mathrm {p}(\mathbb {Q})$![]() with kernel the torsion complexes, does not yield an exact sequence on $\operatorname K$
with kernel the torsion complexes, does not yield an exact sequence on $\operatorname K$![]() -groups after minimalisation, since the map $\operatorname K_1({\mathcal {D}}^\mathrm {p}(\mathbb {Z}) \rightarrow \operatorname K_1({\mathcal {D}}^\mathrm {p}(\mathbb {Q}))$
-groups after minimalisation, since the map $\operatorname K_1({\mathcal {D}}^\mathrm {p}(\mathbb {Z}) \rightarrow \operatorname K_1({\mathcal {D}}^\mathrm {p}(\mathbb {Q}))$![]() is not surjective.
is not surjective.
Corollary 7.2 gains much of its traction from the following:
Theorem 7.3 The functor
induces an equivalence between the full subcategories of Karoubi-localising functors on both sides.
Versions of this result have long been known, again going back to the work of Blumberg, Gepner and Tabuada. The precise version above will appear as part of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle7], and we shall not discuss its proof any further in this note. It implies existence of a unique Karoubi-localising functor $\mathbb {K} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {Sp}$![]() , non-connective algebraic $K$
, non-connective algebraic $K$![]() -theory, with $\Omega ^\infty \mathbb {K}(\mathcal {C}) \simeq \operatorname {\mathcal {K}}(\mathcal {C}^\natural )$
-theory, with $\Omega ^\infty \mathbb {K}(\mathcal {C}) \simeq \operatorname {\mathcal {K}}(\mathcal {C}^\natural )$![]() for stable categories $\mathcal {C}$
for stable categories $\mathcal {C}$![]() . It is this functor which is mostly used in the modern study of algebraic $K$
. It is this functor which is mostly used in the modern study of algebraic $K$![]() -groups and spectra, since it (or more precisely the restriction $X \mapsto \mathbb {K}({\mathcal {D}}^\mathrm {p}(X))$
-groups and spectra, since it (or more precisely the restriction $X \mapsto \mathbb {K}({\mathcal {D}}^\mathrm {p}(X))$![]() , ${\mathcal {D}}^\mathrm {p}(X)$
, ${\mathcal {D}}^\mathrm {p}(X)$![]() being the perfect derived category of any scheme $X$
being the perfect derived category of any scheme $X$![]() ) satisfies Zariski descent for nice enough schemes (as does any Karoubi-localising functor), while $\mathrm {K} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {Sp}$
) satisfies Zariski descent for nice enough schemes (as does any Karoubi-localising functor), while $\mathrm {K} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {Sp}$![]() does not.
does not.
We now turn to the proof of 7.1.
First proof The first proof we give is based on the construction $\operatorname {\mathcal {K}}(\mathcal {C}) \simeq \Omega |\mathrm {Cr}\operatorname {Q}(\mathcal {C})|$![]() and the analysis made for the localisation theorem. From 2.7 applied to $|\mathrm {Cr} \operatorname {Q}-|$
and the analysis made for the localisation theorem. From 2.7 applied to $|\mathrm {Cr} \operatorname {Q}-|$![]() , we obtain a fibre sequence
, we obtain a fibre sequence
and by inspection
as bisimplicial animae. As in § 6, we can identify
But if $\mathcal {A} \rightarrow \mathcal {B}$![]() is dense, so is $\operatorname {Q}_n(\mathcal {A}) \rightarrow \operatorname {Q}_n(\mathcal {B})$
is dense, so is $\operatorname {Q}_n(\mathcal {A}) \rightarrow \operatorname {Q}_n(\mathcal {B})$![]() . Thus, $\operatorname {Q}_n(\mathcal {B})/\operatorname {Q}_n(\mathcal {A}) \simeq 0$
. Thus, $\operatorname {Q}_n(\mathcal {B})/\operatorname {Q}_n(\mathcal {A}) \simeq 0$![]() . As explained in 6.7, this gives that $|\operatorname {Q}_n(\mathcal {B})_{\operatorname {Q}_n(\mathcal {A})}|$
. As explained in 6.7, this gives that $|\operatorname {Q}_n(\mathcal {B})_{\operatorname {Q}_n(\mathcal {A})}|$![]() is discrete with components $\operatorname K_0(\operatorname {Q}_n(\mathcal {B}))/\operatorname K_0(\operatorname {Q}_n(\mathcal {A}))$
is discrete with components $\operatorname K_0(\operatorname {Q}_n(\mathcal {B}))/\operatorname K_0(\operatorname {Q}_n(\mathcal {A}))$![]() . By direct inspection, one finally finds that $\operatorname K_0(\operatorname {Q}(\mathcal {C}))$
. By direct inspection, one finally finds that $\operatorname K_0(\operatorname {Q}(\mathcal {C}))$![]() is the edgewise subdivision of $\mathrm {Bar}(\operatorname K_0(\mathcal {C}))$
is the edgewise subdivision of $\mathrm {Bar}(\operatorname K_0(\mathcal {C}))$![]() , so that in total
, so that in total
is an Eilenberg–Mac Lane space in degree $1$![]() . Looping the fibre sequence from the start of this proof now gives the claim.
. Looping the fibre sequence from the start of this proof now gives the claim.
The second proof of 7.1 we provide rests solely on the universal property of $\mathcal {K} \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() . To emphasise this, we give it in the generality of an arbitrary additive functor $F\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$
. To emphasise this, we give it in the generality of an arbitrary additive functor $F\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$![]() that admits a group completion (i.e. an initial functor $F^\mathrm {grp}$
that admits a group completion (i.e. an initial functor $F^\mathrm {grp}$![]() under $F$
under $F$![]() that is group-like additive); as mentioned this is the case for any additive $F$
that is group-like additive); as mentioned this is the case for any additive $F$![]() but we neither prove nor make use of this fact. The reader may safely consider only $F=\mathrm {Cr}$
but we neither prove nor make use of this fact. The reader may safely consider only $F=\mathrm {Cr}$![]() and $F^\mathrm {grp}=\operatorname {\mathcal {K}}$
and $F^\mathrm {grp}=\operatorname {\mathcal {K}}$![]() if they wish.
if they wish.
Definition 7.4 We call a map $f\colon N\to M$![]() of ${\mathrm {E}_\infty }$
of ${\mathrm {E}_\infty }$![]() -monoids (in $\mathrm {An}$
-monoids (in $\mathrm {An}$![]() ) cofinal if
) cofinal if
(i) $f$
 is an inclusion of a collection of path components, and
is an inclusion of a collection of path components, and(ii) for each $x\in \pi _0(M)$
 there is $x'\in \pi _0(M)$
there is $x'\in \pi _0(M)$ such that $x+x'\in \pi _0(N)$
such that $x+x'\in \pi _0(N)$ . We call such a cofinal map dense if in addition,
. We call such a cofinal map dense if in addition,(iii) an element $x\in \pi _0(M)$
 belongs to $\pi _0(N)$
belongs to $\pi _0(N)$ already if there exists $y\in \pi _0(N)$
already if there exists $y\in \pi _0(N)$ such that $x+y\in \pi _0(N)$
such that $x+y\in \pi _0(N)$ .
.
The last condition is easily seen to be equivalent to the condition that the sequence of monoids
(which might generally fail to be exact in the middle) is indeed exact.
Lemma 7.5 If $f\colon N\to M$![]() is a cofinal map of ${\mathrm {E}_\infty }$
is a cofinal map of ${\mathrm {E}_\infty }$![]() -monoids, then its cofibre $M/N$
-monoids, then its cofibre $M/N$![]() (in the category of ${\mathrm {E}_\infty }$
(in the category of ${\mathrm {E}_\infty }$![]() -monoids) is a discrete group.
-monoids) is a discrete group.
Before proving this lemma, let us derive the cofinality theorem. Recall that every additive functor $F\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$![]() automatically refines to a functor with values in ${\mathrm {E}_\infty }$
automatically refines to a functor with values in ${\mathrm {E}_\infty }$![]() -monoids.
-monoids.
Definition 7.6 We call an additive functor $F\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm{An\ Karoubian}$![]() if
if
(i) every dense inclusion of stable $\infty$
 -categories $\mathcal {A}\to \mathcal {B}$
-categories $\mathcal {A}\to \mathcal {B}$ induces a dense map $F(\mathcal {A})\to F(\mathcal {B})$
induces a dense map $F(\mathcal {A})\to F(\mathcal {B})$ of ${\mathrm {E}_\infty }$
of ${\mathrm {E}_\infty }$ -monoids, and
-monoids, and(ii) $F$
 preserves pullback squares
in $\mathrm {Cat}_\infty ^\mathrm {st}$
preserves pullback squares
in $\mathrm {Cat}_\infty ^\mathrm {st}$
 whose (say) vertical maps are dense.
whose (say) vertical maps are dense.
The groupoid-core functor is indeed Karoubian: The second condition holds because $\mathrm {Cr}$![]() commutes with all limits and for the first condition, we note that the map of ${\mathrm {E}_\infty }$
commutes with all limits and for the first condition, we note that the map of ${\mathrm {E}_\infty }$![]() -monoids $\mathrm {Cr}(\mathcal {A})\to \mathrm {Cr}(\mathcal {B})$
-monoids $\mathrm {Cr}(\mathcal {A})\to \mathrm {Cr}(\mathcal {B})$![]() is clearly cofinal; furthermore, if $b$
is clearly cofinal; furthermore, if $b$![]() is an object in $\mathcal {B}$
is an object in $\mathcal {B}$![]() and $a$
and $a$![]() is an object of $\mathcal {A}$
is an object of $\mathcal {A}$![]() such that $b\oplus a$
such that $b\oplus a$![]() lies in the essential image of $\mathcal {A}$
lies in the essential image of $\mathcal {A}$![]() , then so does $b=\operatorname {fib}(b\oplus a\to a)$
, then so does $b=\operatorname {fib}(b\oplus a\to a)$![]() . Thus, the following version of the Cofinality theorem is indeed a generalisation of 7.1.
. Thus, the following version of the Cofinality theorem is indeed a generalisation of 7.1.
Theorem 7.7 Let $F\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$![]() be an additive and Karoubian functor and $F^{\mathrm {grp}}$
be an additive and Karoubian functor and $F^{\mathrm {grp}}$![]() be a group completion of $F$
be a group completion of $F$![]() . For every dense inclusion $\mathcal {A}\to \mathcal {B}$
. For every dense inclusion $\mathcal {A}\to \mathcal {B}$![]() of stable $\infty$
of stable $\infty$![]() -categories, the canonical map
-categories, the canonical map
of cofibre ${\mathrm {E}_\infty }$![]() -monoids is an equivalence. Hence, $F^\mathrm {grp}$
-monoids is an equivalence. Hence, $F^\mathrm {grp}$![]() induces isomorphisms
induces isomorphisms
and a short exact sequence
of abelian groups, where the last term denotes the quotient in the category of discrete commutative monoids.
Proof. The second statement follows from the first and lemma 7.5: The cofibre sequence of ${\mathrm {E}_\infty }$![]() -groups
-groups
(with last term discrete) is a fibre sequence of animae, with last map $\pi _0$![]() -surjective, and the functor
-surjective, and the functor
commutes with colimits, since it admits the discrete inclusion as a right adjoint.
Let us prove the first statement. The chain of dense inclusions
induces a cofibre sequence of ${\mathrm {E}_\infty }$![]() -groups
-groups
and similarly with $F^{\mathrm {grp}}$![]() , so it suffices to consider the case $\mathcal {B}=\mathcal {A}^\natural$
, so it suffices to consider the case $\mathcal {B}=\mathcal {A}^\natural$![]() .
.
We claim that the functor $F'\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \operatorname {Mon}_{\mathrm {E}_\infty }(\mathrm {An})$![]() given by the formula
given by the formula
(quotient of ${\mathrm {E}_\infty }$![]() -monoids) represents the quotient $(F\circ (-)^\natural )/F$
-monoids) represents the quotient $(F\circ (-)^\natural )/F$![]() in the category of additive functors $\mathrm {Cat}_\infty ^\mathrm {st}\to \operatorname {Mon}_{\mathrm {E}_\infty }(\mathrm {An})$
in the category of additive functors $\mathrm {Cat}_\infty ^\mathrm {st}\to \operatorname {Mon}_{\mathrm {E}_\infty }(\mathrm {An})$![]() . To see this, it will suffice to prove that $F'$
. To see this, it will suffice to prove that $F'$![]() is additive. Since $F'$
is additive. Since $F'$![]() is group-like, we can combine 2.4 and 2.5 with the splitting lemma to see that it suffices to prove that $F'$
is group-like, we can combine 2.4 and 2.5 with the splitting lemma to see that it suffices to prove that $F'$![]() sends the (split) Verdier sequence $\mathcal {A} \rightarrow \operatorname {Ar}(\mathcal {A}) \xrightarrow {t} \mathcal {A}$
sends the (split) Verdier sequence $\mathcal {A} \rightarrow \operatorname {Ar}(\mathcal {A}) \xrightarrow {t} \mathcal {A}$![]() to a (split) fibre sequence. In view of lemma 7.5, we only need to show that it induces a short exact sequences of abelian groups
to a (split) fibre sequence. In view of lemma 7.5, we only need to show that it induces a short exact sequences of abelian groups
For this, we note that short exact sequences of monoids are in particular cofibre sequences of monoids. Since $F$![]() and $F\circ (-)^\natural$
and $F\circ (-)^\natural$![]() are additive, we see by commuting quotients that the sequence in question is a cofibre sequence (of abelian monoids or of abelian groups), and hence right exact. Also, the first map is (split) injective, so the sequence is indeed short exact.
are additive, we see by commuting quotients that the sequence in question is a cofibre sequence (of abelian monoids or of abelian groups), and hence right exact. Also, the first map is (split) injective, so the sequence is indeed short exact.
Similarly, $(F^\mathrm {grp})'$![]() is additive and so represents the quotient of ($F^\mathrm {grp}\circ (-)^\natural )/F^\mathrm {grp}$
is additive and so represents the quotient of ($F^\mathrm {grp}\circ (-)^\natural )/F^\mathrm {grp}$![]() in the category of additive functors $\mathrm {Cat}_\infty ^\mathrm {st}\to \operatorname {Grp}_{\mathrm {E}_\infty }(\mathrm {An})$
in the category of additive functors $\mathrm {Cat}_\infty ^\mathrm {st}\to \operatorname {Grp}_{\mathrm {E}_\infty }(\mathrm {An})$![]() : The short exact sequence
: The short exact sequence
is proven for $n=0$![]() as above, and for $n>0$
as above, and for $n>0$![]() follows from the equivalence
follows from the equivalence
valid for any map of ${\mathrm {E}_\infty }$![]() -groups.
-groups.
Next, we note that the canonical map $F\circ (-)^\natural \to F^\mathrm {grp}\circ (-)^\natural$![]() is a group completion: This follows from the fact that the endofunctor $(-)^\natural$
is a group completion: This follows from the fact that the endofunctor $(-)^\natural$![]() of $\mathrm {Cat}_\infty ^\mathrm {st}$
of $\mathrm {Cat}_\infty ^\mathrm {st}$![]() admits the minimalisation $(-)^\mathrm {min}$
admits the minimalisation $(-)^\mathrm {min}$![]() as a left adjoint (a simple consequence of Thomason's theorem): This adjunction induces an adjunction on $\operatorname {Fun}(\mathrm {Cat}_\infty ^\mathrm {st}, \mathrm {An})$
as a left adjoint (a simple consequence of Thomason's theorem): This adjunction induces an adjunction on $\operatorname {Fun}(\mathrm {Cat}_\infty ^\mathrm {st}, \mathrm {An})$![]() so we have equivalences
so we have equivalences
for every group-like additive functor $G$![]() .
.
Thus, comparing universal properties, we see that the map $F'\to (F^\mathrm {grp})'$![]() is a group completion of $F'$
is a group completion of $F'$![]() : But $F'$
: But $F'$![]() is already group-like, so it is an equivalence.
is already group-like, so it is an equivalence.
The careful reader may have noticed that the second condition of being Karoubian has not been used so far, nor has density (as opposed to cofinality) for the map induced by a dense inclusion. These extra conditions generally ensure that $F^\mathrm {grp} \circ (-)^\natural$![]() is Karoubi-localising, as we will now show. We start by observing:
is Karoubi-localising, as we will now show. We start by observing:
Corollary 7.8 If $F\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$![]() is an additive and Karoubian functor, then so is any group completion $F^\mathrm {grp}$
is an additive and Karoubian functor, then so is any group completion $F^\mathrm {grp}$![]() of $F$
of $F$![]() .
.
Proof. It follows from the cofinality theorem that $F^\mathrm {grp}$![]() sends dense functors to dense maps of ${\mathrm {E}_\infty }$
sends dense functors to dense maps of ${\mathrm {E}_\infty }$![]() -monoids (with the last two conditions being automatic for group-like functors). It remains to prove that $F^\mathrm {grp}$
-monoids (with the last two conditions being automatic for group-like functors). It remains to prove that $F^\mathrm {grp}$![]() preserves pullback squares
preserves pullback squares

in $\mathrm {Cat}_\infty ^\mathrm {st}$![]() whose vertical maps are dense.
whose vertical maps are dense.
By assumption, this is true for $F$![]() and since $\pi _0 F(\mathcal {A}')\to \pi _0 F(\mathcal {B}')$
and since $\pi _0 F(\mathcal {A}')\to \pi _0 F(\mathcal {B}')$![]() is injective, we see that also $\pi _0(F)$
is injective, we see that also $\pi _0(F)$![]() sends the square to a pullback square. From density we then deduce that the map of quotient monoids
sends the square to a pullback square. From density we then deduce that the map of quotient monoids
has kernel zero. But by the cofinality theorem, this identifies with the corresponding map for $\pi _0 (F^\mathrm {grp})$![]() , so we deduce that $\pi _0(F^\mathrm {grp})$
, so we deduce that $\pi _0(F^\mathrm {grp})$![]() also sends the square to a pullback square. Applying the cofinality theorem again, we see that $F^\mathrm {grp}$
also sends the square to a pullback square. Applying the cofinality theorem again, we see that $F^\mathrm {grp}$![]() sends the square to a pullback square of animae.
sends the square to a pullback square of animae.
From 2.13 we now immediately obtain the following generalisation of 7.2:
Corollary 7.9 Let $F\colon \mathrm {Cat}_\infty ^\mathrm {st}\to \mathrm {An}$![]() be additive and Karoubian, and let $F^\mathrm {grp}$
be additive and Karoubian, and let $F^\mathrm {grp}$![]() be a group completion of $F$
be a group completion of $F$![]() . If $F^\mathrm {grp}$
. If $F^\mathrm {grp}$![]() is Verdier-localising, then
is Verdier-localising, then
is Karoubi-localising.
Let us finally give the postponed
Proof of lemma 7.5 We start by observing that $\pi _0(M/N) = \pi _0(M)/\pi _0(N)$![]() is a group by the cofinality assumption. We then need to show that
is a group by the cofinality assumption. We then need to show that
is contractible. Since $\pi _0(N^\mathrm {grp})\to \pi _0(M^\mathrm {grp})$![]() identifies with the discrete group completion of $\pi _0(N)\to \pi _0(M)$
identifies with the discrete group completion of $\pi _0(N)\to \pi _0(M)$![]() , it is injective by cofinality, and we are left to show that the map $N^\mathrm {grp}\to M^\mathrm {grp}$
, it is injective by cofinality, and we are left to show that the map $N^\mathrm {grp}\to M^\mathrm {grp}$![]() induces an equivalence on the base point components. We can prove this by showing it is a homology isomorphism because it is a map of $H$
induces an equivalence on the base point components. We can prove this by showing it is a homology isomorphism because it is a map of $H$![]() -spaces.
-spaces.
To show that the map on base point components is injective on homology, it suffices to prove the same for $N^\mathrm {grp}\to M^\mathrm {grp}$![]() itself. By the group completion theorem, this map is given by the composite
itself. By the group completion theorem, this map is given by the composite
where the first map is injective by the first assumption of cofinality (since localisation is exact), and the second map is an isomorphism by the second assumption.
To show surjectivity on the base point component, we first consider the chain of maps in the homotopy category of spaces
mapping an ${\mathrm {E}_\infty }$![]() -monoid $M$
-monoid $M$![]() into the base point component of its group completion, where the first map is the canonical one and the second one subtracts $x$
into the base point component of its group completion, where the first map is the canonical one and the second one subtracts $x$![]() in the component of $x$
in the component of $x$![]() . On homology, these maps are given by base-change along the canonical ring homomorphisms
. On homology, these maps are given by base-change along the canonical ring homomorphisms
in view of the group completion theorem and the commutativity of $M$![]() for the left map and the decomposition $M^\mathrm {grp} \simeq \pi _0 M^\mathrm {grp} \times M^\mathrm {grp}_0$
for the left map and the decomposition $M^\mathrm {grp} \simeq \pi _0 M^\mathrm {grp} \times M^\mathrm {grp}_0$![]() (natural in the homotopy category of $\mathrm {An}$
(natural in the homotopy category of $\mathrm {An}$![]() ) for the right map. We conclude the existence of a natural isomorphism
) for the right map. We conclude the existence of a natural isomorphism
where in the target we take the quotient of the monoid action in the category of graded abelian groups.
Thus we need to show that the map $N\to M$![]() becomes surjective in homology after modding out the $\pi _0(M)$
becomes surjective in homology after modding out the $\pi _0(M)$![]() -action in the target. So let $a\in H_*(M)$
-action in the target. So let $a\in H_*(M)$![]() where we may assume that $a$
where we may assume that $a$![]() is defined in a single path component $M_x$
is defined in a single path component $M_x$![]() of $M$
of $M$![]() , for some $x\in \pi _0(M)$
, for some $x\in \pi _0(M)$![]() . By the second condition of cofinality, we may assume as well that $x\in \pi _0(N)$
. By the second condition of cofinality, we may assume as well that $x\in \pi _0(N)$![]() , in which case $a$
, in which case $a$![]() lifts to $H_*(N)$
lifts to $H_*(N)$![]() by the first condition of cofinality.
by the first condition of cofinality.
8. The connection to the relative $\operatorname {Q}$ -construction
-construction
Finally, we briefly explain a connection between our version of Waldhausen's fibration theorem, i.e. theorem 2.7, and the relative $\operatorname {Q}$![]() -construction. In particular, this approach generalises the statement to arbitrary exact functors instead of just Verdier inclusions.
-construction. In particular, this approach generalises the statement to arbitrary exact functors instead of just Verdier inclusions.
Definition 8.1 For $f \colon \mathcal {C} \rightarrow \mathcal {D}$![]() an exact functor between stable categories, we define the relative $\operatorname {Q}$
an exact functor between stable categories, we define the relative $\operatorname {Q}$![]()
-construction $\operatorname {Q}(f) \colon \Delta ^\mathrm {op} \rightarrow \mathrm {Cat}_\infty ^\mathrm {st}$![]() by requiring
by requiring

to be cartesian.
There is a canonical map $\mathcal {D} \rightarrow \operatorname {Q}_0(f)$![]() whose components are given by
whose components are given by
Furthermore, the inclusion
induces a functor
whose image lands in the constant functors. Since it is natural for $n \in \Delta$![]() we obtain a map
we obtain a map
We shall prove the following two statements, which together imply 2.7 once more:
Proposition 8.2 For every group-like additive $F \colon \mathrm {Cat}_\infty ^\mathrm {st} \rightarrow \mathrm {An}$![]() and exact $f \colon \mathcal {C} \rightarrow \mathcal {D}$
and exact $f \colon \mathcal {C} \rightarrow \mathcal {D}$![]() , the sequence
, the sequence
is a bifibre sequence of ${\mathrm {E}_\infty }$![]() -groups.
-groups.
Proposition 8.3 If $i \colon \mathcal {C} \rightarrow \mathcal {D}$![]() is fully faithful and exact, then there is an equivalence
is fully faithful and exact, then there is an equivalence
of simplicial categories, such that

commutes.
We shall prove the two statements above in turn.
Proof of proposition 8.2 By the equifibrancy lemma the square

is cartesian, since the map $F \operatorname {Null}(\mathcal {D}) \to F \operatorname {Q}(\mathcal {D})$![]() is equifibred as shown in the proof of 5.2. In other words,
is equifibred as shown in the proof of 5.2. In other words,
is a fibre sequence (the case $\mathcal {C}=0$![]() gave $F(\mathcal {D}) \simeq \Omega |F\operatorname {Q}(\mathcal {C})|$
gave $F(\mathcal {D}) \simeq \Omega |F\operatorname {Q}(\mathcal {C})|$![]() in 5.2, since $\operatorname {Q}(0 \rightarrow \mathcal {D}) \simeq \mathrm {const}_\mathcal {D}$
in 5.2, since $\operatorname {Q}(0 \rightarrow \mathcal {D}) \simeq \mathrm {const}_\mathcal {D}$![]() by inspection). Rotating the fibre sequence above twice to the left therefore gives us the desired fibre sequence
by inspection). Rotating the fibre sequence above twice to the left therefore gives us the desired fibre sequence
To see that it is also a cofibre sequence, it suffices (by the long exact sequence) to check that $\pi _0|F\operatorname {Q}(\mathcal {C})| = 0$![]() . But the functor
. But the functor
induces a homotopy between the $0$![]() and identity maps of $\pi _0|F\operatorname {Q}(\mathcal {C})|$
and identity maps of $\pi _0|F\operatorname {Q}(\mathcal {C})|$![]() , which gives the claim.
, which gives the claim.
Proof of proposition 8.3 We shall realise both $\operatorname {Q}_n(i)$![]() and $\operatorname {Fun}^\mathcal {C}([n] * [n]^\mathrm {op},\mathcal {D})$
and $\operatorname {Fun}^\mathcal {C}([n] * [n]^\mathrm {op},\mathcal {D})$![]() as the following full subcategory $P_n$
as the following full subcategory $P_n$![]() of $\operatorname {Fun}(\operatorname {TwAr^{r}}([0]*[n]*[n]^\mathrm {op}*[0]),\mathcal {D})$
of $\operatorname {Fun}(\operatorname {TwAr^{r}}([0]*[n]*[n]^\mathrm {op}*[0]),\mathcal {D})$![]() : A functor $F$
: A functor $F$![]() lies in $P_n$
lies in $P_n$![]() if under the identification $[0]*[n]*[n]^\mathrm {op}*[0] \cong [1+n]*[1+n]^\mathrm {op}$
if under the identification $[0]*[n]*[n]^\mathrm {op}*[0] \cong [1+n]*[1+n]^\mathrm {op}$![]() ,
,
(i) all squares in the ‘left half’ of $\operatorname {TwAr^{r}}([1+n]*[1+n]^\mathrm {op})$
 go to cartesian squares, i.e.
whenever $j \leq m$
go to cartesian squares, i.e.
whenever $j \leq m$
 (where $\epsilon \in \{l,r\}$
(where $\epsilon \in \{l,r\}$ and $i_\epsilon$
and $i_\epsilon$ denotes the $i$
denotes the $i$ -th element of the left respectively right factor of $[1+n]*[1+n]^\mathrm {op}$
-th element of the left respectively right factor of $[1+n]*[1+n]^\mathrm {op}$ ),
),
(ii) $F$
 vanishes on the ‘right half’ of $\operatorname {TwAr^{r}}([1+n]*[1+n]^\mathrm {op})$
vanishes on the ‘right half’ of $\operatorname {TwAr^{r}}([1+n]*[1+n]^\mathrm {op})$ , i.e. we have $F(i_l \leq k_r) = 0 = F(i_r \leq k_r)$
, i.e. we have $F(i_l \leq k_r) = 0 = F(i_r \leq k_r)$ whenever $i \geq k$
whenever $i \geq k$ , and
, and(iii) $F$
 vanishes on the lower left corner of $\operatorname {TwAr^{r}}([1+n]*[1+n]^\mathrm {op})$
vanishes on the lower left corner of $\operatorname {TwAr^{r}}([1+n]*[1+n]^\mathrm {op})$ , i.e. $F(0_l \leq 0_l) = 0$
, i.e. $F(0_l \leq 0_l) = 0$ , and
, and(iv) $F$
 takes values in $\mathcal {C}$
takes values in $\mathcal {C}$ on all spots not of the form $(0_l \leq k_\epsilon )$
on all spots not of the form $(0_l \leq k_\epsilon )$ .
.
In other words, $P_n$![]() consists of diagrams of the shape
consists of diagrams of the shape

where the lower left corner and the entire right half are zero, the $2n+2$![]() objects on the upper left diagonal marked by empty circles are in $\mathcal {D}$
objects on the upper left diagonal marked by empty circles are in $\mathcal {D}$![]() , the objects marked by filled circles are in the image of $\mathcal {C}$
, the objects marked by filled circles are in the image of $\mathcal {C}$![]() and all squares in the left half are cartesian.
and all squares in the left half are cartesian.
Now consider on the one hand the inclusion
induced by the inclusion $[0] * [n] \subset ([0]*[n])*([0]*[n])^\mathrm {op}$![]() . Since its image lies fully in the ‘left half’, the first and last two conditions guarantee that restriction along $\alpha$
. Since its image lies fully in the ‘left half’, the first and last two conditions guarantee that restriction along $\alpha$![]() yields a map
yields a map
which is clearly natural in $n \in \Delta$![]() .
.
Similarly, consider the map
The first and last conditions imply that any map in the restriction of some $F \in P_n$![]() goes to the pullback of some map in $\mathcal {C}$
goes to the pullback of some map in $\mathcal {C}$![]() , so in particular to an equivalence modulo $\mathcal {C}$
, so in particular to an equivalence modulo $\mathcal {C}$![]() , we therefore obtain a well-defined map
, we therefore obtain a well-defined map
which is again clearly natural in $n \in \Delta$![]() .
.
As mentioned, the claim will now follow from both these maps $\alpha ^*$![]() and $\beta ^*$
and $\beta ^*$![]() being equivalences. We start with $\alpha ^*$
being equivalences. We start with $\alpha ^*$![]() . An inverse is constructed by the following two-step Kan extension. First, let $T_n \subseteq \operatorname {TwAr^{r}}([0]*[n]*[n]^\mathrm {op}*[0])$
. An inverse is constructed by the following two-step Kan extension. First, let $T_n \subseteq \operatorname {TwAr^{r}}([0]*[n]*[n]^\mathrm {op}*[0])$![]() denote the subposet given as the union of $\operatorname {TwAr^{r}}([0]*[n])$
denote the subposet given as the union of $\operatorname {TwAr^{r}}([0]*[n])$![]() and the ‘right half’ of $\operatorname {TwAr^{r}}([0]*[n]*[n]^\mathrm {op}*[0])$
and the ‘right half’ of $\operatorname {TwAr^{r}}([0]*[n]*[n]^\mathrm {op}*[0])$![]() . Then consider
. Then consider
As Kan extensions along fully faithful maps are fully faithful and right inverse to restriction, it remains only to check that the composite takes $\operatorname {Q}_n(i) \subseteq \operatorname {Fun}(\operatorname {TwAr^{r}}([0]*[n]),\mathcal {D})$![]() onto $P_n$
onto $P_n$![]() . But from the pointwise formulae, it is easy to see that the first Kan extension is an extension by $0$
. But from the pointwise formulae, it is easy to see that the first Kan extension is an extension by $0$![]() , and that the pullback condition (i) is equivalent to being right Kan extended from $T_n$
, and that the pullback condition (i) is equivalent to being right Kan extended from $T_n$![]() . This in turn implies immediately that for $F$
. This in turn implies immediately that for $F$![]() satisfying conditions (i) and (ii), condition (iv) is equivalent to $F\rvert _{\operatorname {TwAr^{r}}([n])}$
satisfying conditions (i) and (ii), condition (iv) is equivalent to $F\rvert _{\operatorname {TwAr^{r}}([n])}$![]() taking values in $\mathcal {C}$
taking values in $\mathcal {C}$![]() , which finishes the claim (since the vanishing condition in (iii) is also contained in the definition of $\operatorname {Q}_n(i)$
, which finishes the claim (since the vanishing condition in (iii) is also contained in the definition of $\operatorname {Q}_n(i)$![]() ).
).
We finally treat $\beta ^*$![]() : Again the inverse is given by successive Kan extensions. First add a zero at $(0_l \leq 0_r)$
: Again the inverse is given by successive Kan extensions. First add a zero at $(0_l \leq 0_r)$![]() to a functor defined on the image of $\beta$
to a functor defined on the image of $\beta$![]() by left Kan extension, and then right Kan extend to add zeros at $(0_l \leq 0_l)$
by left Kan extension, and then right Kan extend to add zeros at $(0_l \leq 0_l)$![]() and the ‘right half’, and finally left Kan extend once more to the whole of $\operatorname {TwAr^{r}}([0]*[n]*[n]^\mathrm {op}*[0])$
and the ‘right half’, and finally left Kan extend once more to the whole of $\operatorname {TwAr^{r}}([0]*[n]*[n]^\mathrm {op}*[0])$![]() . Again this process is right inverse to restriction along $\beta$
. Again this process is right inverse to restriction along $\beta$![]() on the whole of $\operatorname {Fun}([n]*[n]^\mathrm {op},\mathcal {D})$
on the whole of $\operatorname {Fun}([n]*[n]^\mathrm {op},\mathcal {D})$![]() , and it remains to check that it takes $\operatorname {Fun}^\mathcal {C}([n]*[n]^\mathrm {op},\mathcal {D})$
, and it remains to check that it takes $\operatorname {Fun}^\mathcal {C}([n]*[n]^\mathrm {op},\mathcal {D})$![]() onto $P_n$
onto $P_n$![]() .
.
But again it follows trivially from the pointwise formulae that the first two Kan extensions really are extensions by zero, precisely as required in conditions (ii) and (iii), and that being in the image of the second left Kan extension is equivalent to the squares in condition (i) being pushouts, so stability implies that these are equivalent conditions. To finally see that the image of $\operatorname {Fun}^\mathcal {C}([n]*[n]^\mathrm {op},\mathcal {D})$![]() also satisfies condition (iv), note that (as just discussed) the value at $(i_l \leq k_\epsilon )$
also satisfies condition (iv), note that (as just discussed) the value at $(i_l \leq k_\epsilon )$![]() , with $i < k$
, with $i < k$![]() or $i=k$
or $i=k$![]() and $\epsilon = l$
and $\epsilon = l$![]() , of the extension $\operatorname {TwAr^{r}}([1+n]*[1+n]^\mathrm {op}) \rightarrow \mathcal {D}$
, of the extension $\operatorname {TwAr^{r}}([1+n]*[1+n]^\mathrm {op}) \rightarrow \mathcal {D}$![]() of some $F \colon \mathrm {im}(\beta ) \rightarrow \mathcal {D}$
of some $F \colon \mathrm {im}(\beta ) \rightarrow \mathcal {D}$![]() sits in a cocartesian square
sits in a cocartesian square

But its right most term is part of the ‘right half’ of $\operatorname {TwAr^{r}}([0]*[n]*[n]^\mathrm {op}*[0])$![]() (in fact it lies on the middle vertical line) and the upper left pointing map is an equivalence module $\mathcal {C}$
(in fact it lies on the middle vertical line) and the upper left pointing map is an equivalence module $\mathcal {C}$![]() by assumption, so $F(i_l \leq k_\epsilon ) \in \mathcal {C}$
by assumption, so $F(i_l \leq k_\epsilon ) \in \mathcal {C}$![]() .
.
Acknowledgements
We heartily thank Dustin Clausen, from whom we first learned a clean proof of the localisation theorem, for several very helpful discussions. We further thank Ferdinand Wagner for the permission to use some of his pretty TikZ diagrams in this note. During the preparation of this manuscript, F. H. was a member of the Hausdorff Center for Mathematics at the University of Bonn funded by the German Research Foundation (DFG) and furthermore a member of the cluster ‘Mathematics Münster: Dynamics-Geometry-Structure’ at the University of Münster (DFG grant nos. EXC 2047 390685813 and EXC 2044 390685587, respectively). F. H. acknowledgesthe Mittag-Leffler Institute for its hospitality during the research programme ‘Higher algebraic structures in algebra, topology and geometry’, supported by the Swedish Research Council under grant no. 2016-06596. A. L. was supported by the Research Training Group ‘Algebro-Geometric Methods in Algebra, Arithmetic and Topology’ at the University of Wuppertal (DFG grant no. GRK 2240) and W. S. by the priority programme ‘Geometry at Infinity’ (DFG grant no. SPP 2026) at the University of Augsburg.