Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-01T05:23:53.883Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear actions of $\mathbb {Z}/p\times \mathbb {Z}/p$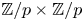 on $S^{2n-1}\times S^{2n-1}$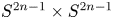

Part of: Topological manifolds

Published online by Cambridge University Press:  16 April 2024

Jim Fowler Open the ORCID record for Jim Fowler [Opens in a new window]  and
Courtney Thatcher
Jim Fowler
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH, USA (fowler@math.osu.edu)
Courtney Thatcher
Affiliation:
Department of Mathematics and Computer Science, University of Puget Sound, Tacoma, WA, USA (courtneythatcher@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

For an odd prime $p$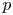, we consider free actions of $(\mathbb {Z}_{/{p}})^2$ 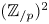on $S^{2n-1}\times S^{2n-1}$ 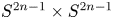given by linear actions of $(\mathbb {Z}_{/{p}})^2$ 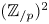on $\mathbb {R}^{4n}$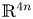. Simple examples include a lens space cross a lens space, but $k$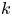-invariant calculations show that other quotients exist. Using the tools of Postnikov towers and surgery theory, the quotients are classified up to homotopy by the $k$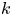-invariants and up to homeomorphism by the Pontrjagin classes. We will present these results and demonstrate how to calculate the $k$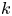-invariants and the Pontrjagin classes from the rotation numbers.

Keywords

group actions on manifoldsPostnikov towerssurgery theory

MSC classification

Primary: 57N65: Algebraic topology of manifolds
Secondary: 57S25: Groups acting on specific manifolds
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 14
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bak, A.. The computation of even dimension surgery groups of odd torsion groups. Communications in Algebra 6 (1978), 1393–1458.CrossRefGoogle Scholar
Bass, H., Milnor, J. and Serre, J.-P.. Solution of the congruence subgroup problem for ${\rm SL_n}(n\geq 3)$ and ${\rm Sp_2n}(n\geq 2)$. Inst. Hautes Études Sci. Publ. Math. 33 (1967), 59–137.CrossRefGoogle Scholar
Chapman, G. R.. The cohomology ring of a finite abelian group. Proc. London Math. Soc. (3) 45 (1982), 564–576.CrossRefGoogle Scholar
Davis, J. F. and Löffler, P.. A note on simple duality. Proceedings of the American Mathematical Society 94 (1985), 343–347.CrossRefGoogle Scholar
Eilenberg, S. and MacLane, S.. Homology of spaces with operators. II. Trans. Amer. Math. Soc. 65 (1949), 49–99.CrossRefGoogle Scholar
Fowler, J. and Thatcher, C.. $\mathbb {Z}_/p\times \mathbb {Z}_/p$ actions on $S^n\times S^n$. Algebr. Geom. Topol. (2023), to appear.Google Scholar
Kwasik, S. and Schultz, R.. All $\mathbb {Z}_q$ lens spaces have diffeomorphic squares. Topology 41 (2002), 321–340.CrossRefGoogle Scholar
Lance, T. (2000) Differentiable structures on manifolds. In Surveys on surgery theory, Vol. 1, volume 145 of Ann. of Math. Stud. (Princeton Univ. Press, Princeton, NJ), pp. 73–104.CrossRefGoogle Scholar
Long, J. H. (2008) The cohomology rings of the special affine group of $\mathbb {F}_p^2$ and of $PSL(3,p)$. ProQuest LLC, Ann Arbor, MI. Thesis (Ph.D.), University of Maryland, College Park.Google Scholar
Milnor, J.. Whitehead torsion. Bull. Am. Math. Soc. 72 (1966), 358.CrossRefGoogle Scholar
Ray, U.. Free linear actions of finite groups on products of spheres. J. Algebra 147 (1992), 456–490.CrossRefGoogle Scholar
Serre, J.-P.. Linear representations of finite groups (Springer-Verlag, New York-Heidelberg, 1977). Translated from the second French edition by Leonard L. Scott, Graduate Texts in Mathematics, Vol. 42.CrossRefGoogle Scholar
Szczarba, R. H.. On tangent bundles of fibre spaces and quotient spaces. Amer. J. Math. 86 (1964), 685–697.CrossRefGoogle Scholar
Thatcher, C. M.. On free $\mathbb {Z}_p$ actions on products of spheres. Geom. Dedicata 148 (2010), 391–415.CrossRefGoogle Scholar