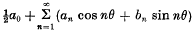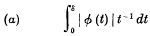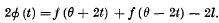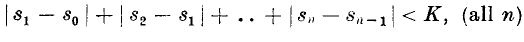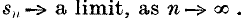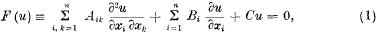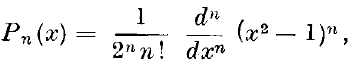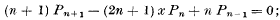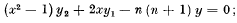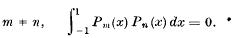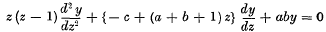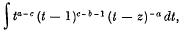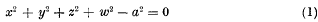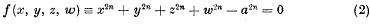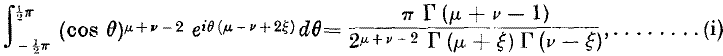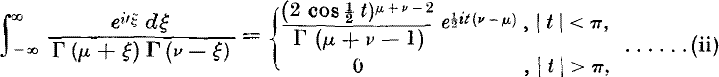Research Article
Generalised Solutions of Laplace's Equation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 181-188
-
- Article
-
- You have access
- Export citation
The Absolute Summability (A) of Fourier Series
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 129-134
-
- Article
-
- You have access
- Export citation
The Absolute Summability of Fourier Series
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-5
-
- Article
-
- You have access
- Export citation
The Complete System of Linear Complexes and one Quaternary Quadric
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 61-70
-
- Article
-
- You have access
- Export citation
Spherical Simplexes in n-dimensions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 6-15
-
- Article
-
- You have access
- Export citation
On the “elementary” solution of Laplace's Equation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 135-139
-
- Article
-
- You have access
- Export citation
On Generating Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 71-82
-
- Article
-
- You have access
- Export citation
On the Solution of Differential Equations by Definite Integrals
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 189-204
-
- Article
-
- You have access
- Export citation
Solution with Axial Symmetry of Einstein's Equations of Teleparallelism
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 140-150
-
- Article
-
- You have access
- Export citation
On Professor Whittaker's solution of differential equations by definite integrals: Part I
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 205-219
-
- Article
-
- You have access
- Export citation
On the Number of Ways of Colouring a Map
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 83-91
-
- Article
-
- You have access
- Export citation
Notes on the Extension of Aitken's Theorem (for Polynomial Interpolation) to the Everett Types.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 16-19
-
- Article
-
- You have access
- Export citation
On some Legendre Function Formulae
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 20-25
-
- Article
-
- You have access
- Export citation
On Rational Solutions of x3 + y3 +z3 = R.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 92-100
-
- Article
-
- You have access
- Export citation
Quadratic Equations in a Cyclic Number System
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 151-157
-
- Article
-
- You have access
- Export citation
On Professor Whittaker's solution of differential equations by definite integrals: Part II: Applications of the methods of non-commutative Algebra
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 220-239
-
- Article
-
- You have access
- Export citation
Bazin's Matrix and other allied Matrices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 240-251
-
- Article
-
- You have access
- Export citation
On The Uniformisation of Algebraic Curves of Genus 3
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 102-107
-
- Article
-
- You have access
- Export citation
A “Cubical” Universe
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 158-163
-
- Article
-
- You have access
- Export citation
On an Integral due to Ramanujan, and some ideas suggested by it
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 26-32
-
- Article
-
- You have access
- Export citation