Research Article
A mathematician among the molasses barrels: Maclaurin's unpublished memoir on volumes Introduction: Maclaurin's memoir and its place in eighteenth-century Scotland
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 193-240
-
- Article
-
- You have access
- Export citation
Multipliers for semigroups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 241-252
-
- Article
-
- You have access
- Export citation
A characterization of noetherian rings by cyclic modules
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 253-262
-
- Article
-
- You have access
- Export citation
On semi-artinian modules and injectivity conditions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 263-270
-
- Article
-
- You have access
- Export citation
The solution via monotonicity methods of some nonscalar reaction-diffusion problems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 271-284
-
- Article
-
- You have access
- Export citation
Minimal permutation representations of the two double covers of Sn
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 285-289
-
- Article
-
- You have access
- Export citation
Compact subsemigroups of (βℕ, +) containing the idempotents
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 291-307
-
- Article
-
- You have access
- Export citation
The maximal operator space of a normed space
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 309-323
-
- Article
-
- You have access
- Export citation
Biorthogonality in the banach spaces ℓp(n)*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 325-336
-
- Article
-
- You have access
- Export citation
Normalizers of finite multiplicity nests
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 337-344
-
- Article
-
- You have access
- Export citation
On primeness and nilpotence in structural matrix near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 345-356
-
- Article
-
- You have access
- Export citation
Upper bounds for the separation of real zeros of polynomials
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 357-363
-
- Article
-
- You have access
- Export citation
Direct finiteness of certain monoid algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 365-369
-
- Article
-
- You have access
- Export citation
Direct finiteness of certain monoid algebras II
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 371-376
-
- Article
-
- You have access
- Export citation
Distance between Hermitian operators in Schatten classes
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 377-380
-
- Article
-
- You have access
- Export citation
Homogeneous structures on Kähler submanifolds of complex projective spaces*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 381-395
-
- Article
-
- You have access
- Export citation
Extrema of principal curvature and symmetry
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 397-402
-
- Article
-
- You have access
- Export citation
Book Reviews
W. R. Bloom and H. Heyer Harmonic analysis of probability measures on hypergroups (de Gruyter Studies in Mathematics Vol. 20, de Gruyter, Berlin, New York 1995) vi + 601pp., 3 11 012105 0, about £140.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 403-405
-
- Article
-
- You have access
- Export citation
A. Ramsay and R. D. Richtmyer, Introduction to hyperbolic geometry (Universitext, Springer-Verlag, Berlin-Heidelberg-New York-London-Paris-Tokyo-Hong Kong 1995), xii + 287 pp., soft-cover, 3 540 94339 0, £30.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 405
-
- Article
-
- You have access
- Export citation
R. Seydel Practical bifurcation and stability analysis: from equilibrium to chaos (2nd edition) (Interdisciplinary Applied Mathematics, Vol. 5, Springer-Verlag, Berlin-Heidelberg-New York-London-Paris-Tokyo-Hong Kong 1994), xv + 407 pp., 3 540 94316 1, £34.50.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 405-406
-
- Article
-
- You have access
- Export citation

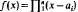 be a polynomial with distinct real zeros whose separation is defined by δ(
be a polynomial with distinct real zeros whose separation is defined by δ(