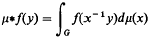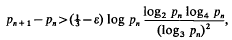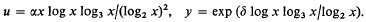Research Article
The Propagation of a Constant Strength Shock through a Simple Wave
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 277-284
-
- Article
-
- You have access
- Export citation
Evaluation of Certain Integrals Involving Bessel Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 285-290
-
- Article
-
- You have access
- Export citation
Existence Theorem for Groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 291-294
-
- Article
-
- You have access
- Export citation
A Note on the Kawada-into Theorem
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 295-296
-
- Article
-
- You have access
- Export citation
An Example of a Plane Shock of Variable Strength
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 297-302
-
- Article
-
- You have access
- Export citation
Some Further Triple Integral Equation Solutions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 303-316
-
- Article
-
- You have access
- Export citation
Integral Equation Formulation of some Three Part Boundary Value Problems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 317-323
-
- Article
-
- You have access
- Export citation
The Laplace Transform of the Modified Bessel Function K(t±mx) where m = 1, 2, 3, …, n
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 325-329
-
- Article
-
- You have access
- Export citation
The Difference between Consecutive Prime Numbers V
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 331-332
-
- Article
-
- You have access
- Export citation
On the Number of Crossings in a Complete Graph
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 333-338
-
- Article
-
- You have access
- Export citation
Book Reviews
C. Berge , Topological Spaces, translated by E. M. Patterson (Oliver and Boyd, 1963), xiii+270 pp., 50s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 339
-
- Article
-
- You have access
- Export citation
J. F. Gray, Sets, Relations and Functions (Holt, Rinehart and Winston, London, 1962), 143 pp., 20s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 339
-
- Article
-
- You have access
- Export citation
Ǐ. P. Kubilyus and J. Kubilius, Veroyatnostnye melody v teorii čisel (2-oe Izd.)(Gos. Izd. politiceskoǐ i naučnoǐ literatury Litovskoǐ SSR, Vil'nyus (Vilna), 1962), 220 pp., 82 Kopeks.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 339-340
-
- Article
-
- You have access
- Export citation
N. Bourbaki, Éléments de mathématique, Fascicule XX (Theorie des ensembles, Chapitre 3–Ensembles ordonnés, cardinaux, nombres entiers) (Hermann, 1963), 152 pp., 36 F.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 340-341
-
- Article
-
- You have access
- Export citation
Infinitistic Methods. Proceedings of the Symposium on Foundations of Mathematics, Warsaw, 2-9 September 1959 (Pergamon, 1961), 362 pp., £5.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 341
-
- Article
-
- You have access
- Export citation
G. T. Kneebone, Mathematical Logic and the Foundations of Mathematics (Van Nostrand, 1963), xiv+435 pp., 65s.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 341-342
-
- Article
-
- You have access
- Export citation
Nathaniel Macon, Numerical Analysis (Wiley, New York and London, 1963), xiv+161 pp., £2.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 342
-
- Article
-
- You have access
- Export citation
w. G. Cochran, Sampling Techniques (John Wiley & Sons, 2nd edition, 1963), ix+413 pp., 72s.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 342-343
-
- Article
-
- You have access
- Export citation
R. L. Goodstein, Boolean Algebra (The Commonwealth and International Library of Science, Technology, Engineering and Liberal Studies, Vol. 6, Pergamon Press, Oxford, 1963), 140 pp., 12s. 6d.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 343
-
- Article
-
- You have access
- Export citation
Ivan Niven, Diophantine Approximations (Interscience Tracts in Pure and Applied Mathematics, No. 14, John Wiley & Sons, New York), viii+68 pp., 36s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 344
-
- Article
-
- You have access
- Export citation