Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-06-22T02:45:38.991Z Has data issue: false hasContentIssue false
  • English
  • Français

The f-decomposition of Artinian modules over hyperfinite groups

Published online by Cambridge University Press:  20 January 2009

Z. Y. Duan
Z. Y. Duan
Affiliation:
Department of MathematicsSouthwest Teachers UniversityChongqing, 630715 P.R., China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A ℤG-module A is said to have an f-decomposition if 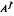in which A∫ is a ℤG-submodule of A such that each irreducible ℤG-factor of A∫ as an abelian group is finite and the ℤG-submodule A∫ has no finite irreducible ℤG-factors. In this paper, we prove that: if G is a hyperfinite group then any artinian ℤG-module A has an f-decomposition, which gives a positive answer to the question raised by D.I. Zaitzev in 1986.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 38 , Issue 1 , February 1995 , pp. 117 - 120
Copyright
Copyright © Edinburgh Mathematical Society 1995

References

REFERENCES

1.Duan, Z. Y., Noetherian modules over hyperflnite groups, (Ph.D thesis, University of Glasgow, 1991).Google Scholar
2.Duan, Z. Y. and Tomkinson, M. J., The decomposition of minmax modules over hyperfinite groups, Arch. Math. 61 (1993), 340–343.CrossRefGoogle Scholar
3.Zaitzev, D. I., Splitting of extensions of abelian groups, Akad. Nauk Ukrain. SSR, Inst. Mat. Kiev (1986), 22–31.Google Scholar