Hostname: page-component-848d4c4894-8kt4b Total loading time: 0 Render date: 2024-06-28T15:04:19.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence theorems on the Dirichlet problem for the equation Δu + f(x, u)=0

Published online by Cambridge University Press:  20 January 2009

Gabriele Bonanno
Gabriele Bonanno
Affiliation:
Istituto Di Matematica, Universitá di Reggio CalabriaVia E. Cuzzocrea, 48 89128 Reggio Calabria, Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we consider the Dirichlet problem Δu + f(x, u)=0 in Ω, u = 0 on ∂Ω here Ω is a bounded domain in ℝn(n≧3), with smooth boundary ∂Ω. We prove the existence of strong solutions to the previous problem, which are positive if f satisfies a suitable condition. As a consequence we find that the problem with 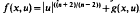, may have positive solutions even if g is not a lower-order perturbation of 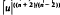Next We examine the case .

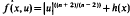Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 39 , Issue 1 , February 1996 , pp. 31 - 36
Copyright
Copyright © Edinburgh Mathematical Society 1996

References

REFERENCES

1. Adams, R. A., Sobolev Space (Academic Press, 1975).Google Scholar
2. Arino, O., Gautier, S. and Penot, J. P., A fixed point theorem for sequentially continuous mappings with application to ordinary differential equations, Funkcial. Ekvac. 27 (1984), 273–279.Google Scholar
3. Dunford, N. and Schwartz, J. T., Linear Operator I (Interscience Publishers, Inc., New York, 1958).Google Scholar
4. Brezis, H. and Nirenberg, L., Positive solutions of nonlinear elliptic equations involving critical Sobolev exponent, Comm. Pure Appl. Math. 36 (1983), 437–477.CrossRefGoogle Scholar
5. Gilbarg, D. and Trudinger, N. S., Elliptic Partial Differential Equations of Second Order, second edition (Springer-Verlag, 1983).Google Scholar
6. Marano, S. A., Existence theorems for a semilinear elliptic boundary value problem, Ann. Polon. Math. 60 (1994), 57–67.CrossRefGoogle Scholar
7. Talenti, G., Elliptic equations and rearrangements, Ann. Scuola Norm. Sup. Pisa Cl. Sci. (IV) 3(1976), 697–718.Google Scholar
8. Zuluaga, M., Existence of solutions for some elliptic problems with critical Sobolev exponents. Rev. Mat. Iberoamericana 5 (1989), 183–193.CrossRefGoogle Scholar