Hostname: page-component-5c6d5d7d68-wpx84 Total loading time: 0 Render date: 2024-08-18T13:45:46.312Z Has data issue: false hasContentIssue false
  • English
  • Français

An application of a theorem of Singer

Published online by Cambridge University Press:  20 January 2009

D. M. Connolly  and
J. H. Williamson
D. M. Connolly
Affiliation:
University of Lethbridge, Canada
J. H. Williamson
Affiliation:
University of York, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The authors have recently treated (2) the problem of finding subsets E of the real line 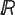, of type Fσ, such that E–E contains an interval and the k-fold vector sum (k)E is of measure zero. Positive results can be obtained, for all k, on the basis of a recent theorem of J. A. Haight (3), following earlier partial results (1), (4) for k ≦ 7; and indeed in these cases the problem has a solution with E a perfect set. An analogous problem, apparently in most respects subtler than the first, is the following. Do there exist finite regular Borel measures μ on 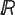such that 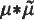is absolutely continuous (where 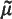is the adjoint of μ) and the kth convolution power μk is singular? Both problems are of interest in the general context of elucidating the properties of the measure algebra 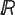or, more generally, M(G) for locally compact abelian G. The second problem may be regarded as an attempt to provide (at least one aspect of) a multiplicity theory for the first.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 2 , September 1974 , pp. 119 - 123
Copyright
Copyright © Edinburgh Mathematical Society 1974

References

REFERENCES

(1) Connolly, D. M., Integer difference-covers which are not K-sum-covers, for k = 6, 7, Proc. Cambridge Philos. Soc. 74 (1973), 17–28.CrossRefGoogle Scholar
(2) Connolly, D. M. and Williamson, J. H., Difference-covers that are not K-sum-covers II, Proc. Cambridge Philos. Soc. 75 (1974), 63–73.CrossRefGoogle Scholar
(3) Haight, J. A., Difference-covers which have small k-sums for any k, Mathe-matika 20 (1973), 109–118.Google Scholar
(4) Jackson, T. H., Williamson, J. H. and Woodall, D. R., Difference-covers that are not k-sum covers I, Proc. Cambridge Philos. Soc. 72 (1972), 425–438.CrossRefGoogle ScholarPubMed
(5) Jessen, B. and Wintner, A., Distribution functions and the Riemann zeta-function, Trans. Amer. Math. Soc. 38 (1935), 48–88.CrossRefGoogle Scholar
(6) Mann, H. B., Addition Theorems (Interscience tracts in pure and applied mathematics no. 18, Interscience Publishers, New York, 1965).Google Scholar
(7) Singer, J., A theorem in finite projective geometry and some applications to number theory, Trans. Amer. Math. Soc. 43 (1938), 377–385.CrossRefGoogle Scholar