Research Article
Transforms on white noise functionals with their applications to Cauchy problems
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-23
-
- Article
-
- You have access
- Export citation
Semi-classical bounds on scattering cross sections in two dimensional magnetic fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 25-61
-
- Article
-
- You have access
- Export citation
A generalization of Kita and Noumi’s vanishing theorems of cohomology groups of local system
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 63-69
-
- Article
-
- You have access
- Export citation
Siegel modular forms and theta series attached to quaternion algebras II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 71-106
-
- Article
-
- You have access
- Export citation
On the stability of pseudoconvexity for certain covering spaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 107-112
-
- Article
-
- You have access
- Export citation
The mixed Hodge structure on the fundamental group of the fiber type 2-arrangement
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 113-135
-
- Article
-
- You have access
- Export citation
On plain lattice points whose coordinates are reciprocals modulo a prime
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 137-146
-
- Article
-
- You have access
- Export citation
Sobolev and Lipschitz estimates for weighted Bergman projections
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 147-178
-
- Article
-
- You have access
- Export citation
Cofiniteness of local cohomology modules for ideals of dimension one
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 179-191
-
- Article
-
- You have access
- Export citation
The genus of curves on the three dimensional quadric
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 193-211
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 147 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 147 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation



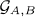 - and
- and 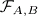 -transforms on white noise functionals are introduced and then prove a characterization theorem for
-transforms on white noise functionals are introduced and then prove a characterization theorem for 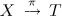 is a proper holomorphic map with one-dimensional fibers and
is a proper holomorphic map with one-dimensional fibers and 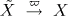 a covering map, a point
a covering map, a point 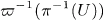 is holomorphically convex if and only if
is holomorphically convex if and only if 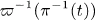 is holomorphically convex.
is holomorphically convex.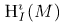 is
is