Research Article
Two algebraic deformations of a K3 surface
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-26
-
- Article
-
- You have access
- Export citation
Seminormal rings and weakly normal varieties
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 27-56
-
- Article
-
- You have access
- Export citation
The coincidence of fields of moduli for non-hyperelliptic curves and for their jacobian varieties
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 57-82
-
- Article
-
- You have access
- Export citation
A generalization of a theorem of marotto
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 83-97
-
- Article
-
- You have access
- Export citation
Tensor products of positive definite quadratic forms, V
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 99-111
-
- Article
-
- You have access
- Export citation
Deformations and equitopological deformations of strongly pseudoconvex manifolds
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 113-129
-
- Article
-
- You have access
- Export citation
Brownian motion parametrized with metric space of constant curvature
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 131-140
-
- Article
-
- You have access
- Export citation
The principle of limiting absorption for uniformly propagative systems with perturbations of long-range class
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 141-174
-
- Article
-
- You have access
- Export citation
Some lie algebras of vector fields and their derivations Case of partially classical type
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 175-207
-
- Article
-
- You have access
- Export citation
On the norm continuity of
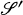 -valued Gaussian processes
-valued Gaussian processes
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 209-220
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 82 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 82 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

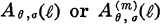
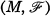 be a smooth foliated manifold, and
be a smooth foliated manifold, and 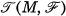 the Lie algebra of all leaf-tangent vector fields on
the Lie algebra of all leaf-tangent vector fields on 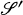 -valued Gaussian processes
-valued Gaussian processes
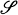 be the Schwartz space of all rapidly decreasing functions on
be the Schwartz space of all rapidly decreasing functions on 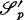 be the space of all elements of
be the space of all elements of