Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Grabowski, J.
and
Poncin, N.
2005.
Derivations of the Lie algebras of differential operators.
Indagationes Mathematicae,
Vol. 16,
Issue. 2,
p.
181.


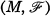 be a smooth foliated manifold, and
be a smooth foliated manifold, and 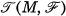 the Lie algebra of all leaf-tangent vector fields on
the Lie algebra of all leaf-tangent vector fields on 