Research Article
Toward a theory of generalized Cohen-Macaulay modules
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-49
-
- Article
-
- You have access
- Export citation
Modular descent of Siegel modular forms of half integral weight and an analogy of the Maass relation
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 51-77
-
- Article
-
- You have access
- Export citation
Homotopy groups of pullbacks of varieties
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 79-90
-
- Article
-
- You have access
- Export citation
Imaginary bicyclic biquadratic fields with the real quadratic subfield of class-number one
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 91-100
-
- Article
-
- You have access
- Export citation
On elliptic surfaces of Mordell-Weil rank 4
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 101-115
-
- Article
-
- You have access
- Export citation
Ternary quadratic forms and Brandt matrices
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 117-126
-
- Article
-
- You have access
- Export citation
Boundedness of singular integral operators of Calderón type, VI
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 127-133
-
- Article
-
- You have access
- Export citation
On the Gorensteinness of Rees algebras over local rings
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 135-154
-
- Article
-
- You have access
- Export citation
Tensor products and localizations of algebras
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 155-161
-
- Article
-
- You have access
- Export citation
Random walks on free products, quotients and amalgams
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 163-180
-
- Article
-
- You have access
- Export citation
Remarks on the paper “Transient Markov convolution semi-groups and the associated negative definite functions”
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 181-184
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 102 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 102 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

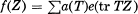 be its Fourier expansion, where
be its Fourier expansion, where 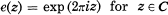 . Then
. Then 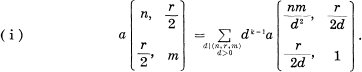
 in a certain range of dimensions with those of its pullback under a holomorphic map in the corresponding range of dimensions. It is asked in [2, § 10] whether here is a corresponding result with
in a certain range of dimensions with those of its pullback under a holomorphic map in the corresponding range of dimensions. It is asked in [2, § 10] whether here is a corresponding result with 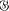 of sections of
of sections of 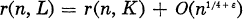 . The main tool utilized for the proof was the theory of modular forms of weight 3/2, especially Shimura’s lifting from the space of cusp forms of weight 3/2 to the space of modular forms of weight 2.
. The main tool utilized for the proof was the theory of modular forms of weight 3/2, especially Shimura’s lifting from the space of cusp forms of weight 3/2 to the space of modular forms of weight 2.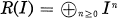 and call this graded
and call this graded 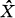 denote the dual group of
denote the dual group of 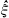 the Haar measure associated with
the Haar measure associated with