Research Article
Minorations d’unités fondamentales—applications
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-18
-
- Article
-
- You have access
- Export citation
On vector bundles on algebraic surfaces and 0-cycles
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 19-23
-
- Article
-
- You have access
- Export citation
On the invariant differential metrics near pseudoconvex boundary points where the Levi form has corank one
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 25-54
-
- Article
-
- You have access
- Export citation
The efimov effect of three-body schrödinger operators: Asymptotics for the number of negative eigenvalues
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 55-83
-
- Article
-
- You have access
- Export citation
Asymptotic dependence of moving average type self-similar stable random Fields*
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 85-100
-
- Article
-
- You have access
- Export citation
Polyhedricity of convex sets in sobolev space
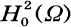
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 101-110
-
- Article
-
- You have access
- Export citation
The uniqueness of positive solutions of parabolic equations of divergence form on an unbounded domain
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 111-121
-
- Article
-
- You have access
- Export citation
L2-boundedness of the cauchy transform on smooth non-Lipschitz curves
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 123-147
-
- Article
-
- You have access
- Export citation
On L-functions associated with the vector space of binary quadratic forms
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 149-176
-
- Article
-
- You have access
- Export citation
Central extensions and rational quadratic forms
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 177-182
-
- Article
-
- You have access
- Export citation
Hankel kernels of higher weight for the ball
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 183-192
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 130 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 130 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation



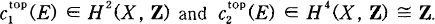 . Viceversa, again a classical theorem of Wu ([Wu]) states that every pair (
. Viceversa, again a classical theorem of Wu ([Wu]) states that every pair (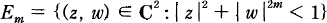 , or the annulus in the plane. Also, there is no hope of getting information about the function
, or the annulus in the plane. Also, there is no hope of getting information about the function 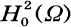
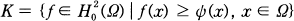
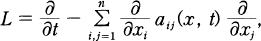
 on the curve
on the curve 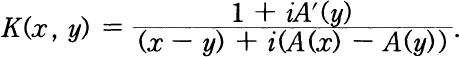
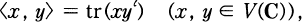
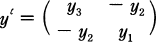 for
for 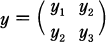 .
.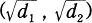 be a bicyclic biquadratic field, and let
be a bicyclic biquadratic field, and let 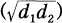 . Denote by
. Denote by 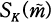 the ray class field mod
the ray class field mod 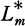 be the maximal abelian extension over Q contained in
be the maximal abelian extension over Q contained in 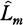 be the maximal extension contained in
be the maximal extension contained in 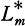 /Q if and only if
/Q if and only if 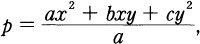
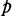 is decomposed completely in
is decomposed completely in 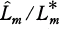 if and only if
if and only if 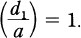 .
.